Spreading of Micrometer-Sized Droplets under the Influence of Insoluble and Soluble Surfactants: A Numerical Study
Abstract
1. Introduction
2. Method
2.1. Model Equations
2.2. Numerical Method
2.3. Parameters for Droplet Spreading
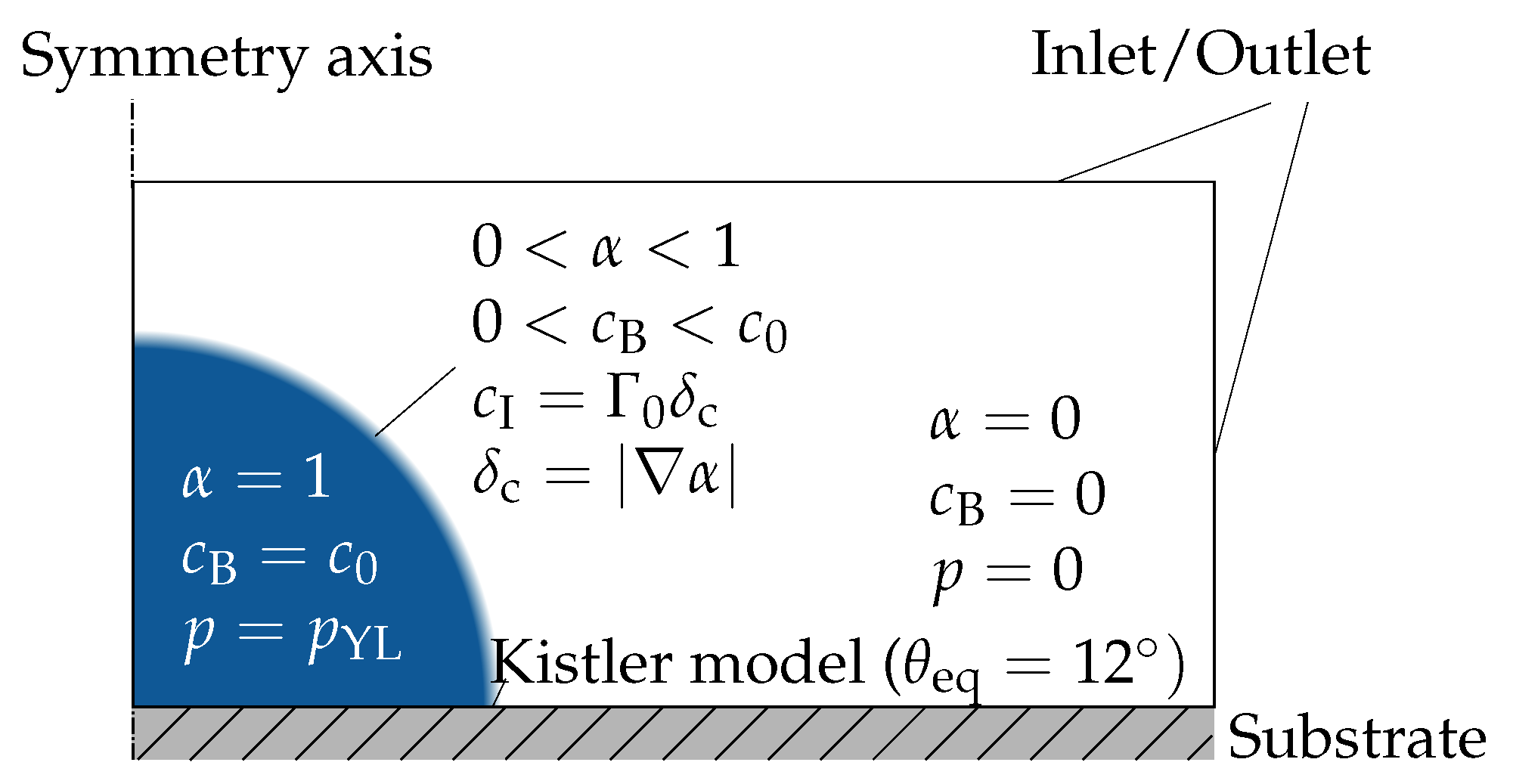
2.4. Numerical Setup for Droplet Spreading
3. Results
3.1. Verification of the Sorption Model
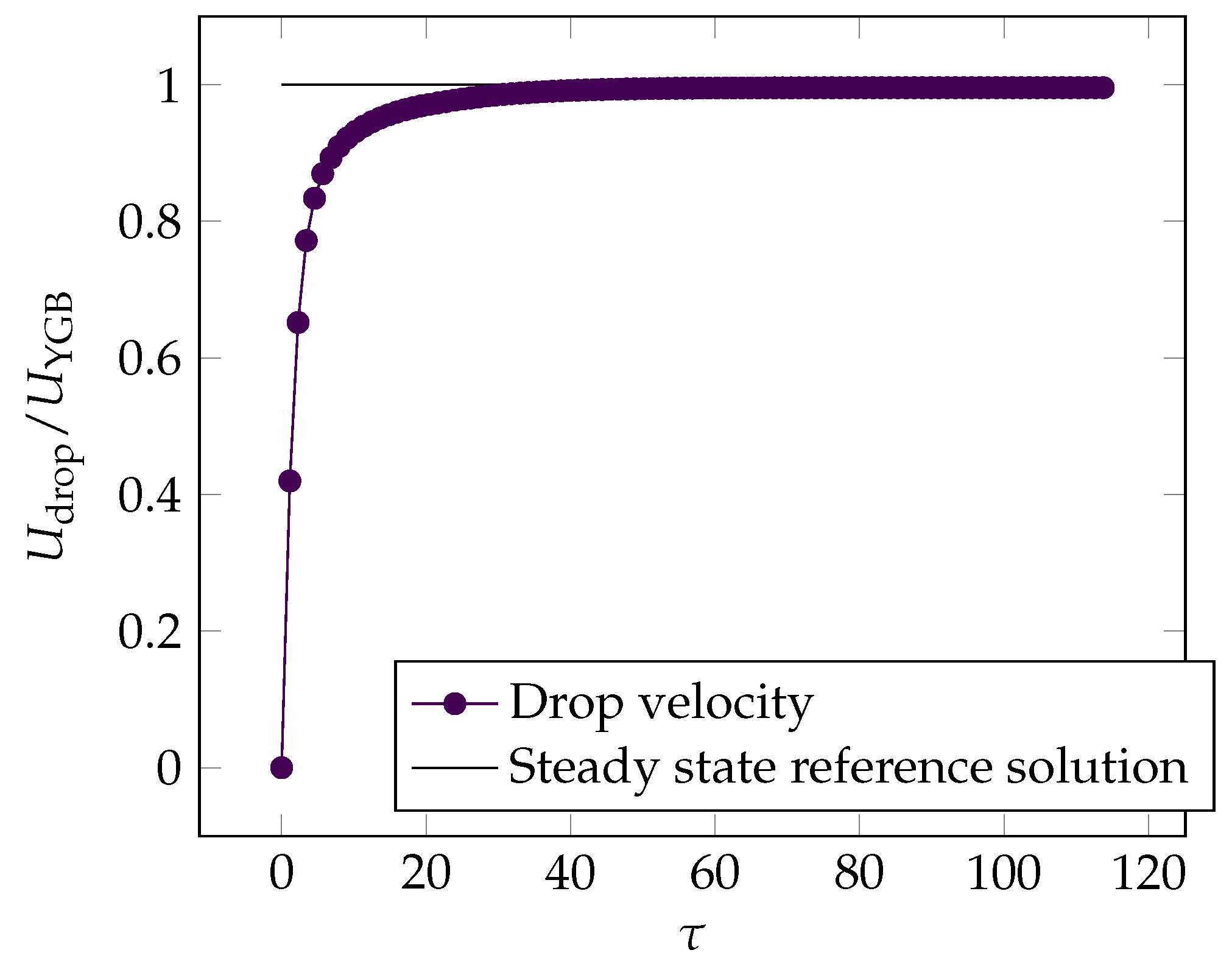
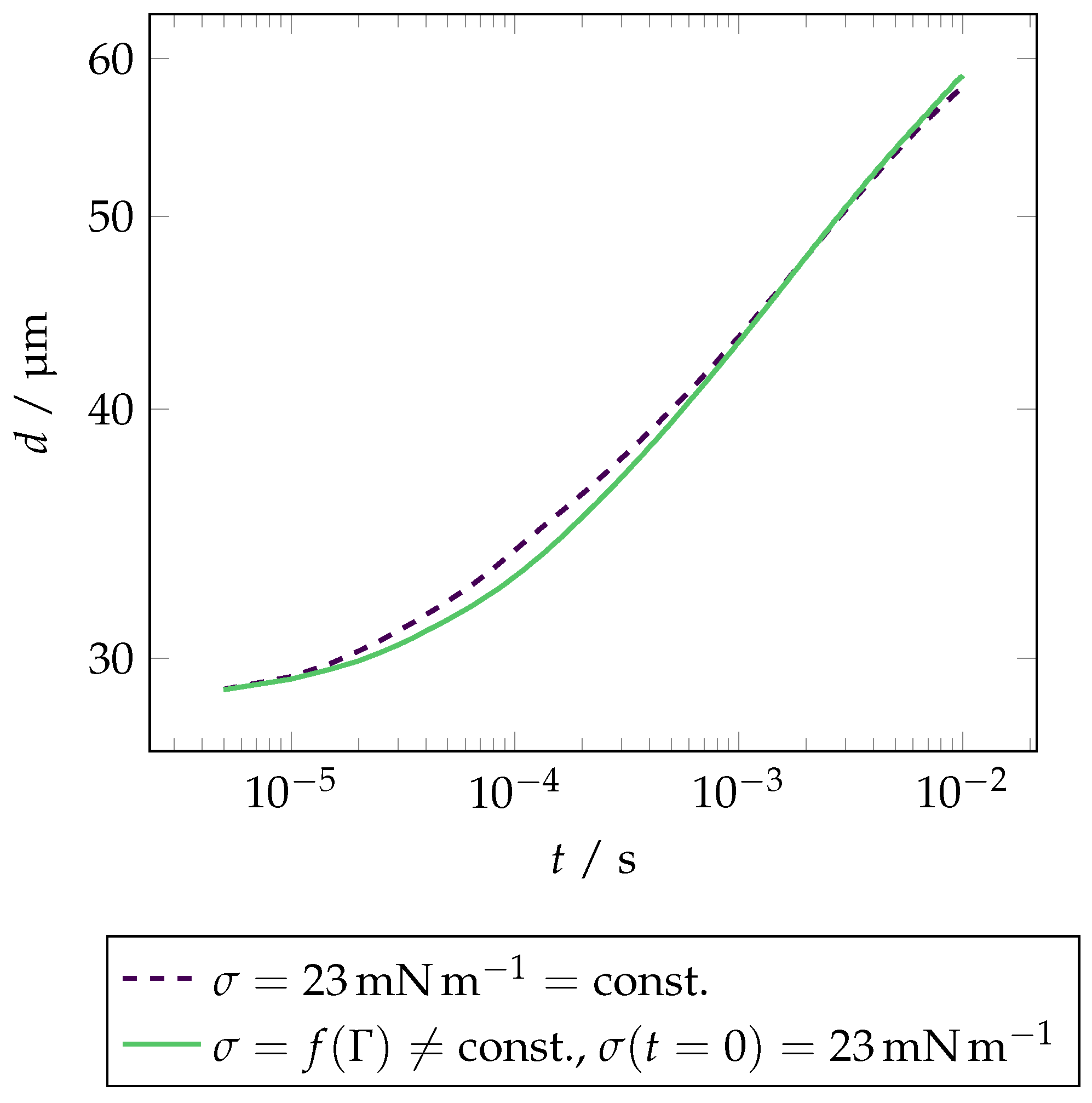
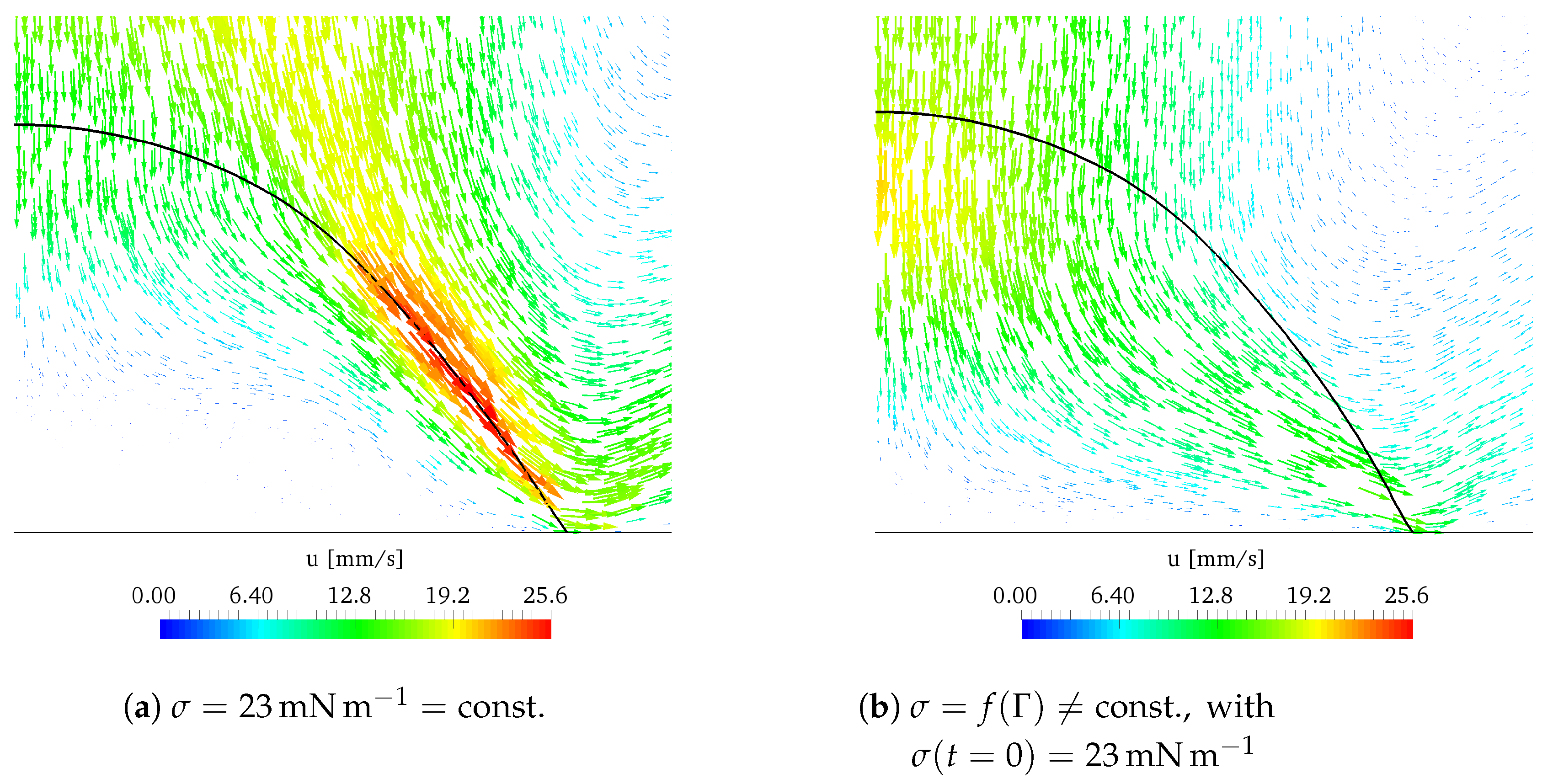
3.2. Verification of the Marangoni Stress Model
3.3. Spreading of Droplet with Insoluble Surfactant
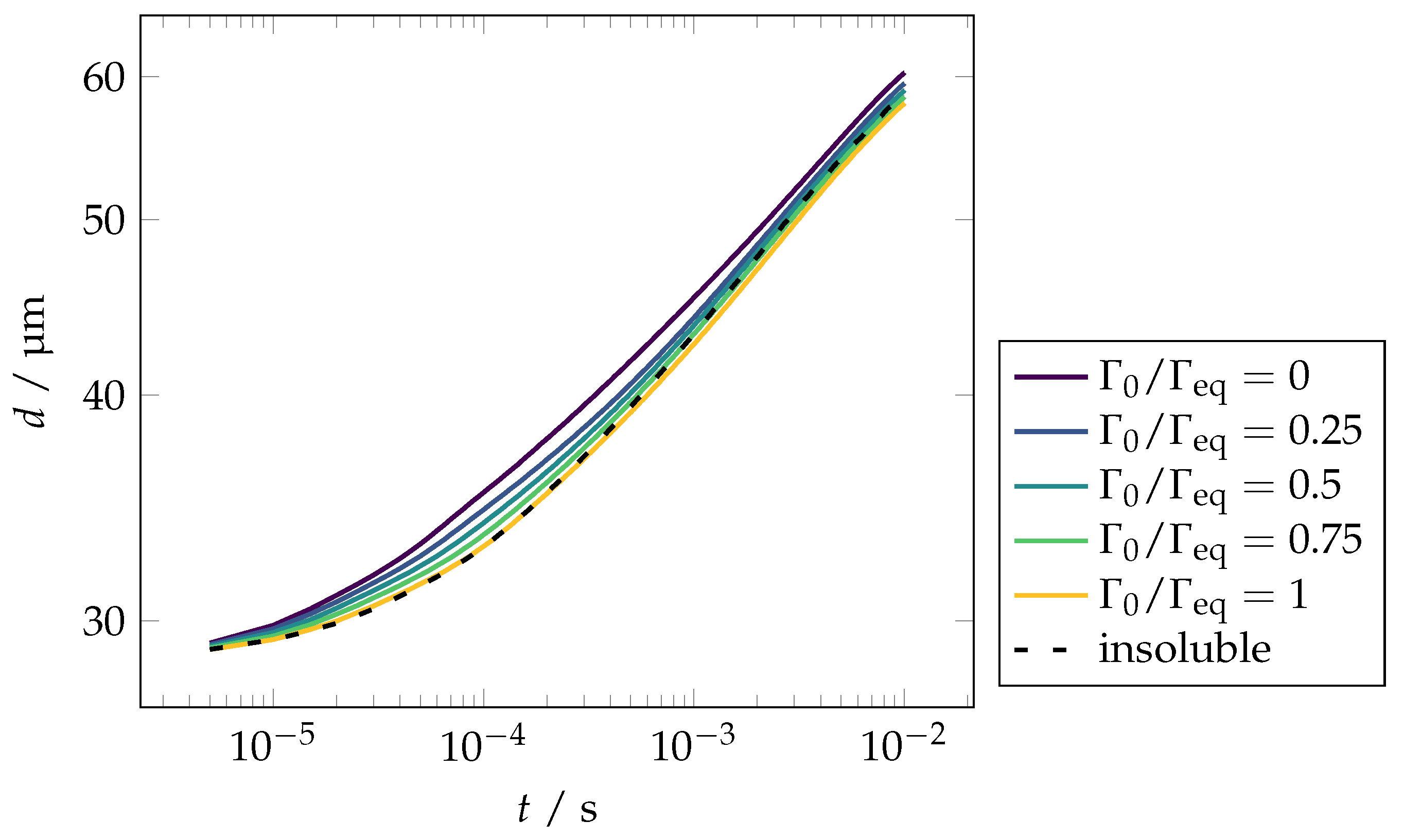
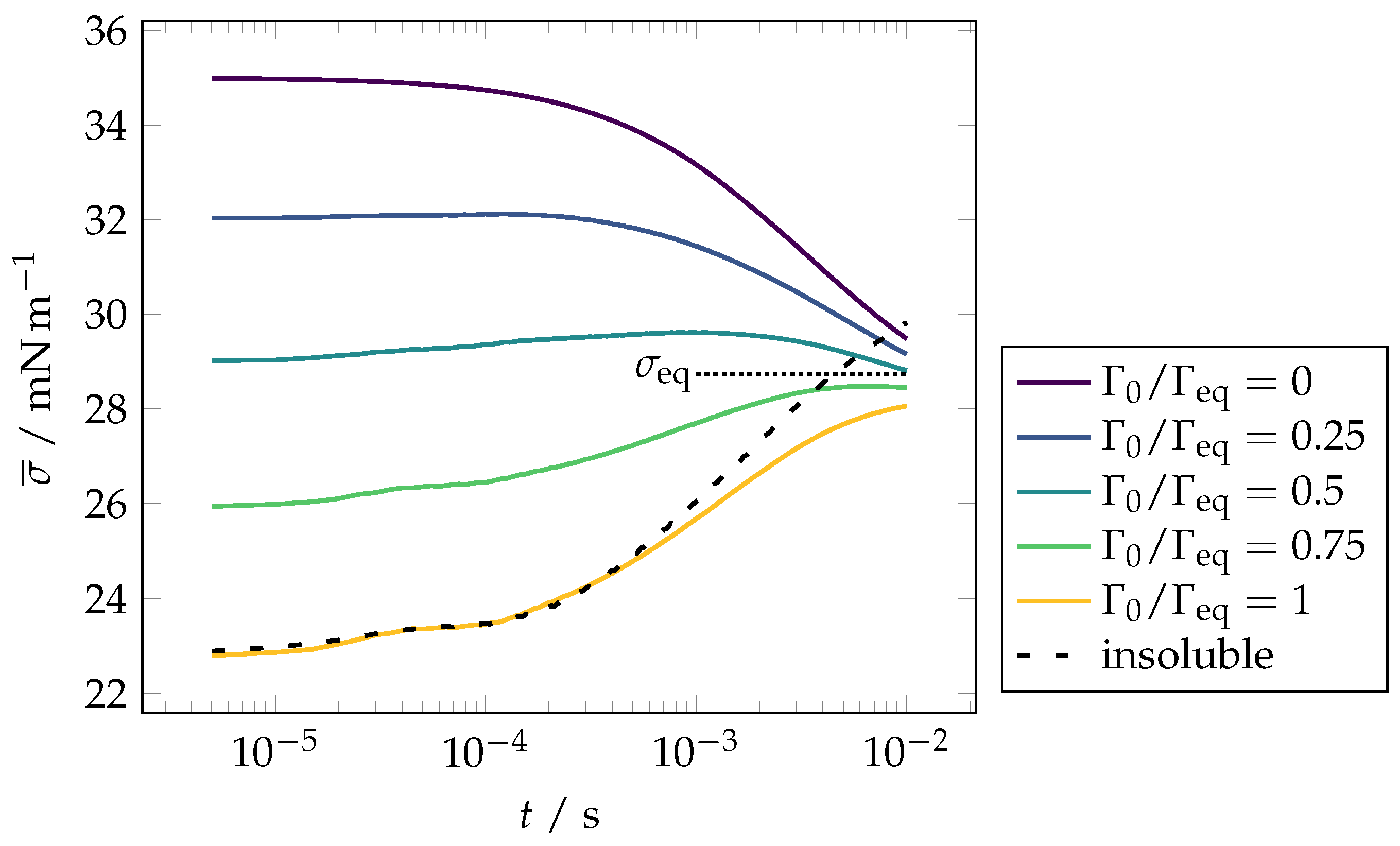
3.4. Spreading with Soluble Surfactant
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Derby, B. Inkjet printing of functional and structural materials: Fluid property requirements, feature stability, and resolution. Ann. Rev. Mater. Res. 2010, 40, 395–414. [Google Scholar] [CrossRef]
- Morita, N.; Hamazaki, T.; Ishiyama, T.; Motosugi, Y.; Hirakata, S. Breakthroughs required in piezo-on-demand inkjets for production printing: Satellite drops, ink penetration and evaporation. Soc. Imaging Sci. Technol. 2016, 2016, 79–82. [Google Scholar]
- Bonn, D.; Eggers, J.; Indekeu, J.; Meunier, J.; Rolley, E. Wetting and spreading. Rev. Mod. Phys. 2009, 81, 739–805. [Google Scholar] [CrossRef]
- Brutin, D.; Starov, V. Recent advances in droplet wetting and evaporation. Chem. Soc. Rev. 2018, 47, 558–585. [Google Scholar] [CrossRef] [PubMed]
- Harikrishnan, A.; Dhar, P.; Gedupudi, S.; Das, S.K. Effect of interaction of nanoparticles and surfactants on the spreading dynamics of sessile droplets. Langmuir 2017, 33, 12180–12192. [Google Scholar] [CrossRef] [PubMed]
- Tanner, L.H. The spreading of silicone oil drops on horizontal surfaces. J. Phys. D Appl. Phys. 1979, 12, 1473–1484. [Google Scholar] [CrossRef]
- Kovalchuk, N.; Matar, O.; Craster, R.; Miller, R.; Starov, V. The effect of adsorption kinetics on the rate of surfactant-enhanced spreading. Soft Matter 2016, 12, 1009–1013. [Google Scholar] [CrossRef]
- Cox, R. The dynamics of the spreading of liquids on a solid surface. Part 2. Surfactants. J. Fluid Mech. 1986, 168, 195–220. [Google Scholar] [CrossRef]
- Joanny, J.F. Kinetics of spreading of a liquid supporting a surfactant monolayer: Repulsive solid surfaces. J. Colloid Interface Sci. 1989, 128, 407–415. [Google Scholar] [CrossRef]
- Clay, M.A.; Miksis, M.J. Effects of surfactant on droplet spreading. Phys. Fluids 2004, 16, 3070–3078. [Google Scholar] [CrossRef]
- Jensen, O.; Naire, S. The spreading and stability of a surfactant-laden drop on a prewetted substrate. J. Fluid Mech. 2006, 554, 5–24. [Google Scholar] [CrossRef]
- Karapetsas, G.; Chandra Sahu, K.; Matar, O.K. Evaporation of sessile droplets laden with particles and insoluble surfactants. Langmuir 2016, 32, 6871–6881. [Google Scholar] [CrossRef] [PubMed]
- Karapetsas, G.; Craster, R.V.; Matar, O.K. On surfactant-enhanced spreading and superspreading of liquid drops on solid surfaces. J. Fluid Mech. 2011, 670, 5–37. [Google Scholar] [CrossRef]
- Teigen, K.E.; Song, P.; Lowengrub, J.; Voigt, A. A diffuse-interface method for two-phase flows with soluble surfactants. J. Comput. Phys. 2011, 230, 375–393. [Google Scholar] [CrossRef] [PubMed]
- Lakshmanan, P.; Ehrhard, P. Marangoni effect caused by contaminants adsorbed on bubble surfaces. J. Fluid Mech. 2010, 647, 143–161. [Google Scholar] [CrossRef]
- Alke, A.; Bothe, D. 3D Numerical Modeling of Soluble Surfactant at Fluidic Interfaces Based on the Volume-of-Fluid Method. Fluid Dyn. Mater. Process. 2009, 5, 345–372. [Google Scholar]
- James, A.J.; Lowengrub, J. A surfactant-conserving volume-of-fluid method for interfacial flows with insoluble surfactant. J. Comput. Phys. 2004, 201, 685–722. [Google Scholar] [CrossRef]
- Open CFD Ltd. OpenFOAM User Guide Version 1.6; Open CFD Ltd.: London, UK, 2009. [Google Scholar]
- Gurumurthy, V.T.; Rettenmaier, D.; Roisman, I.V.; Tropea, C.; Garoff, S. Computations of spontaneous rise of a rivulet in a corner of a vertical square capillary. Colloids Surf. A Physicochem. Eng. Asp. 2018, 544, 118–126. [Google Scholar] [CrossRef]
- Rettenmaier, D. Numerical Simulation of Shear Driven Wetting. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2019. [Google Scholar]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A Continuum Method for Modeling Surface Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Yokoi, K. A density-scaled continuum surface force model within a balanced force formulation. J. Comput. Phys. 2014, 278, 221–228. [Google Scholar] [CrossRef]
- Deising, D.; Marschall, H.; Bothe, D. A unified single-field model framework for Volume-Of-Fluid simulations of interfacial species transfer applied to bubbly flows. Chem. Eng. Sci. 2016, 139, 173–195. [Google Scholar] [CrossRef]
- Hardt, S.; Wondra, F. Evaporation model for interfacial flows based on a continuum-field representation of the source terms. J. Comput. Phys. 2008, 227, 5871–5895. [Google Scholar] [CrossRef]
- Chang, C.H.; Franses, E.I. Adsorption dynamics of surfactants at the air/water interface: A critical review of mathematical models, data, and mechanisms. Colloids Surf. A Physicochem. Eng. Asp. 1995, 100, 1–45. [Google Scholar] [CrossRef]
- Kistler, S.F. Hydrodynamics of Wetting. In Wettability; Berg, J.C., Ed.; Marcel Dekker: New York, NY, USA, 1993. [Google Scholar]
- Antritter, T.; Mayer, M.; Hachmann, P.; Wörner, M. Suppressing artificial equilibrium states caused by spurious currents in droplet spreading simulations with dynamic contact angle model. Prog. Comput. Fluid Dyn. 2019, (in press).
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Anumolu, L.; Trujilo, F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 2012, 5, 014016. [Google Scholar] [CrossRef]
- Hoath, S.D. Fundamentals of Inkjet Printing: The Science of Inkjet And Droplets; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Graindourze, M. UV-Curable Inkjet Inks and Their Applications in Industrial Inkjet Printing, Including Low-Migration Inks for Food Packaging. In Handbook of Industrial Inkjet Printing: A Full System Approach; Zapka, W., Ed.; Wiley Online Library: Hoboken, NJ, USA, 2018; Volume 1, Chapter 6; pp. 129–150. [Google Scholar]
- Bale, M. A System Aproach to Develop New Platforms of Industrial Inkjet Inks. In Handbook of Industrial Inkjet Printing: A Full System Approach, Zapka, W., Ed.; Wiley VCH: Karlsruhe, Germany, 2018; Volume 1, Chapter 3; pp. 23–58. [Google Scholar]
- Joos, P.; Serrien, G. Adsorption kinetics of lower alkanols at the air/water interface: effect of structure makers and structure breakers. J. Colloid Interface Sci. 1989, 127, 97–103. [Google Scholar] [CrossRef]
- Defay, R.; Hommelen, J.R., III. The importance of diffusion in the adsorption process of some alcohols and acids in dilute aqueous solutions. J. Colloid Sci. 1959, 14, 411–418. [Google Scholar] [CrossRef]
- Ward, A.F.H.; Tordai, L. Time-dependence of boundary tensions of solutions I. The role of diffusion in time-effects. J. Chem. Phys. 1946, 14, 453–461. [Google Scholar] [CrossRef]
- Li, X.; Shaw, R.; Evans, G.M.; Stevenson, P. A simple numerical solution to the Ward–Tordai equation for the adsorption of non-ionic surfactants. Comput. Chem. Eng. 2010, 34, 146–153. [Google Scholar] [CrossRef]
- Ferri, J.K.; Stebe, K.J. Which surfactants reduce surface tension faster? A scaling argument for diffusion-controlled adsorption. Adv. Colloid Interface Sci. 2000, 85, 61–97. [Google Scholar] [CrossRef]
- Young, N.O.; Goldstein, J.S.; Block, M.J. The motion of bubbles in a vertical temperature gradient. J. Fluid Mech. 1959, 6, 350–356. [Google Scholar] [CrossRef]
- Jiang, T.S.; Soo-Gun, O.; Slattery, J.C. Correlation for dynamic contact angle. J. Colloid Interface Sci. 1979, 69, 74–77. [Google Scholar] [CrossRef]
- Bracke, M.; De Voeght, F.; Joos, P. The kinetics of wetting: The dynamic contact angle. In Trends in Colloid and Interface Science III; Springer: New York, NY, USA, 1989; pp. 142–149. [Google Scholar]
- Voinov, O. Hydrodynamics of wetting. Fluid Dyn. 1976, 11, 714–721. [Google Scholar] [CrossRef]
- Cox, R.G. The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 1986, 168, 169–194. [Google Scholar] [CrossRef]
- Miller, R.; Aksenenko, E.; Fainerman, V. Dynamic interfacial tension of surfactant solutions. Adv. Colloid Interface Sci. 2017, 247, 115–129. [Google Scholar] [CrossRef]
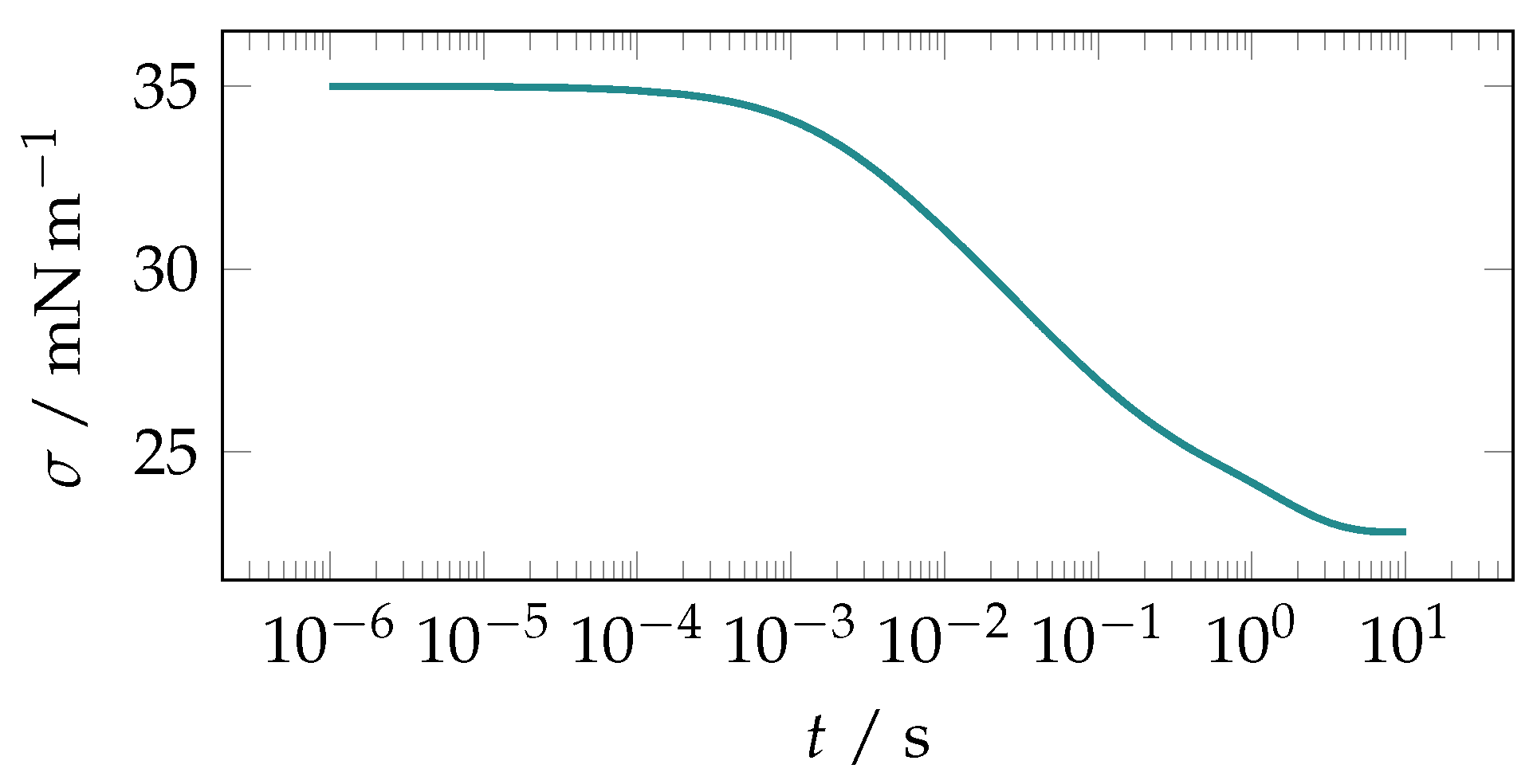
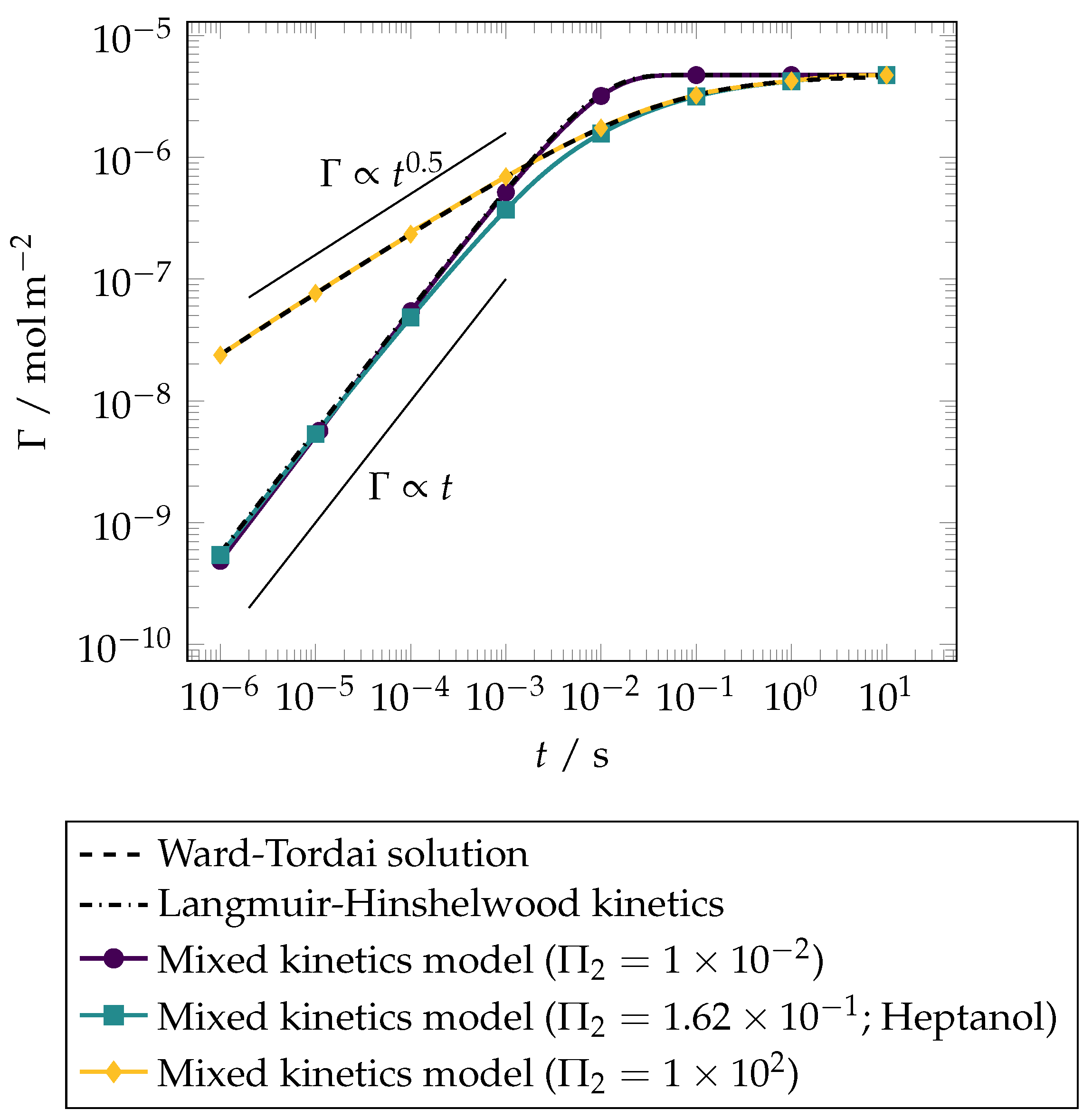

| 0 | 0.25 | 0.5 | 0.75 | 1 | ||
| in mol | 0 | 1.182 | 2.363 | 3.545 | 4.727 | |
| in mol | 1.939 | 1.690 | 1.440 | 1.190 | 0.941 | |
| n | in mol | 1.164 | 1.164 | 1.164 | 1.164 | 1.164 |
| in | 35 | 32.09 | 29.12 | 26.09 | 23 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antritter, T.; Hachmann, P.; Gambaryan-Roisman, T.; Buck, B.; Stephan, P. Spreading of Micrometer-Sized Droplets under the Influence of Insoluble and Soluble Surfactants: A Numerical Study. Colloids Interfaces 2019, 3, 56. https://doi.org/10.3390/colloids3030056
Antritter T, Hachmann P, Gambaryan-Roisman T, Buck B, Stephan P. Spreading of Micrometer-Sized Droplets under the Influence of Insoluble and Soluble Surfactants: A Numerical Study. Colloids and Interfaces. 2019; 3(3):56. https://doi.org/10.3390/colloids3030056
Chicago/Turabian StyleAntritter, Thomas, Peter Hachmann, Tatiana Gambaryan-Roisman, Bernhard Buck, and Peter Stephan. 2019. "Spreading of Micrometer-Sized Droplets under the Influence of Insoluble and Soluble Surfactants: A Numerical Study" Colloids and Interfaces 3, no. 3: 56. https://doi.org/10.3390/colloids3030056
APA StyleAntritter, T., Hachmann, P., Gambaryan-Roisman, T., Buck, B., & Stephan, P. (2019). Spreading of Micrometer-Sized Droplets under the Influence of Insoluble and Soluble Surfactants: A Numerical Study. Colloids and Interfaces, 3(3), 56. https://doi.org/10.3390/colloids3030056






