Abstract
Using neodymium ring magnets (0.5–0.65 T), the experiments on the magnetic field (MF) effects on water evaporation rate and surface tension were performed at room temperature (22–24 °C). In accordance with the literature data, the enhanced evaporation rates were observed in the experiments conducted in a period of several days or weeks. However, the evaporated amounts of water (up to 440 mg over 150 min) in particular experiments differed. The evaporated amounts depended partially on which pole of the ring magnet was directed up. The relatively strong MF (0.65 T) caused a slight decrease in surface tension (−2.11 mN/m) which lasted longer than 60 min and the memory effect vanished slowly. The surface tension data reduced by the MF action are reported in the literature, although contrary results can be also found. The observed effects can be explained based on literature data of molecular simulations and the suggestion that MF affects the hydrogen bonds of intra- and inter-clusters of water molecules, possibly even causing breakage some of them. The Lorentz force influence is also considered. These mechanisms are discussed in the paper.
1. Introduction
The effects of magnetic field (MF) on water treatment have been studied over 50 years in various aspects, and they still attract many researchers. Originally, the studies were focused on the protection of industrial installations or home-heating systems against hard scale formation at elevated temperatures; later and recently, the MF effects in the liquid phase have been studied in various fundamental aspects as well as possible practical applications. A broad scope of such MF effects can be found in several review articles published lately [1,2,3,4,5,6], including an older one published by Baker and Judd [1] in 1996.
Among various investigated MF effects, several papers deal with pure water [7,8,9,10,11,12,13,14], where changes in the evaporation rate, surface tension, viscosity and other parameters were observed [15,16]. The authors reported an increase in water evaporation rate caused by MF which depended also on the experiment setup. Moreover, it was found [7] that the effect depended more on the product of MF strength and its gradient than on the field itself (B·dB/dx). Also, the direction of air or oxygen flow relative to the MF gradient affected the evaporation rate. Larger influence was observed in pure oxygen flow than in air because of its larger-volume magnetic susceptibility χ (= M/H, where M is the magnetization of the material and H is the MF strength, which are in A/m, χox >> χwater). The flow could cause a susceptibility gradient in the vertical direction during the water vaporization and the vaporization from the surface parallel to the field gradient was enhanced. These experiments were conducted in a strong 8 T superconducting solenoid MF which was confirmed later by Guo et al. [12] who also used the superconducting magnet and simulated gravity. These authors also mentioned the importance of Lorentz and magnetization forces for the observed effect as well as that hydrogen bonds must be broken and van der Waals forces weakened during increased water evaporation [13,17].
A 6% increase in water evaporation treated in 0.5 T MF was reported by Rashid et al. [11] but only if the origin of the field was placed at the water/air interface level and no effect was observed if the MF was positioned in the middle or bottom of the sample. However, the evaporated amount calculated from the Fick’s law for diffusion appeared to be much bigger than the experimental amount obtained not only for the MF-treated but also the untreated samples.
Holysz et al. [9] found that the evaporated amount of water from the aqueous solutions of inorganic electrolytes (0.1 M NaCl, KCl, Na3PO4, and CaCl2) was smaller after a weak MF (magnetic stack B = 15 mT) treatment than from pure water. Also, changes in electric conductivity occurred which were related to the thermodynamic hydration functions of these ions. Hence the authors concluded that the hydration shell structures around the ions were changed by the MF. This was proved by molecular simulations made by Chang and Weng [18]. At a relatively low NaCl concentration (1M) and strong MF (1–10T) the coefficient of water self-diffusion decreases if the field increases while at a high concentration the change is opposite. However, the mobility of Na+ and Cl− ions increases regardless of their concentration and the hydrogen bonds damage takes place.
Seyfi et al. [13] interpreted the increased evaporation of water based on the kinetic energy of water molecules and the Lorentz force acting on the charged molecules. It might cause weakening or even breaking of the hydrogen bonding. The experiments were conducted using the ring magnets and the samples were placed inside the ring. The water surface level was at the middle of the magnet height whose north pole was directed up and the MF field was perpendicular to the water surface. After 80 min ca. 19% more water evaporated from MF-treated (75 mT, three ring magnets) than from the untreated sample. The difference increased linearly with the experiment duration. However, there was no difference in the evaporation rate of the samples if the MF was tangentially directed to the water surface (two N-N poles connected magnets). The calculations have shown that under the experimental conditions [13] the difference between the volume magnetic force and the gravity force per unit air volume was too small to influence convection of water molecules if caused by the MF action. Therefore, to explain the effect which was observed only perpendicular but not tangential to the water surface MF field, the authors [13] considered the Lorentz force acting randomly on the bouncing dipoles. The literature reports the data dealing with the presence of the electrostatic potential across the water/vapor interface [19,20]. Thus, the Lorentz force normal to the water surface can influence the momenta of hydrogen bonds in the clusters, weaken or break them, leading to an increased evaporation rate is observed [13].
Recently Amor et al. [14] published a statistically significant MF effect on the rate of evaporation of irrigation water at different temperatures using different commercial magnets (0.33 T, 0.29 T, 0.5 T, and an electromagnet 0.09 T) mounted on a pipe. They found as large as 42% increase in the evaporation at 80 °C during 1 h treatment. Moreover, 24% reduction in the surface tension accompanying the effect of evaporation was measured. The authors have not suggested any mechanism of the observed effects.
Lately Wang et al. [16] reported changes in the evaporated amounts, a decrease in the specific heat and boiling point of tap water after treatment in the 100–400 mT MF composed of 26 magnets for 5 min and at the water flow rate 0.8 m/s.
Finally, it should be mentioned that Otsuka and Ozeki [21] claimed that in pure water (distilled in vacuum with no gas dissolved) MF did not change its properties but it did if oxygen or air was dissolved.
The above brief review of the papers dealing with the MF effects on water properties indicates that still there is a lack of coherent view on the mechanisms of effects, although some interesting explanations have already been put forward. To sum up, the papers published on water evaporation are listed in Table 1. As can be seen some of the experiments are not well specified and it would be difficult to reproduce them. In the light of the above it still seemed interesting for us to carry out more studies on the static MF influence on the evaporation rate of water and its surface tension. We were especially interested whether the experiments conducted in typical environments at room temperature and humidity for several days or even weeks are reproducible and meaningful. If so, such results would have potentially practical importance for faster water evaporation.

Table 1.
Effects of static MF on water evaporation.
2. Experimental
Materials
For the determination of evaporation rate the 65 mL fresh water samples from the Milli-Q Plus system (resistivity 18.2 MΩcm) were used. However, for the surface tension measurements the water from Milli-Q system was distilled in a quartz apparatus and then 50 mL samples were treated in a closed vessel. Prior to the experiments both waters were stored for a short time in a polyethylene tightly closed bottle.
Neodymium ring magnets were used. For water evaporation one 86 × 58 × 35 mm ring magnet and for the surface tension experiments three 101 × 60 × 30 mm neodymium magnets were used. Figure 1 shows the magnets as well as the MF strengths. The MF distribution above the magnet will be shown in the Discussion section. Figure 2 shows the setup for MF water evaporation and surface tension measurements. As can be seen in Figure 2, in the evaporation experiments of the MF-treated and untreated water samples evaporated simultaneously at room temperature (23 ± 1 °C) and the relative humidity 35–38%. After every 30 min the closed samples were weighed and then their location was replaced. To avoid any influence of possible air fluctuations in the room the samples were placed in plastic tubes (Figure 2).

Figure 1.
The magnets and the magnetic field strengths.
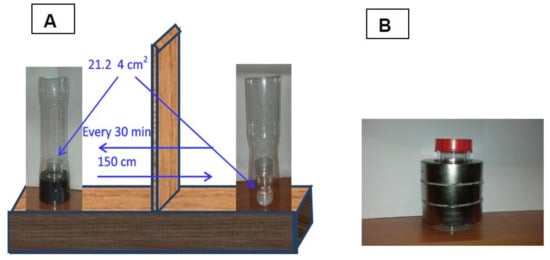
Figure 2.
(A) Evaporation experiment: the MF-treated (left) and untreated (right) samples. (B) MF treatment for surface tension effect.
In the surface tension experiments the samples in closed vessels were MF-treated for 1 h at 25 °C and stirred manually every 15 min. Then the surface tension of MF-treated and untreated water samples was measured using the KSV Sigma 700 ring tensiometer. At least five measurements of each sample were made.
3. Results
3.1. Evaporation Rate
Figure 3 presents the evaporated amounts of water from the MF-treated and untreated samples which were obtained in four independent experiments conducted on different days. The room temperature was 23 °C and the north pole N↑ was on the upper side of the ring magnet. As can be seen up to 440 mg of water were evaporated for 150 min of the experiments and in all cases more water was evaporated from the MF-treated samples although the differences were not exactly the same. For better depictions, the differences are plotted in Figure 4. The maximum difference amounts 35 mg/150 min, and after 1 h MF treatment the increased evaporation of water is 7–15 mg.
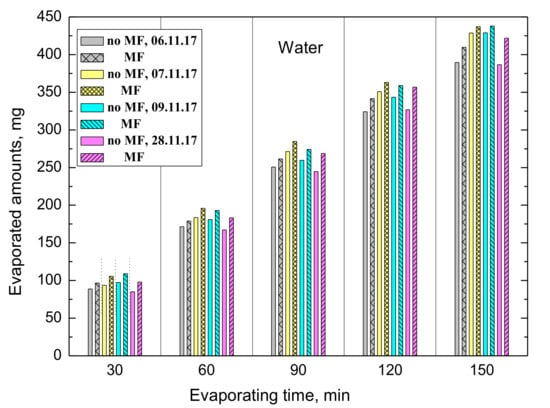
Figure 3.
Evaporated amounts of water from the MF-treated and untreated samples.
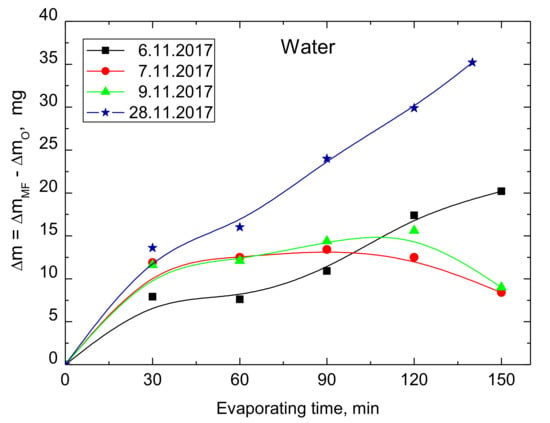
Figure 4.
Differences in the evaporated amounts of water from the MF-treated and untreated samples obtained in four independent experiments.
Then the ring magnet was turned around, thus the south pole S↑ was at the upper side. The results of two evaporating experiments at room temperature with the pole S↑ up and one with the pole N↑ up are presented in Figure 5. The room temperature was 22–22.5 °C and RH = 31–35%. If the north pole N↑ was up more water evaporated than from the untreated sample. However, if the south pole S↑ was up, then during the first 90–120 min of MF treatment less water evaporated from the treated samples than untreated ones. Surprisingly, after that time the water started to evaporate faster from the MF-treated samples and in one experiment the evaporated amount after 3 h was similar to that where the pole N↑ was up.
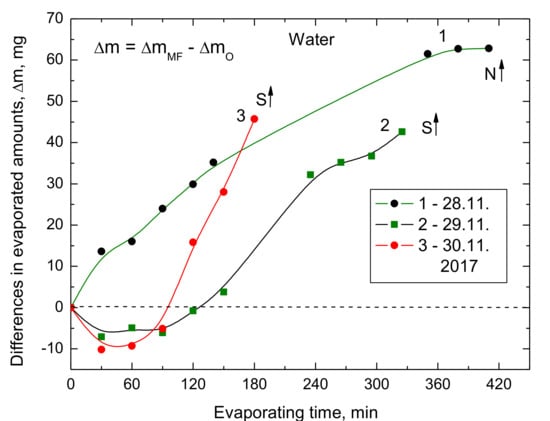
Figure 5.
Differences in the evaporated amounts of water depending on which the magnet pole, north N ↑ or south S↑, was directed upward.
To verify the above different effect of the MF direction, several samples were treated for a long time, even up to 48 h. The results are presented in Figure 6. As it can be seen, in the case of long-term MF treatment the direction of the field does not has direct effect on the evaporated amounts of the treated water. Both with the north or south poles of the magnet directed up more water evaporates from the MF-treated samples. The maximum difference amounts to 175 mg during the 23 h treatment.
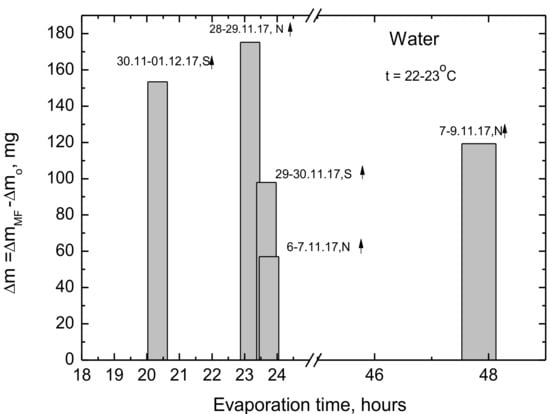
Figure 6.
Differences in the evaporated amounts of water from the long-term MF treated and untreated samples.
Finally, an evaporating experiment was conducted using three ring magnets (see Figure 1 and Figure 2) with the north pole up N↑ and 50 mL sample of water in the same size vessel as previously. Simultaneously one sample of MF-treated water and two samples of the same volume untreated with the magnet were evaporated. These results are plotted in Figure 7. The differences in the evaporated amounts are bigger than in the experiments with the one ring magnet (Figure 4 and Figure 5). This can be due to a stronger MF at the top of three magnets (0.5 T and 0.65 T, Figure 1) and a bit higher room temperature (22 °C and 24 °C, respectively). Although the differences in the evaporated water relative to the two references samples without the MF (Figure 7) are not identical, their run is very similar and 3h duration of the experiment the differences in the evaporated water between the MF-treated sample and the two untreated are practically the same. These results support those presented above and make them plausible. We have also measured (Gausmeter, Model GM-2, AlphaLab Inc., Salt Lake City, UT, USA) the changes in MF intensity B in the perpendicular direction (z-direction) from the magnet top and then the field gradient ∂B/∂z. These results are presented in Figure 8 and Figure 9 and will be used in the discussion below.
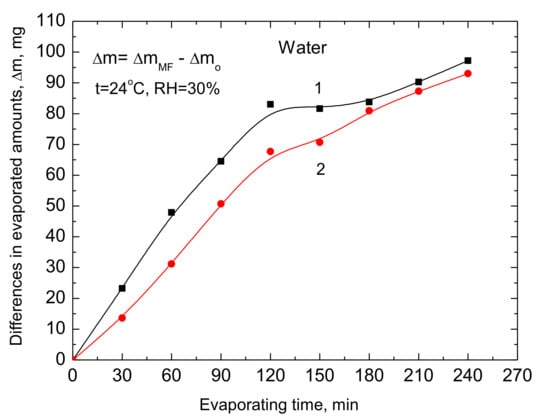
Figure 7.
Differences between the evaporated water from one of the MF-treated samples and two reference untreated samples calculated individually. The evaporation experiment was conducted simultaneously using the three samples.
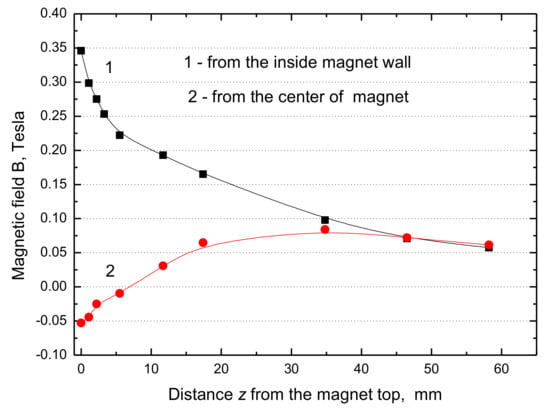
Figure 8.
Changes of MF in the perpendicular direction z from the water surface. Curve 1—from the magnet inside wall and curve 2—from the center of the magnet.
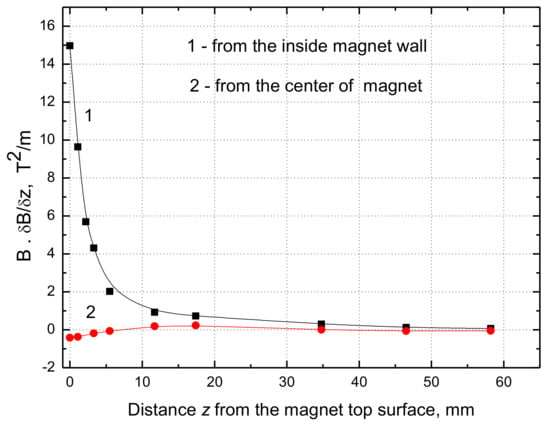
Figure 9.
The product of magnetic field and its gradient along the direction z perpendicular to the water surface from the top of inner magnet wall (curve 1) and from the magnet center (curve 2).
3.2. Surface Tension
The surface tension was measured for the four untreated and six MF-treated for 1 h samples at the room temperature 24.2 ± 0.2 °C. The results of these experiments are shown in Figure 10. First of all, the standard deviation of particular measurements is very small. Moreover, the reproducibility of the experiments is high. The mean surface tension of the untreated samples was 72.30 mN/m and that of 60 min MF treated amounted to 70.19 mN/m. The MF treatment effect appeared in mean value of the surface tension reduced by 2.11 mN/m. Moreover, the memory effect was also found. Figure 11 shows the surface tension changes of the 1h MF sample treated for 60 min when the field had ceased. It increases slowly from 70.00 mN/m right after the treatment via 70.35 mN/m (after 15 min), 70.95 mN/m (after 30 mN/m), to 71.25 mN/m (after 60 min), being still lower than that of the untreated sample 72.36 mN/m.
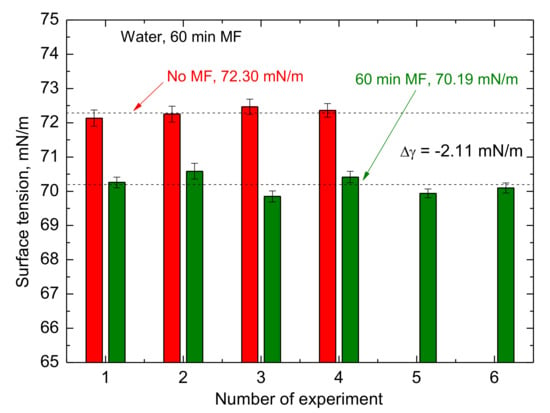
Figure 10.
The surface tension measured for four untreated and six 1 h MF-treated samples at the room temperature 24.2 ± 0.2 °C.
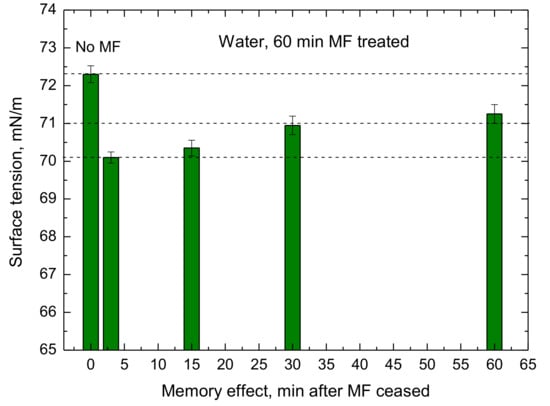
Figure 11.
Changes in the water surface tension of 1 h MF-treated samples as a function of time when the field had ceased—memory effect.
4. Discussion
The presented results show clearly that MF causes changes in the structure of water which appears in the changes of the rate of evaporation and surface tension which was already reported in the earlier published papers [7,8,9,10,11,12,13,14,15,16]. However, some new features of the effects were found. A possible role of dissolved air (oxygen) in the tested water samples should be kept in mind. Both in the case of evaporation and surface tension experiments the water samples contacted with the atmosphere during the deionization (MilliporeQ System) and distillation processes. Otsuka and Ozeki [21] claimed that in the ultrapure water distilled in a vacuum no MF effects occurred even in the 6 T magnetic field. Moreover, no effects were observed in 10 mM NaCl, KCl, CaCl2 if no gas was dissolved. However, if water was saturated with oxygen (700 Torr) and in the presence of air atmosphere, the MF effect appeared. The presence of MF effect was evaluated via the contact angle measurements on a platinum surface which after the MF treatment decreased from 65° to 56°, and by 10° on the copper surface. However, there is no doubt that the contact angle is a sufficiently sensitive parameter to study the MF effects. Based on the analysis of changed Raman bonds and electrolytic potential of water, as well as precipitation of aragonite instead of calcite in the magnetized water, the authors [21] concluded that the observed effects can be assigned to “formation of clathrate-like hydrate of O2 and promotion of hydrogen bonded network”. As the dispersion interactions between two bodies depend on the magnetic susceptibility of the medium, the interactions between the clusters can be affected by MF in the paramagnetic medium [21]. Considering this model, the question arises whether it reflected in the increased evaporation of MF-treated water and a small decrease in its surface tension. Both these effects involve changes in the water structure, at least in its surface layer. Water evaporation relates to breaking of the hydrogen bonding, therefore the above model of “promotion of hydrogen bonded network” should lead to reduced water evaporation instead of increased which was stated in many papers [7,8,9,10,11,12,13,14,15,16]. Nakagawa et al. [7] found that the evaporation rate increased when the vessel was placed off the field center and concluded that rather the MF field gradient B·dB/dx is more important than the field itself. They suggested that oxygen (and air) can cause a susceptibility gradient in normal direction to the evaporating water surface and enhance magnetic convection and hence a decrease in the water vapor density. Volume susceptibility at 293 K of oxygen and air amounts to: χox = +1.8028 × 10−6; χair = +0.3736 × 10−6, while that for nitrogen and water to only −0.0063 × 10−6, and −0.0068 × 10−6, respectively.
where = . The susceptibility χ indicates how given material behaves in MF (attracts into or repels out), as well as it informs about the material structure, energy and bonding. If χ > 0 (the magnetization is higher than that of empty space) the substance is paramagnetic and if χ < 0 the material is diamagnetic. Magnetic susceptibility is the ratio; χ = M/H, where M is the magnetization (magnetic moment per unit volume) and H is the applied magnetizing field intensity. Both M and H have the same unit A/m and hence the volume susceptibility is a dimensionless quantity. The μ is the measure of a material ability to support to form magnetic field in its bulk, i.e., the material magnetization due to the applied MF and μo is the vacuum permeability, (also called as permeability of free space or permeability of vacuum) which is the magnetic constant. It is a measure of resistance appearing when a MF is formed in classical vacuum. The µ0 = 4π × 10−7 H·m−1 ≈ 12.57 × 10−7 H·m−1 [Vs/Am]. The volume magnetic susceptibility χv and magnetic permeability μ are related by the formula: μ = μo (1 + χv), where the term in bracket is the relative permeability of the material and it is dimensionless.
In the MF 8 T and B·dB/dx = 320 T2/m at 60 mm from the force center, the bulk magnetic force difference ∆Fm was equal to 2.2 N/m3 (1.7 N/kg), which is the difference between the force in the wet air near the water surface and the force in the bulk dry air, corresponds to ca. 17% of the gravitational force acting on the air. The authors [7] compared this force effect to the thermal convection effect if the temperature increased by 50 K from 293 K. Moreover, no MF effect on water vaporization was observed in nitrogen contrary to that in oxygen because χox>> χwater. They finally concluded that for the magnetic convection to occur a susceptibility gradient must be present perpendicularly to the MF gradient.
From our results presented in Figure 8 and Figure 9 it can be seen that the maximum value of B·dB/dz = 15 T2/m at the water surface close to the inner magnet wall and only 0.42 T2/m at the magnet center. Hence the maximum force difference ∆Fm (Equation (1)) amounts to 0.089 N/kg, which is only 0.91% of the gravitational force and its contribution in the magnetic convection is minimal, whereas it was 17% if the B·dB/dx = 320 T2/m [7]. Thus, the MF enhancement of the water evaporation is situated close to the inner wall of the ring magnet. Therefore, some other reasons must be considered to explain the observed increase in the evaporation rates (Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7).
Guo et al. [12] used a superconducting magnet which allowed generation of high gradient (from −1500 T2/m to 1313 T2/m) and simulated gravity (~0 g–~2 g, where go = 9.80665 m/s2). Placing the water sample at different positions the amount of evaporated water was determined at different field strengths, its gradient and simulated gravity. The simulated gravity gm (simulated acceleration) in a gradient MF is described following [12]:
where B′ is the field gradient and ρ is the water density.
They considered four reasons influencing enhancement of water vaporization, i.e., effect of MF itself, combined effect of MF and its gradient, changes in the water surface area due to MF, MF effect on the convection. Moreover, also the effect of MF on the hydrogen bonds was discussed. They showed that at the same gravity the homogeneous MF (16.12 T) increased water evaporation. The largest evaporation was at simulated 0 gravity. However, the samples were extremely small 60 μL and the difference in the evaporated water after 24 h experiment was ca. 0.2 mg (Figure 1 in ref. [12]). They concluded that the amount of evaporated water, among others, depended on the surface area of water/gas interface which changed at the “non-center position” and depended on three investigated positions of the sample in the magnet (32.08; 34.65; 44.65 in mm2). An important role of Lorentz force, as well as breaking of hydrogen bonds and weakening of van der Waals interactions [17] were suggested [12]. However, because the published MF effects on the hydrogen bonds are contested [22,23,24] they did not discuss them.
Seyfi et al. [13], who also used ring magnets, the increased evaporation from the MF-treated samples was considered first in the light of kinetic energy of water molecules and Lorentz force which acts on the charged molecules moving at the water/air interface. The water surface was on the same level as the magnet upper height. Having the MF (75 mT) from the north pole directed normally to the water surface, the maximum increase in the evaporated amount during 80 min amounts to ca. 19% at 31 ± 1 °C. However, no effect was observed if the field was parallel to the surface. Similarly to Nakagawa et al. [7], taking into account the volume magnetic and Lorentz forces, they calculated the difference between the gravity and the volume magnetic force and found that it was too small to increase convection of water molecules that would be caused by the MF applied. To explain the observed increase in the evaporation rate, occurring only in the case of MF perpendicular to the water surface, the authors [13] put forward the hypothesis that the Lorentz force affects the kinetic energy of the random motion of the dipoles. This is possible because it is believed that across the water/air interface there exists an electrostatic potential resulting from the bouncing dipoles [19,20]. As a result, changed momenta can occur in the clusters along the hydrogen bonds. This can result in possible weakening or even breaking the hydrogen bonds and escaping of the freed water molecules. Seyfi et al. [13] also suggested that if the water structure is changed due to the MF action, i.e., more monomer water molecules or weakened water clusters are present for a period of time, this would be the origin of the memory effect observed up to 40 min. We are in favor of this hypothesis because it explains our results, both the increased evaporation rate (Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7) and the slightly decreased surface tension (Figure 10), as well as the memory effect (Figure 11).
Also, the theoretical simulations of Toledo et al. [15] help to explain of our results. They applied the GAUSSIAN98 program package and the properties of water were calculated at the Density Functional Theory level using the density functional Becke’s three-parameters exchange functional and the gradient corrected functional [25,26]. Different geometries of the water clusters were considered in the simulated apparent MF (up to 17 T). They considered water clusters of up to 15 molecules that had the same charge. This was due to many possible geometries of larger clusters; hence there might be several minima on the shallow potential/energy surface. This would cause difficulties in determination of the true minimum for each cluster. Anyway, using some literature data the authors [15] calculated the total binding energy of intra- and inter-clusters. However, the energy of inter-clusters is very small in comparison to that of the intra clusters. Thus, calculated value for magnetically untreated water was close to the experimental value (−12.293 and −11.30 kcal/mol, respectively). Moreover, from the calculations it resulted that the clusters of a higher symmetry have lower energy. Although at low MF strengths the changes of the intra cluster binding energy are small but generally the field affects the energy. MF (especially strong one) decreases stability of the clusters consisting of 2, 7, 11, 14 and 15 molecules and stabilizes the clusters with 3, 4, 8 and 12 molecules. Generally, MF can weaken the intra cluster hydrogen bonds thus reducing their average number between water molecules [15]. Also, Zhou et al. [22] concluded from the Monte Carlo simulation that the intra clusters hydrogen bonds are weakened by MF, and the second neighbor solvation shell is affected too, causing increased number of the neighbors. Thus, the final suggestion of Toledo et al. [15] was that MF weakens stronger intra cluster hydrogen bonds; breaks the larger clusters and thus forms smaller clusters which characterize the stronger inter-cluster hydrogen bonds. This can contribute to the paramagnetic term of water. We approve of the conclusions of these simulations because they help to understand the MF effects presented in this paper. Even the observed initial decreased evaporation rate, if the south pole S↑ is up (Figure 5) can result from the competition between the inter and intra clusters whose relative amounts change during the MF treatment time [15].
5. Conclusions
The presented MF effects causing an enhanced water evaporation rate and a small decrease in its surface tension at room temperature agree with many literature data, although in the case of the reduced surface tension there are also reverse results. It can be postulated that the effects, even caused by the same MF strength, depend on many parameters (even the experiment “geometry”) that are difficult to be exactly fixed and reproduced in every experiment. Therefore, it is difficult to obtain exactly reproducible results, especially of the evaporated amounts of water at room temperature. The simulated results are very helpful for better understanding of the observed effects. However, still there is no comprehensive explanation of these interesting effects and more fundamental studies are needed.
Author Contributions
The corresponding author (E.Ch) is the originator to carry out the studies and then has elaborated and discussed the results. A.S. and L.H. kept care on the experimental part and also participated in the results discussion and technical preparation of the manuscript.
Funding
This research was funded by Polish National Centre of Science grant number 2016/21/B/ST4/00987.
Acknowledgments
This work was supported by National Centre of Science, grant 2016/21/B/ST4/00987, which is greatly appreciated. We are grateful to Ms. Weronika Głąb for the surface tension measurements.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Baker, J.S.; Judd, S.J. Magnetic amelioration of scale formation. Water Res. 1996, 3, 247–260. [Google Scholar] [CrossRef]
- Rodgers, C.T. Magnetic field effects in chemical systems. Pure Appl. Chem. 2009, 81, 19–43. [Google Scholar] [CrossRef]
- Zaidi, N.S.; Sohaili, J.; Muda, K.; Sillanpää, M. Magnetic field application and its potential in water and wastewater treatment systems. Sep. Purif. Rev. 2014, 43, 206–240. [Google Scholar] [CrossRef]
- Alabi, A.; Chiesa, M.; Garlisia, C.; Palmisano, G. Advances in anti-scale magnetic water treatment. Environ. Sci. Water Res. Technol. 2015, 1, 408–425. [Google Scholar] [CrossRef]
- Zúñiga, O.; Benavides, J.A.; Ospina-Salazar, D.I.; Jiménez, C.O.; Gutiérrez, M.A. Magnetic treatment of irrigation water and seeds in agriculture. Ingeniería y Competitividad 2016, 18, 217–231. [Google Scholar] [CrossRef]
- Chibowski, E.; Szcześ, A. Magnetic water treatment—A review of the latest approaches. Chemosphere 2018, 203, 54–67. [Google Scholar] [CrossRef]
- Nakagawa, J.; Hirota, N.; Kitazawa, K.; Shoda, M. Magnetic field enhancement of water vaporization. J. Appl. Phys. 1999, 86, 2923–2925. [Google Scholar] [CrossRef]
- Kitazawa, K.; Ikezoe, Y.; Uetake, H.; Hirota, N. Magnetic field effects on water, air and powders. Phys. B 2001, 294–295, 709–714. [Google Scholar] [CrossRef]
- Holysz, L.; Szczes, A.; Chibowski, E. Effects of a static magnetic field on water and electrolyte solutions. J. Colloid Interface Sci. 2007, 316, 996–1002. [Google Scholar] [CrossRef]
- Szcześ, A.; Chibowski, E.; Holysz, L.; Rafalski, P. Effects of static magnetic field on water at kinetic condition. Chem. Eng. Process. 2011, 5, 124–127. [Google Scholar] [CrossRef]
- Rashid, F.L.; Hassan, N.M.; Jafar, A.M.; Hashim, A. Increasing water evaporation rate by magnetic field. Int. Sci. Investig. J. 2013, 2, 61–68. [Google Scholar]
- Guo, Y.-Z.; Yin, D.-C.; Cao, H.-L.; Shi, J.-Y.; Zhang, C.-Y.; Liu, Y.-M.; Huang, H.-H.; Liu, Y.; Wang, Y.; Guo, W.-H.; et al. Evaporation rate of water as a function of a magnetic field and field gradient. Int. J. Mol. Sci. 2012, 13, 16916–16928. [Google Scholar] [CrossRef] [PubMed]
- Seyfi, A.; Afzalzadeha, R.; Hajnorouzi, A. Increase in water evaporation rate with increase in static magnetic field perpendicular to water-air interface. Chem. Eng. Process. 2017, 120, 195–200. [Google Scholar] [CrossRef]
- Amor, H.B.; Elaoud, A.; Salah, N.B.; Elmoueddeb, K. Effect of Magnetic Treatment on Surface Tension and Water Evaporation. Int. J. Adv. Ind. Eng. 2017, 5, 119–124. [Google Scholar]
- Toledo, E.J.L.; Ramalho, T.C.; Magriotis, Z.M. Influence of magnetic field on physical-chemical properties of the liquid water: Insights from experimental and theoretical models. J. Mol. Sci. 2008, 888, 409–415. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, H.; Li, Z. Effect of magnetic field on physical properties of water. Results Phys. 2018, 8, 262–267. [Google Scholar] [CrossRef]
- Krems, R.V. Breaking van der Waals molecules with magnetic fields. Phys. Rev. Lett. 2004, 93, 013201. [Google Scholar] [CrossRef]
- Chang, K.T.; Weng, C.I. An investigation into the structure of aqueous NaCl solutions under magnetic field. Comput. Mater. Sci. 2008, 43, 1048–1055. [Google Scholar] [CrossRef]
- Kathmann, S.M.; Kuo, I.F.W.; Mundy, C.J. Electronic effects on the surface potential at the vapor-liquid interface of water. J. Am. Chem. Soc. 2008, 130, 16556–16561. [Google Scholar] [CrossRef]
- Kathmann, S.M.; Kuo, I.F.W.; Mundy, C.J.; Schenter, G.K. Understanding the surface potential of water. J. Phys. Chem. B 2011, 115, 4369–4377. [Google Scholar] [CrossRef]
- Otsuka, I.; Ozeki, S. Does magnetic treatment of water changes its properties? J. Phys. Chem. B 2006, 110, 1509–1512. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.X.; Lu, G.W.; Zhou, Q.C.; Song, J.H. Monte Carlo simulation of liquid water in a magnetic field. J. Appl. Phys. 2000, 88, 1802–1805. [Google Scholar] [CrossRef]
- Chang, K.T.; Weng, C.I. The effect of an external magnetic field on the structure of liquid water using molecular dynamic simulation. J. Appl. Phys. 2006, 100, 043917. [Google Scholar] [CrossRef]
- Cai, R.; Yang, H.; He, J.; Zhu, W. The effects of magnetic fields on water molecular hydrogen bonds. J. Mol. Struct. 2009, 938, 15–19. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1998, 38, 3089–3100. [Google Scholar] [CrossRef]
- Perdew, P.J. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. J. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).