Waterflooding of Surfactant and Polymer Solutions in a Porous Media Micromodel
Abstract
:1. Introduction
2. Materials and Methods
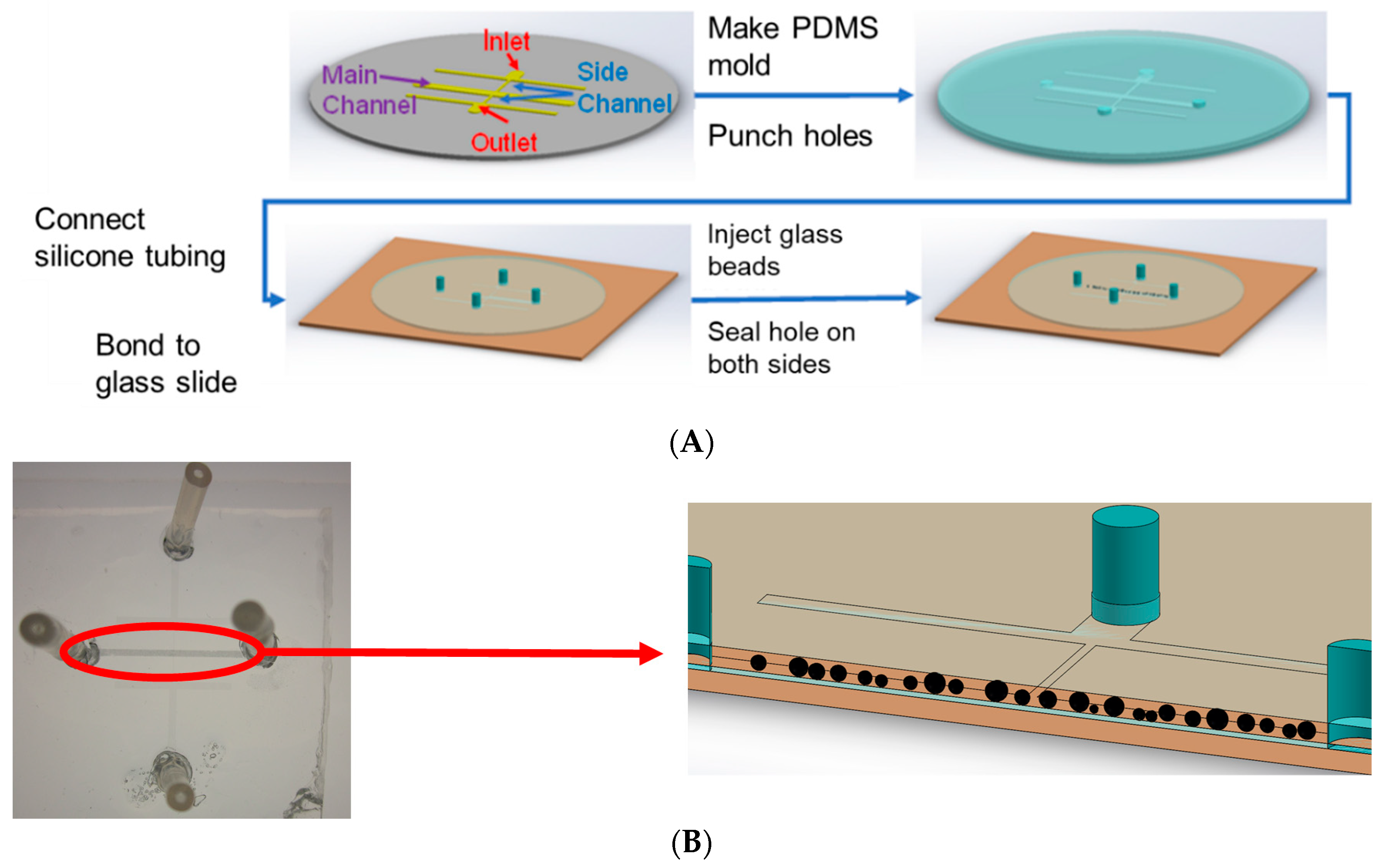
2.1. Device Fabrication
2.2. Image Capture and Processing
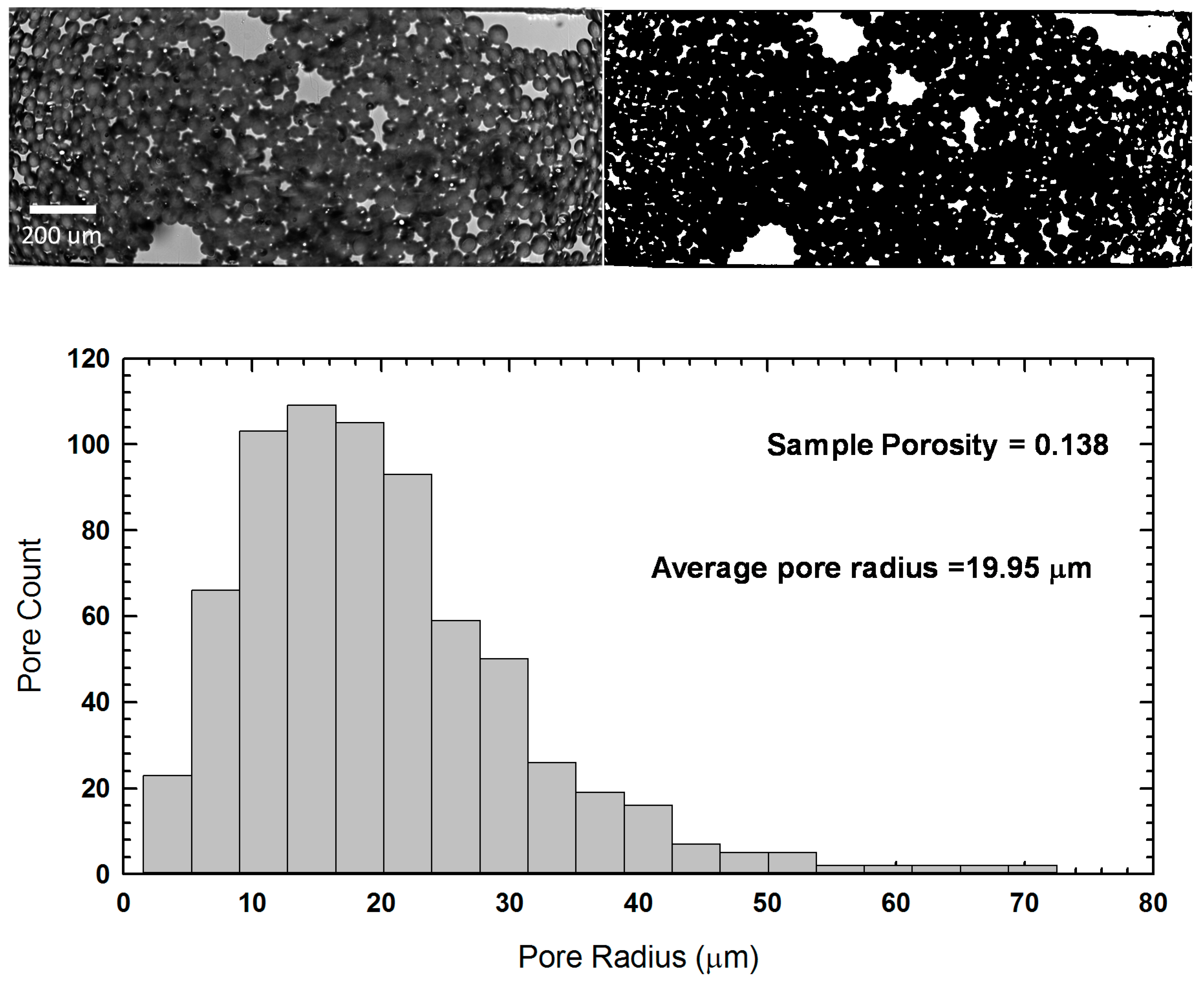
2.3. Device Characterization
2.4. Experimental Details
3. Theory and Simulation
4. Results and Discussion
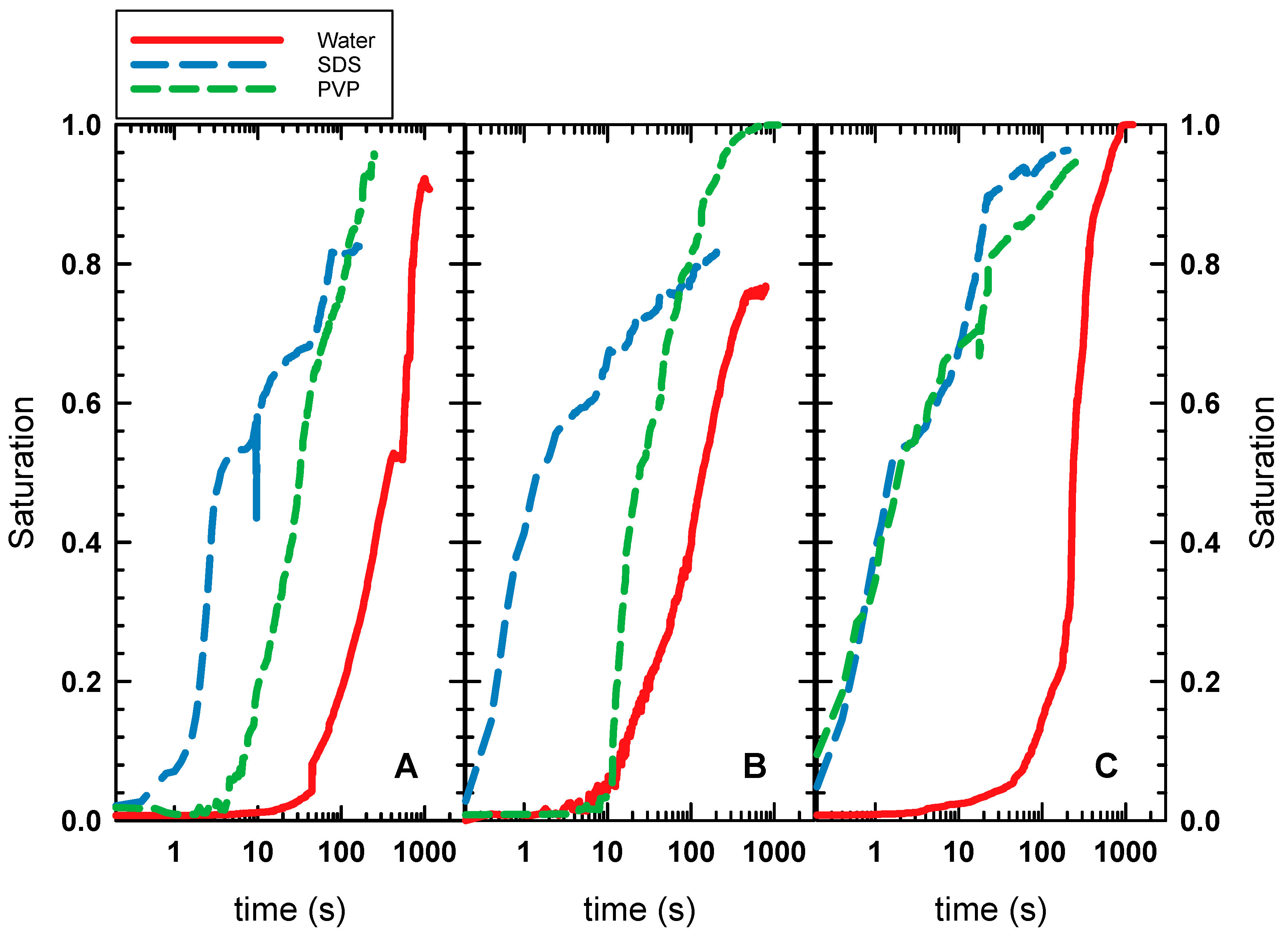
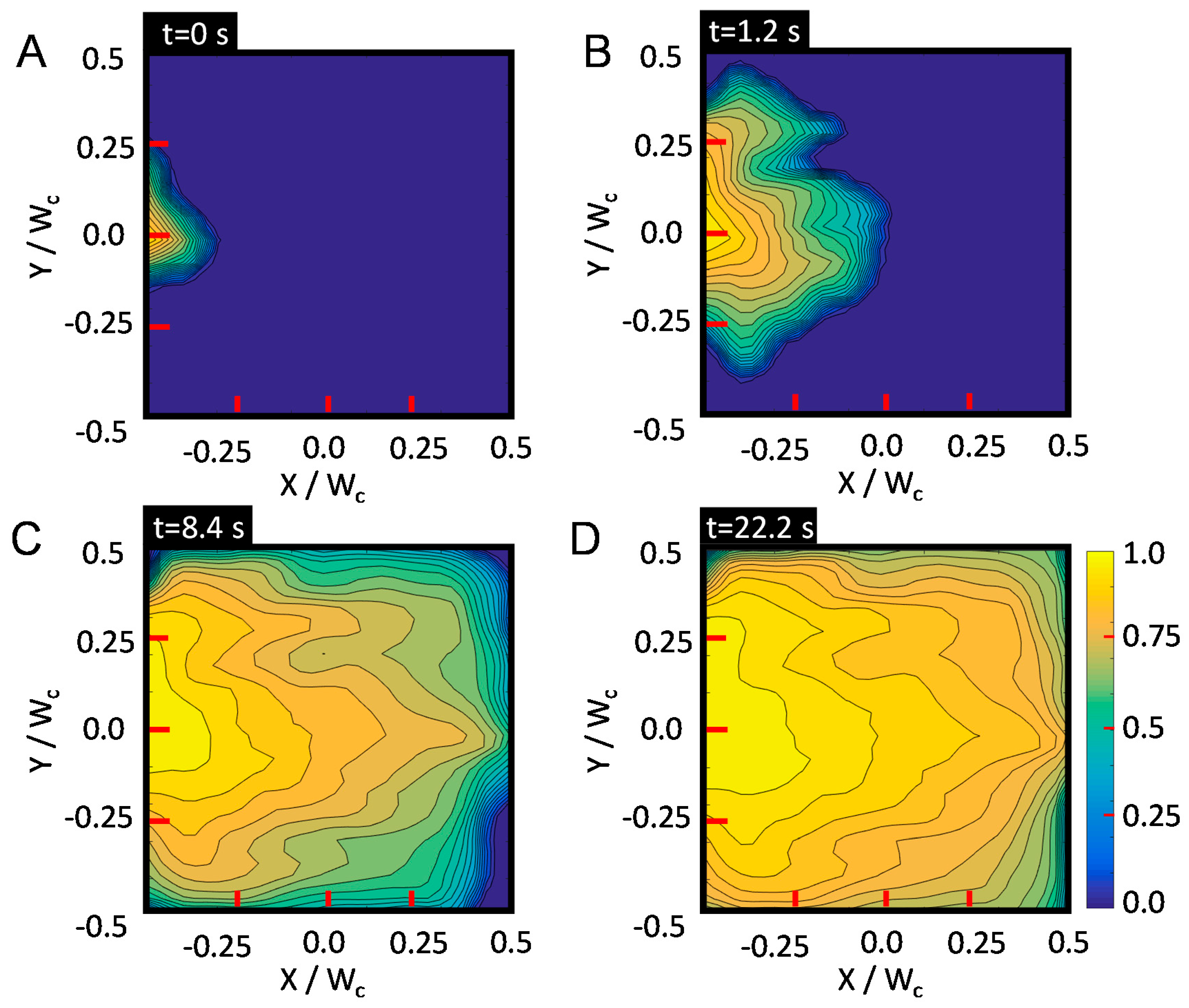
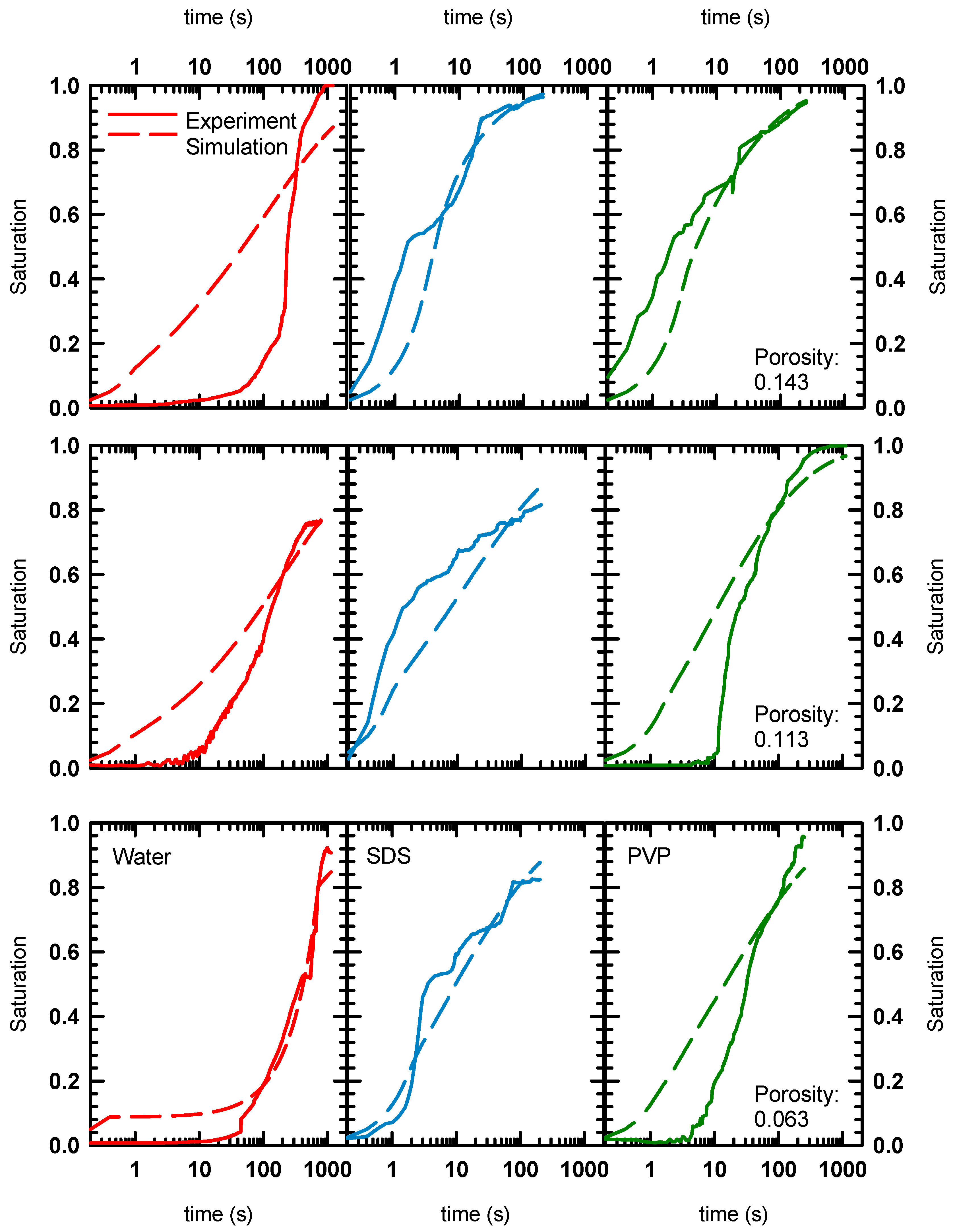
4.1. Oil Displacement Efficiency
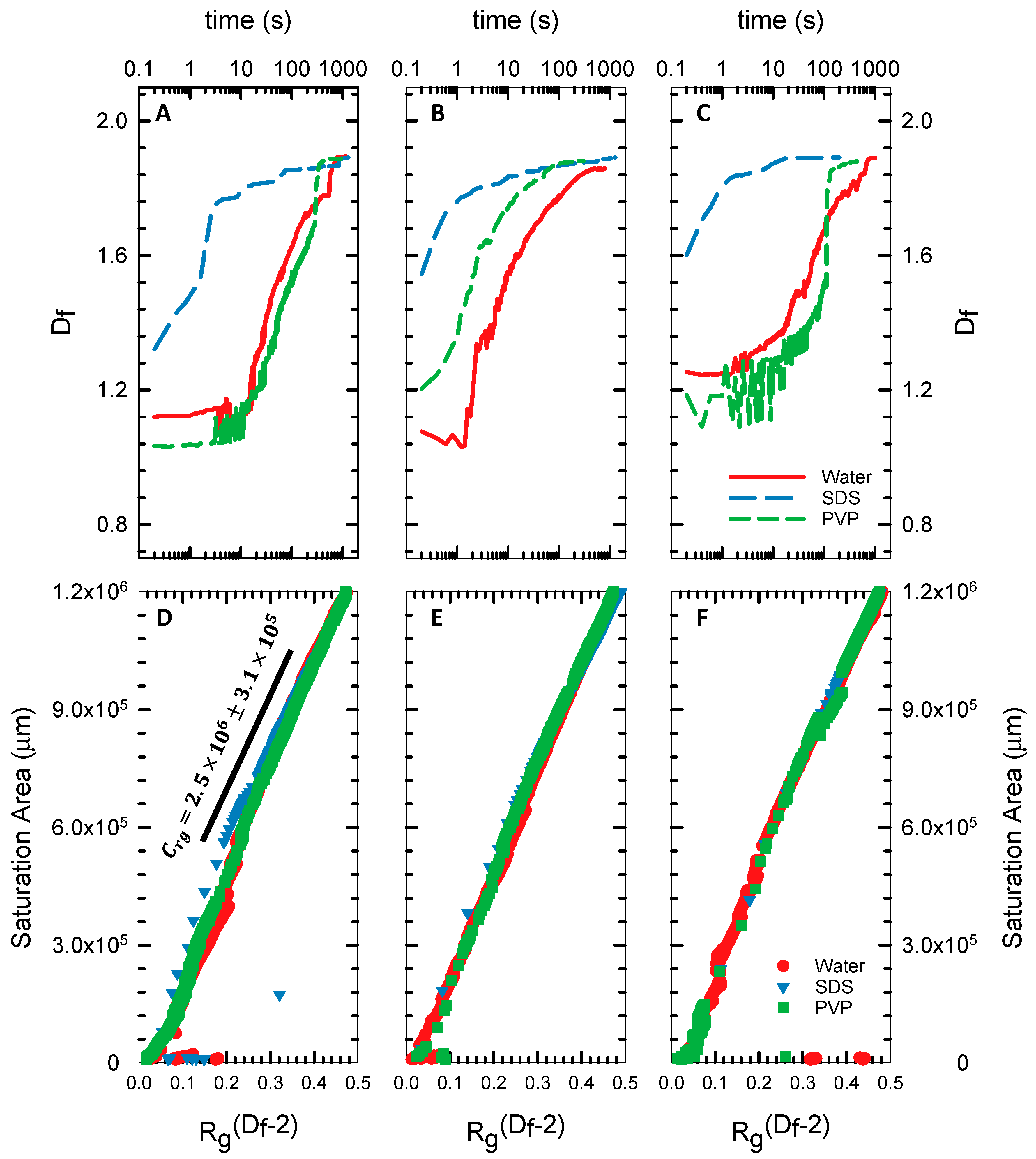
4.2. Fractal Dimension
4.3. IMPES
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karadimitriou, N.K.; Hassanizadeh, S.M. A review of micromodels and their use in two-phase flow studies. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Muggeridge, A.; Cockin, A.; Webb, K.; Frampton, H.; Collins, I.; Moulds, T.; Salino, P. Recovery rates, enhanced oil recovery and technological limits. Philos. Trans. R. Soc. A 2014, 372, 20120320. [Google Scholar] [CrossRef] [PubMed]
- Blunt, M.; Fayers, F.J.; Orr, F.M. Carbon dioxide in enhanced oil recovery. Energy Convers. Manag. 1993, 34, 1197–1204. [Google Scholar] [CrossRef]
- Levitt, D.; Jackson, A.; Heinson, C.; Britton, L.N.; Malik, T.; Dwarakanath, V.; Pope, G.A. Identification and evaluation of high-performance EOR surfactants. SPE Reserv. Eval. Eng. 2009, 12, 243–253. [Google Scholar] [CrossRef]
- Raffa, P.; Broekhuis, A.A.; Picchioni, F. Polymeric surfactants for enhanced oil recovery: A review. J. Pet. Sci. Eng. 2016, 145, 723–733. [Google Scholar] [CrossRef]
- Sagi, A.R. Surfactant Enhanced Oil Recovery. Ph.D. Thesis, Rice University, Houston, TX, USA, 2015. [Google Scholar]
- Hirasaki, G.; Miller, C.A.; Puerto, M. Recent advances in surfactant EOR. SPE J. 2011, 16. [Google Scholar] [CrossRef]
- Wei, B.; Romero-Zerón, L.; Rodrigue, D. Oil displacement mechanisms of viscoelastic polymers in enhanced oil recovery (EOR): A review. J. Pet. Explor. Prod. Technol. 2014, 4, 113–121. [Google Scholar] [CrossRef]
- Sheng, J.J.; Leonhardt, B.; Azri, N. Status of polymer-flooding technology. J. Can. Pet. Technol. 2015, 54, 116–126. [Google Scholar] [CrossRef]
- Ezell, R.G.; McCormick, C.L. Electrolyte- and pH-responsive polyampholytes with potential as viscosity-control agents in enhanced petroleum recovery. J. Appl. Polym. Sci. 2007, 104, 2812–2821. [Google Scholar] [CrossRef]
- Rashidi, M.; Blokhus, A.M.; Skauge, A. Viscosity study of salt tolerant polymers. J. Appl. Polym. Sci. 2010, 117, 1551–1557. [Google Scholar] [CrossRef]
- Elraies, K.A.; Tan, I.M.; Fathaddin, M.T.; Abo-Jabal, A. Development of a new polymeric surfactant for chemical enhanced oil recovery. Pet. Sci. Technol. 2011, 29, 1521–1528. [Google Scholar] [CrossRef]
- Morrow, N.R.; Mason, G. Recovery of oil by spontaneous imbibition. Curr. Opin. Colloid Interface Sci. 2001, 6, 321–337. [Google Scholar] [CrossRef]
- Standnes, D.C.; Austad, T. Wettability alteration in chalk: 2. Mechanism for wettability alteration from oil-wet to water-wet using surfactants. J. Pet. Sci. Eng. 2000, 28, 123–143. [Google Scholar] [CrossRef]
- Blunt, M.; King, M.J.; Scher, H. Simulation and theory of two-phase flow in porous media. Phys. Rev. A 1992, 46, 7680–7699. [Google Scholar] [CrossRef] [PubMed]
- Berejnov, V.; Djilali, N.; Sinton, D. Lab-on-chip methodologies for the study of transport in porous media: Energy applications. Lab Chip 2008, 8, 689–693. [Google Scholar] [CrossRef] [PubMed]
- Chatenever, A.; Calhoun, J.C. Visual examinations of fluid behavior in porous media—Part I. J. Pet. Technol. 1952, 4, 149–156. [Google Scholar] [CrossRef]
- Krummel, A.T.; Datta, S.S.; Münster, S.; Weitz, D.A. Visualizing multiphase flow and trapped fluid configurations in a model three-dimensional porous medium. AIChE J. 2013, 59, 1022–1029. [Google Scholar] [CrossRef] [Green Version]
- Anbari, A.; Chien, H.-T.; Datta, S.S.; Deng, W.; Weitz, D.A.; Fan, J. Microfluidic model porous media: Fabrication and applications. Small 2018, 14, 1703575. [Google Scholar] [CrossRef] [PubMed]
- Lenormand, R.; Touboul, E.; Zarcone, C. Numerical models and experiments on immiscible displacements in porous media. J. Fluid Mech. 1988, 189, 165–187. [Google Scholar] [CrossRef]
- Ferer, M.; Ji, C.; Bromhal, G.S.; Cook, J.; Ahmadi, G.; Smith, D.H. Crossover from capillary fingering to viscous fingering for immiscible unstable flow: Experiment and modeling. Phys. Rev. E 2004, 70. [Google Scholar] [CrossRef] [PubMed]
- Cottin, C.; Bodiguel, H.; Colin, A. Drainage in two-dimensional porous media: From capillary fingering to viscous flow. Phys. Rev. E 2010, 82. [Google Scholar] [CrossRef] [PubMed]
- Lenormand, R.; Zarcone, C.; Sarr, A. Mechanisms of the displacement of one fluid by another in a network of capillary ducts. J. Fluid Mech. 1983, 135, 337–353. [Google Scholar] [CrossRef]
- Chang, L.-C.; Tsai, J.-P.; Shan, H.-Y.; Chen, H.-H. Experimental study on imbibition displacement mechanisms of two-phase fluid using micro model. Environ. Earth Sci. 2009, 59, 901. [Google Scholar] [CrossRef]
- Theodoropoulou, M.A.; Sygouni, V.; Karoutsos, V.; Tsakiroglou, C.D. Relative permeability and capillary pressure functions of porous media as related to the displacement growth pattern. Int. J. Multiph. Flow 2005, 31, 1155–1180. [Google Scholar] [CrossRef]
- Wu, M.; Xiao, F.; Johnson-Paben, R.M.; Retterer, S.T.; Yin, X.; Neeves, K.B. Single- and two-phase flow in microfluidic porous media analogs based on Voronoi tessellation. Lab Chip 2011, 12, 253–261. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Yin, X. Geometry models of porous media based on Voronoi tessellations and their porosity–permeability relations. Comput. Math. Appl. 2016, 72, 328–348. [Google Scholar] [CrossRef]
- Heshmati, M.; Piri, M. Interfacial boundary conditions and residual trapping: A pore-scale investigation of the effects of wetting phase flow rate and viscosity using micro-particle image velocimetry. Fuel 2018, 224, 560–578. [Google Scholar] [CrossRef]
- Roman, S.; Soulaine, C.; AlSaud, M.A.; Kovscek, A.; Tchelepi, H. Particle velocimetry analysis of immiscible two-phase flow in micromodels. Adv. Water Resour. 2016, 95, 199–211. [Google Scholar] [CrossRef]
- Bera, B.; Mitra, S.K.; Vick, D. Understanding the micro structure of Berea Sandstone by the simultaneous use of micro-computed tomography (micro-CT) and focused ion beam-scanning electron microscopy (FIB-SEM). Micron 2011, 42, 412–418. [Google Scholar] [CrossRef] [PubMed]
- Bakke, S.; Øren, P.-E. 3-D Pore-scale modelling of sandstones and flow simulations in the pore networks. SPE J. 1997, 2, 136–149. [Google Scholar] [CrossRef]
- Blunt, M.J. Flow in porous media pore-network models and multiphase flow. Interface Sci. 2001, 6, 197–207. [Google Scholar] [CrossRef]
- Gunda, N.S.K.; Bera, B.; Karadimitriou, N.K.; Mitra, S.K.; Hassanizadeh, S.M. Reservoir-on-a-Chip (ROC): A new paradigm in reservoir engineering. Lab Chip 2011, 11, 3785–3792. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Liang, T.; Zhu, P.; Qi, P.; Lu, J.; Huh, C.; Balhoff, M. A 2.5-D glass micromodel for investigation of multi-phase flow in porous media. Lab Chip 2017, 17, 640–646. [Google Scholar] [CrossRef] [PubMed]
- Marchand, S.; Bondino, I.; Ktari, A.; Santanach-Carreras, E. Consideration on data dispersion for two-phase flow micromodel experiments. Transp. Porous Media 2017, 117, 169–187. [Google Scholar] [CrossRef]
- Kim, M.; Sell, A.; Sinton, D. Aquifer-on-a-Chip: Understanding pore-scale salt precipitation dynamics during CO2 sequestration. Lab Chip 2013, 13, 2508–2518. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; de Haas, T.W.; Fadaei, H.; Sinton, D. Chip-off-the-old-rock: The study of reservoir-relevant geological processes with real-rock micromodels. Lab Chip 2014, 14, 4382–4390. [Google Scholar] [CrossRef] [PubMed]
- Kersting, A.B.; Efurd, D.W.; Finnegan, D.L.; Rokop, D.J.; Smith, D.K.; Thompson, J.L. Migration of plutonium in ground water at the Nevada Test Site. Nature 1999, 397, 56–59. [Google Scholar] [CrossRef]
- Jensen, K.H.; Valente, A.X.C.N.; Stone, H.A. Flow rate through microfilters: Influence of the pore size distribution, hydrodynamic interactions, wall slip, and inertia. Phys. Fluids 2014, 26, 052004. [Google Scholar] [CrossRef]
- Miller, J.S.; Stevens, K.R.; Yang, M.T.; Baker, B.M.; Nguyen, D.-H.T.; Cohen, D.M.; Toro, E.; Chen, A.A.; Galie, P.A.; Yu, X.; et al. Rapid casting of patterned vascular networks for perfusable engineered three-dimensional tissues. Nat. Mater. 2012, 11, 768–774. [Google Scholar] [CrossRef] [PubMed]
- Marschewski, J.; Brenner, L.; Ebejer, N.; Ruch, P.; Michel, B.; Poulikakos, D. 3D-printed fluidic networks for high-power-density heat-managing miniaturized redox flow batteries. Energy Environ. Sci. 2017, 10, 780–787. [Google Scholar] [CrossRef]
- Rabbani, A.; Jamshidi, S.; Salehi, S. Determination of specific surface of rock grains by 2D imaging. J. Geol. Res. 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Rabbani, A.; Jamshidi, S. Specific surface and porosity relationship for sandstones for prediction of permeability. Int. J. Rock Mech. Min. Sci. 2014, 71, 25–32. [Google Scholar] [CrossRef]
- Van der Marck, S.C. Network approach to void percolation in a pack of unequal spheres. Phys. Rev. Lett. 1996, 77, 1785–1788. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Hoang, V.T.; Satik, C.; Rojas, D.H. High-mobility-ratio waterflood performance prediction: Challenges and new insights. SPE Reserv. Eval. Eng. 2008, 11, 186–196. [Google Scholar] [CrossRef]
- Matlab Central Measuring Angle of Intersection—MATLAB & Simulink Example. Available online: https://www.mathworks.com/help/images/examples/measuring-angle-of-intersection.html (accessed on 6 April 2018).
- Stahl, G.A.; Schulz, D.N. Water-Soluble Polymers for Petroleum Recovery; Springer: New York, NY, USA, 1988; ISBN 978-0-306-42915-6. [Google Scholar]
- Taylor, K.C.; Nasr-El-Din, H.A. Water-soluble hydrophobically associating polymers for improved oil recovery: A literature review. J. Pet. Sci. Eng. 1998, 19, 265–280. [Google Scholar] [CrossRef]
- Chari, K.; Antalek, B.; Lin, M.Y.; Sinha, S.K. The viscosity of polymer–surfactant mixtures in water. J. Chem. Phys. 1994, 100, 5294–5300. [Google Scholar] [CrossRef]
- Sadeghi, R.; Azizpour, S. Volumetric, compressibility, and viscometric measurements of binary mixtures of Poly(vinylpyrrolidone) + Water, + Methanol, + Ethanol, + Acetonitrile, + 1-Propanol, + 2-Propanol, and + 1-Butanol. J. Chem. Eng. Data 2011, 56, 240–250. [Google Scholar] [CrossRef]
- Kou, J.; Sun, S. On iterative IMPES formulation for two phase flow with capillarity in heterogeneous porous media. Int. J. Numer. Anal. Model. Ser. B 2010, 1, 20–40. [Google Scholar]
- Aarnes, J.E.; Gimse, T.; Lie, K.-A. An introduction to the numerics of flow in porous media using matlab. In Geometric Modelling, Numerical Simulation, and Optimization; Applied Mathematics at SINTEF; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Li, B.; Chen, Z.; Huan, G. Comparison of solution schemes for black oil reservoir simulations with unstructured grids. Comput. Methods Appl. Mech. Eng. 2004, 193, 319–355. [Google Scholar] [CrossRef]
- Chen, Z.; Huan, G.; Li, B. An improved IMPES method for two-phase flow in porous media. Transp. Porous Media 2004, 54, 361–376. [Google Scholar] [CrossRef]
- Habermann, B. The efficiency of miscible displacement as a function of mobility ratio. Trans. Am. Inst. Min. Metall. Eng. 1960, 219, 264–272. [Google Scholar]
- Fritz, J.L.; Owen, M.J. Hydrophobic recovery of plasma-treated polydimethylsiloxane. J. Adhes. 1995, 54, 33–45. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Datta, A.; Berg, J.M.; Gangopadhyay, S. Studies on surface wettability of poly(dimethyl) siloxane (PDMS) and glass under oxygen-plasma treatment and correlation with bond strength. J. Microelectromech. Syst. 2005, 14, 590–597. [Google Scholar] [CrossRef]
- Bodas, D.; Khan-Malek, C. Formation of more stable hydrophilic surfaces of PDMS by plasma and chemical treatments. Microelectron. Eng. 2006, 83, 1277–1279. [Google Scholar] [CrossRef]
- Bertrand, E.; Blake, T.D.; De Coninck, J. Dynamics of dewetting. Colloids Surf. Physicochem. Eng. Asp. 2010, 369, 141–147. [Google Scholar] [CrossRef]
- Wang, D.; Cheng, J.; Yang, Q.; Wenchao, G.; Qun, L.; Chen, F. Viscous-elastic polymer can increase microscale displacement efficiency in cores. Soc. Pet. Eng. 2000. [Google Scholar] [CrossRef]
- Matlab Central Hausdorff (Box-Counting) Fractal Dimension—File Exchange—MATLAB Central. Available online: http://www.mathworks.com/matlabcentral/fileexchange/30329-hausdorff--box-counting--fractal-dimension (accessed on 21 November 2017).
- Zhong-Can, O.Y.; Gang, Y.; Bai-Lin, H. From fractal to dendritic: Competition between diffusion and field. Phys. Rev. Lett. 1986, 57, 3203–3205. [Google Scholar] [CrossRef] [PubMed]
- Witten, T.A.; Sander, L.M. Diffusion-limited aggregation. Phys. Rev. B 1983, 27, 5686–5697. [Google Scholar] [CrossRef]
- Gharbi, R.B.C.; Qasem, F.; Peters, E.J. A relationship between the fractal dimension and scaling groups of unstable miscible displacements. Exp. Fluids 2001, 31, 357–366. [Google Scholar] [CrossRef]
- Pons, M.-N.; Weisser, E.M.; Vivier, H.; Boger, D.V. Characterization of viscous fingering in a radial Hele-Shaw cell by image analysis. Exp. Fluids 1999, 26, 153–160. [Google Scholar] [CrossRef]
- Maloy, K.J.; Boger, F.; Feder, J.; Jossang, T.; Meakin, P. Dynamics of viscous-fingering fractals in porous media. Phys. Rev. A 1987, 36, 318–324. [Google Scholar] [CrossRef]
- Aronofsky, J.S.; Masse, L.; Natanson, S.G. A model for the mechanism of oil recovery from the porous matrix due to water invasion in fractured reservoirs. Pet. Trans. 1958, 213, 17–19. [Google Scholar]
- Holden, M.A.; Kumar, S.; Castellana, E.T.; Beskok, A.; Cremer, P.S. Generating fixed concentration arrays in a microfluidic device. Sens. Actuators B Chem. 2003, 92, 199–207. [Google Scholar] [CrossRef]
- Kamholz, A.E.; Schilling, E.A.; Yager, P. Optical measurement of transverse molecular diffusion in a microchannel. Biophys. J. 2001, 80, 1967–1972. [Google Scholar] [CrossRef]
- Cheng, J.T.; Pyrak-Nolte, L.J.; Nolte, D.D.; Giordano, N.J. Linking pressure and saturation through interfacial areas in porous media. Geophys. Res. Lett. 2004, 31, L08502. [Google Scholar] [CrossRef]
- Parseval, Y.D.; Pillai, K.M.; Advani, S.G. A simple model for the variation of permeability due to partial saturation in dual scale porous media. Transp. Porous Media 1997, 27, 243–264. [Google Scholar] [CrossRef]
- Niemet, M.R.; Selker, J.S. A new method for quantification of liquid saturation in 2D translucent porous media systems using light transmission. Adv. Water Resour. 2001, 24, 651–666. [Google Scholar] [CrossRef]
- Cai, J.; Yu, B.; Zou, M.; Mei, M. Fractal analysis of invasion depth of extraneous fluids in porous media. Chem. Eng. Sci. 2010, 65, 5178–5186. [Google Scholar] [CrossRef]
- Zhu, T.; Waluga, C.; Wohlmuth, B.; Manhart, M. A study of the time constant in unsteady porous media flow using direct numerical simulation. Transp. Porous Media 2014, 104, 161–179. [Google Scholar] [CrossRef]
- Zheng, Z.; Guo, B.; Christov, I.C.; Celia, M.A.; Stone, H.A. Flow regimes for fluid injection into a confined porous medium. J. Fluid Mech. 2015, 767, 881–909. [Google Scholar] [CrossRef]
- Martys, N.; Cieplak, M.; Robbins, M.O. Critical phenomena in fluid invasion of porous media. Phys. Rev. Lett. 1991, 66, 1058–1061. [Google Scholar] [CrossRef] [PubMed]
- Geistlinger, H.; Ataei-Dadavi, I. Influence of the heterogeneous wettability on capillary trapping in glass-beads monolayers: Comparison between experiments and the invasion percolation theory. J. Colloid Interface Sci. 2015, 459, 230–240. [Google Scholar] [CrossRef] [PubMed]
- Parker, J.C.; Lenhard, R.J. A model for hysteretic constitutive relations governing multiphase flow: 1. Saturation-pressure relations. Water Resour. Res. 1987, 23, 2187–2196. [Google Scholar] [CrossRef]
- Narsilio, G.A.; Buzzi, O.; Fityus, S.; Yun, T.S.; Smith, D.W. Upscaling of Navier–Stokes equations in porous media: Theoretical, numerical and experimental approach. Comput. Geotech. 2009, 36, 1200–1206. [Google Scholar] [CrossRef]
- Wever, D.A.Z.; Picchioni, F.; Broekhuis, A.A. Polymers for enhanced oil recovery: A paradigm for structure–property relationship in aqueous solution. Prog. Polym. Sci. 2011, 36, 1558–1628. [Google Scholar] [CrossRef]
- Sedaghat, M.H.; Mohammadi, H.; Razmi, R. Application of SiO2 and TiO2 nano particles to enhance the efficiency of polymer-surfactant floods. Energy Sources Part Recovery Util. Environ. Eff. 2016, 38, 22–28. [Google Scholar] [CrossRef]
- Mohajeri, M.; Hemmati, M.; Shekarabi, A.S. An experimental study on using a nanosurfactant in an EOR process of heavy oil in a fractured micromodel. J. Pet. Sci. Eng. 2015, 126, 162–173. [Google Scholar] [CrossRef]
- Ma, K.; Liontas, R.; Conn, C.A.; Hirasaki, G.J.; Biswal, S.L. Visualization of improved sweep with foam in heterogeneous porous media using microfluidics. Soft Matter 2012, 8, 10669–10675. [Google Scholar] [CrossRef]
- Conn, C.A.; Ma, K.; Hirasaki, G.J.; Biswal, S.L. Visualizing oil displacement with foam in a microfluidic device with permeability contrast. Lab Chip 2014, 14, 3968–3977. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klinzing, G.R.; Zavaliangos, A. A simplified model of moisture transport in hydrophilic porous media with applications to pharmaceutical tablets. J. Pharm. Sci. 2016, 105, 2410–2418. [Google Scholar] [CrossRef] [PubMed]
- Szulczewski, M.L.; MacMinn, C.W.; Herzog, H.J.; Juanes, R. Lifetime of carbon capture and storage as a climate-change mitigation technology. Proc. Natl. Acad. Sci. USA 2012, 109, 5185–5189. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, B.; MacMinn, C.W.; Juanes, R. Wettability control on multiphase flow in patterned microfluidics. Proc. Natl. Acad. Sci. USA 2016, 113, 10251–10256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Osei-Bonsu, K.; Grassia, P.; Shokri, N. Investigation of foam flow in a 3D printed porous medium in the presence of oil. J. Colloid Interface Sci. 2017, 490, 850–858. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.N.; Chen, Y.; Shu, Y.; Chen, Y.; Tian, Q.; Wu, H. Direct, one-step molding of 3D-printed structures for convenient fabrication of truly 3D PDMS microfluidic chips. Microfluid. Nanofluid. 2015, 19, 9–18. [Google Scholar] [CrossRef]

| Water | 0.1% SDS | 0.1% PVP | |
|---|---|---|---|
| Contact Angle (degrees) | 11.2 ± 0.9 | 42.9 ± 1.4 | 22.3 ± 0.9 |
| γws (mN/m) | 72.2 ± 0.1 | 53.7 ± 0.4 | 66.8 ± 0.5 |
| γwo (mN/m) | 51.9 ± 0.4 | 44.2 ± 1.2 | 49.2 ± 0.7 |
| Average Capillary Number (Ca)/10−3 | 2.3 | 2.7 | 2.4 |
| Water | 0.1% SDS | 0.1% PVP | |||||
|---|---|---|---|---|---|---|---|
| Amax (μm2)/106 | tc (s) | Amax (μm2)/106 | tc (s) | Amax (μm2)/106 | tc (s) | ||
| Porosity | 0.063 | 1.266 | 86.2 | 1.105 | 17.6 | 1.253 | 285.7 |
| 0.11 | 1.059 | 111.1 | 1.241 | 11.0 | 1.209 | 25.3 | |
| 0.143 | 1.258 | 357.1 | 1.269 | 2.1 | 1.209 | 10.4 | |
| Water | SDS | PVP | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Porosity | 0.063 | 0.113 | 0.143 | 0.063 | 0.113 | 0.143 | 0.063 | 0.113 | 0.143 |
| Mobility | 255.8 | 114.7 | 87.2 | 11.2 | 33.3 | 1.9 | 18.2 | 12.5 | 4.6 |
| R2 | 0.95 | 0.87 | 0.54 | 0.87 | 0.29 | 0.88 | 0.8 | 0.79 | 0.87 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, H.-L.; Juárez, J.J. Waterflooding of Surfactant and Polymer Solutions in a Porous Media Micromodel. Colloids Interfaces 2018, 2, 23. https://doi.org/10.3390/colloids2020023
Yeh H-L, Juárez JJ. Waterflooding of Surfactant and Polymer Solutions in a Porous Media Micromodel. Colloids and Interfaces. 2018; 2(2):23. https://doi.org/10.3390/colloids2020023
Chicago/Turabian StyleYeh, Hsiang-Lan, and Jaime J. Juárez. 2018. "Waterflooding of Surfactant and Polymer Solutions in a Porous Media Micromodel" Colloids and Interfaces 2, no. 2: 23. https://doi.org/10.3390/colloids2020023
APA StyleYeh, H.-L., & Juárez, J. J. (2018). Waterflooding of Surfactant and Polymer Solutions in a Porous Media Micromodel. Colloids and Interfaces, 2(2), 23. https://doi.org/10.3390/colloids2020023






