1. Introduction
Flotation is a very interesting phenomenon occurring in nature, which can be seen for example in the movement of insects across the surface of water. It is also an important process in industrial fields such as the flotation separation of valuable minerals and self-assembly. Froth flotation in mining is a classical separation process that selectively separates hydrophobic materials from hydrophilic materials using air bubbles [
1,
2,
3]. When air bubbles are injected into a mineral and water slurry, air bubbles adhere to specific mineral particles through chemical treatments. These particles, combined with air bubbles, are then transported to the surface and removed. Recently, as an environmental issue, the recycling of plastic wastes has received much attention and froth flotation is recommended as a promising approach to selectively separate plastics [
4].
The fluidic assembly method with colloidal components has also been of great interest in many industrial fields for control over nano- and micro-scale assembly processes [
5,
6,
7]. Colloidal crystallization is an efficient method to synthesize microstructured particles that are used as precursors for advanced materials [
8]. The principle of self-assembly combined with lithography technology provides a powerful means of organizing new nanostructures. Liddle et al. [
9] used the characteristics of the local pinning of a moving liquid contact line to concentrate nanoparticles. Recently, a new feedback control technique developed by NIST (National Institute of Standards and Technology) [
10] has been developed to manipulate hundreds of individual micrometer-sized colloidal particles to create quasi-two-dimensional ensembles and crystals. Their control algorithm uses the direct current (DC) field for particles to be removed from the electrode and the alternating current (AC) field to assemble colloidal crystals. Understanding the details of the flotation behavior is necessary in the development of a full-scale self-assembly model.
In order to elucidate the dynamics of flotation and self-assembly, it is important to understand the flotation behavior of assembling particles and its dependence on physical constants such as surface tension and particle density. Even though an object has greater density compared with that of a fluid, the object overcomes the gravitational force and can float at an interface with a higher vertical force induced by surface tension. Singh and Hesla [
11] showed that the interfacial tension cannot rotate a spherical particle about its center when the interfacial tension and the contact angle are constant. When two or more particles are floating nearby, the symmetry of the contact line breaks so that a non-zero horizontal force between particles is induced. Therefore, the particles come closer together, and this results in self-assembly, where interfacial tension plays an important role in propelling floating particles over the free surface. Danov and Kralchevsky [
12] explored the capillary force between non-spherical particles and derived integral expressions for the lateral capillary force in terms of capillary multipoles. This approach was used to study the interactions of particles in the process of self-assembly.
The equilibrium profile of a floating object has been investigated by many research groups. Deryagin [
13] derived analytic solutions for the distorted free surface around the three contact points for small particle radii. Princen [
14] provided much information on the equilibrium shape of interfaces in various systems for gravitational and centrifugal fields. He reported on the critical size for floatability of spheres and cylinders, where the critical radii of spheres are larger than those of cylinders. Huh and Scriven [
15] numerically considered the shapes of axisymmetric fluid interfaces from a circular line of contact. They provided tables of capillary rise data computed by numerical computation and compared their theoretical predictions with experimental observations [
16]. James [
17] supplied the static profile of the distorted meniscus around the small cylinder. He obtained the matched asymptotic solution around the vertical cylinder. A thermodynamic method was developed to solve the Laplace equation in order to determine the critical size of a spherical particle that is able to float at the free interface [
18]. Bindschaedler and Peppas [
19] used the free-energy and force analysis to predict the equilibrium position of a spherical particle during detachment from a liquid in the absence of gravitational effects. The profile of the liquid meniscus was determined to compute the force for detachment as a function of the displacement from the liquid surface. The results are used for predicting the adhesion force of a particle to a biological substrate in the area of bio-adhesion. Vella et al. [
20] considered the equilibrium flotation of a spherical particle to determine the conditions with respect to density and radius that allow it to be able to float at the interface. They obtained the Young–Laplace equation with an axisymmetric geometry, where all lengths were non-dimensionalized by the capillary length. When the radius of the particle is small, the maximum density of particle is approximated by a function of the contact angle. Singh and Joseph [
21] conducted direct numerical experiments in three-dimensional geometry, where the interface was tracked by the level set method and the method of Lagrange multipliers was used for the fluid–particle motion.
The general observation for a floating sphere shows that the deformed shape occurs near the particle surface and an almost flat surface with a tiny slope is also observed as the lateral coordinate goes to infinity. The numerical difficulty for flotation can be summarized with respect to two main topics. Since the Young–Laplance equation is a highly nonlinear equation, it is highly sensitive at the initial estimate when the shooting method as two–point boudnary value problem is used. The other is the infinity boundary condition. It can not be avoided to become very large for the distance bewteen computation nodes because of very wide computational domains. Therefore, an approximation solution is usually adopted to bypass the far-field meniscus.
Recently, Fend and Nguyen [
22] introduced a novel quantitative analysis, where the free surface parameterized by the inclination angle was divided by the total nodes and a cubic polynomial to its nodes was assumed. The nonlinear algebraic system against the unknown coefficients was solved iteratively by linearization, in which they employed different approximate solutions for small and large contact radii and for far-field boundaries. Feng and Nguyen [
23,
24] also explored the effect of contact angle variation and contact angle hysteresis on the floatability of spheres. They showed that the contact angle random hysteresis results from small-scale surface roughness of particles.
The aim of this work is to provide an efficient method to solve the Young–Laplace equation for the meniscus deformed around the floating particle. The highly nonlinear equation is transformed by two ordinary differential equation parametrized with the inclination angle of the deformed surface. If the free surface is equally spaced in the sense of inclination angle, the distance between nodes increases from the three contact points and the length around the far field increases abruptly. It can be an unstable condition in numerical stability for the shooting method. The novel contribution of this work is the introduction of Chebyshev nodes for the discretization of the angle of meniscus inclination, which allows the fine spaces near the three contact points and the infinity boundary without approximated solutions used at the previous studies. Here, the force balance of a spherical particle floating at the interface is combined as a constraint condition to determine the three-phase contact points on the particle surface, where the filling angle depends on the density ratio and contact angle. The next section reviews the formulation of the force balance of a floating object and the governing equations in detail. The numerical implementation to compute the profile of the interface is illustrated, and the effect of particle density, capillary force, and contact angle is discussed.
3. Numerical Implementation
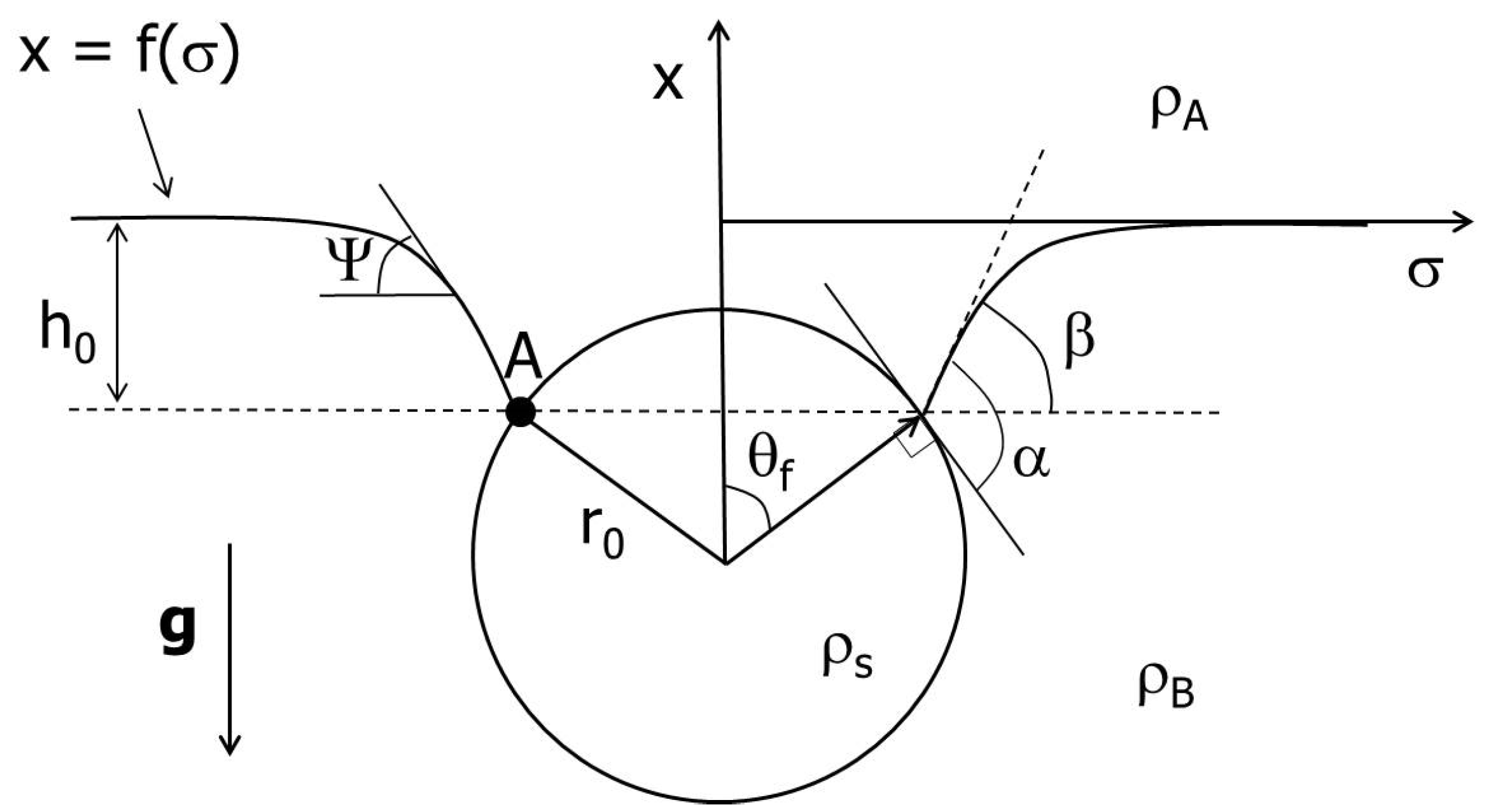
In this numerical study, a single floating sphere is considered, where the free interface is deformed under the action of gravity, buoyancy, and capillary forces. The static equilibrium profile, as illustrated in
Figure 1, depends on the density ratio
D, the filling angle
, the contact angle
, the depth
from the flat interface, and the Bond number
. The position
of contact point A is related to the unsinking condition in Equation (
7). Even though density ratio
D, the Bond number
, and contact angle
are given, the depth
and the filling angle
can not be initially fixed from force balance Equation (
7) at the same time. Equation (
17) then has to be computed iteratively to obtain the position of the three contact points
and the filling angle
, satisfying constraint Equation (
7). This explains why it is difficult to obtain the static profile of the floating particle at the free surface.
In order to calculate the static position of a floating sphere and the equilibrium profile of the axisymmetric curved interface, the shooting method is used to solve a two-point boundary problem of Equation (
17) with boundary condition Equations (
18) and (
19). In this study, the unequal discretization for
is introduced by the Chebyshev nodes, representing the roots of the Chebyshev polynomials of the first kind. Through the characteristics of the nodes it is possible to obtain fine discretization near the three contact points and the region of
.
The Chebyshev nodes in the interval
can be computed by
where
N is the total number of nodes.
can be transformed to
in the interval
by a linear transformation,
Thus,
allows the fine discretization
near
and
. The advantage of this approach is that the distances between nodes are effectively controlled, especially around
and
due to the characteristics of Chebyshev nodes. This is different from the collocation method by Feng and Nguyen [
22].
The numerical implementation can be summarized in five steps. If the density ratio, the Bond number, and the contact angle are given, the first step is to guess the initial filling angle (
). Then,
is derived from the geometrical relation by subtracting the filling angle from the contact angle. The second step is to compute the distance
from the free flat surface using Equation (
7). Then, the boundary conditions are prepared for the governing equation (Equation (
17)). As the third step, Equation (
17) is computed by the secant method, where
goes to zero with a small step of
backwards.
X should approach zero as
. Since the position of
can not be exactly determined, the computation is carried out with
that corresponds approximately to about 0.5 degrees (0.0087 radians) of
. Then, the error (
) is defined by the absolute value of the vertical axis at
, i.e.,
. The fourth step is to obtain the second initial guess of the filling angle (
that is evaluated by adding a small value to
at the first step. The same calculation in the second and third steps is done to obtain the error (
). The final step is to update the filling angle
using by the Newton–Raphson approach,
The computation is iterated and closed until the
value is below the tolerance level of
.
The results in this work are compared with the data provided by Sing and Joseph [
21] in
Table 1. In their numerical study, a flotation experiment with a sphere of radius
cm and density
g/cm
was conducted with fluids of
g/cm
and
g/cm
, where the contact angle was 135
, i.e.,
and the gravitation constant
cm/s
was used. The distance
is slightly different, but the filling angle
can be estimated within 10%.
4. Results
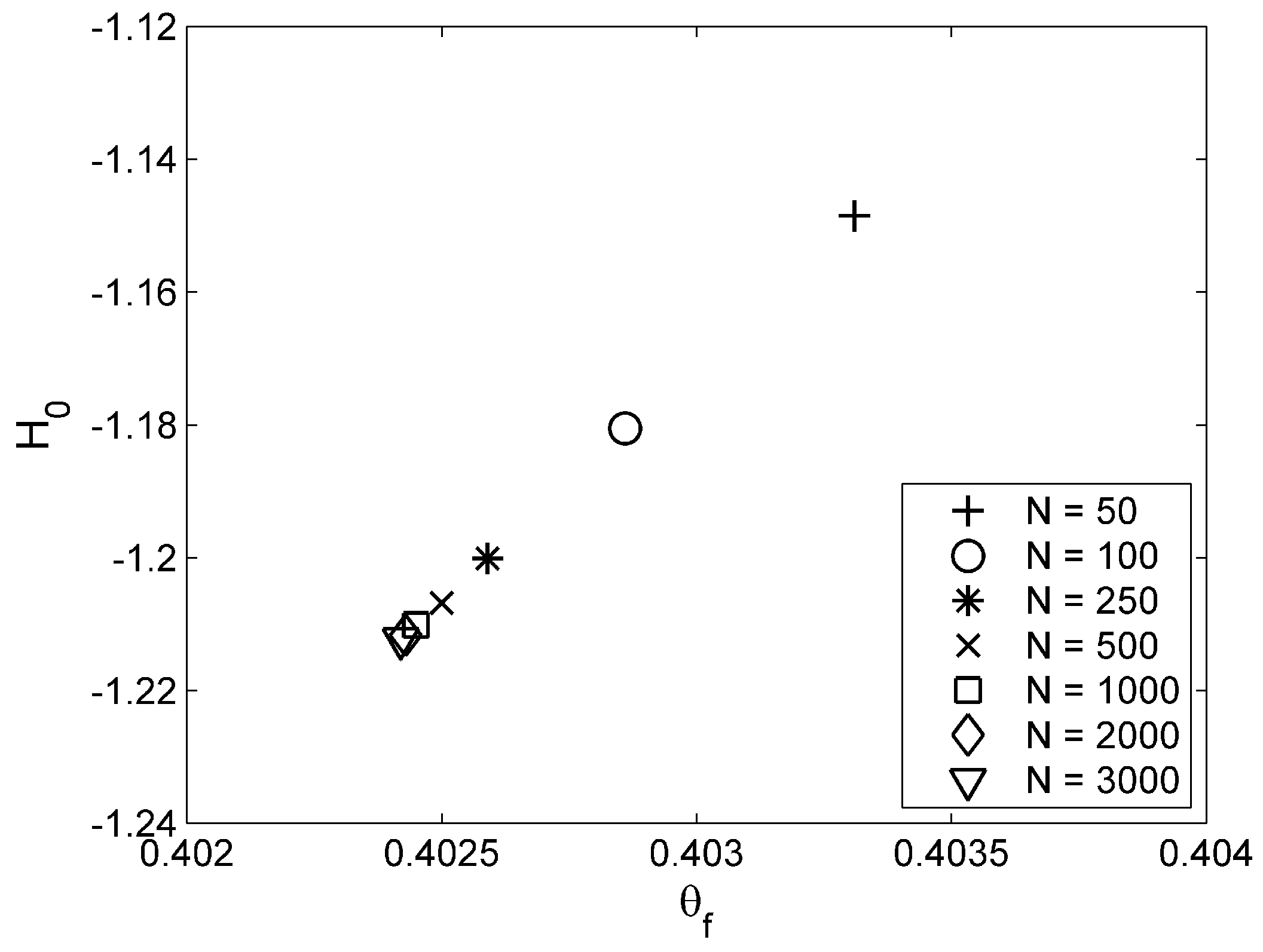
The performance of the numerical method is tested with
N, which is the total number of nodes. As shown in
Figure 2 with the conditions
,
and
, the depth
and the filling angle
converge at the constant value with increasing
N, and the difference over
(square box) is negligible, where the angle step size at
corresponds to 0.00155 radians. This resolution is kept for all computations in this study.
Figure 3 illustrates the typical static profile for a floating object with the same conditions as
Figure 2, with
. Even though the object has a high density ratio, the capillary and buoyancy forces allow sufficient support to float the spherical particle. The free surface near the particle is highly deformed, and it becomes nearly flat as
goes to infinity, where the distance needed to become completely flat is more than 15 times the particle radius. Note that the large contact angle results in the large deformation of the free interface in the case of a high density ratio.
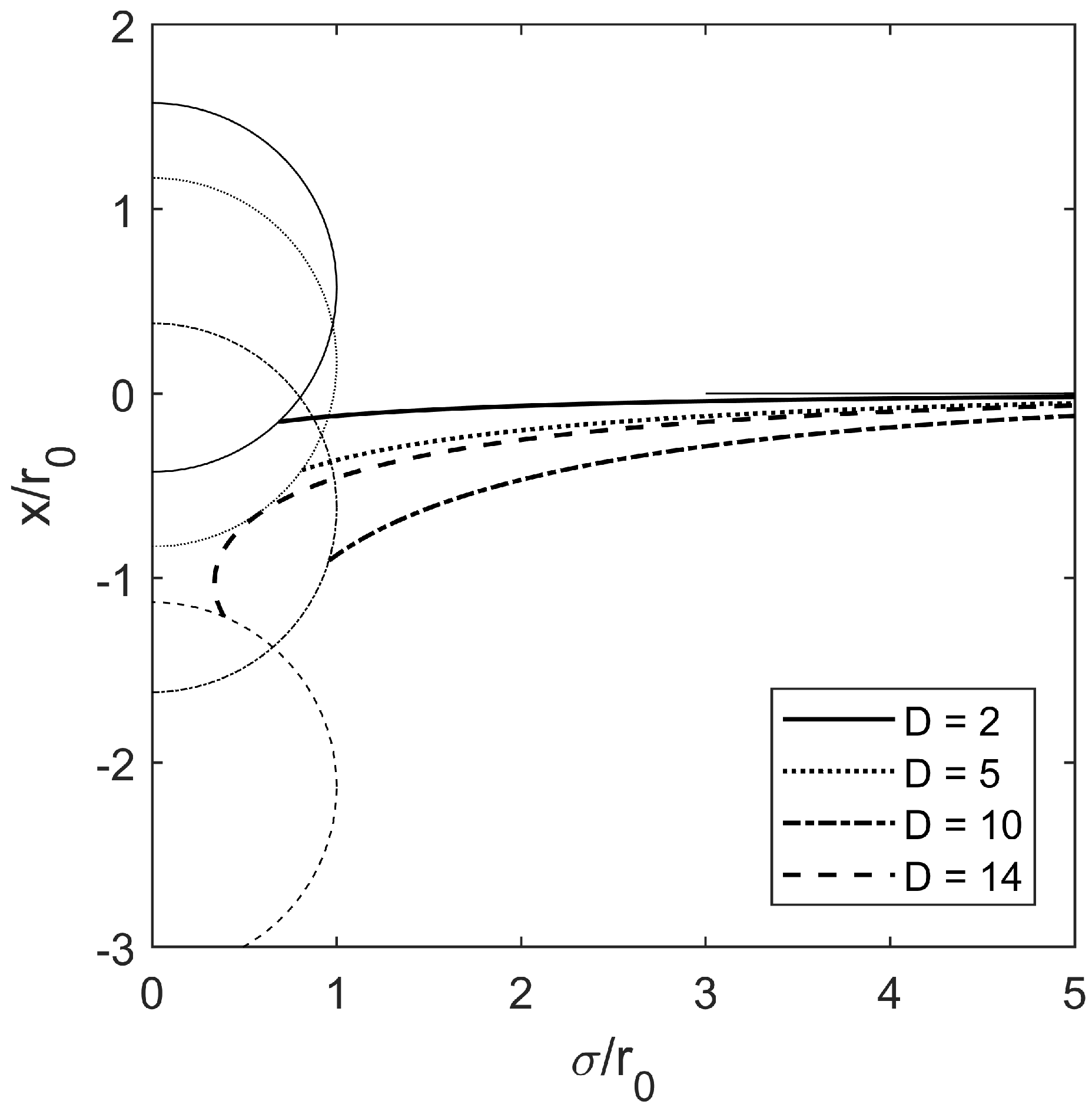
The evolutions of the free interface with different density ratios are displayed in
Figure 4, where
and
. The solid, dotted, dash-dotted, and dashed lines correspond to
,
,
, and
, respectively. As the density ratio increases, the curvature of the free interface becomes steeper and the depth from the flat interface becomes larger. The results show that the static profile is significantly affected by the density ratio. The solid horizontal segment on the right represents the flat interface at
.
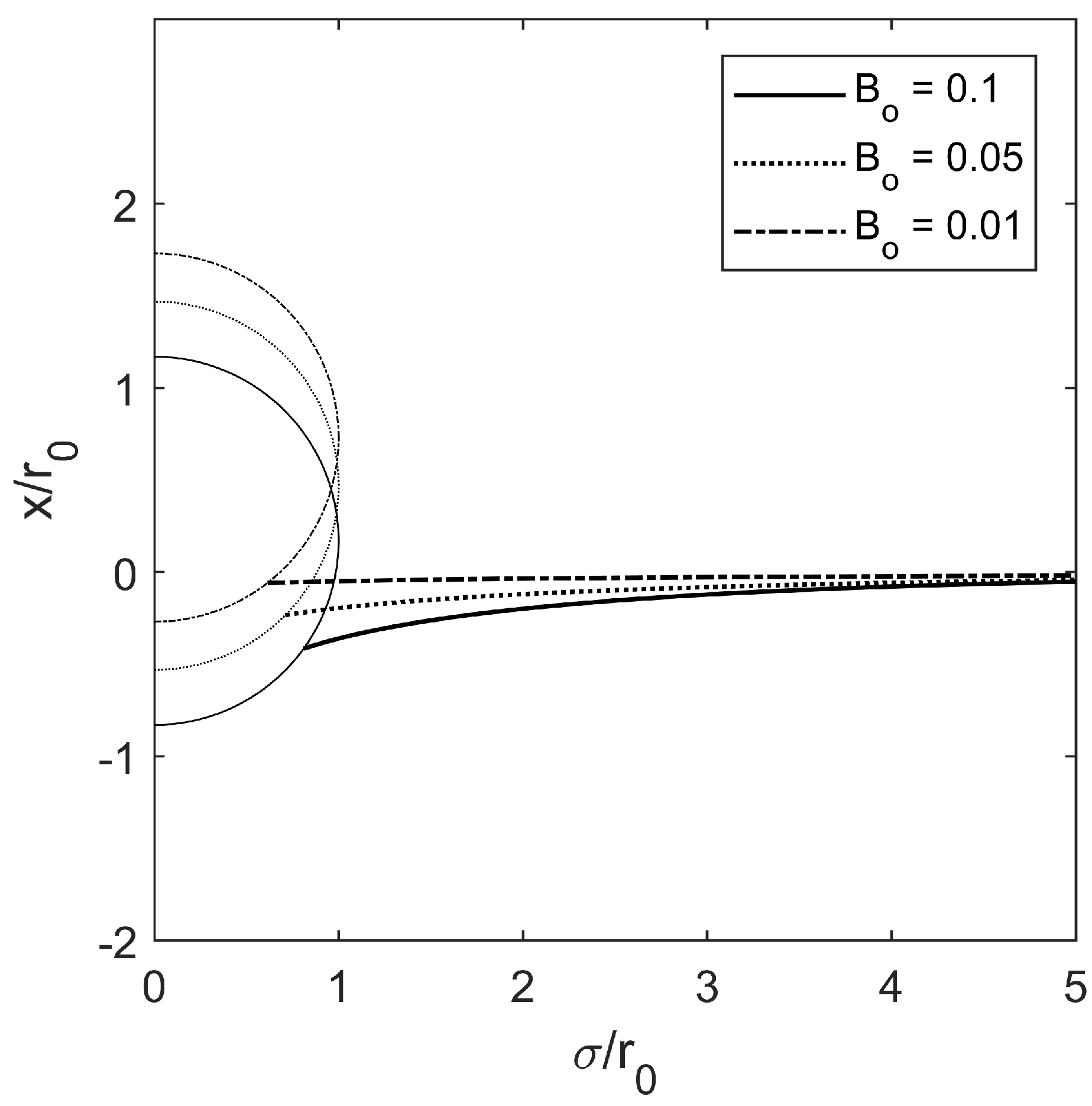
Figure 5 shows the effect of the Bond number on the equilibrium shape of the free interface, where
and
. Note that the Bond number represents the relative measure of surface tension force compared to body force and the ratio of a particle radius to the capillary length. As the size of a spherical object reduces, the surface tension becomes a dominant force and it results into the smaller Bond number. As
decreases, it is readily verified that the variation of the submerged height for a floating particle is negligible and the shape of the profile becomes flat.
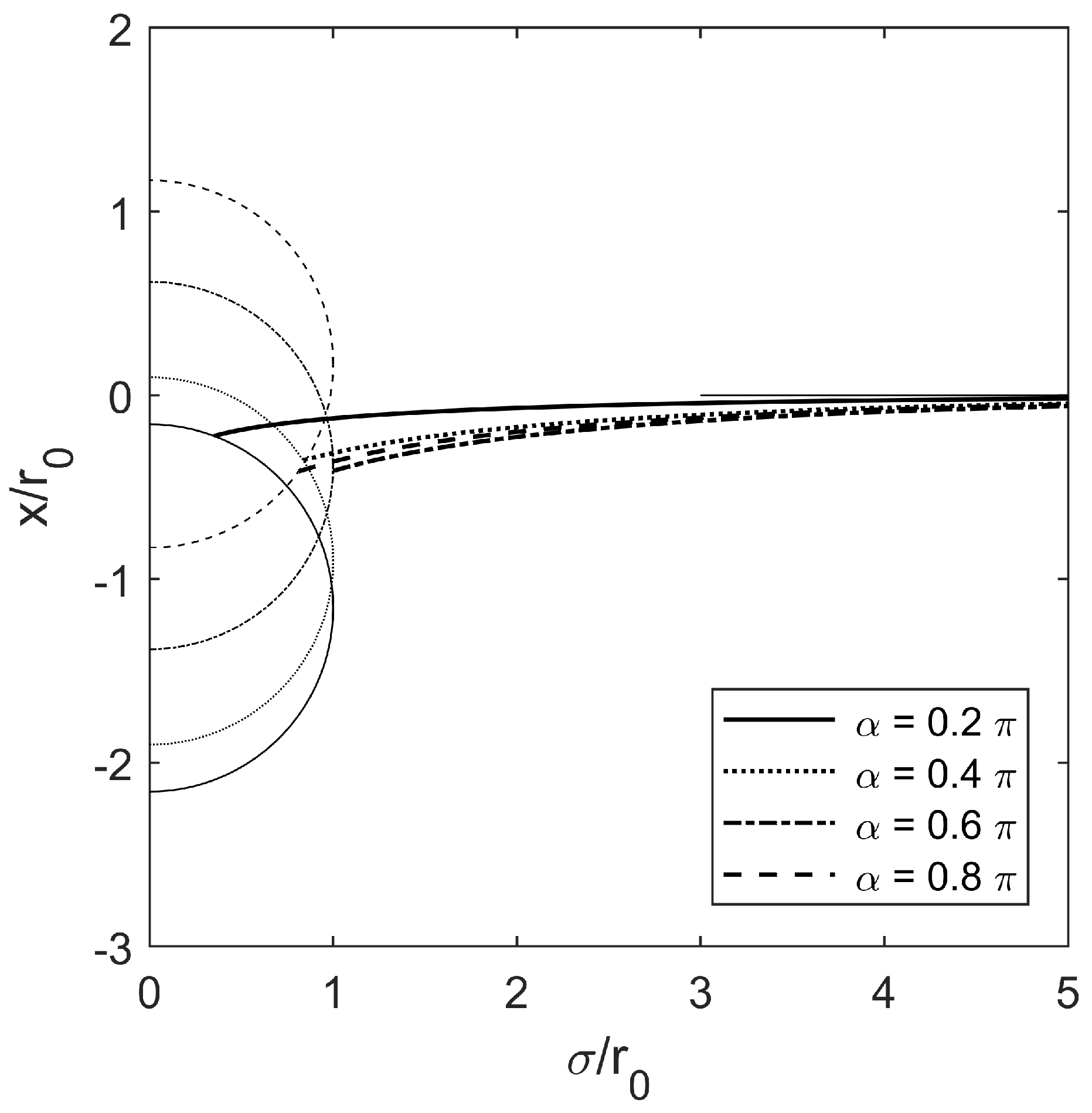
Figure 6 illustrates the effect of the contact angle on the equilibrium shape of the free interface, i.e., the characteristics of hydrophilic and hydrophobic substrates, where
and
. The dashed, dotted, dash-dotted, and solid lines correspond to
,
,
, and
, respectively. As the contact angle increases, there is a very small variation of depth from the flat interface, i.e., the three-phase contact point. However, the floatability can be significantly affected by the contact angle. The hydrophobic surface with contact angle over
allows a huge effect on flotation. The particle with the hydrophilic surface sinks more easily.
5. Discussion
The equilibrium shape of a floating sphere is numerically investigated by the two transformed ordinary differential equations (ODEs), with parametrization of the inclination angle of meniscus which is discretized by the optimal points of Chebyshev nodes. The fine discretization near the three contact points and near the infinity boundary condition allows for fast converged solutions and good stability for numerical solutions. From the force balances of gravity, buoyancy, and capillary forces, the expression of the depth of a floating object from the flat interface is expressed by the density ratio, the filling angle, the contact angle, and the Bond number. This equation indicates the sinking condition for flotation and has to be satisfied during computation.
The equilibrium profile of the free surface around the object is significantly affected by the density ratio and the contact angle. It is observed that the curves of the free interface are deformed more sharply and the depth from the flat interface gets deeper in case of a large density ratio and a large contact angle. As the Bond number decreases, a small particle can float due to strong surface tension even if the density ratio is high.