Classifying with the Fine Structure of Distributions: Leveraging Distributional Information for Robust and Plausible Naïve Bayes

Abstract

In machine learning, the Bayes classifier represents the theoretical optimum for minimizing classification errors. Since estimating high-dimensional probability densities is impractical, simplified approximations such as naïve Bayes and k-nearest neighbor are widely used as baseline classifiers. Despite their simplicity, these methods require design choices—such as the distance measures in kNN, or the feature independence in naïve Bayes. In particular, naïve Bayes relies on implicit assumptions by using Gaussian mixtures or univariate kernel density estimators. Such design choices, however, often fail to capture heterogeneous distributional structures across features. We propose a flexible naïve Bayes classifier that leverages Pareto Density Estimation (PDE), a parameter-free, non-parametric approach shown to outperform standard kernel methods in exploratory statistics. PDE avoids prior distributional assumptions and supports interpretability through visualization of class-conditional likelihoods. In addition, we address a recently described pitfall of Bayes’ theorem: the misclassification of observations with low evidence. Building on the concept of plausible Bayes, we introduce a safeguard to handle uncertain cases more reliably. While not aiming to surpass state-of-the-art classifiers, our results show that PDE-flexible naïve Bayes with uncertainty handling provides a robust, scalable, and interpretable baseline that can be applied across diverse data scenarios.

1. Introduction

In supervised classification the primary objective is to learn a decision rule that minimizes classification error. The Bayes classifier is the theoretical optimum for this criterion when the true class-conditional distributions are known [1,2,3]. In practice, however, estimating a nonparametric, potentially high-dimensional joint density is often infeasible [4,5] (e.g., due to lack of samples since the amount of data required grows exponentially) and building a fully parameterized model to represent the joint distribution can be impractical, because real distributions are too complex to model with simple parametric forms, and high-dimensional feature spaces require the estimation of too many parameters from too little data, leading to unstable or inaccurate models [6].

Consequently, a variety of classifiers have been developed to address classification challenges in practical scenarios, and a wide range of pragmatic approximations has been developed. One class of methods is nonparametric instance-based learning: k-nearest neighbors (kNN) is conceptually simple and, with a suitable choice of k, is a consistent approximation to the Bayes rule as the sample size grows [7]. Another popular approach is the naïve Bayes classifier, which drastically reduces estimation complexity by assuming feature independence and often performs well despite this strong simplification [6,8]. Both kNN and naïve Bayes offer fast and straightforward alternatives to the more intricate Bayes classifier, though they may not always achieve the same level of performance.

Therefore, the naïve Bayes and k-nearest neighbor (kNN) classifiers are commonly used as baseline algorithms for classification. However, in the case of naïve Bayes, the user must determine the most suitable strategy for model fitting based on the specific use case. Available strategies include fitting a mixture of Gaussian distributions or employing a non-parametric approach using kernel density estimation. However, these methods usually do not account for varying distributions across different features (e.g., see Appendix C for varying feature distributions). Moreover, analyzing the distributions of all features to select the optimal strategy for a naïve Bayes classifier is a complex task. Similarly, for kNN, the user must choose an appropriate distance measure, which poses a similar complex decision [9] as well as the number k of nearest neighbors.

Although this feature independence is quite constraining, naïve Bayes classifiers have been reported to achieve high performance in many cases [10,11,12]. Interestingly, it has been observed that a naïve Bayes classifier might perform well even when dependencies exist among features [12], though correlation does not necessarily imply dependence [13]. The impact of feature correlation on performance depends on both the degree of correlation and the specific measure used to evaluate it. Such a performance-dependent relation can be effectively demonstrated by applying multiple correlation measures (see

Table 1. The table presents relevant meta information of the datasets used in the classification benchmark in the subsequent section. “N” states the number of cases, “DIM” the number of features, Class No. the number of classes, the number of cases per class, and the last four columns denote four different measures of dependency, namely Pearson’s correlation coefficient, Spearman’s Rank Correlation Coefficient, Kendall’s Tau, and Xi correlation coefficient.

	N	DIM	Class No.	Cases per Class	Pearson	Spearman	Kendall	XICOR
Cell populations	5121	14	13	1128, 312, 829, 525, 768, 122, 76, 135, 283, 630, 229, 31, 53	0–0.99	0–0.98	0–0.9	0–0.85
CoverType	581,012	55	7	211,840, 283,301, 35,754, 2747, 9493, 17,367, 20,510	0–0.79	0–0.82	0–0.59	0–0.5
Crabs (Sex)	200	5	2	100, 100	0	0–0.07	0–0.03	0.01–0.24
Crabs (SP)	200	5	2	100, 100	0	0–0.07	0–0.03	0.01–0.24
Dermatology	358	34	6	111, 60, 71, 48, 48, 20	0–0.94	0–0.98	0–0.94	0–0.85
Iris	150	4	3	50, 50, 50	0.12–0.96	0.17–0.94	0.08–0.81	0.08–0.72
LetterRecognition	20,000	16	26	796, 755, 805, 783, 773, 748, 766, 789, 747, 792, 787, 753, 758, 775, 736, 734, 752, 761, 803, 768, 764, 786, 783, 813, 739, 734	0–0.85	0–0.87	0–0.79	0–0.61
MiceProtein	1080	77	8	150, 150, 135, 135, 135, 135, 105, 135	0–1	0–1	0–1	0–0.99
Penguins	344	4	3	152, 68, 124	0	0–0.19	0–0.12	0–0.25
Satellite	6435	36	6	1533, 703, 1358, 626, 707, 1508	0–0.96	0–0.96	0.02–0.85	0.02–0.76
Spam	4601	57	2	2788, 1813	0–1	0–0.94	0–0.94	0–0.93
Swiss	200	6	2	100, 100	0.06–0.74	0.05–0.75	0.03–0.59	0.01–0.43
Wine	178	13	3	59, 71, 48	0–0.86	0.01–0.88	0.01–0.7	0–0.6
WCBCD	569	30	2	212, 357	0–1	0–1	0–0.99	0–0.97

). Likewise, the choice of class assignments for cases within a dataset also influences performance, which can be illustrated using a correlated dataset evaluated on two different classifications.

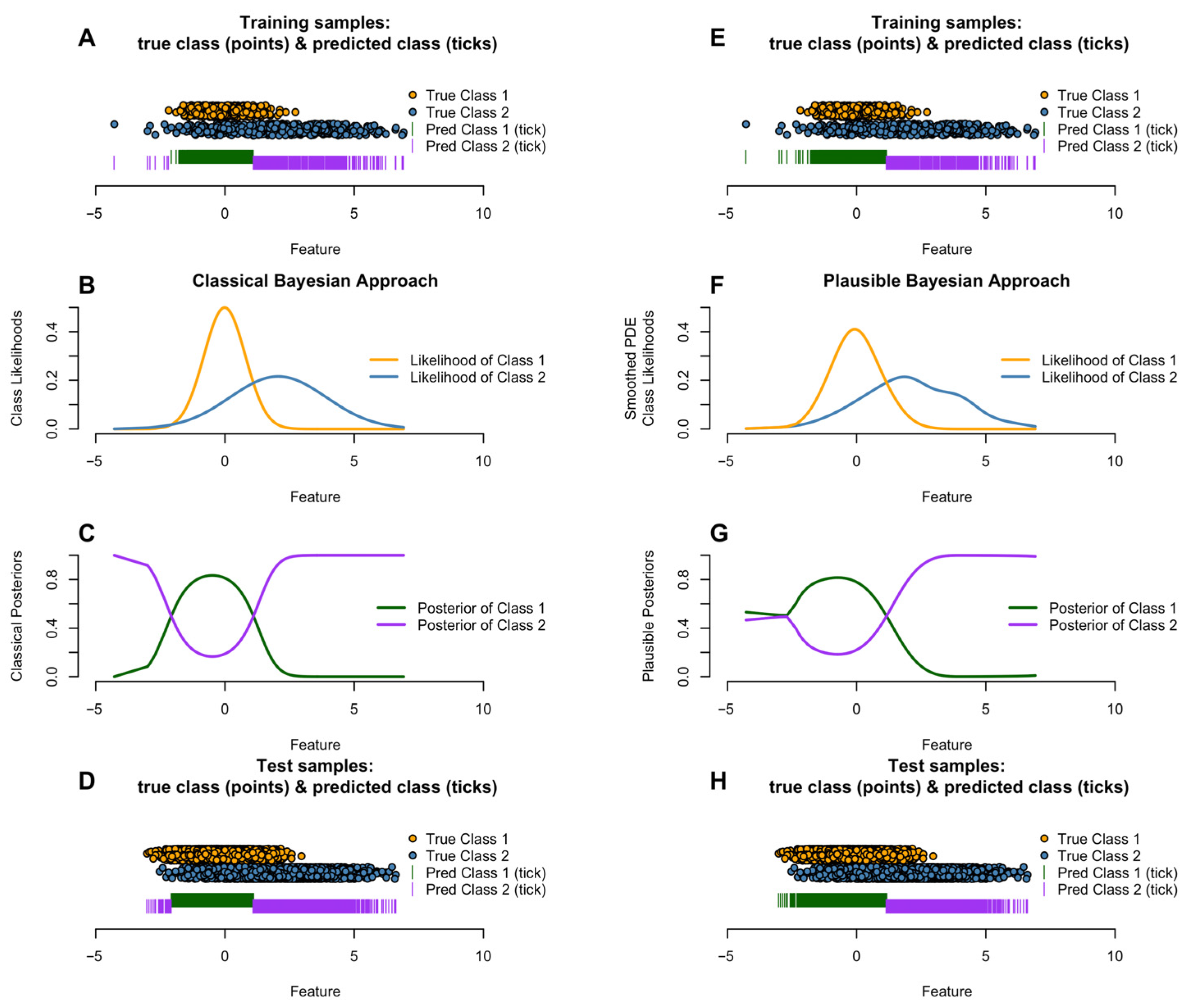
A pitfall in Bayesian theory occurs if observations with low evidence are assigned to a class with a higher likelihood than another, without considering that the probabilities in a probability density with higher variance decay more slowly than in one with lower variance, creating a situation wherein a class assignment chooses a distant class with high variance over a closer class with smaller variance [14]. An example of this would be the size of humans according to gender, where the female (Gaussian) distribution has higher variance than the male (Gaussian) distribution, and the female mean is left of that of males. In that case, the classical Bayes theorem would assign a giant’s size to the class of females, since the likelihood of the males’ distribution would decay faster than that of the females. Instead, the closest mode could be chosen if facing observations with low evidence (the giant size). As a consequence, the non-interpretable choice is to classify all giants as female. Figure 1 outlines this situation for univariate on the left side and sketches the influence of the flexible approach of smoothed Pareto density estimation (PDE) in combination with plausibility correction.

We are proposing a new methodology for the naïve Bayes classifier, overcoming these challenges and improving performance. Our approach does not make any prior assumption about density distribution, creating an algorithm free of assumptions about the data distribution. Furthermore, we dispose of any parameters to be optimized [15]. We use a model of density estimation based on information theory defined by a data-driven kernel radius without intrinsic assumptions about the data, which empirically outperforms typical density estimation approaches [16]. The main contributions of our work are as follows:

• Solution to the above-mentioned pitfall of the Bayes theorem within a Naïve Bayes classifier framework.
• Empirical benchmark showing a robust classification performance of the plausible naïve Bayes classifier using the Pareto Density Estimation (PDE).
• Visualization of class-conditional likelihoods and posteriors to support model interpretability.

The aim of our work is to provide a classifier that can serve as a baseline. Hence, we will show that the performance of naïve Bayes is hard to associate with dependency measures, and that the design decisions are fluid across the degree of correlation and the choice of the correlation measure. We developed an open-access R package (0.2.8) on CRAN https://CRAN.R-project.org/package=PDEnaiveBayes, accessed on 17 November 2025).

2. Materials and Methods

Let a classification $G=C_1\cup \dots \cup C_k$ be a partition of a Dataset D consisting of N = |D| data points into k∈ℕ non-empty, disjoint subsets (classes) [17]. Each class $C_i\subset D$ contains a subset of datapoints $\left\{x_1,..,x_l\right\},$ and each datapoint is assigned is a class label $c_i$∈{1,…,k} via the hypothesis function ℎ: D→{1,…,k}. The task of a classifier is to learn the mapping function h given training data and labels $c_i$.

2.1. Bayes Classification

Assume a set of continuous input variables ${X=\{\stackrel{⃑}{x}}_1,\dots ,{\stackrel{⃑}{x}}_n\}$, with vector $\stackrel{⃑}{x}\in {\mathbb{R}}^d$. In Bayesian classification, the prior is the initial belief (“knowledge”) about class membership.

The Bayesian classifier picks the class whose posterior $p(C_i |\stackrel{⃑}{x})$ has the highest probability

$$p(C_i |\stackrel{⃑}{x})>p(C_j \left|\stackrel{⃑}{x}\right)\forall j \ne i$$

(1)

The posterior probability captures what is known about $C_i$, now that we have incorporated $\stackrel{⃑}{x}$. The posterior probability is obtained with the Bayes Theorem

$$p\left(C_i|\stackrel{⃑}{x}\right)={\displaystyle \frac{p\left(\stackrel{⃑}{x}|C_i\right)p\left(C_i\right)}{{\sum }_{i=1}^{k}p\left(\stackrel{⃑}{x}|C_i\right)p\left(C_i\right)}}$$

(2)

Here $p\left(\stackrel{⃑}{x}|C_i\right)$ is the conditional probability of $\stackrel{⃑}{x}$ given class $C_i$ called class likelihood and the denominator is the evidence. Let H be the hypothesis space and $h_i$ being a MAP hypothesis, $D\subset {\mathbb{R}}^d$ the (not necessarily i.i.d.) data set. Let $H=\{h_1,\dots ,h_M\}$ be the hypothesis space with $h_i$ being a MAP hypothesis, $D\subset {\mathbb{R}}^d$ the (not necessarily i.i.d.) data set and let $f: D->G$ be a classifier that is a function. a Bayes optimal classifier [18] is defined by

$${\mathrm{c}}_{\mathrm{j}}={\mathrm{f}}_{opt}({\stackrel{⃑}{\mathrm{x}}}_{\mathrm{j}})=\underset{C_i}{\mathrm{argmax}}{\sum }_{h_i\in H}p\left(C_i\left|h_i\right({\stackrel{⃑}{\mathrm{x}}}_{\mathrm{j}})\right)\times p\left(h_i\left({\stackrel{⃑}{\mathrm{x}}}_{\mathrm{j}}\right)|D\right)$$

(3)

Equation (3) yields the optimal posterior probability to classify a data point in the sense that it minimizes the average probability error [6].

The general approach to Bayesian modeling is to set up the full probability model, i.e., the joint distribution of all entities in accordance with all that is known about the problem [19]. In practice, given sufficient knowledge about the problem, distributions can be assumed for the $\stackrel{⃑}{x}$ and priors with hyperparameters θ that are estimated.

For the goal of this work, of using a Bayesian classifier to measure a baseline of performance, we make the assumption that the classification of a data point can be computed by the marginal class likelihoods $p_l$ with

$${\mathrm{c}}_{\mathrm{j}}=\underset{C_i}{\mathrm{argmax}} p(C_i){\prod }_{l=1}^d{p}_l\left(x_l|C_i\right)$$

(4)

which is called the naive assumption because it assumes i.d.d. given the classification set G. In some domains, the performance of a naive Bayes classifier has been shown to be comparable to neural networks and decision trees [18]. We will show in the results that for typical datasets, even if this assumption does not hold true, an acceptable baseline performance can be computed.

Our objective is to exploit the empirical information in the training set to derive, in a fully data-driven manner and under as few assumptions as possible, an estimate of each feature’s distribution within every class $C_i$, and then to evaluate classifier performance on unseen test samples. To this end, we adopt a frequentist strategy: we estimate the class-conditional densities directly from the observed data, and we compute the class priors as the relative frequencies of each $C_i$ in the training sample—assuming that the sample faithfully represents the underlying population. Because our decision rule is given by Equation (4), which compares unnormalized scores across classes, the global evidence term (the denominator in Bayes’ theorem) may be treated as a constant and hence omitted.

The challenge is to estimate the likelihood $p\left(\stackrel{⃑}{x}\right|C_i)$, given the samples of the training data. However, by using the naive assumption, the challenge of estimating the $d$-dimensional density is simplified to estimating $d$ one-dimensional densities. In prior works, the first naive Bayes classifier using density estimation was introduced as flexible Bayes [8]. This work improves significantly on the task of parameter-free univariate density estimation without making implicit assumptions about the data (c.f. Ref. [16]).

2.2. Density Estimation

The task of density estimation can be achieved in two general ways. First, through parametric statistics, meaning the fitting of parametrized functions as a superposition, where the fitting can be performed according to some quality measure or some sort of statistical testing. The drawback here is the rich possibility of available assumptions. A default approach could be the use of Gaussian distributions fitted to the data [20]. Second, nonparametric statistics, meaning local parametrized approximations using neighboring data around each available data point. It varies in its use of fixed or variable kernels (global or local estimated radius). The drawback of this approach is the complexity of tuning bandwidths for optimal kernel estimation, which is a computationally hard task [21]. A default approach to solve this problem can be a Gaussian kernel, where the bandwidth is selected according to Silverman’s rule of thumb [5].

In this work, we want to solve the density estimation with the data-driven approach called Pareto Density Estimation (PDE), taken from [15]. In this way, any prior model assumption is dropped. The PDE is a nonparametric estimation method with a variable kernel radius. For each available datapoint in the dataset, the PDE estimates a radius to estimate the density at this point. It uses a rule from information theory: The PDE maximizes the information content (reward) while minimizing the hypersphere radius (effort). Since this rule is historically known as the Pareto rule (or 80-20-rule, reward/effort-trade-off), the method is called the Pareto Density Estimation.

2.3. Pareto Density Estimation

Let a subset $S\subset D$ of data points have a relative size of $\tilde{p} ={\displaystyle \frac{\left|S\right|}{\left|D\right|}}$. If there is an equal probability that an arbitrary point x is observed, then its content is $I\left(\tilde{p}\right)=-\tilde{p} ln(\tilde{p} )$. The optimal set size is the Euclidean distance of S from the ideal point, which is the empty set with 100% information [15]. The unrealized potential is $URP\left(S\right)= \sqrt{{\tilde{p} }^2+{(1+\tilde{p} ln(\tilde{p} \left)\right)}^2}$. Minimizing the $URP\left(S\right)$ yields the optimal set size $\widetilde{p_u}=20.13\%$. This set retrieves 88% of the maximum information [15]. For the purpose of univariate density estimation, computation of the univariate Euclidean distance is required. Under the MMI assumption, the squared Euclidean distances are χ-quadrat-distributed [22] leading to

$$R={\displaystyle \frac{1}{2}}cd\left({\chi }_d^2\right)\left(\widetilde{p_u} \right)$$

(5)

where $cd\left({\chi }_d^2\right)\left(\widetilde{p_u}\right)$ is the Chi-square cumulative distribution function for d degrees of freedom [15]. The pareto Radius is approximated by $R\approx {\tilde{p}}_{18\%}$ for $d=1$.

The PDE is an adaptive technique for estimating the density at a datapoint following the Pareto rule (80-20-rule). The PDE maximizes the information content using a minimum neighborhood size. It is well-suited to estimating univariate feature distributions from sufficiently large samples and to highlighting non-normal characteristics (multimodality, skew, clipped ranges) that standard, default-parameter density estimators often miss. An empirical study, Ref. [16] demonstrated that PDE visualizations (mirrored-density plots, short MD plots) more faithfully revealed fine-scale distributional features than standard visualization defaults (histograms, violin plots, and bean plots) when evaluated across multiple density estimation approaches. Accordingly, PDE frequently yields superior empirical performance relative to commonly used, default-parameter density estimators [16].

Given the Pareto radius R, the raw PDE can be estimated as a discrete function solely at given kernel points $\widehat{x}$ with

$$f_{\widehat{x}}={\displaystyle \frac{1}{A}}{\sum }_{x_i }1\left\{\mid x_i-\widehat{x}\mid \le R\right\}$$

(6)

where 1 is an indicator function that is 1 if the condition holds and 0 otherwise, A normalizes $\sum f_{\widehat{x}}\Delta \widehat{x}=1$, and $f_{\widehat{x}}$ a quantized function that is proportional to the number of samples falling within the interval [$\widehat{x}$−R, $\widehat{x}$+R].

For the mirrored-density (MD) plots used in [16], we previously applied piecewise-linear interpolation of the discrete PDE $f_{\widehat{x}}$ to fill gaps between kernel grid points and obtain a continuous visual approximation of a feature’s pdf $f\left(x\right)$. While linear interpolation produces a visually faithful representation and is adequate for exploratory plots, as it preserves continuity and is trivial to compute, it inherits the small-scale irregularities of the underlying discrete PDE estimate. If linearly interpolated densities are used directly as class-conditional likelihoods in Bayes’ theorem, their high-frequency noise propagates into the posteriors and can produce unstable or incorrect classifications.

Accordingly, in this work, we proceed as follows. After obtaining the raw and discrete conditional PDE $f_{\widehat{x}|C_i}^l$, we replace linear interpolation with several smoothing steps in the next section that produce a class likelihood $p_l\left(x^l|C_i\right),$ which (i) preserves the genuine distributional structure (modes, skewness, tails) and (ii) suppresses spurious high-frequency fluctuations that would destabilize posterior estimates.

2.4. Smoothed Pareto Density Estimation

Although the PDE of class likelihoods captures the overall shape of the distribution, it can be somewhat rough or piecewise constant due to its uniform kernel and finite sampling. This is disadvantageous, as irregular or noisy estimates yield fluctuating posteriors and unstable decisions. Therefore, smoothing the class likelihoods acts as a form of regularization: it suppresses sample-level noise and prevents high-frequency fluctuations like erratic spikes or dips in the likelihoods that lead to brittle posterior assignments. Balancing the fidelity to the PDE’s “true” features with the removal of artificial high-frequency components results in more accurate approximations of the true underlying distributions, leading to more reliable posterior estimates because they are less influenced by random sample noise.

For smoothing, we exploit the insight that the kernel estimate is a convolution of the data with the kernel by using fast Fourier transforms [5] p. 61. To produce a smooth, continuous density estimate, we convolve the PDE output with a Gaussian kernel using the Pareto radius as the bandwidth. Hence, the Gaussian smoothing kernel is defined as

$$K\left(x\right)={\displaystyle \frac{1}{R\sqrt{2\pi }}}\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{x^2}{2R^2}})$$

(7)

where R is the Pareto radius. We use the Fast Fourier Transform (FFT), leveraging the convolution theorem, in order to implement this convolution efficiently, as follows.

First, we evaluate the Gaussian kernel on the same grid ${\left\{{\widehat{x}}_j\right\}}_{j=1}^m$ as the PDE in which $m$ is the number of grid points. Let $\Delta \widehat{x}$ be the grid spacing, then the Gaussian kernel vector

$$k_j=\Delta \widehat{x}\times K\left(x_j\right)$$

(8)

yields a normalized kernel vector aligned with the PDE grid, and we use the mean of adjacent differences to avoid numerical instabilities in spacing.

To perform a linear convolution without wrap-around artifacts, we zero-pad both the density $f_{\widehat{x}}$ and kernel vectors $k_j$ before FFT [23] (part1, p. 260ff). We choose the padding length $L\ge 2^{{\log }_2(2m-1)}$ as the next power of two. This length ensures that circular convolution via FFT corresponds to the linear convolution of the original sequences, and using a power of two leverages FFT efficiency [24]. We create padded vectors $f_{pad}$ (the $f_{\widehat{x}}$ with zero-pad) and $k_{pad}$ ($k_j$ with zeros zero-pad), each of length L. This padding avoids overlap of the signal with itself during convolution.

Next, we compute the FFT of both padded vectors, multiply them element-wise in the frequency domain, and then apply the inverse FFT. By the convolution theorem, the inverse FFT of the product

$$f_{pad}\cdot k_{pad}=IFT\left(FT\right(f_{pad})\cdot FT(k_{pad}\left)\right)/L$$

(9)

yields the linear convolution on the padded length. We divide by L in Equation (9) when taking the inverse FFT, as per the normalization convention.

The central $m$ elements correspond to the convolved density over the original grid. This middle segment is the smoothed density vector ${\tilde{f}}_{\widehat{x}}$, aligned with the original kernel grid. The approach is motivated by the idea from [25].

Finally, the montone Hermite spline approximation of ${\tilde{f}}_{\widehat{x}}$ [26] yields the likelihood function $p\left(x^l\right|C_i)$. and allows for a functional, fast computation of new points.

In sum, the empirical class PDE $f_{\widehat{x}}^l$ in dimension $l$ can be rough due to the data being noisy. If used for a visualization task, the roughness would be inconsequential [16]. In order not to influence the posteriors through data noise, we propose as a solution a combination of filtering by convolution (c.f. Ref. [27]) and monotonous spline approximation (c.f. Ref. [28]) yielding $p_l\left(x^l\right|C_i)$.

2.5. Plausible Naïve Bayes Classification

Ref. [14] showed that misclassification can occur when only low evidence is used in the Bayes’ theorem, i.e., the cases lie below a certain threshold ε. They define cases below ε as uncertain and provide two solutions [14]: reasonable Bayes (i.e., suspending a decision) and plausible Bayes (a correction of Equation (4)). To derive ε, they propose the use of the computed ABC analysis [29]. The algorithm allows users to compute precise thresholds that partition a dataset into interpretable subsets.

Closely related to the Lorenz curve, the ABC curve graphically represents the cumulative distribution function. Using this curve, the algorithm determines optimal cutoffs by leveraging the distributional properties of the data. Positive-valued data are divided into three disjoint subsets: A (the most profitable or largest values, representing the ‘important few’), B (values where yield matches effort), and C (the least profitable or smallest values, representing the ‘trivial many’).

Let $\{x_1,\dots x_n\}$ be a set of n observations, which, for the purpose of defining the plausible Naïve Bayes likelihoods in dimension $l$, are indexed in non-decreasing order in their respective dimensions, i.e., $x_1^l\le ,\dots ,\le x_n^l$. Let $s_i={\sum }_{k=1}^i{x}_k^l$; the $L\left(P\right)$ is defined by [30] as

$$L\left(p_i\right)=\left\{\begin{array}{c}\begin{array}{cc}0& for P_i=0\end{array}\\ \begin{array}{cc}{\displaystyle \frac{s_i}{s_n}}& for p_i={\displaystyle \frac{i}{n}}\end{array}\end{array}\right.$$

(10)

For all other p in [0, 1] with p ≠ pi, L(p) is calculated using a linear, spline, or other suitable interpolation on $L\left(p_i\right)$ [31].

Let L(p) be the Lorenz curve in Equation (11), then the ABC curve is formally defined as

$$ABC\left(p\right)=1-L\left(1-p\right)$$

(11)

Then the break-even point satisfies ${\displaystyle \frac{d\left(ABC\right(p\left)\right)}{d}}{\mid }_{p=B_x}=1$ and the submarginal point $B{C}_p,B{C}_{ABC}$ is located by minimizing the distance from the ABC curve to the maximal-yield point at (1,1) after passing the break-even point with $B{C}_p=\underset{p>B_x}{\mathrm{argmin}}\left[1-ABC\left(p\right)\right]$. The break-even point yields the BC limit, and, hence, the threshold ε with

$$\epsilon =B{C}_{ABC}=ABC\left(B{C}_p\right)$$

(12)

Equation (12) defines the BC Limit.

Inspired by this idea, we reformulate the computation of epsilon from posterior to joint likelihood, as follows. An observation $x$ is considered uncertain in feature $l$ whenever the joint likelihood of every class falls below the confidence threshold ε, i.e.,

$${\Gamma }_{\mathrm{l}}(x^l)={\prod }_{l=1}^k{p}_l\left(x^l|C_i\right)<\varepsilon$$

(13)

where $p_l$ denotes the marginal of the distribution in dimension $l$. We will apply the threshold ε to identify low-evidence regions where the plausibility correction (Equation (15)) may be considered. Such uncertain cases might be classified against human intuition to a class with a probability density center quite far away, despite closer available class centers [14]. Then, a “reasonable” assignment might be to assign the case to the class whose probability centroid is closest, which can be calculated using Voronoi cells for d > 1. For a one-dimensional case, they allow the closest mode to be determined for classification.

We estimate the univariate location of each class’s likelihood mode on a per-feature basis using the half-sample mode [32]. For small sample sizes (n < 100), we use the $L_0$ estimator recommended by [33]. As a safeguard mechanism, estimated modes are only considered for resolving uncertain cases if they are well-separated, i.e., have a distance from each other of at least the 10th percentile within the training data

$$\Delta m_{i,j}=\left|m\left(C_i,x^l\right)-m\left(C_j,x^l\right)\right|>{\tilde{p}}_{10\%}\left(x^l\right), i\ne j,l=1\dots d$$

(14)

This mechanism is motivated by the potential presence of inaccurately estimated modes or overlapping (non-separable) classes.

When the class likelihood $p_l\left(x^l|C_i\right)$ for an observation x is uncertain in feature $l$ (Equation (13) holds true), and there is a class $i$ whose mode is well-separated from the highest-likelihood class (Equation (14)), we perform a conservative, local two-class correction of that feature class likelihoods as follows:

Let $i^{max}=\underset{i}{\mathrm{argmax}} p_l\left(x^l|C_i\right)$ be the index of the uncorrected class likelihood with the largest value and $i^{\prime }$ the index of the class likelihood with the closest mode to $x$ for which Equation (14) holds true for $i=i^{max}$ and $j=i^{\prime }$.

Then we update the two involved class likelihoods by replacing the values of the class likelihood $i^{\prime }$ with the (former) top class likelihood, $i^{max}$. In addition, the operation subtracts δ from the prior top likelihood $i^{max}$ and adds δ to the runner-up, $i^{\prime }$, and the relative advantage of the runner-up versus the former top increases by 2δ, which is sufficient to resolve many marginal posterior ties or implausibilities (as shown in the example in Figure 1) while remaining conservative. All other class likelihoods for this feature remain unchanged in Equation (15):

$$p_{l,corr}\left(x^l|C_i\right)=\left\{\begin{array}{c}\begin{array}{ccc}{p}_l\left(x^l|C_{i^{\prime }}\right)-\delta & \begin{array}{cc} ,{i=i}^{max},& if {\Gamma }_{\mathrm{l}}\left(x^l\right)<\varepsilon \end{array}& \mathrm{a}\mathrm{n}\mathrm{d} \Delta m_{i^{max},i^{\prime }}>{\tilde{p}}_{10\%}\end{array}\\ \begin{array}{ccc}{p}_l\left(x^l|C_{i^{max}}\right)+\delta & ,\begin{array}{cc}i=i^{\prime } ,& if {\Gamma }_{\mathrm{l}}\left(x^l\right)<\varepsilon \end{array}& \mathrm{a}\mathrm{n}\mathrm{d} \Delta m_{i^{max},i^{\prime }}>{\tilde{p}}_{10\%}\end{array}\\ \begin{array}{ccc}{p}_l\left(x^l|C_i\right)& otherwise& \end{array} \end{array}\right.$$

(15)

Equation (4) is then used with the locally corrected class likelihoods $p_{l,corr}\left(x^l|C_i\right)$. Note that as $\delta \to 0$, the correction vanishes and the method reduces to the reasonable-Bayes rule; the transfer introduces a conservative “plausible-Bayes” adjustment, with $\delta$ controlling the strength of the plausibility correction.

2.6. Practical Considerations

In order to avoid numerical overflow, Equation (4), either uncorrected or the with the locally corrected class likelihoods $p_{l,corr}\left(x^l|C_i\right)$ can be computed in log scale

$$c_j=\underset{C_i}{\mathrm{argmax}}\left(\log \left(p\left(C_i\right)\right)+\mathrm{l}\mathrm{o}\mathrm{g}({\sum }_{i=1}^d{p}_l\left(x^l|C_i\right))\right)$$

(16)

to select the label of the class $C_j$ that with the highest probability.

In practice, before this function can be computed, it must be determined if there are enough samples to yield a proper PDE. Based on empirical benchmarks [16], if there are more than 50 samples and at least 12 uniquely defined samples, then $f_{\widehat{x}}^l$ can be estimated, otherwise the estimations might deviate. In case there are too few samples, the density estimation defaults to simple histogram binning with bin width defined by Scott‘s rule [34].

Let $\tau$ be a small constant, then, to ensure numerical stability in Equation 16, the likelihoods $p_l\left(C_i\right)$ are clipped to the range of $[\tau ,1-\tau ]$. The reason is that density after smoothing may result in values slightly below zero due to the convolution (c.f. [5]). In addition, density estimation can have spikes above 1. Moreover, we ensure numerical safety if we clip the corrected likelihoods to be non-negative after applying Equation (15).

There is also a possibility that Equation (4) may not allow a decision as two or more posteriors equal each other after the priors are considered. In such a case, the class assignment is randomly decided.

Equation (15)’s foundation is the assumption that modes can be estimated correctly in the data for each class, which could fail in practice. As a safeguard, we provide the following option for the user. We compute the classification assignments ${\mathrm{C}}_{\mathrm{j},\mathrm{I}}\subset G\left(I\right)$ as defined in Equation (4), transformed according to Equation (16), and likewise without correction ${\mathrm{C}}_{\mathrm{j},\mathrm{I}\mathrm{I}}\subset G\left(II\right)$, using the training data.

Assuming the priors are not excessively imbalanced, we evaluate the Shannon entropy of each classification result ${\mathrm{C}}_{\mathrm{j}}$ and choose the configuration that yields the highest entropy. The Shannon entropy H of $\mathrm{G}$ with priors $p\left(C_j\right)$ for $i=1,\dots ,k$ is defined as

$$H\left(G\right)=-{\displaystyle \frac{1}{Q}}{\sum }_{i=1}^{k}p\left(C_j\right) \mathrm{l}\mathrm{o}\mathrm{g}\left(p\right(C_j\left)\right)$$

(17)

with the normalization factor $Q=-{\displaystyle \frac{1}{k}}\mathrm{l}\mathrm{o}\mathrm{g}({\displaystyle \frac{1}{k}})$.

A higher entropy indicates a potentially more informative classification.

Finally, due to the assumption leading to Equation (4) and subsequent equations, we provide a scalable multicore implementation of the plausible Bayes classifier by computing every feature separately, proceeding as follows: For each feature dimension $l$ we estimate a single Pareto radius $R_l$ independent of class, as defined in Equation (5), rather than separately for each feature–class combination. Empirical evaluations indicate that this approximation is sufficiently accurate for practical applications. For each class $C_i$ in each dimension $l$ we compute the class-wise PDE on an evenly spaced kernel grid ${\left\{\widehat{x_i}\right\}}_i^m$ to compute the raw conditional PDE $f_{\widehat{x}|C_i}^l$ covering the range of the data. Then, we compute the smoothed likelihood functions $p_l\left(x^l\right|C_i)$ per feature dimension $l$ from the discrete conditional PDE $f_{\widehat{x}|C_i}^l$. We call this approach the Plausible Pareto Density Estimation-based flexible Naïve Bayes classifier (PDENB).

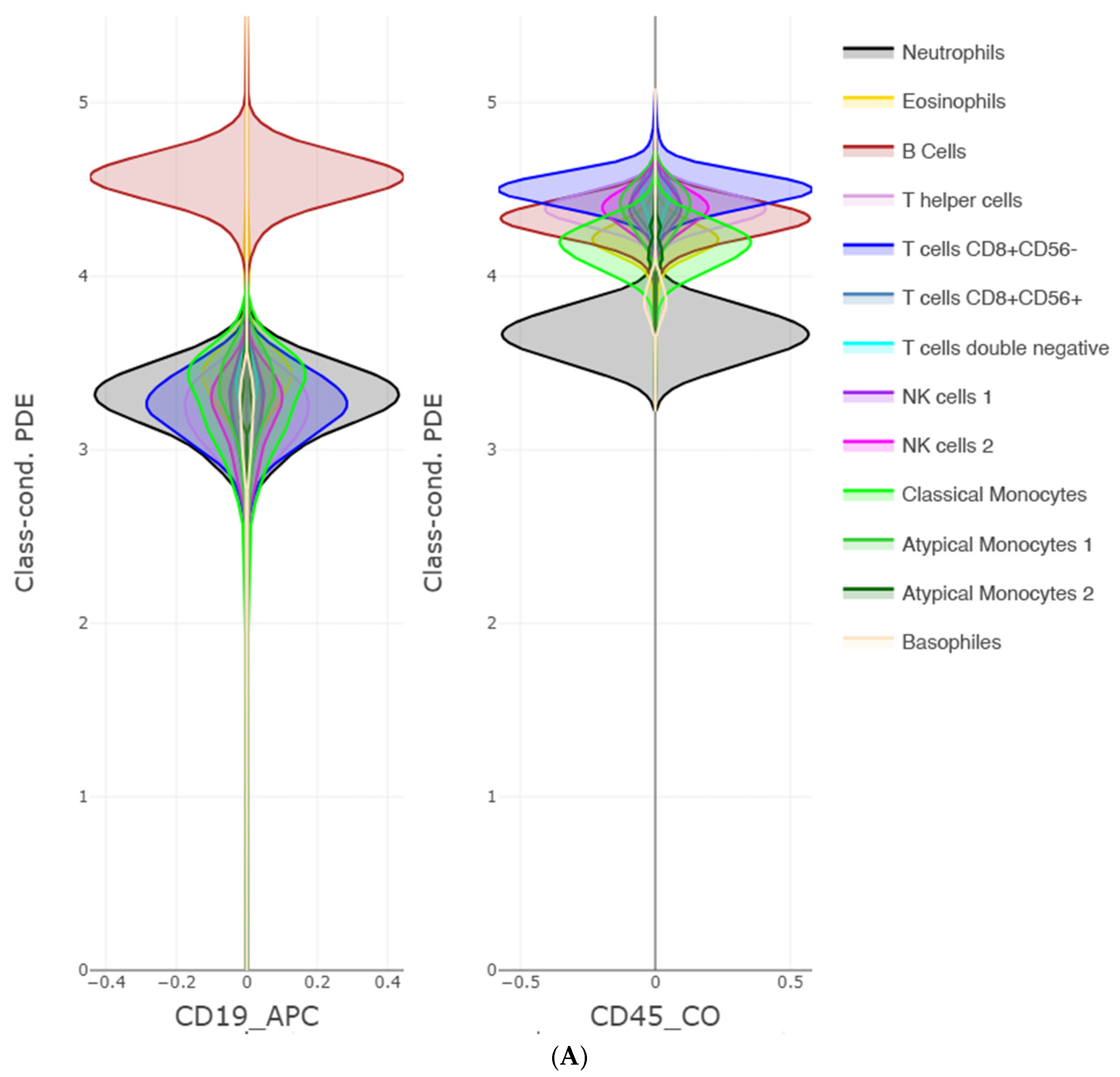
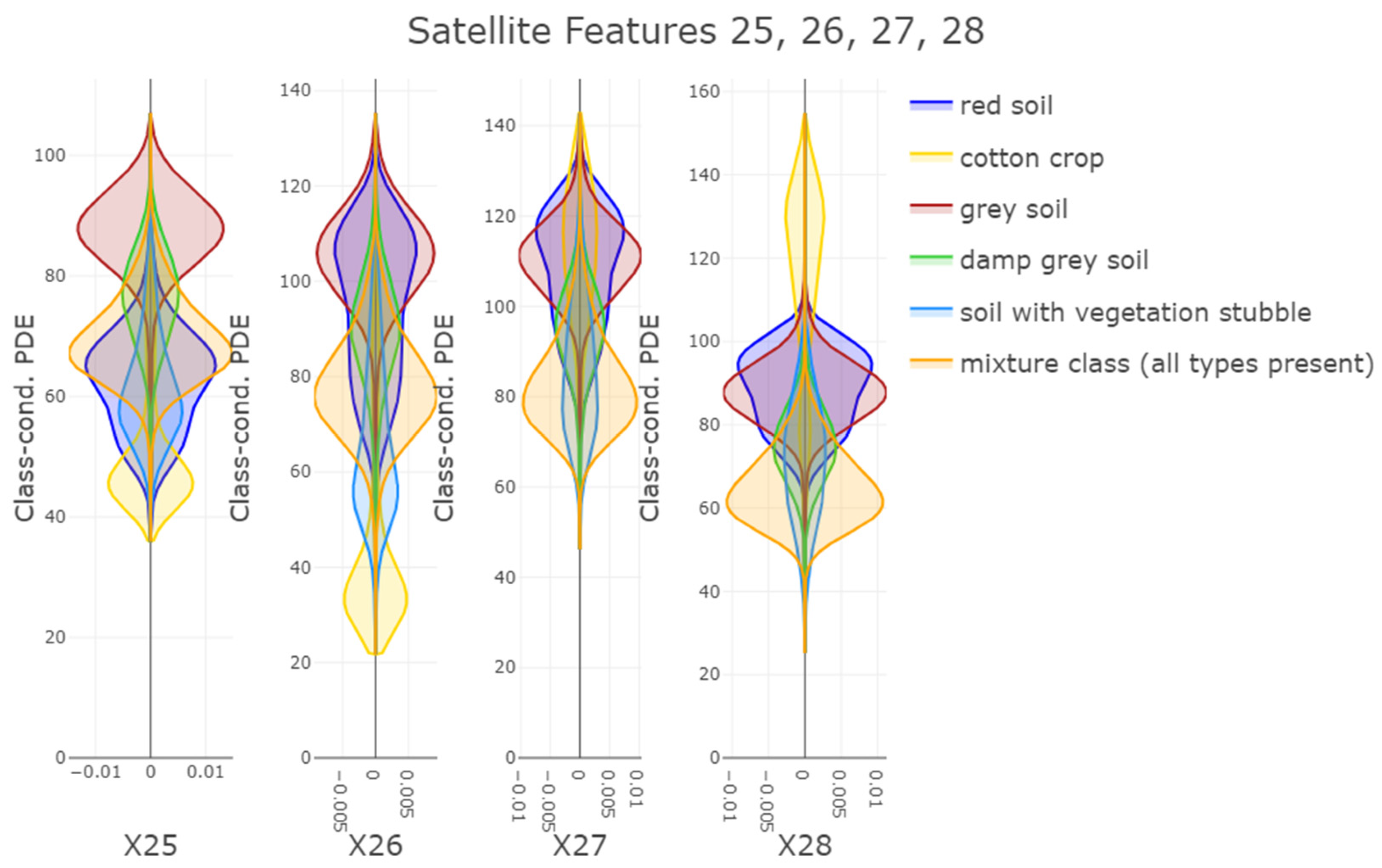
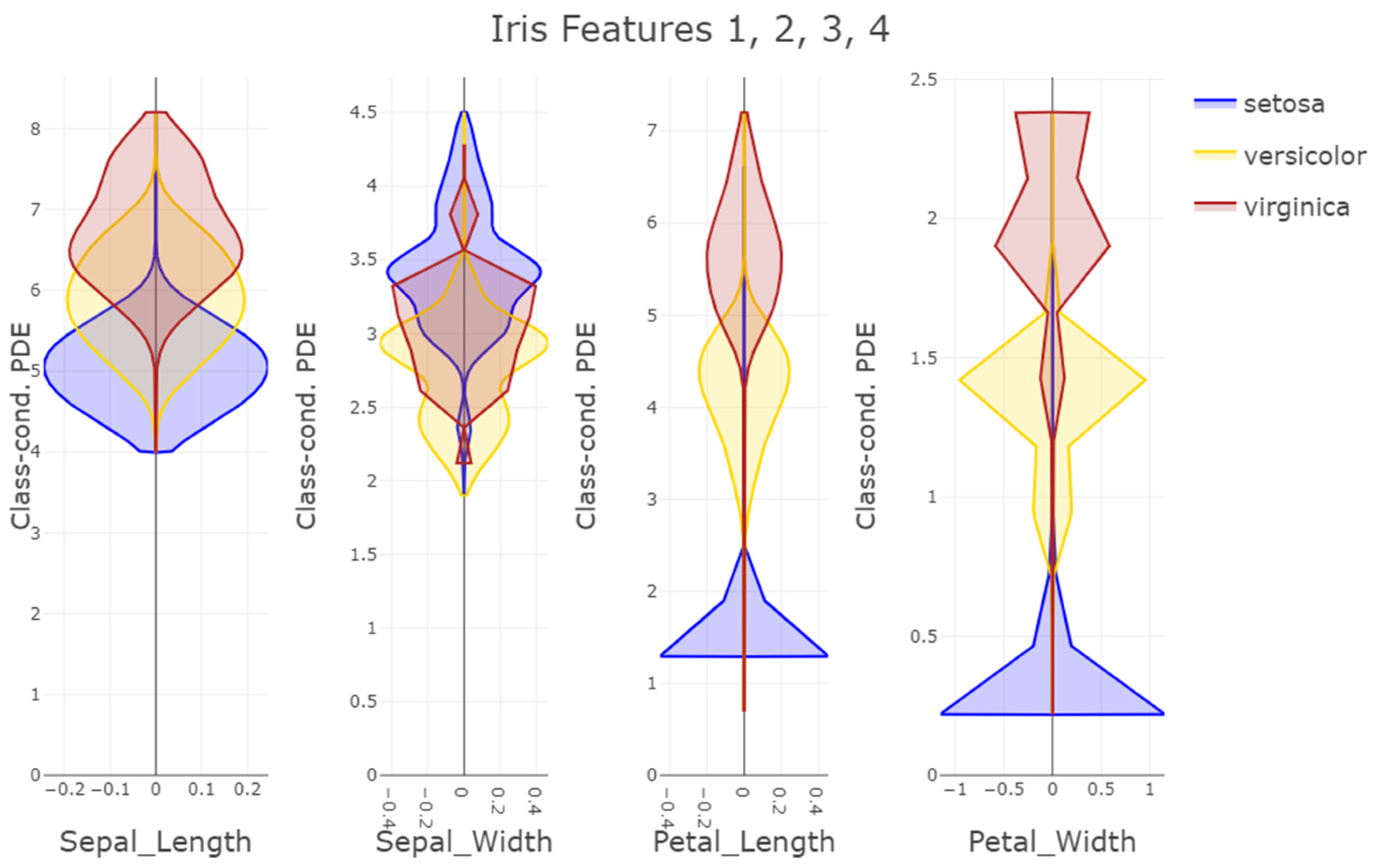
2.7. Interpretability of PDENB

A one-dimensional density estimation is required for the Naïve Bayes Classifier to compute the class-conditional likelihood of a feature as one of three parts of the Bayes theorem, yielding the final Posterior. This class-conditional likelihood allows a two-dimensional visualization as a line plot for a single feature. The plot gives insight into the class-wise distribution of the feature. Scaling the likelihoods with the weight of the prior obtained from the frequentist approach [6] yields correct probabilistic proportions between the class-conditional likelihoods, which can be represented by different colors. Rotating the plots by 90 degrees and mirroring them in a similar way to that used for violin and mirrored density plots [16] allows a lineup of the likelihoods to be created for multiple features at once. Such a visualization allows for interpretation based on the class-wise distribution of features. Most often, the colored class conditional likelihoods are overlapping and non-separable by solely one feature. However, in case of a high performing naïve Bayes classifier, overlaps do not indicate non-separability, but rather, first of all, a class tendency for each feature, and second, the existence of certain combinations and the disqualification of other combinations in question. These visual implications can be the starting point for a domain expert to find relations between features and classes, resulting in explanations.

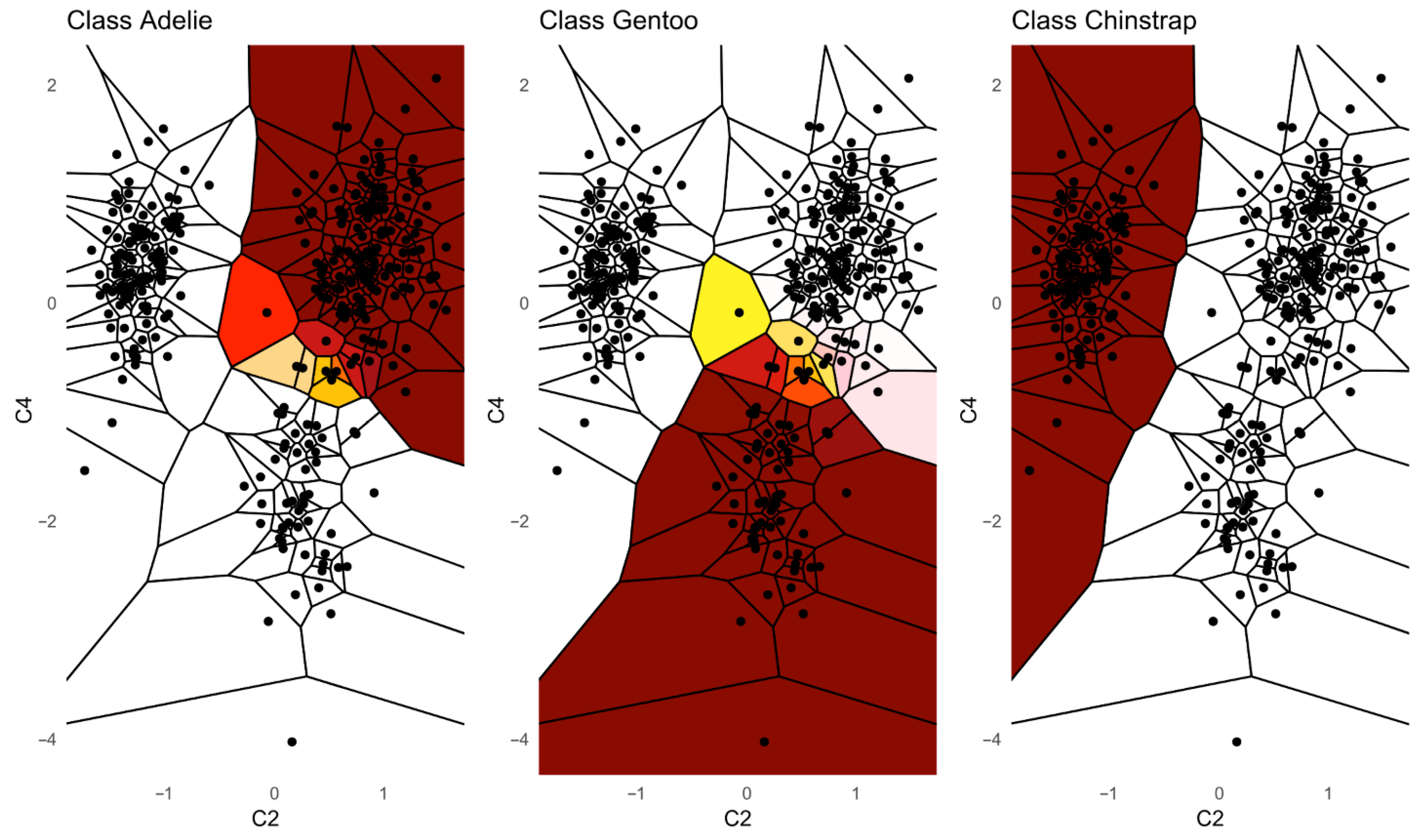
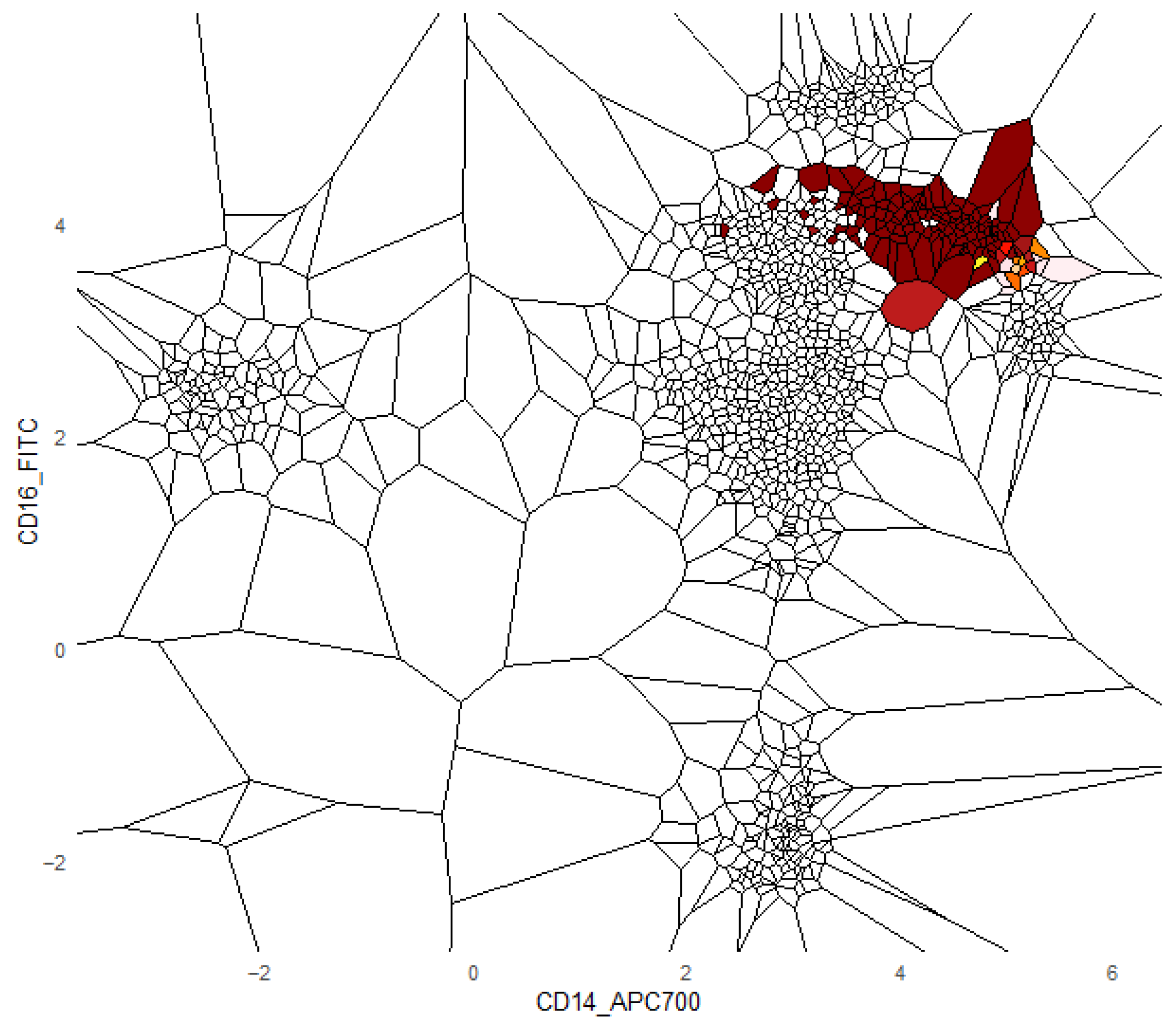
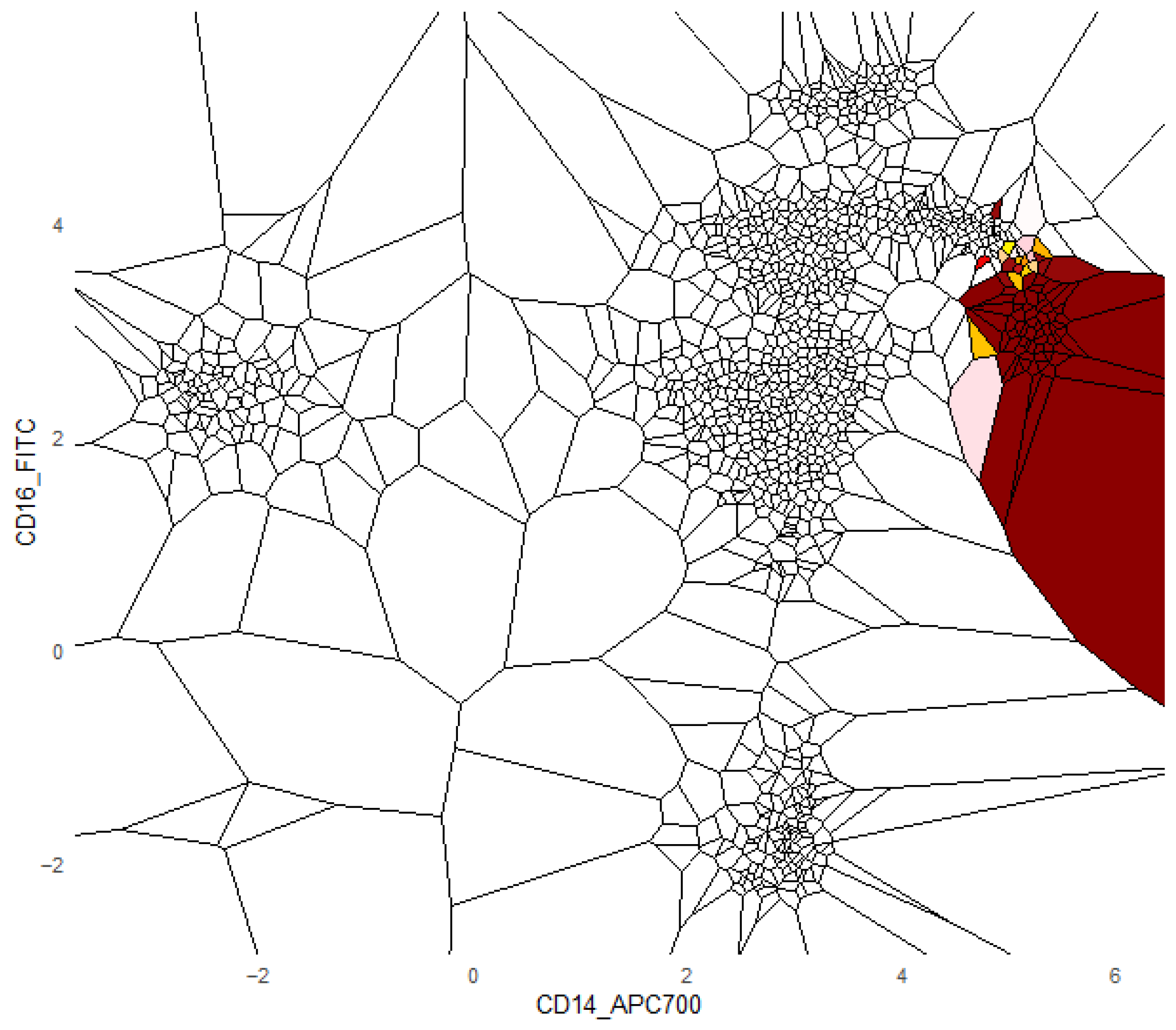
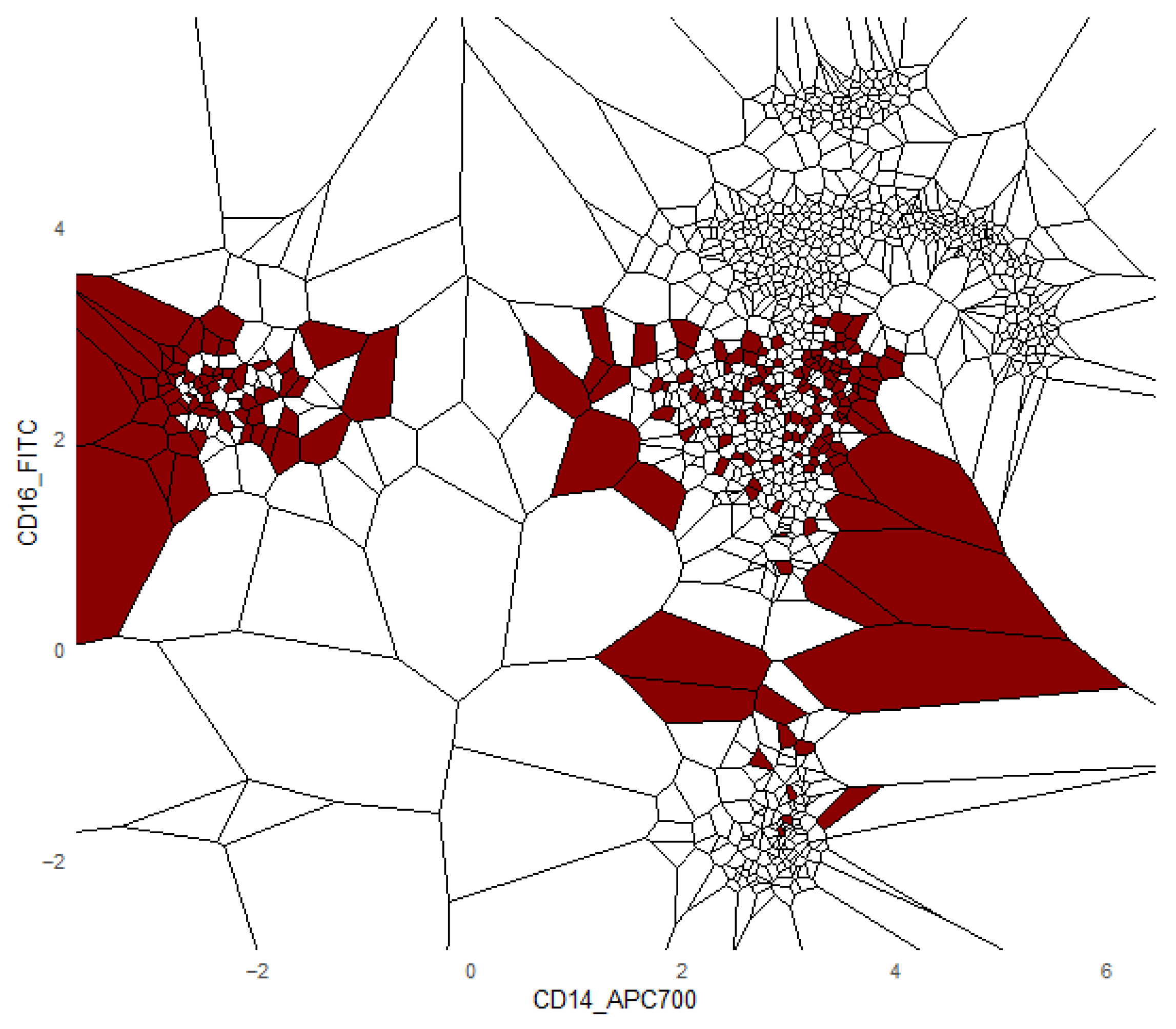
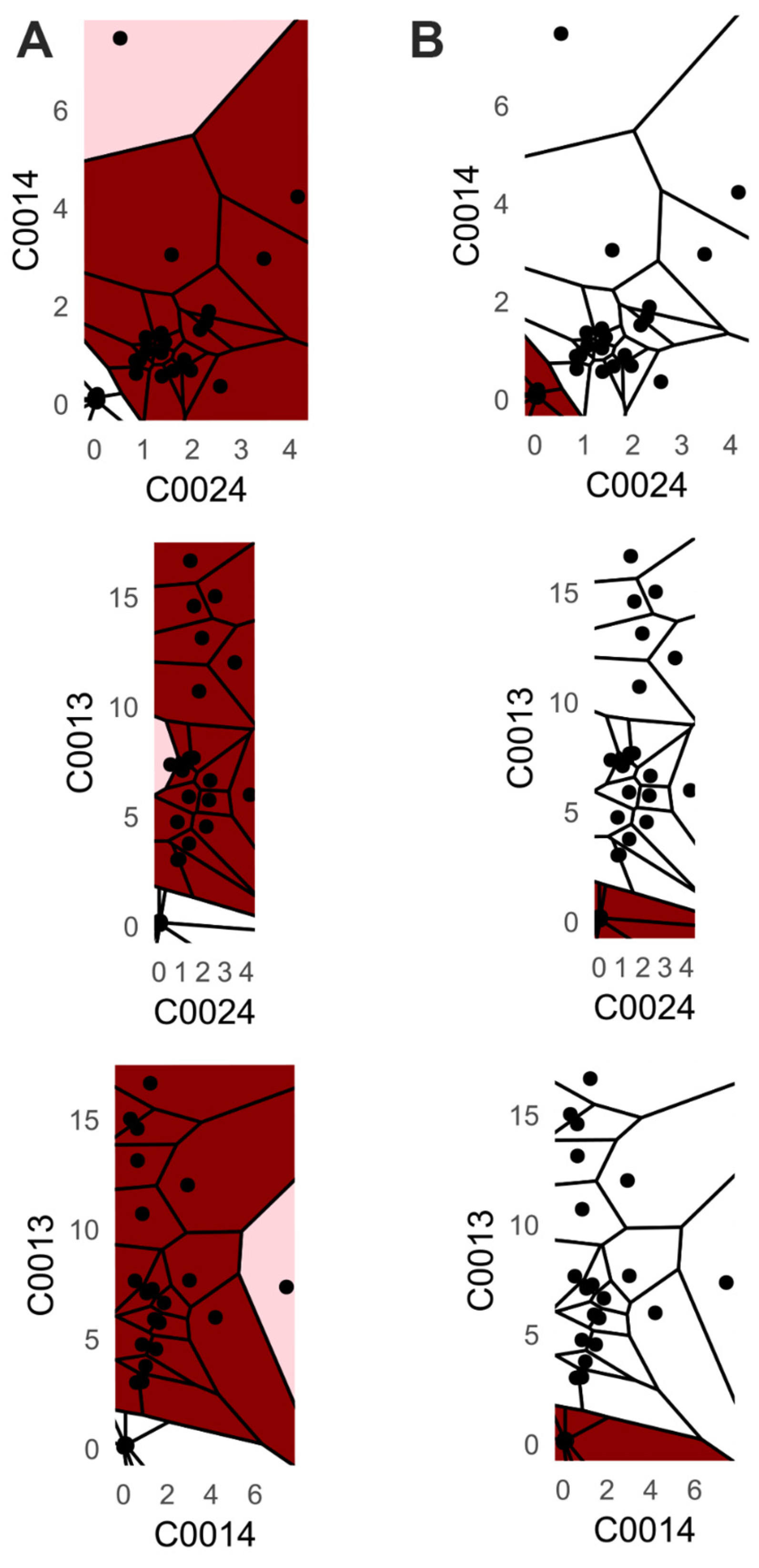
Additionally, we provide a visualization of one class versus all decision boundaries in 2D, as follows. Given a two-dimensional slice $S\subset D\subset {\mathbb{R}}^d$, the Voronoi cell associated with a point g $\in S$ is the region of the plane consisting of all points that are closer to g than to any other point v in the slice, defined by

$$V\left(g\right)=\left\{y\in {\mathbb{R}}^2\right| ‖y-g‖\le ‖y-v‖ \forall g \ne v\}$$

(18)

That is, $V\left(g\right)$ contains all points such that the Euclidean distance from any y to g is less than or equal to the distance to any other v $\in S$. Each Voronoi cell $V\left(g\right)$ is binned according to the binned posterior probability $P\left(C_i|\stackrel{⃑}{x}\right)$, thereby mapping regions of the plane to their inferred class likelihoods by colors. The binning can be either performed in equal sizes, using Scotts rule as bin width [34], or less efficiently, by the DDCAL clustering algorithm [35]. The user can visualize the set of slices of interest. This approach is motivated by human pattern recognition and the subsequent classification of diseases from identified patterns in two-dimensional slices of data [36], which is apparently sufficient for a large variety of multivariate data distributions.

2.8. Benchmark Datasets and Conventional Naïve Bayes Algorithms

For the benchmark we selected 14 datasets: 13 from the UCI repository and a 14th dataset (“Cell populations”) containing manually identified cell populations [37]. Full dataset descriptions of the UCI datasets, attribute definitions, and links to original sources are available on the repository pages for each dataset [38], for example, Iris: https://archive.ics.uci.edu/dataset/53/iris, accessed on the 15 December 2025). The Cell populations dataset is an extended version of the data used by [37]; the set of populations provided here is larger than in that publication because the authors labeled populations at finer granularity. A detailed description of the cell populations dataset is given in [37].

The datasets were preprocessed prior to analysis using the methods of rotation [39,40] taking into consideration Refs. [41,42], as implemented in “ProjectionBasedClustering”, available on CRAN [43]. In it should be noted that although the signed log transformation for better interpretability was applied to the cell populations, no Euclidean optimized variance scaling was used [44]. Thereafter, correlations of features were computed. Important properties, meta information, and correlations of the processed datasets are presented in Table 1. The measure of correlation depends on the choice of algorithm. Here, the Pearson, Spearman’s rank, Kendall’s rank, and the Xi correlation coefficient [45] are summarized using the minimum and maximum values to characterize the correlations of the datasets. The values of the Pearson and Spearman correlation coefficients tend to be higher than the Xi correlation coefficient by around 0.3. Similarly, Kendall’s Tau values tend to be higher than the Xi correlation coefficients, but not as high as the Pearson’s or Spearman’s correlation coefficients. Some important attributes, such as the number of classes, the distribution of cases per class to judge class imbalance, and various dependency measures related to the independent feature assumption of the naïve Bayes classifier, are presented in Table 1.

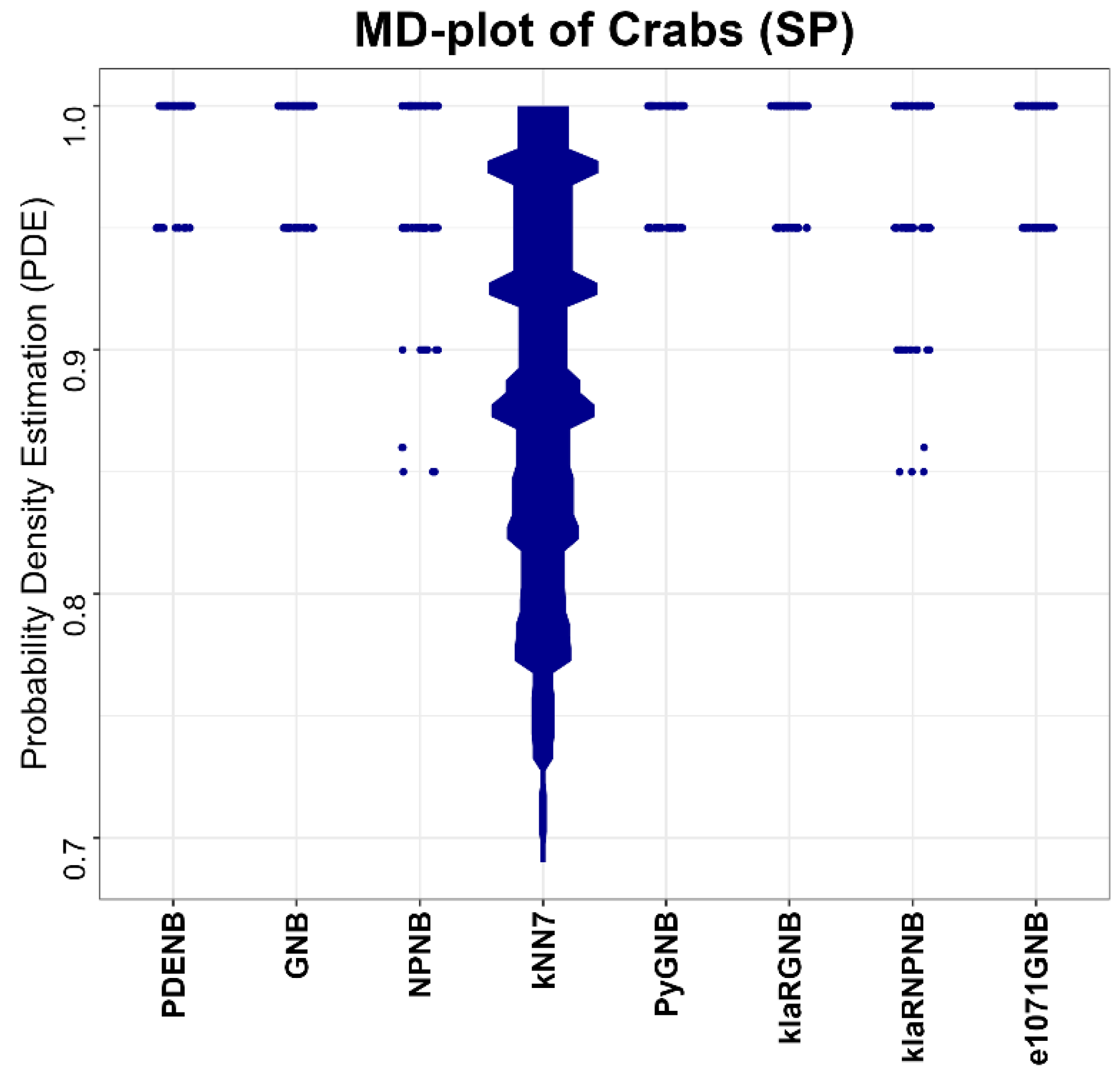
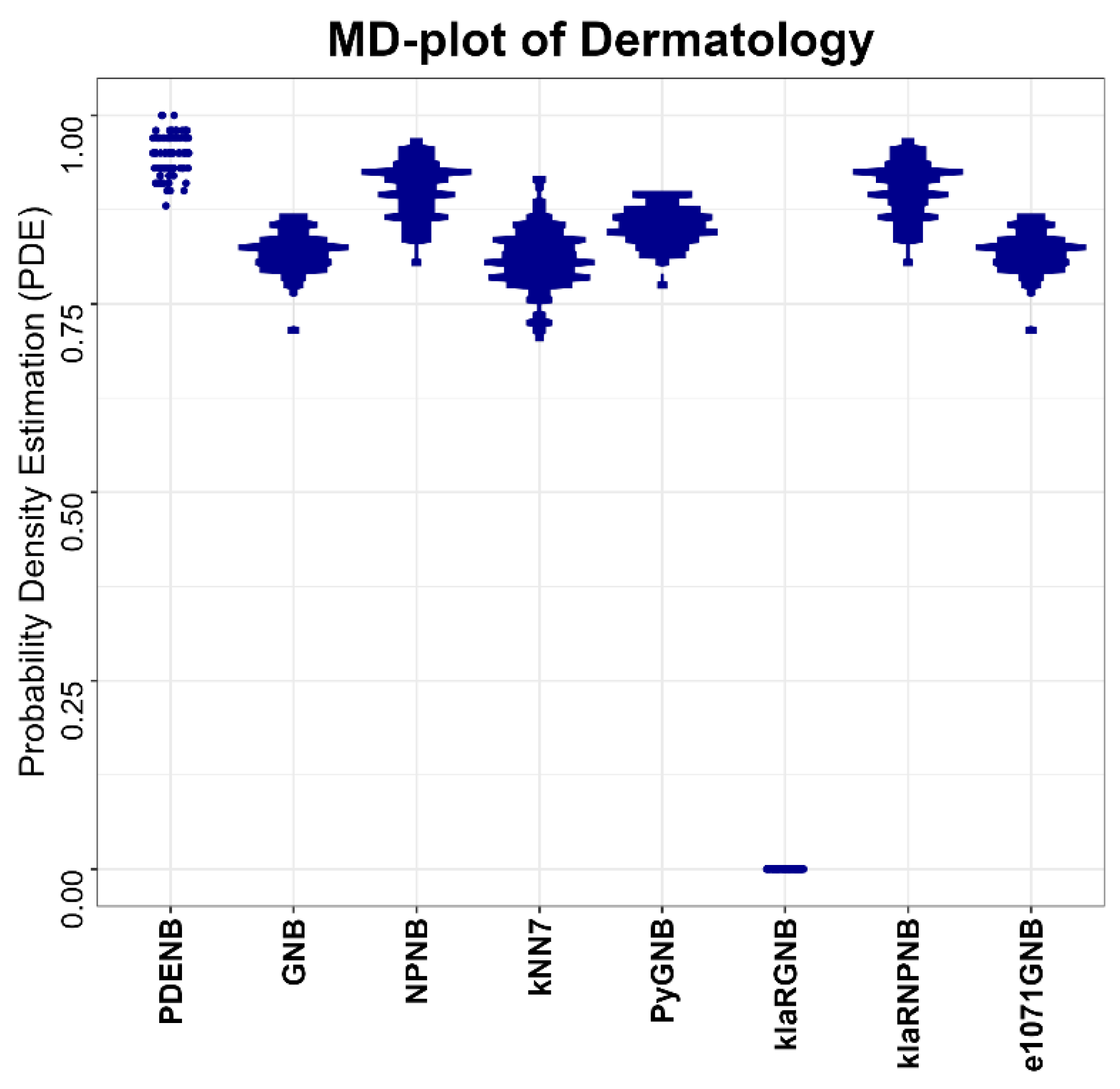
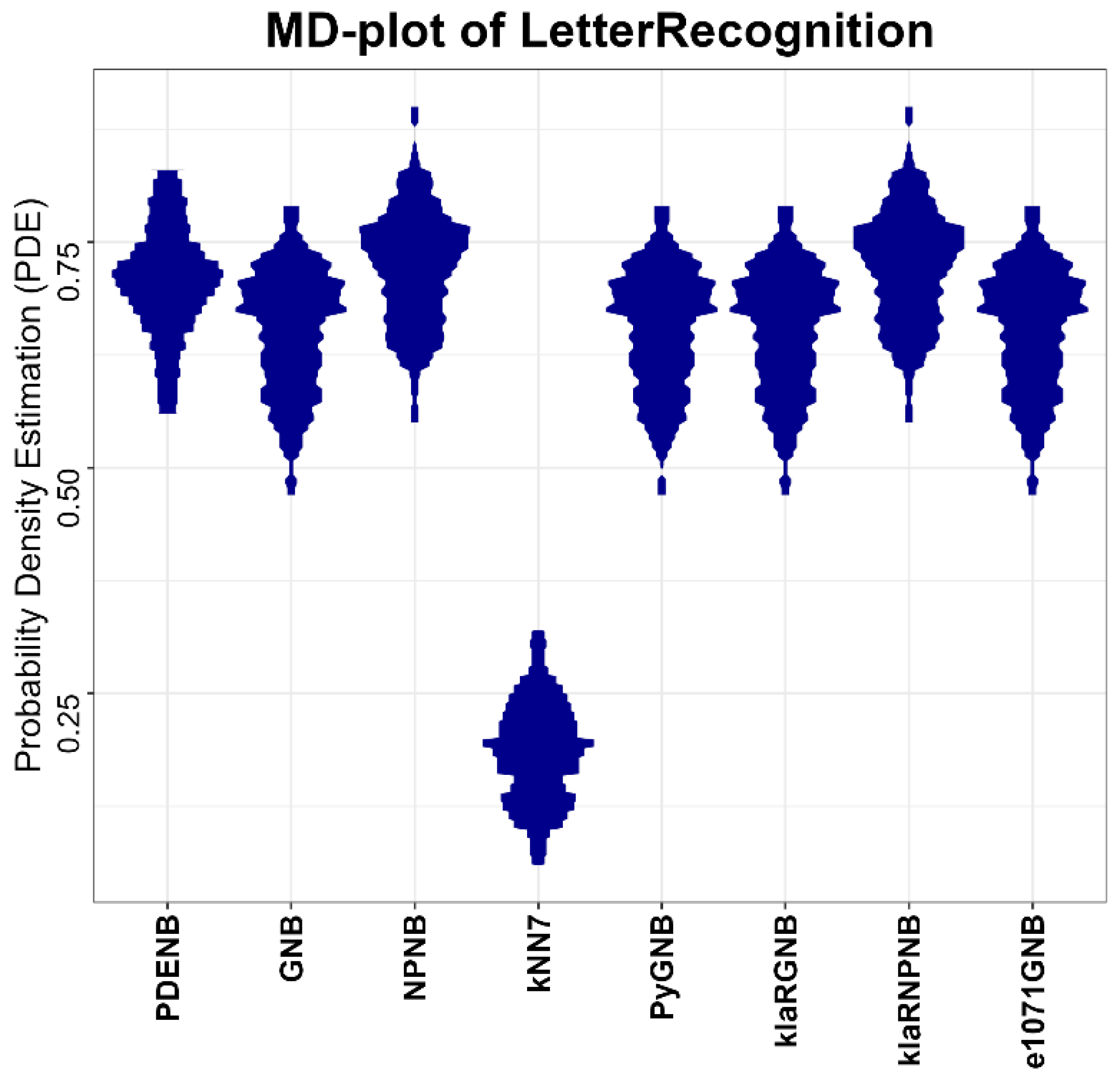
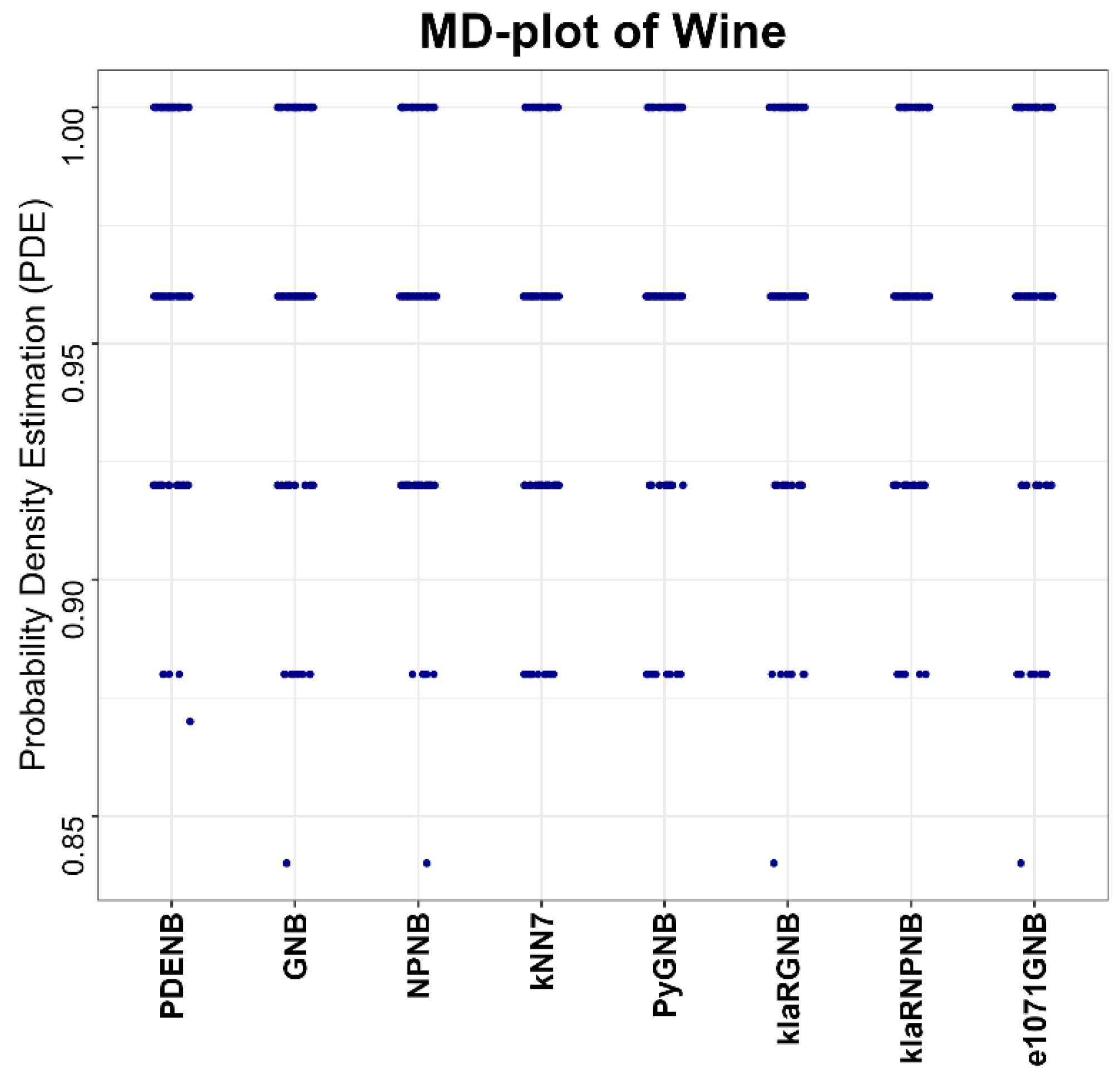
Performance is evaluated for the Plausible Pareto Density Estimation-based flexible Naïve Bayes classifier (PDENB) in comparison to a Gaussian naïve Bayes classifier (GNB) and a nonparametric naïve Bayes classifier (NPNB) from the R package “naivebayes”, available on CRAN [20]); a fast implementation of k-nearest neighbor classifier (kNN as 7NN) from the R package “FNN”, available on CRAN [46]); a Gaussian naïve Bayes from the python package “sklearn” [47] (PyGNB); a Gaussian (klaRGNB) and non-parametric naïve Bayes (klaRNPNB) approach from the R package “klaR”, available on CRAN [48]; and last, but not least, a Gaussian naïve Bayes from the R package “e1071”, available on CRAN [49] (e1071GNB). The algorithms for the naïve Bayes methods were applied in their default settings differencing between “Gaussian” and “nonparametric” versions, while the parameter k for the kNN classifier is set to 7.

3. Results

The first subsection presents the classification performance in detail. Section 2 presents visualizations that support model interpretability, and Section 3 provides an application.

3.1. Classification Performance

Table 1 presents the benchmark across 14 datasets. Following the work of [50,51], small datasets with up to 10.000 samples are evaluated with 100-times repeated hold-out set using the 80–20 rule. Datasets with higher sample sizes are evaluated once with a hold-out set (80–20 rule) and 100 mean samples are obtained with a resampling technique. The performance in each trial is evaluated with the Matthews correlation coefficient (MCC) [52,53]. The results are summarized in tables by means of the 100 trials evaluated in

Table 2. The table presents the final results of the classifier performance evaluation. A total of 14 datasets were evaluated (rows) and 8 classification algorithms were applied. Performance was evaluated with the Matthews Correlation Coefficient (MCC) and the mean (denoted as $\mu$) + AMAD (Adjust Mean Absolute Deviation) (denoted as $\sigma$) are used to determine the overall performance. NA values represent the impossibility of computation in specific cases.

	PDENB		GNB		NPNB		7NN		PyGNB		klaRGNB		klaRNPNB		e1071GNB
	$\mathit{\mu }$	$\mathit{\sigma }$	$\mathit{\mu }$	$\mathit{\sigma }$	$\mathit{\mu }$	$\mathit{\sigma }$	$\mathit{\mu }$	$\mathit{\sigma }$	$\mathit{\mu }$	$\mathit{\sigma }$	$\mathit{\mu }$	$\mathit{\sigma }$	$\mathit{\mu }$	$\mathit{\sigma }$	$\mathit{\mu }$	$\mathit{\sigma }$
Cell populations	0.98	0	0.97	0	0.98	0	0.16	0	0.97	0	0.97	0	0.98	0	0.97	0
CoverType	0.44	0	0.22	0	0.41	0	0.86	0	0.22	0	0.22	0	0.41	0	0.22	0
Crabs (Sex)	0.91	0.1	0.92	0.1	0.92	0.1	0.81	0.1	0.92	0.1	0.92	0.1	0.92	0	0.92	0.1
Crabs (SP)	0.99	0	0.99	0	0.97	0	0.88	0.1	0.99	0	0.99	0	0.97	0	0.99	0
Dermatology	0.95	0	0.82	0	0.9	0.1	0.81	0.1	0.85	0	NA	NA	0.9	0.1	0.82	0
Iris	0.95	0.1	0.94	0.1	0.94	0.1	0.95	0	0.94	0.1	0.94	0.1	0.94	0.1	0.94	0.1
LetterRecognition	0.72	0.1	0.66	0.1	0.72	0.1	0.18	0.1	0.66	0.1	0.66	0.1	0.72	0.1	0.66	0.1
MiceProtein	0.84	0	0.75	0	0.84	0	NA	NA	NA	NA	NA	NA	NA	NA	0.75	0
Penguins	0.98	0	0.98	0	0.97	0	0.97	0	0.98	0	0.98	0	0.97	0	0.98	0
Spam	0.68	0.1	0.52	0	0.38	0	0.58	0	0.68	0	NA	NA	0.37	0	0.52	0
Satellite	0.77	0	0.6	0	0.62	0	0.69	0	0.75	0	0.6	0	0.62	0	0.6	0
Swiss	0.98	0	0.99	0	0.99	0	0.98	0	0.99	0	0.99	0	0.99	0	0.99	0
WCBCD	0.89	0	0.89	0.1	0.87	0	0.93	0	0.89	0.1	0.89	0.1	0.88	0	0.89	0.1
Wine	0.97	0.1	0.96	0.1	0.96	0.1	0.95	0.1	0.96	0.1	0.96	0.1	0.96	0.1	0.96	0.1

. The distributions are shown using Mirrored Density plots (MD plots) in Appendix A. “NA” values indicate a failure of the classification algorithm. For the case of MiceProtein, several classifiers failed due to missing values in the dataset. The remaining cases of “NA” values can be observed for klaRGNB: in the datasets Dermatology, Spam, and Covertype, errors due to the estimation of variance are reported. Furthermore, the results show that high correlation values are not necessarily an indicator of low performance for naïve Bayes classifiers (compare Table 1 to Table 2).

We find that no single algorithm consistently outperforms all others, in line with the no-free-lunch theorem [54]. However, it is still possible to rank algorithms based on their mean performance, considering their best-performing variants across trials, while allowing for ties. To this end, we apply the permutation test [55] pairwise to each evaluation (see

Table A1. The table presents the results of the permutation test for each combination of classifiers in the columns and for all datasets in the rows.

	PDENB.GNB	PDENB.NPNB	PDENB.kNN7	PDENB.PyGNB	PDENB.klaRGNB	PDENB.klaRNPNB	PDENB.e1071GNB	GNB.NPNB	GNB.kNN7	GNB.PyGNB	GNB.klaRGNB	GNB.klaRNPNB	GNB.e1071GNB	NPNB.kNN7
CellPopulations	0	0	0	0	0	0	0	0	0	0	0	0	0	0
CoverType	0	0	0	0	0	0	0	0	0	0	1	0	1	0
Crabs (Sex)	0.437	0.01	0	0.477	0.443	0.01	0.413	0.221	0	1	1	0.133	1	0
Crabs (SP)	0.022	0	0	0.024	0.017	0	0.022	0	0	1	1	0	1	0
Dermatology	0	0	0	0	0	0	0	0	0.038	0	0	0	1	0
Iris	0	0	0.938	0	0	0	0	0.206	0.001	1	1	0.21	1	0.002
LetterRecognition	0	0.189	0	0	0	0.163	0	0	0	0.271	1	0	1	0
MiceProtein	0	0.237	0	0	0	0	0	0	0	0	0	0	1	0
Penguins	0.005	0.01	0.122	0	0.005	0.01	0.001	0	0	1	1	0	1	0.635
Spam	0	0	0	0.994	0	0	0	0	0	0	0	0	0.008	0
Satellite	0	0	0	0	0	0	0	0	0	0	1	0	1	0
Swiss	0.001	0.003	0.887	0	0	0.001	0	1	0	1	1	1	1	0.006
WCBCD	0.231	0	0	0.233	0.231	0	0.22	0	0	1	1	0	1	0
Wine	0.006	0	0	0.005	0.008	0	0.005	0.302	0.077	1	1	0.353	1	0.269
	NPNB.PyGNB	NPNB.klaRGNB	NPNB.klaRNPNB	NPNB.e1071GNB	kNN7.PyGNB	kNN7.klaRGNB	kNN7.klaRNPNB	kNN7.e1071GNB	PyGNB.klaRGNB	PyGNB.klaRNPNB	PyGNB.e1071GNB	klaRGNB.klaRNPNB	klaRGNB.e1071GNB	klaRNPNB.e1071GNB
CellPopulations	0	0	0.07	0	0	0	0	0	0	0	0	0	1	0
CoverType	0	0	0.197	0	0	0	0	0	0	0	0	0	1	0
Crabs (Sex)	0.196	0.201	0.462	0.209	0	0	0	0	1	0.104	1	0.123	1	0.158
Crabs (SP)	0	0	0.471	0	0	0	0	0	1	0	1	0	1	0
Dermatology	0	0	1	0	0	0	0	0.044	0	0	0	0	0	0
Iris	0.208	0.18	1	0.204	0.002	0.003	0	0.001	1	0.189	1	0.209	1	0.19
LetterRecognition	0	0	0.511	0	0	0	0	0	0.232	0	0.24	0	1	0
MiceProtein	0	0	0	0	1	1	1	0	1	1	0	1	0	0
Penguins	0	0	1	0	0	0.001	0.665	0	1	0	1	0	1	0
Spam	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Satellite	0	0	0.26	0	0	0	0	0	0	0	0	0	1	0
Swiss	1	1	1	1	0	0	0.005	0	1	1	1	1	1	1
WCBCD	0	0	0.036	0	0	0	0	0	1	0	1	0	1	0
Wine	0.308	0.306	1	0.308	0.064	0.1	0.194	0.083	1	0.363	1	0.349	1	0.352

in the Appendix). This statistical test determines whether performance differences are significant or not, enabling rankings with possible ties. From these results, we obtain a ranking of classifiers for all datasets (see

Table A2. The table presents the ranks of the permutation test for each combination of classifiers in the columns and for all datasets in the rows.

	PDENB	GNB	NPNB	kNN7	PyGNB	klaRGNB	klaRNP	e1071G
CellPopulations	1	7	2.5	8	4	5.5	2.5	5.5
CoverType	2	7	3.5	1	5	7	3.5	7
Crabs (Sex)	4	4	4	8	4	4	4	4
Crabs (SP)	3	3	6.5	8	3	3	6.5	3
Dermatology	1	6	2.5	6	4	8	2.5	6
Iris	1.5	5.5	5.5	1.5	5.5	5.5	5.5	5.5
LetterRecognition	2	5.5	2	8	5.5	5.5	2	5.5
MiceProtein	1.5	3.5	1.5	6.5	6.5	6.5	6.5	3.5
Penguins	6.5	2.5	6.5	6.5	2.5	2.5	6.5	2.5
Spam	1.5	4.5	6	3	1.5	8	7	4.5
Satellite	1	7	4.5	3	2	7	4.5	7
Swiss	7.5	3.5	3.5	7.5	3.5	3.5	3.5	3.5
WCBCD	4	4	7.5	1	4	4	7.5	4
Wine	4.5	4.5	4.5	4.5	4.5	4.5	4.5	4.5

). Finally, we compute the mean of these ranks to derive an overall score for each algorithm, presented in

Table 3. The table presents the grades computed as the mean of the ranks. Ranks were obtained in Appendix B based on the mean values of the study, and equal ranks are allowed and determined with a Permutation Test.

	PDENB	PyGNB	NPNB	klaRNPNB	e1071GNB	GNB	kNN7	klaRGNB
Grade	2.93	3.96	4.32	4.71	4.75	4.82	5.18	5.32

.

3.2. Interpretable Naïve Bayes Classifier

One advantage of the PDE-based, flexible naïve Bayes classifier is that it relies on one-dimensional density estimates, which we use to visualize the class-dependent fine structure of distributions for each feature. Inspecting all class-conditional likelihoods for a feature at once can reveal interesting relations or patterns when the number of dimensions allows such an overview; otherwise, a targeted feature selection is required. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show class-conditional likelihoods for four representative datasets: Satellite, Iris, Penguin, and the Cell populations dataset on the training data for one arbitrary cross-validation trial.

Figure 2A–D present the features of the annotated biological populations in the Flowcytometry dataset called cell populations. Normally, cell populations are manually distinguished in sequential two-dimensional dot plots. In Figure 2A, CD45 is a pan-leukocyte antigen whose fluorescence intensity separates broad white blood cell compartments (lymphocytes, monocytes, granulocytes) along with side scatter, and helps distinguish hematopoietic from non-hematopoietic events. Within the lymphocytes, CD19 is a B-lineage surface marker used to identify and quantify B cells. In Figure 2B, CD3 separates T-cells, and NK-cells can be separated because they are CD3-negative and positive for CD16 and/or CD56. FS_INT (forward-scatter integral) is a proxy for cell size, and SS_INT (side scatter integral) for granularity in Figure 2D.

Figure 2B,C depict two features, labeled FL4_INT and FL8_INT. These channels correspond to detectors that do not match any used fluorochrome and therefore primarily record detector noise and light spillover from other detectors, see [56] for details. It is clearly visible that no class is distinguishable in FL4_INT in comparison to “CD16_FITC” and “CD4_PC7”. In FL8_INT, we see a spillover effect from another detector (possibly “CD14_APC700”) to FL8_INT, allowing us to distinguish the red class. Without medical knowledge, FL4_INT would be disregarded based on Figure 2C, and FL8_INT would be questioned because it only distinguishes the green class (Monocytes), with negative log light measures based on Figure 2B, which could be a light spillover of CD14, presented in Figure 2C. Based on Figure 2D, for the classification task, it seems that FS_Int and FS_PEAK contain the same information with respect to class likelihoods, which aligns with domain knowledge.

Figure 3 presents class-conditional likelihoods for the Satellite dataset and motivates the need for an assumption-free distribution estimator. The plot illustrates a variety of distributional shapes across classes and features: for example, the “mixture” class in feature 26 is skewed, the “grey soil” class exhibits increased kurtosis, and the “cotton crop” class shows long tails in several features.

Figure 4 shows the well-known Iris dataset, where clear per-class tendencies are evident; the strong performance of naïve Bayes in this example illustrates how informative one-dimensional patterns can be for classification.

Figure 5 displays the Penguin dataset: although class tendencies are visible, substantial class overlap is present. The good performance of naïve Bayes here implies that separability is achieved by combining the information from feature C2 with C4 after the ICA rotation is applied, and that Features C1 and C3 can be disregarded

Across the visualized datasets, PDENB achieves excellent performance (MCC ≥ 0.95). The per-feature PDE visualizations frequently reveal regions of class overlap at the single-feature level—not as a shortcoming, but as an exploratory strength—these plots make the limits of one-dimensional separation explicit and point to which features are complementary. By inspecting class-conditional shapes (modes, tails, skewness) across features we can identify feature combinations that produce clear separation in higher dimensions, guide feature selection, and may even generate meaningful explanations for the classifier’s decisions.

Figure 2. Figures (A–D) show the class-conditional PDE likelihoods of dataset “Cell populations”. The colors depict different classes and are mapped to the cell populations. The range of values per data feature of the y-axis is presented after the transformation to the signed log scale as provided in the package “DataVisualizations” on CRAN [57]. The x-axis presents the range of class-conditional PDE likelihoods. The legend in Figure (A) presents the names of the cell population classes and also applies to the following subfigures (B–D). Figure (A) shows the class-conditional PDE likelihoods for the first two features. Figure (B) shows the class-conditional PDE likelihoods for the next four features. Figure (C) shows the class-conditional PDE likelihoods for the next four features of the dataset “Cell populations”. Figure (D) shows the class-conditional PDE likelihoods for the last three features. For comparison, FS_TOF in a different range is shown again.

Figure 2. Figures (A–D) show the class-conditional PDE likelihoods of dataset “Cell populations”. The colors depict different classes and are mapped to the cell populations. The range of values per data feature of the y-axis is presented after the transformation to the signed log scale as provided in the package “DataVisualizations” on CRAN [57]. The x-axis presents the range of class-conditional PDE likelihoods. The legend in Figure (A) presents the names of the cell population classes and also applies to the following subfigures (B–D). Figure (A) shows the class-conditional PDE likelihoods for the first two features. Figure (B) shows the class-conditional PDE likelihoods for the next four features. Figure (C) shows the class-conditional PDE likelihoods for the next four features of the dataset “Cell populations”. Figure (D) shows the class-conditional PDE likelihoods for the last three features. For comparison, FS_TOF in a different range is shown again.

Figure 3. The figure visualizes the fine distribution structure of the class-conditional PDE likelihoods for a selected subset of features from the Satellite dataset, highlighting differences in skewness, tails, and multimodality across classes. The colors depict different classes as presented in the legend. Each feature contains varying non-classic distributions with different characteristics, such as long and fat tails, and multimodal and skewed distributions, which can be assessed visually.

Figure 3. The figure visualizes the fine distribution structure of the class-conditional PDE likelihoods for a selected subset of features from the Satellite dataset, highlighting differences in skewness, tails, and multimodality across classes. The colors depict different classes as presented in the legend. Each feature contains varying non-classic distributions with different characteristics, such as long and fat tails, and multimodal and skewed distributions, which can be assessed visually.

Figure 4. The figure shows the class-conditional PDE likelihoods for the 4 features of the dataset “Iris”. The colors depict different classes as presented in the legend on the right.

Figure 4. The figure shows the class-conditional PDE likelihoods for the 4 features of the dataset “Iris”. The colors depict different classes as presented in the legend on the right.

Figure 5. The figure shows the class-conditional PDE likelihoods for the 4 features of the dataset “Penguins”, obtained by an ICA transformation. The colors depict different classes as presented in the legend on the right. Features C1–C4 were derived by applying independent component analysis (ICA) to the original variables [58]. Hence, the resulting components are used as rotated features for downstream analysis [59].

Figure 5. The figure shows the class-conditional PDE likelihoods for the 4 features of the dataset “Penguins”, obtained by an ICA transformation. The colors depict different classes as presented in the legend on the right. Features C1–C4 were derived by applying independent component analysis (ICA) to the original variables [58]. Hence, the resulting components are used as rotated features for downstream analysis [59].

Figure 6. The figure shows a customized 2D Voronoi tessellation based on the two ICA components C2 and C4 from the dataset Penguins. The posteriors for the three classes, Adelie, Gentoo, and Chinstrap, are highlighted from left to right. The color palette spans a continuous gradient from dark red through orange and yellow to white. Dark red corresponds to posterior values approaching one, with intermediate hues representing progressively lower posterior values, and white indicating posterior values equal to zero. A compact area consisting mainly of a dark red color can be detected, indicating a specific location of very high posterior values for each class in the relationship between the two features. See Figure 5 for comparison to class likelihoods.

Figure 6. The figure shows a customized 2D Voronoi tessellation based on the two ICA components C2 and C4 from the dataset Penguins. The posteriors for the three classes, Adelie, Gentoo, and Chinstrap, are highlighted from left to right. The color palette spans a continuous gradient from dark red through orange and yellow to white. Dark red corresponds to posterior values approaching one, with intermediate hues representing progressively lower posterior values, and white indicating posterior values equal to zero. A compact area consisting mainly of a dark red color can be detected, indicating a specific location of very high posterior values for each class in the relationship between the two features. See Figure 5 for comparison to class likelihoods.

Figure 7. The figure shows a customized 2D Voronoi tessellation based on the two features CD16_FITC and CD14_APC700 from the Cell populations dataset. The color palette is identical to Figure 6, with dark red indicating high posterior values and white indicating zero. The posterior for the class of atypical monocytes 1 is highlighted. A compact area consisting mainly of a dark red color can be detected, indicating a specific location of high posterior values for this class in the relationship between the two features. Both features are typically used to detect atypical monocytes in Flow Cytometry.

Figure 7. The figure shows a customized 2D Voronoi tessellation based on the two features CD16_FITC and CD14_APC700 from the Cell populations dataset. The color palette is identical to Figure 6, with dark red indicating high posterior values and white indicating zero. The posterior for the class of atypical monocytes 1 is highlighted. A compact area consisting mainly of a dark red color can be detected, indicating a specific location of high posterior values for this class in the relationship between the two features. Both features are typically used to detect atypical monocytes in Flow Cytometry.

Figure 8. The figure shows a customized 2D Voronoi tessellation based on the two features CD16_FITC and CD14_APC700 from the Cell populations dataset. The color palette is identical to Figure 6, with dark red indicating high posterior values and white indicating zero. The posterior for the class of classical monocytes is highlighted. The color palette is identical to Figure 6, with dark red indicating high posterior values and white indicating zero. A compact area consisting mainly of a dark red color can be detected, indicating a specific location of high posterior values for class 10 in the relationship between the two features. Both features are typically used to detect classical monocyte cells in Flow Cytometry.

Figure 8. The figure shows a customized 2D Voronoi tessellation based on the two features CD16_FITC and CD14_APC700 from the Cell populations dataset. The color palette is identical to Figure 6, with dark red indicating high posterior values and white indicating zero. The posterior for the class of classical monocytes is highlighted. The color palette is identical to Figure 6, with dark red indicating high posterior values and white indicating zero. A compact area consisting mainly of a dark red color can be detected, indicating a specific location of high posterior values for class 10 in the relationship between the two features. Both features are typically used to detect classical monocyte cells in Flow Cytometry.

See Figure 6 for comparison to posteriors. Another take on visualizing patterns detected by the naïve Bayes classifier would be to visualize the posterior computed in high dimensions in a two-dimensional plot. An informative plot in two dimensions can be derived from a 2D scatter plot. Given the two-dimensional coordinates, a Voronoi tessellation can be used to partition the area defined by the coordinates, as is performed in Figure 6, Figure 7, Figure 8 and Figure 9 for the training data. This representation allows a coloration of decision areas based on the posterior. High posterior values are colored as dark red, zero values as white, and intermediate values as a gradient in between the range of these two colors, with yellow as the color for values in the middle. Within the 2D Voronoi visualization of the posterior decision boundaries, the recognition of a single compact area with high posterior values for a certain class suggests a decision pattern. For example, the hypothesis derived from Figure 8 is clearly visible in the high posterior values depending on the class in Figure 9.

Figure 7 and Figure 8 present the posteriors computed for the classes of atypical monocytes, classical monocytes, and B-cells on feature CD 14 vs. CD16. CD14 vs. CD16 is a standard plot for innate-cell phenotyping: it cleanly separates atypical monocyte subsets (classical CD14+ CD16- CD4+ and atypical CD14+/- CD16+ CD4 and CD14+/- CD16- CD4+. However, CD16 is not specific to classical monocytes (it is also found on neutrophils and some monocytes), so classical monocytes should be confirmed with CD56 and the exclusion of CD3/CD14. B cells are not identifiable on CD14 vs. CD16 in Figure 9, because they are typically CD14⁻CD16⁻ and overlap with many other CD14⁻CD16⁻ populations; a positive B-cell marker (e.g., CD19 or CD20) is required for reliable detection.

In sum, the proposed visualization approaches is meaningful because it reveals decision boundaries in the two-dimensional feature space that are not only predictive (i.e., yield good classification performance) but also explanatory, making the underlying decision patterns interpretable.

3.3. A Baseline for the Distinction of Blood vs. Bone Marrow in Biological Population Frequencies

Distinguishing bone marrow (BM) from peripheral blood (pB) is a routine but clinically important task in diagnostic hematology. BM and pB differ in their cellular composition and in the relative frequencies of their hematopoietic progenitors, immature myeloid and lymphoid populations, and other subpopulations; these differences are routinely exploited by clinicians in flow-cytometric two-dimensional scatter plots to identify diagnostically relevant populations. Accurate separation of BM from pB is also important for downstream tasks such as assessing Minimal Residual Disease (MRD), because inadvertent dilution of BM aspirates with peripheral blood can bias clinical interpretation. For background on aspiration and dilution effects, see [60].

We used the Dresden cohort from the public Flow Cytometry collection [61]. The Dresden data comprise N = 44 sample files measured on a BD FACSCanto II instrument: 22 bone marrow and 22 peripheral blood samples. Each sample consists of a high-event flow cytometry file comprising approximately 130,000–880,000 single-cell events. For each event, 10 parameters were recorded, including forward scatter and side scatter for cell size and granularity, as well as eight fluorescence channels corresponding to the antigens CD34, CD13, CD7, CD56, CD33, CD117, HLA-DR, and CD45. All files are anonymized, instrument-compensated, and log-scaled into the range [0, 6] for analysis. We follow the patient-level evaluation used in the dataset’s original benchmarking by identifying cell population frequencies through ALPODS [62]. This yields one label per sample file (BM vs. pB) and permits direct comparison with previously reported results [62]. Contrary to Ref. [62], we do not identify meaningful cell populations with ALPODS but use all generated cell population frequencies as a baseline.

Using the PDENB and 80/20% cross validation of 100 trials, PDENB achieves a classification accuracy of 99.3 ± 0.03% accuracy (98.8+-0.5 MCC) on the Dresden dataset (sample-level decision). This outperforms the previously reported accuracy of 96.8 ± 0.09% for the ALPODS explainable-AI pipeline on the same dataset. Figure 10 presents selected posterior decision boundaries in 2D. It is visible that low cell population frequencies of population C0024 (defined by CD45 < 2.0735 and CD13 ≥ 3.0485 and CD34 ≥ 3.4125), C0013 (CD45 < 2.0735 and CD13 ≥ 2.4105 and CD13 < 2.8655 and CD7 < 3.377 and FS < 5.464 and CD34 < 5.871 and CD33 ≥ 3.37451.91 and CD117 1.91 and CD117 < 3.4675 and CD117 ≥ 3.3245 & HLA_DR ≥ 2.2005) and C0014 (CD45 < 2.0735 and CD13 ≥ 2.4105 and CD13 < 2.8655 and CD7 < 3.377 and FS < 5.464 and CD34 < 5.871 & CD33 ≥ 3.3745 and CD56 ≥ 1.91 & CD117 ≥ 3.4675) depict peripheral blood and high cell population frequencies of bone marrow.

The improvement demonstrates that robust, nonparametric, PDE-based likelihood estimation combined with conservative smoothing and plausibility correction can yield a stronger baseline for this task, and that highly accurate classification is achievable for high-event flow-cytometry samples without bespoke gating rules.

4. Discussion

We introduced PDENB, a Pareto Density-based Plausible Naïve Bayes classifier that combines assumption-free, neighborhood-based density estimation with smoothing and visualization tools to produce robust, interpretable classification. Our empirical benchmark across 14 datasets and its dedicated application to multicolor flow cytometry demonstrate several consistent advantages of this approach.

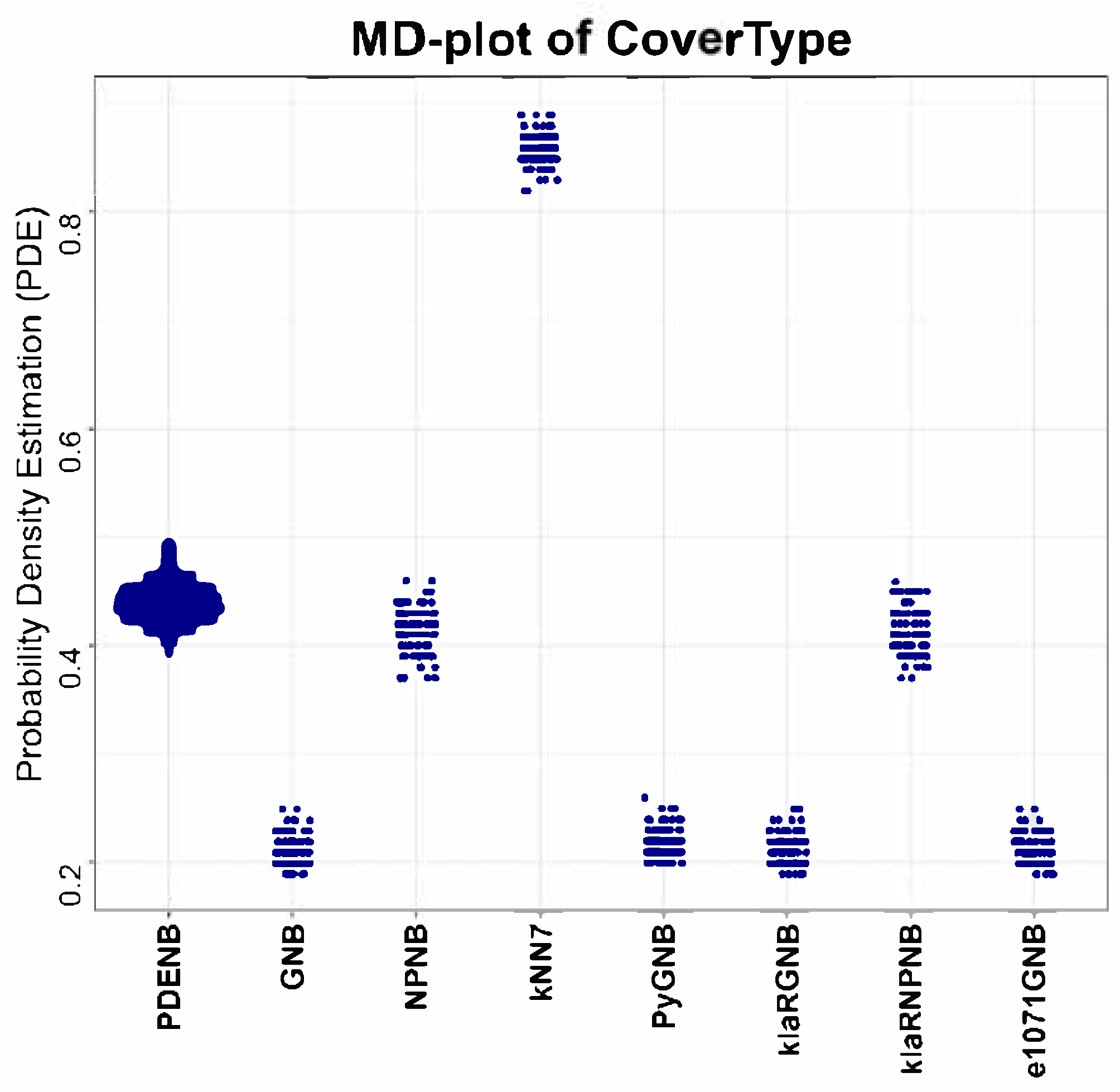
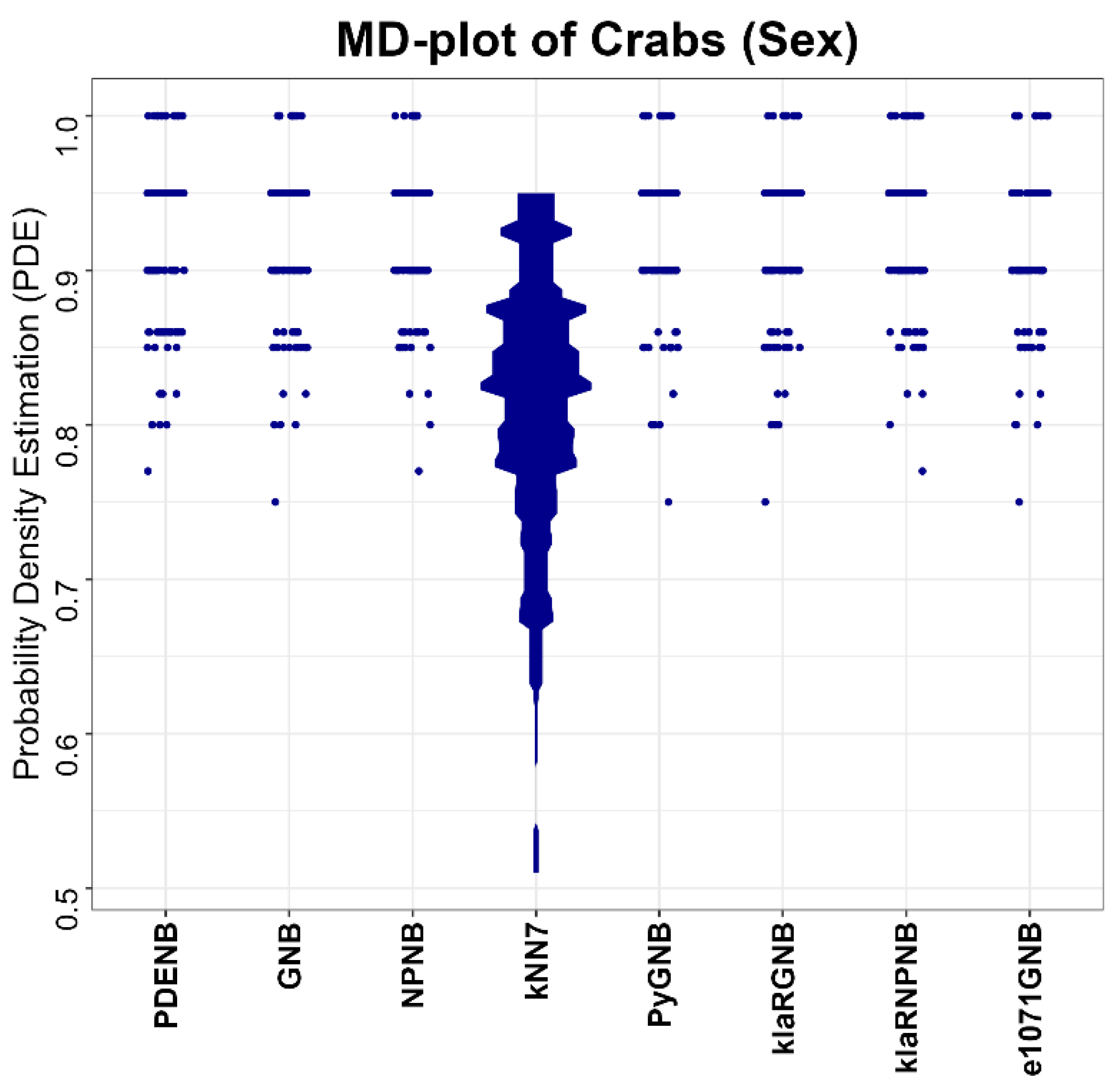
First, PDENB is competitive with—and frequently superior to—established Naïve Bayes implementations and non-parametric variants. Using repeated 80/20 hold-out evaluations (or resampling for very large datasets) and Matthews Correlation Coefficient (MCC) as the performance measure, PDENB attains top average ranks (Table 3) and achieves very high per-dataset performance on several problems (e.g., MCC ≥ 0.95 for Iris, Penguins, Wine, Dermatology, and the Cell populations dataset). The permutation tests (with multiple-comparison correction) aggregated in Table 3 indicate that these improvements are not merely random fluctuations: they translate into statistically detectable differences for many dataset–classifier pairs (see also Appendix Table A1 and Table A2). Note that we did not apply variance-optimized feature scaling for the benchmark; because k-nearest neighbors’ decisions are distance-based, kNN is not expected to attain its best possible performance under our preprocessing. The choice of scaling and distance is often empirical and context-dependent, and there is no single universally “correct” recipe.

Second, PDENB’s core strength is its flexibility in modeling complex, non-Gaussian feature distributions without parametric assumptions. The Satellite dataset illustrates this point: feature distributions (see Appendix C) and class-conditional distributions for this set display long tails, multimodality, and skewness that violate Gaussian assumptions. In that setting, PDENB captures the fine structure that classical Gaussian Naïve Bayes misses, yielding substantially better discriminative performance. This example underscores the value of highly adaptive density estimation methods when confronted with complex, non-Gaussian data structures. This pattern—non-parametric methods outperforming Gaussian approximations when data depart from normality—is borne out across the benchmark: non-parametric Naïve Bayes variants tend to outrank their Gaussian counterparts (see Table 2).

Third, PDENB directly supports interpretability through visualization. The class-conditional mirrored density (MD) plots and the customized 2D Voronoi posterior maps provide intuitive, feature-level, and case-level explanations as outlined using Figure 2, Figure 3, Figure 4 and Figure 5: users can inspect class-conditional likelihood shapes (modes, skewness, overlaps) and identify the feature combinations that produce compact, high-posterior decision areas. These visual diagnostics do not replace formal model evaluation, but they materially aid exploratory analysis and hypothesis generation, and they help explain why a particular prediction was made in cases where two or more features jointly determine a compact posterior region (see Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10).

The FlowCytometry application of distinguishing blood vs. bone marrow illustrates a practical use case where PDENB’s combination of sensitivity to distributional fine structure, feature selection, and interpretability is valuable. In such features of cell population frequencies, absolute counts, and percentages, classical Gaussian assumptions are violated (see Appendix C Figure A16 and Figure A17). PDENB achieved 98.8 MCC under cross-validation. The improved baseline performance is practically meaningful because higher sample-level accuracy reduces the risk of mislabeling the origin of aspirates of bone marrow vs. peripheral blood, which in turn can reduce downstream diagnostic errors. This result is a first indication that PDENB could potentially support clinically relevant classification tasks even with modest sample sizes, provided that careful feature selection and validation are applied.

The influence of dependency was tracked with four different measures in Table 1 after preprocessing. High correlation values (>0.8) using all four measures are depicted in Table 1 for all datasets except for the following three: CoverType, Swiss, and Wine (Crabs and Penguin had low correlations due to rotation by ICA or PCA). Although naïve Bayes theoretically assumes feature independence, in practice, correlated features did not necessarily imply a low performance (<0.8). For example, the Cell populations dataset retained high performance despite correlated features above 0.9. The removal of correlated features did not necessarily improve performance. Still, correlations can affect interpretability and sometimes classifier reliability; feature decorrelation, conditional modeling, or methods that explicitly capture dependencies may further improve the model’s performance in specific domains. In our benchmark, we observed that high feature correlation does not uniformly impair PDENB.

Our benchmark covers a diverse but limited set of datasets; broader evaluations—especially in high-dimensional, noisy, or highly imbalanced settings—would strengthen generality claims, although benchmarking against all families of classifiers is a controversial topic [63,64]. We emphasize several methodological points and caveats. PDENB’s robust performance hinges on three design choices: (i) estimating a single, class-independent Pareto radius per feature; (ii) applying smoothing to the raw class-conditional PDE output prior to using it as a likelihood; and (iii) applying a plausibility correction to the class likelihoods. While these design choices increase estimator stability and interpretability, they come at the cost of greater computational demand. To mitigate the computational cost, we provide a multicore, shared-memory [65] implementation for large-scale applications. Finally, embedding PDENB visualizations within formal explainable-AI workflows (e.g., counterfactual analyses, local-explanation wrappers) would enhance their utility for decision-makers.

Several design alternatives (e.g., kernels, global or local Pareto radii) were explored during preliminary experimentation. For example, we approximate the Pareto radius through a single, class-independent parameter rather than estimating separate radii for each feature–class combination. While this could reduce the model’s flexibility, preliminary internal experiments and benchmarking indicate that the resulting approximation error is small and that the simplification is sufficiently accurate for practical applications. The final architecture and parameter configuration were fixed after extensive testing, as this setup consistently provided the most stable and reliable performance across validation settings. Therefore, we fixed the parameters, especially regarding the radius estimation, which could be estimated through class-dependent or global methods, the choice of kernel, and several competing approaches to assess low evidence areas in the naïve Bayes theorem. The curious reader will find even more possibilities for changing parameters in the presented setting.

As an example, we present results from our preliminary experimentation to support the process of deciding between a global versus a local (class-dependent) Pareto radius in Appendix D and showcase our reasoning. As Appendix D shows, the strategy using a global Pareto radius achieves better results in the high-performing examples, while the local radius achieves better results in the low-performing and moderately performing examples. Therefore, it is justifiable that the global strategy is the default setting, although the user is able to change the radius estimation to the local mode.

The computation of PDENB’s plausibility threshold ε is a data-driven optimal selection of the group of cases with smallest joint likelihood across all classes (see ABC-Analysis [29]). Therefore, the relevant cases for which a plausible class assignment could be considered are determined automatically.

The δ-based adjustment provides a controlled way to nudge likelihood mass from the current top class towards a nearby mode without distorting the global posterior landscape. The parameter δ governs the trade-off between conservatism and decisiveness: a small δ produces minor, local adjustments that yield stable and interpretable posterior changes, whereas a larger δ would raise the likelihood of MAP flips in low-evidence regions. Because Equation (15) transfers a bounded amount of mass from one class to another, the overall likelihood geometry is preserved and posterior trajectories remain smooth rather than exhibiting abrupt thresholding, particularly near class boundaries. This produces a gradual change in the likelihood profile (illustrated in Figure 1 and resembling a fading-variance effect) and enhances the MAP estimate for the closest-mode class while retaining Bayesian coherence and interpretability.

In Appendix E we show that random forest (RF) yields a small but consistent edge in raw MCC on four imbalanced datasets, while PDENB provides a transparent, well-calibrated, and parameter-free baseline the errors of which are interpretable from its class-conditional likelihood plots. The benchmark on four imbalanced datasets hints that PDENB cannot necessarily achieve high performance for minority classes if there is a lack of samples, since the minority might be underrepresented. When two classes overlap strongly in feature space, one class can suffer disproportionately poor performance—especially if it is less prevalent or more heterogeneous. Differences in class prevalence (priors) or in within-class variability shift posterior probabilities toward the dominant (or more concentrated) class, which increases misclassification of the disadvantaged class. An estimation of a risk leading to a reweighting of the posteriori might be helpful if the false negative rate of a specific minority class must be minimized.

The PDENB is applicable to numeric tabular data as shown in the benchmark study. Theoretically, it is limited to independent features, however in practice it shows high performance despite significant dependency measures within the data. The PDENB can process big and high-dimensional data, as was shown in the benchmark study. In the case of Covertype (over 450.000 training samples and over 100.000 test samples with 17 features), the model training time is under 35 s and the classification requires around 3 s. Larger datasets with millions of cases could be processed within a few minutes. A more explicit runtime test was executed and documented in Appendix F. The PDENB can compute large datasets of a million cases with up to 100 feature dimensions within a few minutes (<7 min). The computational speed of the training drastically decreases for hundreds of features and multiple millions of observations; however, it is still feasible, with a runtime of under an hour. Its prediction remains comparably fast, with a runtime of under 13 min for 4 million cases and 100 features.

PDENB assumes continuous feature domains. For features with only a few distinct numeric values or very small class-specific sample sizes, we therefore fall back to a simple histogram-based likelihood with an automatically chosen number of bins [16], as described in Appendix G. Truly categorical variables, i.e., unordered labels without a meaningful numeric scale, are mathematically different: they do not admit a probability density in the sense defined in the Section 2.3 ff., and we do not implement a dedicated categorical likelihood model for them in the present work. In principle, PDENB could be extended to such features by replacing the continuous density with a multinomial/Dirichlet class-conditional model over categories, or by embedding categories into a continuous representation and applying PDE in that space. We regard this as a natural direction for future work and, in this study, deliberately restrict ourselves to continuous and quasi-continuous features, for which PDE and the histogram fallback are well defined and interpretable.

The plausible correction in PDENB relies on effective mode separation, which is determined using quantile-based criteria. If class separation is not feasible, instead of plausible correction, the classical Bayes theorem will be used. Conversely, when class separation exists, skewed distributions do not affect the computation of the plausible correction, provided that mode recognition remains accurate. However, incorrect mode recognition may deteriorate the correction outcome. The presented framework offers a foundation for the development of autogating approaches. In future work, the two-dimensional representation based on Voronoi cells, together with the a posteriori probability derived from PDENB, could be utilized to identify regions of interest within the feature space. Convex hulls may then be employed to characterize specific properties associated with particular feature–class combinations. By combining these properties, it would be possible to define automated and data-driven class assignment strategies, thereby enabling fully autonomous gating within this framework.

The advantage of the PDENB is clearly its assumption-free modeling of the data and robust performance. PDENB can be applied to data to leverage fine details of the distributions. Its assumption-free smoothed density estimation, combined with a plausibility correction of the Bayes theorem, yields reliable and robust posterior estimates.

Patterns arising from the multiplicative combination of feature-wise likelihoods can be recognized by the user and serve as intuitive explanations of how different features jointly contribute to the final class assignment.

5. Conclusions

This work presents a novel way of solving the naïve Bayes classification considering critical decision details. An parameter-free density estimation allows for the adaptive modeling of continuous one-dimensional features. The result is a robust classifier achieving results in line with the state of the art. The advantage of the proposed classifier is its robust and adaptive modeling. Furthermore, its resulting class-conditional likelihoods can be visualized with Mirrored-Density plots, enabling an interpretable and explorative approach to machine learning. Interpretable visualizations allow swift hypothesis exploration. Future work will tackle the challenge of identifying the most important visualizations of likelihoods and posteriors. These robust results allow for its benchmarks to be referenced against other methods. The algorithm is accessible via https://CRAN.R-project.org/package=PDEnaiveBayes, accessed on the 17 November 2025.