Interleaved Fusion Learning for Trustworthy AI: Improving Cross-Dataset Performance in Cervical Cancer Analysis

Abstract

This study introduces a novel Interleaved Fusion Learning (IFL) methodology leveraging transfer learning to generate a family of models optimized for specific datasets while maintaining superior generalization performance across others. The approach is demonstrated in cervical cancer screening, where cytology image datasets present challenges of heterogeneity and imbalance. By interleaving transfer steps across dataset partitions and regulating adaptation through a dynamic learning parameter, IFL promotes both domain-specific accuracy and cross-domain robustness. To evaluate its effectiveness, complementary metrics are used to capture not only predictive accuracy but also fairness in performance distribution across datasets. Results highlight the potential of IFL to deliver reliable and unbiased models in clinical decision support. Beyond cervical cytology, the methodology is designed to be scalable to other medical imaging tasks and, more broadly, to domains requiring equitable AI solutions across multiple heterogeneous datasets.

1. Introduction

Cervical cancer remains one of the leading health threats for women worldwide, especially in low- and middle-income countries, where it is the second-most prevalent cancer among women [1,2]. Globally, over 600,000 new cases and over 340,000 deaths were reported in 2020, of which about 90% occurred in resource-limited regions [3]. The high mortality in these areas largely stems from inadequate access to screening, human papillomavirus (HPV) vaccination, and timely medical intervention [4]. HPV infection is recognized as the primary cause of cervical cancer, yet barriers to implementing preventive measures persist due to economic and healthcare disparities [5]. Advances in diagnostic tools, including machine learning and artificial intelligence, show promise for enhancing early detection, which is critical given that early-stage intervention could reduce cervical cancer mortality by up to 60% [6]. More broadly, AI and machine learning (ML) applications are increasingly transforming healthcare by improving diagnostics, optimizing treatments, and enhancing patient outcomes [7,8]

The integration of Deep Learning (DL) in cervical cancer diagnostics has advanced significantly in recent years, with applications that enhance automated image analysis and assist in early detection [9,10]. DL techniques now focus extensively on cervical cell classification, leveraging large datasets to train models, although publicly available data remains limited [11]. For this reason, transfer learning has been widely employed to address data scarcity by adapting pre-trained models from large, general datasets [12]. This method has shown particular promise in cervical cell detection tasks, allowing networks to achieve higher accuracy despite constrained data [13]. As DL continues to evolve, its impact on cervical cancer detection grows, offering scalable solutions that aid in screening and reduce the diagnostic burden on pathologists.

Ensuring trustworthiness in AI models is essential, especially in healthcare, where biases in training data or model structures can disproportionately impact certain demographic groups. Recent research emphasizes the need for fairness-focused metrics and strategies to mitigate these biases, which are present in diverse applications such as environmental security and semantic segmentation, and now in clinical predictions as well [14,15,16]. Despite advances in algorithmic fairness, the evaluation and reduction in biases within clinical models remains challenging due to the limited accessibility of representative health data and the complexity of high-dimensional medical information [17]. In healthcare, these biases can lead to disparities in diagnostic outcomes, reinforcing existing inequities. Addressing these issues requires a comprehensive approach involving data quality enhancement, explicitly fair algorithms, and interdisciplinary collaboration to ensure ethical, equitable AI deployment in clinical settings [18].

Transfer learning has emerged as a powerful technique to mitigate the effects of data scarcity and to address biases in medical image analysis by leveraging pre-trained models from tasks with varying dataset sizes, regardless of their relative scale [19,20]. In medical applications, transfer learning enables models to inherit feature representations from large, well-curated datasets, which can be fine-tuned to perform effectively even with limited domain-specific data [21,22]. This is particularly useful for complex tasks like cervical cell detection, where annotated data is often limited. Studies show that using domain-specific transfer learning can significantly improve model accuracy and reduce bias by aligning features more closely with the target medical context [13,22]. This approach not only enhances model robustness but also minimizes the need for extensive manual labeling, making it a viable solution to achieve fairer and more accurate predictions in clinical settings. Building on these foundations, this study introduces a novel dataset fusion methodology that further addresses the challenge of balancing domain-specific optimization with cross-domain adaptability.

The purpose of this work is to develop a methodology for creating more robust and Trustworthy Artificial Intelligence (TAI) models for health applications that mitigate bias effects and address the challenges described above. This objective will be achieved by developing a novel methodology, Interleaved Fusion Learning, that can be applied to a family of models, each specialized for a specific dataset, while also benefiting from shared knowledge across all datasets. By allowing models to share knowledge while maintaining specialization for their respective datasets, this methodology facilitates a synergistic fusion of diverse data sources, integrating heterogeneous data to enhance enhance predictive performance across a broader range of data. The proposed methodology will be evaluated using cervical cancer datasets to demonstrate its potential in improving screening solutions.

The organization of this paper is outlined as follows: initially, Section 2 provides an overview of the materials and techniques essential for conducting this research. Subsequently, Section 3 provides an explanation of the proposed approach for the development and evaluation of the interleaved fusion learned models. In Section 4, we detail our implementation of the methodology and present a selection of the data obtained through our algorithm. Finally, in Section 5 and Section 6 , we engage in an analysis of the data and seek to draw some definitive conclusions.

2. Materials and Methods

2.1. Open Cervical Cancer Datasets

To develop robust models for cervical cell segmentation and classification, large and well-annotated datasets are essential. Among the most comprehensive publicly available resources, the APACC (Annotated PAp cell images and smear slices for Cell Classification) dataset and the CRIC (Center for Recognition and Inspection of Cells) Cervix collection stand out for their extensive cell annotations and segmentation data, which make them highly suitable for DL applications [23,24]. Both datasets offer the detailed, large-scale data necessary for effective model training and evaluation in the context of cervical cancer screening, supporting a range of tasks from detection to classification. Given their quality and scope, APACC dataset and CRIC Cervix collection provide an invaluable foundation for advancing automated cytological analysis.

In contrast, other commonly used datasets in cervical cell research, such as SIPaKMeD, Herlev and Mendeley, are less suited to our objectives. SIPaKMeD and Herlev datasets focus on isolated cells and are primarily used for image-based classification rather than full-image detection and segmentation, limiting their application for models requiring comprehensive smear data [25,26,27]. On the other hand, the Mendeley dataset includes images with pointed-out cells but lacks full cell labeling, which restricts its effectiveness for segmentation-focused tasks [27,28].

2.1.1. CRIC Cervix Collection

The CRIC Cervix collection is a robust dataset, specifically curated to support automated analysis and detection in cervical cytology. Created as part of the CRIC initiative, this dataset includes 400 high-resolution RGB images (1376 × 1020 pixels), each containing manually classified cells. With a total of over 11,000 annotated cells, the CRIC Cervix collection offers the high-quality labels needed for machine learning models focused on cytopathological tasks [24].

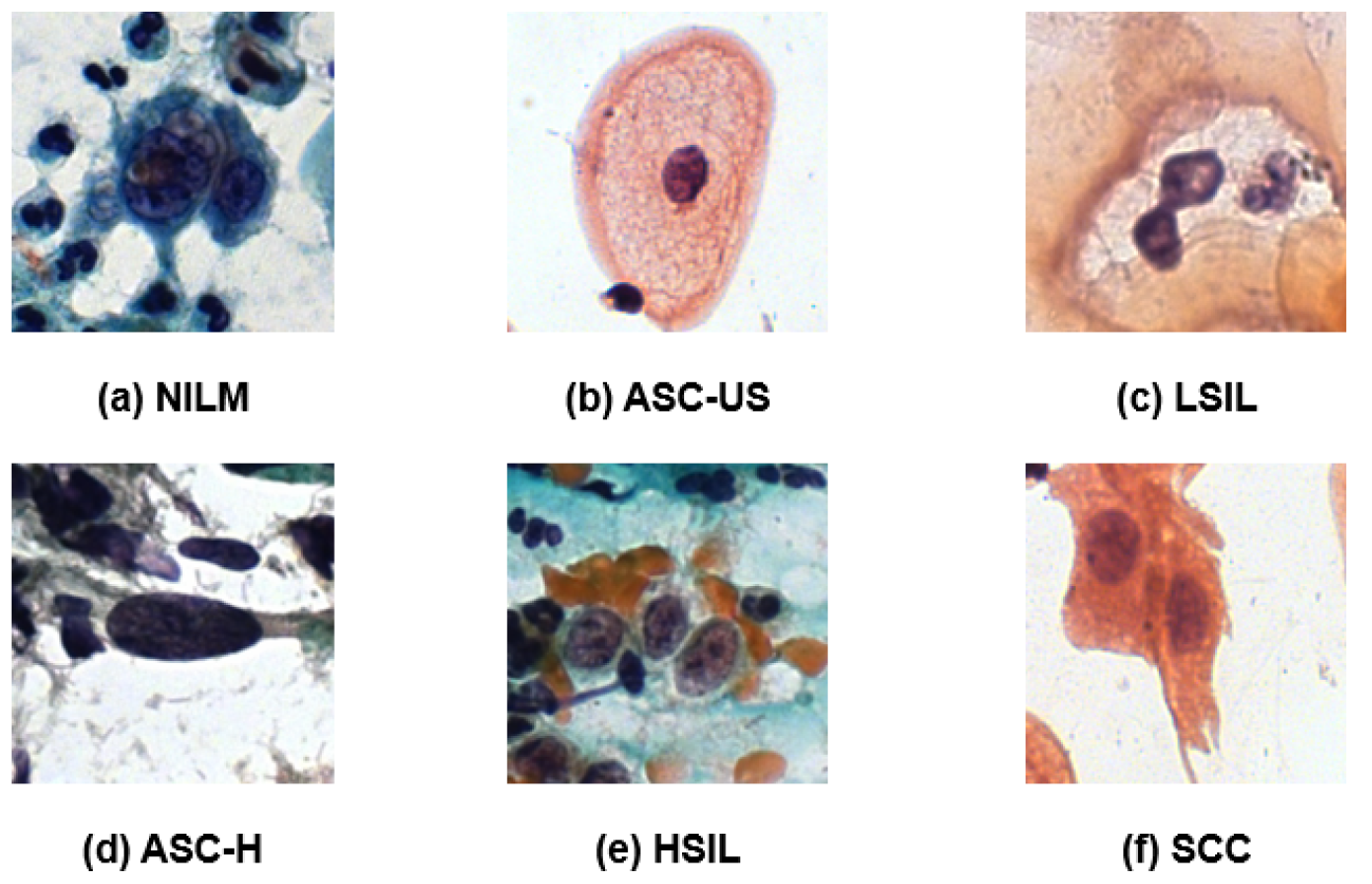
The CRIC Cervix collection uses the Bethesda System, which is the standardized terminology most widely adopted worldwide for cervical cytopathology, ensuring uniformity and reproducibility across laboratories and pathologists [29]. This dataset classifies cells into six categories based on Bethesda nomenclature: (1) negative for intraepithelial lesion or malignancy (NILM), (2) atypical squamous cells of undetermined significance, possibly non-neoplastic (ASC-US), (3) low-grade squamous intraepithelial lesion (LSIL), (4) atypical squamous cells that cannot exclude a high-grade lesion (ASC-H), (5) high-grade squamous intraepithelial lesion (HSIL), and (6) squamous cell carcinoma (SCC). To streamline model development and enhance classification homogeneity with the APACC database, we have unified these categories into a binary classification system. The NILM category is maintained as is, while all other categories are combined and labeled as “Positive”.

The reference images for each category are shown in Figure 1, with subfigures (a) through (f) illustrating representative cells from each class.

2.1.2. APACC Dataset

The APACC dataset is one of the most recent and comprehensive publicly available resources for cervical cell analysis. This dataset includes 103,675 annotated cell images, extracted from 107 whole Pap smears, and divided into over 21,000 sub-regions to support finer analysis [23]. This sub-regions are RGB images with a resolution of 1984 × 1984 pixels.

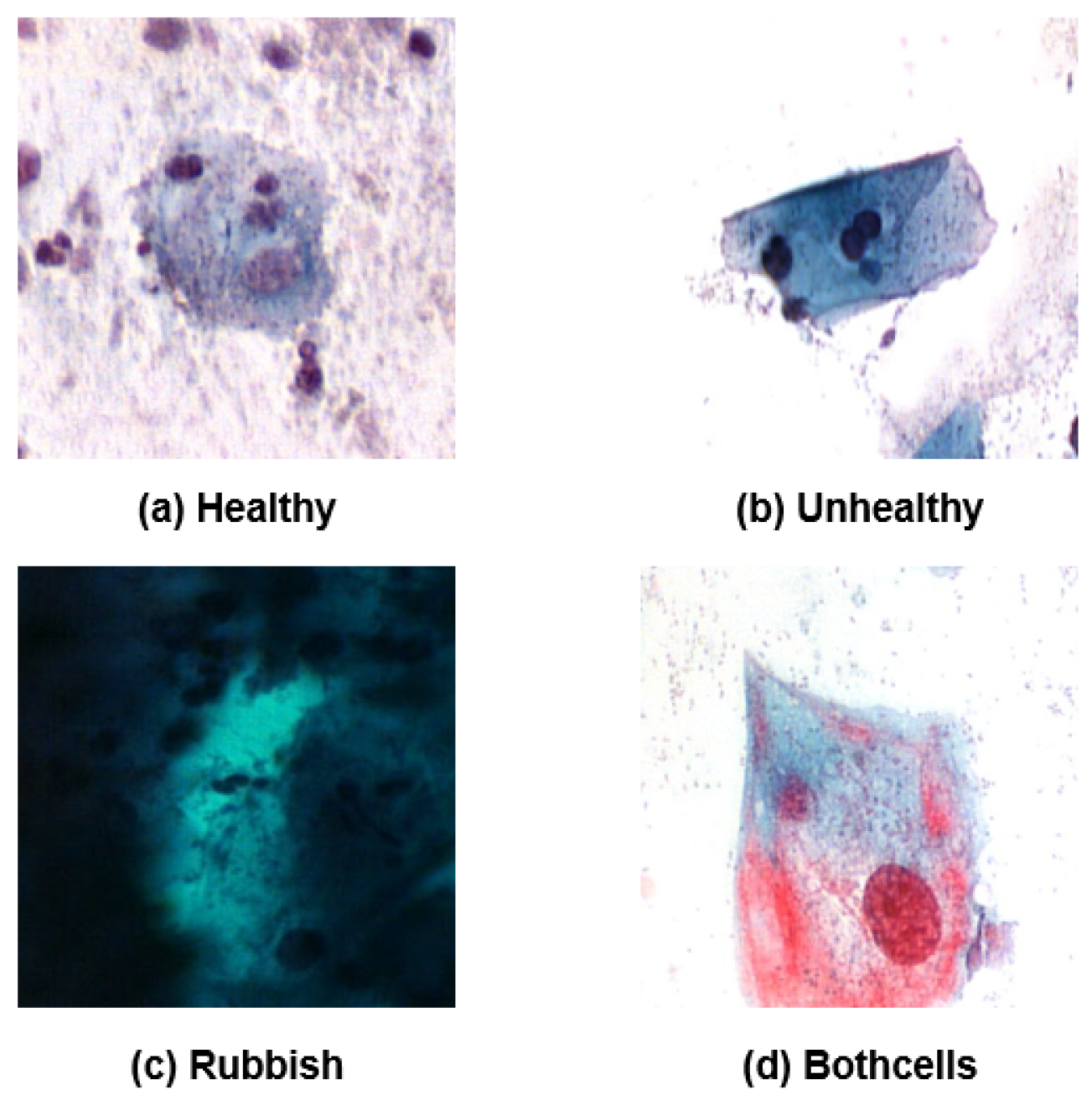
The APACC dataset categorizes cells into four classes: healthy (normal), unhealthy (abnormal), rubbish (not valid), and bothcells (a mixture of healthy and unhealthy cells). These classes loosely map onto Bethesda categories, where “healthy” corresponds to the NILM category, “unhealthy” represents cells from the broader Epithelial cell abnormality category (though without subdivisions like ASC, LSIL, or HSIL), “rubbish” aligns with Unsatisfactory for evaluation, and “bothcells” also falls within Epithelial cell abnormality as it includes malignant cells intermingled with normal cells. For our analysis, we have simplified the dataset by applying the same binary classification approach as in the CRIC database: NILM cells remain as “Negative,” while both “unhealthy” and “bothcells” are consolidated under a “Positive” label. The “rubbish” class has been excluded to ensure data relevance and consistency.

Representative examples of each original class from APACC are shown in Figure 2, with subfigures (a) through (d) illustrating these types.

2.2. Deep Learning Architectures for Object Recognition: YOLOv8

YOLOv8 (You Only Look Once, Version 8), developed by Ultralytics, is one of the most advanced and efficient architectures for real-time object detection in medical imaging [30,31]. This DL model combines high accuracy with speed, making it ideal for applications requiring rapid identification of abnormalities, such as cervical cancer screening. With its optimized structure, YOLOv8 is particularly effective in identifying abnormal cells within complex, high-resolution images, which is crucial for early detection of precancerous and malignant lesions.

Its flexibility also allows it to be adapted to clinical environments where both diagnostic precision and processing speed are essential. Supporting both detection and classification tasks, YOLOv8 enhances the efficiency of cytological analysis, contributing to faster and more reliable early cancer screening workflows.

YOLOv8 provides several adjustable parameters that allow fine-tuning for specific tasks and datasets. The initial learning rate. controls the speed of weight updates during training, while the optimizer manages how the model minimizes the loss function. Early stopping prevents overfitting by halting training when validation metrics cease to improve. Data augmentation enhances generalization by applying random transformations to the training data. The batch size defines the number of samples processed before updating model weights, and the image size determines the resolution at which images are resized for input, balancing accuracy and computational efficiency.

2.3. Transfer Learning

Transfer learning is a DL approach that enables models to leverage knowledge acquired from one task (source task) to improve performance on a related task (target task), especially useful when the target domain has limited labeled data [32].

Formally, a domain is defined as $D=\{𝒳,𝒴,d(·\left)\right\}$, where $𝒳$ is a feature space, $𝒴$ is a label space, and the function $d:𝒳\to 𝒴$ ensures that each feature $x\in 𝒳$ has a corresponding label $y\in 𝒴$, such that $d\left(x\right)=y$. Given a specific domain D, we define a task $T=\{X,𝒴\}$, where $X\subset 𝒳$ is a subset of the feature space. For a specific task T, any function $f(·)$ learned based on the relationships determined by the image of $d\left(X\right)$ is referred to as a predictive function.

In transfer learning, the objective is to enhance a predictive function $f_T(·)$ in a target domain $D_T=\{{𝒳}_T,{𝒴}_T,d_T(·)\}$ with a corresponding target task $T_T=\{X_T,{𝒴}_T\}$, by leveraging knowledge from a source predictive function $f_S(·)$ learned from a source domain $D_S=\{{𝒳}_S,{𝒴}_S,d_S(·)\}$ and a source task $T_S=\{X_S,{𝒴}_S\}$. This process is valid under the assumption that either $D_S\ne D_T$ or $T_S\ne T_T$.

The condition $D_S\ne D_T$ implies that the feature spaces, label spaces, or mapping functions differ between the source and target domains, i.e., ${𝒳}_S\ne {𝒳}_T$, ${𝒴}_S\ne {𝒴}_T$, or $d_S(·)\ne d_T(·)$. Conversely, $T_S\ne T_T$ implies that the tasks differ, either in the subset of the feature space $X_S\ne X_T$ or in the label space ${𝒴}_S\ne {𝒴}_T$.

Enhancing Transfer Learning

Two primary strategies for improving transfer learning outcomes are fine-tuning and weight initialization. Fine-tuning involves initializing a new model with pre-trained weights from the source domain and adapting specific layers to target domain data. This can involve adjusting all layers, or selectively fine-tuning only the last layers tailored to the target task. Weight initialization, by contrast, freezes certain pre-trained layers to retain general feature representations while adapting to the new domain through the remaining layers [19].

Let ${\theta }_S$ represent the learned parameters of the source function $f_S(·)$. In fine-tuning, we initialize the target model $f_T(·)$ with parameters ${\theta }_T={\theta }_S$ and proceed to optimize a subset or the entirety of ${\theta }_T$ using labeled data from $D_T$ to better fit $T_T$. On the other hand, weight initialization can be expressed by partitioning ${\theta }_S$ into two parameter sets, ${\theta }_S^{\mathrm{frozen}}$ and ${\theta }_S^{\mathrm{tunable}}$, such that ${\theta }_T=\{{\theta }_S^{\mathrm{frozen}},{\theta }_S^{\mathrm{tunable}}\}$, where only ${\theta }_S^{\mathrm{tunable}}$ is optimized with the target domain data, preserving the general representations from ${\theta }_S^{\mathrm{frozen}}$ for use in $D_T$.

3. Method

In this section we present Interleaved Fusion Learning (IFL), a new methodology designed to enhance model robustness and bias mitigation. The core concept behind this approach is to develop a sequence of models that effectively perform in their source datasets while adding essential knowledge from other datasets in the sequence. To determine whether this objective is achieved, a comprehensive evaluation framework will be established to assess and compare results across an arbitrary number n of datasets.

In Figure 3, we present a schematic representation of the methodology pipeline. The diagram illustrates the IFL process: initially, each dataset ${𝒟}_i$ is employed to obtain a specific model $f_i$ trained only on this dataset. Furthermore, a global model f is trained on the combined dataset $𝒟={\bigcup }_{i=1}^n{𝒟}_i$. The specific models $f_i$ then undergo the IFL pipeline, to produce a set of final models ${\left\{f_{T_i}\right\}}_{i=1}^n$, each model $f_{T_i}$ specialized in ${𝒟}_i$. Each final model $f_{T_i}$ is evaluated against the global model f on the dataset ${𝒟}_i$, and against its corresponding initial model $f_i$ on the remaining datasets ${𝒟}_j$, with $j\ne i$.

To optimize performance across datasets while ensuring robustness and fairness, we start by formally defining the problem, which serves as the foundation for the proposed methodology.

3.1. Problem Definition

Building on the concepts introduced in Section 2.3, transfer learning offers several key advantages for developing TAI systems. By leveraging transfer learning, models can be designed with enhanced robustness and fairness, mitigating biases inherent in training data while preserving performance specific to the target domain.

One approach to enhancing trustworthiness is through integrating a primary, potentially biased dataset $D_{\mathrm{B}}$, which represents the model’s main objective, with a secondary, less biased or unbiased dataset $D_{\mathrm{U}}$. Transfer learning between these datasets can adjust parameters in a way that preserves key knowledge from $D_{\mathrm{B}}$ while mitigating bias through fine-tuning with $D_{\mathrm{U}}$. Formally, let ${\theta }_{\mathrm{B}}$ and ${\theta }_{\mathrm{U}}$ denote the learned parameters from $D_{\mathrm{B}}$ and $D_{\mathrm{U}}$, respectively. Let ${\theta }_T=\{{\theta }_{\mathrm{B}}^{\mathrm{frozen}},{\theta }_{\mathrm{B}}^{\mathrm{tunable}}\}$ be a partition of ${\theta }_{\mathrm{B}}$, and we can then optimize ${\theta }_T$ such that only ${\theta }_{\mathrm{B}}^{\mathrm{tunable}}$ is fine-tuned using samples from $D_{\mathrm{U}}$, adding robustness against bias while retaining essential information from $D_{\mathrm{B}}$.

The principles outlined above set the foundation for applying sequential transfer learning, where each dataset contributes to refining the model parameters progressively.

3.2. Sequential Transfer Learning

The methodology we propose defines a domain $D=\{𝒳,𝒴,d(·\left)\right\}$ for each dataset, where $𝒳$ is the set of features in the elements of the dataset, $𝒴$ is the set of their possible labels, and d is the optimal function that correctly classifies the features with their corresponding labels. We also define the task $T=\{X,𝒴\}$, where X represents the labeled features of the dataset, i.e., the $x\in 𝒳$ for which the image of $d\left(x\right)$ is known. Specifically, each dataset can be represented as ${𝒟}_i=\{D_i,T_i\}$, where $D_i=\{{𝒳}_i,{𝒴}_i,d_i(·)\}$ defines the domain with feature space ${𝒳}_i$, label space ${𝒴}_i$, and mapping function $d_i(·)$, and $T_i=\{X_i,{𝒴}_i\}$ represents the unique task associated with the labeled subset $X_i\subset {𝒳}_i$ and label space ${𝒴}_i$. Each trained model $f_i$ on a dataset ${𝒟}_i$ functions as a predictive function $f_i(·)$, and its learned parameters ${\theta }_i$ correspond to the weights of $f_i(·)$.

The process is repeated sequentially for every $i\in \{1,\dots ,n\}$, where n is the total number of available datasets. To begin, we define a baseline model $f_i(·)$, trained from scratch using only the source dataset ${𝒟}_i$ , resulting in initial weights ${\theta }_i$. We then construct a sequence by choosing a subsequent index j defined by

$$j=1+\left(\right(i+k-1)modn),$$

(1)

where $k\in \{1,\dots ,n-1\}$ represents the step within the sequence. For each j in this sequence, a model $f_{ij}(·)$ is obtained by training a model in the dataset ${𝒟}_i\cup {𝒟}_j$, initializing it with the weights from training on the previous dataset in the sequence, denoted as ${\theta }_{j_{\left(prev\right)}}$, where

$$j_{\left(prev\right)}=1+((j+k-2)modn).$$

(2)

This sequence continues iteratively through each dataset until we reach $j=i$, obtaining a final model $f_{T_i}(·)$ that has been adapted across all datasets in $\{{𝒟}_1,{𝒟}_2,\dots ,{𝒟}_n\}$. After completing this sequence for a given i, the process is repeated for each $i\in \{1,\dots ,n\}$, resulting in a set of n models ${\left\{f_{T_i}(·)\right\}}_{i=1}^n$, each initialized with a different dataset. A schematic representation of this method is shown in Figure 4.

Let $f(·)$ represent a model trained from scratch on the combined dataset $𝒟={\bigcup }_{i=1}^n{𝒟}_i$. Our goal for each transfer-learned model $f_{T_i}(·)$ is to outperform $f(·)$ when evaluated on its initial dataset ${𝒟}_i$. Additionally, each $f_{T_i}(·)$ should yield better results on any other dataset ${𝒟}_j$ (where $j\ne i$) compared to the baseline model $f_i(·)$, which is trained solely on ${𝒟}_i$. This criterion aims to demonstrate the advantage of transfer learning in enhancing performance consistency and fairness across diverse domains.

Learning Rate Selection for Transfer Learning

For each new dataset ${𝒟}_j$, this methodology aims to set a learning rate that reflects the model’s performance on ${𝒟}_j$. A high learning rate can reduce bias but may cause the model to lose specificity for the source datasets. To balance this trade-off, the new learning rate for transfer learning from ${𝒟}_{j_{\left(\mathrm{prev}\right)}}$ to ${𝒟}_j$ is determined as

$${\eta }_j=min\left({\displaystyle \frac{\sqrt{\lambda }}{|X_j|}}\sum _{x_j\in X_j}𝒜(f_{i{j}_{(\mathrm{prev})}}(x_t)),\lambda \right),$$

(3)

where

$$𝒜\left(f\left(x_t\right)\right)=\left\{\begin{array}{cc}\hfill 1\hfill & \hfill \mathrm{if}{f}_{i{j}_{\left(\mathrm{prev}\right)}}\left(x_t\right)\ne y_t,\hfill \\ \hfill 0\hfill & \hfill \mathrm{if}{f}_{i{j}_{\left(\mathrm{prev}\right)}}\left(x_t\right)=y_t,\hfill \end{array}\right.$$

(4)

with $\lambda \in [0,1]$ controlling the maximum learning rate, and $y_t$ representing the label corresponding each $x_t\in X_j$ in the dataset ${𝒟}_j$.

The choice of this learning rate definition is motivated by several factors. Primarily, we aim for ${\eta }_j\in [0,1]$, as is typical in transfer learning. This holds because the sum ${\sum }_{x_t\in X_j}𝒜(f_{i{j}_{\left(\mathrm{prev}\right)}}\left(x_t\right))$ is an integer in $[0,|X_j\left|\right]$, so dividing by $|X_j|$ normalizes it to $[0,1]$. Multiplying by $\sqrt{\lambda }$, where $\lambda \in [0,1]$, ensures

$$\sqrt{\lambda }·{\displaystyle \frac{{\sum }_{x_t\in X_j}𝒜(f_{i{j}_{\left(\mathrm{prev}\right)}}\left(x_t\right))}{|X_j|}}\in [0,1].$$

(5)

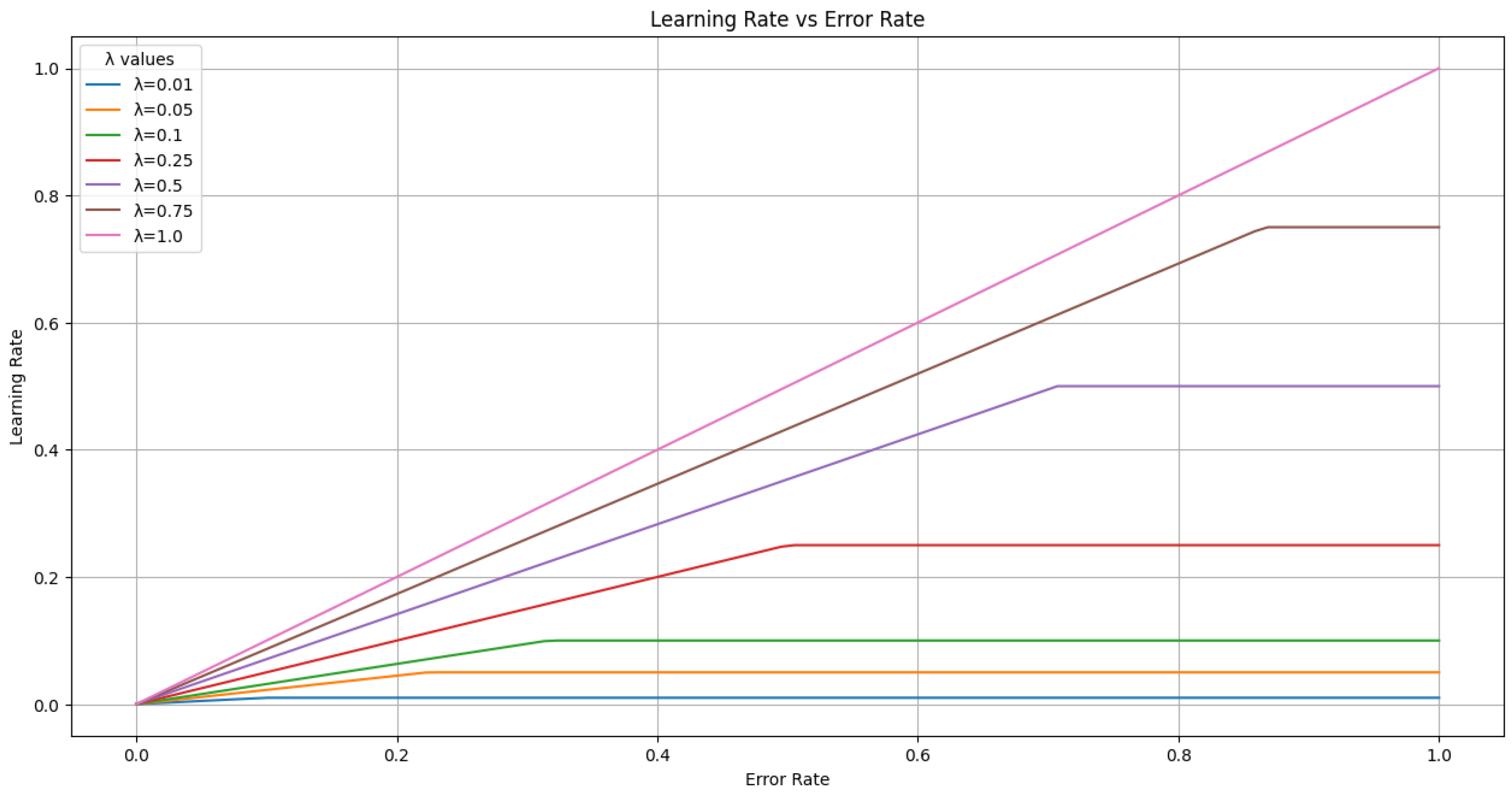
Since ${\eta }_j$ is the minimum of this product and $\lambda$, both in $[0,1]$, it follows that ${\eta }_j\in [0,1]$. The parameter $\lambda$ controls the maximum learning rate, setting an upper bound of ${\eta }_j\le \lambda$. By using $\sqrt{\lambda }$ in the other term of the minimum function, the learning rate is modulated by $\lambda$ even when the error measure is low. This setup allows flexibility to adjust $\lambda$ based on specific model requirements, enabling either a higher or lower learning rate as needed.

In Figure 5, we present a graph to illustrate the possible values of ${\eta }_j$ based on the error rate on the new dataset, ${\sum }_{x_t\in X_j}𝒜(f_{i{j}_{\left(\mathrm{prev}\right)}}\left(x_t\right))/\left|X_j\right|$, and the chosen value of $\lambda$.

3.3. Evaluation

Once $f_{T_i}$ is trained, it is evaluated through two comparisons. First, $f_{T_i}$ is compared to the model f on the initial dataset ${𝒟}_i$. Second, $f_{T_i}$ is compared to $f_i$ on datasets different from ${𝒟}_i$. Figure 6 illustrates these comparisons.

To comprehensively evaluate the performance of our methodology, we designed an evaluation protocol that focuses on three key aspects: (1) measuring cross-domain generalization through a structured performance matrix, (2) analyzing performance deviations to assess consistency and robustness, and (3) benchmarking IFL models against baseline and global models to validate their effectiveness.

3.3.1. Cross-Domain Performance Matrix

To systematically evaluate the IFL models, we propose a cross-domain performance matrix M, where each entry $M_{ij}\left(\mathrm{Metric}\right)$ represents the performance of model $f_{T_i}(·)$ when evaluated on dataset ${𝒟}_j$ using a chosen evaluation metric. The matrix is constructed as follows:

$$M_{ij}\left(\mathrm{Metric}\right)=\mathrm{Metric}\left(f_{T_i}\left({𝒟}_j\right)\right),$$

(6)

where Metric is a user-specified evaluation metric, such as Accuracy, F1-score, or AUC-ROC. The diagonal entries $M_{ii}\left(\mathrm{Metric}\right)$ quantify the model’s performance on its source dataset using the selected metric, while off-diagonal entries $M_{ij}\left(\mathrm{Metric}\right)$ (for $i\ne j$) measure its generalization to other datasets.

3.3.2. Performance Deviation Analysis

We define two aggregate metric vectors to summarize cross-domain performance using the elements of the Cross-Domain Performance Matrix ($M_{ij}\left(\mathrm{Metric}\right)$):

• Cross-Domain Generalization Score (CDGS): The vector whose elements are the average performance of $f_{T_i}(·)$ on all datasets other than its source, computed as

  $${\mathrm{CDGS}}_i\left(\mathrm{Metric}\right)={\displaystyle \frac{1}{n-1}}\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^n{M}_{ij}\left(\mathrm{Metric}\right),$$

  (7)

  where Metric determines the range of ${\mathrm{CDGS}}_i\left(\mathrm{Metric}\right)$. For normalized metrics such as accuracy or F1-score, ${\mathrm{CDGS}}_i\left(\mathrm{Metric}\right)\in [0,1]$. Higher values indicate better generalization across datasets.
• Performance Variance (PV): The vector whose elements are the variance of each $M_{ij}\left(\mathrm{Metric}\right)$ across all datasets, reflecting the consistency of the model’s performance:

  $${\mathrm{PV}}_i\left(\mathrm{Metric}\right)={\displaystyle \frac{1}{n}}\sum _{j=1}^n{\left(M_{ij}\left(\mathrm{Metric}\right)-\overline{M_i}\left(\mathrm{Metric}\right)\right)}^2,$$

  (8)

  where ${\overline{M}}_i\left(\mathrm{Metric}\right)={\displaystyle \frac{1}{n}}{\sum }_{j=1}^n{M}_{ij}\left(\mathrm{Metric}\right)$ is the mean performance of $f_{T_i}(·)$ across all datasets. Lower PV values indicate more consistent performance, while higher values suggest variability or bias. Again, for normalized metrics, we have $M_{ij}\left(\mathrm{Metric}\right)\in [0,1]$, and consequently ${\mathrm{PV}}_i\left(\mathrm{Metric}\right)\in [0,1]$, with smaller values indicating greater consistency across datasets in this case.

3.3.3. Benchmark Comparison Matrix

To validate the effectiveness of our methodology, we construct a benchmark comparison matrix B, which directly mirrors the structure of the cross-domain performance matrix M. The entries of B are defined as follows:

$$B_{ij}\left(\mathrm{Metric}\right)=\left\{\begin{array}{cc}\hfill \mathrm{Metric}\left(f\left({𝒟}_i\right)\right),\hfill & \hfill \mathrm{if}i=j,\hfill \\ \hfill \mathrm{Metric}\left(f_i\left({𝒟}_j\right)\right),\hfill & \hfill \mathrm{if}i\ne j.\hfill \end{array}\right.$$

(9)

The diagonal entries $B_{ii}\left(\mathrm{Metric}\right)$ represent the performance of the global model $f(·)$ on dataset ${𝒟}_i$, while the off-diagonal entries $B_{ij}\left(\mathrm{Metric}\right)$ (for $i\ne j$) capture the performance of the baseline model $f_i(·)$ on the other datasets ${𝒟}_j$.

By directly comparing the cross-domain performance matrix M with the benchmark comparison matrix B, we can evaluate the improvements introduced by the IFL models $f_{T_i}(·)$. Specifically, this comparison enables the following:

• Assessment of Cross-Domain Generalization: Comparing $M_{ij}\left(\mathrm{Metric}\right)$ against $B_{ij}\left(\mathrm{Metric}\right)$ (for $i\ne j$) reveals whether the IFL model $f_{T_i}(·)$ generalizes better to other datasets ${𝒟}_j$ than the baseline model $f_i(·)$.
• Evaluation of Source Dataset Performance: Comparing $M_{ii}\left(\mathrm{Metric}\right)$ with $B_{ii}\left(\mathrm{Metric}\right)$ indicates whether the IFL model $f_{T_i}(·)$ outperforms the global model $f(·)$ on its original dataset ${𝒟}_i$.

This benchmarking approach allows for a straightforward comparison, as each element in both matrices represents a single value of the chosen metric. This simplicity ensures that performance differences can be directly interpreted while preserving the properties of the utilized metric, such as normalization or scale consistency.

4. Results

In this section, we present the results obtained from the application of the proposed IFL methodology, as described in Section 3. The implementation of the IFL methodology was applied with the APACC and CRIC Cervix datasets defined in Section 2.1. In order to increase the dimensionality of the experiment, each dataset was first divided into two halves, resulting in four distinct datasets to facilitate multidimensional analysis: ${𝒟}_{1a}$, ${𝒟}_{1b}$, ${𝒟}_{2a}$, and ${𝒟}_{2b}$, without losing generality. Each of these datasets was further partitioned into training (80%) and validation (20%) subsets, with an equal split to ensure a balanced distribution of “Negative” and “Positive” classes across all partitions. The YOLOv8 architecture, as detailed in Section 2.2, was employed as the base DL model.

4.1. Implementation Details

We begin by providing details about the code implementation specific to our methodology. All code was specifically implemented for this study and executed on an NVIDIA A100 GPU to ensure efficient training and inference.

4.1.1. Training Cost and Deployment Feasibility

Each baseline YOLOv8 model required approximately 4–5 GPU-hours on the NVIDIA A100. Transfer steps were faster, taking around 1–2 GPU-hours each, resulting in a total training cost close to 30 GPU-hours for the full set of experiments. With partial freezing, approximately 35% of the parameters were updated at each step, while the remaining layers were kept frozen to preserve previously acquired features. These figures provide a reference for the computational budget and the feasibility of applying the proposed methodology in practice.

4.1.2. Dataset Preparation and Binary Label Mapping

The datasets were organized in the YOLO format, where each sample $x_t\in X_j$ was an annotated cell with associated bounding boxes and labels $y_t\in 𝒴$. For consistency, the class mappings were defined as

$$𝒴=\{‘‘\mathrm{Negative}’’:0,‘‘\mathrm{Positive}’’:1\}.$$

Both datasets (${𝒟}_j$) were processed to align with the binary classification framework:

• CRIC Cervix: The six Bethesda categories (Figure 1) were mapped to two labels: “Negative” ($y=0$) and “Positive” ($y=1$) as outlined in Section 2.1.
• APACC: The original four classes (Figure 2) were similarly consolidated, with “rubbish” excluded from analysis, resulting in “Negative” ($y=0$) and “Positive” ($y=1$) labels as outlined in Section 2.1.

4.1.3. Model Initialization and Sequential Transfer

The sequential transfer learning methodology was implemented by first training four distinct models, each initialized using one of the four datasets (${𝒟}_{1a}$, ${𝒟}_{1b}$, ${𝒟}_{2a}$, ${𝒟}_{2b}$) as the starting point. The YOLOv8 model $f_j$ for each dataset ${𝒟}_j$ was trained from scratch using the training subset of the dataset. The model was trained for 300 epochs using the hyperparameters detailed in Section 2.2. For each dataset, the training was conducted using

• Initial learning rate (${\eta }_0$): $0.001$.
• Optimizer: Adam.
• Early stopping: Patience of 50 epochs.
• Data augmentation: Enabled.
• Batch size: 16.
• Image size: $640\times 640$ pixels.

After training the initial models $f_{1a}$, $f_{1b}$, $f_{2a}$, and $f_{2b}$, sequential transfer learning was applied to each, reusing the trained weights as initialization for subsequent fine-tuning on the remaining three datasets. During this process, the initial layers were manually frozen to retain previously acquired features. The learning rate ${\eta }_j$ for fine-tuning was calculated dynamically as described in Equation (3), being

• $\lambda =0.001$: Maximum learning rate.
• $|X_j^{\mathrm{val}}|$: Cardinality of the validation set.
• IoU threshold: $0.5$, ensuring prediction–ground truth alignment.
• $𝒜\left(f\left(x_t\right)\right)$: Indicates prediction errors, as defined in Section Learning Rate Selection for Transfer Learning.

This resulted in a total of 12 transfer learning processes, each involving

1.

Validation of the current model $f_{i{j}_{\mathrm{prev}}}$ on $X_j^{\mathrm{val}}$ to calculate ${\eta }_j$.

2.

Fine-tuning the model $f_{ij}$ on the training subset $X_j^{\mathrm{train}}$ of the new dataset ${𝒟}_i$ using the dynamically adjusted ${\eta }_j$.

At the end of each fine-tuning iteration, the model performance was evaluated on $X_j^{\mathrm{val}}$ to assess the impact of the IFL process.

4.2. Evaluation of Performance Matrices

In this section, we focus on evaluating the results summarized in two matrices previously defined in Section 3.3: the Cross-Domain Performance Matrix M, which captures the performance of the IFL models, and the Benchmark Comparison Matrix B, which serves as a baseline for comparison.

4.2.1. Cross-Domain Performance Matrix

The cross-domain performance matrix M summarizes the evaluation of each model $f_{T_i}(·)$ on all datasets ${𝒟}_j$ using accuracy. Results are presented in

Table 1. Cross-Domain Performance Matrix M for F1-score.

Model	${\mathbf{𝒟}}_{1\mathit{a}}$	${\mathbf{𝒟}}_{1\mathit{b}}$	${\mathbf{𝒟}}_{2\mathit{a}}$	${\mathbf{𝒟}}_{2\mathit{b}}$
$f_{T_{1a}}$	0.52	0.59	0.15	0.10
$f_{T_{1b}}$	0.54	0.61	0.14	0.09
$f_{T_{2a}}$	0.50	0.55	0.28	0.19
$f_{T_{2b}}$	0.49	0.56	0.30	0.20

.

Diagonal entries ($M_{ii}$) correspond to evaluations of models on their source datasets, while off-diagonal entries reflect performance on other datasets. This table highlights the cross-domain generalization behavior of the IFL models when measured with F1-score.

4.2.2. Benchmark Comparison Matrix

As stated in Section 3.3, the benchmark comparison matrix B mirrors the structure of M, facilitating a direct comparison. Each entry in B represents the performance of the baseline or global model using the same F1-score metric. Results are shown in

Table 2. Benchmark Comparison Matrix B for F1-score.

${\mathbf{𝒟}}_{1\mathit{a}}$	${\mathbf{𝒟}}_{1\mathit{b}}$	${\mathbf{𝒟}}_{2\mathit{a}}$	${\mathbf{𝒟}}_{2\mathit{b}}$
0.55	0.60	0	0
0.53	0.62	0	0.02
0	0	0.26	0.18
0	0	0.21	0.17

.

Diagonal entries ($B_{ii}$) capture the performance of the global model f on each dataset ${𝒟}_i$, while off-diagonal entries reflect the baseline models $f_i$ evaluated on other datasets ${𝒟}_j$ ($j\ne i$). As the matrix contains results of two different models in each row, the column models. In order to evaluate the IFL models performance, we compare the elements of matrix B with their corresponding entries in matrix M. For any $i,j\in \{1,\dots ,n\}$, if $M_{ij}>B_{ij}$, it indicates that the IFL model outperforms its corresponding baseline model on the given dataset.

4.3. Generalization and Consistency Analysis

The generalization and consistency of the models are analyzed using Cross-Domain Generalization Score (CDGS) and Performance Variance (PV) for the Accuracy, as defined in Equations (7) and (8), respectively:

$$\mathrm{CDGS}=[0.2567,0.2333,0.4200,0.4700],\mathrm{PV}=[0.0621,0.0711,0.0284,0.0245].$$

CDGS reflects the average performance of a model on datasets other than its source, while PV measures the variability in performance across datasets. Blank cells indicate entries where indices coincide, as they are not relevant for cross-domain evaluation. These tables allow direct comparison between IFL models ($f_{T_i}$) and their respective baselines ($f_i$).

5. Discussion

The results of this study offer valuable insights into the application of the novel IFL method, specifically in the context of cervical cytology image analysis. The methodology presented is versatile and holds significant potential for broader applications across various domains. However, several important considerations arise when interpreting these findings.

In our experiment, 2 out of the 16 models do not improve their specific benchmark models. Specifically, the model $f_{T_{1a}}$ did not surpass the global model f on dataset ${𝒟}_{1a}$, and the model $f_{T_{1b}}$ has the same accuracy as the global model f on dataset ${𝒟}_{1b}$, even though the rest of the models either matched or exceeded the anticipated performance. This discrepancy highlights the challenges in ensuring consistent improvement across all models and datasets.

The APACC and CRIC Cervix datasets, while extensive and well-annotated, are the only publicly available datasets that meet the requirements for this study, particularly the detailed labeling and high resolution needed for both detection and classification tasks. Splitting these datasets allows for multidimensional analysis and IFL experimentation, but it may also reduce the diversity and variability within each subset. Future work could address this limitation by incorporating additional datasets, either from the domain of cervical cancer or from other medical imaging fields, to test the generalizability of the methodology across entirely different domains. This expansion could further validate the robustness of the proposed approach and explore its applicability to other pathologies. We also have to note that the selected order of the experiment could have varied. We chose the assignments $\{{𝒟}_{1a}={𝒟}_1,{𝒟}_{1b}={𝒟}_2,{𝒟}_{2a}={𝒟}_3,{𝒟}_{2b}={𝒟}_4\}$, but there are $4!=24$ possible permutations, and we can choose $3!=6$ different permutations with different cycle order. Each permutation could potentially yield specific results due to differences in training order influencing the observed outcomes. Future research could explore the impact of such permutations systematically. This analysis could provide additional insights into the stability and optimality of the training process for transfer learning and multidimensional experiments.

Another critical factor in the methodology is the choice of the parameter $\lambda$, which governs the maximum learning rate during transfer learning. As shown in Section Learning Rate Selection for Transfer Learning, $\lambda$ directly influences the adaptability of the model to new datasets. A higher $\lambda$ allows for faster adaptation but risks overfitting to the target dataset, potentially causing the model to lose important information from its source domain. Conversely, a lower $\lambda$ enforces more conservative updates, which can preserve knowledge from the source dataset but might limit the model’s ability to effectively learn features specific to the new domain. Optimizing $\lambda$ for each transfer step is therefore crucial, and future studies could explore adaptive or data-driven methods for determining this parameter to achieve an optimal balance between source retention and target adaptation. As illustrated in Figure 5, the learning rate cap $\lambda$ mainly scales the error-dependent update. Preliminary checks showed that values in the range $[{10}^{-4},{10}^{-2}]$ produced near-identical accuracy, with fluctuations comparable to the variance observed across random seeds. While this indicates that $\lambda$ has limited influence under the present conditions, we acknowledge its potential relevance in larger or more heterogeneous settings and identify it as a promising direction for future work. In addition, Equation (3) offers a more stable and interpretable alternative to validation loss or gradient-based schedulers, which can fluctuate under class imbalance or noisy labels.

Preliminary checks indicated that variations in interleaving, learning rate schedule (fixed vs. dynamic), dataset order, and freezing policy produced only marginal changes, generally within the variance observed across random seeds. While this suggests that these design factors are not decisive in our current datasets, we acknowledge that they may become more influential in larger or more heterogeneous settings. For this reason, we did not include a full ablation grid in the main results, but we explicitly note this as a limitation and highlight it as a relevant direction for future research.

YOLOv8 was selected as it integrates detection and classification in a single pipeline and represents the state of the art in many recent medical imaging works, making it especially suitable for cytology where abnormal cells must be first localized. Alternative backbones such as ViT, Swin, or ConvNeXt achieve strong results on isolated cell crops, but do not address whole-slide detection. Importantly, our Interleaved Fusion Learning framework is architecture-agnostic: the sequential transfer and dynamic learning rate adaptation can be applied to any network supporting fine-tuning, and could in future be explored with CNN or transformer backbones.

For the evaluation, in Section 3.3, by explicitly incorporating Metric into the definitions of $M_{ij}\left(\mathrm{Metric}\right)$, ${\mathrm{CDGS}}_i\left(\mathrm{Metric}\right)$, and ${\mathrm{PV}}_i\left(\mathrm{Metric}\right)$, this framework remains adaptable to different evaluation needs. For example, if fairness is a key concern, one might prioritize metrics such as the F1-score or balanced accuracy, as they are particularly suited to scenarios with class imbalances or where equitable performance across classes is critical. We acknowledge that the absolute accuracies remain modest. However, the focus here is not on achieving state-of-the-art single-dataset results, but on showing consistent improvements over global and local baselines, indicating that residual knowledge can indeed be preserved and transferred. Direct comparison with alternative approaches was intentionally avoided, as their objectives and setups differ substantially. Depending on the chosen metric, these methods could appear either superior or inferior, leading to potentially misleading conclusions. Instead, the most meaningful baselines for assessing IFL are the global and local training strategies across datasets, which directly reflect its goal of preserving and transferring residual knowledge between domains.

The structured methodology relies on curated binary class mappings and dynamic learning rate adjustments. While these choices have been effective for the current datasets, they may require modifications for datasets with more complex label distributions or larger imbalances. Investigating methods to handle multi-class problems or severe label imbalances within this IFL framework could expand its utility and improve its fairness in real-world applications.

In Section 2.3, a new notation for domains in transfer learning was introduced to address inconsistencies identified in previous literature. Although these studies provide initial domain definitions, their practical application often involves inconsistent alterations, resulting in discrepancies between the theoretical framework and its implementation. The revised notation seeks to promote a consistent and coherent use of domain definitions, improving the clarity and reproducibility of transfer learning methodologies.

Although the present study employed binary mappings to simplify the evaluation, it is important to acknowledge that many medical applications, including cervical cytology, are inherently multi-class in nature, with diagnostic categories such as NILM, ASC-US, LSIL, HSIL, and SCC. Extending the IFL framework to these settings is not trivial, as class overlap, hierarchical relationships, and unequal misclassification costs become critical factors. Furthermore, severe class imbalance remains a pervasive challenge in medical data, where minority categories, although clinically decisive, are often underrepresented. While balanced accuracy and F1-score partially mitigate these effects, future work should explore the integration of imbalance-aware strategies such as cost-sensitive losses, resampling techniques, or hierarchical classification schemes within the IFL pipeline. Addressing these two aspects—multi-class complexity and class imbalance—is essential to ensure that performance improvements are equitably distributed across categories.

In conclusion, while the IFL methodology demonstrates clear advantages in improving performance and robustness, the study also underscores the need for broader dataset diversity, careful parameter selection, and enhanced interpretability. These factors should guide future research to maximize the impact and applicability of IFL in medical imaging and beyond.

6. Conclusions

The results, summarized in Section 4, highlight key advantages of the IFL models ($f_{T_i}$) over both the baseline models ($f_i$) trained solely on their respective source datasets and the combined dataset model ($f(·)$) trained on the entire dataset $𝒟$.

This work not only advances the field by proposing a novel IFL methodology but also provides a comprehensive set of practical tools to support future research. These tools include methods for the informed and systematic selection of learning rates, offering a structured optimization process based on our proposed dynamic learning rate for transfer steps. In the method, we provide a novel evaluation stage designed to accommodate diverse performance metrics, such as fairness, robustness, or domain-specific criteria. In addition, we address longstanding inconsistencies in transfer learning notation by presenting an enhanced and standardized framework. Collectively, these contributions establish a solid foundation for further developments in IFL and transfer learning methodologies.

In the studied cervix datasets, the IFL models exhibit consistent improvements in cross-domain generalization, as evidenced by values presented in Table 1. These models generally achieve higher accuracy on datasets other than their sources compared to the baseline models, demonstrating their ability to retain critical knowledge from the source dataset while adapting to new domains. The low PV values further support the robustness of the IFL models, indicating a relatively consistent performance across datasets.

These findings underscore the potential of IFL to enhance the robustness and fairness of DL models in complex multi-domain settings. Future work will focus on expanding the methodology to incorporate additional metrics, such as fairness measures, and exploring its applicability to other medical imaging domains. Furthermore, integrating explainability techniques could provide additional insights into the decision-making processes of the IFL models, facilitating their adoption in clinical practice.