Large Language Models for Structured Task Decomposition in Reinforcement Learning Problems with Sparse Rewards
Abstract
1. Introduction
- We perform a detailed evaluation of different LLMs, identifying the most effective models for the teacher role in our proposed framework.
- We identify the most effective subgoal encoding that enables agents to perceive and act on them.
- We develop a scalable method for LLM integration, reducing computational costs and ensuring practical applicability in real-world settings.
2. Related Work
2.1. Curriculum Learning
2.2. Hierarchical Reinforcement Learning
2.3. LLM-Enhanced RL
2.4. Contribution
3. Proposed Framework and Methodology
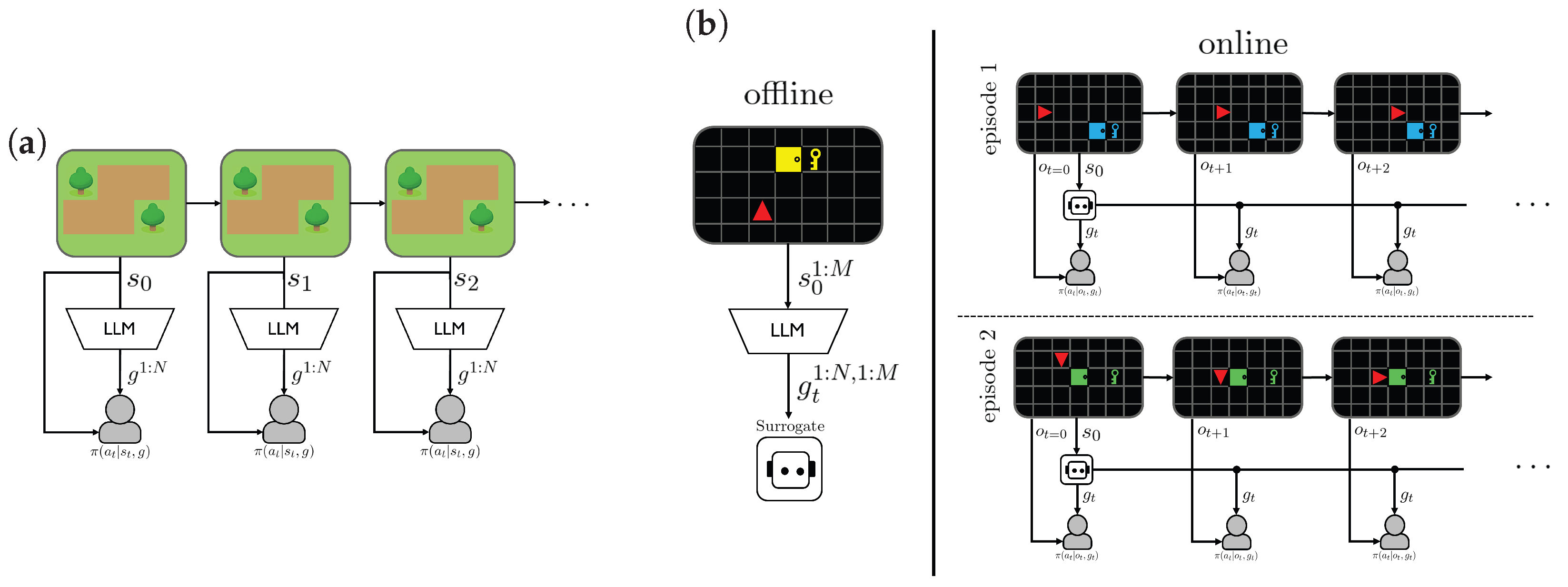
3.1. Subgoal Generation
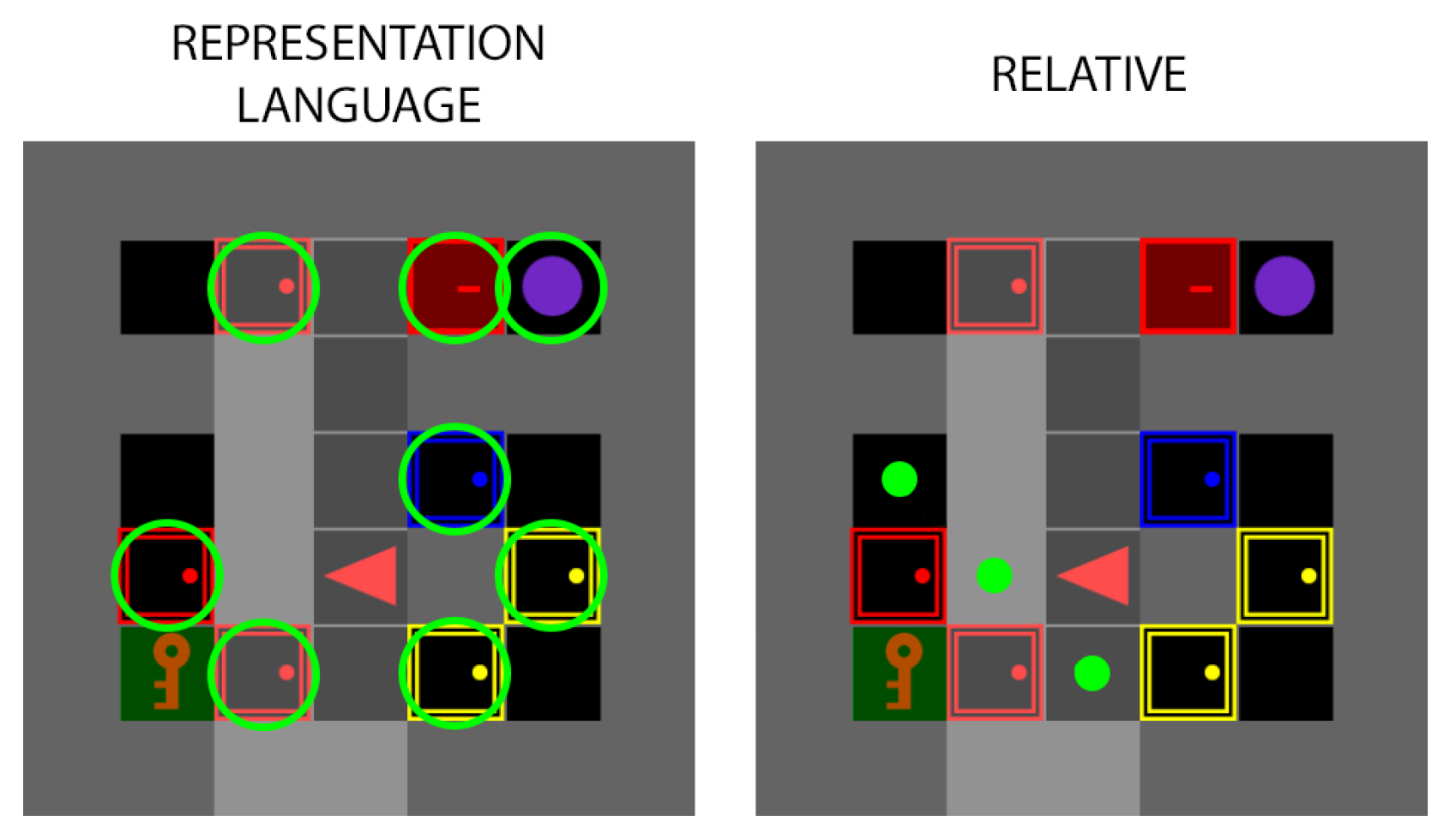
3.2. Subgoal Representation
- Position-based subgoals are defined in terms of coordinates provided by the environment (e.g., in 2D or in 3D). In discrete domains, these subgoals represent a point in space, whereas in continuous domains they denote a target region. While intuitive, this approach assumes the agent can infer directional relationships and may suffer from misalignment when the LLM inaccurately predicts object positions.
- Representation-based subgoals are defined in terms of identifiable components or features of the environment’s state, which the agent perceives through its observations . In object-based domains, this could correspond to the representation of a specific object, while in image-based domains, it could correspond to an element detected through perception modules. This approach can be limited in novel or unseen scenarios since subgoals are tightly linked to predefined state representations.
- Language-based subgoals are derived from LLM-generated text, which is especially effective when the task cannot be directly expressed as an element of the environment. The text is then converted into embeddings using a pretrained language encoder, allowing the subgoals to be represented in a continuous vector space. To reduce the complexity of handling diverse natural language instructions, we first construct a fixed pool of environment-relevant subgoals. This pool is generated by enumerating all objects and their attributes and combining them with a set of predefined actions. Each resulting subgoal phrase is then converted into a vector embedding. When a new instruction is received, it is similarly converted into an embedding and matched to the closest canonical subgoal in the pool using cosine similarity.
3.3. Modeling LLM–Surrogate Subgoal Generation
- Positional errors: For position-based subgoals, we measure the distance between the LLMs’ proposed coordinates and the oracle’s optimal coordinates .
- Semantic errors: For representation-based and language-based subgoals, we evaluate mismatches in object type, state, or sequence.
| Algorithm 1 Surrogate LLM framework |
|
4. Experimental Setup
- MultiRoomN2S4 and MultiRoomN4S5: Navigation tasks requiring the agent to traverse multiple rooms.
- KeyCorridorS3R3 and KeyCorridorS6R3: Tasks involving key retrieval and door unlocking in increasingly complex layouts.
- ObstructedMaze1Dlh and ObstructedMaze1Dlhb: Challenging maze navigation tasks with obstructed paths and objects.
4.1. Algorithm and Model Architecture
4.2. Hyperparameter Configuration
4.3. Metrics
- Accuracy: The ratio of correct subgoal predictions to total predicted subgoals:
- Correct SGs/Total: The number of correct subgoals identified by the LLM compared to the total number of subgoals.
- Correct EPs/Total: The number of complete episodes where all subgoals were correctly predicted.
- Manhattan distance: Average distance between predicted and actual subgoal positions:with standard deviation:
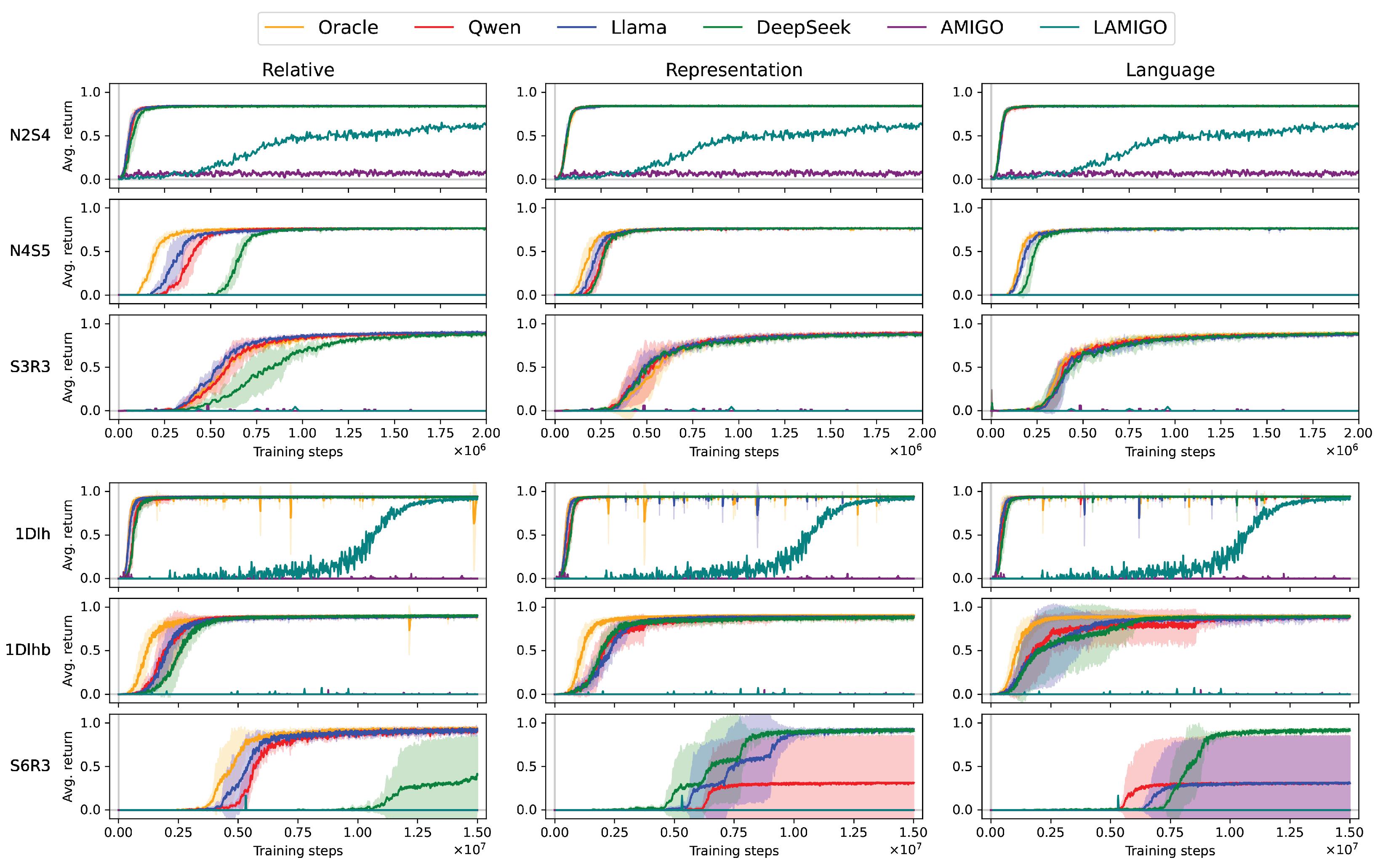
5. Results
5.1. Surrogate LLM Evaluation
5.2. Policy Training Evaluation
5.2.1. LLMs’ Lack of Spatial Reasoning
5.2.2. Analysis of Subgoal Strategies
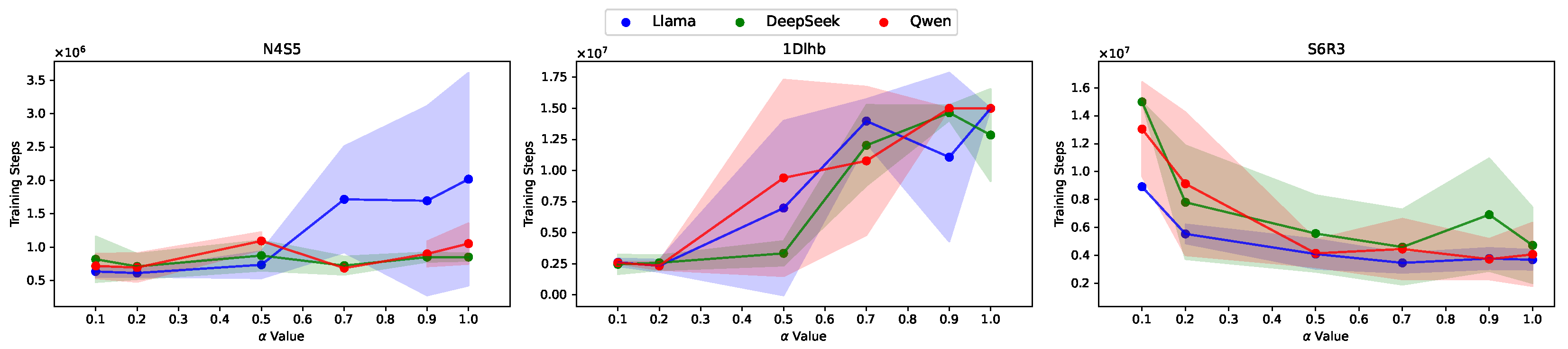
5.2.3. Sensitivity Analysis of Subgoal Reward Balance
5.3. Ablation Study: Impact of Subgoals and Rewards
- No Reward: In this setup, agents receive representation-based subgoals in their observation, but no supplementary rewards for achieving them. Results show that agents fail to learn in environments with long reward horizons, namely, MultiRoomN4S5, KeyCorridorS3R3, KeyCorridorS6R3, and ObstructedMaze1Dlhb (Figure 5, first and third columns). This highlights the critical role of rewards in guiding exploration and reinforcing task completion, particularly in complex scenarios where subgoals alone are insufficient to bridge the reward gap. However, in environments with shorter reward horizons, such as MultiRoomN2S4 and ObstructedMaze1Dlh, agents successfully learn the task even without supplementary rewards, as the reduced complexity allows subgoals to provide sufficient guidance.
- No Subgoal: Agents receive supplementary rewards for subgoal completion but do not have access to subgoals in their observation space. Agents still perform well in this condition, achieving convergence comparable to setups where subgoals are explicitly provided (compare Figure 5, which shows training without subgoals, to Figure 3, which shows training with subgoals). For example, in ObstructedMaze1Dlh, access to subgoals leads to substantially faster convergence, with Qwen and Llama improving by roughly 20% and DeepSeek by about 12.5%. A similar trend is observed in KeyCorridorS6R3, where all models converge approximately 15% faster when subgoals are available. However, once the underlying policy has been fully acquired, subgoals in the observation space are no longer necessary for successful task completion, suggesting that incorporating subgoals into the agent’s observation space primarily serves to accelerate training.
6. Conclusions and Future Work
Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Prompts Used for Subgoal Generation



Appendix B. Training Solely with Oracle Data Is Insufficient
Appendix B.1. Experimental Setup
- Oracle-generated data: The agent is trained on a perfectly curated data set.
- Surrogate LLM data: The agent is trained on data generated by a surrogate LLM (e.g., Llama or DeepSeek).
- Training: Agents are trained on either oracle-generated data or surrogate LLM data.
- Evaluation: The trained agents are evaluated on real-world LLMs to measure their effectiveness.

| Oracle → Llama | Oracle → DeepSeek | Llama → Llama | DeepSeek → DeepSeek | ||
|---|---|---|---|---|---|
| Metric | Subgoal Type | ||||
| Mean | Position | 72.77 | 55.15 | 97.87 | 99.79 |
| Representation | 62.95 | 73.87 | 89.61 | 91.88 | |
| Language | 63.01 | 72.07 | 78.21 | 85.54 | |
| Median | Position | 83.60 | 53.50 | 99.50 | 99.80 |
| Representation | 81.35 | 84.60 | 98.70 | 99.80 | |
| Language | 93.30 | 87.00 | 99.70 | 100.00 | |
| IQR | Position | 36.58 | 34.75 | 1.47 | 0.30 |
| Representation | 66.93 | 43.55 | 3.60 | 1.75 | |
| Language | 90.32 | 50.20 | 38.15 | 0.30 |
Appendix B.2. Insights and Implications of Training with Surrogate LLM Data
Appendix C. LLM Accuracy Evaluation
| Algorithm A1 LLM Accuracy Evaluation |
|
Appendix D. Subgoal Types with Illustrative Examples
Appendix D.1. Position-Based Subgoals

Appendix D.2. Representation-Based Subgoals
Appendix D.3. Language-Based Subgoals
Appendix E. Adaptive Closer Subgoals
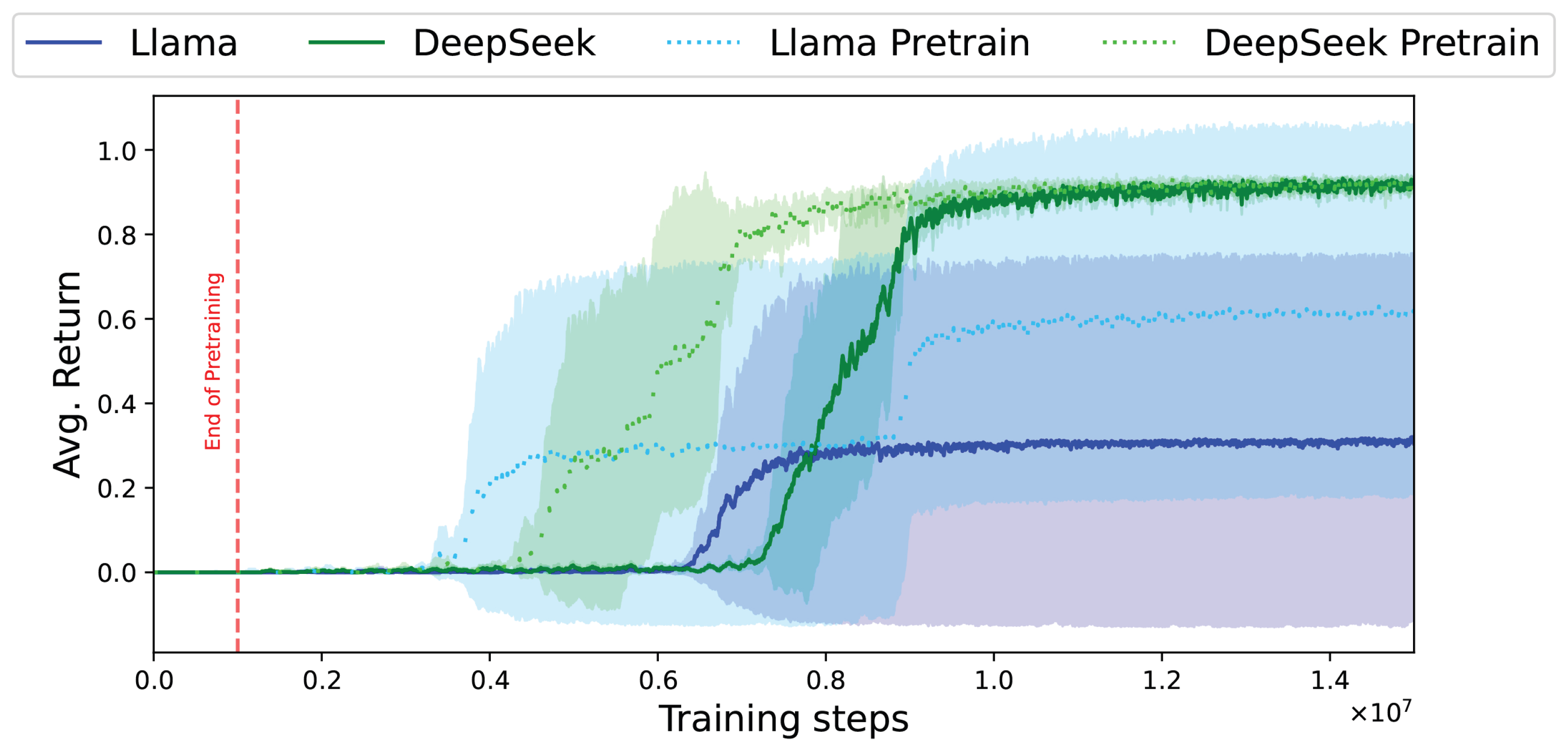
- Pretraining phase: The RL agent is initially trained for 1 million steps using subgoals that are close to the agent’s starting position, making them easily achievable. This phase mimics the behavior of a less accurate LLM by providing subgoals that are relatively simple, ensuring the agent can achieve them with minimal effort.
- Training phase: After pretraining, the agent transitions to standard training using subgoals generated by the surrogate LLM. By this stage, the agent has already developed an understanding of how to follow subgoals provided by the LLM, which enhances training efficiency.
References
- Pathak, D.; Agrawal, P.; Efros, A.A.; Darrell, T. Curiosity-driven exploration by self-supervised prediction. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, NSW, Australia, 6–11 August 2017. [Google Scholar]
- Rengarajan, D.; Vaidya, G.; Sarvesh, A.; Kalathil, D.; Shakkotta, S. Reinforcement Learning with Sparse Rewards using Guidance from Offline Demonstration. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual, 25–29 April 2022. [Google Scholar]
- Klink, P.; D’Eramo, C.; Peters, J.R.; Pajarinen, J. Self-paced deep reinforcement learning. In Proceedings of the Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 6–12 December 2020; Volume 33, pp. 9216–9227. [Google Scholar]
- Andres, A.; Schäfer, L.; Albrecht, S.V.; Del Ser, J. Using offline data to speed up reinforcement learning in procedurally generated environments. Neurocomputing 2025, 618, 129079. [Google Scholar] [CrossRef]
- Vezhnevets, A.S.; Osindero, S.; Schaul, T.; Heess, N.; Jaderberg, M.; Silver, D.; Kavukcuoglu, K. Feudal networks for hierarchical reinforcement learning. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, NSW, Australia, 6–11 August 2017. [Google Scholar]
- Anand, D.; Gupta, V.; Paruchuri, P.; Ravindran, B. An enhanced advising model in teacher-student framework using state categorization. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 6653–6660. [Google Scholar]
- Hu, S.; Huang, T.; Liu, G.; Kompella, R.R.; Ilhan, F.; Tekin, S.F.; Xu, Y.; Yahn, Z.; Liu, L. A survey on large language model-based game agents. arXiv 2024, arXiv:2404.02039. [Google Scholar] [CrossRef]
- Pham, D.H.; Le, T.; Nguyen, H.T. How rationals boost textual entailment modeling: Insights from large language models. Comput. Electr. Eng. 2024, 119, 109517. [Google Scholar] [CrossRef]
- Ruiz-Gonzalez, U.; Andres, A.; Bascoy, P.G.; Ser, J.D. Words as Beacons: Words as Beacons: Guiding RL Agents with High-Level Language Prompts. In Proceedings of the NeurIPS 2024 Workshop on Open-World Agents, Vancouver, BC, Canada, 15 December 2024. [Google Scholar]
- Chevalier-Boisvert, M.; Dai, B.; Towers, M.; de Lazcano, R.; Willems, L.; Lahlou, S.; Pal, S.; Castro, P.S.; Terry, J. Minigrid & Miniworld: Modular & customizable reinforcement learning environments for goal-oriented tasks. In Proceedings of the 37th International Conference on Neural Information Processing System, Orleans, LA, USA, 10–16 December 2023; Volume 36, pp. 73383–73394. [Google Scholar]
- Elman, J.L. Learning and development in neural networks: The importance of starting small. Cognition 1993, 48, 71–99. [Google Scholar] [CrossRef] [PubMed]
- Mu, J.; Zhong, V.; Raileanu, R.; Jiang, M.; Goodman, N.; Rocktäschel, T.; Grefenstette, E. Improving intrinsic exploration with language abstractions. In Proceedings of the Neural Information Processing Systems (NeurIPS), New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum learning. In Proceedings of the International Conference on Machine Learning (ICML), Montreal, QC, Canada, 14–18 June 2009; pp. 41–48. [Google Scholar]
- Graves, A.; Bellemare, M.G.; Menick, J.; Munos, R.; Kavukcuoglu, K. Automated curriculum learning for neural networks. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, NSW, Australia, 6–11 August 2017; pp. 1311–1320. [Google Scholar]
- Hacohen, G.; Weinshall, D. On the power of curriculum learning in training deep networks. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 10–15 June 2019; pp. 2535–2544. [Google Scholar]
- Platanios, E.A.; Stretcu, O.; Neubig, G.; Poczos, B.; Mitchell, T.M. Competence-based curriculum learning for neural machine translation. In Proceedings of the Nations of the Americas Chapter of the Association for Computational Linguistics (NAACL), Minneapolis, MN, USA, 2–7 June 2019; pp. 1151–1161. [Google Scholar]
- Matiisen, T.; Oliver, A.; Cohen, T.; Schulman, J. Teacher–student curriculum learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3732–3740. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Grefenstette, E.; Rocktaschel, T. Prioritized Level Replay. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; Volume 139, pp. 4940–4950. [Google Scholar]
- Kanitscheider, I.; Huizinga, J.; Farhi, D.; Guss, W.H.; Houghton, B.; Sampedro, R.; Zhokhov, P.; Baker, B.; Ecoffet, A.; Tang, J.; et al. Multi-task curriculum learning in a complex, visual, hard-exploration domain: Minecraft. arXiv 2021, arXiv:2106.14876. [Google Scholar]
- Racanière, S.; Lampinen, A.K.; Santoro, A.; Reichert, D.P.; Firoiu, V.; Lillicrap, T.P. Automated curricula through setter-solver interactions. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Campero, A.; Raileanu, R.; Kuttler, H.; Tenenbaum, J.B.; Rocktaschel, T.; Grefenstette, E. Learning with AMIGo: Adversarially motivated intrinsic goals. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual, 3–7 May 2021. [Google Scholar]
- Florensa, C.; Held, D.; Geng, X.; Abbeel, P. Automatic goal generation for reinforcement learning agents. In Proceedings of the International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 1515–1528. [Google Scholar]
- Dayan, P.; Hinton, G.E. Feudal Reinforcement Learning. In Proceedings of the Neural Information Processing Systems (NeurIPS), Denver, CO, USA, 30 November–3 December 1992; Volume 5, pp. 271–278. [Google Scholar]
- Jiang, Y.; Gu, S.S.; Murphy, K.P.; Finn, C. Language as an abstraction for hierarchical deep reinforcement learning. In Proceedings of the Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Goecks, V.G.; Waytowich, N.R.; Watkins-Valls, D.; Prakash, B. Combining learning from human feedback and knowledge engineering to solve hierarchical tasks in minecraft. In Proceedings of the Machine Learning and Knowledge Engineering for Hybrid Intelligence (AAAI-MAKE), Stanford University, Palo Alto, CA, USA, 21–23 March 2022. [Google Scholar]
- Prakash, R.; Pavlamuri, S.; Chernova, S. Interactive Hierarchical Task Learning from Language Instructions and Demonstrations; Association for Computational Linguistics: Stroudsburg, PA, USA, 2021. [Google Scholar]
- Prakash, B.; Oates, T.; Mohsenin, T. Using LLMs for augmenting hierarchical agents with common sense priors. In Proceedings of the International FLAIRS Conference, Daytona Beach, FL, USA, 20–23 May 2024; Volume 37. [Google Scholar]
- Shridhar, M.; Yuan, X.; Cote, M.A.; Bisk, Y.; Trischler, A.; Hausknecht, M. ALFWorld: Aligning Text and Embodied Environments for Interactive Learning. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual, 3–7 May 2021. [Google Scholar]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language Models Are Unsupervised Multitask Learners; OpenAI Blog: San Francisco, CA, USA, 2019. [Google Scholar]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. In Proceedings of the Neural Information Processing Systems (NeurIPS), Virtual, 6–12 December 2020; Volume 33, pp. 1877–1901. [Google Scholar]
- Achiam, J.; Adler, S.; Agarwal, S.; Ahmad, L.; Akkaya, I.; Aleman F., L.; Almeida, D.; Altenschmidt, J.; Altman, S.; Anadkat, S.; et al. GPT-4 Technical Report; OpenAI Blog: San Francisco, CA, USA, 2023. [Google Scholar]
- Touvron, H.; Lavril, T.; Izacard, G.; Martinet, X.; Lachaux, M.; Lacroix, T.; Rozière, B.; Goyal, N.; Hambro, E.; Azhar, F.; et al. Llama: Open and efficient foundation language models. arXiv 2023, arXiv:2302.13971. [Google Scholar] [CrossRef]
- Bai, J.; Bai, S.; Chu, Y.; Cui, Z.; Dang, K.; Deng, X.; Fan, Y.; Ge, W.; Han, Y.; Huang, F.; et al. Qwen Technical Report. arXiv 2023, arXiv:2309.16609. [Google Scholar] [CrossRef]
- Bi, X.; Chen, D.; Chen, G.; Chen, S.; Dai, D.; Deng, C.; Ding, H.; Dong, K.; Du, Q.; Fu, Z.; et al. DeepSeek LLM: Scaling open-source language models with longtermism. arXiv 2024, arXiv:2401.02954. [Google Scholar]
- Cao, Y.; Zhao, H.; Cheng, Y.; Shu, T.; Chen, Y.; Liu, G.; Liang, G.; Zhao, J.; Yan, J.; Li, Y.; et al. Survey on large language model-enhanced reinforcement learning: Concept, taxonomy, and methods. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 9737–9757. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Puig, X.; Paxton, C.; Du, Y.; Wang, C.; Fan, L.; Chen, T.; Huang, D.; Akyürek, E.; Anandkumar, A.; et al. Pre-trained language models for interactive decision-making. In Proceedings of the Neural Information Processing Systems (NeurIPS), New Orleans, LA, USA, 28 November–9 December 2022; Volume 35, pp. 31199–31212. [Google Scholar]
- Carta, T.; Romac, C.; Wolf, T.; Lamprier, S.; Sigaud, O.; Oudeyer, P. Grounding large language models in interactive environments with online reinforcement learning. In Proceedings of the International Conference on Machine Learning (ICML), Honolulu, HI, USA, 23–29 July 2023; pp. 3676–3713. [Google Scholar]
- Ma, Y.J.; Liang, W.; Wang, G.; Huang, D.; Bastani, O.; Jayaraman, D.; Zhu, Y.; Fan, L.; Anandkumar, A. Eureka: Human-level reward design via coding large language models. arXiv 2023, arXiv:2310.12931. [Google Scholar]
- Kwon, M.; Xie, S.M.; Bullard, K.; Sadigh, D. Reward design with language models. In Proceedings of the International Conference on Learning Representations (ICLR), Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Klissarov, M.; D’Oro, P.; Sodhani, S.; Raileanu, R.; Bacon, P.; Vincent, P.; Zhang, A.; Henaff, M. Motif: Intrinsic motivation from artificial intelligence feedback. In Proceedings of the International Conference on Learning Representations (ICLR), Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Klissarov, M.; Henaff, M.; Raileanu, R.; Sodhani, S.; Vincent, P.; Zhang, A.; Bacon, P.; Precup, D.; Machado M., C.; D’Oro, P. MaestroMotif: Skill Design from Artificial Intelligence Feedback. In Proceedings of the International Conference on Learning Representations (ICLR), Singapore, 24–28 April 2025. [Google Scholar]
- Wang, Z.; Cai, S.; Chen, G.; Liu, A.; Ma, X.; Liang, Y. Describe, Explain, Plan and Select: Interactive planning with large language models enables open-world multi-task agents. In Proceedings of the Neural Information Processing Systems (NeurIPS), New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Du, Y.; Watkins, O.; Wang, Z.; Colas, C.; Darrell, T.; Abbeel, P.; Gupta, A.; Andreas, J. Guiding Pretraining in reinforcement learning with large language models. In Proceedings of the International Conference on Machine Learning (ICML), Honolulu, HI, USA, 23–29 July 2023; pp. 8657–8677. [Google Scholar]
- Pignatelli, E.; Ferret, J.; Rockaschel, T.; Grefenstette, E.; Paglieri, D.; Coward, S.; Toni, L. Assessing the Zero-Shot Capabilities of LLMs for Action Evaluation in RL. arXiv 2024, arXiv:2409.12798. [Google Scholar]
- Ahn, M.; Brohan, A.; Brown, N.; Chebotar, Y.; Cortes, O.; David, B.; Finn, C.; Fu, C.; Gopalakrishnan, K.; Hausman, K.; et al. Do as i can, not as i say: Grounding language in robotic affordances. In Proceedings of the Conference on Robot Learning (CoRL), Auckland, New Zealand, 14–18 December 2022; pp. 287–318. [Google Scholar]
- Wang, Z.; Cai, S.; Liu, A.; Jin, Y.; Hou, J.; Zhang, B.; Lin, H.; He, Z.; Zheng, Z.; Yang, Y.; et al. JARVIS-1: Open-world multi-task agents with memory-augmented multimodal language models. arXiv 2023, arXiv:2311.05997. [Google Scholar] [CrossRef]
- Cobbe, K.; Hesse, C.; Hilton, J.; Schulman, J. Leveraging Procedural Generation to Benchmark Reinforcement Learning. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; Volume 119, pp. 2048–2056. [Google Scholar]
- Emani, M.; Foreman, S.; Sastry, V.; Xie, Z.; Raskar, S.; Arnold, W.; Thakur, R.; Vishwanath, V.; Papka, M.E. A Comprehensive Performance Study of Large Language Models on Novel AI Accelerators. arXiv 2023, arXiv:2310.04607. [Google Scholar] [CrossRef]
- Reynolds, L.; McDonell, K. Prompt programming for large language models: Beyond the few-shot paradigm. In Proceedings of the CHI Conference on Human Factors in Computing Systems, Yokohama, Japan, 8–13 May 2021. [Google Scholar]
- Kojima, T.; Gu, S.S.; Reid, M.; Matsuo, Y.; Iwasawa, Y. Large language models are zero-shot reasoners. In Proceedings of the 36th International Conference on Neural Information Processing System, New Orleans, LA, USA, 28 November–9 December 2022; Volume 35, pp. 22199–22213. [Google Scholar]
- Reimers, N.; Gurevych, I. all-MiniLM-L6-v2: Sentence Embeddings Using MiniLM-L6-v2. 2024. Available online: https://huggingface.co/sentence-transformers/all-MiniLM-L6-v2 (accessed on 22 August 2025).
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Andres, A.; Villar-Rodriguez, E.; Del Ser, J. An evaluation study of intrinsic motivation techniques applied to reinforcement learning over hard exploration environments. In Proceedings of the International Cross-Domain Conference for Machine Learning and Knowledge Extraction; Springer: Vienna, Austria, 2022; pp. 201–220. [Google Scholar]
- Padakandla, S. A Survey of Reinforcement Learning Algorithms for Dynamically Varying Environments. ACM Comput. Surv. 2021, 54, 1–35. [Google Scholar] [CrossRef]

| Method | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| AMIGO [21] | ✗ | ✗ | ✓ | Trains an adversarial teacher to generate subgoals that guide the agent to explore the state space efficiently. |
| LAMIGO [12] | ✗ | ✗ | ✓ | Extends AMIGO by representing subgoals as natural language instructions, enabling text-based guidance. |
| LLMxHRL [27] | ✓ | ✗ | ✓ | Leverages an LLM to provide commonsense priors, which guide a hierarchical agent in generating and interpreting subgoals. |
| ELLM [43] | ✗ | ✓ | ✓ | Uses LLM to propose non-sequential, diverse skills, without task-specific sequencing. |
| CALM [44] | ✓ | ✓ | ✗ | LLM to decompose tasks into subgoals, evaluating only the accuracy of proposed subgoals without assessing RL performance. |
| Ours | ✓ | ✓ | ✓ | Generates sequential, task-specific subgoals with surrogate models from LLMs, guiding agents while reducing computational cost. |
| Hyperparameter | Description | Value |
|---|---|---|
| Subgoal magnitude | 0.2 | |
| Discount factor | 0.99 | |
| Generalized Advantage Estimation (GAE) factor | 0.95 | |
| Number of steps to collect in each rollout per worker | 256 | |
| Number of epochs for each PPO update | 4 | |
| Learning rate for the Adam optimizer | 0.0001 | |
| Epsilon parameter for numerical stability | 1 × | |
| Maximum gradient norm for clipping | 0.5 | |
| Clip value for PPO policy updates | 0.2 | |
| Coefficient for the value function loss | 0.5 | |
| Coefficient for the entropy term in the loss function | 0.0005 |
| Environment | LLM | Accuracy | Correct SGs /Total | Correct EPs /Total | Manhattan Distance |
|---|---|---|---|---|---|
| MultiRoomN2S4 (Position) | Llama | 0.9210 | 1842/2000 | 859/1000 | 0.26 ± 1.01 |
| DeepSeek | 0.3310 | 662/2000 | 125/1000 | 2.91 ± 2.54 | |
| Qwen | 0.7135 | 1427/2000 | 581/1000 | 1.12 ± 2.05 | |
| MultiRoomN2S4 (Semantic) | Llama | 0.9295 | 1859/2000 | 871/1000 | - |
| DeepSeek | 0.2570 | 514/2000 | 21/1000 | - | |
| Qwen | 0.5585 | 1117/2000 | 286/1000 | - | |
| MultiRoomN4S5 (Position) | Llama | 0.5397 | 2159/4000 | 179/1000 | 3.69 ± 4.65 |
| DeepSeek | 0.1200 | 480/4000 | 3/1000 | 7.92 ± 4.64 | |
| Qwen | 0.3600 | 1440/4000 | 56/1000 | 5.23 ± 4.94 | |
| MultiRoomN4S5 (Semantic) | Llama | 0.5480 | 2192/4000 | 166/1000 | - |
| DeepSeek | 0.1625 | 650/4000 | 7/1000 | - | |
| Qwen | 0.3517 | 1407/4000 | 38/1000 | - | |
| KeyCorridorS3R3 (Position) | Llama | 0.9743 | 2923/3000 | 962/1000 | 0.18 ± 1.20 |
| DeepSeek | 0.3337 | 1001/3000 | 18/1000 | 2.57 ± 2.54 | |
| Qwen | 0.9810 | 2943/3000 | 958/1000 | 0.07 ± 0.63 | |
| KeyCorridorS3R3 (Semantic) | Llama | 0.9847 | 2954/3000 | 963/1000 | - |
| DeepSeek | 0.9063 | 2719/3000 | 770/1000 | - | |
| Qwen | 0.9957 | 2987/3000 | 993/1000 | - | |
| KeyCorridorS6R3 (Position) | Llama | 0.9137 | 2741/3000 | 802/1000 | 1.47 ± 5.02 |
| DeepSeek | 0.3650 | 1095/3000 | 44/1000 | 7.24 ± 7.47 | |
| Qwen | 0.8810 | 2643/3000 | 732/1000 | 1.34 ± 4.25 | |
| KeyCorridorS6R3 (Semantic) | Llama | 0.9323 | 2797/3000 | 806/1000 | - |
| DeepSeek | 0.7617 | 2285/3000 | 536/1000 | - | |
| Qwen | 0.9587 | 2876/3000 | 895/1000 | - | |
| ObstructedMaze1Dlh (Position) | Llama | 0.9870 | 2961/3000 | 984/1000 | 0.08 ± 0.82 |
| DeepSeek | 0.4300 | 1290/3000 | 155/1000 | 2.98 ± 3.41 | |
| Qwen | 0.6687 | 2006/3000 | 486/1000 | 2.18 ± 3.53 | |
| ObstructedMaze1Dlh (Semantic) | Llama | 0.9877 | 2963/3000 | 986/1000 | - |
| DeepSeek | 0.7390 | 2217/3000 | 452/1000 | - | |
| Qwen | 0.7417 | 2225/3000 | 561/1000 | - | |
| ObstructedMaze1Dlhb (Position) | Llama | 0.4485 | 1794/4000 | 0/1000 | 4.33 ± 4.21 |
| DeepSeek | 0.2288 | 915/4000 | 2/1000 | 4.49 ± 3.39 | |
| Qwen | 0.4050 | 1620/4000 | 1/1000 | 3.85 ± 3.71 | |
| ObstructedMaze1Dlhb (Semantic) | Llama | 0.4858 | 1943/4000 | 0/1000 | - |
| DeepSeek | 0.5182 | 2073/4000 | 14/1000 | - | |
| Qwen | 0.4820 | 1928/4000 | 1/1000 | - |
| LLM 1 AvgRank (pos/Semantic) | LLM 2 AvgRank (pos/Semantic) | Exact p-Value (Position) | Exact p-Value (Semantic) |
|---|---|---|---|
| Llama (1.33/1.83) | DeepSeek (2.66/2.00) | 0.0312 | 0.0625 |
| Llama (1.33/1.83) | Qwen (2.00/2.16) | 0.0625 | 0.3125 |
| DeepSeek (2.66/2.00) | Qwen (2.00/2.16) | 0.0312 | 0.0938 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Gonzalez, U.; Andres, A.; Del Ser, J. Large Language Models for Structured Task Decomposition in Reinforcement Learning Problems with Sparse Rewards. Mach. Learn. Knowl. Extr. 2025, 7, 126. https://doi.org/10.3390/make7040126
Ruiz-Gonzalez U, Andres A, Del Ser J. Large Language Models for Structured Task Decomposition in Reinforcement Learning Problems with Sparse Rewards. Machine Learning and Knowledge Extraction. 2025; 7(4):126. https://doi.org/10.3390/make7040126
Chicago/Turabian StyleRuiz-Gonzalez, Unai, Alain Andres, and Javier Del Ser. 2025. "Large Language Models for Structured Task Decomposition in Reinforcement Learning Problems with Sparse Rewards" Machine Learning and Knowledge Extraction 7, no. 4: 126. https://doi.org/10.3390/make7040126
APA StyleRuiz-Gonzalez, U., Andres, A., & Del Ser, J. (2025). Large Language Models for Structured Task Decomposition in Reinforcement Learning Problems with Sparse Rewards. Machine Learning and Knowledge Extraction, 7(4), 126. https://doi.org/10.3390/make7040126







