Hybrid Deep Learning Approaches for Accurate Electricity Price Forecasting: A Day-Ahead US Energy Market Analysis with Renewable Energy
Abstract
1. Introduction
2. Motivation and Contribution
2.1. Problem Statement
- (i)
- Training effective machine learning models requires large amounts of quality data. Unfortunately, accessing such data is frequently problematic because they are scarce. Previous research has struggled with this limitation, often having to work with limited datasets covering just a year or two.
- (ii)
- The performance and reliability of deep learning models can be compromised by poor data quality. When working with historical energy data, problems like noise, gaps in the data, and inconsistencies can lead to less accurate predictions.
- (iii)
- The growing adoption of renewable energy has made electricity prices more unpredictable and unstable.
- (iv)
- It is crucial to recognize what drives electricity production. While many studies have been criticized for using only 2–5 input variables, incorporating more diverse factors beyond price can significantly improve price forecasting accuracy.
- (v)
- Sequential data often have variable-length sequences, which can be challenging to handle using machine learning methods.
- (vi)
- Current prediction models, including neural networks, struggle to simultaneously capture both short-term and long-term patterns in electricity prices, reducing their forecasting accuracy.
- (vii)
- Models that memorize training data rather than learning true patterns will fail on new data. Testing performance on separate validation data helps identify whether a model has truly learned useful patterns or just memorized examples.
- (viii)
- Reproduction of existing research is important in machine learning to validate results, provide benchmarks for innovative approaches, educate researchers, and improve efficiency.
2.2. Our Research Contribution
- (i)
- We propose, design, and develop four state-of-the-art hybrid deep learning models to forecast electricity prices in the US energy market, namely, (a) VMD-DNN, (b) VMD-CNN, (c) VMD-LSTM, and (d) VMD-BiLSTM.
- (ii)
- Our dataset covers a 5-year period, providing enough data to effectively train the deep learning model. We also include data augmentation to create Supplementary Data.
- (iii)
- To ensure data integrity, we use VMD for denoising, apply spline interpolation to address missing data, and standardize the dataset with Z-score normalization to reduce discrepancies.
- (iv)
- To reduce volatility and uncertainty in price forecasting, we include temperature data to capture solar energy effects and wind speed data to account for wind energy’s impact on the electricity market.
- (v)
- We ensure the dataset is up-to-date, covering 2018 to 2022, to capture the impact of renewable energy integration on wholesale electricity prices.
- (vi)
- We include 24 time-sensitive input features to capture underlying patterns and enhance electricity price forecasting.
- (vii)
- We implement a sliding window technique to handle variable-length sequences, capture temporal dependencies, and optimize batch processing for training, validating, and testing the VMD-DL hybrid model.
- (viii)
- We validate our hybrid model using a separate validation dataset during training and apply mean squared error (MSE) to address the overfitting–underfitting issue, ensuring reliable model validation.
- (ix)
- We ensure transparency by detailing the data splitting process and making both our dataset and state-of-the-art model publicly available to support reproducibility of the research.
- (x)
- We deliver a set of best-practice guidelines in the field of electricity price forecasting.
3. Electricity Markets in the United States
4. A Day-Ahead Electricity Market
5. Background Study
- (i)
- Statistical models;
- (ii)
- Deep neural network models;
- (iii)
- Hybrid models.
5.1. Statistical Models
5.2. Deep Neural Network Models
5.3. Hybrid Models
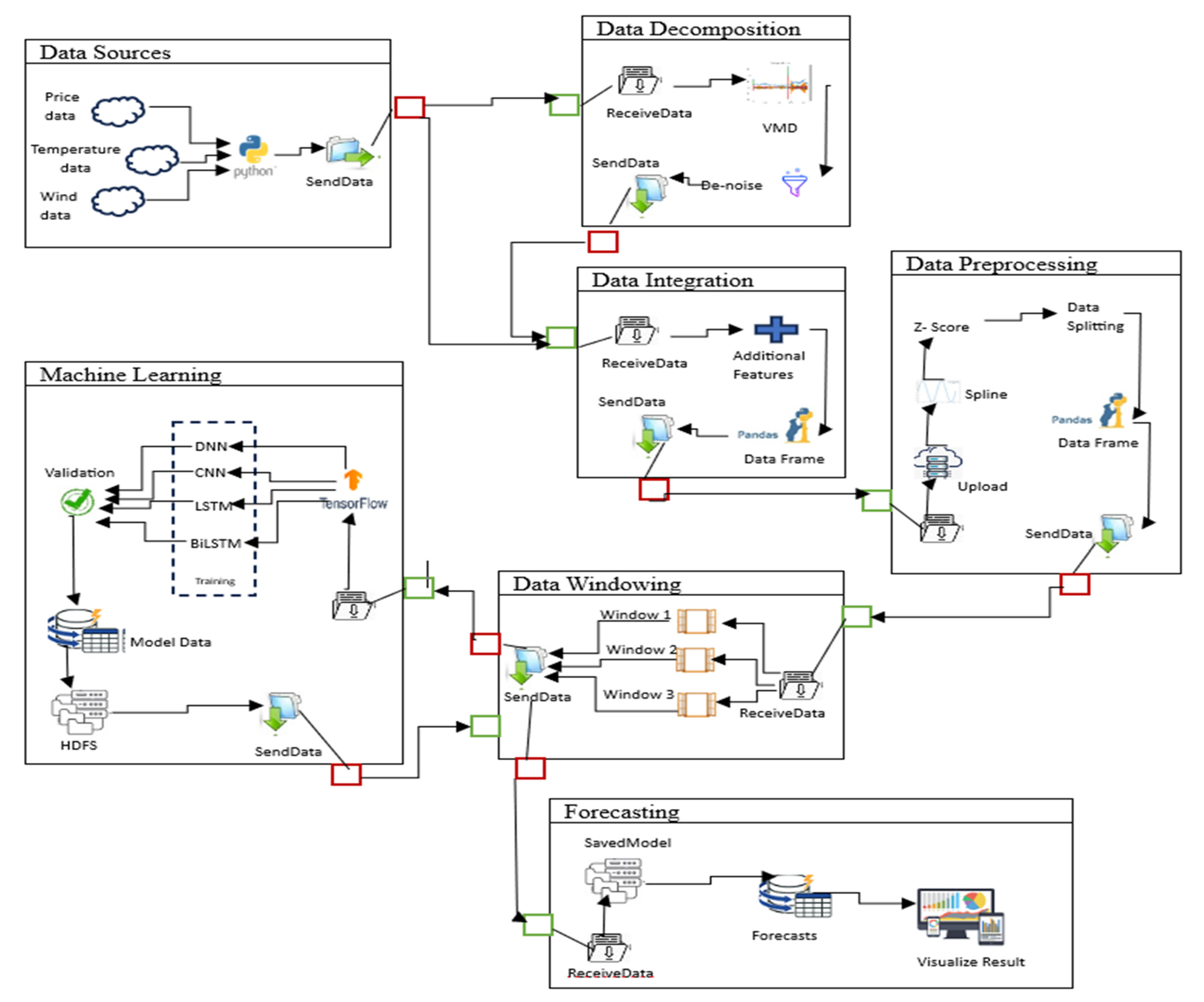
6. Research Methodology
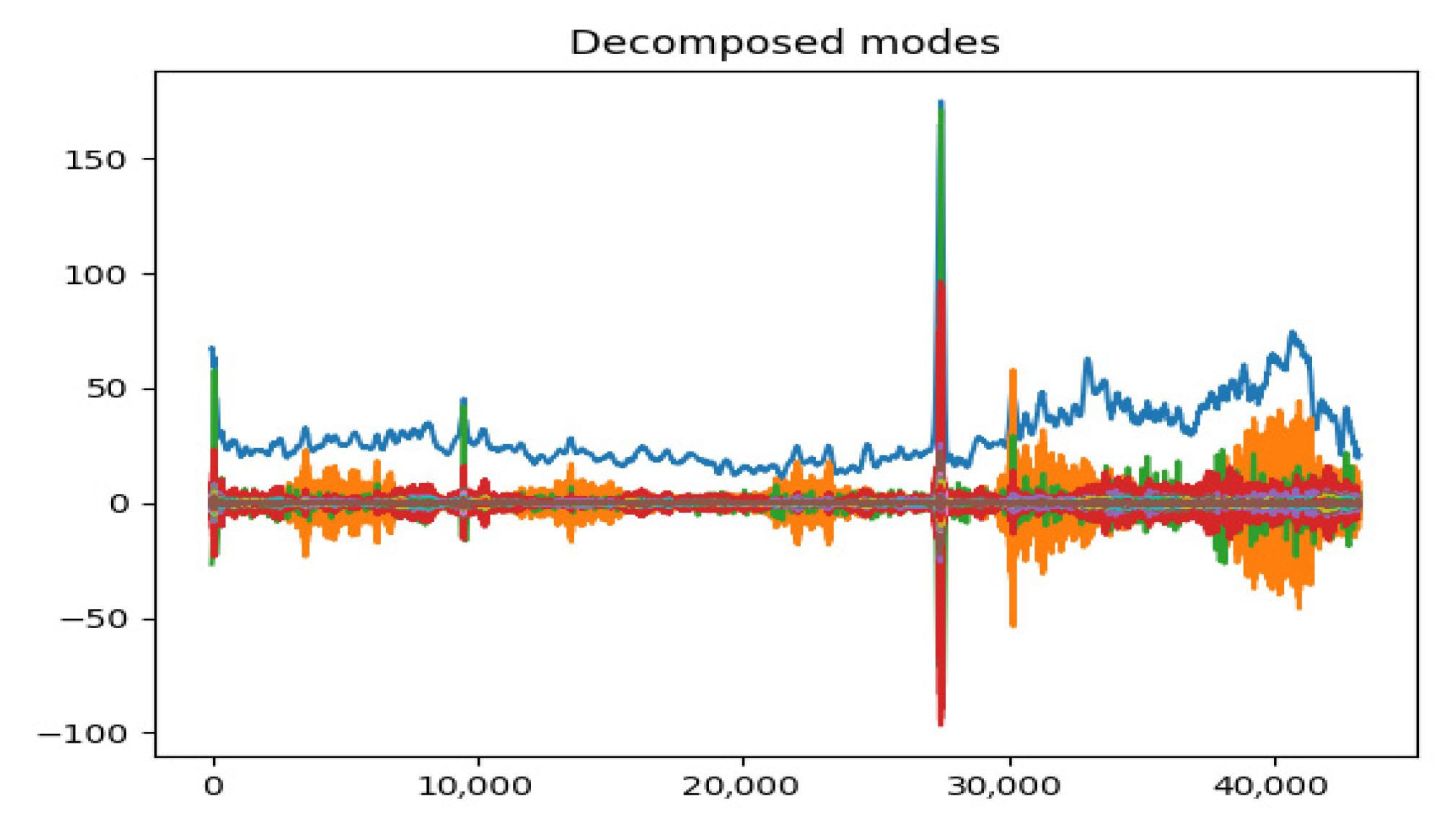
6.1. VMD
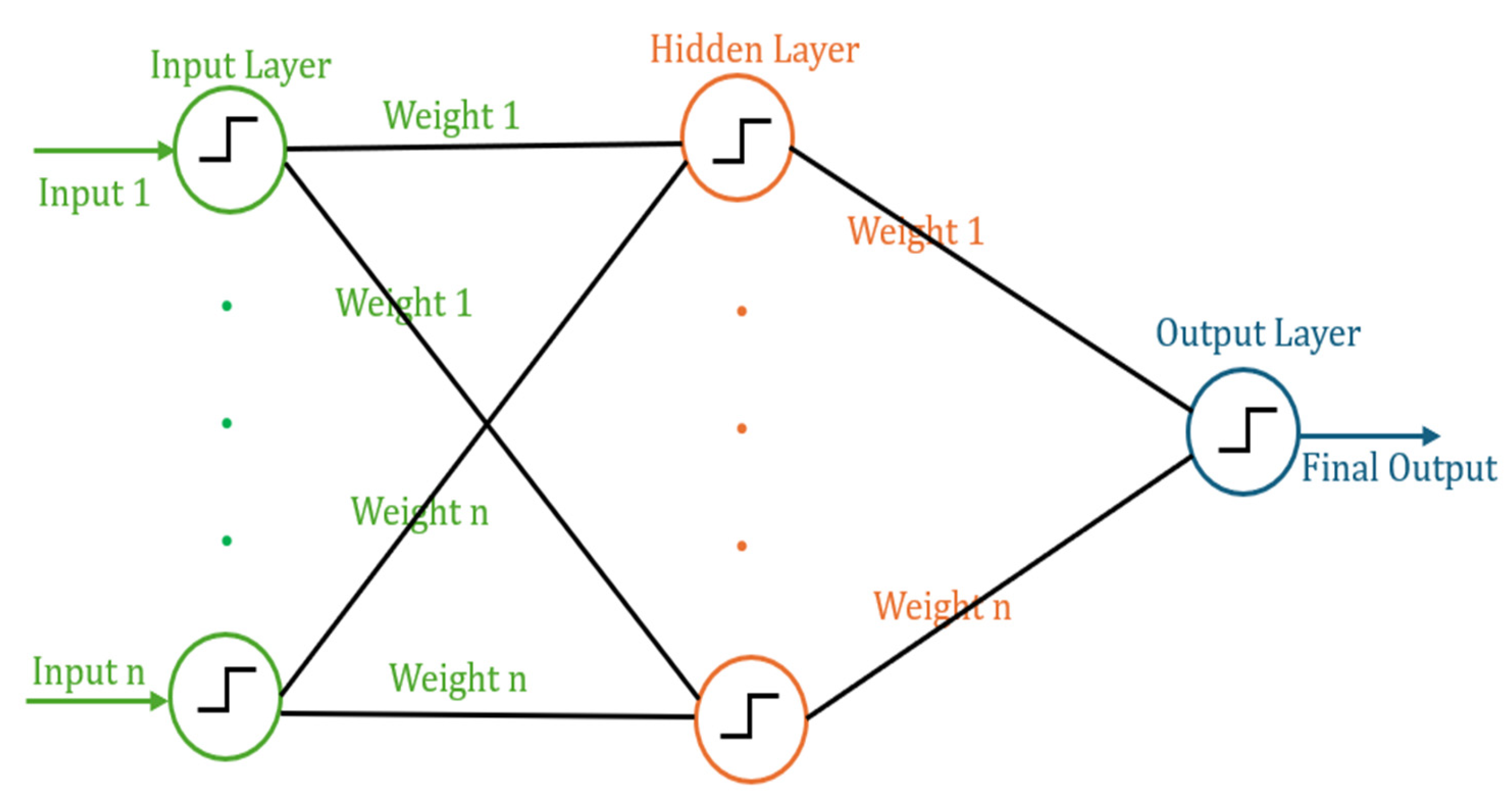
6.2. DNN
6.3. CNN
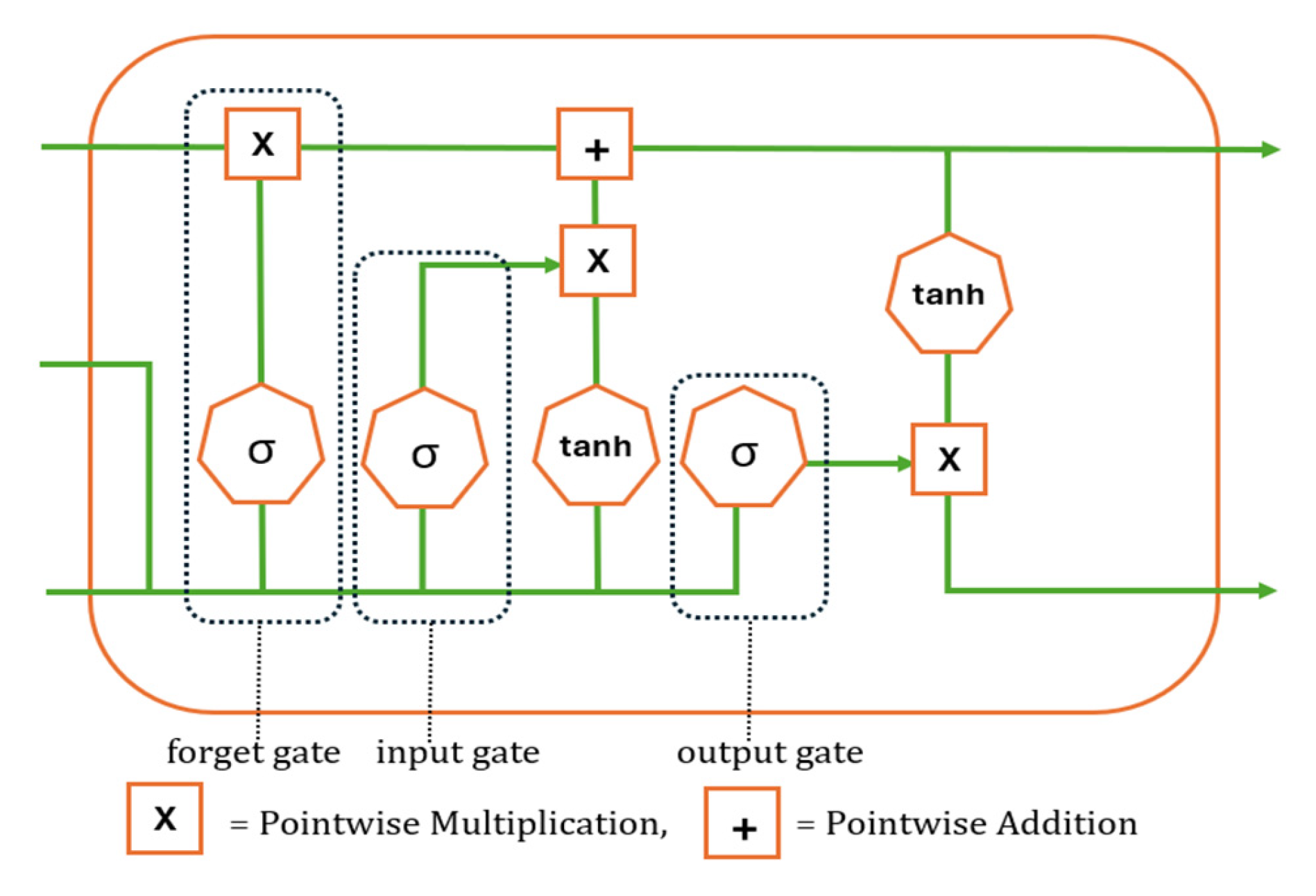
6.4. LSTM
6.5. Bi-LSTM
7. Proposed Model Architecture
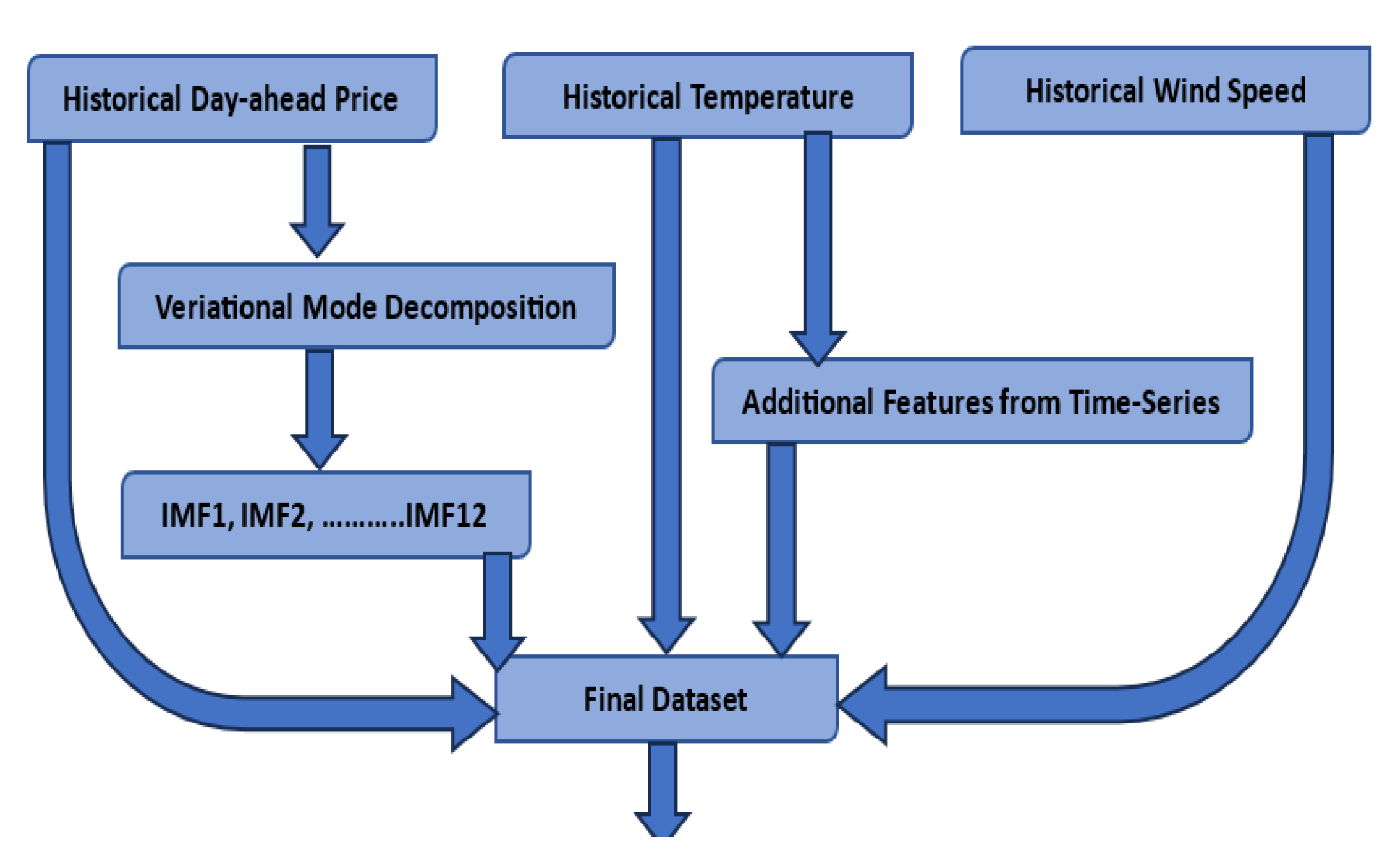
8. Data Description and Preprocessing
8.1. MISO Market Data
8.2. Feature Selection
- (i)
- Hourly historical day-ahead electricity prices ($);
- (ii)
- Hourly historical temperature (°F);
- (iii)
- Hourly historical wind speed (mph);
- (iv)
- Twelve decomposed signals from historical prices (IMF 1–12);
- (v)
- Weekday/weekend identification (weekdays = 0, weekends = 1);
- (vi)
- Hour of the day (0–23);
- (vii)
- Day of the week (0–6);
- (viii)
- Day of the month (1–28/30/31);
- (ix)
- Month of the year (1–12);
- (x)
- Midweek/non-midweek (Tue/Wed/Thu = 1, others = 0);
- (xi)
- Daily sine signal for the time series;
- (xii)
- Daily cosine signal for the time series;
- (xiii)
- Yearly sine signal for the time series;
- (xiv)
- Yearly cosine signal for the time series.
8.3. Data Interpolation
8.4. Data Normalization
8.5. Data Windowing
8.6. Data Preparation
9. Computational Efficiency and Experimental Setup
- Machine Learning Framework: TensorFlow 2.0;
- Programming Language: Python 3, Pandas 2.3, NumPy 2.3, Matplotlib 3.10, Seaborn 0.13;
- Processing Unit: GPU (NVIDIA T4 Tensor Core) [88];
- Notebook: Google CoLab;
- Dataset Market: MISO;
- Dataset Length: 5 years;
- Total Inputs: 24 input features;
- Data Augmentation: VMD;
- Data Interpolation Method: Spline;
- Data Normalization Method: Z-score;
- Data Splitting: Training, Validation, and Test;
- Window Sliding Method: (i) Window 1 (14 + 1 days), (ii) Window 2 (7 + 1 days), and (iii) Window 3 (1 + 1 days);
- Deep Learning Neural Network: VMD, DNN, CNN, LSTM, and BiLSTM;
- Optimization Algorithms: Adam;
- Model Validation and Performance Matrices: MSE, MAE;
- Forecasting Timeframe: 24 h.
10. Model Validation Matrices
10.1. MSE
10.2. MAE
11. Result Analysis and Discussion
11.1. Model Loss
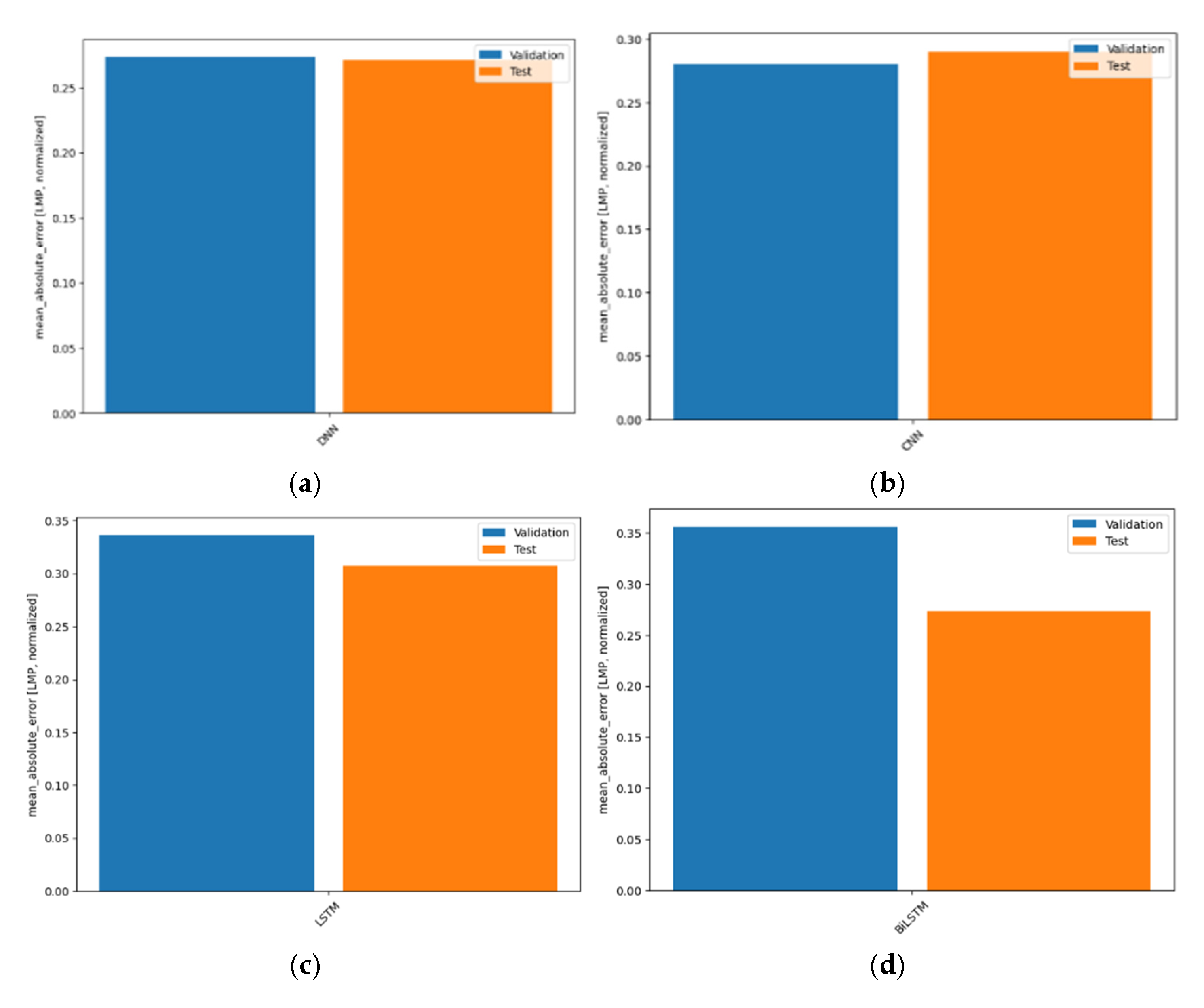
11.2. Model Performance
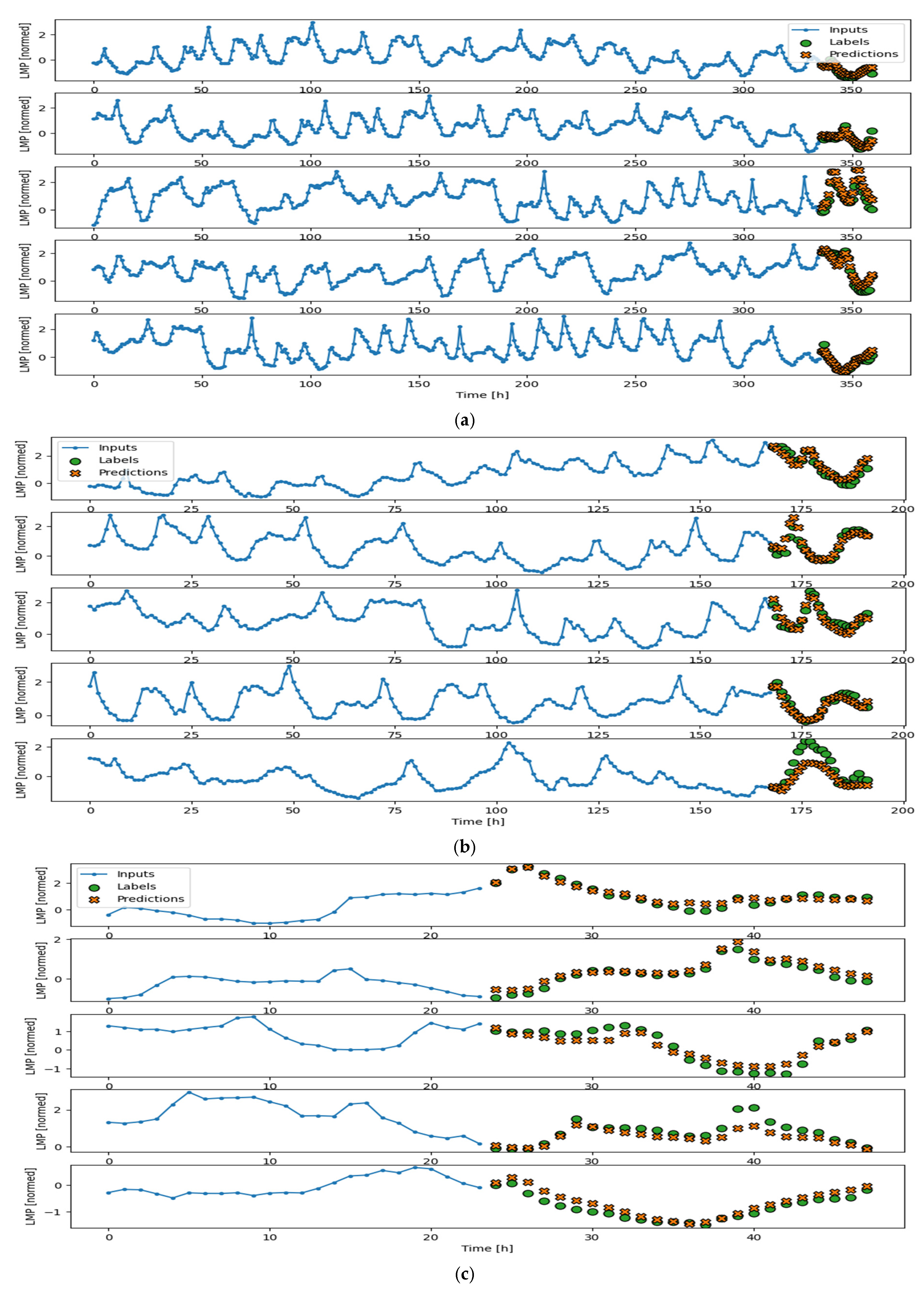
11.3. Electricity Price Forecasting Using Hybrid Models
12. The Best Practices in Electricity Price Forecasting
- (i)
- Integration of the data from renewable energy sources, like solar, wind, etc., has a great influence on achieving a notable accuracy in electricity price forecasting.
- (ii)
- The dataset must be long enough, e.g., five years, and also recent enough to capture the impact of the renewable energy sources in the electricity grid market.
- (iii)
- The test dataset comprises at least a year of data to achieve the best outcome.
- (iv)
- We proposed, designed, and developed four state-of-the-art hybrid deep learning models to forecast electricity prices in the US energy market, namely, (a) VMD-DNN, (b) VMD-CNN, (d) VMD-LSTM, and (d) VMD-BiLSTM. The VMD-BiLSTM hybrid model outperforms all other hybrid models.
- (v)
- To ensure data quality, a data de-noising technique like VMD is useful to achieve high accuracy.
- (vi)
- Data interpolation to handle missing data points and data normalization techniques to standardize the data are very helpful in price forecasting.
- (vii)
- Increasing the amount of time-sensitive features has the potential to improve the accuracy of the forecasting approach. We considered 24 time-sensitive input features that can capture underlying patterns in data to improve electricity price forecasting.
- (viii)
- Sliding Window techniques are significant in machine learning model training because they enable the model to handle variable-length sequences, capture temporal dependencies, increase the amount of training data, and improve batch processing.
- (ix)
- A validation dataset is very beneficial for balancing the overfitting–underfitting issues of the model.
13. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Heydari, A.; Majidi Nezhad, M.; Pirshayan, E.; Astiaso Garcia, D.; Keynia, F.; de Santoli, L. Short-term electricity price and load forecasting in isolated power grids based on composite neural network and gravitational search optimization algorithm. Appl. Energy 2020, 277, 115503. [Google Scholar] [CrossRef]
- Chai, J.; Zhang, Z.-Y.; Wang, S.-Y.; Lai, K.K.; Liu, J. Aviation fuel demand development in China. Energy Econ. 2014, 46, 224–235. [Google Scholar] [CrossRef]
- Lago, J.; de Ridder, F.; Vrancx, P.; de Schutter, B. Forecasting day-ahead electricity prices in Europe: The importance of considering market integration. Appl. Energy 2018, 211, 890–903. [Google Scholar] [CrossRef]
- U.S. Electricity Grid & Markets. Available online: https://www.epa.gov/green-power-markets/us-electricity-grid-markets (accessed on 5 May 2022).
- Hoff, S. U.S. Electric System is Made Up of Interconnections and Balancing Authorities. Available online: https://www.Eia.Gov/Todayinenergy/Detail.Php?Id=27152 (accessed on 20 July 2016).
- Fasching, E. In the First Half of 2022, 24% of U.S. Electricity Generation Came from Renewable Sources. Available online: https://www.Eia.Gov/Todayinenergy/Detail.Php?Id=53779#:~:Text=In%20the%20first%20half%20of,Generation%20came%20from%20renewable%20sources&text=In%20the%20first%20six%20months,From%20our%20Electric%20Power%20Monthly (accessed on 9 September 2022).
- Brancucci Martinez-Anido, C.; Brinkman, G.; Hodge, B.-M. The impact of wind power on electricity prices. Renew. Energy 2016, 94, 474–487. [Google Scholar] [CrossRef]
- Grossi, L.; Nan, F. Robust forecasting of electricity prices: Simulations, models and the impact of renewable sources. Technol. Forecast. Soc. Change 2019, 141, 305–318. [Google Scholar] [CrossRef]
- Maciejowska, K. Assessing the impact of renewable energy sources on the electricity price level and variability—A quantile regression approach. Energy Econ. 2020, 85, 104532. [Google Scholar] [CrossRef]
- Singh, N.; Hussain, S.; Tiwari, S. A PSO-based ANN model for short-term electricity price forecasting. In Advances in Intelligent Systems and Computing; Springer Nature: Berlin/Heidelberg, Germany, 2018; pp. 553–563. [Google Scholar] [CrossRef]
- Aggarwal, A.; Tripathi, M.M. A novel hybrid approach using wavelet transform, time series time delay neural network, and error predicting algorithm for day-ahead electricity price forecasting. In Proceedings of the International Conference on Computer Applications in Electrical Engineering-Recent Advances, Roorkee, India, 5–7 October 2017; pp. 199–204. [Google Scholar] [CrossRef]
- Hong, Y.-Y.; Liu, C.-Y.; Chen, S.-J.; Huang, W.-C.; Yu, T.-H. Short-term LMP forecasting using an artificial neural network incorporating empirical mode decomposition. Int. Trans. Electr. Energy Syst. 2014, 25, 1952–1964. [Google Scholar] [CrossRef]
- Talari, S.; Shafie-khah, M.; Osório, G.; Wang, F.; Heidari, A.; Catalão, J. Price forecasting of electricity markets in the presence of high penetration of wind power generators. Sustainability 2017, 9, 2065. [Google Scholar] [CrossRef]
- Singh, N.; Mohanty, S.R.; Shukla, R.D. Short-term electricity price forecast based on an environmentally adapted generalized neuron. Energy 2017, 125, 127–139. [Google Scholar] [CrossRef]
- Zhu, Y.; Dai, R.; Liu, G.; Wang, Z.; Lu, S. Power market price forecasting via deep learning. In Proceedings of the 44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018. [Google Scholar] [CrossRef]
- Bento, P.; Pombo, J.; Calado, M.; Mariano, S. A bat-optimized neural network and wavelet transform approach for short-term price forecasting. Appl. Energy 2018, 210, 88–97. [Google Scholar] [CrossRef]
- Khajeh, M.G.; Maleki, A.; Rosen, M.A.; Ahmadi, M.H. Electricity price forecasting using neural networks with an improved iterative training algorithm. Int. J. Ambient. Energy 2017, 39, 147–158. [Google Scholar] [CrossRef]
- Afrasiabi, M.; Mohammadi, M.; Rastegar, M.; Kargarian, A. Multi-agent microgrid energy management based on deep learning forecaster. Energy 2019, 186, 115873. [Google Scholar] [CrossRef]
- Wang, D.; Luo, H.; Grunder, O.; Lin, Y.; Guo, H. Multi-step ahead electricity price forecasting using a hybrid model based on two-layer decomposition technique and BP neural network optimized by the firefly algorithm. Appl. Energy 2017, 190, 390–407. [Google Scholar] [CrossRef]
- Jiang, P.; Ma, X.; Liu, F. A new hybrid model based on data preprocessing and an intelligent optimization algorithm for electrical power system forecasting. Math. Probl. Eng. 2015, 2015, 815253. [Google Scholar] [CrossRef]
- Zhang, J.L.; Zhang, Y.J.; Li, D.Z.; Tan, Z.F.; Ji, J.F. Forecasting day-ahead electricity prices using a new integrated model. Int. J. Electr. Power Energy Syst. 2019, 105, 541–548. [Google Scholar] [CrossRef]
- Dastile, X.; Celik, T.; Potsane, M. Statistical and machine learning models in credit scoring: A systematic literature survey. Appl. Soft Comput. J. 2020, 91. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Raviv, E.; Bouwman, K.E.; Van Dijk, D. Forecasting day-ahead electricity prices: Utilizing hourly prices. Energy Econ. 2015, 50, 227–239. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; Houm, Y.E. Short-Term Load Forecasting: Based on Hybrid CNN-LSTM Neural Network. In Proceedings of the 2021 6th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 17–20 September 2021. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, Z.; Wei, Y. An adaptive hybrid model for short term electricity price forecasting. Appl. Energy 2020, 258, 114087. [Google Scholar] [CrossRef]
- Jaimes, D.M.; López, M.Z.; Zareipour, H.; Quashie, M. A Hybrid Model for Multi-Day-Ahead Electricity Price Forecasting considering Price Spikes. Forecasting 2023, 5, 499–521. [Google Scholar] [CrossRef]
- Acaroğlu, H.; Márquez, F.P.G. Comprehensive Review on Electricity Market Price and Load Forecasting Based on Wind Energy. Energies 2021, 14, 7473. [Google Scholar] [CrossRef]
- Contreras, J.; Espinola, R.; Nogales, F.; Conejo, A. ARIMA models to predict next-day electricity prices. IEEE Trans. Power Syst. 2003, 18, 1014–1020. [Google Scholar] [CrossRef]
- Conejo, A.; Plazas, M.; Espinola, R.; Molina, A. Day-Ahead Electricity Price Forecasting Using the Wavelet Transform and ARIMA Models. IEEE Trans. Power Syst. 2005, 20, 1035–1042. [Google Scholar] [CrossRef]
- Shivanipickl. Mastering Data: Exploring 5 Statistical Data Analysis Techniques with Real-World Examples. Available online: https://medium.com/@shivanipickl/mastering-data-exploring-5-statistical-data-analysis-techniques-with-real-world-examples-5e9064be6d46 (accessed on 2 November 2022).
- Uniejewski, B.; Nowotarski, J.; Weron, R. Automated variable selection and shrinkage for day-ahead electricity price forecasting. Energies 2016, 9, 621. [Google Scholar] [CrossRef]
- Lago, J.; De Ridder, F.; De Schutter, B. Forecasting spot electricity prices: Deep learning approaches and empirical comparison of traditional algorithms. Appl. Energy 2018, 221, 386–405. [Google Scholar] [CrossRef]
- Ziel, F.; Weron, R. Day-ahead electricity price forecasting with high-dimensional structures: Univariate vs. multivariate modeling frameworks. Energy Econ. 2018, 70, 396–420. [Google Scholar] [CrossRef]
- Ziel, F.; Steinert, R.; Husmann, S. Forecasting day ahead electricity spot prices: The impact of the EXAA to other European electricity markets. Energy Econ. 2015, 51, 430–444. [Google Scholar] [CrossRef]
- Ziel, F. Forecasting electricity spot prices using lasso: On capturing the autoregressive intraday structure. IEEE Trans. Power Syst. 2016, 31, 4977–4987. [Google Scholar] [CrossRef]
- Uniejewski, B.; Weron, R. Efficient forecasting of electricity spot prices with expert and LASSO models. Energies 2018, 11, 2039. [Google Scholar] [CrossRef]
- Uniejewski, B.; Marcjasz, G.; Weron, R. Understanding intraday electricity markets: Variable selection and very short-term price forecasting using LASSO. Int. J. Forecast. 2019, 35, 1533–1547. [Google Scholar] [CrossRef]
- Karakatsani, N.; Bunn, D. Fundamental and behavioural drivers of electricity price volatility. Stud. Nonlinear Dyn. Econom. 2010, 14, 4. [Google Scholar] [CrossRef]
- Isaac Abiodun, O.; Jantan, A.; Esther Omolara, A.; Victoria Dada, K.; AbdElatif Mohamed, N.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, 938. [Google Scholar] [CrossRef]
- Rahman, M.S. A Hybrid Deep Neural Network Model to Forecast Day-Ahead Electricity Prices in the USA Energy Market. Ph.D. Thesis, University of North Dakota, Grand Forks, ND, USA, 2023. Available online: https://commons.und.edu/theses/5330 (accessed on 5 September 2025).
- Wang, L.; Zhang, Z.; Chen, J. Short-Term Electricity Price Forecasting With Stacked Denoising Autoencoders. In IEEE Transactions on Power Systems; IEEE: New York, NY, USA, 2017; Volume 32, pp. 2673–2681. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Ma, J.; Jin, Q. BRIM: An accurate electricity spot price prediction scheme-based bidirectional recurrent neural network and integrated market. Energies 2019, 12, 2241. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, L.; Mao, M.; Tai, H.; Wan, Y. An optimized heterogeneous structure LSTM network for electricity price forecasting. IEEE Access 2019, 7, 108161–108173. [Google Scholar] [CrossRef]
- Mujeeb, S.; Javaid, N.; Ilahi, M.; Wadud, Z.; Ishmanov, F.; Afzal, M. Deep long short term memory: A new price and load forecasting scheme for big data in smart cities. Sustainability 2019, 11, 987. [Google Scholar] [CrossRef]
- Xu, J.; Baldick, R. Day-ahead price forecasting in ERCOT market using neural network approaches. In Proceedings of the Tenth ACM International Conference on Future Energy Systems, Phoenix, AZ, USA, 25–28 June 2019; pp. 486–491. [Google Scholar] [CrossRef]
- Meier, J.-H.; Schneider, S.; Schmidt, I.; Schüller, P.; Schönfeldt, T.; Wanke, B. ANN-based electricity price forecasting under special consideration of time series properties. In Information and Communication Technologies in Education, Research, and Industrial Applications; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 262–275. [Google Scholar] [CrossRef]
- Chang, Z.; Zhang, Y.; Chen, W. Effective Adam-optimized LSTM neural network for electricity price forecasting. In Proceedings of the 2018 IEEE International Conference on Software Engineering and Service Science, Beijing, China, 23–25 November 2018; pp. 245–248. [Google Scholar] [CrossRef]
- Chinnathambi, R.A.; Plathottam, S.J.; Hossen, T.; Nair, A.S.; Ranganathan, P. Deep neural networks (DNN) for day-ahead electricity price markets. In Proceedings of the 2018 IEEE Electrical Power and Energy Conference, Toronto, ON, Canada, 10–11 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Luo, S.; Weng, Y. A two-stage supervised learning approach for electricity price forecasting by leveraging different data sources. Appl. Energy 2019, 242, 1497–1512. [Google Scholar] [CrossRef]
- Atef, S.; Eltawil, A.B. A comparative study using deep learning and support vector regression for electricity price forecasting in smart grids. In Proceedings of the 2019 IEEE International Conference on Industrial Engineering and Applications, Tokyo, Japan, 12–15 April 2019; pp. 603–607. [Google Scholar] [CrossRef]
- Chang, Z.; Zhang, Y.; Chen, W. Electricity price prediction based on a hybrid model of Adam optimized LSTM neural network and wavelet transform. Energy 2019, 187, 115804. [Google Scholar] [CrossRef]
- Zahid, M.; Ahmed, F.; Javaid, N.; Abbasi, R.; Zainab Kazmi, H.; Javaid, A.; Bilal, M.; Akbar, M.; Ilahi, M. Electricity price and load forecasting using enhanced convolutional neural network and enhanced support vector regression in smart grids. Electronics 2019, 8, 122. [Google Scholar] [CrossRef]
- Jahangir, H.; Tayarani, H.; Baghali, S.; Ahmadian, A.; Elkamel, A.; Aliakbar Golkar, M.; Castilla, M. A novel electricity price forecasting approach based on dimension reduction strategy and rough artificial neural networks. IEEE Trans. Ind. Inf. 2019, 16, 2369–2381. [Google Scholar] [CrossRef]
- Ahmad, W.; Javaid, N.; Chand, A.; Shah, S.Y.R.; Yasin, U.; Khan, M.; Syeda, A. Electricity price forecasting in smart grid: A novel E-CNN model. In Web, Artificial Intelligence and Network Applications; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 1132–1144. [Google Scholar] [CrossRef]
- Aineto, D.; Iranzo-Sánchez, J.; Lemus-Zúñiga, L.G.; Onaindia, E.; Urchueguía, J.F. On the influence of renewable energy sources in electricity price forecasting in the Iberian market. Energies 2019, 12, 2082. [Google Scholar] [CrossRef]
- Nazar, M.S.; Fard, A.E.; Heidari, A.; Shafie-khah, M.; Catalão, J.P. Hybrid model using a three-stage algorithm for simultaneous load and price forecasting. Electr. Power Syst. Res. 2018, 165, 214–228. [Google Scholar] [CrossRef]
- Yang, Z.; Ce, L.; Lian, L. Electricity price forecasting by a hybrid model, combining wavelet transform, ARMA, and kernel-based extreme learning machine methods. Appl. Energy 2017, 190, 291–305. [Google Scholar] [CrossRef]
- Victoire, A.A.; Gobu, B.; Jaikumar, S.; Arulmozhi, N.; Kanimozhi, P.; Victoire, A. Two-stage machine learning framework for simultaneous forecasting of price-load in the smart grid. In Proceedings of the 2018 IEEE International Conference on Machine Learning and Applications, Orlando, FL, USA, 17–20 December 2018; pp. 1081–1086. [Google Scholar] [CrossRef]
- Lahmiri, S. Comparing variational and empirical mode decomposition in forecasting day-ahead energy prices. IEEE Syst. J. 2017, 11, 1907–1910. [Google Scholar] [CrossRef]
- Pourdaryaei, A.; Mokhlis, H.; Illias, H.A.; Kaboli, S.H.A.; Ahmad, S. Short-term electricity price forecasting via hybrid backtracking search algorithm and ANFIS approach. IEEE Access 2019, 7, 77674–77691. [Google Scholar] [CrossRef]
- Abedinia, O.; Amjady, N.; Shafie-khah, M.; Catalão, J. Electricity price forecast using Combinatorial Neural Network trained by a new stochastic search method. Energy Convers. Manag. 2015, 105, 642–654. [Google Scholar] [CrossRef]
- Bisoi, R.; Dash, P.K.; Das, P.P. Short-term electricity price forecasting and classification in smart grids using optimized multi kernel extreme learning machine. Neural Comput. Appl. 2018, 32, 1457–1480. [Google Scholar] [CrossRef]
- Saifur, R.M.; Reza, H.; Kim, E. A Hybrid Deep Neural Network Model to Forecast Day-Ahead Electricity Prices in the USA Energy Market. In Proceedings of the 2023 IEEE World AI IoT Congress (AIIoT), Seattle, WA, USA, 7–10 June 2023; pp. 525–534. [Google Scholar] [CrossRef]
- Kazienko, P.; Lughofer, E.; Trawiński, B. Hybrid and Ensemble Methods in Machine Learning, J. UCS Special Issue. J. Univers. Comput. Sci. 2013, 19, 457–461. [Google Scholar]
- Memarzadeh, G.; Keynia, F. Short-term electricity load and price forecasting by a new optimal LSTM-NN based prediction algorithm. Electr. Power Syst. Res. 2021, 192, 106995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Data Sci. Adapt. Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Sezer, O.B.; Gudelek, M.U.; Ozbayoglu, A.M. Financial Time Series Forecasting with Deep Learning: A Systematic Literature Review: 2005–2019. arXiv 2019, arXiv:1911.13288. [Google Scholar] [CrossRef]
- Lago, J.; Marcjasz, G.; De Schutter, B.; Weron, R. Forecasting day-ahead electricity prices: A review of state-of-the-art algorithms, best practices, and an open-access benchmark. arXiv 2020. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Dwivedi, S.A.; Attry, A.; Parekh, D.; Singla, K. Analysis and forecasting of Time-Series data using S-ARIMA, CNN and LSTM. In Proceedings of the 2021 International Conference on Computing, Communication, and Intelligent Systems (ICCCIS), Greater Noida, India, 19–20 February 2021; pp. 131–136. [Google Scholar] [CrossRef]
- Bahri, M.Z.; Vahidnia, S. Time Series Forecasting Using Smoothing Ensemble Empirical Mode Decomposition and Machine Learning Techniques. In Proceedings of the 2022 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Maldives, Maldives, 16–18 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Selvin, S.; Vinayakumar, R.; Gopalakrishnan, E.A.; Menon, V.K.; Soman, K.P. Stock price prediction using LSTM, RNN and CNN-sliding window model. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; pp. 1643–1647. [Google Scholar] [CrossRef]
- Contributors, W. Long Short-Term Memory. 2021. Available online: https://en.wikipedia.org/w/index.php?title=Long_short-term_memory&oldid=1005032489 (accessed on 11 December 2022).
- Phi, M. Illustrated Guide to LSTM’s and GRU’s: A Step By-Step Explanation. 2018. Available online: https://towardsdatascience.com/illustrated-guide-to-lstms-and-gru-s-a-step-by-step-explanation-44e9eb85bf21 (accessed on 10 December 2022).
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, D.; Xiang, W.; Guan, Z.; Huang, J. Power Load Forecasting Based on COA-Bi-LSTM Method. In Proceedings of the 2022 2nd International Conference on Electrical Engineering and Control Science (IC2ECS), Nanjing, China, 16–18 December 2022; pp. 842–845. [Google Scholar] [CrossRef]
- Sharma, U.; Sharma, C. Deep Learning Based Prediction of Weather Using Hybrid_Stacked Bi-Long Short Term Memory. In Proceedings of the 2022 12th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 27–28 January 2022; pp. 422–427. [Google Scholar] [CrossRef]
- Midcontinent Independent System Operator, Inc. Historical Annual Day-Ahead LMPs (zip). Available online: https://www.Misoenergy.Org/Markets-and-Operations/Real-Time--Market-Data/Market-Reports/#nt=%2FMarketReportType%3AHistorical%20LMP%2FMarketReportName%3AHistorical%20Annual%20Day-Ahead%20LMPs%20(Zip)&t=10&p=0&s=MarketReportPublished&sd=desc (accessed on 11 December 2022).
- LCG Consulting. MISO (Midwest Independent Transmission System Operator) Day-Ahead Energy Price. 2022. Available online: http://Energyonline.Com/Data/GenericData.Aspx?DataId=9&MISO___Day-Ahead_Energy_Price (accessed on 11 December 2022).
- Iowa AWOS. Automated Airport Weather Observations from Around the World. 2022. Available online: https://mesonet.agron.iastate.edu/request/download.phtml (accessed on 11 December 2022).
- Wikipedia.org. Spline Interpolation. Available online: https://en.wikipedia.org/wiki/Spline_interpolation (accessed on 6 July 2023).
- Patro, S.G.; Sahu, K.K. Normalization: A Preprocessing Stage. arXiv 2015. [Google Scholar] [CrossRef]
- Al Machot, F.; Mayr, H.C.; Ranasinghe, S. A windowing approach for activity recognition in sensor data streams. In Proceedings of the 2016 Eighth International Conference on Ubiquitous and Future Networks (ICUFN), Vienna, Austria, 5–8 July 2016; pp. 951–953. [Google Scholar] [CrossRef]
- tensorflow.org. Colab’s ‘Pay As You Go’ Offers More Access to Powerful NVIDIA Compute for Machine Learning. Available online: https://blog.tensorflow.org/2022/09/colabs-pay-as-you-go-offers-more-access-to-powerful-nvidia-compute-for-machine-learning.html (accessed on 29 September 2022).
- Wikipedia Contributors. Mean Squared Error. Wikipedia.org, The Free Encyclopedia. 2021. Available online: https://en.wikipedia.org/w/index.php?title=Mean_squared_error&oldid=1020706752 (accessed on 10 December 2022).
- Wikipedia.org. Mean Absolute Error. Available online: https://en.wikipedia.org/wiki/Mean_absolute_error (accessed on 10 December 2022).




| Techniques | Previous Hours | Forecasting Hours | Total Window Size |
|---|---|---|---|
| Window 1 | 336 (14 days/2 weeks) | 24 (1 day) | 360 h (14 + 1 days) |
| Window 2 | 168 (7 days/1week) | 24 (1 day) | 192 h (7 + 1 days) |
| Window 3 | (1 day) | 24 (1 day) | hours (1 + 1 days) |
| Dataset Name | Start Date | End Date | Hours |
|---|---|---|---|
| Training | 1 January 2018 | 25 December 2021 | 34,920 |
| Validation | 26 December 2021 | 20 September 2022 | 6456 |
| Test | 21 September 2022 | 12 April 2022 | 1800 |
| Model Name | Model Summary |
|---|---|
| VMD-DNN | 5-layer network, batch size 336 (varies depending on window type), Adam optimizer, learning rate 0.001, ReLU activation, and a total of 259,928 trainable parameters |
| VMD-CNN | 4-layer network, batch size 336 (varies depending on window type), Adam optimizer, learning rate 0.001, ReLU activation, and a total of 1,984,792 trainable parameters |
| VMD-LSTM | 4-layer network, batch size 336 (varies depending on window type), Adam optimizer, learning rate 0.001, ReLU activation, and a total of 16,224 trainable parameters |
| VMD-BiLSTM | 4-layer network, batch size 336 (varies depending on window type), Adam optimizer, learning rate 0.001, ReLU activation, and a total of 38,024 trainable parameters |
| Window Techniques | Hybrid Model | Model Loss (MSE) |
|---|---|---|
| Window 1 (14 + 1 days) | VMD-DNN | 0.3312 |
| VMD-CNN | 0.2637 | |
| VMD-LSTM | 0.1796 | |
| VMD-BiLSTM | 0.1517 | |
| Window 2 (7 + 1 days) | VMD-DNN | 0.2824 |
| VMD-CNN | 0.1956 | |
| VMD-LSTM | 0.1730 | |
| VMD-BiLSTM | 0.1318 | |
| Window 3 (1 + 1 days) | VMD-DNN | 0.1229 |
| VMD-CNN | 0.1418 | |
| VMD-LSTM | 0.1590 | |
| VMD-BiLSTM | 0.1236 |
| Window Techniques | Hybrid Model | Model Performance (MAE) |
|---|---|---|
| Window 1 (14 + 1 days) | VMD-DNN | 0.4623 |
| VMD-CNN | 0.4083 | |
| VMD-LSTM | 0.3312 | |
| VMD-BiLSTM | 0.3014 | |
| Window 2 (7 + 1 days) | VMD-DNN | 0.4161 |
| VMD-CNN | 0.3472 | |
| VMD-LSTM | 0.3238 | |
| VMD-BiLSTM | 0.2782 | |
| Window 3 (1 + 1 days) | VMD-DNN | 0.2710 |
| VMD-CNN | 0.2930 | |
| VMD-LSTM | 0.3077 | |
| VMD-BiLSTM | 0.2733 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.S.; Reza, H. Hybrid Deep Learning Approaches for Accurate Electricity Price Forecasting: A Day-Ahead US Energy Market Analysis with Renewable Energy. Mach. Learn. Knowl. Extr. 2025, 7, 120. https://doi.org/10.3390/make7040120
Rahman MS, Reza H. Hybrid Deep Learning Approaches for Accurate Electricity Price Forecasting: A Day-Ahead US Energy Market Analysis with Renewable Energy. Machine Learning and Knowledge Extraction. 2025; 7(4):120. https://doi.org/10.3390/make7040120
Chicago/Turabian StyleRahman, Md. Saifur, and Hassan Reza. 2025. "Hybrid Deep Learning Approaches for Accurate Electricity Price Forecasting: A Day-Ahead US Energy Market Analysis with Renewable Energy" Machine Learning and Knowledge Extraction 7, no. 4: 120. https://doi.org/10.3390/make7040120
APA StyleRahman, M. S., & Reza, H. (2025). Hybrid Deep Learning Approaches for Accurate Electricity Price Forecasting: A Day-Ahead US Energy Market Analysis with Renewable Energy. Machine Learning and Knowledge Extraction, 7(4), 120. https://doi.org/10.3390/make7040120





