Learning to Partition: Dynamic Deep Neural Network Model Partitioning for Edge-Assisted Low-Latency Video Analytics
Abstract
1. Introduction
- Design an edge-assisted DNN model partitioning technique, DNN-Scissor, for cost-efficient, low-latency video analytics. DNN-Scissor optimizes long-term system performance including system workload, bandwidth consumption, and video frame drop.
- Design a deep reinforcement learning-based algorithm to learn the optimal DNN splitting policy for each video frame to minimize the system cost over time.
- Implement a real-world video analytics system testbed and conduct experiments to evaluate the performances.
2. Literature Review
2.1. DNN Model Partition
2.2. Edge-Assisted Low-Latency Video Analytics
2.3. Conclusions of the Literature Review
3. System Overview
3.1. System Architecture
3.2. Workflow
- The local device reads a video frame from the camera at a specified reading interval and pre-processes (e.g., resizes) the frame.
- The DNN-Scissor agent, running on the local device, observes the current system state such as the length of local queues and current network bandwidth, and makes a decision on where to split the DNN for frame .
- Together with this splitting decision, frame is then put into the local queue waiting for local inference.
- DNN-Scissor monitors the waiting time of . Once the waiting time exceeds a time-out threshold, will be dropped directly.
- The local device calculates the DNN layer by layer for until the split location.
- The intermediate features from the split location are then put into the offloading queue for transmitting to the edge. The features will also be dropped once the waiting time exceeds the time-out threshold.
- The edge continues the feed-forward calculations for the rest of the DNN layers and outputs analysis results.
4. Methodology
4.1. Preliminaries
4.2. DNN Partitioning as a Dynamic Graph Cut Problem
- State-Dependent Costs: The true cost or expense of a partition is not a static property of the graph. It is dynamic and state-dependent. The data transfer cost (latency) depends on the real-time network bandwidth, and the computational cost (latency) depends on the current workloads of the local and edge devices. Classic graph algorithms typically operate on graphs with fixed, pre-defined weights.
- Long-Term Sequential Objective: We do not seek a single, static optimal partition. Instead, the goal is to learn a dynamic policy that selects the best partition for each incoming video frame to maximize a cumulative, long-term reward. This objective requires a farsighted approach that considers the future consequences of a current action (e.g., preventing future queue build-up), which is a characteristic of sequential decision problems.
4.3. Deep Reinforcement Learning Modeling
4.4. Splitting Policy Learning Algorithm
| Algorithm 1 DNN splitting policy learning with A2C |
| Input: Initialized actor and critic , empty replay buffer M 1: while rewards not converged do 2: Read a frame from camera 3: Obtain lengths of local queue and offloading queue 4: Obtain current network bandwidth 5: Estimate time delay and data amount by Equations (1) and (2) 6: Get state s by Equation (3) 7: Sample split location 8: Put into the local queue 9: Update state 10: if then 11: Drop 12: Get reward 13: else 14: Split the DNN at a and inference 15: Get reward 16: end if 17: Store to M 18: if time to update then 19: sample set of transitions B from M 20: Update actor by 21: Update critic by 22: end if 23: end while |
4.5. Algorithmic Complexity
5. Results
5.1. Experimental Settings
5.1.1. Experimental Environment
5.1.2. Hyperparameters and Settings
5.1.3. DRL Agent Training Setup
5.1.4. Data Set
5.1.5. Human-in-the-Loop Configuration
- Choice of Analytics DNN: The specific DNN model used for the vision task (e.g., YOLOv3, ResNet18) is a manual design choice based on the application’s requirements for accuracy and performance.
- Selection of Candidate Split Points: The set of potential layers where a partition can occur is pre-defined by a human. This selection is guided by the DNN’s architecture, targeting layers where the output feature maps form a logical bottleneck or transition point. The DRL agent’s role is to automatically select the best option from this pre-defined set.
- DRL Agent Architecture and Hyperparameters: The structure of the DRL agent’s neural networks (e.g., number of layers and neurons in the actor and critic networks) is a manual design choice. Additionally, key training hyperparameters are set by a human, including the learning rate, the reward discount factor (), the trade-off weight (w) in the reward function, and the penalty (F) for dropping a frame.
- System Operational Parameters: The operational settings for the video analytics pipeline are configured manually. This includes the video frame reading rate (e.g., 1000 ms per frame for YOLOv3) and the time-out threshold (T) that determines when a waiting frame is dropped. These are typically set based on the specific application’s latency requirements and the available hardware resources.
5.1.6. Baselines
- Device Only: This method runs deep neural networks at the local device.
- Edge Only [36]: This method receives the original video frames and runs deep neural networks at the edge.
- Semi-Fixed [2]: This method either splits DNNs at a fixed layer (not the first one) or directly processes video frames at the edge when the number of waiting frames exceeds a threshold. We set the fifth layer to split for each DNN partition task, and the threshold is set to 10.
- Greedy [8]: This method selects the best split location that maximizes the current system performance measured by the transmitted data amount and processing delay for each video frame independently. The overall delay for this approach is estimated by predicting the queuing delay and the transmission delay under an estimated bandwidth.
5.1.7. Metrics
- Transmitted Data Amount, i.e., , is the data size to be transmitted from the local device to the edge per video frame, measured by bytes.
- Total Delay, i.e., , is the total time delay per video frame, including the local inference and edge inference times, waiting times in queues, and transmission time.
- Local Delay is the local inference time per frame.
- Edge Delay is the edge inference time per frame.
- Drop Rate is the percentage of frames dropped because of long waiting times in either local queue or offloading queue. All the compared methods have the same time threshold dropping frames.
- System Cost is the average magnitude of reward per frame. It is either the weighted sum of the transmitted data amount plus the total delay, i.e., , when a frame got computed, or 10 when a drop is dropped. The trade-off weight w is set to 1 by default.
5.2. Experimental Results
5.2.1. Comparison Results
5.2.2. Verification of Inference Accuracy
5.2.3. Effects of Network Bandwidth
5.2.4. Sensitivity Analysis of the Reward Trade-Off Weight (w)
5.2.5. Analysis of Latency Components and System Adaptability
5.2.6. Effects of Frame Reading Rate
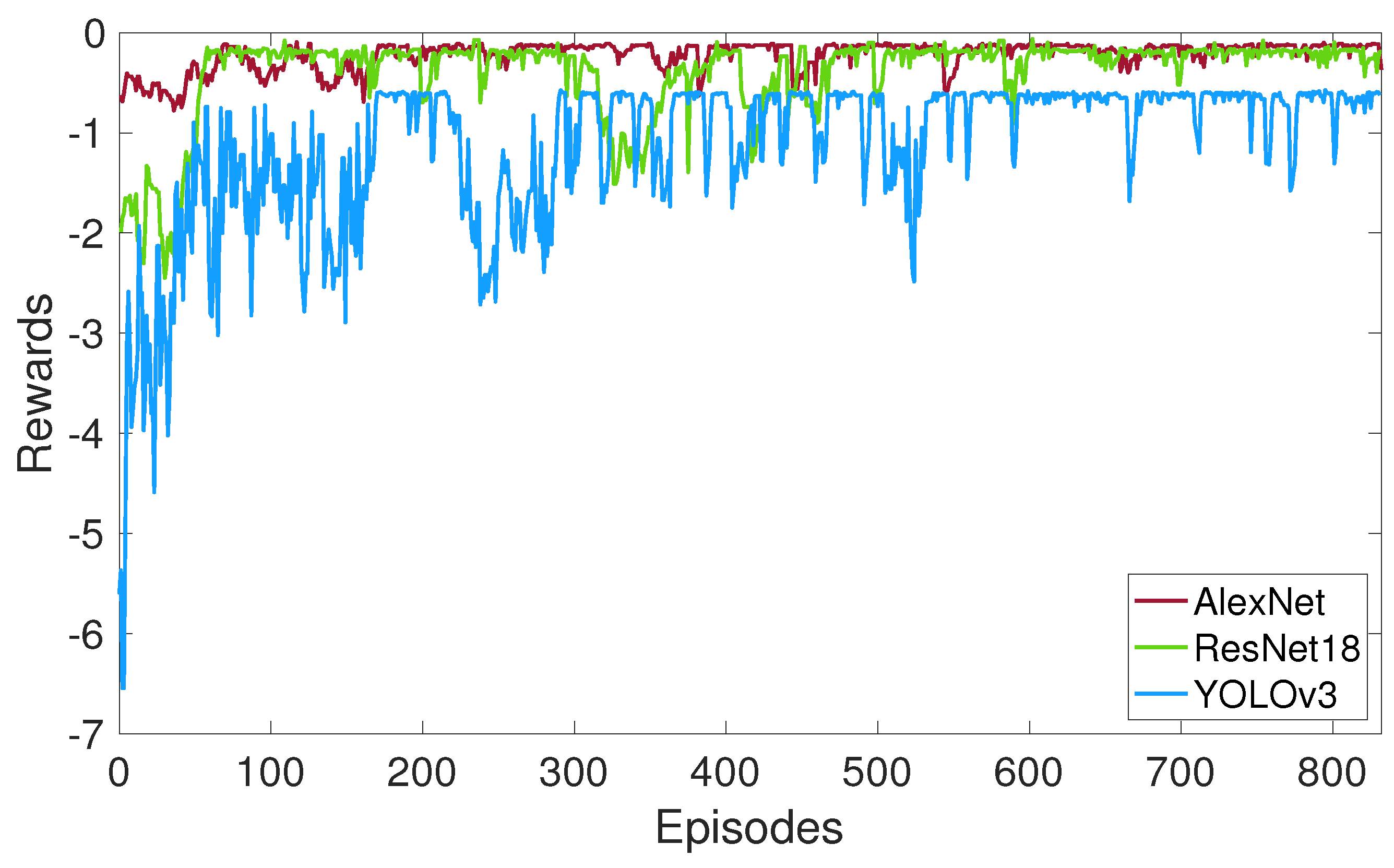
5.2.7. Reward Convergence
5.2.8. Robustness to Dynamic Conditions
5.3. Computational Cost Analysis
5.3.1. Pre-Processing Expenses
- Tasks: The pipeline begins by capturing a frame from the video stream. The frame is then decoded and resized to the required input dimensions of the target DNN (e.g., 416 × 416 for YOLOv3). Finally, pixel values are normalized.
- Expenses: These are standard, efficient computer vision operations. On a typical CPU like the one in our testbed, the combined latency for these tasks is minimal, generally in the range of 5–15 ms per frame. The computational cost is low and predictable.
5.3.2. Processing Expenses
- 1. Partition Decision:
- –
- Location: Local device (CPU).
- –
- Task: The DRL agent performs a forward pass through its policy network to select the optimal split point.
- –
- Expense: As established, the complexity is O(1) with respect to the analytic DNN’s size. This is an extremely fast operation, incurring a latency of only 1–2 ms.
- 2. Local Inference:
- –
- Location: Local device (CPU).
- –
- Task: The local device executes the initial layers of the DNN up to the chosen split point.
- –
- Expense: This is a major variable cost. The latency depends directly on the partition decision. A shallow split (fewer layers processed locally) results in low latency, while a deep split results in high latency. This cost can range from a few milliseconds to several seconds, as shown in our experimental results.
- 3. Data Transmission:
- –
- Location: Network.
- –
- Task: The intermediate feature map is serialized and transmitted from the local device to the edge server.
- –
- Expense: The cost is network latency, which depends on the size of the feature map (determined by the split point) and the available network bandwidth. This cost is also highly variable and is a key factor in the DRL agent’s decision-making.
- 4. Edge Inference:
- –
- Location: Edge server (GPU).
- –
- Task: The edge server executes the remaining layers of the DNN.
- –
- Expense: Due to the powerful GPU, the per-layer processing time is significantly lower than on the local CPU. The total latency on the edge depends on the number of layers it needs to process (the inverse of the local inference cost).
5.3.3. Post-Processing Expenses
- Tasks: For an object detection model like YOLOv3, this includes applying non-maximum suppression (NMS) to filter redundant bounding boxes and decoding the final tensor into class labels and coordinates. For a classification model, this is a simple operation to find the class with the highest probability score.
- Expenses: These operations are computationally inexpensive compared to the DNN inference itself. On the edge server, the post-processing latency is typically very low, in the range of 2–5 ms.
6. System Development and Operational Costs
6.1. Data Collection
- Skills Needed: Graduate Researcher with basic knowledge of computer vision datasets.
- Task Description: Our experiments utilize a publicly available traffic video dataset. This stage involved searching for suitable datasets, selecting one that met our criteria for complexity and resolution, and downloading the video files.
- Estimated Person-Hours: 4–6 h.
6.2. Data Cleaning
- Skills Needed: Graduate Researcher.
- Task Description: As we used a standard, pre-existing dataset, extensive data cleaning was not required. The effort was limited to verifying the integrity of the video files and ensuring consistent formatting for our video reader module.
- Estimated Person-Hours: 2–3 h.
6.3. Data Labeling
- Skills Needed: Not applicable.
- Task Description: This stage is not applicable to our project for two key reasons:
- For the video analytics task, we use DNN models (YOLOv3, ResNet18, etc.) that are already pre-trained on large, labeled datasets (like COCO and ImageNet). We did not perform any new labeling for the analytics models.
- For our DRL agent, the training is performed online by interacting with the system environment. The “labels” are the reward signals () generated automatically by the system based on performance metrics (latency, data size). Therefore, no manual data labeling is required.
- Estimated Person-Hours: 0 h.
6.4. Data Transformation
- Skills Needed: Python/PyTorch Developer.
- Task Description: This refers to the pre-processing of video frames (e.g., resizing, normalization) before they are fed into the DNN. This is an automated step within our software pipeline. The cost is the one-time effort to write and integrate this pre-processing code. This effort is included in the “Training, Validation, and Tests” stage below as part of the overall system development.
- Estimated Person-Hours: Included in Stage 5.
6.5. Training, Validation, and Tests
- Skills Needed: Researcher/Engineer with strong skills in Python, PyTorch, Deep Reinforcement Learning, and systems networking.
- Task Breakdown and Person-Hour Estimation:
- –
- System and Testbed Development (80–100 h): This includes writing the code for client–server communication, implementing the model partitioning logic for each DNN, creating the DRL agent environment, and setting up the hardware testbed.
- –
- DRL Agent Training and Tuning (30–40 h): This involves writing the training scripts, setting up experiments with different hyperparameters (learning rate, reward weights, etc.), and monitoring the training processes to ensure convergence.
- –
- System Evaluation and Analysis (40–50 h): This includes running all the baseline comparisons, executing the experiments under different network conditions and configurations, collecting the performance logs, and processing the data to generate the figures and tables for the manuscript.
- Total Estimated Person-Hours for this stage: 150–190 h.
7. Discussion on Scalability and Adaptability
7.1. Adaptation to Limited Bandwidth Environments
7.2. Scaling to Resource-Constrained Edge Devices
8. Conclusions and Future Work
- Expanding the System Topology: The current architecture is limited to a single-edge setup. A natural extension is to investigate multi-device and multi-edge scenarios, which would require more complex state representations and potentially multi-agent reinforcement learning techniques to manage resource coordination and selection.
- Enhanced Adaptability and Flexibility: To address the reliance on static configurations, future work could explore methods for automatically discovering optimal split points in arbitrary DNN architectures. Furthermore, using meta-learning or online learning would allow the DRL agent to rapidly adapt to new models or drastic shifts in network behavior, reducing the high offline training cost.
- Adaptive Control Parameters: Instead of using hardcoded thresholds and penalties, a more advanced implementation could learn these parameters dynamically or employ an adaptive control mechanism that adjusts them based on the application’s quality-of-service requirements.
- Holistic Co-optimization with Accuracy Guarantees: To overcome the limitations of a fixed model and the assumption of neutral accuracy, a more holistic framework is needed. This would involve expanding the DRL agent’s action space to co-optimize partitioning with feature compression and dynamic model adaptation (e.g., switching between large and small models). A key challenge would be to incorporate the resulting accuracy trade-offs directly into the agent’s reward function.
- Energy-Aware and Secure Partitioning: For battery-powered or sensitive applications, future work could incorporate energy consumption models and privacy-preserving techniques (e.g., lightweight encryption) into the optimization process, creating a truly multi-objective partitioning policy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
| Term/Symbol | Definition and Properties |
| Key Terms | |
| Edge Server | In the context of this paper, an edge server is a computing resource with significant processing power (e.g., equipped with a GPU) located at the network edge, such as on-premises or at a local data center. It is geographically closer to the end-user (local device) than the centralized cloud. Its primary role is to act as a powerful computational offloader, executing the intensive portions of DNN inference tasks to reduce latency. |
| Feature | A feature is a learned, numerical representation of a specific pattern or attribute in the input data. |
| Feature Map | A feature map is a 3D tensor with dimensions corresponding to height, width, and channels. Each channel represents a specific learned feature detected across the spatial dimensions (height and width) of the input. |
| Model Partitioning | The process of splitting a single DNN’s computational graph, , into two sequential sub-graphs, corresponding to two sets of layers: and . The sub-graph for runs on the local device, and its output (an intermediate feature map) is transmitted to the edge server, which executes the sub-graph for . |
| Candidate Split Point | A pre-defined layer in a DNN’s architecture where a valid partition can be made. The DRL agent’s action space is the discrete set of all such candidate points for a given DNN. |
| Acronyms | |
| A2C | Advantage Actor–Critic. A model-free, on-policy, deep reinforcement learning algorithm used for policy learning. |
| CPU | Central Processing Unit. The primary component of a computer that executes instructions. |
| DNN | Deep Neural Network. A class of machine learning models with multiple layers between the input and output layers. |
| DRL | Deep Reinforcement Learning. A subfield of machine learning that combines reinforcement learning with deep neural networks. |
| GPU | Graphics Processing Unit. A specialized electronic circuit designed to rapidly manipulate and alter memory to accelerate the creation of images for output to a display device; their highly parallel structure makes them effective for training and running DNNs. |
| Key Mathematical Symbols | |
| A single video frame captured at time step t. | |
| The system state observed at time step t. | |
| The action taken at time step t, representing the chosen DNN partition point. | |
| The reward received after taking action in state . | |
| The number of frames waiting in the local processing queue at time step t. | |
| The number of intermediate feature maps waiting in the offloading queue at time step t. | |
| The data size (amount) of the intermediate features transmitted for frame . | |
| The total end-to-end processing delay for frame . | |
| w | A hyperparameter weight to balance the trade-off between data transmission cost and time delay cost in the reward function. |
| F | A large, constant penalty value for dropping a frame. |
| T | The time-out threshold. If a frame’s waiting time exceeds T, it is dropped. |
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Gao, G. SmartEye: An Open Source Framework for Real-Time Video Analytics with Edge-Cloud Collaboration. In Proceedings of the 29th ACM International Conference on Multimedia, Chengdu, China, 20–24 October 2021; pp. 3767–3770. [Google Scholar]
- Ananthanarayanan, G.; Bahl, P.; Bodík, P.; Chintalapudi, K.; Philipose, M.; Ravindranath, L.; Sinha, S. Real-time video analytics: The killer app for edge computing. Computer 2017, 50, 58–67. [Google Scholar] [CrossRef]
- Chen, J.; Ran, X. Deep learning with edge computing: A review. Proc. IEEE 2019, 107, 1655–1674. [Google Scholar] [CrossRef]
- Matsubara, Y.; Levorato, M.; Restuccia, F. Split computing and early exiting for deep learning applications: Survey and research challenges. ACM Comput. Surv. 2022, 55, 1–30. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, J. Communication-computation trade-off in resource-constrained edge inference. IEEE Commun. Mag. 2020, 58, 20–26. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar] [CrossRef]
- Kang, Y.; Hauswald, J.; Gao, C.; Rovinski, A.; Mudge, T.; Mars, J.; Tang, L. Neurosurgeon: Collaborative intelligence between the cloud and mobile edge. ACM SIGARCH Comput. Archit. News 2017, 45, 615–629. [Google Scholar] [CrossRef]
- Hu, C.; Li, B. Distributed inference with deep learning models across heterogeneous edge devices. In Proceedings of the IEEE INFOCOM 2022-IEEE Conference on Computer Communications, Virtual, 2–5 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 330–339. [Google Scholar]
- Mohammed, T.; Joe-Wong, C.; Babbar, R.; Di Francesco, M. Distributed inference acceleration with adaptive DNN partitioning and offloading. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, Virtual, 2–5 May 2022; IEEE: Piscataway, NJ, USA, 2020; pp. 854–863. [Google Scholar]
- Li, H.; Hu, C.; Jiang, J.; Wang, Z.; Wen, Y.; Zhu, W. Jalad: Joint accuracy-and latency-aware deep structure decoupling for edge-cloud execution. In Proceedings of the 2018 IEEE 24th International Conference on Parallel and Distributed Systems (ICPADS), Singapore, 11–13 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 671–678. [Google Scholar]
- Shao, J.; Zhang, J. Bottlenet++: An end-to-end approach for feature compression in device-edge co-inference systems. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Laskaridis, S.; Venieris, S.I.; Almeida, M.; Leontiadis, I.; Lane, N.D. SPINN: Synergistic progressive inference of neural networks over device and cloud. In Proceedings of the 26th Annual International Conference on Mobile Computing and Networking, London, UK, 21–25 September 2020; pp. 1–15. [Google Scholar]
- Dong, C.; Hu, S.; Chen, X.; Wen, W. Joint optimization with DNN partitioning and resource allocation in mobile edge computing. IEEE Trans. Netw. Serv. Manag. 2021, 18, 3973–3986. [Google Scholar] [CrossRef]
- Tang, X.; Chen, X.; Zeng, L.; Yu, S.; Chen, L. Joint multiuser dnn partitioning and computational resource allocation for collaborative edge intelligence. IEEE Internet Things J. 2020, 8, 9511–9522. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Raha, A.; Raghunathan, V.; Raghunathan, A. Partnner: Platform-agnostic adaptive edge-cloud dnn partitioning for minimizing end-to-end latency. ACM Trans. Embed. Comput. Syst. 2024, 23, 1–38. [Google Scholar] [CrossRef]
- Peng, S.; Shen, Z.; Zheng, Q.; Hou, X.; Jiang, D.; Yuan, J.; Jin, J. APT-SAT: An Adaptive DNN Partitioning and Task Offloading Framework within Collaborative Satellite Computing Environments. IEEE Trans. Netw. Sci. Eng. 2025. [Google Scholar] [CrossRef]
- Zhang, M.; Fang, J.; Teng, Z.; Liu, Y.; Wu, S. Joint DNN Partitioning and Task Offloading Based on Attention Mechanism-Aided Reinforcement Learning. IEEE Trans. Netw. Serv. Manag. 2025, 22, 2914–2927. [Google Scholar] [CrossRef]
- Fang, W.; Xu, W.; Yu, C.; Xiong, N.N. Joint Architecture Design and Workload Partitioning for DNN Inference on Industrial IoT Clusters. ACM Trans. Internet Technol. (TOIT) 2022, 23, 7. [Google Scholar] [CrossRef]
- Hu, C.; Bao, W.; Wang, D.; Liu, F. Dynamic adaptive DNN surgery for inference acceleration on the edge. In Proceedings of the IEEE INFOCOM 2019-IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1423–1431. [Google Scholar]
- Zeng, L.; Chen, X.; Zhou, Z.; Yang, L.; Zhang, J. Coedge: Cooperative dnn inference with adaptive workload partitioning over heterogeneous edge devices. IEEE/ACM Trans. Netw. 2020, 29, 595–608. [Google Scholar] [CrossRef]
- Xiao, Z.; Xia, Z.; Zheng, H.; Zhao, B.Y.; Jiang, J. Towards performance clarity of edge video analytics. In Proceedings of the 2021 IEEE/ACM Symposium on Edge Computing (SEC), San Jose, CA, USA, 14–17 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 148–164. [Google Scholar]
- Du, K.; Zhang, Q.; Arapin, A.; Wang, H.; Xia, Z.; Jiang, J. Accmpeg: Optimizing video encoding for video analytics. arXiv 2022, arXiv:2204.12534. [Google Scholar] [CrossRef]
- Chen, B.; Yan, Z.; Nahrstedt, K. Context-aware image compression optimization for visual analytics offloading. In Proceedings of the 13th ACM Multimedia Systems Conference, Athlone, Ireland, 14–17 June 2022; pp. 27–38. [Google Scholar]
- Wang, X.; Gao, G.; Wu, X.; Lyu, Y.; Wu, W. Dynamic DNN model selection and inference off loading for video analytics with edge-cloud collaboration. In Proceedings of the 32nd Workshop on Network and Operating Systems Support for Digital Audio and Video, Athlone, Ireland, 17 June 2022; pp. 64–70. [Google Scholar]
- Ran, X.; Chen, H.; Zhu, X.; Liu, Z.; Chen, J. Deepdecision: A mobile deep learning framework for edge video analytics. In Proceedings of the IEEE INFOCOM 2018-IEEE Conference on Computer Communications, Honolulu, HI, USA, 15–19 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1421–1429. [Google Scholar]
- Zhao, K.; Zhou, Z.; Chen, X.; Zhou, R.; Zhang, X.; Yu, S.; Wu, D. EdgeAdaptor: Online Configuration Adaption, Model Selection and Resource Provisioning for Edge DNN Inference Serving at Scale. IEEE Trans. Mob. Comput. 2022, 22, 5870–5886. [Google Scholar] [CrossRef]
- Gao, G.; Dong, Y.; Wang, R.; Zhou, X. EdgeVision: Towards collaborative video analytics on distributed edges for performance maximization. IEEE Transactions on Multimedia 2024, 26, 9083–9094. [Google Scholar] [CrossRef]
- Dong, Y.; Gao, G. EdgeCam: A Distributed Camera Operating System for Inference Scheduling and Continuous Learning. In Proceedings of the 2024 IEEE/ACM Ninth International Conference on Internet-of-Things Design and Implementation (IoTDI), Hong Kong, China, 13–16 May 2024; pp. 225–226. [Google Scholar]
- Jiang, J.; Luo, Z.; Hu, C.; He, Z.; Wang, Z.; Xia, S.; Wu, C. Joint model and data adaptation for cloud inference serving. In Proceedings of the 2021 IEEE Real-Time Systems Symposium (RTSS), Dortmund, Germany, 7–10 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 279–289. [Google Scholar]
- Zhang, H.; Ananthanarayanan, G.; Bodik, P.; Philipose, M.; Bahl, P.; Freedman, M.J. Live video analytics at scale with approximation and delay-tolerance. In Proceedings of the 14th USENIX Symposium on Networked Systems Design and Implementation, Boston, MA, USA, 27–29 March 2017. [Google Scholar]
- Jiang, J.; Ananthanarayanan, G.; Bodik, P.; Sen, S.; Stoica, I. Chameleon: Scalable adaptation of video analytics. In Proceedings of the 2018 Conference of the ACM Special Interest Group on Data Communication, Budapest, Hungary, 20–25 August 2018; pp. 253–266. [Google Scholar]
- Liu, J.; Gao, G. CSVA: Complexity-Driven and Semantic-Aware Video Analytics via Edge-Cloud Collaboration. In Proceedings of the International Conference on Wireless Artificial Intelligent Computing Systems and Applications, Tokyo, Japan, 24–26 June 2025; pp. 107–116. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Liu, L.; Li, H.; Gruteser, M. Edge assisted real-time object detection for mobile augmented reality. In Proceedings of the 25th Annual International Conference on Mobile Computing and Networking, Los Cabos, Mexico, 21–25 October 2019; pp. 1–16. [Google Scholar]
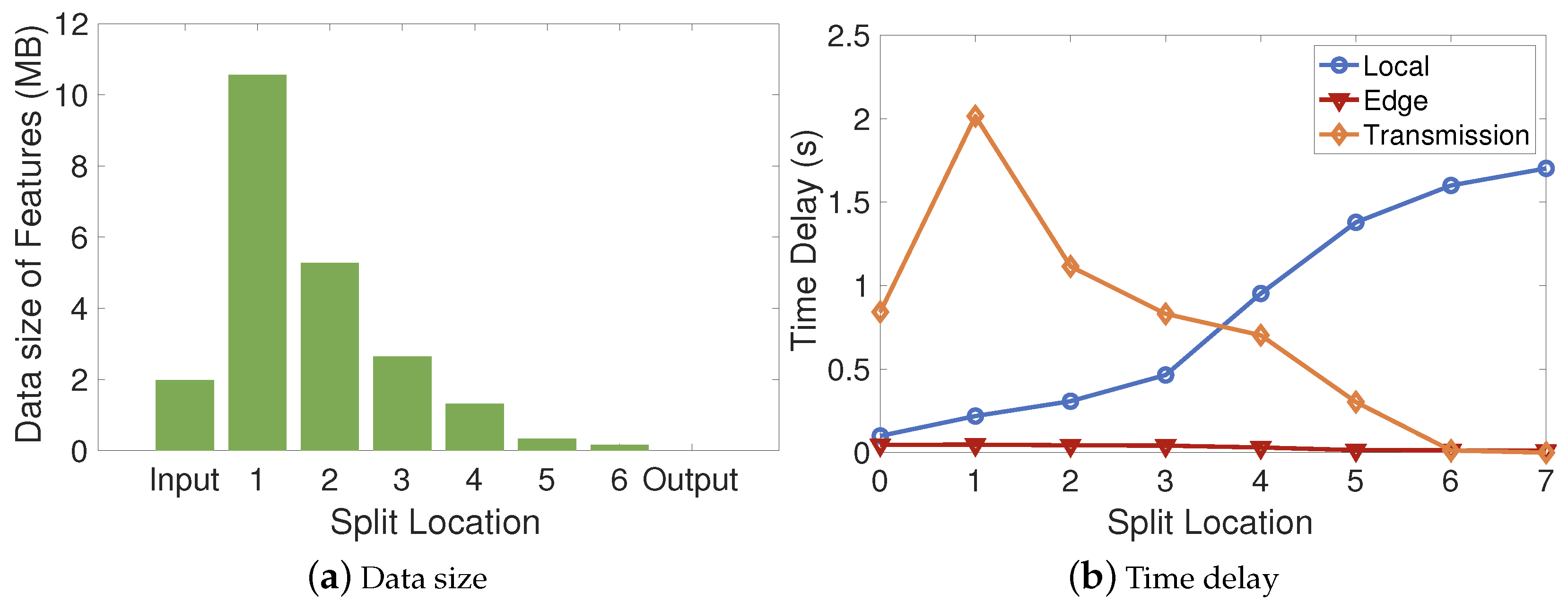

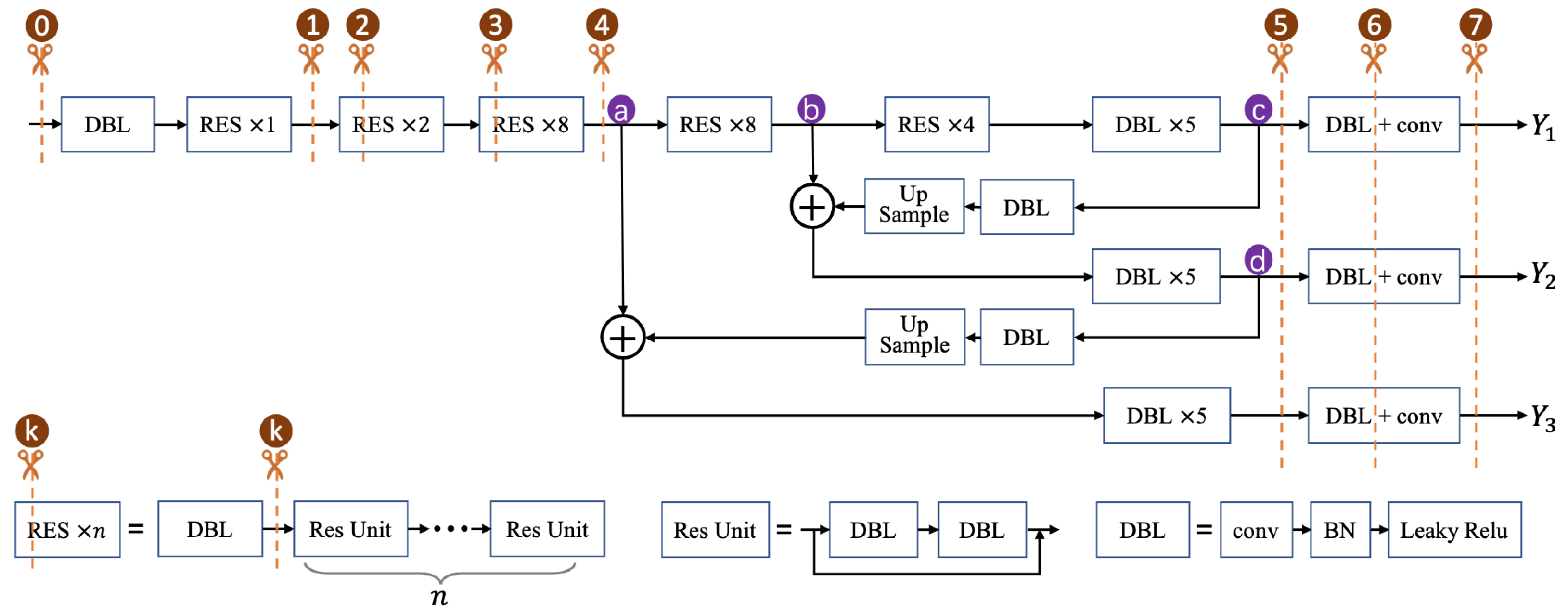


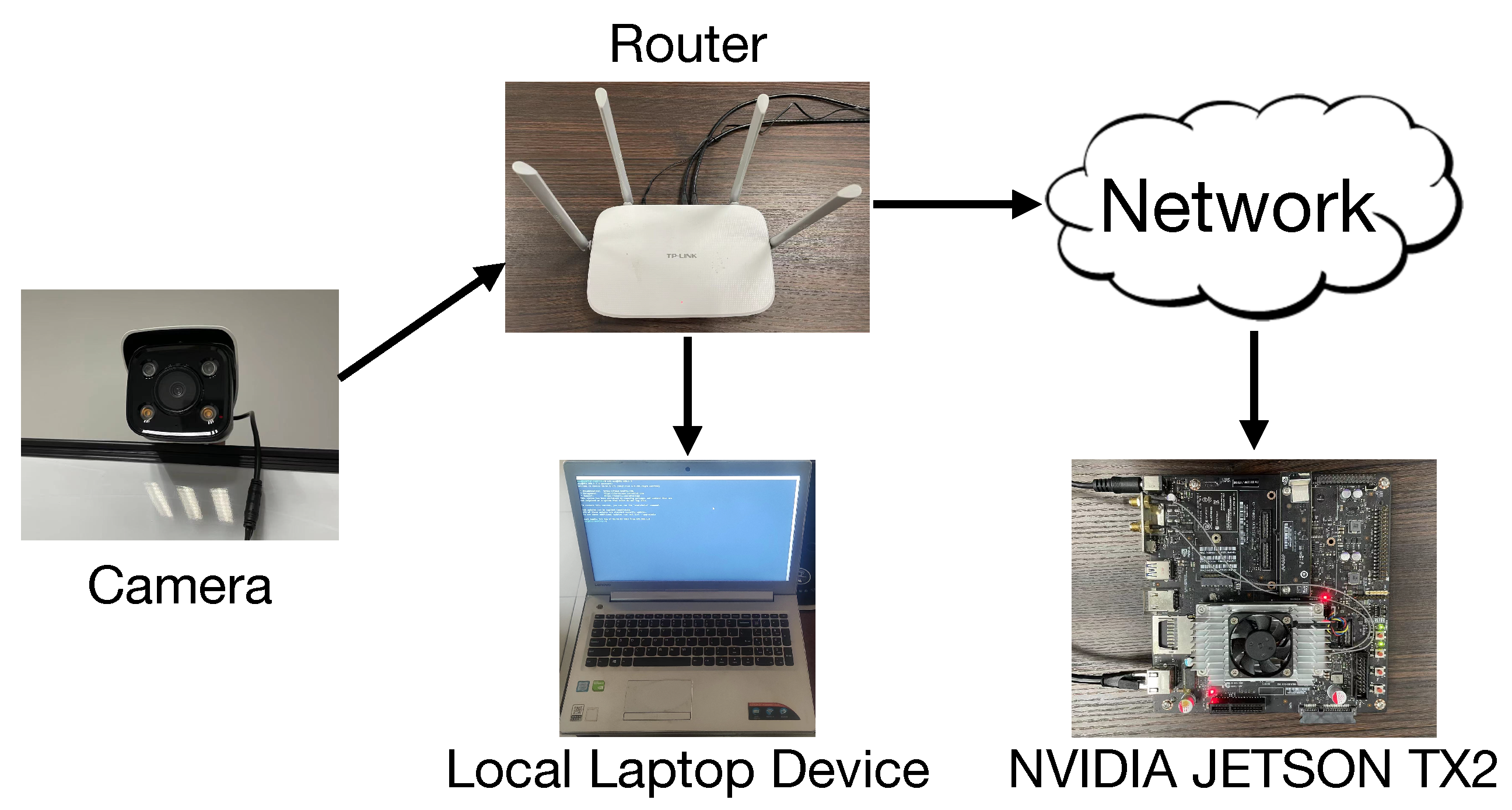
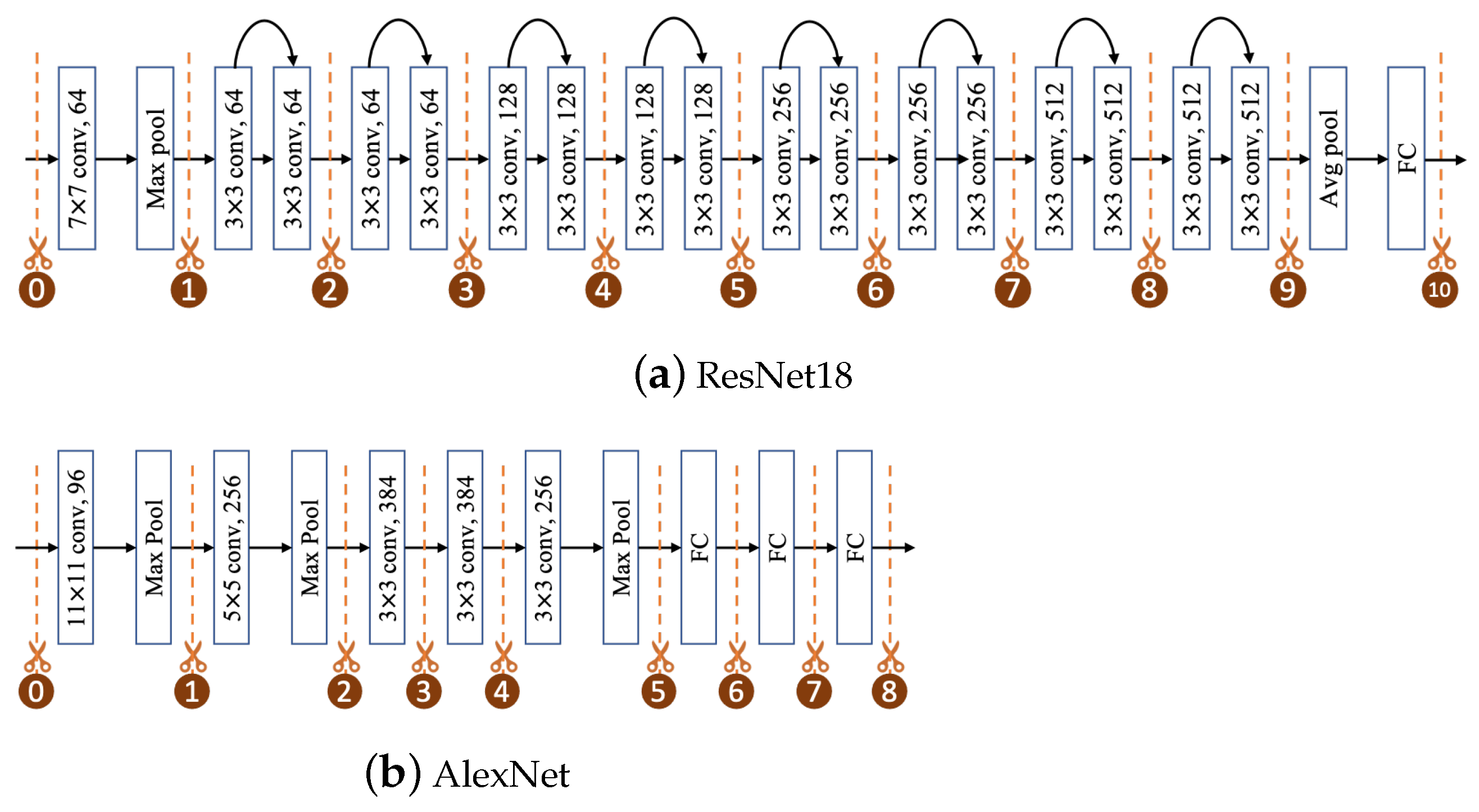





| DNN | Size | # Parameters | Local Inference Time | Edge Inference Time |
|---|---|---|---|---|
| YOLOv3 | 236 MB | 61.53 M | 4.347 s | 0.759 s |
| ResNet18 | 44.6 MB | 11.7 M | 0.187 s | 0.5 s |
| AlexNet | 233 MB | 62.37 M | 0.136 s | 0.616 s |
| Metric | vs. LocalOnly | vs. EdgeOnly | vs. SemiFixed | vs. Greedy |
|---|---|---|---|---|
| Transmitted Data Amount | NA | 49% | −66% | 26% |
| Total Delay Reduction | 86% | 25% | 77% | 83% |
| Drop Rate Reduction | 56% | −68% | 6% | 30% |
| System Cost Reduction | 63% | 42% | 50% | 67% |
| Partitioning Strategy | Top 1 Predicted Class | Top 1 Logit Value |
|---|---|---|
| No Partition (Executed Locally) | ‘golden retriever’ | 9.3985 |
| Split at Layer 2 | ‘golden retriever’ | 9.3985 |
| Split at Layer 5 | ‘golden retriever’ | 9.3985 |
| Split at Layer 8 | ‘golden retriever’ | 9.3985 |
| No Partition (Executed on Edge) | ‘golden retriever’ | 9.3985 |
| Learned Policy: | Split Point | Local Comp. | Trans. | Edge Comp. | Total Delay |
|---|---|---|---|---|---|
| High Bandwidth | Shallow (e.g., 2) | 260 | 145 | 390 | 795 |
| (Low w policy) | (33%) | (18%) | (49%) | ||
| Low Bandwidth | Deep (e.g., 4) | 1150 | 48 | 165 | 1363 |
| (High w policy) | (84%) | (4%) | (12%) |
| DNN | I | II | III |
|---|---|---|---|
| YOLOv3 | 800 ms | 1000 ms | 1200 ms |
| ResNet18 | 100 ms | 150 ms | 200 ms |
| AlexNet | 100 ms | 150 ms | 200 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, Y.; Liu, L.; Wang, X.; Fan, Z.; Wang, J.; Gao, G. Learning to Partition: Dynamic Deep Neural Network Model Partitioning for Edge-Assisted Low-Latency Video Analytics. Mach. Learn. Knowl. Extr. 2025, 7, 117. https://doi.org/10.3390/make7040117
Lyu Y, Liu L, Wang X, Fan Z, Wang J, Gao G. Learning to Partition: Dynamic Deep Neural Network Model Partitioning for Edge-Assisted Low-Latency Video Analytics. Machine Learning and Knowledge Extraction. 2025; 7(4):117. https://doi.org/10.3390/make7040117
Chicago/Turabian StyleLyu, Yan, Likai Liu, Xuezhi Wang, Zhiyu Fan, Jinchen Wang, and Guanyu Gao. 2025. "Learning to Partition: Dynamic Deep Neural Network Model Partitioning for Edge-Assisted Low-Latency Video Analytics" Machine Learning and Knowledge Extraction 7, no. 4: 117. https://doi.org/10.3390/make7040117
APA StyleLyu, Y., Liu, L., Wang, X., Fan, Z., Wang, J., & Gao, G. (2025). Learning to Partition: Dynamic Deep Neural Network Model Partitioning for Edge-Assisted Low-Latency Video Analytics. Machine Learning and Knowledge Extraction, 7(4), 117. https://doi.org/10.3390/make7040117





