Abstract
Deploying deep learning (DL) models in real-world environments remains a major challenge, particularly under resource-constrained conditions where achieving both high accuracy and compact architectures is essential. While effective, Conventional pruning methods often suffer from high computational overhead, accuracy degradation, or disruption of the end-to-end training process, limiting their practicality for embedded and real-time applications. We present Dynamic Attention-Guided Pruning (DAGP), a Dynamic Attention-Guided Soft Channel Pruning framework that overcomes these limitations by embedding learnable, differentiable pruning masks directly within convolutional neural networks (CNNs). These masks act as implicit attention mechanisms, adaptively suppressing non-informative channels during training. A progressively scheduled L1 regularization, activated after a warm-up phase, enables gradual sparsity while preserving early learning capacity. Unlike prior methods, DAGP is retraining-free, introduces minimal architectural overhead, and supports optional hard pruning for deployment efficiency. Joint optimization of classification and sparsity objectives ensures stable convergence and task-adaptive channel selection. Experiments on CIFAR-10 (VGG16, ResNet56) and PlantVillage (custom CNN) achieve up to 98.82% FLOPs reduction with accuracy gains over baselines. Real-world validation on an enhanced PlantDoc dataset for agricultural monitoring achieves 60 ms inference with only 2.00 MB RAM on a Raspberry Pi 4, confirming efficiency under field conditions. These results illustrate DAGP’s potential to scale beyond agriculture to diverse edge-intelligent systems requiring lightweight, accurate, and deployable models.
1. Introduction
Convolutional Neural Networks (CNNs) have become a cornerstone of modern artificial intelligence, underpinning applications in precision agriculture, medical diagnostics, automatic speech recognition (ASR), and real-time Unmanned Aerial Vehicle (UAV) control [1]. Their ability to extract rich hierarchical features with relatively compact architectures makes them attractive for embedded and edge deployment, particularly in latency-sensitive and resource-constrained environments. Compared to emerging transformer-based architectures, CNNs offer a favorable balance between accuracy, generalization, and computational efficiency [2].
While efficient, deploying CNNs in real-world scenarios—especially on edge devices—remains challenging due to strict constraints on memory, processing power, and energy consumption [3]. Especially in medium or large datasets, where model size tends to grow proportionally with the dataset size, this increase significantly hinders real-world applications, where responsiveness and real-time inference are critical. Model compression has emerged as a key strategy to address these challenges, with structured channel pruning being particularly preferable due to its compatibility with standard hardware and reduced inference cost without architectural redesign [4]. Yet, conventional pruning methods often suffer from high computational overhead, accuracy degradation, or disruption of end-to-end optimization, limiting their scalability [5].
To overcome these limitations, we propose DAGP—a Dynamic Attention-Guided Soft Channel Pruning framework that integrates lightweight, learnable pruning masks directly into CNNs. These masks act as implicit attention mechanisms, dynamically suppressing non-informative channels during training. A progressively scheduled L1 regularization, activated after a warm-up phase, preserves early learning capacity while promoting stable convergence. Unlike traditional pipelines, DAGP is fully differentiable, retraining-free, and optionally supports hard pruning for deployment efficiency. Its design enables robust compression with enhanced accuracy, validated on the CIFAR-10 benchmark and the PlantVillage agricultural dataset. The compressed model obtained from PlantVillage is further fine-tuned on the real-world PlantDoc agricultural dataset before being deployed on a Raspberry Pi 4 for real-time edge inference.
The main contributions of this work are as follows:
- An end-to-end differentiable pruning strategy that jointly optimizes classification and sparsity objectives
- A progressive regularization scheme for adaptive structured sparsity, without impairing early training dynamics.
- Empirical evidence of substantial compression with accuracy gains, validated on CIFAR-10 and the PlantVillage agricultural benchmark.
- A deployment-ready architecture in which the hard-pruned model from PlantVillage is fine-tuned on an enhanced PlantDoc dataset, addressing class imbalance through curated public samples, targeted augmentation, and LoRA-based synthetic image generation.
- Edge-device validation via Raspberry Pi 4 deployment, with metrics confirming suitability for real-time applications in resource-constrained environments.
The remainder of this paper is structured as follows. Section 2 reviews relevant related works and foundational methods. Section 3 details materials used in this study. Section 4 presents the proposed pruning methodology and its integration into CNN architectures. Section 5 reports and analyzes the experimental results. Section 6 provides an in-depth discussion of key findings. Finally, the last section concludes the paper and outlines directions for future research.
2. Related Works
2.1. Static and Structured Pruning
Structured pruning techniques aim to reduce the computational cost of CNNs by permanently removing entire filters or channels, leading to dense, hardware-friendly architectures.
Early and foundational methods include L1-norm-based filter pruning by Li et al. [6], which removes filters with the smallest weight magnitudes based on their L1-norm. Building on this, Network Slimming by Liu et al. [7] introduces L1 regularization on BatchNorm scaling factors to induce channel sparsity. To further improve compression in deep architectures, He et al. [8] proposed a LASSO regression-based channel pruning method, which iteratively identifies redundant filters and reconstructs intermediate outputs, allowing precise control over pruning sensitivity across layers. Wang et al. [9] proposed RFPruning, a retraining-free structured pruning framework that integrates ADMM-based sparse learning during training with a genetic algorithm to fine-tune pruning rates per layer. Lian et al. [10] proposed DAAR, a dual-attention structured pruning method that combines spatial and channel attention with per-layer adaptive pruning rates. Jiang et al. [11] modeled channel pruning as a multi-objective optimization task over feature-map selection, using evolutionary search with search-space heuristics to compress CNNs with minimal accuracy loss. Hedegaard et al. [12] proposed Structured Pruning Adapters (SPAs) that integrate structured channel pruning with adapter-based task adaptation to accelerate and specialize neural networks for new tasks. Two variants, SPLoRA and SPPaRA, fuse low-rank or residual adapters with channel-pruned layers to achieve high compression while preserving accuracy. Lu et al. [13] proposed a Growing-before-Pruning (GbP) framework that overcomes the rigid limitations of traditional filter pruning by first expanding the network’s filter space through multi-branch architectures, then applying a progressive pruning strategy guided by a global group sparsity model based on a Gaussian Scale Mixture (GSM). A deterministic annealing schedule further improves convergence and avoids local minima during sparsity control.
Despite their effectiveness in reducing FLOPs and parameter counts, these methods rely on static filter-importance metrics, fixed thresholds, and multi-stage prune–retrain pipelines. Such constraints break end-to-end differentiability, hinder adaptability across datasets and tasks, and limit real-time applicability in embedded or resource-constrained systems.
DAGP addresses these shortcomings by replacing static importance metrics with learnable, continuous pruning masks jointly optimized with network weights. Its fully differentiable design enables seamless integration into the standard training loop without iterative retraining, while its lightweight architecture ensures deployment readiness in real-time, resource-constrained environments.
2.2. Differentiable and Soft Pruning
Differentiable and soft pruning techniques address the rigidity of static approaches by incorporating differentiable masks, enabling the attenuation of less informative channels during training. This integration allows pruning decisions to be optimized jointly with the network’s learning objective, preserving end-to-end differentiability.
He et al. [14] introduced Soft Filter Pruning (SFP), which gradually zeroes out low-importance filters during training while allowing their recovery. Kang and Han [15] proposed an operation-aware pruning method, deriving probabilistic masks from BatchNorm parameters via Gaussian Cumulative Distribution Function (CDF) and sigmoid relaxation to guide channel suppression during optimization. AutoPruner by Luo & Wu [16] introduces a differentiable, end-to-end trainable filter pruning layer that learns binary index codes for channel selection during fine-tuning. By gradually binarizing activation-based codes, the method jointly optimizes accuracy and sparsity, enabling structured compression without iterative retraining.
While improving flexibility, these approaches often rely on fixed sparsity targets, manually tuned regularization terms, or post-training thresholds. Such dependencies increase tuning complexity, reduce adaptability across architectures and datasets, and limit seamless deployment in embedded or real-time scenarios.
DAGP integrates differentiable, learnable masks into the optimization process, coupled with a progressively scheduled L1 regularization. This warm-up-based scheduling preserves early learning capacity while gradually inducing structured sparsity, enabling the model to adaptively suppress uninformative channels during training. By jointly learning masks and network weights, DAGP eliminates the need for fixed thresholds or manually tuned sparsity targets, ensuring stability, adaptability, and efficiency without additional tuning stages.
2.3. Dynamic Channel Pruning
Dynamic pruning techniques adapt pruning decisions at runtime or per input, enhancing inference efficiency. Gao et al. [17] introduced Feature Boosting and Suppression (FBS), a dynamic framework that predicts channel saliency per input using a lightweight auxiliary module. It selectively amplifies or suppresses channels through a differentiable winner-take-all mechanism, enabling both input- and output-side sparsity. Chen et al. [18] proposed a reinforcement learning-based method that employs separate agents to learn both static and runtime channel importance, aiming to balance dynamic flexibility with storage efficiency. Liu et al. [19] introduced Dynamic Channel Pruning via Activation Gates (DCPAG), embedding an auxiliary pruning module and dynamic ReLU gate to enable input-dependent channel control and targeted fine-tuning of challenging samples.
While these approaches improve pruning granularity and inference adaptability, they often introduce architectural complexity, require additional components and depend on costly training strategies such as reinforcement learning. These factors may hinder ease of deployment, increase latency, and reduce compatibility with constrained or real-time environments.
Extending beyond the limitations of prior pruning approaches, we propose DAGP—a lightweight, retraining-free, attention-guided soft pruning framework that is fully differentiable and seamlessly integrated into standard training pipelines. DAGP employs learnable, continuous pruning masks optimized jointly with model weights, enabling task-adaptive channel selection without architectural modification, external solvers, or multi-stage retraining. A warm-up-based sparsity schedule delays regularization to preserve early learning capacity while ensuring gradual and stable pruning. These masks act as implicit attention scores, selectively suppressing less informative channels while maintaining network expressiveness. Beyond efficient compression, DAGP functions as a unified data–model optimization framework that simultaneously reduces model size and enhances accuracy and generalization. By combining the strengths of soft and dynamic pruning, DAGP delivers a practical, end-to-end, deployment-ready solution for real-time inference in resource-constrained environments.
3. Materials
Dataset Description
To evaluate the effectiveness and deployment readiness of our Dynamic Attention-Guided Pruning (DAGP) strategy, we performed evaluations on both standardized benchmarks and a real-world deployment scenario, using a consistent split of 70% for training, 20% for validation, and 10% for testing across all datasets.
We first assessed performance on the CIFAR-10 dataset (Figure 1a) with VGG16 and ResNet56, providing a controlled benchmark for compression and accuracy under structured pruning [20]. Standard data augmentation techniques (Table 1) were applied during training to enhance generalization. For domain-specific validation in precision agriculture, we employed a custom CNN on the PlantVillage dataset (Figure 1b) [21], enabling lightweight modeling in moderately imbalanced conditions.

Figure 1.
Samples from CIFAR-10 and PlantVillage datasets.

Table 1.
Parameters used for data augmentation in the training dataset.
To demonstrate real-world applicability, we fine-tuned the hard-pruned version pre-trained on the PlantVillage model on the PlantDoc dataset (Figure 2a) using a Raspberry Pi 4, simulating deployment in resource-constrained environments. We enhanced PlantDoc by addressing class imbalance—particularly for spider mite—through curated public data, standard augmentations, and synthetic images generated with a LoRA-finetuned Stable Diffusion model. Figure 2a includes real and synthetic images for the rare spider mite class, while Figure 2b illustrates their t-SNE embeddings. The t-SNE plot reveals that synthetic samples are tightly embedded within the real data cluster, confirming their distributional realism and task-relevance. This close interference reinforces intra-class cohesion without distorting the semantic space, demonstrating the effectiveness of our targeted data-generation pipeline.

Figure 2.
Enhanced PlantDoc dataset and t-SNE visualization for spider mite class.
4. Methodology
4.1. Preliminary Mathematical Formulation
Let C denote a deep convolutional neural network composed of L learnable layers. Each layer has output channels. The model is trained on a dataset
where each input is associated with a one-hot encoded label for a classification task with K classes and . The output of the network is denoted as follows:
computed via softmax activation.
- A.
- Classification Loss
The network is trained to minimize the cross-entropy loss over the dataset:
- B.
- Learnable Soft Pruning Masks
To enable dynamic soft pruning, we associate each convolutional block ℓ with a learnable differentiable attention mask defined as:
where are trainable logits, and denotes the element-wise sigmoid activation function. These masks modulate the output channels during training, dynamically suppressing less informative features.
- C.
- Mask-Guided Channel Modulation
The output feature map of layer is modulated by the learned soft pruning mask through element-wise channel-wise multiplication:
where is the activation map of the j-th output channel before pruning of layer , is the corresponding learned soft mask value and is the resulting masked (attenuated) output channel.
- D.
- Sparsity-Inducing Regularization
To promote sparsity in the learned masks, we incorporate an regularization term:
where is a sparsity coefficient that evolves over training epochs e, controlling the strength of regularization for layer ℓ and denote the norm.
- E.
- Sparsity Schedule with Warm-Up
To preserve learning capacity during early training, we delay the onset of sparsity with a warm-up mechanism:
where is the warm-up epoch and is the maximum regularization strength.
- F.
- Composite Objective Function
The total loss is defined as a combination of the task-specific classification loss and the sparsity regularization:
- G.
- Joint Gradient-Based Optimization
Both network weights and mask logits are updated via standard gradient descent:
with η denoting the learning rate and ∇ representing the gradient of the total loss with respect to the corresponding parameter.
- H.
- Post-Training Hard Pruni
After training, hard pruning can be applied by thresholding the learned masks:
where is a pruning threshold and is the indicator function.
According to Table 2, our method reformulates pruning from static thresholds or handcrafted rules into a fully learnable process. Instead of layer-level or globally fixed pruning rates, we introduce pruning weights associated with each channel, activated by a sigmoid function to produce pruning masks that act as attention scores and are optimized end-to-end with the network. This enables precise, channel-customized pruning that is locally adaptive yet globally supervised by task accuracy and overall loss. This attention mechanism enables selective channel pruning, leading to jointly optimizing both performance and sparsity, thereby enhancing accuracy while compressing models. Sparsity strength is directly controlled through L2 regularization on these pruning weights, ensuring a joint optimization of pruning and accuracy. A warm-up phase is further integrated to allow early feature learning before pruning begins, preventing the loss of important representations. By balancing local channel-level decisions with global task guidance, the approach avoids sensitivity to local data distributions while remaining lightweight and computationally efficient. To the best of our knowledge, we are the first to introduce pruning ratios as learnable attention weights together with a warm-up phase, providing a novel framework for dynamic, task-guided pruning.

Table 2.
Overview: prior main pruning approaches and proposed contribution.
4.2. Dynamic Attention-Guided Pruning Mechanism
The proposed Dynamic Attention-Guided Pruning (DAGP) strategy enables an end-to-end, lightweight, and retraining-free framework that supervises structured channel pruning during training through task-driven accuracy signals. At its core, the method integrates Attention-Guided Pruning Blocks after each convolutional layer. These blocks introduce learnable, continuous-valued mask vectors , computed via a sigmoid activation over trainable logits as defined in Equation (4). Each element of the mask modulates the activation of a specific output channel (Equation (5)), functioning as an attention-guided gate that softly suppresses less informative channels during forward propagation.
To promote sparsity while preserving the model’s learning capacity, an L1 regularization term is applied to the learned masks (Equation (6)). Crucially, DAGP introduces a delayed sparsity schedule (Equation (7)), wherein the regularization strength remains null during an initial warm-up phase. This design prevents premature suppression, allowing the network to first discover relevant features before inducing sparsity—enhancing stability and convergence.
Unlike conventional approaches that decouple pruning and training or rely on fixed heuristics, our method jointly optimizes both the classification objective and sparsity constraints within a unified, differentiable loss function (Equation (8)). The non-convex optimization is handled directly via standard optimizers (Adam), ensuring that both network weights and mask logits are updated simultaneously during backpropagation (Equation (9)). As a result, the pruning process becomes fully accuracy-supervised and inherently task-adaptive, with the network autonomously determining which channels to suppress based on their contribution to the end objective.
This strategy serves not only as a compression mechanism but also as an implicit regularizers, enhancing generalization and mitigating overfitting. As a result, it outperforms baseline unpruned models in accuracy under identical training conditions.
For deployment, hard pruning is optionally performed post-training by thresholding the learned mask values (Equation (10)). The corresponding kernels are removed, and the model is reconstructed accordingly. The proposed method is formally outlined in Algorithm 1, which summarizes the core steps of our strategy.
| Algorithm 1: Dynamic soft channel pruning with adaptive sparsity scheduling |
| Input: Training dataset , Pruning threshold ), maximum sparsity coefficient Warm-up epoch , Total training epochs ; Baseline CNN initialized randomly and trained jointly with pruning. Initialization: For each layer , initialize trainable mask logits ; Compute the soft pruning masks using Equation (4). Apply attention-guided channel modulation via mask-based reweighting as defined in Equation (5). Set Training Loop: for do for each mini-batch in do 1. Forward propagation using masked CNN ; 2. Compute the classification loss as per Equation (3). 3. Compute sparsity-inducing loss using Equation (6). 4. Compute the total loss using using Equation (8). 5. Update and jointly using Equation (9). 6. Update if else keep 0 Equation (7). end for end for Post-Training Hard Pruning: For each layer , retrieve the learned soft masks ; Prune channels whose mask values satisfy ; Reconstruct C’ by pruning C. Return: Pruned network . |
4.3. Instantiations and Computational Complexity
The proposed DAGP (Dynamic Attention-Guided Pruning) framework is modular, lightweight, and architecture-agnostic, enabling seamless integration into diverse CNNs such as VGG-16, ResNet-56, and custom architectures. DAGP is exemplarily integrated into the custom CNN architecture, as illustrated in Figure 3. Its block-wise design allows insertion after any convolutional layer, preserving architectural flexibility without structural modifications. In addition to standard training hyperparameters, DAGP introduces two key pruning-specific controls: the maximum sparsity strength , and the pruning onset epoch , which defers regularization to stabilize early training. Its model-agnostic and task-independent design supports broad applicability across both academic benchmarks and real-world, resource-constrained deployments.
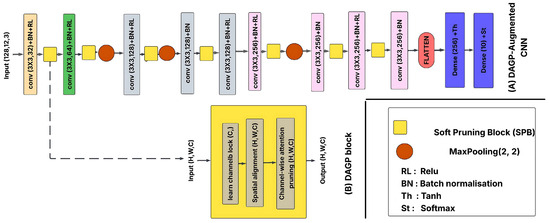
Figure 3.
Structural integration of the DAGP framework into the custom CNN model.
Importantly, DAGP introduces minimal computational overhead. Each pruning block adds two learnable parameters per channel—yielding an analytical overhead expressed as:
where denotes the number of output channels in layer , and AP denotes the total number of additional trainable parameters introduced by DAGP.
This linear complexity ensures scalability, making the approach efficient even for deep models. A detailed breakdown of the adopted models, their architectural configurations, and the associated DAGP overhead is provided in Table 3.

Table 3.
Model summaries with computational overhead.
4.4. Theoretical Justification of the Proposed Strategy
The proposed DAGP framework is conceptually grounded in a set of foundational principles from information theory and statistical learning. These principles not only inspire the design of the proposed masks but also offer rigorous justifications for their effectiveness in guiding sparsity during training. In what follows, we discuss four core theoretical perspectives that collectively support our method.
4.4.1. Attention Mechanisms as Soft Feature Selectors
DAGP integrates sigmoid-based learnable masks applied element-wise to convolutional outputs at each layer. The resulting masked activations are defined using an element-wise multiplication as defined in Equation (5). This operation is structurally equivalent to attention, where weights are assigned to feature channels according to their task relevance. While conceptually related to the attention mechanisms introduced by Vaswani et al. [22], DAGP’s design aligns more closely with the lightweight formulation of Squeeze-and-Excitation (SE) blocks by Hu et al. [23], focusing on implicit channel modulation. However, unlike these classical attention mechanisms, DAGP employs input-independent, learnable masks jointly optimized with network weights via backpropagation. Their differentiable design enables seamless insertion into any layer without modifying the architecture. By selectively suppressing less informative channels during training, these masks function as implicit regularizers—driving task-aware compression, enhancing generalization, and enabling lightweight architectural adaptation akin to implicit neural architecture search within standard training regimes.
4.4.2. Information Bottleneck Principle
From an information–theoretic standpoint, the masked activations function as compressed representations of the input that retain maximal information about the output . This perspective aligns with the Information Bottleneck (IB) principle proposed by Tishby et al. [24], which formalizes the learning objective as:
where denotes mutual information, controls the trade-off between compression and relevance, and
By learning sparse masks, DAGP reduces redundancy in (minimizing ) while maintaining predictive capacity (maximizing ), effectively realizing the Information Bottleneck in a structured, layer-wise manner, aligning compression with discriminative performance during training.
4.4.3. Structural Risk Minimization (SRM)
The proposed DAGP framework also aligns with the principle of Structural Risk Minimization from Statistical Learning Theory introduced by Vapnik et al. [25]. It balances empirical risk and model complexity according to:
where is the true risk, the empirical risk, and a measure of hypothesis complexity.
Initially, the model’s learning capacity is fully preserved through a warm-up schedule to enable effective data fitting. As training progresses, L1-based sparsity regularization gradually reduces by pushing mask values toward zero. This structured sparsity acts as a form of complexity control, guiding the network toward simpler, more generalizable hypotheses without compromising task performance.
4.4.4. Minimum Description Length (MDL) Principle
Finally, DAGP embodies the Minimum Description Length (MDL) principle introduced by Rissanen et al. [26], aiming to minimize the total cost of representing both the model and the data:
where denotes coding length. The soft-to-hard pruning strategy reduces by eliminating redundant filters while preserving performance, thereby keeping low. The resulting models are compact yet effective, satisfying the MDL criterion of efficient description.
Collectively, these theoretical frameworks provide a cohesive foundation for DAGP by unifying efficient representation learning, model compactness, and generalization control. This synergy enables DAGP to dynamically adapt sparsity during training while maintaining high predictive performance.
4.5. Evaluation Metrics
We evaluated all models—both the baselines and those pruned—using standard classification metrics: accuracy, precision, recall, and F1-score. To assess computational efficiency and deployment readiness, we report model size, number of parameters, FLOPs, and inference time on both a high-performance workstation and a resource-constrained Raspberry Pi 4 (2 GB RAM). Training convergence was monitored via accuracy and loss curves. To analyze the sparsity behavior and dynamic pruning effects, we employed visual diagnostics, including accuracy versus sparsity curves during training, channel retention distributions, and block-wise mask evolution plots.
4.6. Implementation Specification
All experiments were conducted on a workstation equipped with an NVIDIA GeForce RTX 4070 Ti (12 GB GPU) and an AMD Ryzen 9 7950X 16-core processor (x32 architecture). No hyperparameter tuning was applied beyond standard values (Table 4). Additionally, the custom CNN model, initially trained using DAGP on PlantVillage and fine-tuned on PlantDoc, was implemented on a Raspberry Pi 4 (2 GB RAM) to validate embedded deployment feasibility. For all pruning-related experiments, the mask threshold τ was fixed at 0.5. This value was rigorously chosen as it aligns with binary selection logic and coincides with the inflection point of the sigmoid activation function (σ (0) = 0.5), which represents a natural decision boundary (positive weights output > 0.5, negative weights < 0.5), and was further validated as a statistically grounded choice in the ablation study. This setting ensures that pruning decisions are made at a stable and semantically meaningful point where the model’s learned importance values transition from suppressing to preserving feature channels.

Table 4.
Hyperparameter configurations.
5. Experimental Results
Throughout all pruning experiments, we observe that classification accuracy improves, even as the total training loss increases after the warm-up phase. This behavior is expected: all pruning masks are trained under accuracy supervision, as evidenced by the formulation of the total loss (Equation (8)). Once sparsity regularization activates, the increase in total loss is driven by the L1 penalty on mask values, not by classification error. This decoupling ensures that the model prioritizes predictive performance while progressively learning compact, efficient representations.
5.1. Classification on CIFAR-10
5.1.1. Training and Validation Dynamics
Figure 4 presents the training and validation accuracy curves for the baseline models (VGG16 and ResNet56) and their corresponding versions integrated with the proposed DAGP strategy. The learning dynamics reveal that DAGP improves generalization and stabilizes the training process. This effect is particularly evident in the VGG-16 model, where DAGP acts as an implicit regularizer that effectively mitigates overfitting. It enables the construction of compact yet highly accurate models without introducing additional optimizers or training complexity. By integrating learnable, task-adaptive pruning masks directly into the training pipeline, DAGP provides a unified framework that simultaneously achieves accuracy preservation, model size reduction, and improved training robustness.
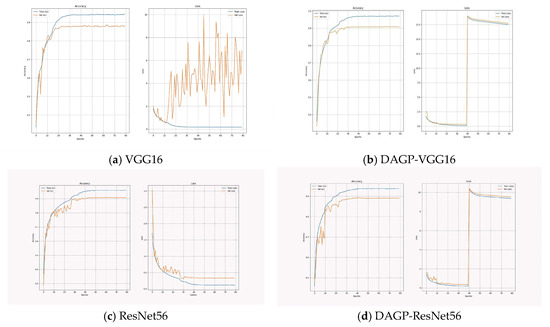
Figure 4.
Training and validation curves of baseline and DAGP-integrated models (VGG-16 and ResNet-56).
5.1.2. Performance Summary on CIFAR-10 Test Set
To evaluate the effectiveness of DAGP on a standard image classification benchmark, we report results on the CIFAR-10 dataset using two representative CNN architectures—VGG16 and ResNet56—as summarized in Table 5. DAGP consistently improves test accuracy (+3.27% for VGG16, +1.29% for ResNet56) despite applying aggressive pruning (up to 93.92%), and with high stability across multiple runs, confirming its ability to enhance both performance and compactness. These improvements are further evidenced by the confusion matrices shown in Figure 5a,b. These improvements grow with model complexity, highlighting DAGP’s dual role: an explicit, structured pruning strategy for compression and an implicit optimization mechanism that adapts to the model–dataset interaction. The observed accuracy improvements, along with substantial reductions in FLOPs and parameters for both VGG-16 and ResNet-56, demonstrate DAGP’s effectiveness as a task-adaptive, architecture-agnostic compression framework. These results affirm its suitability for deploying high-performing CNNs in real-world, resource-constrained environments.

Table 5.
Performance comparison on CIFAR-10 test set.
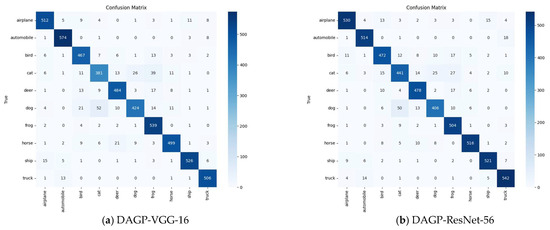
Figure 5.
Confusion matrices on CIFAR-10 test set of DAGP-integrated models (VGG-16 and ResNet-56).
5.1.3. Visualization-Based Analysis of DAGP Effect
Figure 6, depicting VGG-16 and ResNet-56 on CIFAR-10, shows that global sparsity evolves in tandem with accuracy after the warm-up phase (Figure 6b,e), with the accuracy–sparsity curves remaining stable throughout, showing stable and effective joint optimization of accuracy and sparsity that enables task-guided, accuracy-supervised pruning. This indicates effective regularization and confirms that DAGP maintains performance even under high compression. The curves converge smoothly without instability, achieving final accuracies of 91.30 ± 0.0017% and 91.32 ± 0.0005%, and final global sparsity levels of 93.92% for VGG-16 and 84.28% for ResNet-56, respectively. Moreover, the average mask values per block (Figure 6c,f) converge with high stability to mean values generally below 0.5, indicating effective pruning of a considerable number of channels. Importantly, these values differ across layers, demonstrating adaptive and selective pruning guided by hierarchical feature importance and attention-based selection, achieving a task adaptive sparsity. A notable distinction appears between the two architectures: ResNet-56, with its deeper structure and higher redundancy, exhibits many layers whose masks converge close to zero, effectively eliminating redundant channels, while VGG-16 prunes fewer channels due to its more compact design. This dynamic aligns with the channel retention patterns (Figure 6a,d), where more channels are preserved at low, mid, and high hierarchical stages—supporting rich feature extraction—while intermediate layers are pruned more aggressively to remove redundancy. Together, these findings confirm that DAGP enhances performance and compression simultaneously through attention-guided, selective pruning that reduces overfitting, preserves task-relevant features, and drives stable convergence.
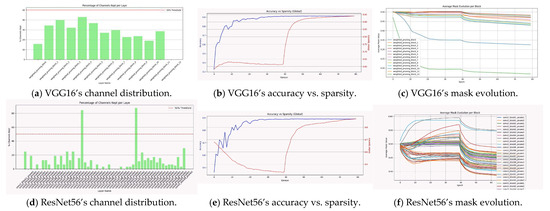
Figure 6.
Visualization of DAGP dynamics on CIFAR-10: accuracy–sparsity trade-off, mask evolution, and channel retention for VGG16 and ResNet56.
5.2. Classification on PlantVillage
5.2.1. Training and Validation Dynamics
The integration of DAGP into the custom CNN (Figure 7a) model yields noticeable improvements in training stability and generalization, as illustrated in Figure 7b. Once the warm-up phase concludes, the model maintains a consistent learning trajectory, with a reduced generalization gap and smoother convergence. These improvements highlight the strategy’s ability to enforce implicit regularization while preserving task-relevant discriminative capacity. This behavior confirms DAGP’s effectiveness not only in benchmark settings but also in task-specific scenarios such as tomato disease classification in agriculture.
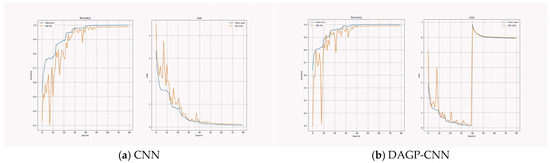
Figure 7.
Training and validation curves of baseline and DAGP-integrated custom CNN.
5.2.2. Performance Summary on PlantVillage Test Set
To evaluate DAGP’s effectiveness in task-specific scenarios, we assessed its integration into a custom CNN model on the PlantVillage dataset. As shown in Table 6, DAGP achieves significant reductions in model complexity—over 99.3% in parameters and 98.82% in FLOPs—while improving test accuracy by +1.7% with high stability across multiple runs, demonstrating that it not only compresses but also enhances performance. The strong classification capability of the model is further demonstrated by the confusion matrix in Figure 8a. These results confirm DAGP’s ability to act as an implicit, end-to-end attention-driven optimization mechanism, enabling compact and accurate models without additional tuning.

Table 6.
Performance comparison on PlantVillage test set.
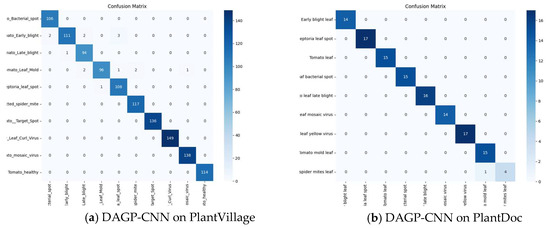
Figure 8.
Confusion matrices of the soft- and hard-pruned CNN models on the PlantVillage and PlantDoc test sets, respectively.
Importantly, this behavior persists in a task-specific agricultural context, further demonstrating its model-agnostic character—already validated on CIFAR-10 across two distinct architectures—and reinforcing its dataset-independent applicability. Its capacity to align architectural sparsity with task relevance makes it a valuable task-adaptive strategy for embedded and edge AI deployments, where efficiency and precision must co-exist.
5.2.3. Visualization-Based Analysis of DAGP Effect
DAGP’s effectiveness extends beyond benchmark settings, demonstrating strong adaptability to task-specific domains such as agricultural disease classification. On the PlantVillage dataset, the DAGP-augmented custom CNN preserves high classification accuracy while enabling substantial compression. As shown in Figure 9b, accuracy and sparsity evolve jointly and remain stable after the warm-up phase, confirming task-driven and consistent pruning dynamics.
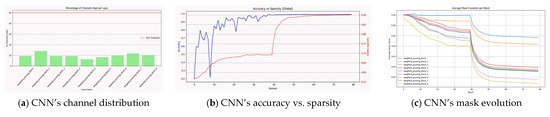
Figure 9.
Visualization of DAGP behavior on PlantVillage: accuracy–sparsity dynamics, mask evolution, and channel retention for the custom CNN.
The convergence of mask evolution (Figure 9c) with high stability and the structured channel retention across hierarchical blocks reflect selective feature preservation. Given the medium complexity of the PlantVillage dataset, relatively small numbers of filters across layers are sufficient to capture discriminative patterns. DAGP adapts by suppressing a considerable proportion of channels, especially in intermediate layers, which explains the tendency of several block-level mean mask values to converge toward lower ranges under pruning pressure. This retention pattern reveals a consistent trend of keeping essential channels in critical layers while pruning less informative ones, reinforcing the model’s capacity to preserve discriminative features. This structured behavior indicates that DAGP consistently identifies and retains task-relevant features (Figure 9a), underscoring its robustness and generalizability as a principled pruning strategy.
5.3. Adaptation to PlantDoc via Fine-Tuning the Compressed Baseline
To validate DAGP’s applicability in real-world conditions and enable practical deployment pathways, the compressed CNN model (DAGP-CNN trained on PlantVillage) was transferred to the PlantDoc dataset. A hard-pruned version was reconstructed by permanently removing kernels associated with suppressed channels. Fine-tuning was conducted on an enhanced PlantDoc dataset. The successful adaptation of the pruned model across datasets highlights DAGP’s transferability and effectiveness under domain shift, reinforcing its potential for deployment in precision agriculture under real-world constraints.
The findings reported in Table 7 clearly confirm that the fine-tuned, compressed CNN preserves high classification accuracy (99.23%) with high stability across multiple runs, while substantially reducing model size and inference latency. Starting from a backbone of 4.82 M parameters, the pruned model is 3.75× smaller than MobileOne-S0 (2.1 M), 15.36× smaller than MobileOne-S4 (4.8 M) [27], and 71.78× smaller than ConvNeXt-Tiny (29 M) [28]. The confusion matrix presented in Figure 8b highlights the model’s strong performance on this real-world dataset. This demonstrates the viability of the proposed compression approach for real-world, resource-constrained applications without compromising accuracy and supports ongoing research trends in lightweight and transferable deep learning models.

Table 7.
Evaluation of the fine-tuned compressed custom CNN on the PlantDoc test set.
5.4. Embedded Deployment: Raspberry Pi Evaluation
To align with realistic embedded AI deployment practices, inference using the fine-tuned, compressed model was conducted on a Raspberry Pi 4 [29]. This setup reflects typical real-world constraints, where training is performed offline and efficient on-device inference is required under limited computational resources.
After converting the compressed model weights into TensorFlow-Lite, the DAGP-pruned CNN was deployed on a Raspberry Pi 4 (2 GB RAM) to assess its viability for embedded agricultural monitoring systems under resource-constrained conditions. As presented in Table 8, the pruned custom CNN achieved a notably low memory footprint of 2.00 MB, minimal CPU utilization of 0.25%, and fast inference latency of 60 ms. These results highlight the strength of our DAGP-based strategy in producing a lightweight and accurate architecture suitable for real-time agricultural applications. The enhanced PlantDoc dataset further reinforces the robustness of our approach in field-ready conditions. This deployment confirms that the proposed solution is both scalable and operationally efficient for real-world, real-time agricultural monitoring on constrained edge devices, and further validates the capability of our DAGP framework as a practical and effective strategy for low-resource, real-time intelligent systems.

Table 8.
Inference performance on the PlantDoc test set of the compressed model using Raspberry Pi 4.
5.5. Ablation Study
To reinforce the theoretical foundations underlying the DAGP architecture, we conduct an ablation study to empirically assess the influence of key sparsity control hyperparameters. Specifically, we evaluate the effects of the maximum sparsity strength (λmax) and the pruning onset epoch (estar), and the hard pruning threshold (τ) on model accuracy and sparsity. While τ is primarily applied post-training for model reconstruction and FLOPs estimation, we further analyze its impact by comparing manually fixed thresholds with adaptive thresholds obtained using Otsu’s method. These ablations are performed across models of different depths and on two datasets, providing a robust evaluation of how hyperparameter choices collectively affect performance and compression.
As reported in Table 9, increasing the maximum sparsity strength (λmax) consistently results in greater pruning ratios, as stronger L1 regularization encourages mask values to approach zero. However, this gain in sparsity must be balanced carefully, as excessive regularization may slightly compromise accuracy. Conversely, smaller λmax values yield limited sparsity due to insufficient penalization, leading to near-dense models.

Table 9.
Performance on test set of ablation study across models and datasets.
The pruning onset epoch (estart) also has a notable effect: removing the warm-up phase—applying regularization from the start—negatively impacts both learning stability and accuracy. This premature pruning constrains the model before sufficient feature learning occurs, leading to suboptimal compression. Delaying pruning too much, however, leaves insufficient epochs for effective sparsity.
The hard pruning threshold (τ) also has a decisive impact: high values cause aggressive pruning, leading to over-pruning and reduced recovery capacity, while low values result in near-dense models with limited compression benefits. This trade-off highlights the need for a balanced threshold to ensure effective binarization of masks without compromising learning. Otsu’s method further validates this balance, yielding thresholds close to 0.5 and confirming it as a simple yet statistically grounded choice, which also coincides with the inflection point where sigmoid activations separate retained and pruned weights—aligning with our previous hypothesis on the role of the inflection point in guiding effective pruning. The effectiveness of this threshold is further empirically supported by the strong performance of the hard-pruned models on real-world datasets such as PlantDoc.
These findings underscore the importance of a principled balance: a moderately strong λmax combined with an early but not immediate estart, along with a balanced threshold choice, yields the most favorable trade-off between performance and efficiency, confirming the practical flexibility of DAGP across tasks and architectures.
6. Discussion
To conduct a comprehensive and rigorous comparison, Table 10 summarizes representative pruning strategies across four main categories: static, differentiable soft, dynamic, and hybrid approaches. Our method (DAGP) is evaluated against state-of-the-art techniques using multiple architectures (VGG-16, ResNet-56, Custom CNN) and datasets (CIFAR-10, PlantVillage), ensuring fairness and diversity in benchmarking. Notably, DAGP consistently achieves the highest ∆-Acc.↑ (%) across all tested models and datasets, demonstrating that it not only reduces parameters and FLOPs significantly (up to 98.82%) but also improves baseline accuracy—a rare property among pruning methods. This highlights DAGP’s effectiveness as a model optimization-aware pruning strategy, capable of inducing sparsity without compromising discriminative power.

Table 10.
Comparative performance of pruning strategies across categories, architectures, and datasets.
Unlike most existing methods that decouple pruning from learning or rely on rigid sparsity heuristics, DAGP leverages learned differentiable masks after a warm-up phase, enabling the network to discover and adapt its optimal sparsity configuration in an end-to-end, accuracy-supervised fashion. Furthermore, as a retraining-free approach, DAGP reduces the complexity typically associated with iterative fine-tuning cycles. In sum, DAGP redefines pruning not as a trade-off between efficiency and accuracy, but as a synergistic optimization process that enables accuracy enhancement through sparsity, outperforming prior static, dynamic, and hybrid strategies on all key metrics.
7. Conclusions
This work introduced DAGP, a unified, differentiable, and dynamic soft-pruning framework that enables CNNs to learn task-guided sparsity in an end-to-end manner with negligible overhead. DAGP jointly optimizes compression and accuracy by reformulating pruning as a dynamic, learnable process, achieving substantial reductions in parameters and FLOPs while maintaining or improving performance. Beyond theoretical support, the effectiveness of the proposed approach has been validated across multiple CNN architectures and datasets further validation was demonstrated through a real-world deployment on Raspberry Pi 4 confirms its suitability for latency-critical edge applications. These results confirm the architecture-agnostic nature and cross-dataset generalization capabilities of DAGP, offering a foundation for future extensions. Further work could explore other task scenarios such as object detection and semantic segmentation, scaling to larger benchmarks like ImageNet, and extending to additional application domains where efficiency and accuracy are equally critical. Overall, DAGP demonstrates that intelligent sparsity learning can simultaneously advance model compression and performance, providing a robust and generalizable pathway toward edge-ready deep learning.
Author Contributions
Conceptualization, A.C. and R.E.A.; methodology, A.C. and K.E.M.; software and implementation, A.C., I.E.M. and Y.A.; validation and experiments, A.C., I.E.M., Y.A., M.E.G., B.B. and R.E.A.; writing– original draft, A.C.; formal analysis, A.C., M.E.G., B.B. and R.E.A.; visualization, A.C., K.E.M. and I.E.M.; supervision, R.E.A. and Y.A.; project administration; R.E.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets used in this research (PlantVillage, CIFAR-10, and PlantDoc) are publicly available: PlantVillage: https://www.kaggle.com/datasets/emmarex/plantdisease (accessed on 12 April 2025). CIFAR-10: https://www.cs.toronto.edu/~kriz/cifar.html (accessed on April 2025). PlantDoc: https://github.com/pratikkayal/PlantDoc-Dataset (accessed on 14 April 2025). The source code and experimental results are available at: https://github.com/Anouar-usmba/DAGP-paper (accessed on 14 April 2025).
Acknowledgments
We wish to acknowledge the support of Nextronic by ABA Technology, through its Dakaï laboratory, which enabled the birth of this work, and the University Sidi Mohamed Ben Abdellah for its contribution to research, innovation, and fruitful collaboration.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNN | Convolutional Neural Network |
| DAGP | Dynamic Attention-Guided Pruning |
| DL | Deep Learning |
| LoRA | Low-Rank Adaptation |
References
- Khaoula, E.M.; Hassan, S. Moroccan Arabic Darija Automatic Speech Recognition System Using CNN Model for Drone Control Application. In Proceedings of the 2024 3rd International Conference on Embedded Systems and Artificial Intelligence (ESAI), Fez, Morocco, 19–20 December 2024; pp. 1–7. [Google Scholar]
- Rahman, N.; Khan, M.; Ullah, I.; Kim, D.H. A novel lightweight CNN for constrained IoT devices: Achieving high accuracy with parameter efficiency on the MSTAR dataset. IEEE Access 2024, 12, 160284–160298. [Google Scholar] [CrossRef]
- El Manaa, K.; Laaidi, N.; Ezzine, A.; Satori, H. Phoneme-based automatic speech recognition for real-time Arabic command drone control. Iran J. Comput. Sci. 2025, 1–17. [Google Scholar] [CrossRef]
- Dantas, P.V.; Sabino da Silva, W., Jr.; Cordeiro, L.C.; Carvalho, C.B. A comprehensive review of model compression techniques in machine learning. Appl. Intell. 2024, 54, 11804–11844. [Google Scholar] [CrossRef]
- Lyu, Z.; Zhu, G.; Xu, J.; Ai, B.; Cui, S. Semantic communications for image recovery and classification via deep joint source and channel coding. IEEE Trans. Wirel. Commun. 2024, 23, 8388–8404. [Google Scholar] [CrossRef]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning Filters for Efficient ConvNets. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Liu, Z.; Li, J.; Shen, Z.; Huang, G.; Yan, S.; Zhang, C. Learning Efficient Convolutional Networks Through Network Slimming. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2736–2744. [Google Scholar]
- He, Y.; Zhang, X.; Sun, J. Channel Pruning for Accelerating very Deep Neural Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1389–1397. [Google Scholar]
- Wang, Z.; Xie, X.; Shi, G. RFPruning: A retraining-free pruning method for accelerating convolutional neural networks. Appl. Soft Comput. 2021, 113, 107860. [Google Scholar] [CrossRef]
- Lian, S.; Zhao, Y.; Pei, J. DAAR: Dual attention cooperative adaptive pruning rate by data-driven for filter pruning. Appl. Intell. 2025, 55, 402. [Google Scholar] [CrossRef]
- Jiang, P.; Xue, Y.; Neri, F. Convolutional neural network pruning based on multi-objective feature map selection for image classification. Appl. Soft Comput. 2023, 139, 110229. [Google Scholar] [CrossRef]
- Hedegaard, L.; Alok, A.; Jose, J.; Iosifidis, A. Structured pruning adapters. Pattern Recognit. 2024, 156, 110724. [Google Scholar] [CrossRef]
- Lu, X.; Dong, W.; Fang, Z.; Lin, J.; Li, X.; Shi, G. Growing-before-pruning: A progressive neural architecture search strategy via group sparsity and deterministic annealing. Pattern Recognit. 2025, 166, 111697. [Google Scholar] [CrossRef]
- He, Y.; Kang, G.; Dong, X.; Fu, Y.; Yang, Y. Soft Filter Pruning for Accelerating Deep Convolutional Neural Networks. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 2234–2240. [Google Scholar]
- Kang, M.; Han, B. Operation-Aware Soft Channel Pruning Using Differentiable Masks. In Proceedings of the International Conference on Machine Learning, Virtual, 12–18 November 2020; pp. 5122–5131. [Google Scholar]
- Luo, J.H.; Wu, J. Autopruner: An end-to-end trainable filter pruning method for efficient deep model inference. Pattern Recognit. 2020, 107, 107461. [Google Scholar] [CrossRef]
- Gao, X.; Zhao, Y.; Dudziak, Ł.; Mullins, R.; Xu, C.Z. Dynamic channel pruning: Feature boosting and suppression. arXiv 2018, arXiv:1810.05331. [Google Scholar]
- Chen, J.; Chen, S.; Pan, S.J. Storage efficient and dynamic flexible runtime channel pruning via deep reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 14747–14758. [Google Scholar]
- Liu, S.Q.; Yang, Y.X.; Gao, X.J.; Cheng, K. Dynamic channel pruning via activation gates. Appl. Intell. 2022, 52, 16818–16831. [Google Scholar] [CrossRef]
- Feldsar, B.; Mayer, R.; Rauber, A. Detecting adversarial examples using surrogate models. Mach. Learn. Knowl. Extr. 2023, 5, 1796–1825. [Google Scholar] [CrossRef]
- Yan, W.; Feng, Q.; Yang, S.; Zhang, J.; Yang, W. Prune-FSL: Pruning-based lightweight few-shot learning for plant disease identification. Agronomy 2024, 14, 1878. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems 30; Curran Associates Inc.: Brooklyn, NY, USA, 2017. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. arXiv 2020, arXiv:physics/0004057. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Vasu, P.K.A.; Gabriel, J.; Zhu, J.; Tuzel, O.; Ranjan, A. Mobileone: An Improved One Millisecond Mobile Backbone. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7907–7917. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A Convnet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. [Google Scholar]
- Raspberry Pi Foundation, Raspberry Pi 4 documentation. Available online: https://www.raspberrypi.com/products/raspberry-pi-4-model-b (accessed on 5 June 2025).
- Li, B.; Wu, B.; Su, J.; Wang, G. Eagleeye: Fast Sub-Net Evaluation for Efficient Neural Network Pruning. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 639–654. [Google Scholar]
- Hua, W.; Zhou, Y.; De Sa, C.M.; Zhang, Z.; Suh, G.E. Channel gating neural networks. Adv. Neural Inf. Process. Syst. 2019, 32, 1884–1894. [Google Scholar]
- Gao, S.; Zhang, Y.; Huang, F.; Huang, H. Bilevelpruning: Unified Dynamic and Static Channel Pruning for Convolutional Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 16090–16100. [Google Scholar]
- Chen, R.; Qi, H.; Liang, Y.; Yang, M. Identification of plant leaf diseases by deep learning based on channel attention and channel pruning. Front. Plant Sci. 2022, 13, 1023515. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, T.; Jannat, S.; Islam, M.F.; Noor, J. Involution-Infused DenseNet with Two-Step Compression for Resource-Efficient Plant Disease Classification. arXiv 2025, arXiv:2506.00735. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).