Leveraging DNA-Based Computing to Improve the Performance of Artificial Neural Networks in Smart Manufacturing
Abstract
1. Introduction
2. Literature Review
2.1. Studies Related to Analyzing the Role of Window Size
2.2. Studies Related to Using Long Window Data
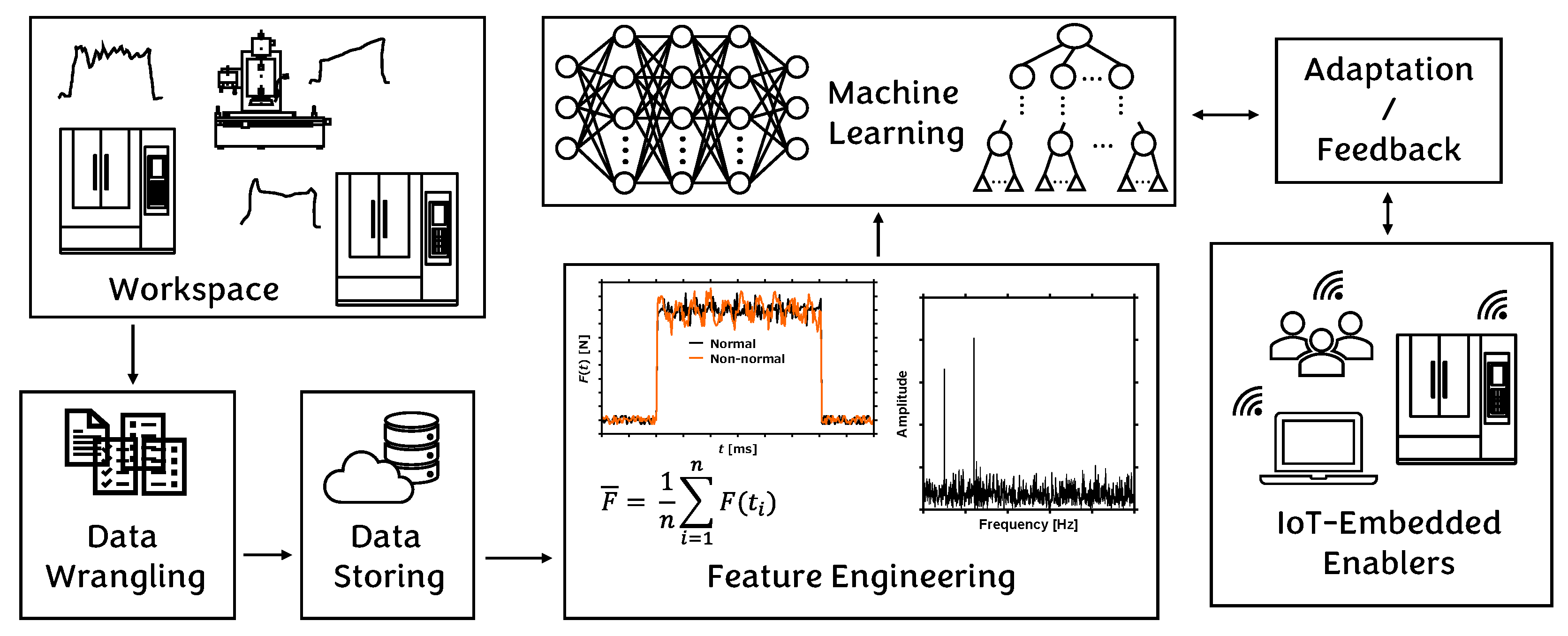
3. Data Preparation
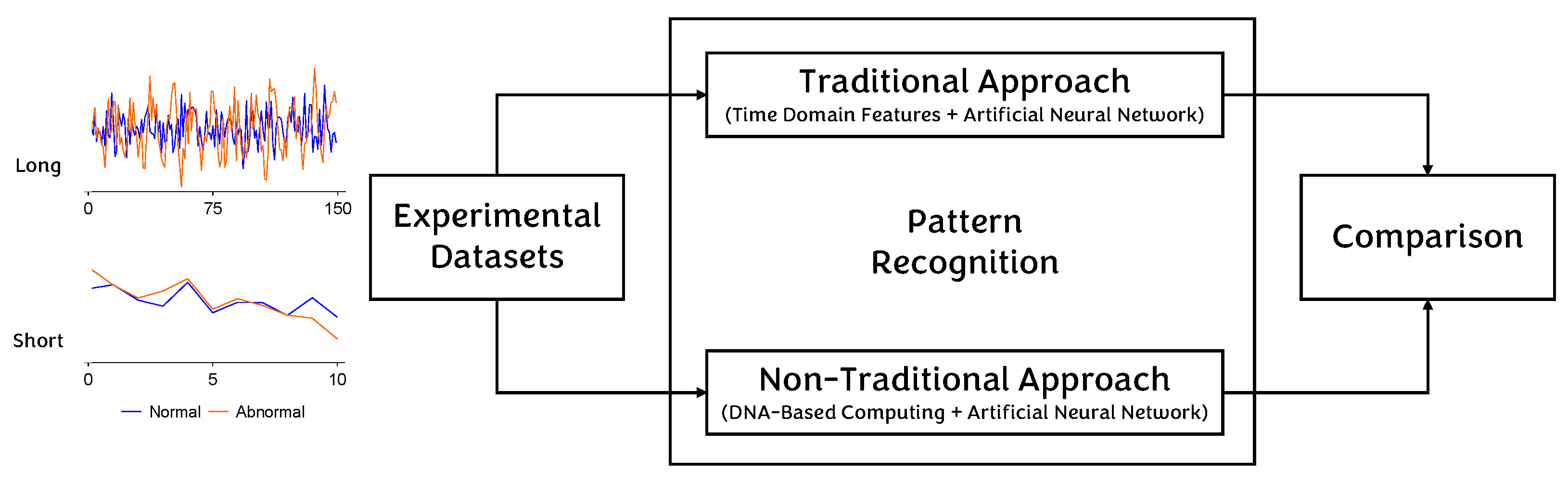
4. Methodology
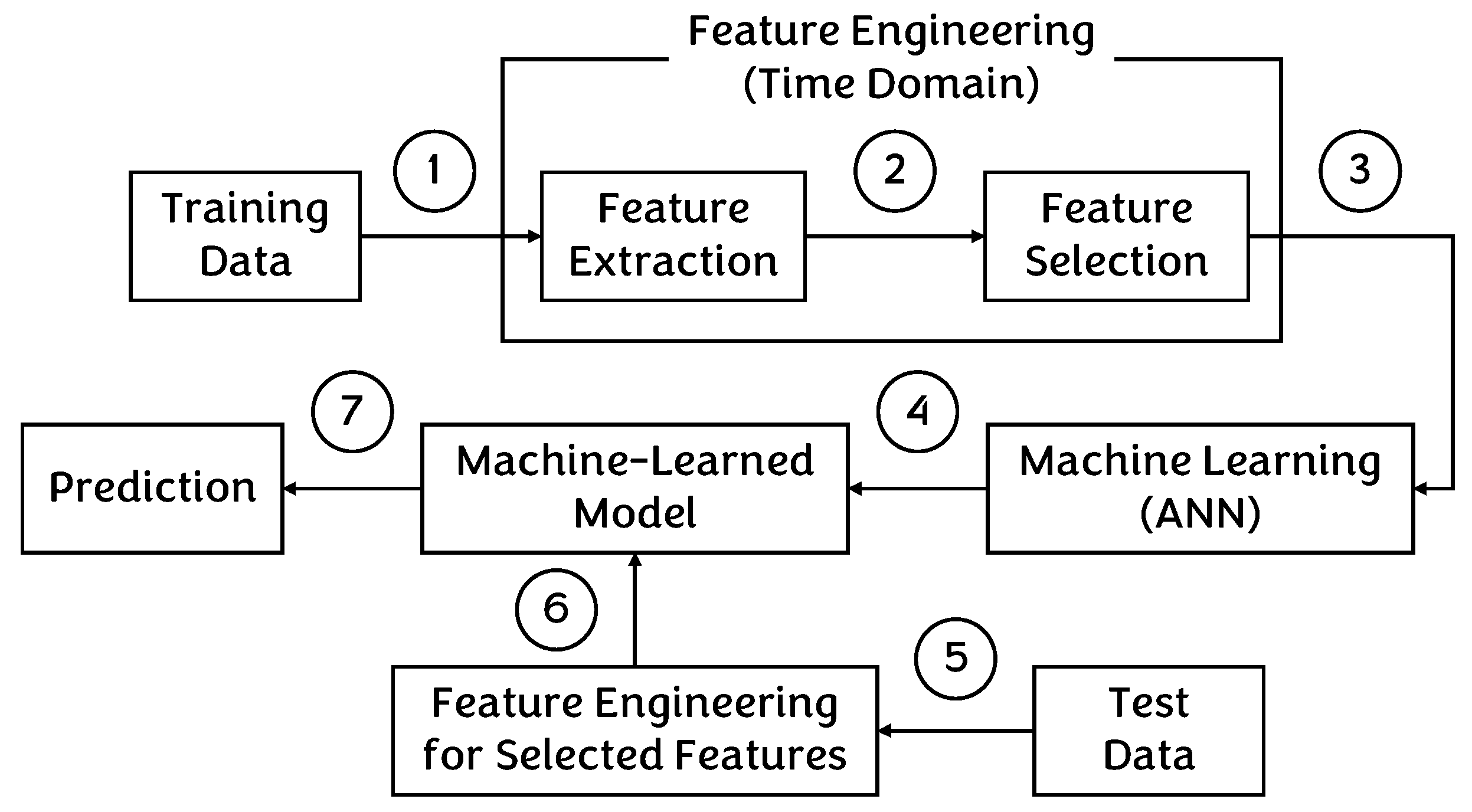
4.1. Traditional Approach
4.2. Non-Traditional Approach
5. Results
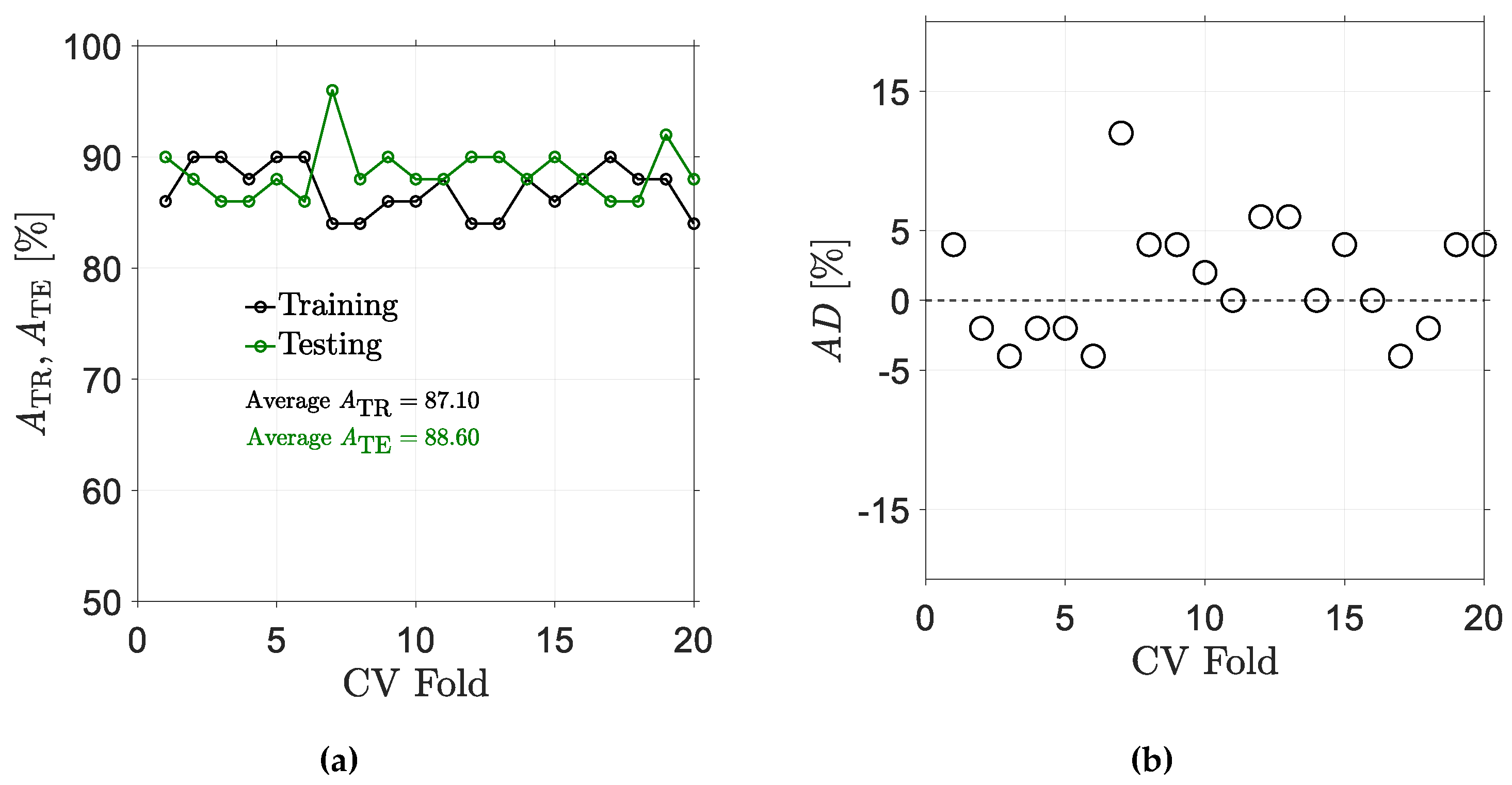
5.1. Results for Traditional Approach
5.2. Results for Non-Traditional Approach
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Glossary of Symbols Related to Section 3 and Section 4
| Symbols | Meaning | Sections |
|---|---|---|
| Z | Set of all generated datasets (100 total, 50 Normal and 50 Abnormal). | 3 |
| Zk | The k-th dataset in Z, where k = 1, …, 100. | 3 |
| Zk(i) | The i-th point in dataset Zk, where i = 0, …, N and N is the window size. | 3 |
| X, Y | Sets of training and test datasets, respectively. Mutually exclusive subsets of Z, each containing 50 Normal/Abnormal datasets. | 3 |
| Nl, Ns | Long window size (=150) and short window size (=10), respectively. | 3 |
| Xl, Xs | Long and short window training datasets, respectively. | 3, 4 |
| Yl, Ys | Long and short window test datasets, respectively. | 3, 4 |
| Fl, Fs | Sets of extracted time-domain features from Xl and Xs, respectively. | 4 |
| Flj, Fsj | Individual features where j = 1, …, 7. Fl1 = Fs1 = Average, Fl2 = Fs2 = Standard Deviation, Fl3 = Fs3 = Minimum Value, Fl4 = Fs4 = Maximum Value, Fl5 = Fs5 = Range, Fl6 = Fs6 = Skewness, and Fl7 = Fs7 = Kurtosis | 4 |
| Fltrain, Fstrain | Selected subsets of Fl and Fs, respectively, after feature selection process. | 4 |
| Fltest, Fstest | Extracted features from Yl and Ys, respectively, corresponding to Fltrain and Fstrain. | 4 |
| ANN1, ANN2, ANN3, ANN4 | ANN models trained on different inputs. ANN1 is trained on Fltrain, ANN2 is trained on Fstrain, ANN3 is trained on RFXl, and ANN4 is trained on RFXs. | 4 |
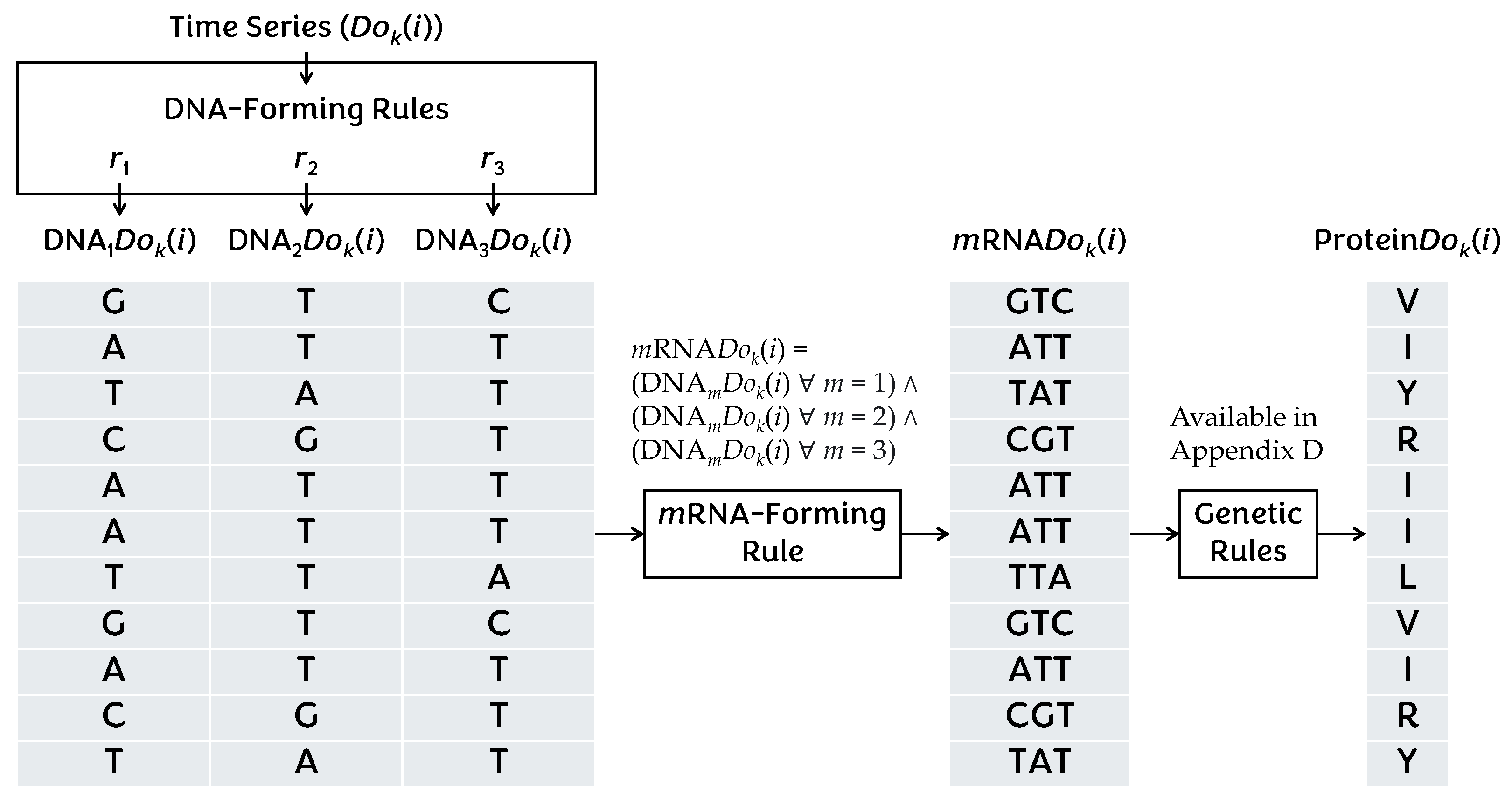
| Dok(i) | Time series dataset element, where D ∈ {X, Y}, o ∈ {l, s}, k = {1, …, 100}, i = {0, …, No}. | 4 |
| r1, r2, r3 | DNA-forming rules applied to Dok(i). | 4 |
| DNAm(Dok(i)) | DNA array element derived from Dok(i) under rule rm (m = 1,2,3). | 4 |
| DNAm(Dok) | DNA array of dataset Dok, generated using the rule rm (m = 1,2,3). | 4 |
| mRNADok(i) | Codon (3-letter mRNA symbol) formed from DNA arrays. | 4 |
| ProteinDok(i) | Protein symbol (1-letter amino acid) derived from codon mRNADok(i). | 4 |
| ProteinDok | Sequence (array) of protein symbols for dataset Dok. | 4 |
| g | Genetic rules mapping codons to amino acids. | 4 |
| P | Set of all possible amino acids encoded in a protein array. | 4 |
| p | A particular amino acid in P. | 4 |
| Cp | Number of times amino acid p appears in P. | 4 |
| C | Total number of proteins in P. | 4 |
| RF(p) | Relative frequency of amino acid p, defined as Cp/C. | 4 |
| RFDok | Set of relative frequencies for dataset Dok. | 4 |
| RFDo | Aggregated set of relative frequencies for datasets under condition o. | 4 |
| RFXl, RFXs | Sets of DBC-driven features for long- and short-windowed training datasets, respectively. | 4 |
| RFYl, RFYs | Sets of DBC-driven features for long- and short-windowed test datasets, respectively. | 4 |
Appendix B. Pseudocode for the Feature Extraction Process
| Steps | Description |
|---|---|
| Step 1 | START |
| Step 2 | Specify the input folder path containing text (*.txt) files of the datasets. |
| Step 3 | Enumerate all files matching ‘*.txt’ in the folder. |
| Step 4 | Initialize empty containers for each output column: patternTypes, datasetIDs, F1, …, F7. |
| Step 5 | FOR each file in the list: 5.1 Open file for reading. 5.2 Read Line 1; parse substring after ‘Pattern Type:’ → ‘ptype’. 5.3 Read Line 2; parse integer after ‘Dataset ID:’ → ‘id’. 5.4 Read ‘numeric data’ from Line 3 to end into vector ‘x’. 5.5 Compute: F1 ← average (x), F2 ← standard deviation (x), F3 ← min (x), F4 ← max (x), F5 ← range (x), F6 ← skewness (x), and F7 ← kurtosis (x). 5.6 Append records (ptype, id, F1, …, F7) to outputs (patternTypes, datasetIDs, F1, …, F7). 5.7 Close file. END FOR |
| Step 6 | Assemble all records into a table in the column order specified in Step 4. |
| Step 7 | Write the table to ‘Features.csv’ in the same folder mentioned in Step 1. |
| Step 8 | END |
| Code |
|---|
| % Configure paths folderPath = ‘INPUT_FOLDER_PATH’; % e.g., ‘C:\path\to\data’ outCSV = ‘OUTPUT_CSV_NAME.csv’; % e.g., ‘Features.csv’ % Enumerate files files = dir(fullfile(folderPath, ‘*.txt’)); n = numel(files); % Preallocate containers patternTypes = strings(n,1); datasetIDs = zeros(n,1); F1 = zeros(n,1); F2 = zeros(n,1); F3 = zeros(n,1); F4 = zeros(n,1); F5 = zeros(n,1); F6 = zeros(n,1); F7 = zeros(n,1); % Process each file for i = 1:n fp = fullfile(files(i).folder, files(i).name); % Read header lines fid = fopen(fp, ‘r’); line1 = fgetl(fid); % “Pattern Type: <label>” line2 = fgetl(fid); % “Dataset ID: <int>” fclose(fid); % Parse header values patternTypes(i) = strtrim(erase(line1, ‘Pattern Type:’)); datasetIDs(i) = sscanf(line2, ‘Dataset ID: %d’); % Read numeric data from line 3 onward x = readmatrix(fp, ‘NumHeaderLines’, 2); x = x(:); % Compute features F1(i) = mean(x); % Average F2(i) = std(x); % Standard Deviation F3(i) = min(x); % Minimum F4(i) = max(x); % Maximum F5(i) = F4(i)–F3(i); % Range F6(i) = skewness(x); % Skewness F7(i) = kurtosis(x); % Kurtosis end % Assemble table in the exact column order T = table(patternTypes, datasetIDs, F1, F2, F3, F4, F5, F6, F7, ‘VariableNames’, {‘PatternType’, ‘DatasetID’, ‘F1’, ‘F2’, ‘F3’, ‘F4’, ‘F5’, ‘F6’, ‘F7’}); % Write CSV writetable(T, fullfile(folderPath, outCSV)); |
Appendix C. Pseudocode for the Feature Selection Process
| Steps | Description |
|---|---|
| Step 1 | START |
| Step 2 | Get features and class labels: 2.1 Input features and pattern type for datasets (e.g., from the file ‘Features.csv’ created in Appendix B). 2.2 Select feature columns (e.g., features listed in the ‘F1, …, F7’ columns in ‘Features.csv’) as predictors. 2.3 Select pattern types (e.g., Normal/Abnormal patterns listed in the ‘PatternType’ column in ‘Features.csv’) as class labels. |
| Step 3 | Convert class labels to categorical (if needed). |
| Step 4 | Run MATLAB®-based Random Forest Classifier (TreeBagger): 4.1 Set random seed for reproducibility. 4.2 Set number of trees (e.g., 30). 4.3 Train classifier with OOB prediction and permutation importance enabled, keeping other parameters at MATLAB® defaults. |
| Step 5 | Display feature importance: 5.1 Obtain permutation importance scores. 5.2 Sort scores descending and reorder feature names accordingly. 5.3 Plot feature importance scores as a bar chart. 5.4 Print feature importance scores. |
| Step 6 | END. |
| Code |
|---|
| % Getting features and the class label % Input features and pattern type; e.g., ‘Features.csv’ from Appendix B) TrainingFeatures = readtable(‘INPUT_FEATURES_PATH.csv’); % e.g., ‘C:\path\to\Features.csv’ featuresRF = TrainingFeatures(:, 3:end); % Select predictors F1–F7 classLabelsRF = TrainingFeatures.PatternType; % Use PatternType as class label % Convert class labels to categorical if they aren’t already classLabelsRF = categorical(classLabelsRF); % Random forest classifier rng(1); % Set random seed for reproducibility numTrees = 30; % Number of trees model = TreeBagger(numTrees, featuresRF, classLabelsRF, ‘Method’, ‘classification’, ‘OOBPrediction’, ‘On’, ‘OOBVarImp’, ‘On’); % Display feature importance featureImportance = model.OOBPermutedVarDeltaError; [sortedImportance, sortedIndices] = sort(featureImportance, ‘descend’); sortedFeatures = featuresRF.Properties.VariableNames(sortedIndices); % Plot feature importance figure; bar(sortedImportance); % Customize plot xlabel(‘Feature’, ‘FontSize’, 24); ylabel(‘Score’, ‘FontSize’, 24); set(gca, ‘XTick’, 1:numel(sortedFeatures), ‘XTickLabel’, sortedFeatures, ‘XTickLabelRotation’, 0, ‘TickLabelInterpreter’, ‘none’); set(gca, ‘XGrid’, ‘on’, ‘YGrid’, ‘on’); set(gca, ‘TickDir’, ‘out’); set(gca, ‘Box’, ‘on’); grid on; % Print out the names and importance scores of the features disp(‘Features by importance:’); disp(table(sortedFeatures(:), sortedImportance(:), ‘VariableNames’, {‘Feature’, ‘Score’})); |
Appendix D. Pseudocode for the Machine Learning
| Steps | Description |
|---|---|
| Step 1 | START |
| Step 2 | Prepare training data: 2.1 Load the table of selected features and one-hot labels for training. 2.2 Define inputs as all selected feature columns. 2.3 Define targets as the final two one-hot columns (one-hot: Normal, Abnormal). 2.4 Convert inputs and targets to numeric arrays and transpose so columns represent samples, as required by MATLAB®. |
| Step 3 | Define and train ANN: 3.1 Create a pattern recognition feed-forward network. 3.2 Train the network on training inputs and targets. |
| Step 4 | Prepare test data: 4.1 Load the table of selected features and one-hot labels for testing. 4.2 Define test inputs as all selected feature columns. 4.3 Define test targets as the final two one-hot columns (one-hot: Normal, Abnormal). 4.4 Convert test inputs and targets to numeric arrays and transpose so columns represent samples, as required by MATLAB®. |
| Step 5 | Evaluate on test data: 5.1 Compute outputs for the test inputs. 5.2 Convert outputs to predicted class indices. 5.3 Display predicted indices. 5.4 Plot the confusion matrix using true one-hot targets vs. predicted outputs. |
| Step 6 | END. |
| Code |
|---|
| % Training data % Load the table (selected features + one-hot labels from a csv file) trainTbl = readtable(‘INPUT_SELECTED_FEATURES_TRAIN.csv’); % e.g., ‘C:\path\to\SelectedFeatures_Train.csv’ % Creating inputs and targets for training % Assumes layout: [ … feature columns …, Normal, Abnormal ] train_input = trainTbl(:, 2:end-2); train_target = trainTbl(:, end-1:end); % two one-hot columns: [Normal, Abnormal] % Convert table to array and transpose (columns = samples) train_input = table2array(train_input)’; train_target = table2array(train_target)’; % Define & Train the ANN % MATLAB®-based Two-layer feed-forward net for pattern recognition with 3 hidden neurons (number of hidden neurons can be configured if needed) net = patternnet(3); % Train the network [net, tr] = train(net, train_input, train_target); % Test data % Load the table (selected features + one-hot labels from a csv file) testTbl = readtable(‘INPUT_SELECTED_FEATURES_TEST.csv’); % e.g., ‘C:\path\to\SelectedFeatures_Test.csv’ % Creating inputs and targets for testing test_input = testTbl(:, 2:end-2); test_target_real = testTbl(:, end-1:end); % Convert and transpose test_input = table2array(test_input)’; test_target_real = table2array(test_target_real)’; % Inference & evaluation % Network predictions (continuous outputs; each column sums ~1 due to softmax) test_output_pred = net(test_input); % Convert outputs to predicted class indices (1=Normal, 2=Abnormal if that order) test_pred_idx = vec2ind(test_output_pred); % Inspect predicted indices disp(‘Predicted class indices:’); disp(test_pred_idx); % Confusion matrix plot (targets: one-hot; outputs: network predictions) figure; plotconfusion(test_target_real, test_output_pred); title(‘Confusion Matrix’); |
Appendix E. The Central Dogma of Molecular Biology

| No. | Genetic Rules (Codon = C, Amino Acid = AA) |
|---|---|
| 1 | IF C ∈ {ATT, ATC, ATA} THEN AA = I |
| 2 | IF C ∈ {CTT, CTC, CTA, CTG, TTA, TTG} THEN AA = L |
| 3 | IF C ∈ {GTT, GTC, GTA, GTG} THEN AA = V |
| 4 | IF C ∈ {TTT, TTC} THEN AA = F |
| 5 | IF C ∈ {ATG} THEN AA = M |
| 6 | IF C ∈ {TGT, TGC} THEN AA = C |
| 7 | IF C ∈ {GCT, GCC, GCA, GCG} THEN AA = A |
| 8 | IF C ∈ {GGT, GGC, GGA, GGG} THEN AA = G |
| 9 | IF C ∈ {CCT, CCC, CCA, CCG} THEN AA = P |
| 10 | IF C ∈ {ACT, ACC, ACA, ACG} THEN AA = T |
| 11 | IF C ∈ {TCT, TCC, TCA, TCG, AGT, AGC} THEN AA = S |
| 12 | IF C ∈ {TAT, TAC} THEN AA = Y |
| 13 | IF C ∈ {TGG} THEN AA = W |
| 14 | IF C ∈ {CAA, CAG} THEN AA = Q |
| 15 | IF C ∈ {AAT, AAC} THEN AA = N |
| 16 | IF C ∈ {CAT, CAC} THEN AA = H |
| 17 | IF C ∈ {GAA, GAG} THEN AA = E |
| 18 | IF C ∈ {GAT, GAC} THEN AA = D |
| 19 | IF C ∈ {AAA, AAG} THEN AA = K |
| 20 | IF C ∈ {CGT, CGC, CGA, CGG, AGA, AGG} THEN AA = R |
| 21 | IF C ∈ {TAA, TAG, TGA} THEN AA = X |
Appendix F. Type-2 DNA-Based Computing (DBC)
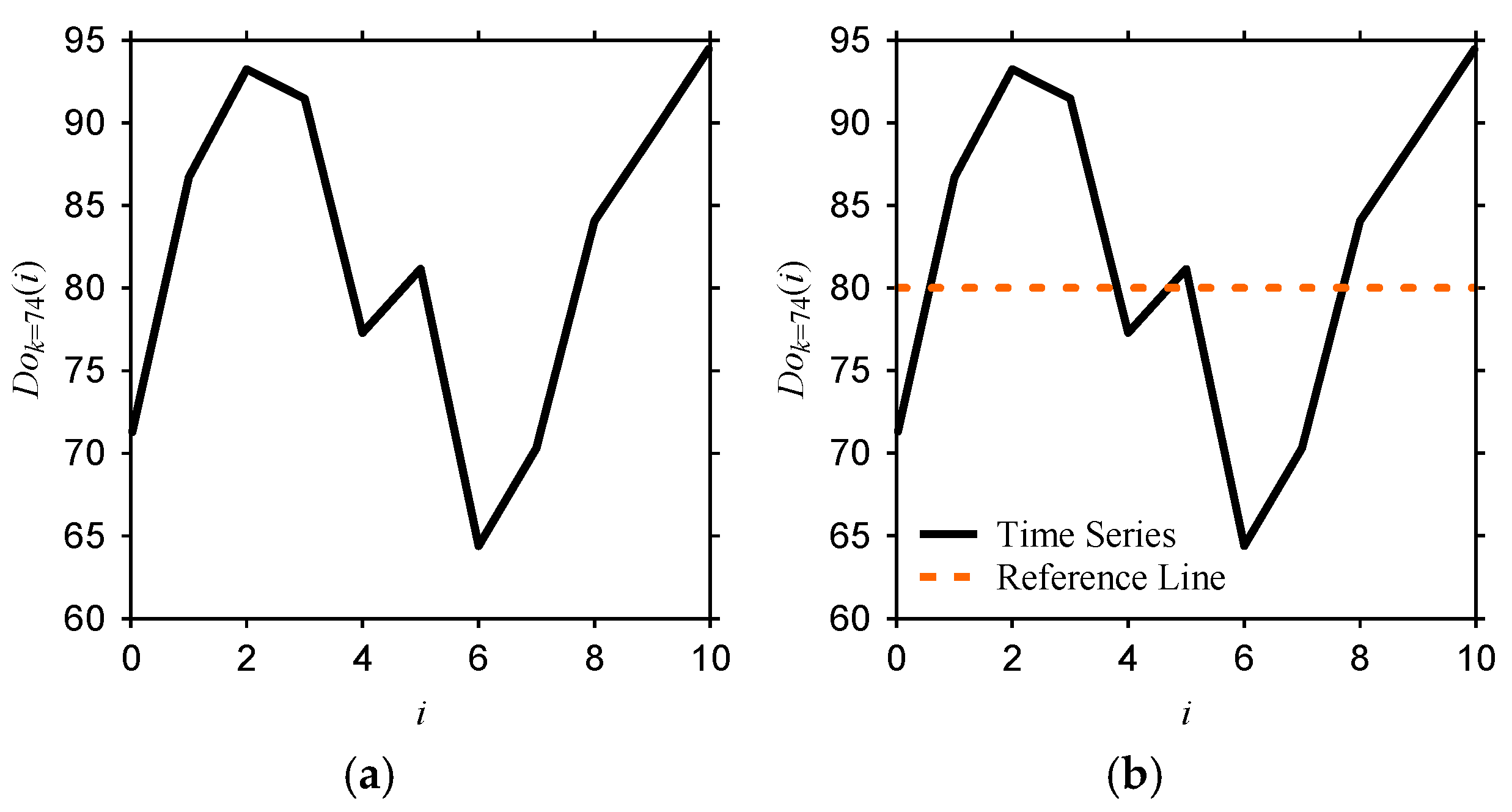

| Rule 1 (r1) | Rule 2 (r2) | Rule 3 (r3) |
|---|---|---|
| Reference = 80 a = 12.5 b = 7.5 c = −7.5 d = −12.5 | Reference = 100 a = 12.5 b = 7.5 c = −7.5 d = −12.5 | Reference = 60 a = 12.5 b = 7.5 c = −7.5 d = −12.5 |
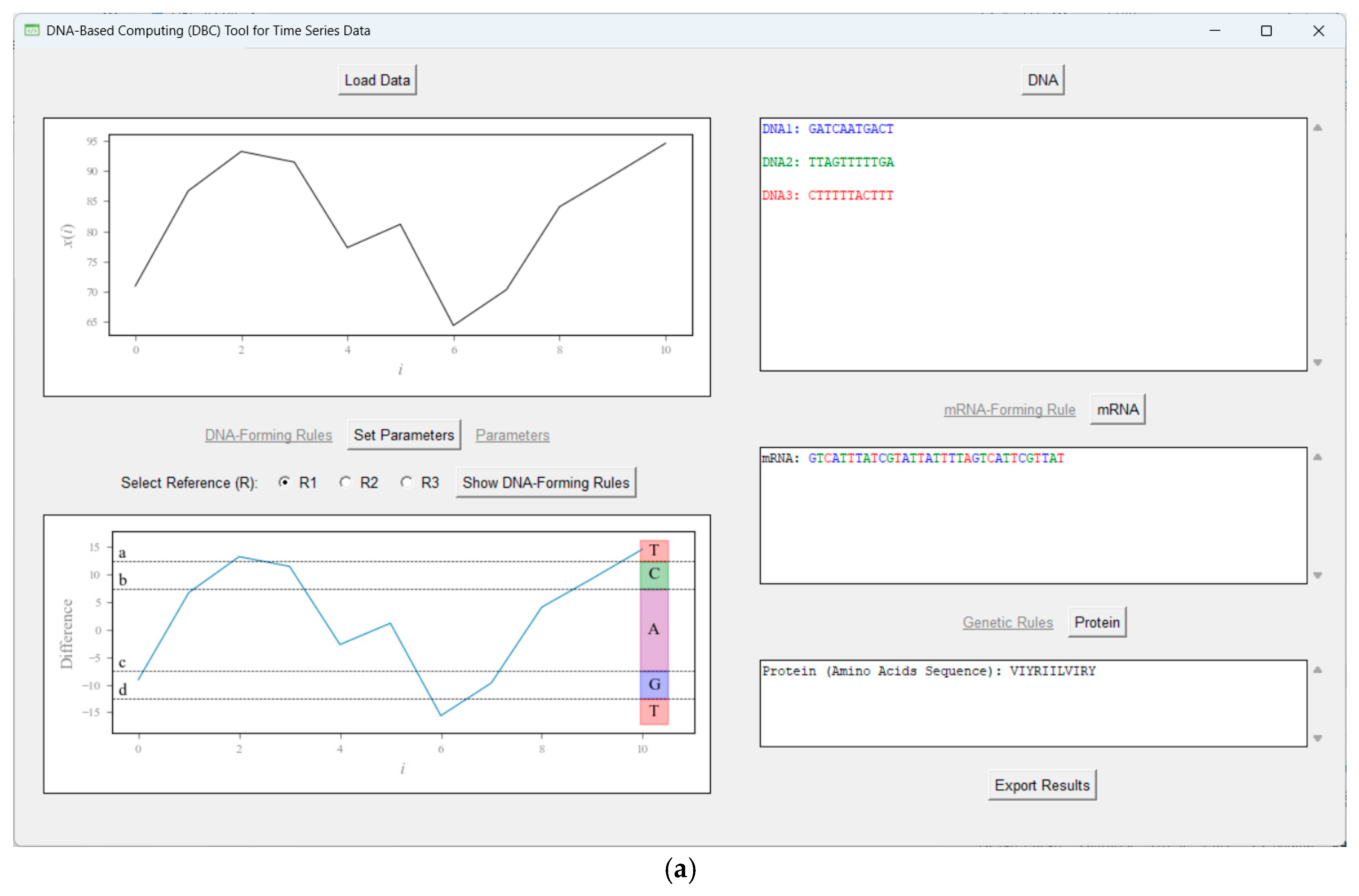
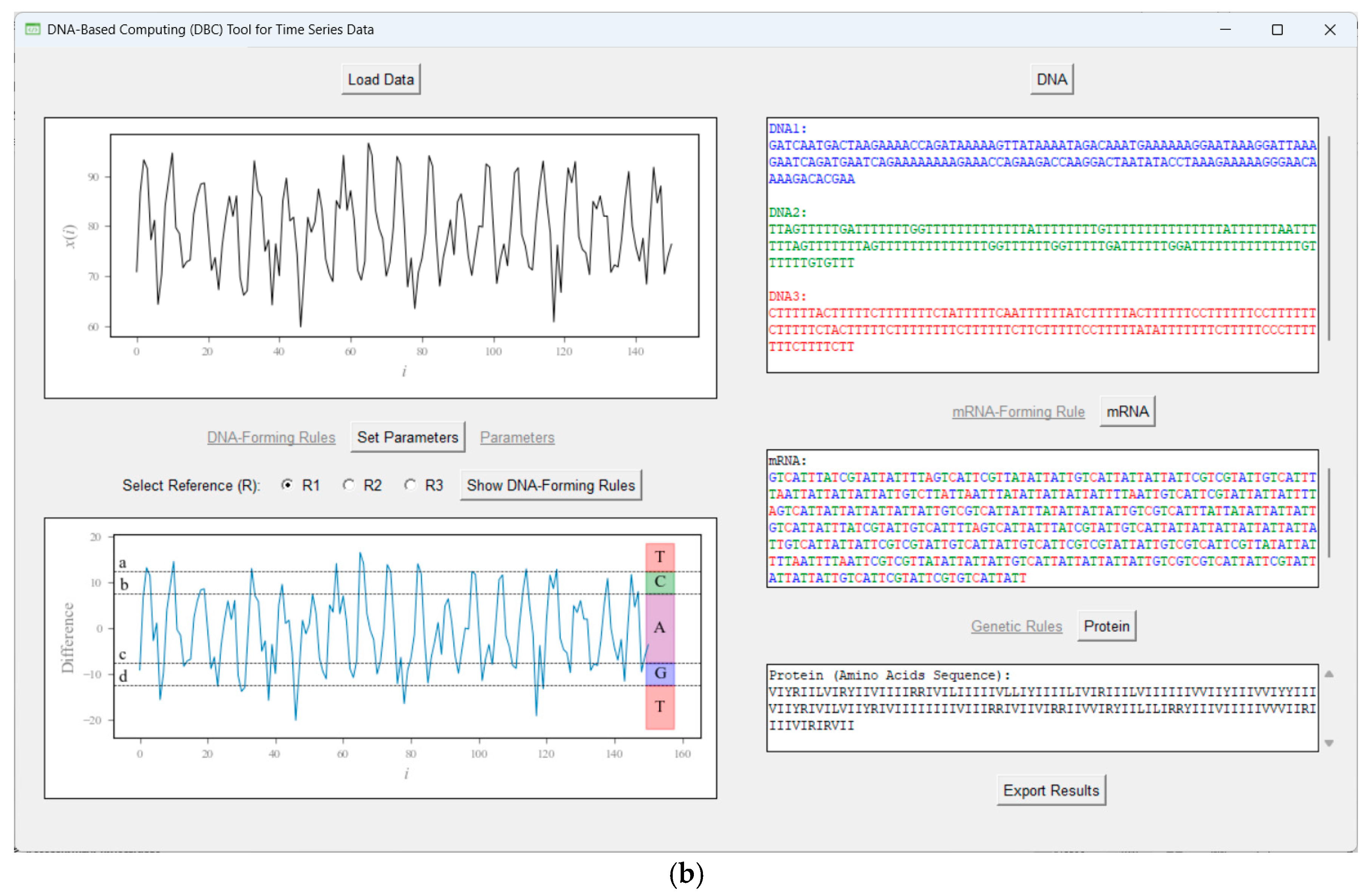
References
- Kusiak, A. Smart Manufacturing. Int. J. Prod. Res. 2018, 56, 508–517. [Google Scholar] [CrossRef]
- Oztemel, E.; Gursev, S. Literature Review of Industry 4.0 and Related Technologies. J. Intell. Manuf. 2020, 31, 127–182. [Google Scholar] [CrossRef]
- Monostori, L.; Kádár, B.; Bauernhansl, T.; Kondoh, S.; Kumara, S.; Reinhart, G.; Sauer, O.; Schuh, G.; Sihn, W.; Ueda, K. Cyber-Physical Systems in Manufacturing. CIRP Ann. 2016, 65, 621–641. [Google Scholar] [CrossRef]
- Yao, X.; Zhou, J.; Lin, Y.; Li, Y.; Yu, H.; Liu, Y. Smart Manufacturing Based on Cyber-Physical Systems and Beyond. J. Intell. Manuf. 2019, 30, 2805–2817. [Google Scholar] [CrossRef]
- Lu, Y.; Cecil, J. An Internet of Things (IoT)-Based Collaborative Framework for Advanced Manufacturing. Int. J. Adv. Manuf. Technol. 2016, 84, 1141–1152. [Google Scholar] [CrossRef]
- Bi, Z.; Jin, Y.; Maropoulos, P.; Zhang, W.-J.; Wang, L. Internet of Things (IoT) and Big Data Analytics (BDA) for Digital Manufacturing (DM). Int. J. Prod. Res. 2023, 61, 4004–4021. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Fattahi, S.; Ura, S. Towards Developing Big Data Analytics for Machining Decision-Making. J. Manuf. Mater. Process. 2023, 7, 159. [Google Scholar] [CrossRef]
- Fattahi, S.; Okamoto, T.; Ura, S. Preparing Datasets of Surface Roughness for Constructing Big Data from the Context of Smart Manufacturing and Cognitive Computing. Big Data Cogn. Comput. 2021, 5, 58. [Google Scholar] [CrossRef]
- Iwata, T.; Ghosh, A.K.; Ura, S. Toward Big Data Analytics for Smart Manufacturing: A Case of Machining Experiment. Proc. Int. Conf. Des. Concurr. Eng. Manuf. Syst. Conf. 2023, 2023, 33. [Google Scholar] [CrossRef]
- Segreto, T.; Teti, R. Machine Learning for In-Process End-Point Detection in Robot-Assisted Polishing Using Multiple Sensor Monitoring. Int. J. Adv. Manuf. Technol. 2019, 103, 4173–4187. [Google Scholar] [CrossRef]
- Aheleroff, S.; Xu, X.; Zhong, R.Y.; Lu, Y. Digital Twin as a Service (DTaaS) in Industry 4.0: An Architecture Reference Model. Adv. Eng. Inform. 2021, 47, 101225. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Ullah, A.S.; Teti, R.; Kubo, A. Developing Sensor Signal-Based Digital Twins for Intelligent Machine Tools. J. Ind. Inf. Integr. 2021, 24, 100242. [Google Scholar] [CrossRef]
- Bijami, E.; Farsangi, M.M. A Distributed Control Framework and Delay-Dependent Stability Analysis for Large-Scale Networked Control Systems with Non-Ideal Communication Network. Trans. Inst. Meas. Control 2018, 41, 768–779. [Google Scholar] [CrossRef]
- Ura, S.; Ghosh, A.K. Time Latency-Centric Signal Processing: A Perspective of Smart Manufacturing. Sensors 2021, 21, 7336. [Google Scholar] [CrossRef]
- Beckmann, B.; Giani, A.; Carbone, J.; Koudal, P.; Salvo, J.; Barkley, J. Developing the Digital Manufacturing Commons: A National Initiative for US Manufacturing Innovation. Procedia Manuf. 2016, 5, 182–194. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Ullah, A.M.M.S. Delay Domain-Based Signal Processing for Intelligent Manufacturing Systems. Procedia CIRP 2022, 112, 268–273. [Google Scholar] [CrossRef]
- Jauregui, J.C.; Resendiz, J.R.; Thenozhi, S.; Szalay, T.; Jacso, A.; Takacs, M. Frequency and Time-Frequency Analysis of Cutting Force and Vibration Signals for Tool Condition Monitoring. IEEE Access 2018, 6, 6400–6410. [Google Scholar] [CrossRef]
- Teti, R.; Segreto, T.; Caggiano, A.; Nele, L. Smart Multi-Sensor Monitoring in Drilling of CFRP/CFRP Composite Material Stacks for Aerospace Assembly Applications. Appl. Sci. 2020, 10, 758. [Google Scholar] [CrossRef]
- Segreto, T.; Karam, S.; Teti, R. Signal Processing and Pattern Recognition for Surface Roughness Assessment in Multiple Sensor Monitoring of Robot-Assisted Polishing. Int. J. Adv. Manuf. Technol. 2017, 90, 1023–1033. [Google Scholar] [CrossRef]
- Hameed, S.; Junejo, F.; Amin, I.; Qureshi, A.K.; Tanoli, I.K. An Intelligent Deep Learning Technique for Predicting Hobbing Tool Wear Based on Gear Hobbing Using Real-Time Monitoring Data. Energies 2023, 16, 6143. [Google Scholar] [CrossRef]
- Pan, Y.; Zhou, P.; Yan, Y.; Agrawal, A.; Wang, Y.; Guo, D.; Goel, S. New Insights into the Methods for Predicting Ground Surface Roughness in the Age of Digitalisation. Precis. Eng. 2021, 67, 393–418. [Google Scholar] [CrossRef]
- Byrne, G.; Dimitrov, D.; Monostori, L.; Teti, R.; Van Houten, F.; Wertheim, R. Biologicalisation: Biological Transformation in Manufacturing. CIRP J. Manuf. Sci. Technol. 2018, 21, 1–32. [Google Scholar] [CrossRef]
- Ura, S.; Zaman, L. Biologicalization of Smart Manufacturing Using DNA-Based Computing. Biomimetics 2023, 8, 620. [Google Scholar] [CrossRef]
- Wegener, K.; Damm, O.; Harst, S.; Ihlenfeldt, S.; Monostori, L.; Teti, R.; Wertheim, R.; Byrne, G. Biologicalisation in Manufacturing—Current State and Future Trends. CIRP Ann. 2023, 72, 781–807. [Google Scholar] [CrossRef]
- Murphy, K.P. Probabilistic Machine Learning: An Introduction; Adaptive Computation and Machine Learning Series; The MIT Press: Cambridge, MA, USA, 2022; ISBN 978-0-262-04682-4. [Google Scholar]
- Wahid, M.F.; Tafreshi, R.; Langari, R. A Multi-Window Majority Voting Strategy to Improve Hand Gesture Recognition Accuracies Using Electromyography Signal. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 427–436. [Google Scholar] [CrossRef]
- Kausar, F.; Mesbah, M.; Iqbal, W.; Ahmad, A.; Sayyed, I. Fall Detection in the Elderly Using Different Machine Learning Algorithms with Optimal Window Size. Mob. Netw. Appl. 2023, 29, 413–423. [Google Scholar] [CrossRef]
- Maged, A.; Xie, M. Recognition of Abnormal Patterns in Industrial Processes with Variable Window Size via Convolutional Neural Networks and AdaBoost. J. Intell. Manuf. 2023, 34, 1941–1963. [Google Scholar] [CrossRef]
- Haoua, A.A.; Rey, P.-A.; Cherif, M.; Abisset-Chavanne, E.; Yousfi, W. Material Recognition Method to Enable Adaptive Drilling of Multi-Material Aerospace Stacks. Int. J. Adv. Manuf. Technol. 2024, 131, 779–796. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S. A DNA-Based Computing Method for Solving Control Chart Pattern Recognition Problems. CIRP J. Manuf. Sci. Technol. 2010, 3, 293–303. [Google Scholar] [CrossRef]
- Batool, S.; Khan, M.H.; Farid, M.S. An Ensemble Deep Learning Model for Human Activity Analysis Using Wearable Sensory Data. Appl. Soft Comput. 2024, 159, 111599. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S.; D’Addona, D.; Arai, N. DNA Based Computing for Understanding Complex Shapes. Biosystems 2014, 117, 40–53. [Google Scholar] [CrossRef]
- Alyammahi, H.; Liatsis, P. Non-Intrusive Appliance Identification Using Machine Learning and Time-Domain Features. In Proceedings of the 2022 29th International Conference on Systems, Signals and Image Processing (IWSSIP), Sofia, Bulgaria, 1 June 2022; pp. 1–5. [Google Scholar]
- Feiner, L.; Chamoulias, F.; Fottner, J. Real-Time Detection of Safety-Relevant Forklift Operating States Using Acceleration Data with a Windowing Approach. In Proceedings of the 2021 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Mauritius, 7 October 2021; pp. 1–6. [Google Scholar]
- Clerckx, B.; Huang, K.; Varshney, L.; Ulukus, S.; Alouini, M. Wireless Power Transfer for Future Networks: Signal Processing, Machine Learning, Computing, and Sensing. IEEE J. Sel. Top. Signal Process. 2021, 15, 1060–1094. [Google Scholar] [CrossRef]
- Cuentas, S.; García, E.; Peñabaena-Niebles, R. An SVM-GA Based Monitoring System for Pattern Recognition of Autocorrelated Processes. Soft Comput. 2022, 26, 5159–5178. [Google Scholar] [CrossRef]
- Derakhshi, M.; Razzaghi, T. An Imbalance-Aware BiLSTM for Control Chart Patterns Early Detection. Expert. Syst. Appl. 2024, 249, 123682. [Google Scholar] [CrossRef]
- D’Addona, D.M.; Matarazzo, D.; Ullah, A.M.M.S.; Teti, R. Tool Wear Control through Cognitive Paradigms. Procedia CIRP 2015, 33, 221–226. [Google Scholar] [CrossRef]
- D’Addona, D.M.; Ullah, A.M.M.S.; Matarazzo, D. Tool-Wear Prediction and Pattern-Recognition Using Artificial Neural Network and DNA-Based Computing. J. Intell. Manuf. 2017, 28, 1285–1301. [Google Scholar] [CrossRef]
- Caggiano, A.; Nele, L. Artificial Neural Networks for Tool Wear Prediction Based on Sensor Fusion Monitoring of CFRP/CFRP Stack Drilling. Int. J. Autom. Technol. 2018, 12, 275–281. [Google Scholar] [CrossRef]
- Guo, W.; Wu, C.; Ding, Z.; Zhou, Q. Prediction of Surface Roughness Based on a Hybrid Feature Selection Method and Long Short-Term Memory Network in Grinding. Int. J. Adv. Manuf. Technol. 2021, 112, 2853–2871. [Google Scholar] [CrossRef]
- Lee, W.J.; Mendis, G.P.; Triebe, M.J.; Sutherland, J.W. Monitoring of a Machining Process Using Kernel Principal Component Analysis and Kernel Density Estimation. J. Intell. Manuf. 2020, 31, 1175–1189. [Google Scholar] [CrossRef]
- Zhou, Y.; Xue, W. A Multisensor Fusion Method for Tool Condition Monitoring in Milling. Sensors 2018, 18, 3866. [Google Scholar] [CrossRef] [PubMed]
- Bagga, P.J.; Makhesana, M.A.; Darji, P.P.; Patel, K.M.; Pimenov, D.Y.; Giasin, K.; Khanna, N. Tool Life Prognostics in CNC Turning of AISI 4140 Steel Using Neural Network Based on Computer Vision. Int. J. Adv. Manuf. Technol. 2022, 123, 3553–3570. [Google Scholar] [CrossRef]
- Crick, F. Central Dogma of Molecular Biology. Nature 1970, 227, 561–563. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi-Kambs, M.; Hölz, K.; Somoza, M.M.; Ott, A. Hamming Distance as a Concept in DNA Molecular Recognition. ACS Omega 2017, 2, 1302–1308. [Google Scholar] [CrossRef]
- Shan, G. Monte Carlo Cross-Validation for a Study with Binary Outcome and Limited Sample Size. BMC Med. Inform. Decis. Mak. 2022, 22, 270. [Google Scholar] [CrossRef]
- Bernard, G.; Achiche, S.; Girard, S.; Mayer, R. Condition Monitoring of Manufacturing Processes under Low Sampling Rate. J. Manuf. Mater. Process. 2021, 5, 26. [Google Scholar] [CrossRef]
- Baillieul, J.; Antsaklis, P.J. Control and Communication Challenges in Networked Real-Time Systems. Proc. IEEE 2007, 95, 9–28. [Google Scholar] [CrossRef]
- Lalouani, W.; Younis, M.; White-Gittens, I.; Emokpae, R.N.; Emokpae, L.E. Energy-Efficient Collection of Wearable Sensor Data through Predictive Sampling. Smart Health 2021, 21, 100208. [Google Scholar] [CrossRef]
- Halgamuge, M.N.; Zukerman, M.; Ramamohanarao, K.; Vu, H.L. An Estimation of Sensor Energy Consumption. Prog. Electromagn. Res. B 2009, 12, 259–295. [Google Scholar] [CrossRef]
- Tingting, Y.; Botong, X. Green Innovation in Manufacturing Enterprises and Digital Transformation. Econ. Anal. Policy 2025, 85, 571–578. [Google Scholar] [CrossRef]
- Yang, J.; Shan, H.; Xian, P.; Xu, X.; Li, N. Impact of Digital Transformation on Green Innovation in Manufacturing under Dual Carbon Targets. Sustainability 2024, 16, 7652. [Google Scholar] [CrossRef]
- Abilakimova, A.; Bauters, M.; Afolayan Ogunyemi, A. Systematic Literature Review of Digital and Green Transformation of Manufacturing SMEs in Europe. Prod. Manuf. Res. 2025, 13, 2443166. [Google Scholar] [CrossRef]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 4th ed.; Garland Science: New York, NY, USA, 2002. [Google Scholar]
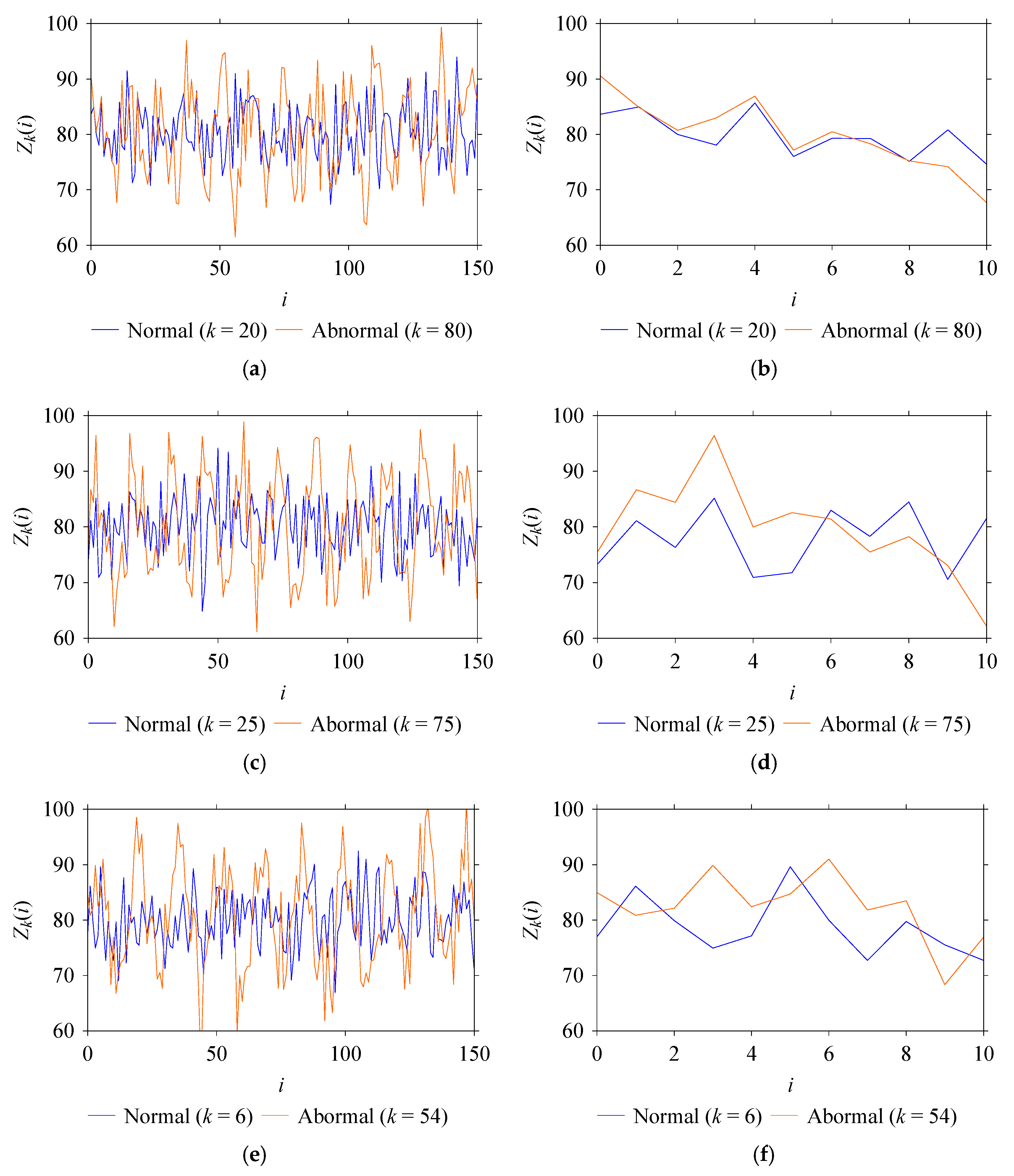
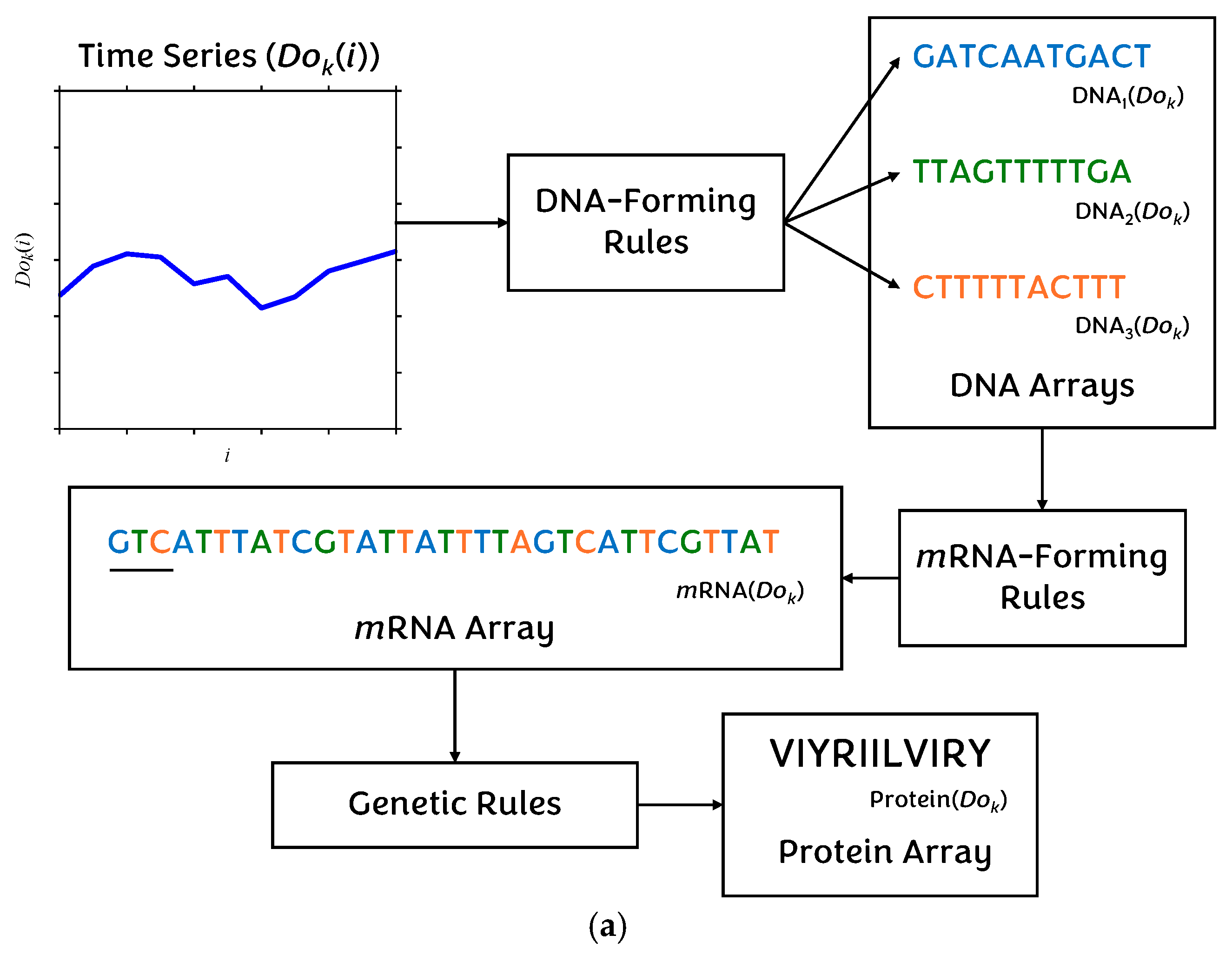



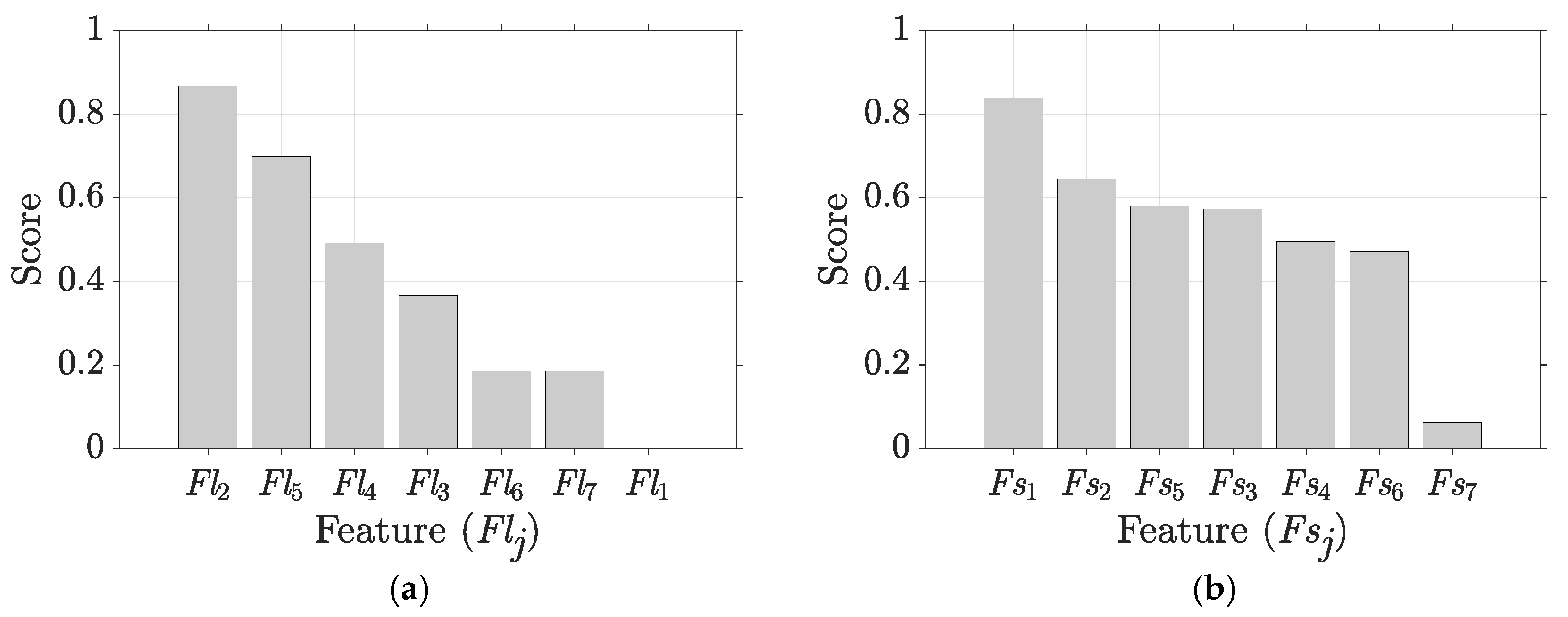
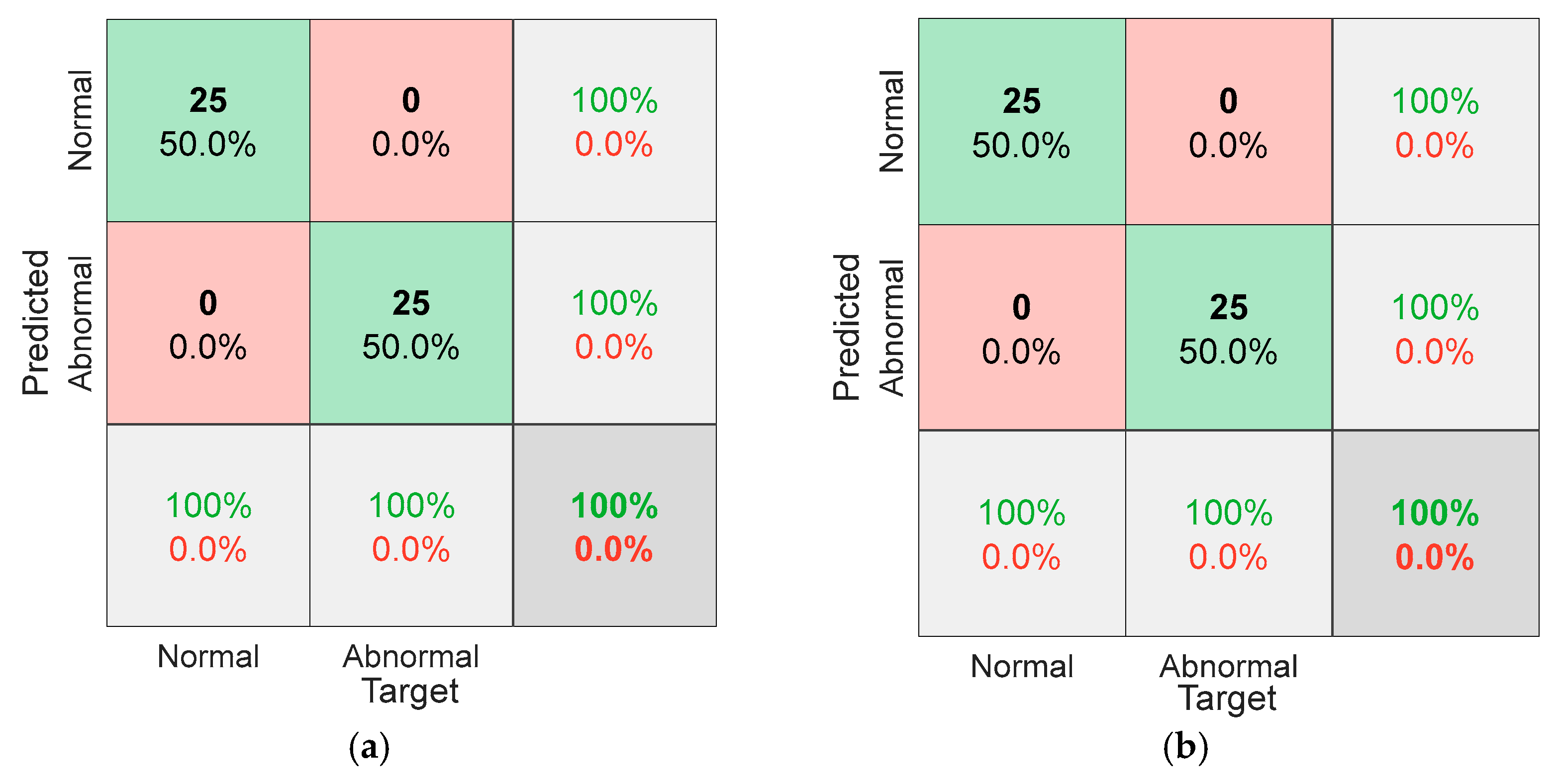

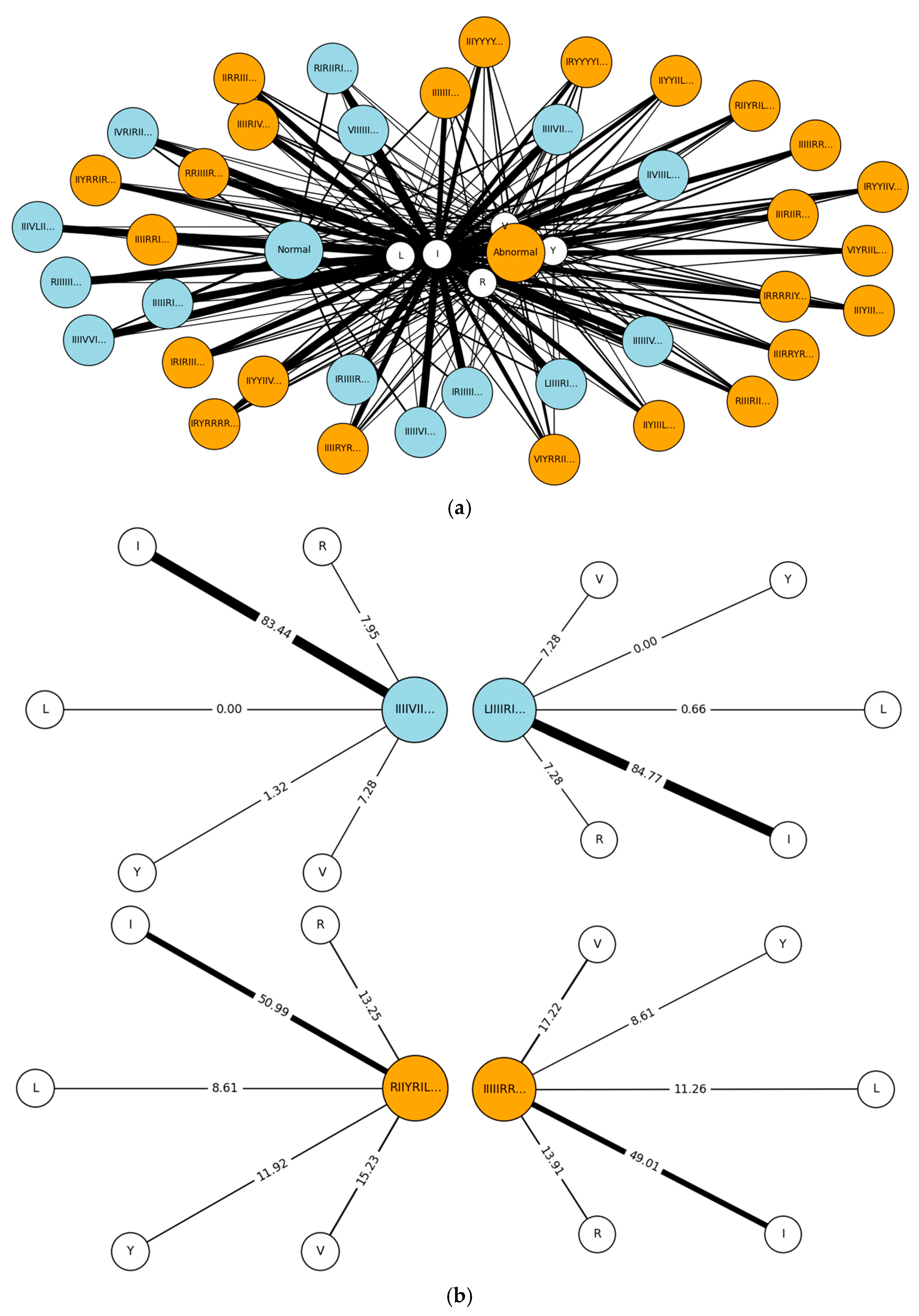
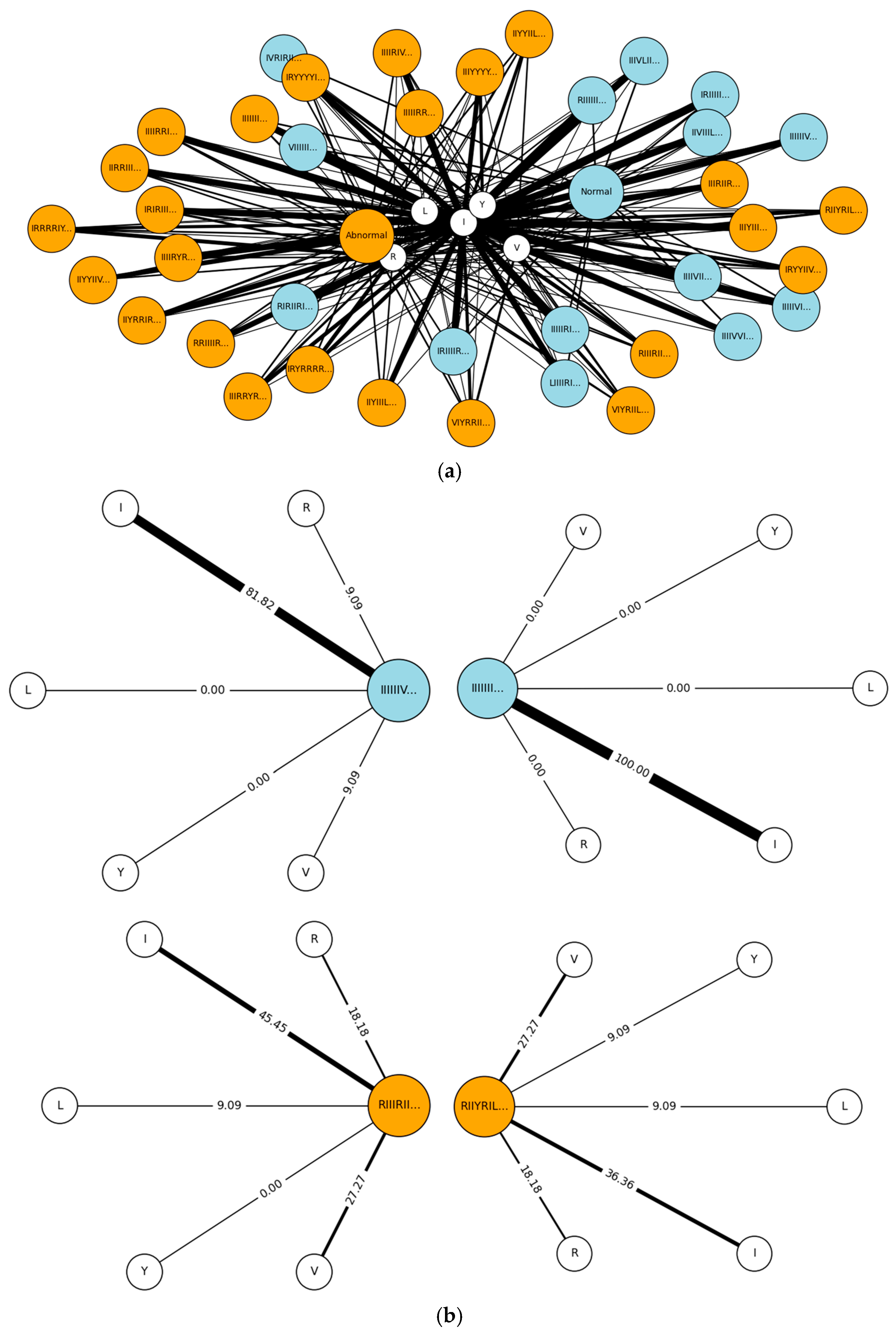
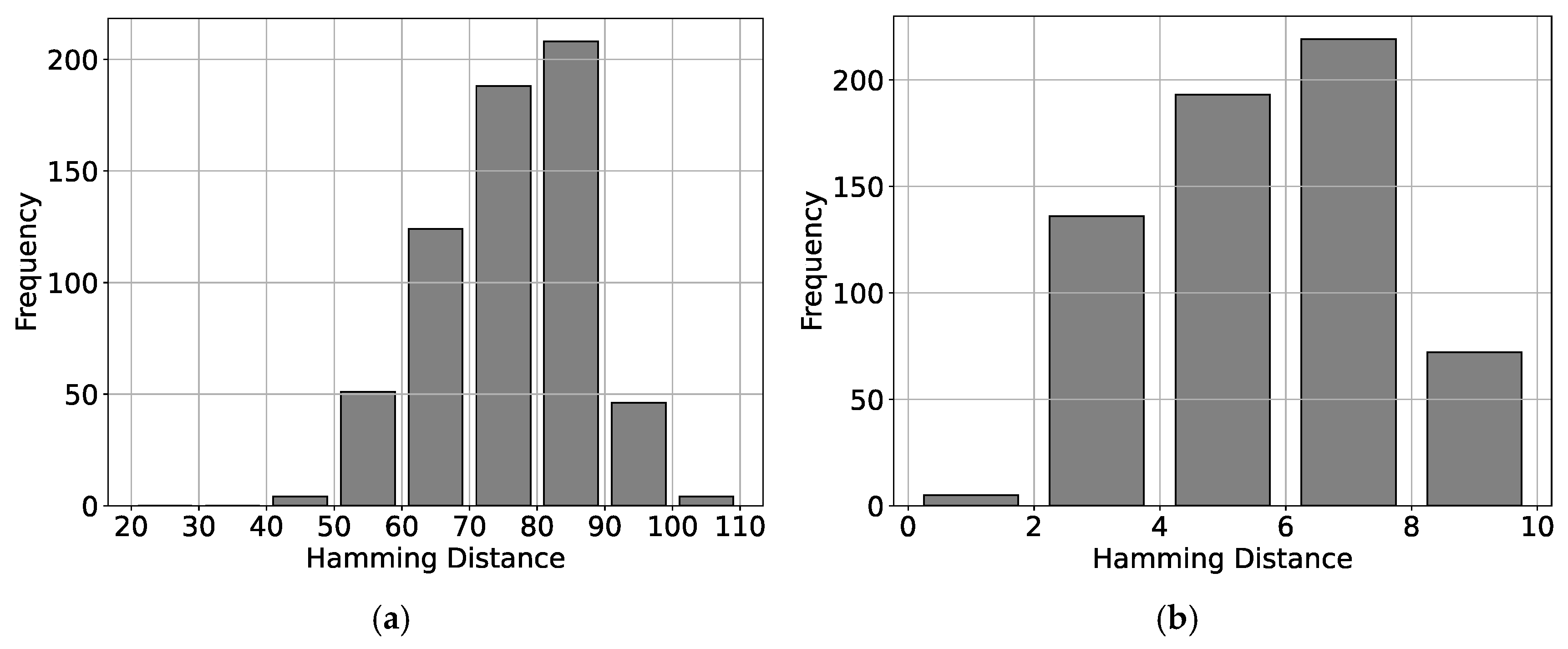
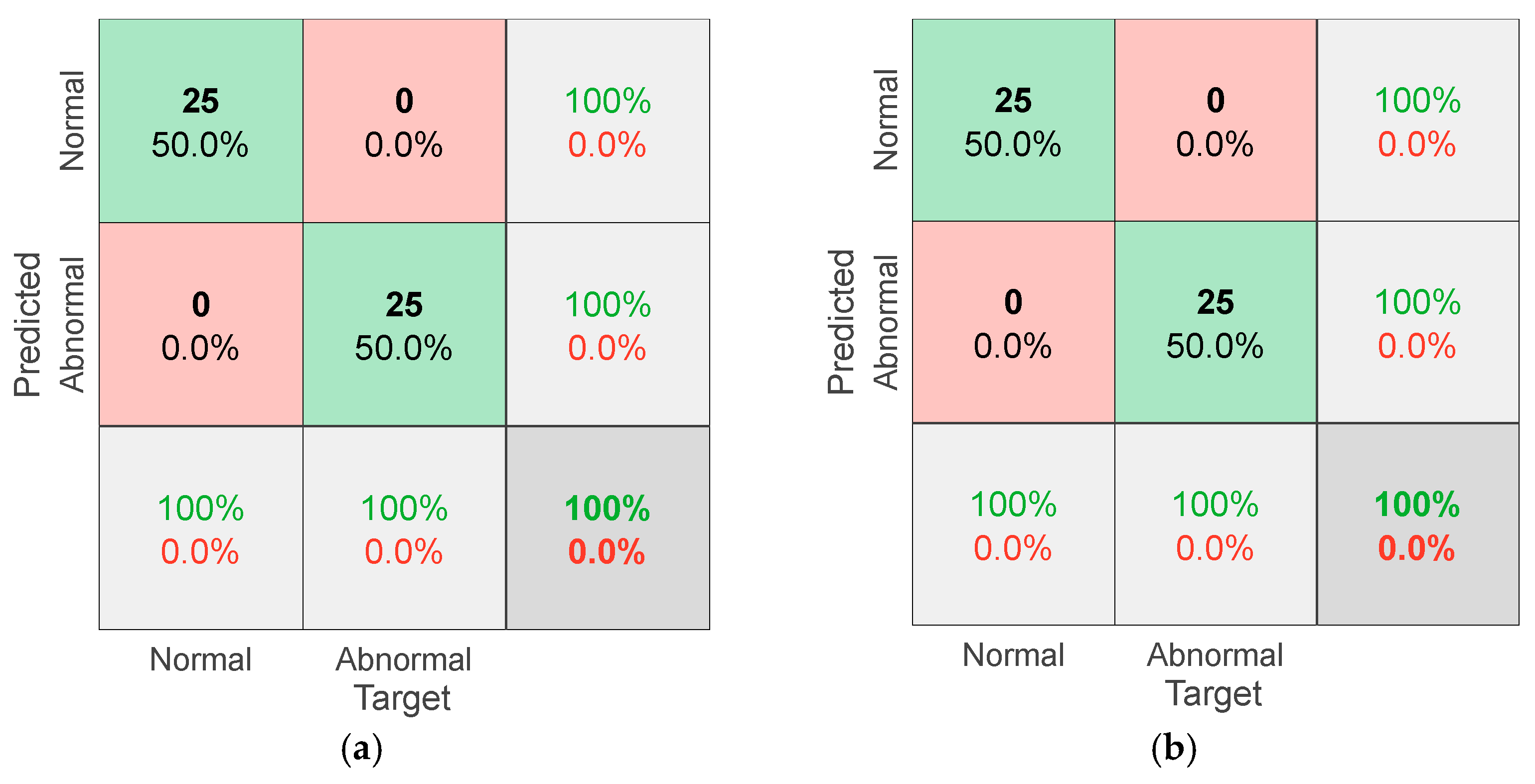

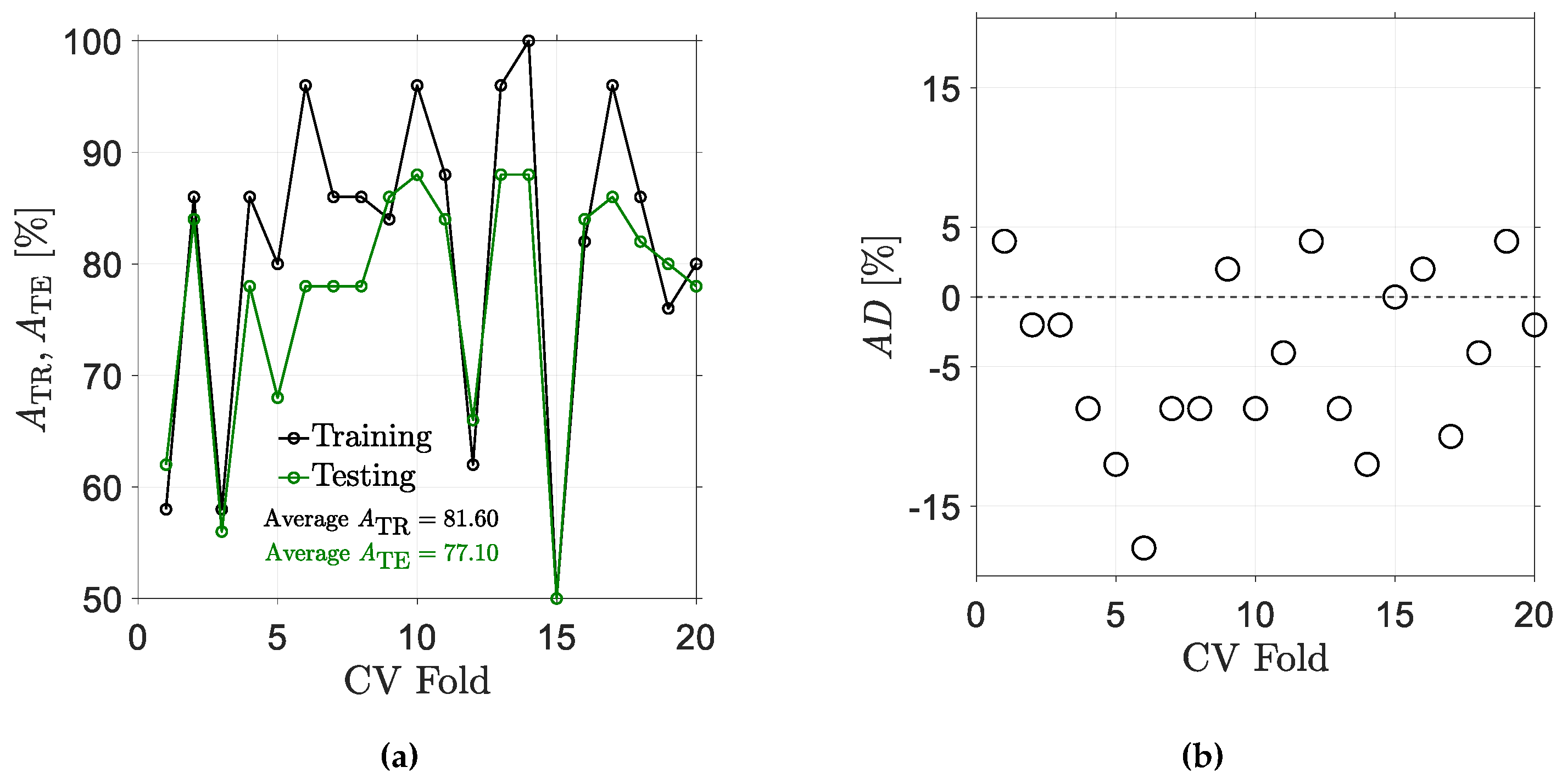
| Steps | Descriptions | |
|---|---|---|
| Creation | 100 datasets are created: 50 Normal, 50 Abnormal, following the definitions in [30]. | |
| Splitting | Using stratified sampling, the datasets are divided into training and test sets, each containing 50. | |
| Windowing | Long | The training and test sets are processed with a long window size of 150, resulting in long-windowed datasets. |
| Short | The training and test sets are processed with a short window size of 10, resulting in short-windowed datasets. | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghosh, A.K.; Ura, S. Leveraging DNA-Based Computing to Improve the Performance of Artificial Neural Networks in Smart Manufacturing. Mach. Learn. Knowl. Extr. 2025, 7, 96. https://doi.org/10.3390/make7030096
Ghosh AK, Ura S. Leveraging DNA-Based Computing to Improve the Performance of Artificial Neural Networks in Smart Manufacturing. Machine Learning and Knowledge Extraction. 2025; 7(3):96. https://doi.org/10.3390/make7030096
Chicago/Turabian StyleGhosh, Angkush Kumar, and Sharifu Ura. 2025. "Leveraging DNA-Based Computing to Improve the Performance of Artificial Neural Networks in Smart Manufacturing" Machine Learning and Knowledge Extraction 7, no. 3: 96. https://doi.org/10.3390/make7030096
APA StyleGhosh, A. K., & Ura, S. (2025). Leveraging DNA-Based Computing to Improve the Performance of Artificial Neural Networks in Smart Manufacturing. Machine Learning and Knowledge Extraction, 7(3), 96. https://doi.org/10.3390/make7030096







