Quantum Machine Learning and Deep Learning: Fundamentals, Algorithms, Techniques, and Real-World Applications

Abstract

Quantum computing, with its foundational principles of superposition and entanglement, has the potential to provide significant quantum advantages, addressing challenges that classical computing may struggle to overcome. As data generation continues to grow exponentially and technological advancements accelerate, classical machine learning algorithms increasingly face difficulties in solving complex real-world problems. The integration of classical machine learning with quantum information processing has led to the emergence of quantum machine learning, a promising interdisciplinary field. This work provides the reader with a bottom-up view of quantum circuits starting from quantum data representation, quantum gates, the fundamental quantum algorithms, and more complex quantum processes. Thoroughly studying the mathematics behind them is a powerful tool to guide scientists entering this domain and exploring their connection to quantum machine learning. Quantum algorithms such as Shor’s algorithm, Grover’s algorithm, and the Harrow–Hassidim–Lloyd (HHL) algorithm are discussed in detail. Furthermore, real-world implementations of quantum machine learning and quantum deep learning are presented in fields such as healthcare, bioinformatics and finance. These implementations aim to enhance time efficiency and reduce algorithmic complexity through the development of more effective quantum algorithms. Therefore, a comprehensive understanding of the fundamentals of these algorithms is crucial.

1. Introduction

Quantum technologies have experienced remarkable growth in recent years. Since the mid-20th century, when Richard Feynman first introduced the concept of quantum computing, extensive research has been conducted in this field. Quantum computers leverage quantum mechanical principles such as superposition and entanglement. Unlike classical computers, which encode information using bits that represent either 0 or 1, quantum computers use qubits, which can represent both values simultaneously due to their quantum properties [1].

Machine learning (ML) problems fundamentally involve two key tasks: efficiently managing large volumes of data and developing algorithms that process these data as quickly as possible. Quantum registers offer a significant advantage over classical registers in addressing the first task. While an n-bit classical register can store only a single n-bit binary string, an n-qubit register can represent $2^n$ n-bit binary strings simultaneously by encoding the information in quantum amplitudes. However, extracting all these strings is challenging, as measurement causes the quantum state to collapse, yielding only one string or amplitude as the output. Despite this limitation, qubits enable inherent parallelism, allowing algorithms to operate on all $2^n$ strings simultaneously, which can lead to exponential speedups over their classical counterparts [2].

Quantum algorithms are the foundation of quantum computing, with decades of research driving significant progress and breakthroughs. Among the nine key quantum algorithms—Deutsch’s algorithm, Deutsch–Josza algorithm, Bernstein–Vazirani algorithm, Simon’s algorithm, quantum Fourier transform, phase estimation algorithm, Shor’s algorithm, Grover’s algorithm and the HHL algorithm— Shor’s algorithm, introduced in 1994 [3], was a major breakthrough, enabling the efficient factoring of large numbers—a problem believed to be computationally hard for classical computers, as no known polynomial-time classical algorithm exists for it. The algorithm leverages the quantum phase estimation (QPE) algorithm to estimate the eigenvalues of unitary operators [4]. In 1996, Lov Grover further advanced the field with Grover’s algorithm [5], achieving a quadratic speedup for searching unsorted databases.

Quantum machine learning (QML) is an interdisciplinary field that lies at the intersection of quantum computing (QC) and ML. The scope of this field leverages the principles of quantum mechanics to process and analyze data more efficiently. Due to the rapid growth of data, classical computers struggle to handle it effectively. As a result, QML presents a promising solution to address these challenges.

The progression of QML can be divided into two main stages. The first stage, from the mid-1990s to 2007, was mainly focused on the development of theoretical models. The second stage, which is ongoing, is concentrated on the practical application and implementation of these models [6].

In 1995, Kak [7] introduced a novel computational framework that integrates quantum mechanics with neural network models to enhance learning, memory, and processing efficiency. Building on this foundation, Ventura and Martinez proposed a quantum associative memory in 1999 [8], capable of retrieving stored patterns exponentially faster than classical models. Around the same time, the concept of a qubit-like neuron was introduced [9], followed by the proposal of a quantum neural network (QNN) [10]. After these breakthrough proposals, other quantum machine learning techniques emerged, including the quantum support vector machine [11] and the quantum k-means algorithm [12].

The first comprehensive monograph on QML [13] was published in 2014. This was followed by key implementations, including the first demonstration of a quantum neuron on a quantum processor as outlined in [14]. In 2020, Google introduced Quantum TensorFlow [15], seamlessly integrating quantum computing capabilities into the TensorFlow platform.

The aim of this work is to provide a tutorial for beginners to enter the field of QML by thoroughly studying the mathematics behind quantum algorithms and QML algorithms. Additionally, real-world applications are presented to illustrate the practical use of these concepts.

There are several review articles that present QML. What differentiates our work from previous studies is the following. In [16], there is a comprehensive analysis covering both NISQ and fault-tolerant quantum algorithms. However, our study specifically focuses on fault-tolerant quantum algorithms and their mathematical preliminaries, which are missing in [16]. While [17] is a review on QML, it lacks a tutorial character, and quantum algorithms are not presented in detail. Our work, in contrast, provides a more structured and explanatory approach. In [18], a review on QML is presented, but it does not include mathematical equations, which we explicitly cover in our study. In [19], some quantum algorithms are presented in significant detail, but the article lacks a tutorial character and does not discuss possible applications in QML and QDL, which our study addresses. In [20], the scope does not include an in-depth mathematical explanation of the algorithms, whereas our work aims to bridge this gap.

The paper is organized as follows: Section 2 presents the fundamental theory of quantum computing. An analytic mathematical explanation of basic quantum algorithms is provided in Section 3. Section 4 and Section 5 cover the fundamentals of quantum machine learning and quantum deep learning, respectively, along with some applications. Section 6 highlights real-world applications of quantum machine learning. Finally, the conclusions are presented in Section 7.

2. Overview of Quantum Computing

2.1. History and Evolution of QC

Quantum computing is an emerging field that leverages principles of quantum mechanics to perform computations. It sits at the intersection of mathematics, physics and computer science. While quantum computers exist today, their practical use remains minimal. Despite its immense potential, quantum computing is still in its early stages. Preskill [21] first introduced the term “noisy intermediate-scale quantum (NISQ) era” because the current quantum circuits are susceptible to noise. However, there is optimism that NISQ-era devices will soon demonstrate practical applications, marking a significant step toward more advanced quantum computing.

The theoretical idea of quantum computing began in the mid-20th century and has since evolved into a rapidly advancing field of research and technological development. The development of quantum mechanics by physicists such as Niels Bohr, Werner Heisenberg, Erwin Schrödinger, and Paul Dirac in the 1920s and 1930s laid the groundwork for understanding the strange behavior of subatomic particles, such as superposition and entanglement—principles central to quantum computing. Einstein is considered the principal founder of quantum theory because he explained the photoelectric effect by proposing that light behaves as particles called quanta. The idea of quantum computing was introduced by Nobel laureate Richard Feynman. While working on a simulation for quantum physics models, he discovered that the values in his calculations were growing exponentially, requiring computational power far beyond what traditional computers could handle [22].

Between 1980 and 2000, the foundational concepts of quantum computing emerged. In 1981, Richard Feynman proposed that a quantum computer could be used to simulate quantum systems, which classical computers could not perform efficiently. This is widely considered the first concrete proposal for a quantum computer [22]. In 1985, David Deutsch, a British physicist, formalized the idea of a quantum Turing machine, a theoretical model for a universal quantum computer. His work demonstrated that a quantum computer could solve problems that classical computers could not. During the late 1980s, researchers began developing early quantum algorithms, including Deutsch’s algorithm. One of the most significant breakthroughs occurred in 1994 when Peter Shor developed an efficient quantum algorithm for integer factorization [23].

In the early 2000s, researchers built small-scale quantum computers that could run simple algorithms. In 2001, researchers from IBM and Stanford University successfully implemented a small version of Shor’s algorithm on a 7-qubit quantum computer, factorizing the number 15. In 2011, D-Wave Systems, a Canadian company, launched its first commercial quantum computing system based on quantum annealing [23].

After 2010, several companies began investing more heavily in the development of efficient quantum computers, aiming to build systems with a greater number of qubits. Nowadays, large companies such as Google, IBM and Microsoft, along with startups such as Rigetti, D-Wave, and Xanadu, have made breakthroughs in building quantum computers with increasing qubit capacities. Additionally, there has been active research in developing quantum algorithms and exploring the applications of quantum computers in real-world scenarios, including finance, machine learning, drug discovery and cryptography.

Quantum algorithms have been developed for both NISQ and fault-tolerant devices. For NISQ devices, the most important are variational algorithms, including the Variational Quantum Eigensolver (VQE) [24], the Quantum Approximate Optimization Algorithm (QAOA) [25] and Parameterized Quantum Circuits [26].

A variational quantum circuit is a hybrid approach that combines quantum and classical computation, utilizing the advantages of both. It consists of a quantum circuit with adjustable parameters that a classical computer optimizes iteratively. These parameters function similarly to the weights in artificial neural networks [27].

The algorithms described below refer to fault-tolerant quantum computing.

2.2. Bra–Ket Notation

States and operators in quantum mechanics are represented as vectors and matrices, respectively [28]. Bra–Ket Notation, or Dirac notation, was introduced as an easier way to write quantum mechanical expressions.

A ket, denoted as $|\psi \rangle$, represents a quantum state in a Hilbert space. It is a column vector that encapsulates all the information about the state of a quantum system. If $|a\rangle$ is a quantum state in a two-level system, it can be represented as

$$|a\rangle =\left(\begin{array}{c}{a}_1\\ a_2\end{array}\right)$$

(1)

A bra is denoted as $\langle \varphi |$. It is a row vector and is obtained by taking the conjugate transpose of a ket. If $|b\rangle$ is a quantum state, its corresponding bra is represented as

$$\langle b|={|b\rangle }^{†}={\left(\begin{array}{c}{b}_1\\ b_2\end{array}\right)}^{†}=\left(\begin{array}{cc}{b}_1^{*}& b_2^{*}\end{array}\right)$$

(2)

2.3. Quantum Bits

The fundamental component of QC is known as a quantum bit or qubit for short. Qubits are basic units of quantum information and function according to the principles of quantum mechanics. Quantum characteristics are not limited to subatomic particles, as larger systems can also exhibit quantum behavior. A qubit can be realized using various entities, including photons, electrons, neutrons, and even atoms [29]. A qubit can be represented as a vector in a two-dimensional complex vector space. The states $|0\rangle$ and $|1\rangle$ are written in vector form as

$$|0\rangle =\left(\begin{array}{c}1\\ 0\end{array}\right),|1\rangle =\left(\begin{array}{c}0\\ 1\end{array}\right)$$

(3)

A qubit can exist in a state of 0, a state of 1 or in a superposition of both states simultaneously, a phenomenon referred to as superposition. In contrast, classical bits are limited to a single value at any given time, either 0 or 1. Mathematically, a qubit can be expressed by the following equation:

$$|\psi \rangle =\alpha |0\rangle +\beta |1\rangle$$

(4)

where $|\psi \rangle$ is the qubit’s state and $\alpha$ and $\beta$ represent the the probabilistic amplitude of the waveform of the state for being in the |0> state and |1> state, respectively. It must be noted that

$${|\alpha |}^2+{|\beta |}^2=1$$

(5)

Thus, the general state of a qubit $|\psi \rangle$ can also be written as

$$|\psi \rangle =\alpha \left(\begin{array}{c}1\\ 0\end{array}\right)+\beta \left(\begin{array}{c}0\\ 1\end{array}\right)$$

(6)

When we conduct a measurement, we retrieve a single bit of information, either 0 or 1. The simplest form of measurement occurs in the computational basis, represented by $|0\rangle$ and $|1\rangle$. For instance, measuring the state $\alpha |0\rangle +\beta |1\rangle$ on this basis yields a result of 0 with a probability of ${|\alpha |}^2$ and a result of 1 with a probability of ${|\beta |}^2$.

In quantum mechanics, the inner product between two vectors representing qubit states in a Hilbert space provides valuable information about their similarities. Specifically, the inner product is a mathematical operation that takes two quantum states, denoted as $|\varphi \rangle$ and $|\psi \rangle$ and is represented as $\langle \varphi |\psi \rangle$.

This inner product reveals important properties of the states:

1. Orthogonality: If the states $|\varphi \rangle$ and $|\psi \rangle$ are orthogonal, meaning they are completely independent and share no information, the inner product equals zero:

$$\langle \varphi |\psi \rangle =0$$

(7)

Consequently, the inner product $\langle 0|1\rangle$ can be computed as

$$\langle 0|1\rangle =\left(\begin{array}{cc}1& 0\end{array}\right)\left(\begin{array}{c}0\\ 1\end{array}\right)=1·0+0·1=0$$

(8)

2. Normalization: If the states are identical, that is $|\varphi \rangle =|\psi \rangle$, the inner product equals one:

$$\langle \varphi |\varphi \rangle =1$$

(9)

Consequently, the inner product $\langle 0|0\rangle$ can be computed as

$$\langle 0|0\rangle =\left(\begin{array}{cc}1& 0\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=1·1+0·0=1$$

(10)

Quantum computing uses quantum physics principles including superposition and entanglement to process data. Superposition is described by Equation (4). This property allows for the exponential speedup of quantum computing, as a qubit can exist in a combination of both states simultaneously. Quantum entanglement will be described in detail below.

2.4. Quantum Gates

The fundamental components of quantum circuits are quantum gates, which act on qubits. These quantum gates are realized through unitary operators, which serve to transform the state of a closed quantum system. Therefore, quantum gates are represented by unitary matrices. Unitary operators play a crucial role in evolving the quantum state, preserving the overall probabilities and maintaining the reversibility of the quantum process. The unitary operator maps the quantum state $|\varphi \rangle$ into the state $U|\psi \rangle$ as follows:

$$|\varphi \rangle =U|\psi \rangle$$

(11)

An operator U is a unitary transformation if the following condition is satisfied:

$$U{U}^{†}=U^{†}U=I$$

(12)

where $U^{†}$ is the conjugate transpose of the unitary operator U, and I is the identity operator.

The equation above describes the reversibility of a quantum system and ensures that the information contained in a quantum state can be recovered after the application of a quantum gate, allowing for the reconstruction of the original state prior to the operation. Every quantum gate operation is inherently reversible due to the unitary nature of quantum mechanics, unlike many classical operations.

Quantum gates operate on single-qubit, two-qubit or multi-qubit systems. Therefore, quantum gates can be categorized into three main categories: single-qubit gates, two-qubit gates and multi-qubit gates [30]. Below is a concise representation of the most significant quantum gates in each category.

2.4.1. Single-Qubit Gates

Single-qubit gates operate on a single qubit. Common single-qubit gates are illustrated in Figure 1 and include the following:

• Pauli (X) Gate: Acts like a quantum NOT gate, flipping the state $|0\rangle$ to $|1\rangle$ and vice versa.

  $$X=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$$

  (13)
  For example, applying the X gate to the state $|0\rangle$,

  $$X|0\rangle =\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)=|1\rangle$$

  (14)
  Similarly, applying the X gate to the state $|1\rangle$,

  $$X|1\rangle =\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{c}1\\ 0\end{array}\right)=|0\rangle$$

  (15)
• Pauli (Y) Gate: Introduces both a flip and a phase change.

  $$Y=\left[\begin{array}{cc}0& -i\\ i& 0\end{array}\right]$$

  (16)
  For example, applying the Y gate to the state $|0\rangle$,

  $$Y|0\rangle =\left[\begin{array}{cc}0& -i\\ i& 0\end{array}\right]\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ i\end{array}\right)=i|1\rangle$$

  (17)
  Similarly, applying the Y gate to the state $|1\rangle$,

  $$Y|1\rangle =\left[\begin{array}{cc}0& -i\\ i& 0\end{array}\right]\left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{c}-i\\ 0\end{array}\right)=-i|0\rangle$$

  (18)
• Pauli (Z) Gate: Applies a phase flip to the $|1\rangle$ state.

  $$Z=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$$

  (19)
  For example, applying the Z gate to the state $|0\rangle$,

  $$Z|0\rangle =\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}1\\ 0\end{array}\right)=|0\rangle$$

  (20)
  Applying the Z gate to the state $|1\rangle$,

  $$Z|1\rangle =\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ -1\end{array}\right)=-|1\rangle$$

  (21)
• Hadamard (H) Gate: It is one of the most frequently used quantum gates, transforming a basis state ($|0\rangle$ or $|1\rangle$ ) into a superposition state.

  $$H={\displaystyle \frac{1}{\sqrt{2}}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$$

  (22)
  For example, applying the H gate to the state $|0\rangle$,

  $$H|0\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]\left(\begin{array}{c}1\\ 0\end{array}\right)={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{c}1\\ 1\end{array}\right)={\displaystyle \frac{1}{\sqrt{2}}}(|0\rangle +|1\rangle )$$

  (23)
  Similarly, applying the H gate to the state $|1\rangle$,

  $$H|1\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]\left(\begin{array}{c}0\\ 1\end{array}\right)={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{c}1\\ -1\end{array}\right)={\displaystyle \frac{1}{\sqrt{2}}}(|0\rangle -|1\rangle )$$

  (24)

2.4.2. Two-Qubit Gates

Two-qubit gates operate on two qubits simultaneously. A two-qubit system consists of two qubits, which together form a composite system. Each qubit can be in the state $|0\rangle$ or $|1\rangle$, so the two-qubit system can be in one of four possible basis states:

$$|00\rangle ,|01\rangle ,|10\rangle ,|11\rangle$$

(25)

The two-qubit system is described using the tensor product of the individual qubit states. If qubit 1 is in the state $|{\psi }_1\rangle$ and qubit 2 is in the state $|{\psi }_2\rangle$, the combined state is

$$|{\psi }_{12}\rangle =|{\psi }_1\rangle \otimes |{\psi }_2\rangle$$

(26)

For example,

If $|{\psi }_1\rangle =|0\rangle$ and $|{\psi }_2\rangle =|1\rangle$, then the combined state is

$$|0\rangle \otimes |1\rangle =\left[\begin{array}{c}1\\ 0\end{array}\right]\otimes \left[\begin{array}{c}0\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]=|01\rangle$$

(27)

Common two-qubit gates include the following:

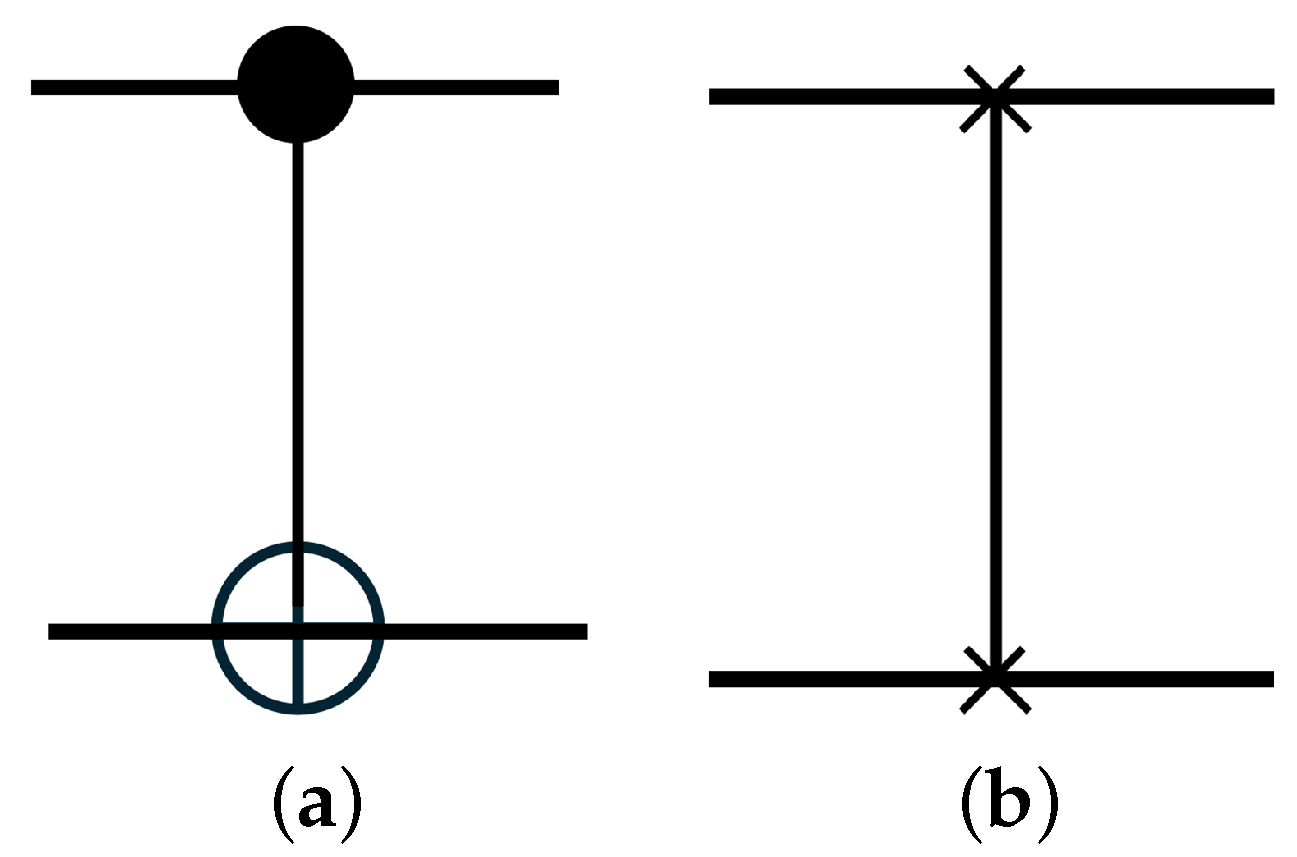
• CNOT (Controlled-NOT) Gate: Flips the target qubit if the control qubit is $|1\rangle$ (Figure 2a).

  $$\mathrm{CNOT}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right]$$

  (28)
  For example, applying the CNOT gate to the state $|00\rangle$,

  $$\mathrm{CNOT}|00\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right]\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right)=|00\rangle$$

  (29)
  Similarly, applying the CNOT gate to the state $|01\rangle$,

  $$\mathrm{CNOT}|01\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right]\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right)=|01\rangle$$

  (30)
  Similarly, applying the CNOT gate to the state $|10\rangle$,

  $$\mathrm{CNOT}|10\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right]\left(\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right)=|11\rangle$$

  (31)
  Finally, applying the CNOT gate to the state $|11\rangle$,

  $$\mathrm{CNOT}|11\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right]\left(\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right)=|10\rangle$$

  (32)
  The information above is summarized in the following

  Table 1. Truth table for CNOT gate.

  Control (Input)	Target (Input)	Control (Output)	Target (Output)
  $|0\rangle$	$|0\rangle$	$|0\rangle$	$|0\rangle$
  $|0\rangle$	$|1\rangle$	$|0\rangle$	$|1\rangle$
  $|1\rangle$	$|0\rangle$	$|1\rangle$	$|1\rangle$
  $|1\rangle$	$|1\rangle$	$|1\rangle$	$|0\rangle$

  .
  Table 1 shows that the output state of the target qubit corresponds to that of a standard XOR gate. The target qubit is $|0\rangle$ when both inputs are identical and $|1\rangle$ when the inputs differ.
• SWAP Gate: Swaps the states of two qubits (Figure 2b).

  $$\mathrm{SWAP}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

  (33)
  For example, applying the SWAP gate to the state $|00\rangle$,

  $$\mathrm{SWAP}|00\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right)=|00\rangle$$

  (34)
  Similarly, applying the SWAP gate to the state $|01\rangle$,

  $$\mathrm{SWAP}|01\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right)=|10\rangle$$

  (35)
  Similarly, applying the SWAP gate to the state $|10\rangle$,

  $$\mathrm{SWAP}|10\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]\left(\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right)=|01\rangle$$

  (36)
  Finally, applying the SWAP gate to the state $|11\rangle$,

  $$\mathrm{SWAP}|11\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]\left(\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right)=|11\rangle$$

  (37)
  The information above is summarized in the following

  Table 2. Truth table for the SWAP gate.

  Input Qubit 1	Input Qubit 2	Output Qubit 1	Output Qubit 2
  $|0\rangle$	$|0\rangle$	$|0\rangle$	$|0\rangle$
  $|0\rangle$	$|1\rangle$	$|1\rangle$	$|0\rangle$
  $|1\rangle$	$|0\rangle$	$|0\rangle$	$|1\rangle$
  $|1\rangle$	$|1\rangle$	$|1\rangle$	$|1\rangle$

  .

2.4.3. Multi-Qubit Gates

Multi-qubit gates operate on multiple qubits simultaneously. A multi-qubit system consists of n qubits, which together form a composite quantum system. Each qubit can be in the state $|0\rangle$ or $|1\rangle$, allowing the multi-qubit system to exist in one of $2^n$ possible basis states. The states of the multi-qubit system are represented using the tensor product of the individual qubit states. If qubit 1 is in the state $|{\psi }_1\rangle$, qubit 2 is in the state $|{\psi }_2\rangle$ and so on, the combined state of the system is given by

$$|{\psi }_{1\dots n}\rangle =|{\psi }_1\rangle \otimes |{\psi }_2\rangle \otimes \dots \otimes |{\psi }_n\rangle$$

(38)

For example, if $|{\psi }_1\rangle =|0\rangle$, $|{\psi }_2\rangle =|1\rangle$, and $|{\psi }_3\rangle =|0\rangle$, then the combined state of the three-qubit system is

$$|0\rangle \otimes |1\rangle \otimes |0\rangle =\left[\begin{array}{c}1\\ 0\end{array}\right]\otimes \left[\begin{array}{c}0\\ 1\end{array}\right]\otimes \left[\begin{array}{c}0\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]\otimes \left[\begin{array}{c}0\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\end{array}\right]=|010\rangle$$

(39)

Fredkin Gate: Swaps the states of two target qubits based on the state of a control qubit. If the control qubit is $|1\rangle$, the states of the two target qubits are swapped. If the control qubit is $|0\rangle$, the target qubits remain unchanged (Figure 3). The Fredkin gate is also known as the controlled-SWAP gate.

$$\mathrm{Fredkin}=\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]$$

(40)

For example, applying the Fredkin gate to the state $|001\rangle$,

$$\mathrm{Fredkin}|001\rangle =\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\left(\begin{array}{c}0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right)=|001\rangle$$

(41)

Similarly, applying the Fredkin gate to the state $|110\rangle$,

$$\mathrm{Fredkin}|110\rangle =\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\left(\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\end{array}\right)=|101\rangle$$

(42)

The information above is summarized in the following

Table 3. Truth table for the Fredkin gate.

Control	Target 1	Target 2	Output Control	Output Target 1	Output Target 2
0	0	0	0	0	0
0	0	1	0	0	1
0	1	0	0	1	0
0	1	1	0	1	1
1	0	0	1	0	0
1	0	1	1	1	0
1	1	0	1	0	1
1	1	1	1	1	1

.

2.5. Quantum Measurement

After the application of quantum gates, the measurement process is initiated. Measurement in quantum computing constitutes a fundamental concept that significantly influences the operation of quantum systems and their interaction with classical information. Following the execution of a series of quantum gates, the state of a quantum system can be represented by a quantum state vector $|\psi \rangle$. This state vector encapsulates the information regarding the quantum system and can be expressed as a superposition of orthonormal basis states:

$$|\psi \rangle =\sum _i{\alpha }_i|{\psi }_i\rangle$$

(43)

where $|{\psi }_i\rangle$ denotes the orthonormal basis states and ${\alpha }_i$ are the complex coefficients that characterize the probability amplitudes associated with each basis state. Upon measurement, the quantum state collapses to one of the possible basis states, with the probability of obtaining a particular state $|{\psi }_i\rangle$ given by the square of the magnitude of the corresponding coefficient [31]:

$$P\left(i\right)=|{\alpha }_i{|}^2$$

(44)

The measurement process is essential, as it facilitates the extraction of information and enables decision-making based on the results of quantum computations.

2.6. Quantum Entanglement

An important principle of quantum computing is called entanglement, which has no classical analogue. Qubits can become entangled, a phenomenon in which the state of one qubit is directly related to the state of another, regardless of the distance between them [32]. In simple terms, two quantum systems are entangled when their combined state cannot be written as tensor product of basic states.

Suppose that two qubits $q_{s_0}$ and $q_{s_1}$ are in the state $|q_s\rangle$, which is given by

$$|q_s\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|10\rangle +|11\rangle \right)$$

(45)

$|q_s\rangle$ can also be written as

$$|q_s\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|10\rangle +|11\rangle \right)=|1\rangle \otimes \left[{\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +|1\rangle \right)\right]$$

(46)

That is, the states of $q_{s_0}$ and $q_{s_1}$ are

$$|q_{s_1}\rangle =|1\rangle$$

(47)

$$|q_{s_0}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +|1\rangle \right)$$

(48)

Therefore, $|q_s\rangle$ can be written as

$$|q_s\rangle =|q_{s_1}\rangle \otimes |q_{s_0}\rangle$$

(49)

Specifically, $|q_s\rangle$ can be written as the tensor product of the states of the two qubits, so that $q_{s_0}$ and $q_{s_1}$ are not in quantum entanglement but in a separable state.

Let us consider two other qubits, $q_{e_0}$ and $q_{e_1}$, which are in the state $|q_e\rangle$, given by

$$|q_e\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|00\rangle +|11\rangle \right)$$

(50)

The state $|q_e\rangle$ cannot be written as the tensor product of the states of the two qubits, so $q_{e_0}$ and $q_{e_1}$ are in quantum entanglement. The difference between separability and entanglement is explained as follows.

When qubit $q_{s_1}$ is measured in state $|q_s\rangle$, it is always found in $|1\rangle$. Afterward, qubit $q_{s_0}$ has a 50% chance of being in $|0\rangle$ or $|1\rangle$, meaning $q_{s_1}$’s measurement does not affect $q_{s_0}$. When qubit $q_{e_1}$ is measured in state $|q_e\rangle$, it has a 50% chance of being in $|0\rangle$ or $|1\rangle$. If $q_{e_1}$ is found in $|0\rangle$, $q_{e_0}$ will be $|0\rangle$; if in $|1\rangle$, $q_{e_0}$ will be $|1\rangle$. This shows that measuring one entangled qubit determines the state of the other.

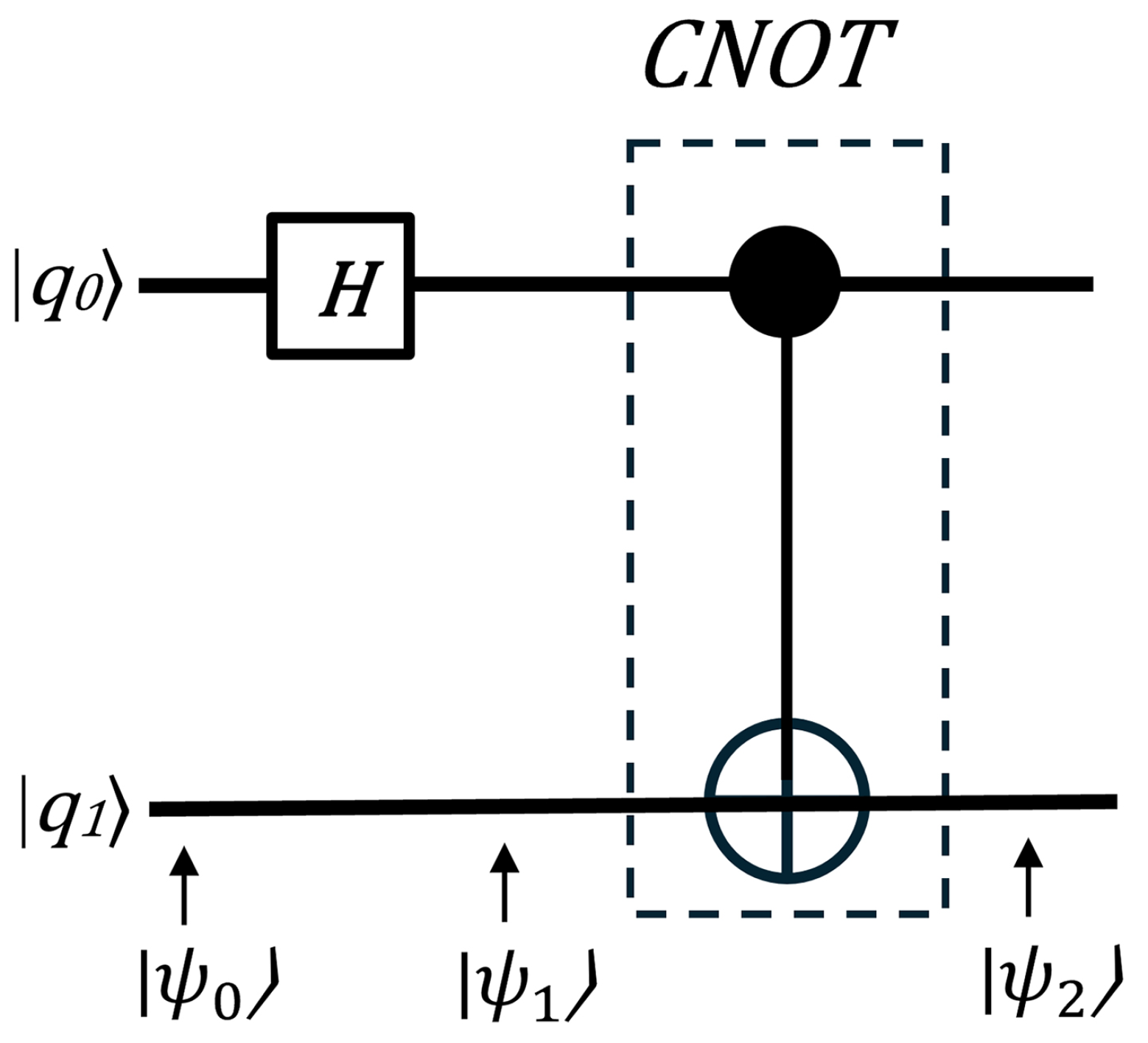
Bell states are quantum states involving two qubits that represent the simplest form of quantum entanglement. The quantum circuit that creates Bell states is shown in Figure 4. While there are various ways to generate entangled Bell states using quantum circuits, the most basic approach starts with a computational basis as the input and employs a Hadamard gate followed by a CNOT gate.

Suppose that the input state is given by the following equation:

$$|{\psi }_0\rangle =|00\rangle$$

(51)

Next, a Hadamard gate is applied to the q0 qubit, putting it into a superposition state using Equation (23).

$$|{\psi }_1\rangle =H|0\rangle \otimes |0\rangle =\left[{\displaystyle \frac{|0\rangle +|1\rangle }{\sqrt{2}}}\right]|0\rangle ={\displaystyle \frac{|00\rangle +|10\rangle }{\sqrt{2}}}$$

(52)

Then, q0 acts as a control input to the CNOT gate and the target qubit (q1) gets inverted only when the control is 1. The output is as follows:

$$|{\psi }_2\rangle ={\displaystyle \frac{|00\rangle +|11\rangle }{\sqrt{2}}}$$

(53)

Table 4. Bell state circuit computation.

Input	Intermediate State	Bell State
$|00\rangle$	${\displaystyle \frac{|00\rangle +|10\rangle }{\sqrt{2}}}$	${\displaystyle \frac{|00\rangle +|11\rangle }{\sqrt{2}}}$
$|01\rangle$	${\displaystyle \frac{|01\rangle +|11\rangle }{\sqrt{2}}}$	${\displaystyle \frac{|01\rangle +|10\rangle }{\sqrt{2}}}$
$|10\rangle$	${\displaystyle \frac{|00\rangle -|10\rangle }{\sqrt{2}}}$	${\displaystyle \frac{|00\rangle -|11\rangle }{\sqrt{2}}}$
$|11\rangle$	${\displaystyle \frac{|01\rangle -|11\rangle }{\sqrt{2}}}$	${\displaystyle \frac{|01\rangle -|10\rangle }{\sqrt{2}}}$

summarizes the results of the Bell state circuit computation. For example, knowing the state of two input qubits and measuring one of the output qubits allows us to determine the state of the other qubit, as the two qubits are entangled.

The expression $\mathrm{Tr}\left[{\rho }_A^2\right]$ is a measurement of the degree of entanglement. The following equation shows whether two states, A and B, are completely separable or have some degree of entanglement:

$$\mathrm{Tr}\left[{\rho }_A^2\right]=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{A}\mathrm{and}\mathrm{B}\mathrm{are}\mathrm{completely}\mathrm{separable}\hfill \\ ({\displaystyle \frac{1}{2}},1]\hfill & \mathrm{if}\mathrm{there}\mathrm{is}\mathrm{a}\mathrm{degree}\mathrm{of}\mathrm{entanglement}\hfill \end{array}\right.$$

(54)

Here, $\mathrm{Tr}\left[{\rho }_A^2\right]$ represents the trace of the square of a density matrix ${\rho }_A$.

Two states are completely entangled when

$$\mathrm{Tr}\left[{\rho }_A^2\right]={\displaystyle \frac{1}{2}}$$

(55)

The density matrix $\rho$ can be computed by the following equation:

$$\rho =|q\rangle \langle q|=\left(\begin{array}{c}\alpha \\ \beta \end{array}\right)\left(\begin{array}{cc}{\alpha }^{*}& {\beta }^{*}\end{array}\right)=\left(\begin{array}{cc}\alpha {\alpha }^{*}& \alpha {\beta }^{*}\\ \beta {\alpha }^{*}& \beta {\beta }^{*}\end{array}\right)=\left(\begin{array}{cc}{|\alpha |}^2& \alpha {\beta }^{*}\\ \beta {\alpha }^{*}& {|\beta |}^2\end{array}\right)$$

(56)

The reduced density matrix ${\rho }_A$ can be computed by the following equation:

$${\rho }_A={\mathrm{Tr}}_B\left({\rho }^{AB}\right)={\mathrm{Tr}}_B(|a_1\rangle \langle a_2|\otimes |b_1\rangle \langle b_2|)=\langle a_1|a_2\rangle \mathrm{Tr}(|b_1\rangle \langle b_2|)=\langle a_1|a_2\rangle \langle b_2|b_1\rangle$$

(57)

As an instance, consider the following Bell state:

$$|q_{AB}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|00\rangle +|11\rangle \right)$$

(58)

The density matrix of qubit A is given by

$$\begin{array}{cc}\hfill {\rho }_A& ={\mathrm{Tr}}_B\left({\rho }^{AB}\right)={\mathrm{Tr}}_B\left({\displaystyle \frac{1}{\sqrt{2}}}\left(|00\rangle +|11\rangle \right){\displaystyle \frac{1}{\sqrt{2}}}\left(\langle 00|+\langle 11|\right)\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\mathrm{Tr}}_B\left(|00\rangle \langle 00|+|11\rangle \langle 11|+|00\rangle \langle 11|+|11\rangle \langle 00|\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\left({\mathrm{Tr}}_B(|00\rangle \langle 00|)+{\mathrm{Tr}}_B(|00\rangle \langle 11|)+{\mathrm{Tr}}_B(|11\rangle \langle 00|)+{\mathrm{Tr}}_B(|11\rangle \langle 11|)\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\left((|0\rangle \langle 0|)(\langle 0|0\rangle )+(|0\rangle \langle 1|\left)\right(\langle 1|0\rangle )+(|1\rangle \langle 0|)(\langle 0|1\rangle )+(|1\rangle \langle 1|\left)\right(\langle 1|1\rangle )\right)\hfill \end{array}$$

(59)

Considering that the basis states are orthogonal, we have

$${\rho }_A={\displaystyle \frac{1}{2}}\left(|0\rangle \langle 0|+|1\rangle \langle 1|\right)$$

(60)

The corresponding density matrix is

$${\rho }_A={\displaystyle \frac{1}{2}}\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

(61)

Therefore, ${\rho }_A^2$ can be computed as

$${\rho }_A^2={\displaystyle \frac{1}{2}}\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]{\displaystyle \frac{1}{2}}\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]={\displaystyle \frac{1}{4}}\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

(62)

Thus,

$$\mathrm{Tr}\left({\rho }_A^2\right)={\displaystyle \frac{1}{4}}(1+1)={\displaystyle \frac{2}{4}}={\displaystyle \frac{1}{2}}$$

(63)

The above computation indicates that the initial states are completely entangled.

As another example, the initial state of the two-qubit system is given by

$$|q_{AB}\rangle =|00\rangle$$

(64)

The density matrix of qubit A is given by

$$\begin{array}{cc}\hfill {\rho }_A& ={\mathrm{Tr}}_B\left({\rho }^{AB}\right)={\mathrm{Tr}}_B(|00\rangle \langle 00|)\hfill \\ \hfill & =(|0\rangle \langle 0|)\hfill \end{array}$$

(65)

The corresponding density matrix is

$${\rho }_A=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]$$

(66)

Therefore, ${\rho }_A^2$ can be computed as

$${\rho }_A^2=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]$$

(67)

Thus,

$$\mathrm{Tr}\left({\rho }_A^2\right)=1+0=1$$

(68)

The above computation indicates that the initial states are completely separable.

2.7. Quantum Computing Models

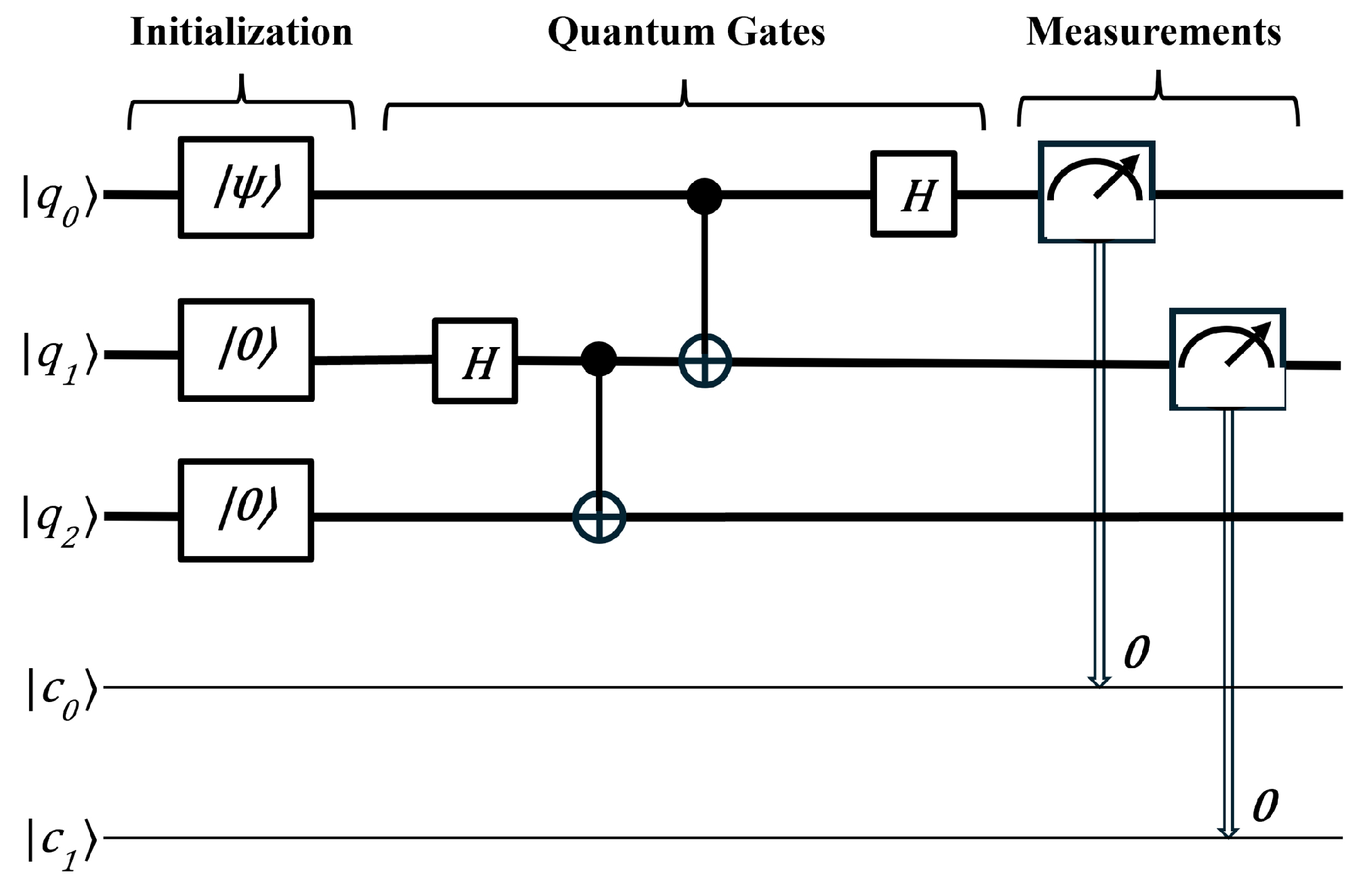
Quantum computing models provide abstract frameworks that define how quantum information is processed, specifying how qubits are manipulated and how computation proceeds in a quantum system. The quantum computing model described above is the quantum circuit model, also known as the gate-based model. This is the most widely used and familiar framework for quantum computing, analogous to classical digital circuits. Figure 5 depicts the main idea of this model. The quantum circuit model consists of three stages: initialization of quantum gates, implementation of quantum gates, and measurement. This model serves as the foundation for most current quantum computers, including those developed by companies like IBM and Google.

However, several other models have also been proposed, such as the adiabatic model (used by D-Wave Systems) [33], the topological model (explored by Microsoft) [34], and the quantum annealing model (also used by D-Wave Systems) [35].

2.8. Physical Representation of Quantum Computers

The physical representation of quantum computers encompasses a variety of methodologies, each with unique advantages and challenges. Ongoing research in these areas aims to optimize performance, enhance scalability and develop practical quantum computing systems. As the field progresses, these diverse approaches contribute to the broader goal of achieving functional and effective quantum computing technologies. The most important technologies that demonstrate quantum computers are

• Ion Trap Quantum Computing. This method involves trapping individual ions using electromagnetic fields. The ions serve as qubits and their quantum states are manipulated using laser beams [36].
• Superconducting Quantum Computing. This approach involves circuits made from superconducting materials that exhibit quantum behavior at low temperatures. The qubits are manipulated using microwave pulses, allowing for fast and efficient operations [37].
• Linear Optical Quantum Computing. This method uses photons as qubits and leverages the properties of linear optical elements (like beam splitters, phase shifters, and detectors) to process quantum information [38].
• Semiconductor Spin-Based Quantum Computing. This approach uses the spin states of electrons in semiconductor materials (like silicon) as qubits. Spin qubits can be created using quantum dots or by doping silicon with specific atoms [36].
• Nuclear Magnetic Resonance (NMR)-Based Quantum Computing. NMR quantum computing employs the nuclear spins of molecules as qubits. Magnetic fields and radiofrequency pulses are used to manipulate the spins [36]. It was the initial approach to building quantum computers, but it has since become less favored [37].
• Quantum Computing with Defects. This approach uses defects in solid-state materials (like nitrogen-vacancy centers in diamond or silicon vacancies in silicon carbide) as qubits [38].

Several companies are actively working on the physical implementation of quantum computers using various approaches. For instance, IBM and Google are focusing on superconducting qubits, while IonQ is advancing the trapped ion approach. Xanadu is exploring linear optical quantum computing [37]. These companies are making significant investments in quantum technology and frequently achieving new milestones, contributing to a clearer understanding of how these machines function. Their ongoing efforts are steadily advancing toward unlocking the true potential of quantum computers [22].

2.9. Quantum Noise

Quantum noise refers to the inherent uncertainty and random fluctuations found in quantum systems as a result of quantum physics’ fundamental principles. Unlike classical noise, which is caused by external sources such as heat disturbances or electromagnetic interference, quantum noise inevitably arises from the fundamental features of quantum particles. This is the result of the Heisenberg Uncertainty Principle, which asserts that some pairs of physical quantities, such as position and momentum, cannot be correctly measured at the same time.

In quantum information science, quantum noise can produce decoherence, which occurs when quantum systems lose their unique quantum features and behave more like classical systems. This issue poses a major barrier to the creation of reliable quantum computers. To limit the influence of quantum noise, researchers use approaches like quantum error correction, which detect and correct noise-induced errors [39].

3. Quantum Algorithms

As one group of researchers made progress on the physical implementation of quantum computers, others advanced in identifying algorithms that would run on a quantum computer with a speedup over classical computers.

Just as classical computers rely on classical algorithms for their functionality, quantum computers depend on quantum algorithms. These algorithms aim to demonstrate the advantages of quantum computing over classical computing. The investigation of quantum algorithms has constituted a dynamic area of research for over 20 years; however, the development of a fully operational quantum computer remains a work in progress [40].

As previously mentioned, the quantum circuit model is the most widely utilized framework in quantum computing. Quantum algorithms are typically represented by quantum gates that operate on a set of qubits and conclude with a measurement process.

After proposing the concept of a quantum Turing machine, Deutsch [41] developed an algorithm to demonstrate faster performance on a quantum computer. The Deutsch algorithm solves the problem of determining whether a function is constant or balanced using just one query, whereas a classical computer requires two queries. This algorithm showcases the strength of quantum parallelism. Deutsch, together with Richard Jozsa, later extended this idea into the more general Deutsch–Jozsa algorithm [42].

In 1993, Bernstein and his student Vazirani published a paper [43] introducing an algorithm that outperforms the best-known classical approach to a specific problem. Furthermore, they contributed by presenting a quantum version of the Fourier transform within the same paper.

Following the contributions of Bernstein and Vazirani, Daniel Simon made further advancements in 1994. Simon presented a problem [44] that could be solved exponentially faster by a quantum computer compared to a classical one.

One of the most important breakthroughs in quantum computing was Shor’s algorithm [3], developed in 1994. Shor built on earlier work by Deutsch, the Bernstein–Vazirani algorithm and Simon’s algorithm to create a way to quickly factor large numbers into two prime factors. While classical computers find this task extremely hard, Shor’s algorithm can complete it efficiently on a quantum computer, thanks in part to the quantum phase estimation algorithm, which is essential for estimating the eigenvalues of the unitary operators involved in the computation. Factoring large numbers is fundamental for the Rivest–Shamir–Adleman (RSA) encryption system, which secures most online communication today. This includes protecting credit card info, bank transfers and private messages [32].

Following Shor’s groundbreaking work, Lov Grover developed another significant quantum algorithm in 1996. His algorithm [5] focuses on searching through an unsorted database and provides a substantial quadratic speedup compared to classical algorithms.

The last fundamental quantum algorithm proposed by Harrow, Hassidim and Lloyd is called HHL algorithm [45]. This algorithm is designed to solve linear systems of equations and demonstrates the potential for exponential speedup under certain conditions compared to classical methods.

Table 5. Short description of quantum algorithms.

Algorithm	Description
Deutsch’s Algorithm	Determines whether a given function is constant or balanced using a single query to the oracle.
Deutsch–Josza Algorithm	Extends Deutsch’s algorithm to multiple inputs, identifying whether a function is constant or balanced with just one query, showcasing exponential speedup.
Bernstein–Vazirani Algorithm	Finds a hidden binary string by querying an oracle only once, providing a polynomial speedup over classical algorithms.
Simon’s Algorithm	Solves the hidden string problem for functions satisfying $f\left(x\right)=f(x\oplus s)$, demonstrating exponential speedup compared to classical methods.
Quantum Fourier Transform	Computes the discrete Fourier transform of a quantum state efficiently, essential for algorithms like Shor’s.
Phase Estimation Algorithm	Estimates the phase of an eigenvalue of a unitary operator, playing a crucial role in many quantum algorithms, including Shor’s.
Shor’s Algorithm	Efficiently factors large integers using the quantum Fourier transform, posing a threat to classical cryptographic systems.
Grover’s Algorithm	Provides a quadratic speedup for searching an unstructured database, allowing the identification of a marked item in $O\left(\sqrt{N}\right)$ time.
HHL Algorithm	Provides an exponential speedup for solving system of equations.

contains all the aforementioned algorithms with a brief description of their function. These nine quantum algorithms are fault-tolerant.

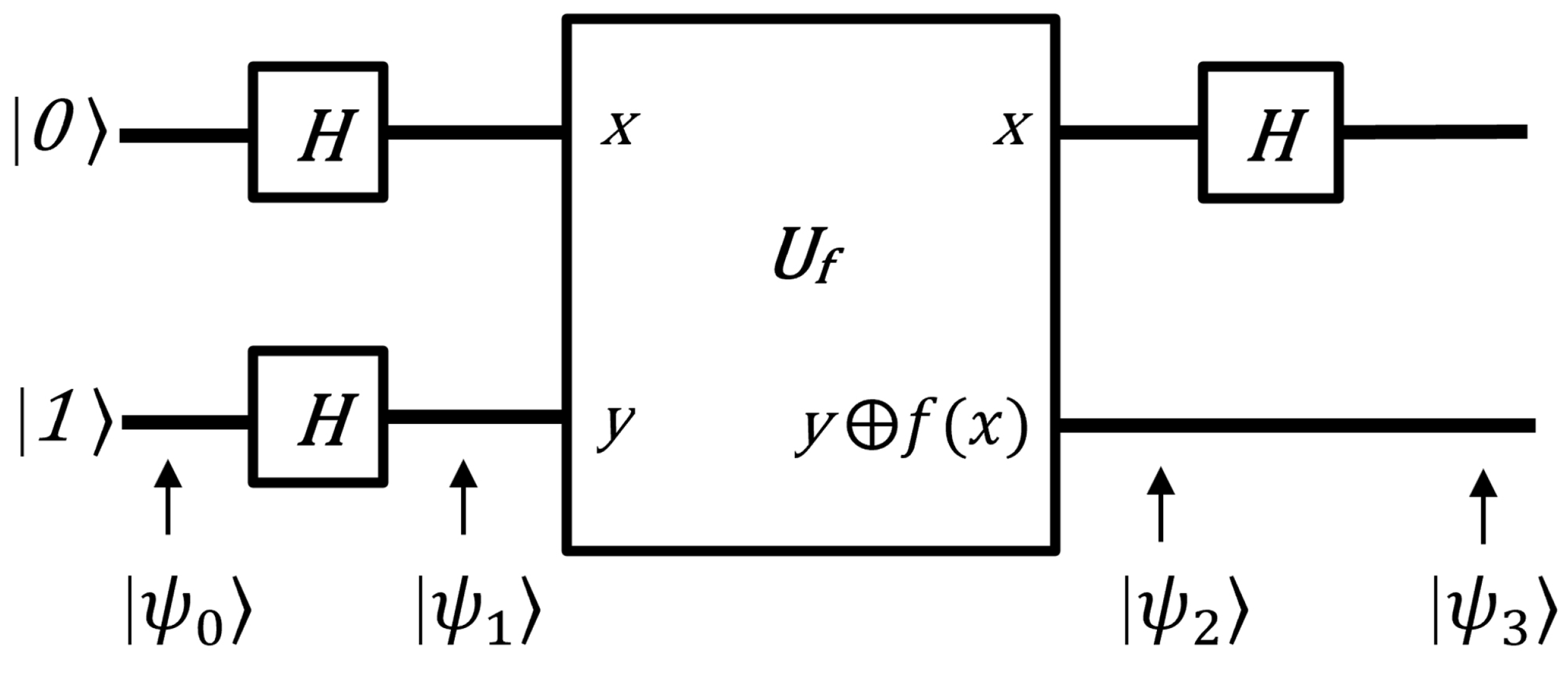
3.1. Deutsch’s Algorithm

Deutsch’s algorithm was one of the first quantum algorithms to demonstrate that quantum computers could solve certain problems more efficiently than classical ones. Deutsch’s problem involves a black-box function, $f:\{0,1\}\to \{0,1\}$, that takes a single bit as input and outputs a single bit. This algorithm is designed to determine whether function $f\left(x\right)$ is constant or balanced. A function $f\left(x\right)$ is classified as constant if the output is the same for both inputs (either always 0 or always 1) while it is classified as balanced if the output differs for each input (0 for one input, 1 for the other). This can be expressed mathematically as follows:

$$f\left(x\right)=\left\{\begin{array}{cc}\mathrm{constant},\hfill & \mathrm{if}f\left(0\right)=f\left(1\right)\hfill \\ \mathrm{balanced},\hfill & \mathrm{if}f\left(0\right)\ne f\left(1\right)\hfill \end{array}\right.$$

(69)

Before the mathematical representation of the algorithm, it is crucial to explain an important property known as the phase oracle property. Figure 6 represents the quantum circuit of the phase oracle property.

Let $U_f$ be a unitary operator that maps the state $|x\rangle |y\rangle$ to $|x\rangle |y\oplus f\left(x\right)\rangle$. This can be expressed mathematically as follows:

$$U_f|x\rangle |y\rangle =|x\rangle |y\oplus f\left(x\right)\rangle$$

(70)

where ⊕ denotes addition modulo 2 (XOR operation).

Set $y=|0\rangle$. Then, the unitary operator $U_f$ acts as follows:

$$U_f|x\rangle |0\rangle =|x\rangle |0\oplus f\left(x\right)\rangle =|x\oplus f\left(x\right)\rangle$$

(71)

since $0\oplus 0=0$ and $0\oplus 1=1$.

The final state does not depend on the y state.

Set $|y\rangle$= $|-\rangle$. Thus, the operation of $U_f$ becomes

$$U_f|x\rangle |-\rangle =U_f|x\rangle {\displaystyle \frac{1}{\sqrt{2}}}(|0\rangle -|1\rangle )={\displaystyle \frac{1}{\sqrt{2}}}(U_f|x\rangle |0\rangle -U_f|x\rangle |1\rangle )={\displaystyle \frac{1}{\sqrt{2}}}(|x\rangle |f\left(x\right)\rangle -|x\rangle |\overline{f\left(x\right)}\rangle )$$

(72)

$$=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\sqrt{2}}}(|x\rangle |0\rangle -|x\rangle |1\rangle )\hfill & \mathrm{if}f\left(x\right)=0\hfill \\ {\displaystyle \frac{1}{\sqrt{2}}}(|x\rangle |1\rangle -|x\rangle |0\rangle )\hfill & \mathrm{if}f\left(x\right)=1\hfill \end{array}\right.$$

(73)

$$=\left\{\begin{array}{cc}(|x\rangle |-\rangle )\hfill & \mathrm{if}f\left(x\right)=0\hfill \\ -(|x\rangle |-\rangle )\hfill & \mathrm{if}f\left(x\right)=1\hfill \end{array}\right.$$

(74)

$$={(-1)}^{f\left(x\right)}|x\rangle |-\rangle$$

(75)

Thus, let $U_f$ be a unitary operator that maps the state $|x\rangle |-\rangle$ to ${(-1)}^{f\left(x\right)}|x\rangle |-\rangle$. This property is mathematically expressed as

$$U_f\left(|x\rangle |-\rangle \right)={(-1)}^{f\left(x\right)}|x\rangle |-\rangle$$

(76)

The Deutsch–Jozsa algorithm can be implemented following a common five-step procedure. The quantum circuit for this algorithm is depicted in Figure 7.

First, initial input states are set up.

$$|{\psi }_0\rangle =|0\rangle |1\rangle$$

(77)

Next, a Hadamard gate is applied to each qubit, putting it into a superposition state using Equations (23) and (24).

$$|{\psi }_1\rangle =H|0\rangle \otimes H|1\rangle =[{\displaystyle \frac{|0\rangle +|1\rangle }{\sqrt{2}}}][{\displaystyle \frac{|0\rangle -|1\rangle }{\sqrt{2}}}]$$

(78)

In the third step, an oracle operation is applied. Thus, using Equation (76), $|{\psi }_2\rangle$ is expressed as follows:

$$|{\psi }_2\rangle =U_f|{\psi }_1{\rangle =(-1)}^{f\left(x\right)}{\displaystyle \frac{|0\rangle +|1\rangle }{\sqrt{2}}}|-\rangle =\left\{\begin{array}{cc}\pm {\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +|1\rangle \right)|-\rangle \hfill & \mathrm{if}f\left(0\right)=f\left(1\right),\hfill \\ \pm {\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle -|1\rangle \right)|-\rangle \hfill & \mathrm{if}f\left(0\right)\ne f\left(1\right)\hfill \end{array}\right.$$

(79)

In the fourth step, Hadamard gates are applied. Therefore,

$$|{\psi }_3\rangle =\left\{\begin{array}{cc}\pm H{\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +|1\rangle \right)|-\rangle \hfill & \mathrm{if}f\left(0\right)=f\left(1\right)\hfill \\ \pm H{\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle -|1\rangle \right)|-\rangle \hfill & \mathrm{if}f\left(0\right)\ne f\left(1\right)\hfill \end{array}\right.=\left\{\begin{array}{cc}\pm |0\rangle |-\rangle \hfill & \mathrm{if}f\left(0\right)=f\left(1\right)\hfill \\ \pm |1\rangle |-\rangle \hfill & \mathrm{if}f\left(0\right)\ne f\left(1\right)\hfill \end{array}\right.$$

(80)

Therefore, by measuring the first qubit, the function f can be determined to be either constant or balanced. If the measurement of the first qubit yields $|0\rangle$, then f is constant; if the measurement yields $|1\rangle$, then f is balanced.

A classical computer would require at least two evaluations, while a quantum computer requires only one. This algorithm is based on quantum parallelism and highlights the power of quantum computers. However, it does not have any practical applications.

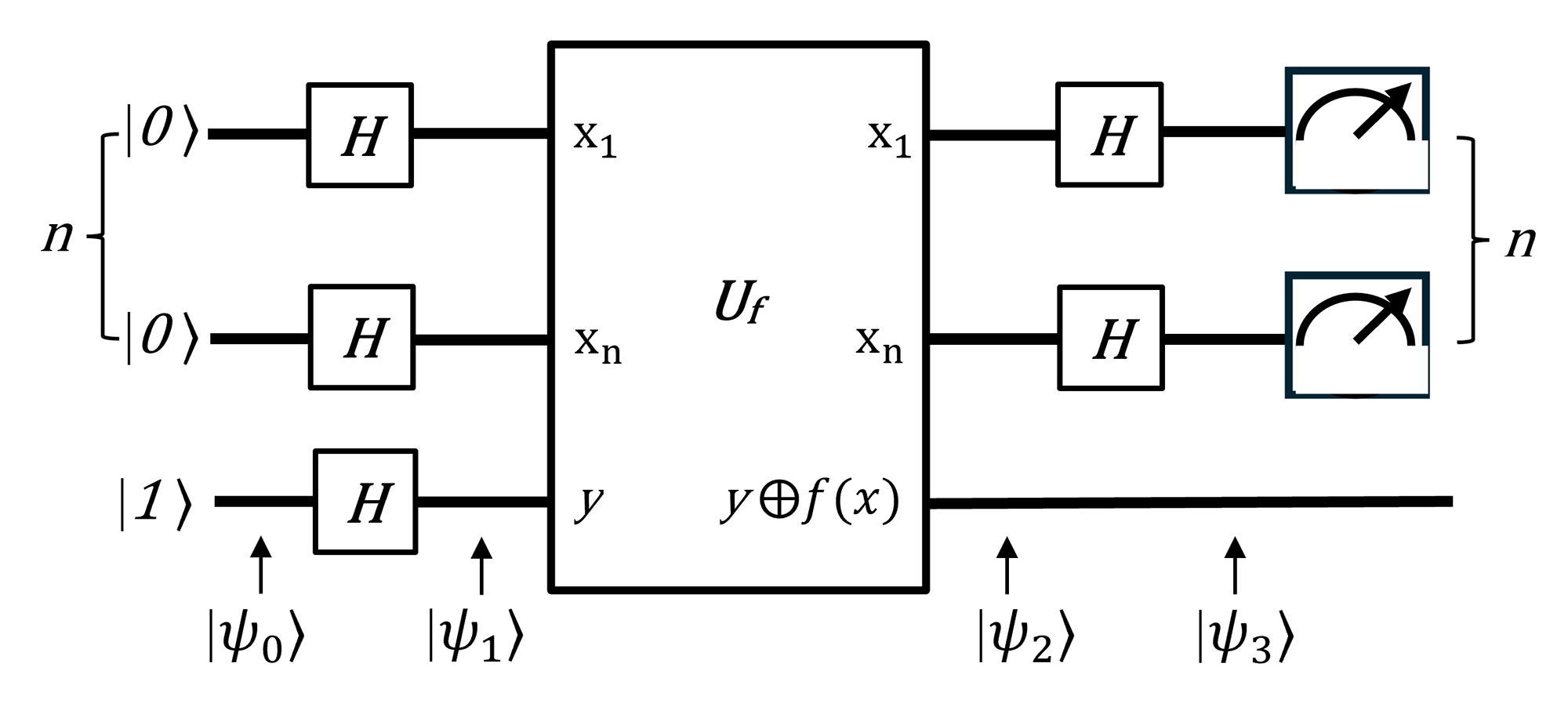
3.2. Deutsch–Josza Algorithm

The Deutsch–Jozsa algorithm is a generalization of the Deutsch algorithm and it is designed to determine whether a given Boolean function $f:{\{0,1\}}^n\to \{0,1\}$ is constant or balanced. The Deutsch–Jozsa algorithm can be implemented following a common five-step procedure. The quantum circuit for this algorithm is depicted in Figure 8.

First, initial input states are set up.

$$|{\psi }_0\rangle =|0^n\rangle |1\rangle$$

(81)

Next, a Hadamard gate is applied to each qubit, putting it into a superposition state.

$$|{\psi }_1\rangle =H^{\otimes n}|0^n\rangle \otimes H|1\rangle$$

(82)

$$H^{\otimes n}|0^n\rangle ={\left({\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +|1\rangle \right)\right)}^{\otimes n}={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{k=0}^{2^n-1}|k\rangle$$

(83)

With the help of Equation (83), $|{\psi }_1\rangle$ can be expressed as

$$|{\psi }_1\rangle ={\displaystyle \frac{1}{\sqrt{2^{n+1}}}}\sum _{x=0}^{2^n-1}|x\rangle \left(|0\rangle -|1\rangle \right)={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}|x\rangle |-\rangle )$$

(84)

In the third step, an oracle operation is applied. Thus, using Equation (76), $|{\psi }_2\rangle$ is expressed as follows:

$$|{\psi }_2\rangle =U_f|{\psi }_1\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}{U}_f|x\rangle |-\rangle )={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}{(-1)}^{f\left(x\right)}|x\rangle |-\rangle$$

(85)

In the fourth step, Hadamard gates are applied. Therefore,

$$|{\psi }_3\rangle =H^{\otimes n}|{\psi }_2\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}{(-1)}^{f\left(x\right)}{H}^{\otimes n}|x\rangle |-\rangle$$

(86)

For the measurement, the state $|-\rangle$ is not of interest.

$$H^{\otimes n}|x\rangle =H^{\otimes n}\left(|x_1\rangle |x_2\rangle \dots |x_n\rangle \right)=$$

$$={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +{(-1)}^{x_1}|1\rangle \right)\otimes {\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +{(-1)}^{x_2}|1\rangle \right)\otimes \dots \otimes {\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +{(-1)}^{x_n}|1\rangle \right)=$$

$$={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{y=0}^{2^n-1}{(-1)}^{x·y}|y\rangle$$

(87)

Therefore, $|{\psi }_3\rangle$ is expressed as follows:

$$|{\psi }_3\rangle ={\displaystyle \frac{1}{2^n}}\sum _{x=0}^{2^n-1}\sum _{y=0}^{2^n-1}{(-1)}^{f\left(x\right)}{(-1)}^{x·y}|y\rangle$$

(88)

Finally, a measurement of the qubits is performed to obtain the answer.

The probability of measuring the $|000...0\rangle$ state is

$${\displaystyle \frac{1}{2^n}}\sum _{x=0}^{2^n-1}{(-1)}^{f\left(x\right)}$$

(89)

If f is constant:

If f(x) = 0 for all x, then:

$${\displaystyle \frac{1}{2^n}}\sum _{x=0}^{2^n-1}1={\displaystyle \frac{1}{2^n}}{2}^n=1$$

(90)

If f(x) = 1 for all x, then:

$${\displaystyle \frac{1}{2^n}}\sum _{x=0}^{2^n-1}(-1)={\displaystyle \frac{1}{2^n}}(-2^n)=-1$$

(91)

Amplitude of $|000...0\rangle$ state is $\pm 1$.

If f is balanced:

$${\displaystyle \frac{1}{2^n}}\left({(-1)}^0+{(-1)}^1+\dots +{(-1)}^0\right)=0$$

(92)

Thus, if the state $|00\dots 0\rangle$ is measured, then the function f is confirmed to be constant. Conversely, if any other state is measured, it indicates that f is balanced.

Some positive aspects of the Deutsch–Jozsa algorithm include its ability to provide an exponential speedup over classical algorithms for the specific problem it addresses. While a classical algorithm might require up to $2^{n-1}+1$ queries to the function to determine if it is constant or balanced, the Deutsch–Jozsa algorithm requires only one quantum query. However, the Deutsch–Jozsa algorithm solves a very specific problem, leading to its limited practical application. The Deutsch–Jozsa algorithm served as a foundational milestone for the advancement of more important quantum algorithms.

3.3. Bernstein–Vazirani Algorithm

The Bernstein–Vazirani algorithm is designed to determine an n-bit “hidden string” s by querying a function $f\left(x\right)$, which is defined as

$$f\left(x\right)=s·x(mod2)$$

(93)

where x is any n-bit binary string, representing the input to the algorithm, and $s·x$ denotes the bitwise dot product of s and x, calculated as

$$s·x=\sum _{i=1}^n{s}_i{x}_i(mod2)$$

The Bernstein–Vazirani algorithm can be implemented following a common five-step procedure. The quantum circuit for this algorithm is depicted in Figure 9. The quantum topology of this circuit is the same as that of the Deutsch–Josza algorithm.

First, initial input states are set up.

$$|{\psi }_0\rangle =|0^n\rangle |1\rangle$$

(94)

Next, a Hadamard gate is applied to each qubit, putting the system into a superposition state as described by Equations (24) and (83).

$$|{\psi }_1\rangle =H^{\otimes n}|0^n\rangle \otimes H|1\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}|x\rangle |-\rangle )$$

(95)

In the third step, an oracle operation is applied. Thus, using Equation (76), $|{\psi }_2\rangle$ is expressed as follows:

$$|{\psi }_2\rangle =U_f|{\psi }_1\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}{U}_f|x\rangle |-\rangle )={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}{(-1)}^{f\left(x\right)}|x\rangle |-\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}{(-1)}^{s·x}|x\rangle |-\rangle$$

(96)

For the measurement, the state $|-\rangle$ is not of interest.

In the fourth step, Hadamard gates are applied. Therefore,

$$|{\psi }_3\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}{(-1)}^{s·x}{H}^{\otimes n}|x\rangle$$

(97)

With the aim of Equation (87), $|{\psi }_3\rangle$ can be expressed as

$$|{\psi }_3\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}{(-1)}^{s·x}{\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{y=0}^{2^n-1}{(-1)}^{x·y}|y\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}\sum _{y=0}^{2^n-1}{(-1)}^{(s+y)·x}|y\rangle$$

(98)

The term $(s+y)$ can be expressed as $(s\oplus y)$ because

• If $y\ne s$, the sum

  $$\sum _{x=0}^{2^n-1}{(-1)}^{x·(s\oplus y)}$$

  (99)

  evaluates to zero for all $y\ne s$. This is because $x·(s\oplus y)$ takes on an equal number of 0 and 1 values as x varies over the $2^n$ possible n-bit strings, resulting in equal numbers of $+1$ and $-1$ terms, which sum to 0.
• If y = s

  $$\sum _{x=0}^{2^n-1}{(-1)}^{(s+s)·x}=\sum _{x=0}^{2^n-1}{(-1)}^{2s·x}=\sum _{x=0}^{2^n-1}1=2^n$$

  (100)

Thus, $|{\psi }_3\rangle$ can be expressed as

$$|{\psi }_3\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}\sum _{y=0}^{2^n-1}{(-1)}^{x·(s\oplus y)}|y\rangle$$

(101)

Finally, $|y\rangle$ is measured to obtain the answer.

The amplitude of $|s\rangle$ is

$${\displaystyle \frac{1}{2^n}}\sum _{x=0}^{2^n-1}{(-1)}^{(s+s)·x}={\displaystyle \frac{1}{2^n}}\sum _{x=0}^{2^n-1}{(-1)}^{2s·x}={\displaystyle \frac{1}{2^n}}\sum _{x=0}^{2^n-1}1={\displaystyle \frac{1}{2^n}}·2^n=1$$

(102)

The probability of measuring the $|s\rangle$ state is 1.

The output of the Bernstein–Vazirani algorithm is the hidden bit string s, which is retrieved with just one query to the oracle, demonstrating the efficiency of QC over classical methods for this specific problem.

3.4. Simon’s Algorithm

Simon’s problem can be defined as follows:

A function $f:{\{0,1\}}^n\to {\{0,1\}}^m$ that maps bit strings to bit strings. The unknown function f maps either each unique input to a unique output or maps two distinct inputs to one unique output. In mathematical terms, this can be expressed as

$$f\left(x\right)=f\left(y\right)\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}x\oplus y=s$$

(103)

for some $x,y\in {\{0,1\}}^n$. The goal is to determine whether f is one-to-one or two-to-one by finding the hidden string s with as few evaluations of f as possible.

In order to solve this problem, a classical approach requires $2^{n/2}$ queries, while Simon’s algorithm promises to solve this using n queries.

Simon’s Algorithm Example:

Consider the function $f:{\{0,1\}}^3\to {\{0,1\}}^3$ defined by the truth

Table 6. Truth table of function $f\left(x\right)$.

x	$\mathit{f}\left(\mathit{x}\right)$
000	101
001	010
010	100
011	111
100	101
101	010
110	100
111	111

.

Each output $f\left(x\right)$ appears twice for two distinct inputs. For example,

$$f\left(000\right)=f\left(100\right)\Rightarrow s=001\oplus 010=011.$$

Simon’s algorithm can be implemented following a common five-step procedure. The quantum circuit for this algorithm is depicted in Figure 10.

First, initial input states are set up.

$$|{\psi }_0{\rangle =|0\rangle }^{\otimes n}{|0\rangle }^{\otimes n}$$

(104)

Next, a Hadamard gate is applied to each qubit, putting them into a superposition state.

$$|{\psi }_1\rangle =H^{\otimes n}{|0\rangle }^{\otimes n}{|0\rangle }^{\otimes n}$$

(105)

Using Equation (83),

$$|{\psi }_1\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}{|x\rangle |0\rangle }^{\otimes n}$$

(106)

In the third step, an oracle operation is applied. Thus, $|{\psi }_2\rangle$ is expressed as follows:

$$|{\psi }_2\rangle =U_f|{\psi }_1\rangle =U_f{\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}{|x\rangle |0\rangle }^{\otimes n}={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x=0}^{2^n-1}|x\rangle |f\left(x\right)\rangle$$

(107)

The output of f corresponds to an input of either x or y where x and y are two different inputs to f that gave the same output. Hence, the n bits are in the state

$${\displaystyle \frac{1}{\sqrt{2}}}(|x\rangle +|y\rangle )$$

In the fourth step, Hadamard gates are applied. Therefore,

$$|{\psi }_3\rangle =H^{\otimes n}|{\psi }_2\rangle =H^{\otimes n}{\displaystyle \frac{1}{\sqrt{2}}}(|x\rangle +|y\rangle )$$

(108)

Using Equation (87), $|{\psi }_3\rangle$ is expressed as follows:

$$|{\psi }_3\rangle ={\displaystyle \frac{1}{\sqrt{2^n+1}}}\sum _{z=0}^{2^n-1}[{(-1)}^{x·z}+{(-1)}^{y·z}]|z\rangle$$

(109)

Finally, a measurement of the qubits is performed to obtain the answer. The measurement returns a random bit string z such that

$$x·z=y·zmod2$$

(110)

Therefore,

$$\begin{array}{cc}\hfill x·z& =(x\oplus s)·zmod2\hfill \end{array}$$

(111)

$$\begin{array}{cc}\hfill x·z& =x·z\oplus s·zmod2\hfill \end{array}$$

(112)

$$\begin{array}{cc}\hfill 0& =s·zmod2\hfill \end{array}$$

(113)

Thus, the bit string z is orthogonal to the secret string s.

From the measurement results $\{z_1,\dots ,z_k\}$, a system of equations is formed such that

$$\begin{array}{cc}\hfill z_1·smod2& =0\hfill \\ \hfill z_2·smod2& =0\hfill \\ \hfill ⋮& \hfill \\ \hfill z_k·smod2& =0\hfill \end{array}$$

(114)

There are k equations and n unknowns. The secret string s can be solved by solving the system of equations derived above.

Simon’s algorithm demonstrates the power of quantum algorithms. while the best classical algorithms for the same problem may require exponential time, Simon’s algorithm can solve it in polynomial time.

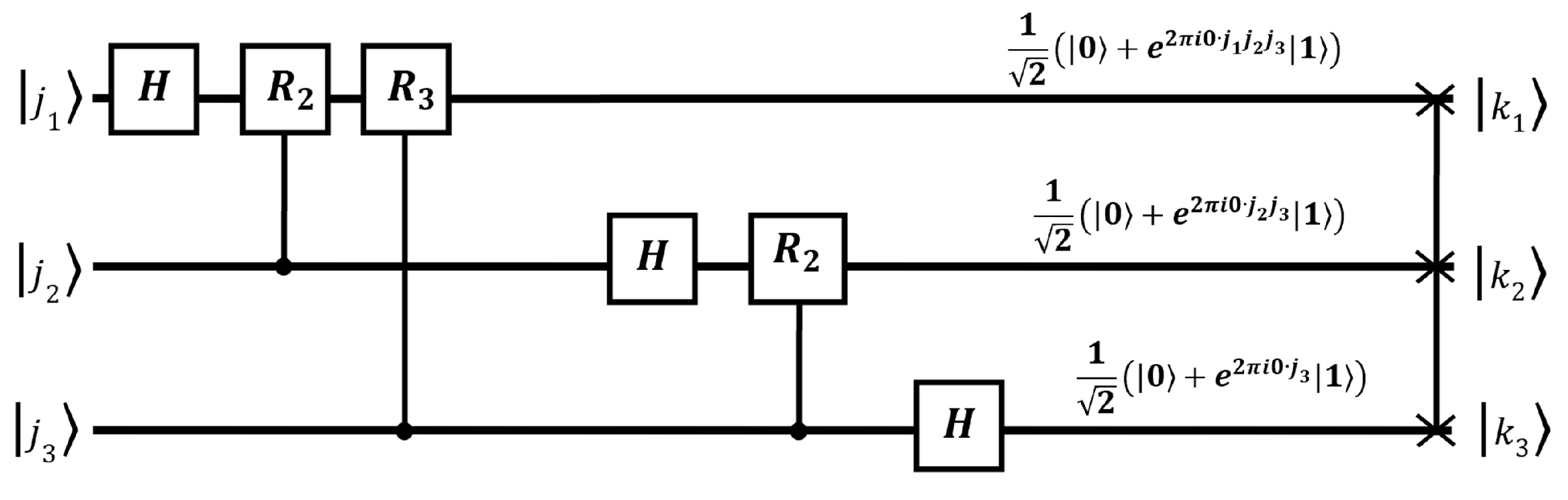
3.5. Quantum Fourier Transform

The quantum Fourier transform, or QFT for short, transforms a qubit from the computational basis $\{|0\rangle ,|1\rangle \}$ to the Fourier basis $\{|+\rangle ,|-\rangle \}$. Although the QFT does not speed up the classical task of computing Fourier transforms of classical data [39], it is an important component of the quantum phase estimation algorithm, which will be explained in detail later.

Consider the computational basis $\{|0\rangle ,|1\rangle ,\dots ,|N-1\rangle \}$ (in decimal notation) with $N=2^n$, where n is the number of qubits. The action of the QFT on a basis state $|j\rangle$ is given by

$$|j\rangle \stackrel{\mathrm{QFT}}{\to }{\displaystyle \frac{1}{\sqrt{N}}}\sum _{k=0}^{N-1}{e}^{2\pi ijk/N}|k\rangle$$

(115)

Any quantum state $|\psi \rangle$ can be written as a linear combination of the basis states. Therefore, QFT acts on a general quantum state $|\psi \rangle$ as follows:

$$|\psi \rangle =\sum _{j=0}^{N-1}{x}_j|j\rangle \stackrel{\mathrm{QFT}}{\to }{\displaystyle \frac{1}{\sqrt{N}}}\sum _{k=0}^{N-1}\left(\sum _{j=0}^{N-1}{x}_j{e}^{2\pi ijk/N}\right)|k\rangle$$

(116)

However,

$$y_k={\displaystyle \frac{1}{\sqrt{N}}}\sum _{j=0}^{N-1}{x}_j{e}^{{\displaystyle \frac{2\pi ijk}{N}}}={\displaystyle \frac{1}{\sqrt{N}}}\sum _{j=0}^{N-1}{x}_j{\omega }^{kj}$$

(117)

where $\omega =e^{2\pi i/N}$.

The matrix representation of QFT is as follows:

$$\mathrm{QFT}={\displaystyle \frac{1}{\sqrt{N}}}\left[\begin{array}{ccccc}1& 1& 1& \dots & 1\\ 1& \omega & {\omega }^2& \dots & {\omega }^{N-1}\\ 1& {\omega }^2& {\omega }^4& \dots & {\omega }^{2(N-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }^{N-1}& {\omega }^{2(N-1)}& \dots & {\omega }^{(N-1)(N-1)}\end{array}\right]$$

(118)

where $\omega =e^{2\pi i/N}$.

Another representation of the QFT is described by the following equation:

$$\begin{array}{cc}\hfill & |j\rangle \stackrel{\mathrm{QFT}}{\to }{\displaystyle \frac{1}{2^{n/2}}}\sum _{k=0}^{2^n-1}{e}^{2\pi ijk/2^n}|k\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{2^{n/2}}}\sum _{k_1=0}^1\dots \sum _{k_n=0}^1{e}^{2\pi ij\left({\sum }_{l=1}^n{k}_l{2}^{-l}\right)}|k_1\dots k_n\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{2^{n/2}}}\sum _{k_1=0}^1\dots \sum _{k_n=0}^1\underset{l=1}{\overset{n}{⨂}}{e}^{2\pi ij\left({\sum }_{l=1}^n{k}_l{2}^{-l}\right)}|k_l\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{2^{n/2}}}\underset{l=1}{\overset{n}{⨂}}\left(\sum _{k_l=0}^1{e}^{2\pi ij{k}_l{2}^{-l}}|k_l\rangle \right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2^{n/2}}}\underset{l=1}{\overset{n}{⨂}}\left(|0\rangle +e^{2\pi ij{2}^{-l}}|1\rangle \right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2^{n/2}}}\left(|0\rangle +e^{2\pi i0.j_n}|1\rangle \right)\left(|0\rangle +e^{2\pi i0.j_{n-1}{j}_n}|1\rangle \right)\dots \left(|0\rangle +e^{2\pi i0.j_1{j}_2\dots j_n}|1\rangle \right)\hfill \end{array}$$

(119)

The above equation can be summarized as

$${\displaystyle \frac{1}{\sqrt{2^n}}}\prod _{j=0}^{n-1}\left(|0\rangle +e^{2\pi i0.j_1{j}_2\dots j_n}|1\rangle \right)$$

(120)

The above representation has adopted the notation $0.j_l{j}_{l+1}\dots j_m$ to represent the binary fraction ${\displaystyle \frac{j_l}{2}}+{\displaystyle \frac{j_{l+1}}{4}}+\dots +{\displaystyle \frac{j_m}{2^{m-l+1}}}$. The quantum circuit for this algorithm is depicted in Figure 11. Each qubit went from $|j_n\rangle$ to $|0\rangle +e^{2\pi i0.j_n{j}_{n-1}\dots j_{n-k}}|1\rangle$.

The QFT consists of two types of quantum gates: the Hadamard gate and the controlled $R_k$ gate. If a Hadamard gate is applied to any $|j_n\rangle$, the result will be as follows, in accordance with Equations (23) and (24):

$$H|j_n\rangle =\left\{\begin{array}{cc}{\displaystyle \frac{1}{\sqrt{2}}}(|0\rangle +|1\rangle ),\hfill & \mathrm{if}{j}_n=0\hfill \\ {\displaystyle \frac{1}{\sqrt{2}}}(|0\rangle -|1\rangle ),\hfill & \mathrm{if}{j}_n=1\hfill \end{array}\right.$$

(121)

This can be generalized by the following expression:

$${\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i{j}_n/2}|1\rangle \right)$$

(122)

Because the term $e^{2\pi i{j}_n/2}$ is equal to $+1$ if $j_n=0$ and $-1$ if $j_n=1$.

The controlled $URO{T}_k$ gate is described mathematically using the following equation:

$$URO{T}_k=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& e^{2\pi i/2^k}\end{array}\right]$$

(123)

For example, applying the $URO{T}_k$ gate to the state $|00\rangle$, where the first qubit indicates the control qubit while the second qubit indicates the target,

$$URO{T}_k|00\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& e^{2\pi i/2^k}\end{array}\right]\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right)=|00\rangle$$

(124)

Similarly, applying the $URO{T}_k$ gate to the state $|01\rangle$,

$$URO{T}_k|01\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& e^{2\pi i/2^k}\end{array}\right]\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right)=|01\rangle$$

(125)

Similarly, applying the $URO{T}_k$ gate to the state $|10\rangle$,

$$URO{T}_k|10\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& e^{2\pi i/2^k}\end{array}\right]\left(\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right)=|10\rangle$$

(126)

Finally, applying the $URO{T}_k$ gate to the state $|11\rangle$,

$$URO{T}_k|11\rangle =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& e^{2\pi i/2^k}\end{array}\right]\left(\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right)=e^{2\pi i/2^k}\left(\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right)=e^{2\pi i/2^k}|11\rangle$$

(127)

This gate applies a phase of $e^{2\pi i/2^k}$ for the state $|1\rangle$ on the target qubit and acts only if the control qubit is in the state $|1\rangle$.

The action of $CRO{T}_k$ on a two-qubit state $|x_i{x}_j\rangle$ where the first qubit is the control and the second is the target is given by

$$\begin{array}{cc}\hfill CRO{T}_k|0x_j\rangle & =|0x_j\rangle \hfill \\ \hfill CRO{T}_k|1x_j\rangle & =exp\left({\displaystyle \frac{2\pi i}{2^k}}{x}_j\right)|1x_j\rangle \hfill \end{array}$$

(128)

In the quantum circuit design for the QFT, the following gates are required:

• For the first line, only 1 Hadamard gate is required.
• For the second line, there are 1 Hadamard gate and $(n-2)$ R gates.
• For the ${(n-1)}^{\mathrm{th}}$ line, we need 1 Hadamard gate and 1 R gate.
• Additionally, there are ${\displaystyle \frac{n}{2}}$ swap gates.

To summarize, the total number of quantum gates required can be calculated as follows:

$$n+{\displaystyle \frac{n(n-1)}{2}}+{\displaystyle \frac{n}{2}}$$

(129)

where n represents the number of qubits in the system.

In terms of complexity, QFT requires $n^2$ operations while the classical Fourier transform requires $n{2}^n$. Therefore, QFT demonstrates superior performance in terms of complexity.

Let us present a simple example of a 3-qubit system and calculate the QFT of number 5. Figure 12 represents this circuit.

The binary representation of the number 5 is 101. Since qubits in Qiskit are initialized in the $|0\rangle$ state, the first and third qubits should have an X gate applied to initialize them in the $|1\rangle$ state. Next, Hadamard gates are applied to every qubit. Sequentially, UROT gates are applied. Finally, swap gates are used to reverse the order of the qubits.

Generally, the number $|j\rangle$ can be represented in the binary system as $|j_1{j}_2{j}_3\rangle$.

Firstly, the Hadamard gate is applied to $|j_1\rangle$. The output is as follows:

$$H|j_1\rangle ={\displaystyle \frac{1}{\sqrt{2}}}(|0\rangle +e^{2\pi i{j}_1/2}|1\rangle )$$

(130)

Next, the $R_2$ gate is applied using Equation (128):

$$\begin{array}{c}\hfill R_{2}H|j_1\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i(j_1/2+j_2/2^2)}|1\rangle \right)\end{array}$$

(131)

Next, the $R_3$ gate is applied using Equation (128):

$$\begin{array}{c}\hfill R_3{R}_{2}H|j_1\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i(j_1/2+j_2/2^2+j_3/2^3)}|1\rangle \right)\end{array}$$

(132)

In the next step, a similar process is applied to $|j_2\rangle$.

$$H|j_2\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i{j}_2/2}|1\rangle \right)$$

(133)

Next, the $R_2$ gate is applied using Equation (128):

$$\begin{array}{c}\hfill R_{2}H|j_2\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i(j_2/2+j_3/2^2)}|1\rangle \right)\end{array}$$

(134)

Finally, a similar process is applied to $|j_3\rangle$.

$$H|j_3\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i{j}_3/2}|1\rangle \right)$$

(135)

The output is as follows:

$$\begin{array}{cc}\hfill QFT|j\rangle & ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i\left({\displaystyle \frac{j_1}{2}}+{\displaystyle \frac{j_2}{2^2}}+{\displaystyle \frac{j_3}{2^3}}\right)}|1\rangle \right)\otimes \hfill \\ \hfill & {\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i\left({\displaystyle \frac{j_2}{2}}+{\displaystyle \frac{j_3}{2^2}}\right)}|1\rangle \right)\otimes \hfill \\ \hfill & {\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i{\displaystyle \frac{j_3}{2}}}|1\rangle \right)\hfill \end{array}$$

(136)

Finally, a swap gate is applied:

$$\begin{array}{cc}\hfill QFT|j\rangle & ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i{\displaystyle \frac{j_3}{2}}}|1\rangle \right)\otimes \hfill \\ \hfill & {\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i\left({\displaystyle \frac{j_2}{2}}+{\displaystyle \frac{j_3}{2^2}}\right)}|1\rangle \right)\otimes \hfill \\ \hfill & {\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{2\pi i\left({\displaystyle \frac{j_1}{2}}+{\displaystyle \frac{j_2}{2^2}}+{\displaystyle \frac{j_3}{2^3}}\right)}|1\rangle \right)\hfill \end{array}$$

(137)

Therefore, the number 5 can be represented by QFT by the following:

$$\begin{array}{cc}\hfill QFT|101\rangle & ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{\pi i}|1\rangle \right)\otimes \hfill \\ \hfill & {\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{{\displaystyle \frac{\pi i}{2}}}|1\rangle \right)\otimes \hfill \\ \hfill & {\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +e^{{\displaystyle \frac{5\pi i}{4}}}|1\rangle \right)\hfill \end{array}$$

(138)

In addition to the QFT, there is also the inverse IQFT. Mathematically, this is described as follows. If $|\psi \rangle$ is the result of the application of the QFT algorithm to $|j\rangle$,

$$|\psi \rangle =\mathrm{QFT}|j\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\left(|0\rangle +e^{2\pi i0.j_{n-1}}|1\rangle \right)\otimes \left(|0\rangle +e^{2\pi i0.j_{n-2}}|1\rangle \right)\otimes \dots \otimes \left(|0\rangle +e^{2\pi i0.j_0}|1\rangle \right)$$

(139)

The result of the inverse QFT is as follows:

$$\mathrm{IQFT}|\psi \rangle =|j\rangle$$

(140)

Although the QFT requires fewer operations in comparison with the classical Fourier transform, practical implementations of QFT are limited. The QFT’s exponential speedup in certain quantum algorithms, such as quantum phase estimation and Shor’s algorithm, demonstrates its significance in quantum computing.

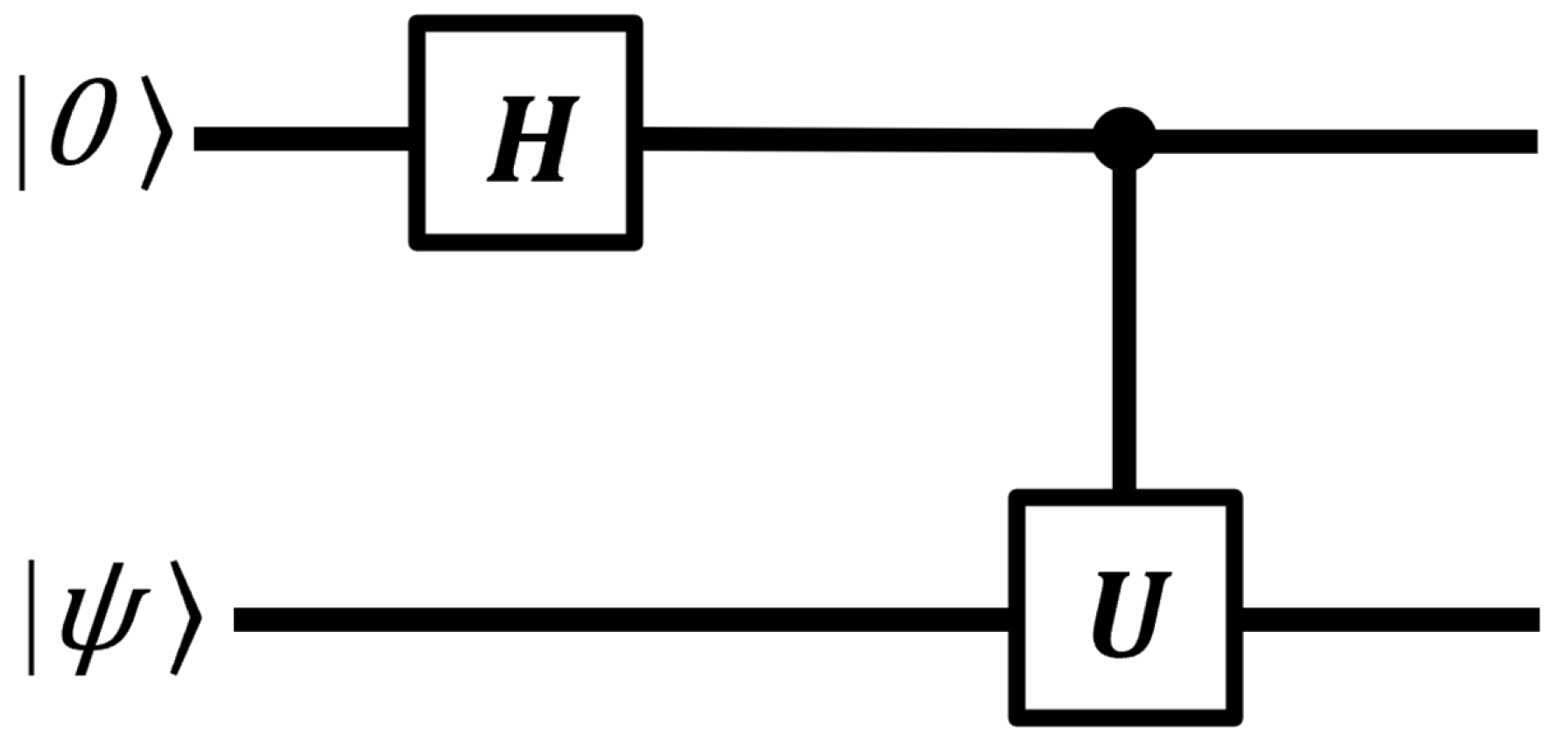
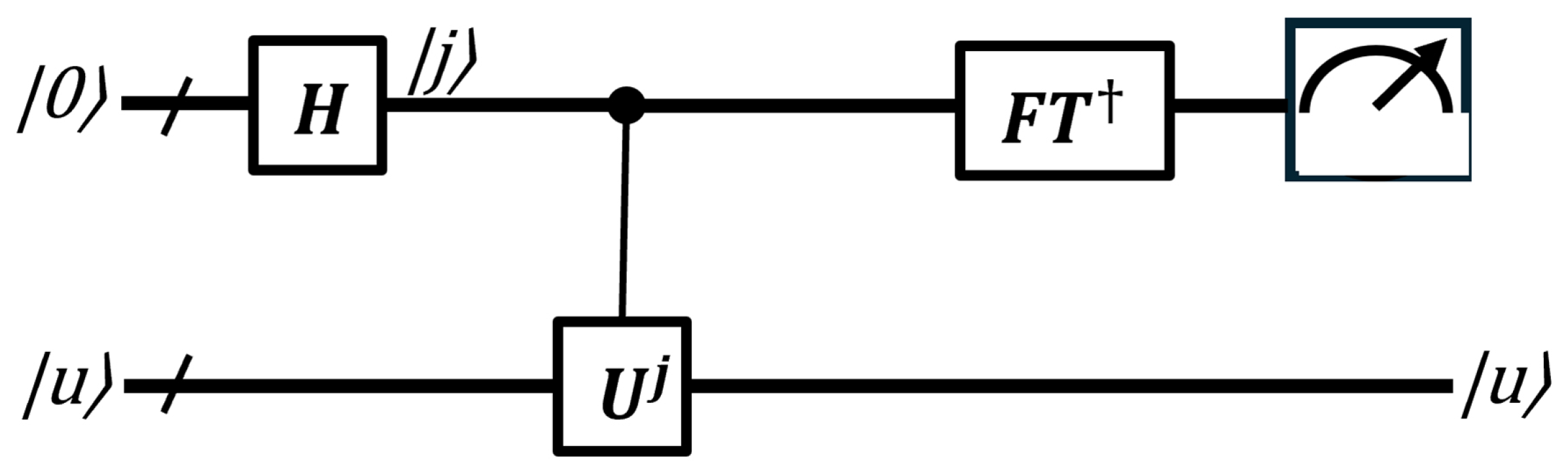
3.6. Quantum Phase Estimation

Quantum phase estimation is a key subroutine for important quantum algorithms, including Shor’s algorithm. Suppose a unitary operator U has an eigenvector $|u\rangle$ with eigenvalue $e^{2\pi i\phi }$, where the value of $\phi$ is unknown [39]. The goal of the phase estimation algorithm is to estimate $\phi$. This can be expressed mathematically using the following equation:

$$U|u\rangle =e^{2\pi i\phi }|u\rangle$$

(141)

Before explaining QPE in detail, it is essential to understand the concept of phase kickback. Phase kickback occurs when a controlled phase gate is applied to a control qubit in superposition. Figure 13 illustrates the quantum circuit that demonstrates this property.

In this setup, the target qubit in the controlled operation—in our case, $|\psi \rangle$—must be an eigenvector of the unitary operator U. This condition is expressed mathematically as follows:

$$U|\psi \rangle =e^{2\pi i\phi }|\psi \rangle$$

(142)

With this requirement in place, the controlled operation modifies the phase of the control qubit, effectively encoding the phase information $\phi$ from the target eigenstate onto the control qubit.

The matrix representation of U for a two-qubit system is expressed by the following equation:

$$CU=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& e^{i\varphi }\end{array}\right)$$

(143)

The above matrix applies a phase $e^{i\phi }$ to the target qubit only when the control qubit is $|1\rangle$.

First, initial input states are set up.

$$|0\rangle |\psi \rangle$$

(144)

Next, a Hadamard gate is applied to control qubit, putting it into a superposition state using the Equation (23).

$$H|0\rangle |\psi \rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +|1\rangle \right)|\psi \rangle$$

(145)

Finally, a controlled-U gate is applied.

$$CU{\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +|1\rangle \right)|\psi \rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle |\psi \rangle +|1\rangle e^{i\theta }|\psi \rangle \right)={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +|1\rangle e^{i\theta }\right)|\psi \rangle$$

(146)

Therefore, the phase of the target qubit is transferred, or “kicked back,” to the control qubit.

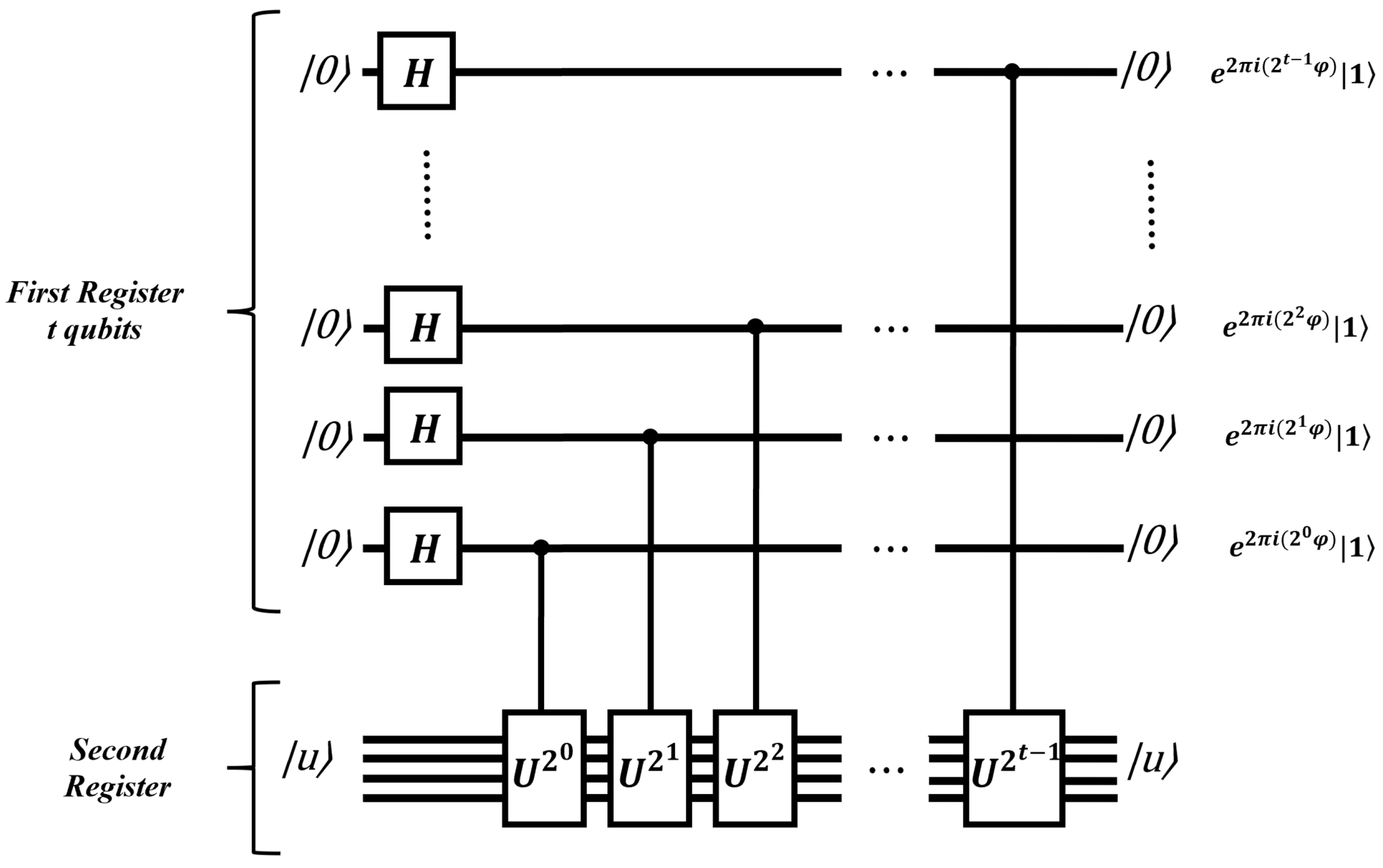
Phase estimation is performed in two stages. The first stage includes initialization, Hadamard gates and controlled-U gates, while the second stage includes the inverse QFT and measurement. Figure 14 depicts the first stage of the algorithm and Figure 15 shows the full quantum circuit for phase estimation.

Suppose a unitary operator U has an eigenvector $|\psi \rangle$ with an eigenvalue of the form $e^{2\pi i\varphi }$:

$$U|\psi \rangle =e^{2\pi i\varphi }|\psi \rangle$$

(147)

The quantum phase estimation procedure utilizes two registers. The first register holds t qubits, all initialized to the state $|0\rangle$. The choice of t is determined by the desired level of precision for estimating $\phi$. The second register contains enough qubits to store the state $|u\rangle$.

This is expressed by the following:

$${|0\rangle }^{\otimes n}\otimes |\psi \rangle$$

(148)

Next, Hadamard gates are applied to the first register with the aim of Equation (83).

$$H^{\otimes n}|0^n\rangle \otimes |\psi \rangle ={\left({\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle +|1\rangle \right)\right)}^{\otimes n}|\psi \rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{k=0}^{2^n-1}|k\rangle |\psi \rangle$$

(149)

Next, controlled-U operations are applied on the second register, with U raised to successive powers of two.

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{k=0}^{2^n-1}|k\rangle \otimes U^k|\psi \rangle & ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{k=0}^{2^n-1}{e}^{2\pi ik\varphi }|k\rangle \otimes |\psi \rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{2^n}}}\left(|0\rangle +e^{i2\pi \varphi ·2^{n-1}}|1\rangle \right)\hfill \\ \hfill & \otimes \left(|0\rangle +e^{i2\pi \varphi ·2^{n-2}}|1\rangle \right)\hfill \\ \hfill & \otimes \dots \hfill \\ \hfill & \otimes \left(|0\rangle +e^{i2\pi \varphi ·2^0}|1\rangle \right)\otimes |\psi \rangle .\hfill \end{array}$$

(150)

The above equation resembles Equation (119), but with $\varphi \to {\displaystyle \frac{j}{2^n}}$.

The second stage contains the IQFT and the measurement. With the aim of Equation (140), what we obtain is

$$\mathrm{IQFT}\left({\displaystyle \frac{1}{\sqrt{2^n}}}\left(|0\rangle +e^{i2\pi \varphi 2^{n-1}}|1\rangle \right)\otimes \left(|0\rangle +e^{i2\pi \varphi 2^{n-2}}|1\rangle \right)\otimes \dots \otimes \left(|0\rangle +e^{i2\pi \varphi 2^0}|1\rangle \right)\right)=|m\rangle$$

(151)

where $|m\rangle$ represents the measurement result with $m=2^n\varphi .$

QPE is a key quantum algorithm that can be used as a subroutine in various applications, including machine learning algorithms. The central component of the algorithm, as described earlier, is the application of the IQFT.

3.7. Shor’s Algorithm

As mentioned earlier, QPE is an essential component of Shor’s algorithm. Before analyzing Shor’s algorithm or the factoring problem, it is necessary to understand the order-finding problem. Before diving into the order-finding problem, some basic knowledge of number theory is required.

Suppose a function is defined by the following equation:

$$f\left(a\right)=a^{x}modN$$

(152)

The goal is to estimate the period r, which is the smallest positive integer such that $a^r\equiv 1modN$.

Consider the example with $a=2$ and $N=9$:

$$\begin{array}{cc}\hfill 2^1& \equiv 2mod9\hfill \\ \hfill 2^2& \equiv 4mod9\hfill \\ \hfill 2^3& \equiv 8mod9\hfill \\ \hfill 2^4& \equiv 7mod9\hfill \\ \hfill 2^5& \equiv 5mod9\hfill \\ \hfill 2^6& \equiv 1mod9\hfill \\ \hfill 2^7& \equiv 2mod9\hfill \\ \hfill 2^8& \equiv 4mod9\hfill \\ \hfill 2^9& \equiv 8mod9\hfill \\ \hfill 2^{10}& \equiv 7mod9\hfill \\ \hfill 2^{11}& \equiv 5mod9\hfill \\ \hfill 2^{12}& \equiv 1mod9\hfill \end{array}$$

We observe the following repeated pattern: $2,4,8,7,5,1$. Therefore, the period r is 6, as the sequence repeats every 6 steps.

Suppose that

$$U|u_s\rangle =|xymodN\rangle$$

(153)

and

$$|u_s\rangle ={\displaystyle \frac{1}{\sqrt{r}}}\sum _{k=0}^{r-1}{e}^{-2\pi ikt/r}|x^{k}modU\rangle$$

(154)

Applying U to $u_s$,

$$\begin{array}{cc}\hfill U|u_s\rangle & =U{\displaystyle \frac{1}{\sqrt{r}}}\sum _{k=0}^{r-1}{e}^{-2\pi ikt/r}|x^{k}modN\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{r}}}\sum _{k=0}^{r-1}{e}^{-2\pi ikt/r}|x^{k+1}modN\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{r}}}\sum _{k=0}^{r-1}{e}^{-2\pi i(k-1)t/r}|x^{k}modN\rangle \hfill \\ \hfill & =e^{2\pi it/r}|u_s\rangle \hfill \end{array}$$

(155)

From the above equation, $u_s$ is the eigenvector of U.

The reduction of order-finding to phase estimation is completed by explaining how to extract the desired answer r from the output of the phase estimation algorithm, which yields ${\displaystyle \frac{t}{r}}$. Here, ${\displaystyle \frac{t}{r}}$ is a rational number and by computing the nearest fraction to ${\displaystyle \frac{t}{r}}$, it may be possible to obtain r. The continued fractions algorithm efficiently accomplishes this task.

The continued fraction algorithm is a mathematical method for finding the best rational approximation to a real number. This can be expressed mathematically by the following equation:

$$[a_0,\dots ,a_M]\equiv a_0+{\displaystyle \frac{1}{a_1+\frac{1}{a_2+\frac{1}{\dots +\frac{1}{a_M}}}}}$$

(156)

The last denominator less than N is the candidate for r. The optimal r can be calculated by the following:

$$r_n=a_n{r}_{n-1}+r_{n-2}$$

(157)

Example:

$${\displaystyle \frac{427}{512}}={\displaystyle \frac{1}{\frac{512}{427}}}={\displaystyle \frac{1}{1+\frac{85}{427}}}={\displaystyle \frac{1}{1+\frac{1}{\frac{427}{85}}}}={\displaystyle \frac{1}{1+\frac{1}{5+\frac{2}{85}}}}={\displaystyle \frac{1}{1+\frac{1}{5+\frac{1}{\frac{85}{2}}}}}={\displaystyle \frac{1}{1+\frac{1}{5+\frac{1}{42+\frac{1}{2}}}}}$$

(158)

Using the continued fraction expansion,

$$\begin{array}{cc}\hfill r_0& =1\hfill \end{array}$$

(159)

$$\begin{array}{cc}\hfill r_1& =a_1=1\hfill \end{array}$$

(160)

$$\begin{array}{cc}\hfill r_2& =a_2{r}_1+r_0=5·1+1=6\hfill \end{array}$$

(161)

Therefore, r equals 6.

The order-finding algorithm can be implemented following a common 6-step procedure. The quantum circuit for this algorithm is depicted in Figure 16.

First, initial input states are set up.

$$|{\psi }_0\rangle =|0^t\rangle |1^L\rangle$$

(162)

Next, a Hadamard gate is applied to each qubit, putting it into a superposition state.

$$|{\psi }_1\rangle =H^{\otimes t}|0^t\rangle |1^L\rangle ={\displaystyle \frac{1}{\sqrt{2^t}}}\sum _{j=0}^{2^t-1}|j\rangle |1^L\rangle$$

(163)

In the third step, $U_{xN}$ is applied. Thus,

$$|{\psi }_2\rangle =U_{x,N}{\displaystyle \frac{1}{\sqrt{2^t}}}\sum _{j=0}^{2^t-1}|j\rangle |1^L\rangle =\sqrt{{\displaystyle \frac{1}{2^t}}}\sum _{j=0}^{2^t-1}|j\rangle |x^{j}modN\rangle =\sqrt{{\displaystyle \frac{1}{r{2}^t}}}\sum _{s=0}^{r-1}\sum _{j=0}^{2^t-1}{e}^{{\displaystyle \frac{2\pi isj}{r}}}|j\rangle |u_s\rangle$$

(164)

In the fourth step, IQFT is applied to first register. Therefore,

$$|{\psi }_3\rangle =\sqrt{{\displaystyle \frac{1}{r}}}\sum _{s=0}^{r-1}\left|{\displaystyle \frac{s}{r}}\right||u_s\rangle$$

(165)

Therefore, by measuring the first register, the term ${\displaystyle \frac{s}{r}}$ can be extracted.

The last step involves the application of continued fractions algorithm to obtain r.

The order-finding problem turns out to be equivalent to the factoring problem or, in other words, to Shor’s algorithm. The goal of Shor’s algorithm is to find the prime factors of a large number $N=p·q$. The steps to achieve this are as follows:

• Choose a random number $1<a<N-1$.
• Compute $gcd(a,N)$.
• If $gcd(a,N)\ne 1$, go back to step 1.
• Use the order-finding subroutine to find r such that $a^r\equiv 1modN$.
• If r is odd, go back to step 1.
• If $a^{r/2}\equiv -1modN$, go back to step 1.
• The factors of N are $p=gcd(a^{r/2}-1,N)$ and $q=gcd(a^{r/2}+1,N)$.

An example of factoring the number 15 by implementing Shor’s algorithm is presented below.

• Choose $a=7$.
• Compute $gcd(15,7)=1$.
• Calculate r:

  $$7^{1}mod15=7$$

  $$7^{2}mod15=4$$

  $$7^{3}mod15=13$$

  $$7^{4}mod15=1$$
  Thus, $r=4$.
• Check if ${\displaystyle \frac{r}{2}}=2$ is valid:

  $$7^2\equiv -1mod15$$
• Find factors:

  $$p=gcd(7^2-1,15)=gcd(48,15)=3$$

  $$q=gcd(7^2+1,15)=gcd(50,15)=5$$

Therefore, the prime factors of number 15 are 3 and 5.

Shor’s algorithm does not consist entirely of quantum components. The quantum part is limited to the order-finding subroutine. However, Shor’s algorithm runs in polynomial time in $logN$, whereas the best classical factoring methods run in sub-exponential time in $logN$. As a result, Shor’s algorithm achieves a super-polynomial (often referred to as exponential) speedup, offering an efficient solution to a problem that remains challenging for classical computers. This algorithm has significant implications for cryptographic applications.

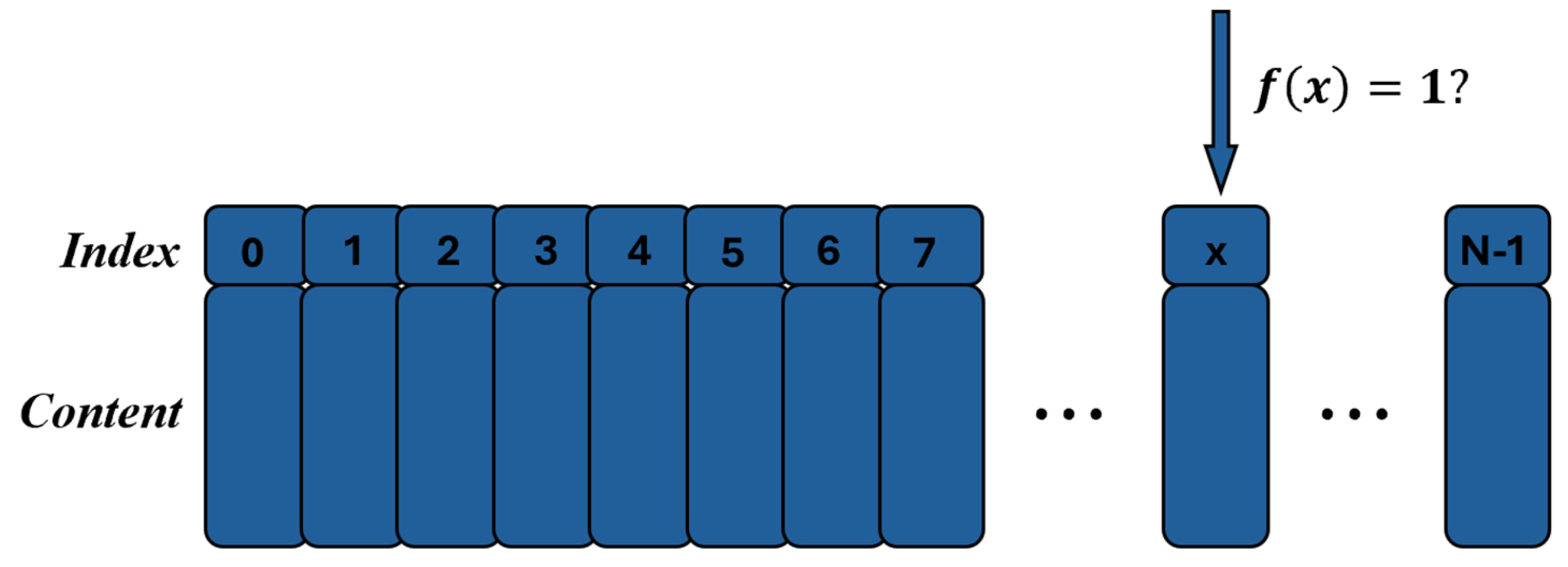
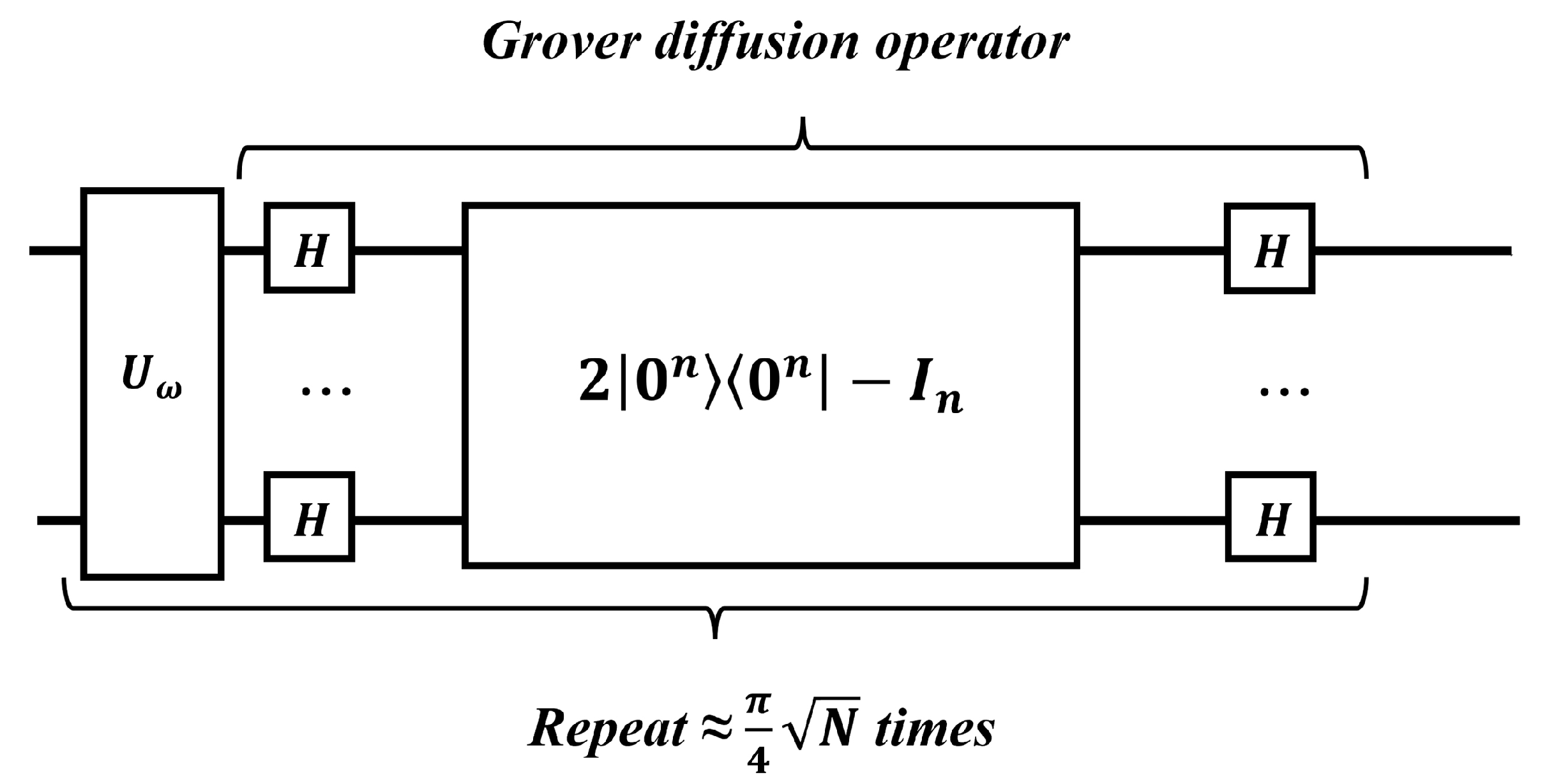
3.8. Grover’s Algorithm

Grover’s algorithm is a quantum search algorithm designed to find a target item in an unstructured database with N entries. Instead of directly searching the database elements, we focus on the index of those elements, denoted by x. The search is guided by a function $f\left(x\right)$, which computes whether a given index x matches the desired criteria.

The goal of Grover’s algorithm is to find an index x such that $f\left(x\right)=1$, indicating that the corresponding database entry is the target item. Figure 17 briefly describes the search process.

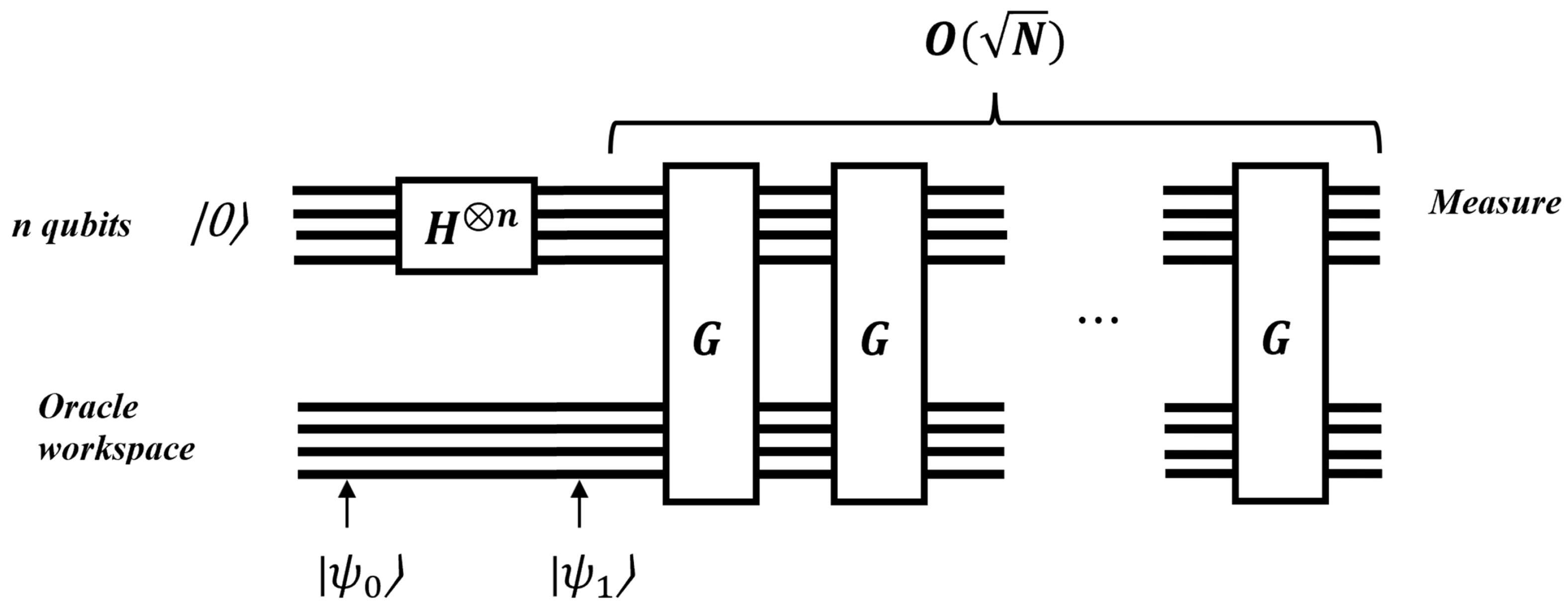
In a classical approach, the search complexity is $O\left(N\right)$. However, Grover’s algorithm provides a quadratic speedup, reducing the complexity to $O\left(\sqrt{N}\right)$. This quantum speedup makes Grover’s algorithm significantly faster than classical search methods for large databases.

The quantum circuit for Grover’s algorithm is depicted in Figure 18.

First, initial input states are set up.

$$|{\psi }_0\rangle =|0^n\rangle$$

(166)

Next, a Hadamard gate is applied to each qubit, putting the system into a superposition state as described by Equation (83).

$$|{\psi }_1\rangle =H^{\otimes n}|0^n\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{k=0}^{2^n-1}|k\rangle$$

(167)

Next, a quantum subroutine, known as the Grover iteration, is applied repeatedly. The quantum circuit for Grover’s iteration is shown in Figure 19. The optimal number of iterations, denoted by t, will be defined later.

Grover’s iteration can be described by the following mathematical equation:

$$G=H^{\otimes n}{Z}_0{H}^{\otimes n}{Z}_f$$

(168)

It consists of an oracle to mark the correct state and a diffusion operation to amplify the amplitude of the marked state.

The oracle can be denoted as $Z_f$ and can be expressed mathematically by the following equation:

$$Z_f:|x\rangle \mapsto {(-1)}^{f\left(x\right)}|x\rangle$$

(169)

The oracle acts similarly to the oracle in the Deutsch–Jozsa algorithm. If x is not a solution to the search problem, applying the oracle does not change the state. On the other hand, if x is a solution to the search problem (meaning $f\left(x\right)=1$), it shifts the phase of the solution.

The diffusion operator can be denoted as $Z_{OR}$ and can be expressed mathematically by the following equation:

$$Z_{O}R:H^{\otimes n}\left({2|0\rangle }^{\otimes n}{\langle 0|}^{\otimes n}-I\right)H^{\otimes n}$$

(170)

The above equation can also be written as

$$\begin{array}{cc}\hfill H^{\otimes n}\left({2|0\rangle }^{\otimes n}{\langle 0|}^{\otimes n}-I\right)H^{\otimes n}& =2\left(H^{\otimes n}{|0\rangle }^{\otimes n}{\langle 0|}^{\otimes n}{H}^{\otimes n}\right)-H^{\otimes n}I{H}^{\otimes n}\hfill \\ \hfill & =2\left(H^{\otimes n}{|0\rangle }^{\otimes n}{\langle 0|}^{\otimes n}{H}^{\otimes n}\right)-I{H}^{\otimes n}{H}^{\otimes n}\hfill \\ \hfill & =2\left(H^{\otimes n}{|0\rangle }^{\otimes n}{\langle 0|}^{\otimes n}{H}^{\otimes n}\right)-I\hfill \\ \hfill & =2\left(H^{\otimes n}{|0\rangle }^{\otimes n}{\langle 0|}^{\otimes n}{\left(H^{\otimes n}\right)}^{†}\right)-I\hfill \\ \hfill & =2|u\rangle \langle u|-I\hfill \end{array}$$

(171)

Suppose that there are the sets of non-solutions and solutions such that

$$A_0=\{x\in {\Sigma }^n:f\left(x\right)=0\}$$

$$A_1=\{x\in {\Sigma }^n:f\left(x\right)=1\}$$

Therefore,

$$Z_f|A_0\rangle =|A_0\rangle$$

$$Z_f|A_1\rangle =-|A_1\rangle$$

The state $|u\rangle$ can be described by the following equation:

$$|u\rangle =\sqrt{{\displaystyle \frac{|A_0|}{N}}}|A_0\rangle +\sqrt{{\displaystyle \frac{|A_1|}{N}}}|A_1\rangle$$

(172)

After applying G to $|A_0\rangle$,

$$\begin{array}{cc}\hfill G|A_0\rangle & =(2|u\rangle \langle u|-1)Z_f|A_0\rangle \hfill \\ \hfill & =(2|u\rangle \langle u|-1)|A_0\rangle \hfill \\ \hfill & =2\sqrt{{\displaystyle \frac{|A_0|}{N}}}|u\rangle -|A_0\rangle \hfill \\ \hfill & =2\sqrt{{\displaystyle \frac{|A_0|}{N}}}\left(\sqrt{{\displaystyle \frac{|A_0|}{N}}}|A_0\rangle +\sqrt{{\displaystyle \frac{|A_1|}{N}}}|A_1\rangle \right)-|A_0\rangle \hfill \\ \hfill & ={\displaystyle \frac{|A_0|-|A_1|}{N}}|A_0\rangle +2\sqrt{{\displaystyle \frac{|A_0|·|A_1|}{N}}}|A_1\rangle \hfill \end{array}$$

(173)

After applying G to $|A_1\rangle$,

$$\begin{array}{cc}\hfill G|A_1\rangle & =(2|u\rangle \langle u|-1)Z_f|A_1\rangle \hfill \\ \hfill & =(1-2|u\rangle \langle u|)|A_1\rangle \hfill \\ \hfill & =|A_1\rangle -2\sqrt{{\displaystyle \frac{|A_1|}{N}}}|u\rangle \hfill \\ \hfill & =|A_1\rangle -2\sqrt{{\displaystyle \frac{|A_0|}{N}}}\left(\sqrt{{\displaystyle \frac{|A_0|}{N}}}|A_0\rangle +\sqrt{{\displaystyle \frac{|A_1|}{N}}}|A_1\rangle \right)\hfill \\ \hfill & =-2\sqrt{{\displaystyle \frac{|A_0|·|A_1|}{N}}}|A_0\rangle +{\displaystyle \frac{|A_0|-|A_1|}{N}}|A_1\rangle \hfill \end{array}$$

(174)

Therefore, the action of G on $\mathrm{span}\{|A_0\rangle ,|A_1\rangle \}$ can be described by a $2\times 2$ matrix:

$$M=\left(\begin{array}{cc}{\displaystyle \frac{|A_0|-|A_1|}{N}}& -2\sqrt{{\displaystyle \frac{|A_0|·|A_1|}{N}}}\\ \sqrt{{\displaystyle \frac{|A_0|·|A_1|}{N}}}& {\displaystyle \frac{|A_0|-|A_1|}{N}}\end{array}\right)={\left(\begin{array}{cc}\sqrt{{\displaystyle \frac{|A_0|}{N}}}& -\sqrt{{\displaystyle \frac{|A_1|}{N}}}\\ \sqrt{{\displaystyle \frac{|A_1|}{N}}}& \sqrt{{\displaystyle \frac{|A_0|}{N}}}\end{array}\right)}^2$$

(175)

The above matrix is a rotation matrix. Therefore,

$$\left(\begin{array}{cc}{\displaystyle \frac{\sqrt{|A_0|}}{N}}& -{\displaystyle \frac{\sqrt{|A_1|}}{N}}\\ {\displaystyle \frac{\sqrt{|A_1|}}{N}}& {\displaystyle \frac{\sqrt{|A_0|}}{N}}\end{array}\right)=\left(\begin{array}{cc}cos\left(\theta \right)& -sin\left(\theta \right)\\ sin\left(\theta \right)& cos\left(\theta \right)\end{array}\right)\theta ={sin}^{-1}\left({\displaystyle \frac{\sqrt{|A_1|}}{N}}\right)$$

(176)

Therefore,

$$M=\left(\begin{array}{cc}cos\left(2\theta \right)& -sin\left(2\theta \right)\\ sin\left(2\theta \right)& cos\left(2\theta \right)\end{array}\right)$$

(177)

The state $|u\rangle$ can also be written as follows:

$$|u\rangle ={\displaystyle \frac{\sqrt{|A_0|}}{N}}|A_0\rangle +{\displaystyle \frac{\sqrt{|A_1|}}{N}}|A_1\rangle =cos\left(\theta \right)|A_0\rangle +sin\left(\theta \right)|A_1\rangle$$

(178)

Each time the Grover operation is performed, the state is rotated by an angle $2\theta$.

$$\begin{array}{cc}\hfill G|u\rangle & =cos\left(3\theta \right)|A_0\rangle +sin\left(3\theta \right)|A_1\rangle \hfill \\ \hfill G^2|u\rangle & =cos\left(5\theta \right)|A_0\rangle +sin\left(5\theta \right)|A_1\rangle \hfill \\ \hfill ⋮\\ \hfill G^t|u\rangle & =cos\left((2t+1)\theta \right)|A_0\rangle +sin\left((2t+1)\theta \right)|A_1\rangle \hfill \end{array}$$

(179)

The above procedure can also be described geometrically, as shown in Figure 20.

After t iterations, the probability of measuring the desired output $A_1$ is given by

$$P\left(A_1\right)={sin}^2\left((2t+1)\theta \right)$$

(180)

This probability should be close to 1. Therefore,

$$(2t+1)\theta \approx {\displaystyle \frac{\pi }{2}}$$

(181)

Thus,

$$t\approx {\displaystyle \frac{\pi }{4\theta }}-{\displaystyle \frac{1}{2}}\mathrm{closest}\mathrm{integer}\Rightarrow t=⌊{\displaystyle \frac{\pi }{4\theta }}⌋$$

(182)

Grover’s algorithm has the potential to be used in a wide variety of applications, especially in ML. This algorithm can be used as a black box, offering a quadratic advantage compared to classical algorithms.

3.9. HHL Algorithm

Consider a system of N linear equations with N unknowns, represented as

$$Ax=b,$$

(183)

where x is the vector of unknowns, A is the coefficient matrix and b is the constants vector.

If A is an invertible matrix, the solution can be obtained as

$$x=A^{-1}b$$

(184)

The HHL algorithm is a quantum algorithm specifically designed to solve this linear system efficiently.

The best classical algorithms require $O\left(N\right)$ complexity time for this problem. However, the HHL algorithm provides an exponential speedup, reducing the time complexity to $O(logN)$.

Before explaining HHL in detail, it is essential to clarify some linear algebra. A is a Hermitian matrix. This means it can be written as a sum of the outer products of its eigenvectors, scaled by its eigenvalues. Therefore,

$$A=\sum _{i=0}^{N-1}{\lambda }_i\left|v_i\right.〉\left.〈v_i\right|$$

(185)

Therefore, the inverse A can be written as

$$A^{-1}=\sum _{i=0}^{N-1}{\displaystyle \frac{1}{{\lambda }_i}}\left|v_i\right.〉\left.〈v_i\right|$$

(186)

Suppose that b is one eigenvector of A, which is one of the inputs in the quantum circuit. Since A is invertible and Hermitian, it must have an orthogonal basis of eigenvectors. Therefore, b can be written as

$$|b\rangle =\sum _{j=0}^{N-1}{b}_j|v_j\rangle$$

(187)

Therefore, the desired output has the following form:

$$|x\rangle =A^{-1}|b\rangle =(\sum _{i=0}^{N-1}{\displaystyle \frac{1}{{\lambda }_i}}\left|v_i\right.〉\left.〈v_i\right|)(\sum _{j=0}^{N-1}{b}_j|v_j\rangle )=\sum _{i=0}^{N-1}\sum _{j=0}^{N-1}{\displaystyle \frac{1}{{\lambda }_i}}{b}_j\left|v_i\right.〉\left.〈v_i\right|v_j\rangle =\sum _{i=0}^{N-1}{\displaystyle \frac{1}{{\lambda }_i}}{b}_i|v_i\rangle$$

(188)

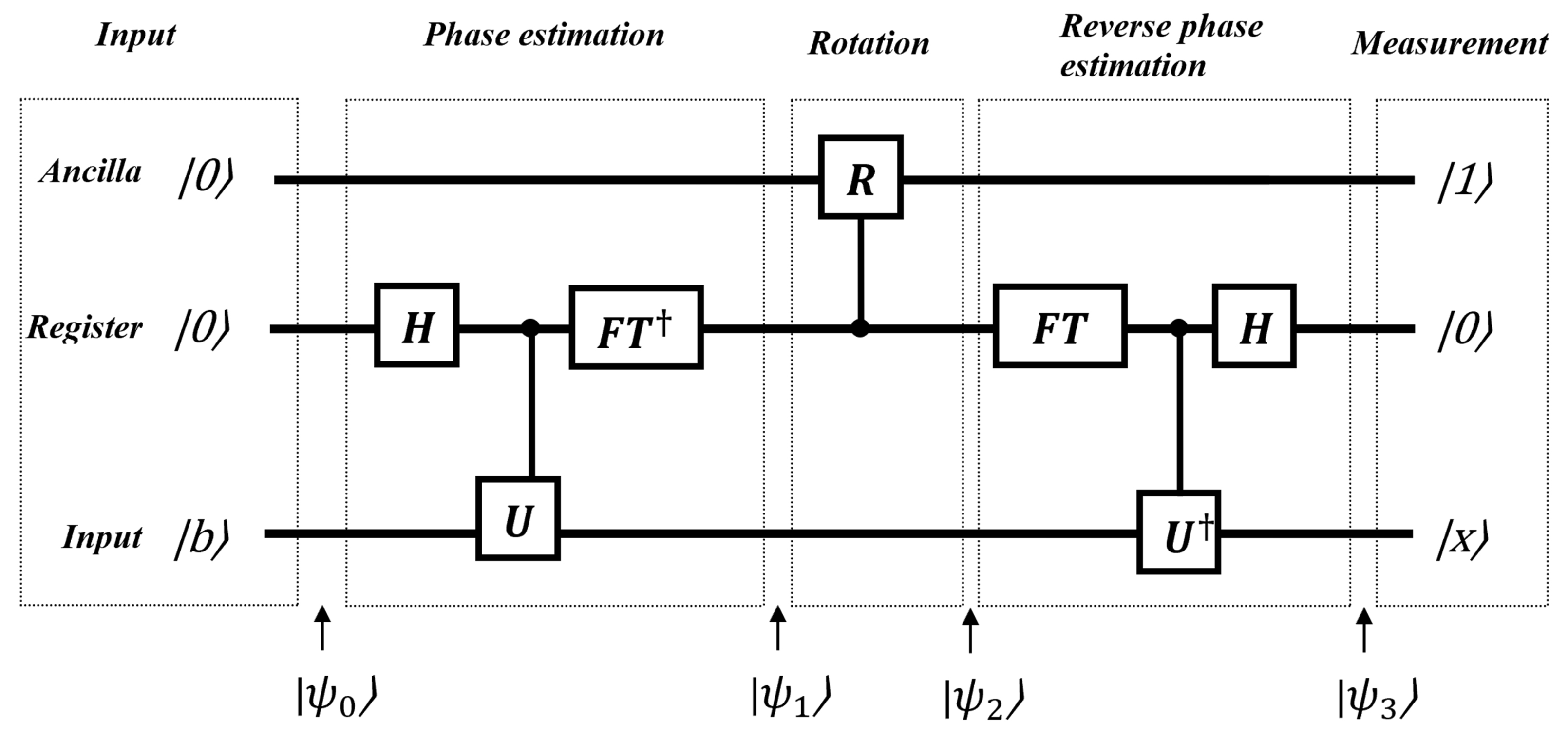
The HHL algorithm can be implemented following a common 5-step procedure. The quantum circuit for the HHL algorithm is depicted in Figure 21.

As inputs, the circuit requires an ancilla qubit, a register and one eigenvector of A, named b. An ancilla qubit is commonly used in many quantum algorithms. It serves as an auxiliary qubit to assist in implementing quantum operations and is not part of the circuit’s input or output. The HHL algorithm consists of three stages. In the first state, a phase estimation module computes the eigenvalues of A, which are subsequently stored in a quantum register. In the second stage, the inverse of the eigenvalues obtained in the first stage is computed using a controlled $R_y$ gate. The result of this computation is then encoded into an ancilla qubit. The final stage involves uncomputing the phase estimation and the unitary operations. The ancilla qubit is then measured. If the measurement outcome is 1, this indicates that the quantum state approximates $|x\rangle$.

First, initial input states are set up.

$$|{\psi }_0{\rangle =|0\rangle }_A{|0\rangle }_R^{\otimes n}{|b\rangle }_I$$

(189)

Next, the QPE algorithm is applied using the unitary operator $U=exp\left(iAt\right)$, which can be expressed as

$$U=exp\left(iAt\right)=\sum _{i=0}^{N-1}exp\left(i{\lambda }_{i}t\right)|v_i\rangle \langle v_i|$$

(190)

where A is a Hermitian matrix with eigenstates $|u_i\rangle$ and corresponding eigenvalues ${\lambda }_i$.

Since A is Hermitian, the operator $exp\left(iAt\right)$ is unitary. Its eigenvalues are $exp\left(i{\lambda }_{j}t\right)$, and its eigenstates are the same as those of A. Therefore, after applying U to $|b\rangle$, the output is as follows:

$$U|b\rangle =\sum _{i=0}^{N-1}exp\left(i{\lambda }_{i}t\right)|b\rangle =\sum _{i=0}^{N-1}|{\tilde{\lambda }}_i\rangle |b\rangle$$

(191)

Therefore,

$$|{\psi }_1{\rangle =|0\rangle }_A\sum _{j=0}^{N-1}{b}_j|v_j{\rangle }_I\sum _{i=0}^{N-1}{|{\tilde{\lambda }}_i\rangle }_R$$

(192)

Next, a controlled Y rotation gate is applied to the ancilla qubit. The matrix representation of this gate is as follows:

$$R_y\left(\theta \right)=\left[\begin{array}{cc}cos\left({\displaystyle \frac{\theta }{2}}\right)& -sin\left({\displaystyle \frac{\theta }{2}}\right)\\ sin\left({\displaystyle \frac{\theta }{2}}\right)& cos\left({\displaystyle \frac{\theta }{2}}\right)\end{array}\right]$$

(193)

with $\theta =2arcsin\left({\displaystyle \frac{C}{\tilde{\lambda }}}\right)$.

After applying $R_y\left(\theta \right)$ into the ancilla qubit, the result is as follows:

$$R_y{\left(\theta \right)|0\rangle }_A=\left[\begin{array}{cc}cos\left({\displaystyle \frac{\theta }{2}}\right)& -sin\left({\displaystyle \frac{\theta }{2}}\right)\\ sin\left({\displaystyle \frac{\theta }{2}}\right)& cos\left({\displaystyle \frac{\theta }{2}}\right)\end{array}\right]\left[\begin{array}{c}1\\ 0\end{array}\right]=\left[\begin{array}{c}cos\left({\displaystyle \frac{\theta }{2}}\right)\\ sin\left({\displaystyle \frac{\theta }{2}}\right)\end{array}\right]=cos\left({\displaystyle \frac{\theta }{2}}\right)|0\rangle +sin\left({\displaystyle \frac{\theta }{2}}\right)|1\rangle$$

(194)

Therefore, the circuit is in the following state:

$$|{\psi }_2\rangle =\sum _{j=0}^{N-1}{b}_j|v_j{\rangle }_I\sum _{i=0}^{N-1}{|{\tilde{\lambda }}_i\rangle }_R{\left(\sqrt{1-{\displaystyle \frac{c^2}{{\lambda }_j^2}}}|0\rangle +{\displaystyle \frac{c}{{\lambda }_j}}|1\rangle \right)}_A$$

(195)

The fourth step involves the application of an inverse QPE algorithm. Thus, the following state is obtained:

$$|{\psi }_3\rangle =\sum _{j=0}^{N-1}{b}_j|v_j{\rangle }_I{|0\rangle }_R^{\otimes n}{\left(\sqrt{1-{\displaystyle \frac{c^2}{{\lambda }_j}}}|0\rangle +{\displaystyle \frac{c}{{\lambda }_j}}|1\rangle \right)}_A$$

(196)

Finally, a measurement of the ancilla qubit is performed to obtain the answer. If 1 is obtained, the state is

$$|{\psi }_4\rangle =\sum _{j=0}^{N-1}{b}_j|v_j\rangle {\displaystyle \frac{c}{{\lambda }_j}}=\sum _{j=0}^{N-1}{b}_j|u_j\rangle {\displaystyle \frac{c}{{\lambda }_j}}$$

(197)

which is proportional to the desired output.

We consider a practical example of the HHL algorithm using a $2\times 2$ Hermitian matrix A defined as

$$A=\left[\begin{array}{cc}{\displaystyle \frac{3}{4}}& {\displaystyle \frac{1}{4}}\\ {\displaystyle \frac{1}{4}}& {\displaystyle \frac{17}{12}}\end{array}\right]$$

(198)

and the input vector:

$$\overrightarrow{b}=\left[\begin{array}{c}0\\ 1\end{array}\right]$$

(199)

The solution vector for this system is

$$\overrightarrow{x}=\left[\begin{array}{c}-{\displaystyle \frac{1}{4}}\\ {\displaystyle \frac{3}{4}}\end{array}\right]$$

(200)

The matrix A has the following eigenvalues and their corresponding normalized eigenvectors, where each normalized eigenvector is given by $\widehat{v}={\displaystyle \frac{v}{\parallel v\parallel }}$.

$${\lambda }_1={\displaystyle \frac{3}{2}},{\lambda }_2={\displaystyle \frac{2}{3}}$$

(201)

$$|v_1\rangle ={\displaystyle \frac{1}{\sqrt{10}}}\left[\begin{array}{c}1\\ 3\end{array}\right],|v_2\rangle ={\displaystyle \frac{1}{\sqrt{10}}}\left[\begin{array}{c}-3\\ 1\end{array}\right]$$

(202)

Since $\overrightarrow{b}$ can be decomposed in terms of A’s eigenbasis, we write

$$|b\rangle ={\displaystyle \frac{3}{\sqrt{10}}}|v_1\rangle +{\displaystyle \frac{1}{\sqrt{10}}}|v_2\rangle$$

(203)

The HHL algorithm proceeds in five main steps: initialization, quantum phase estimation, controlled rotation, inverse QPE, and measurement.

The initial state of the system (ancilla qubit A, register R, input qubit I) is

$$|{\psi }_0\rangle ={|0\rangle }_A{|0\rangle }_R^{\otimes 2}{|b\rangle }_I$$

(204)

After applying QPE, we obtain

$$|{\psi }_1\rangle ={|0\rangle }_A\sum _{j=0}^1{|{\tilde{\lambda }}_j\rangle }_R{|v_j\rangle }_I={|0\rangle }_A\left({\displaystyle \frac{3}{\sqrt{10}}}{|v_1\rangle }_I{|{\displaystyle \frac{3}{2}}\rangle }_R+{\displaystyle \frac{1}{\sqrt{10}}}{|v_2\rangle }_I{|{\displaystyle \frac{2}{3}}\rangle }_R\right)$$

(205)

A controlled Y-rotation is applied to the ancilla qubit, conditioned on the register. Assuming the rotation constant $C=0.5$, we get

$$|{\psi }_2\rangle ={\displaystyle \frac{3}{\sqrt{10}}}{|v_1\rangle }_I{|{\displaystyle \frac{3}{2}}\rangle }_R{\left({\displaystyle \frac{2\sqrt{2}}{3}}|0\rangle +{\displaystyle \frac{1}{3}}|1\rangle \right)}_A+{\displaystyle \frac{1}{\sqrt{10}}}{|v_2\rangle }_I{|{\displaystyle \frac{2}{3}}\rangle }_R{\left({\displaystyle \frac{\sqrt{7}}{4}}|0\rangle +{\displaystyle \frac{3}{4}}|1\rangle \right)}_A$$

(206)

Applying the inverse QPE yields

$$|{\psi }_3\rangle ={\displaystyle \frac{3}{\sqrt{10}}}{|v_1\rangle }_I\left({\displaystyle \frac{2\sqrt{2}}{3}}{|0\rangle }_A+{\displaystyle \frac{1}{3}}{|1\rangle }_A\right){|0\rangle }_R+{\displaystyle \frac{1}{\sqrt{10}}}{|v_2\rangle }_I{\left({\displaystyle \frac{\sqrt{7}}{4}}|0\rangle +{\displaystyle \frac{3}{4}}|1\rangle \right)}_A{|0\rangle }_R$$

(207)

A measurement is performed on the ancilla qubit. If the outcome is ${|1\rangle }_A$, the resulting (non-normalized) state of the input register is

$$|{\psi }_4\rangle =\sum _{j=0}^1{b}_j|v_j\rangle {\displaystyle \frac{C}{{\lambda }_j}}={\displaystyle \frac{1}{\sqrt{10}}}\left(|v_1\rangle +{\displaystyle \frac{3}{4}}|v_2\rangle \right)$$

(208)

Substituting the eigenvectors,

$$|x\rangle ={\displaystyle \frac{1}{\sqrt{10}}}\left({\displaystyle \frac{1}{\sqrt{10}}}\left[\begin{array}{c}1\\ 3\end{array}\right]+{\displaystyle \frac{3}{4}}·{\displaystyle \frac{1}{\sqrt{10}}}\left[\begin{array}{c}-3\\ 1\end{array}\right]\right)={\displaystyle \frac{1}{10}}\left(\left[\begin{array}{c}1\\ 3\end{array}\right]+\left[\begin{array}{c}-{\displaystyle \frac{9}{4}}\\ {\displaystyle \frac{3}{4}}\end{array}\right]\right)={\displaystyle \frac{1}{2}}\left[\begin{array}{c}-{\displaystyle \frac{1}{4}}\\ {\displaystyle \frac{3}{4}}\end{array}\right]$$

(209)

This is proportional to the true solution of the system.

Overall, HHL solves a linear system of equations providing an exponential speedup over the classical algorithms. This indicates a potential quantum advantage. HHL is used as a subroutine in many QML algorithms particularly for tasks such as matrix inversion and solving differential equations.

4. Quantum Machine Learning

Machine learning is a prominent area of research in computer science. However, with the substantial expansion of data sizes, researchers are increasingly exploring innovative methods to address this challenge. QC has emerged as a potential solution for managing these limitations. Consequently, researchers are investigating how the integration of quantum computing with machine learning can be effectively realized [19].

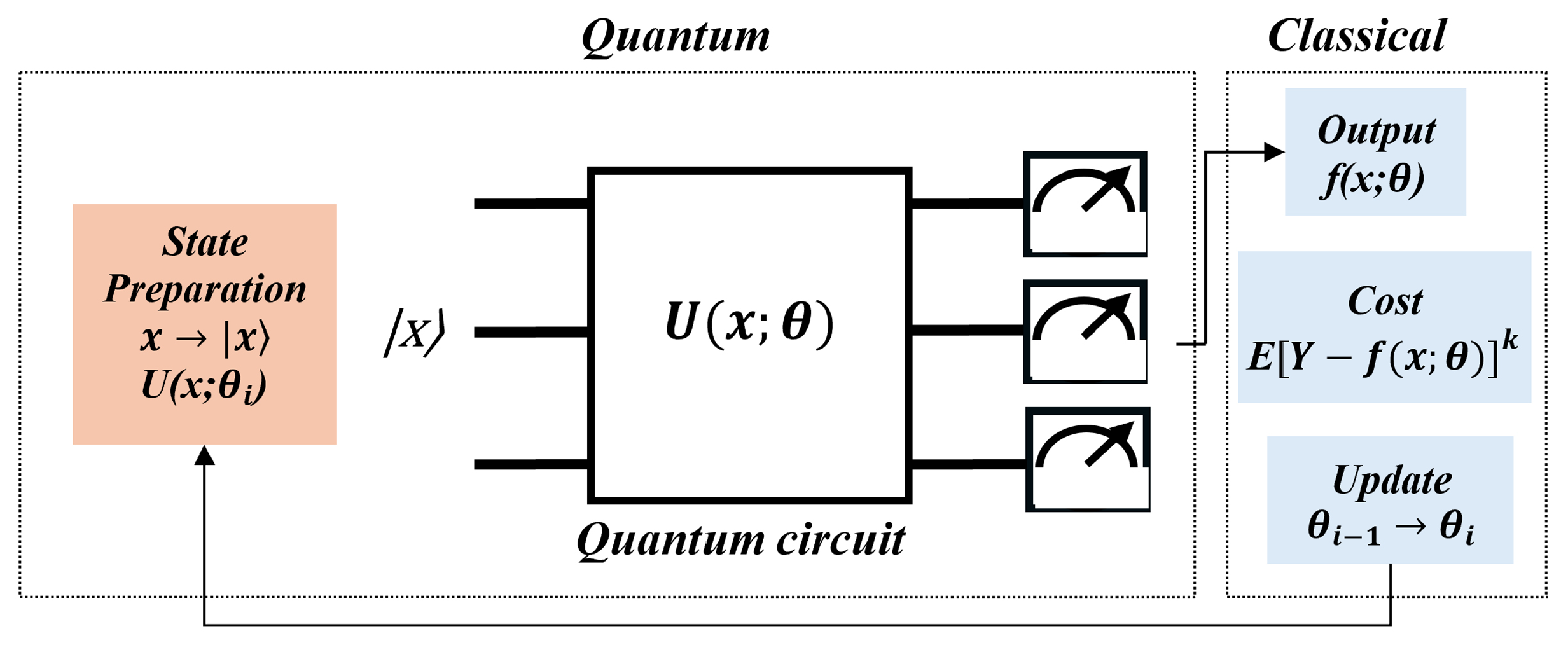
The general procedure for quantum machine learning algorithms comprises three main steps: encoding, quantum computation and measurement, as illustrated in Figure 22. The initial step (encoding) entails the transformation of data from classical forms into quantum states. The second step (quantum computation) varies based on the specific type of quantum machine learning algorithm being employed. The final step (measurement) involves converting the output data from quantum states back into classical formats [31].

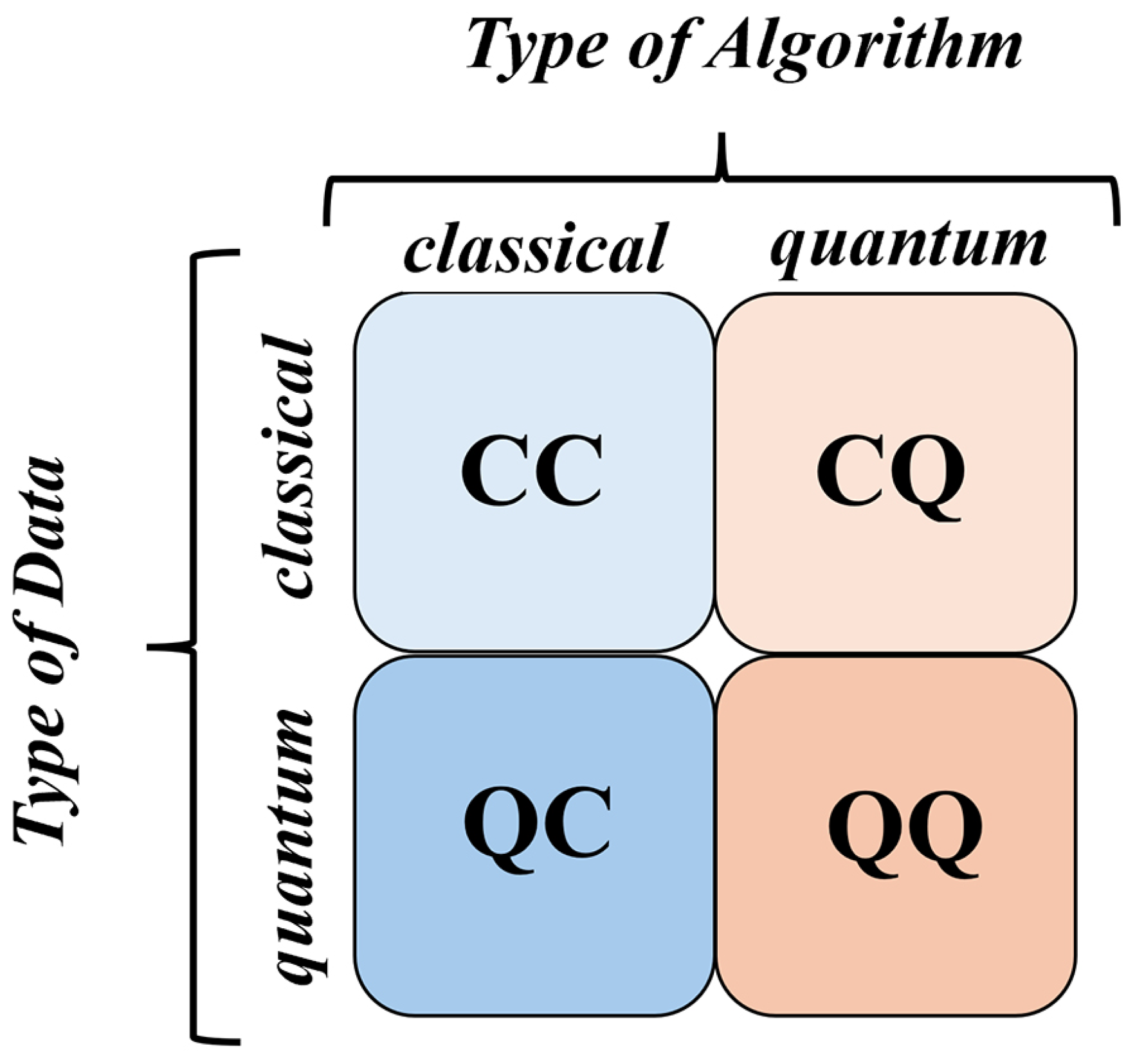
QML is developed by modifying classical algorithms or their subroutines to run on future quantum computers. These devices are expected to become broadly available soon, helping manage the increasing amounts of data being produced globally [46]. The emerging field of QML can be approached in four main ways, determined by two factors: the nature of the data (classical or quantum) and the type of algorithm used (classical or quantum). Figure 23 presents these four distinct approaches [28].

The Classical–Classical (CC) approach utilizes classical data and algorithms that are inspired by ideas from quantum computing. These algorithms, termed “quantum-inspired,” are applied to classical data and run on conventional computers.

The Classical–Quantum (CQ) approach involves applying quantum algorithms to classical data.There are two main approaches to developing QML models within this approach. This approach involves developing quantum versions of traditional machine learning algorithms by leveraging quantum subroutines, such as Grover’s algorithm, the HHL algorithm and quantum phase estimation, to achieve algorithmic speedups. It also requires converting classical data into quantum data through a process known as quantum encoding [28].

The Quantum–Classical (QC) approach applies classical machine learning algorithms to quantum data with the goal of obtaining meaningful insights.

The Quantum–Quantum (QQ) approach involves applying quantum algorithms to quantum data in order to uncover underlying patterns and gain insights from the data. This approach is referred to as purely QML.

Among the four approaches, the CQ and CC methods have been more thoroughly investigated in the field of QML. Numerous studies examine the potential of these approaches to address real-world problems and demonstrate a quantum advantage [2].

Classical machine learning methods can be replaced by quantum algorithms to solve problems more effectively. With numerous potential applications and a broad range of theoretical approaches, QML is a very promising and quickly developing area of study.

4.1. Data Encoding

One of the main problems in QML is encoding data into quantum states. The process of converting classical data, such as images or big datasets, into quantum data requires a substantial investment of time and computing power. Thus, creating novel methods for effective data encoding is an important area for further study [31].

4.1.1. Basis Encoding

Basis encoding is the most elementary method for converting classical data into quantum states. This technique maps a binary string of classical data $x=x_1\dots x_n$ onto the computational basis state $|x\rangle =|x_1\dots x_n\rangle$, requiring n qubits to represent n bits of classical information [48]. For instance, the classical input string (1100) is encoded as the quantum state $|1100\rangle$ using four qubits [28]. In order to encode a dataset using the basis encoding method, the following equation must typically be used:

$$|\mathcal{D}\rangle ={\displaystyle \frac{1}{\sqrt{M}}}\sum _{m=1}^M|X_m\rangle$$

(210)

where $\mathcal{D}=X_1,X_2,\dots ,X_M$ represents classical data in the form of binary strings, where $X_m=b_1,b_2,\dots ,b_N$ and $b_i\in \{0,1\}$ for $i\in \{1,2,\dots ,N\}$. Here, N denotes the number of features and M indicates the number of samples in the dataset $\mathcal{D}$ [31].

Additionally, in order to convert the vector $\mathbf{x}=(2,3)$ into a quantum state, each component must first be transformed into its binary representation, requiring 2 bits: $x_1=10$ and $x_2=11$. The corresponding basis encoding then utilizes two qubits to represent the data as follows [28]:

$$|\mathbf{x}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}|10\rangle +{\displaystyle \frac{1}{\sqrt{2}}}|11\rangle$$

(211)

4.1.2. Amplitude Encoding

Amplitude encoding is one of the most widely used and preferred techniques for encoding data in QML algorithms [31]. In this method, a classical data vector

$$\mathbf{x}=(x_1,x_2,\dots ,x_n)$$

is mapped onto the amplitudes of a quantum state.

A normalized vector $\mathbf{x}$ is encoded into a quantum state $|\psi \rangle$ as

$$|\psi \rangle =\sum _{i=1}^n{\displaystyle \frac{x_i}{\parallel \mathbf{x}\parallel }}|i\rangle$$

(212)

where $|\psi \rangle$ is the quantum state, $x_i$ are the components of the classical vector, $\parallel \mathbf{x}\parallel$ is the normalization of the vector, and $|i\rangle$ are the computational basis states.

For example, the vector

$$\mathbf{x}=(0.1,-0.7,1.0)$$

can be encoded using the following procedure:

First, compute the normalization of the vector:

$$\parallel \mathbf{x}\parallel =\sqrt{x_1^2+x_2^2+\dots +x_n^2}=\sqrt{0.01+0.49+1.00}=\sqrt{1.5}\approx 1.225$$

(213)

Subsequently,

$${\mathbf{x}}^{\prime }={\displaystyle \frac{1}{\parallel \mathbf{x}\parallel }}\mathbf{x}=\left({\displaystyle \frac{0.1}{1.225}},{\displaystyle \frac{-0.7}{1.225}},{\displaystyle \frac{1.0}{1.225}}\right)=(0.081,-0.571,0.816,0.000)$$

(214)

The vector $\mathbf{x}$ will be encoded into a quantum state as follows:

$$|\psi \rangle =0.081|00\rangle -0.571|01\rangle +0.816|10\rangle +0.000|11\rangle$$

(215)

The above state can also be represented as a matrix:

$$A=\left[\begin{array}{cc}0.081& -0.571\\ 0.816& 0.000\end{array}\right]$$

(216)

There are also other encoding methods, including Angle Encoding [31], QSample Encoding [28] and Hamiltonian Encoding [48]. Proper data encoding is crucial for the future of QML to fully leverage the computational power of quantum computing.

4.2. QML Algorithms

Machine learning is divided into supervised and unsupervised types. In both, models gain insights by analyzing data. Supervised learning uses labeled data, where input–output pairs are provided, allowing the model to learn relationships between them. Unsupervised learning uses only input data, and the model finds patterns or structures on its own. This section covers two quantum machine learning algorithms: the quantum support vector machine (supervised) and quantum k-means (unsupervised). We focus on quantum models using quantum algorithms, where learning happens directly at the quantum level.

4.2.1. Quantum Support Vector Machine

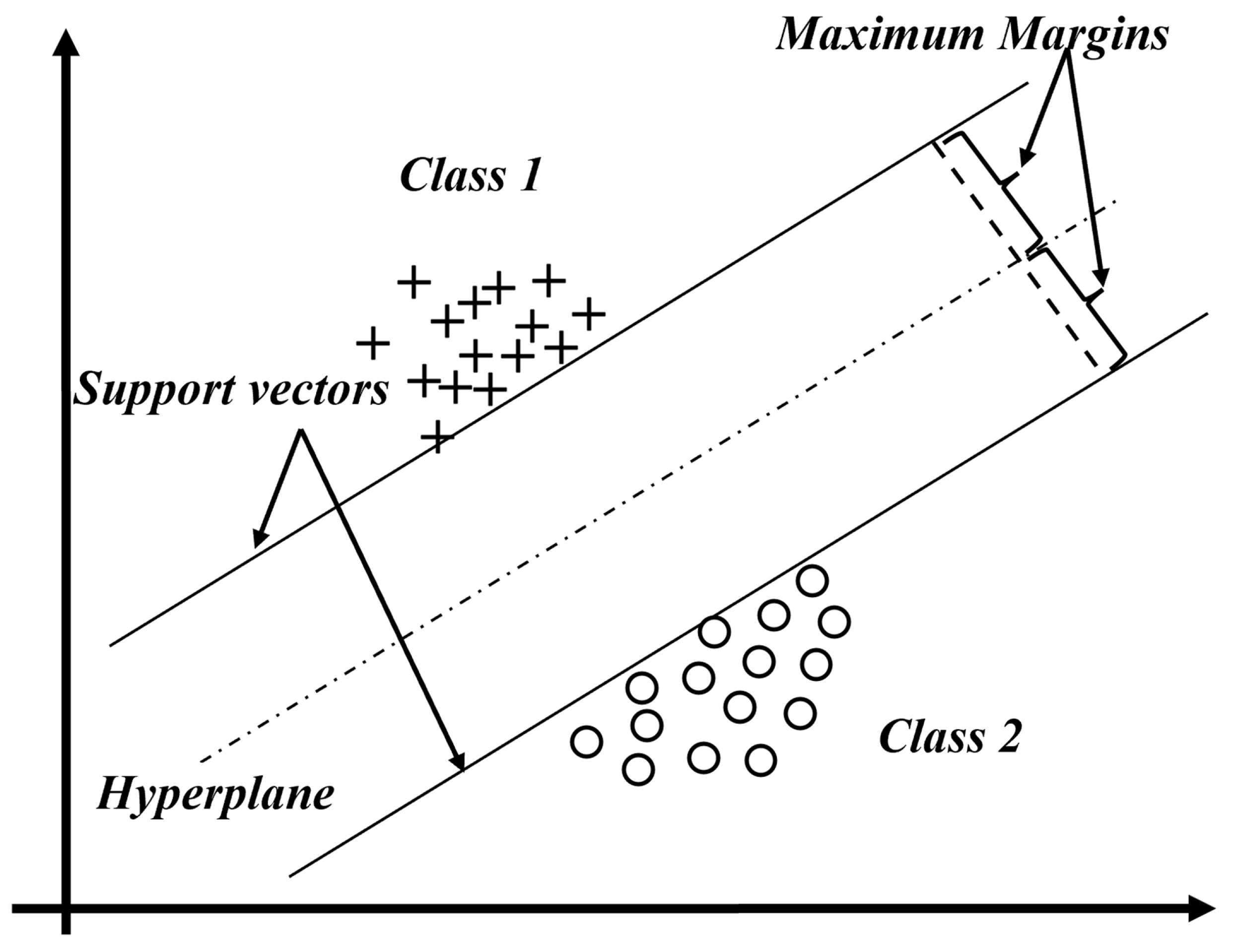
The support vector machine (SVM) algorithm is a popular supervised learning method, especially useful for binary classification tasks. Its key idea is to find a hyperplane that separates two different classes of data based on their features, which then acts as a decision boundary for classifying new data.

As shown in Figure 24, SVM works to maximize the margin between the hyperplane and the closest data points, ensuring the boundary between the two classes is as wide as possible. In this figure, two distinct classes are illustrated: class 1 and class 2. A sectional view of the dataset reveals that the data can be separated linearly when projected into higher dimensions. The points closest to the hyperplane, shown on the dashed lines, are called support vectors, while the hyperplane itself, dividing the two classes, is defined by a specific mathematical equation. The equation of the hyperplane can then be given as [19]

$$\overrightarrow{w}·\overrightarrow{x}+b=0$$

(217)

Additionally, w and b should be adjusted such that

$$\overrightarrow{w}·\overrightarrow{x_i}+b\ge 1,\mathrm{for}\overrightarrow{x_i}\mathrm{in}\mathrm{the}\mathrm{positive}\mathrm{class},$$

(218)

$$\overrightarrow{w}·\overrightarrow{x_i}+b\le -1,\mathrm{for}\overrightarrow{x_i}\mathrm{in}\mathrm{the}\mathrm{negative}\mathrm{class}$$

(219)

The distance between two hyperplanes can be expressed as ${\displaystyle \frac{2}{\parallel \mathbf{w}\parallel }}$.

Minimizing $\parallel \mathbf{w}\parallel$ leads to a maximum margin and adding constraints ensures that the margin correctly classifies the data. This can be represented by the following optimization problem:

$$\underset{w,b}{min}{\displaystyle \frac{1}{2}}{\parallel \mathbf{w}\parallel }^2$$

(220)

subject to the constraint

$$y^{\left(i\right)}(w^T{x}^{\left(i\right)}-b)\ge 1$$

(221)

for all training examples $i=1,\dots ,M$ with labels $y^{\left(i\right)}\in \{-1,1\}$, the constraint can be incorporated into the objective function using Lagrange multipliers ${\alpha }^{\left(i\right)}$. This leads to the following formulation of the problem:

$$\underset{w,b}{min}\underset{{\alpha }^{\left(i\right)}\ge 0}{max}\left({\displaystyle \frac{1}{2}}{\parallel w\parallel }^2-\sum _{i=1}^M{\alpha }^{\left(i\right)}\left(y^{\left(i\right)}(w^T{x}^{\left(i\right)}-b)-1\right)\right)$$

(222)

In order to solve the maximization of the objective function F with respect to ${\alpha }^{\left(i\right)}$, we set the following derivatives to zero:

$${\displaystyle \frac{\partial F}{\partial w}}=w-\sum _{i=1}^M{\alpha }^{\left(i\right)}{y}^{\left(i\right)}{x}^{\left(i\right)}=0$$

(223)

$${\displaystyle \frac{\partial F}{\partial b}}=\sum _{i=1}^M{\alpha }^{\left(i\right)}{y}^{\left(i\right)}=0$$

(224)

As a consequence, we can express the weights w as

$$w=\sum _{i=1}^M{\alpha }^{\left(i\right)}{y}^{\left(i\right)}{x}^{\left(i\right)}$$

(225)

Therefore,

$$\begin{array}{cc}\hfill F& ={\displaystyle \frac{1}{2}}\sum _{i=1}^M{\alpha }^{\left(i\right)}{y}^{\left(i\right)}{x}^{\left(i\right)}\sum _{j=1}^M{\alpha }^{\left(j\right)}{y}^{\left(j\right)}{x}^{\left(j\right)}-\sum _{i=1}^M{\alpha }^{\left(i\right)}{y}^{\left(i\right)}{x}^{\left(i\right)}\sum _{j=1}^M{\alpha }^{\left(j\right)}{y}^{\left(j\right)}{x}^{\left(j\right)}+\sum _{i=1}^M{\alpha }^{\left(i\right)}{y}^{\left(i\right)}b+\sum _{i=1}^M{\alpha }^{\left(i\right)}\hfill \\ \hfill & =\sum _{i=1}^M{\alpha }^{\left(i\right)}-{\displaystyle \frac{1}{2}}\sum _{i=1}^M\sum _{j=1}^M{\alpha }^{\left(i\right)}{\alpha }^{\left(j\right)}{y}^{\left(i\right)}{y}^{\left(j\right)}(x^{\left(i\right)}·x^{\left(j\right)})\hfill \end{array}$$

(226)

Given that

$${\alpha }^{\left(i\right)}\ge 0$$

for each training example $i=1,\dots ,M$, and

$$\sum _{i=1}^M{\alpha }^{\left(i\right)}{y}^{\left(i\right)}=0.$$

The optimization problem can be extended to incorporate an arbitrary kernel function $K({\mathbf{x}}^{\left(i\right)},{\mathbf{x}}^{\left(j\right)})$, introducing non-linearity to the model. By replacing the dot product in the previous dual formulation with the kernel function, the problem is reformulated as

$$\underset{{\alpha }^{\left(i\right)}}{min}\left\{{\displaystyle \frac{1}{2}}\sum _{i=1}^M\sum _{j=1}^M{\alpha }^{\left(i\right)}{\alpha }^{\left(j\right)}{y}^{\left(i\right)}{y}^{\left(j\right)}K({\mathbf{x}}^{\left(i\right)},{\mathbf{x}}^{\left(j\right)})-\sum _{i=1}^M{\alpha }^{\left(i\right)}\right\}$$

(227)

The type of kernel function $K({\mathbf{x}}^{\left(i\right)},{\mathbf{x}}^{\left(j\right)})$ depends on the problem being solved. Common choices include the linear kernel, polynomial kernel and sigmoid kernel.

The quantum SVM can be implemented in two ways. The first method utilizes Grover’s algorithm [11], which performs a maximum search across all possible solutions to identify the hyperplane, achieving a quadratic speedup. A detailed description of each algorithm’s step is described below.

• Initialization
  The kernel function and kernel matrix should be determined for the specific problem.
• Data encoding
  Classical data should be converted into quantum data as described previously.
• Find the objective function
  Grover’s algorithm is used to solve the objective function to find an optimal set of ${\alpha }^{\left(i\right)}$, which solves for the parameters w and b.

The second method employs the HHL algorithm [49], transforming the optimization problem into a linear system of equations that is solved using the HHL algorithm. This approach offers an exponential speedup.

As explained before, the dual problem involves finding the optimal $\alpha =[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_M]$ by solving a system of equations derived from the dual optimization.

At the optimal solution, the dual problem’s conditions ensure that

$$A\alpha =b$$

(228)

where

• A is the kernel matrix, defined as

  $$A_{ij}=y^{\left(i\right)}{y}^{\left(j\right)}K(x^{\left(i\right)},x^{\left(j\right)})$$

  where $K(x^{\left(i\right)},x^{\left(j\right)})$ is the kernel function.
• $\alpha$ is the vector of Lagrange multipliers.
• b is a vector derived from the constraints:

  $$\sum _{i=1}^M{\alpha }_i{y}^{\left(i\right)}=0$$

In other words, $A\alpha =b$ encapsulates the optimization process to compute the multipliers ${\alpha }_i$. A detailed description of each algorithm’s step is described below.

• Initialization
  The kernel function and kernel matrix should be determined for the specific problem.
• Data encoding
  Classical data should be converted into quantum data as described previously.
• Find the Lagrange multipliers
  The HHL algorithm is used to solve the system of equations $A\alpha =b$ to find an optimal set of ${\alpha }^{\left(i\right)}$.

Table 7. Overview of quantum SVM variants.

Author	Description	Application	Complexity
M. Senekane, B. M. Taele [50]	This study introduces a quantum SVM aimed at predicting solar irradiation, using data from the Digital Technology Group (DTG) Weather Station at Cambridge University. The proposed algorithm incorporates the HHL algorithm as a quantum subroutine. The original problem is transformed into a linear system of equations, which is then solved using the HHL method. The algorithm has been implemented in Python.	Solar irradiation prediction	Not mentioned
Yuan et al. [51]	This study presents a quantum support vector algorithm designed to detect flow separation in aeronautic applications. Beyond binary classification, a multiclass quantum SVM was developed to classify various wing angles of attack. The quantum algorithms showed improvements in accuracy of 11.1% and 17.9%, respectively, compared to the classical SVM. These algorithms are based on a quantum annealing model and have been implemented on the Advantage 4.1 system from D-Wave.	Aerodynamic classification	Not mentioned
Shubham Vashisth et al. [52]	This study introduces a quantum SVM algorithm designed for binary classification in the diagnosis of malignant breast cancer. The proposed algorithm was implemented using the existing components of the quantum SVM from the Qiskit library and its performance was assessed on the IBM Quantum Experience platform.	Breast cancer diagnosis	$O(logNM)$
Yang et al. [53]	This study presents a new quantum SVM algorithm that improves classification accuracy for OCR and Iris datasets. The proposed algorithm is based on the HHL algorithm and its performance was evaluated on the IBMQX2 quantum computer.	Classification	$O(logNM)$

contains an overview of the applications of the quantum SVM.

4.2.2. Quantum K-Means Algorithm

K-means clustering is one of the most widely recognized methods in unsupervised machine learning. Through the process of clustering, data points are grouped into distinct classes or clusters based on the underlying structure of the input data. The primary objective of clustering is to identify similarities among data points and to organize those that exhibit similar characteristics into cohesive clusters [2].

The classical k-means algorithm categorizes data into k clusters by assigning each data point to the nearest centroid during each iteration. New centroids are computed by averaging the data points within each cluster and this process continues until cluster assignments no longer change. A notable limitation of the k-means algorithm is that the number of clusters must be predetermined. Furthermore, it relies on the assumption that similarity can be quantified using Euclidean distance, implying that smaller distances signify greater similarity [2].

The quantum version of the k-means algorithm consists of three quantum subroutines: the swap test, distance calculation and Grover’s algorithm. The swap test is used to measure the overlap between two vectors, $\langle a|b\rangle$, which serves as a measure of similarity. The quantum circuit for this subroutine is shown in Figure 25.

First, initial input states are set up.

$$|{\psi }_0\rangle =|0\rangle |a\rangle |b\rangle$$

(229)

Next, a Hadamard gate is applied to control qubit, putting it into a superposition state.

$$|{\psi }_1\rangle =H|0\rangle |a\rangle |b\rangle ={\displaystyle \frac{1}{\sqrt{2}}}(|0\rangle +|1\rangle )(|a\rangle |b\rangle )={\displaystyle \frac{1}{\sqrt{2}}}(|0,a,b\rangle +|1,a,b\rangle )$$

(230)

In the third step, a Fredkin gate is applied. Thus, $|{\psi }_2\rangle$ is expressed as follows:

$$|{\psi }_2\rangle ={\displaystyle \frac{1}{\sqrt{2}}}(|0,a,b\rangle +|1,b,a\rangle )$$

(231)

In the fourth step, a Hadamard gate is applied to the control qubit. Therefore,

$$|{\psi }_3\rangle ={\displaystyle \frac{1}{2}}|0\rangle (|a,b\rangle +|b,a\rangle )+{\displaystyle \frac{1}{2}}|1\rangle (|a,b\rangle -|b,a\rangle )$$

(232)

The probability of measuring the control qubit being in state $|0\rangle$ is given by

$$\begin{array}{cc}\hfill P(|0\rangle )& ={\displaystyle \frac{1}{4}}{\left||a,b\rangle +|b,a\rangle \right|}^2\hfill \\ \hfill & ={\displaystyle \frac{1}{4}}{\left(|a\rangle |b\rangle +|b\rangle |a\rangle \right)}^{†}\left(|a\rangle |b\rangle +|b\rangle |a\rangle \right)\hfill \\ \hfill & ={\displaystyle \frac{1}{4}}(\langle a|\langle b|a\rangle |b\rangle +\langle a|\langle b|b\rangle |a\rangle \hfill \\ \hfill & +\langle b|\langle a|a\rangle |b\rangle +\langle b|\langle a|b\rangle |a\rangle )\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}{|\langle a|b\rangle |}^2\hfill \end{array}$$

(233)

where $\langle a|b\rangle |$ represents the inner product between the quantum states $|a\rangle$ and $|b\rangle$. In case of $P(|0\rangle )=0.5$, it implies that the states $|a\rangle$ and $|b\rangle$ are orthogonal. On the other hand, if $P(|0\rangle )=1$ it implies that the states are identical.

The swap test subroutine can be used as part of the distance calculation algorithm in order to calculate the Euclidean distance ${|a-b|}^2$.

First, initial input states are set up.

$$|\psi \rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0,a\rangle +|1,b\rangle \right)$$

(234)

$$|\varphi \rangle ={\displaystyle \frac{1}{\sqrt{Z}}}\left(|a||0\rangle +|b||1\rangle \right)$$

(235)

Next, $\langle \varphi |\psi \rangle$ can be calculated using the swap test. Therefore,

$$\begin{array}{cc}\langle \varphi |\psi \rangle \hfill & ={\displaystyle \frac{1}{\sqrt{2}}}\left(|a|\langle 0|+|b|\langle 1|\right){\displaystyle \frac{1}{\sqrt{Z}}}\left(|0,a\rangle +|1,b\rangle \right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{2Z}}}(|a|\langle 0|0,a\rangle +|a|\langle 0|1,b\rangle +|b|\langle 1|0,a\rangle +|b|\langle 1|1,b\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{2Z}}}\left(|a||a\rangle +|b||b\rangle \right)\hfill \end{array}$$

(236)

Using the equation from amplitude encoding, the above equation can be translated into

$$\langle \varphi |\psi \rangle ={\displaystyle \frac{1}{\sqrt{2Z}}}(a+b)$$

(237)

The Euclidean distance can be calculated by squaring the above equation:

$${|a-b|}^2=2Z{|\langle \varphi |\psi \rangle |}^2$$

(238)

In the quantum version of the k-means algorithm, the swap test and distance calculation subroutines are used to measure the Euclidean distance between data points and centroids, while Grover’s algorithm is applied to select the closest centroid for each cluster. Since the above subroutines have been explained in detail, the quantum k-means algorithm should now be described thoroughly to integrate these components effectively.

• Initialization
  The number of clusters, k, must be selected and k cluster centroids ${\overrightarrow{\mu }}_1,{\overrightarrow{\mu }}_2,\dots ,{\overrightarrow{\mu }}_k\in {\mathbb{R}}^N$ should be initialized. These initial centroids can be assigned using any standard method commonly employed in the classical k-means algorithm, such as random selection or the k-means initialization technique.
• Main loops until convergence is reached.
  Inner Loop (i): Choose the closest cluster centroid.
  Loop over training examples $i=\{1,\dots ,M\}$, and for each training example $x^{\left(i\right)}$ to assign data points to clusters, compute the distances $\parallel x^{\left(i\right)}-{\overrightarrow{\mu }}_k\parallel$ for each cluster centroid. Then, use Grover’s algorithm to efficiently determine the index

  $$c^{\left(i\right)}:=arg\underset{k}{min}{\parallel x^{\left(i\right)}-{\overrightarrow{\mu }}_k\parallel }^2$$

  (239)
  Inner Loop (j): New cluster centroids should be chosen.
  For each cluster j, the centroid should be updated bu computing the mean of all points assigned to that cluster. Looping over clusters $j=\{1,\dots ,k\}$, the new centroid ${\overrightarrow{\mu }}_j$ is computed as

  $${\overrightarrow{\mu }}_j={\displaystyle \frac{1}{|C_j|}}\sum _{i\in C_j}{x}^{\left(i\right)}$$

  (240)

  where $|C_j|$ represents the set of data points assigned to cluster j and $C_j$ is the number of such points. The updated ${\overrightarrow{\mu }}_j$ then becomes the new cluster centroid.
• Convergence.
  Convergence is achieved when iterations of the algorithm do not change the positions of the cluster centroids [54].

The quantum version of the k-means algorithm offers an exponential speedup over its classical counterpart.

Table 8. Overview of quantum k-means algorithm variants.

Author	Description	Application	Complexity
Changqing Gong et al. [55]	The proposed quantum k-means algorithm, which leverages trusted servers in quantum cloud computing, is designed to simplify complex quantum computations and reduce the frequency of quantum state superposition and de-superposition, utilizing a quantum cloud server. The proposed algorithm incorporates key subroutines such as SwapTest and GroverOptim. This algorithm has been implemented using IBM’s Qiskit platform.	Security	$O\left(Mlog\left(n\right)\sqrt{kt}\right)$
S.S. Kavitha, N. Kaulgud [56]	This work proposes a quantum k-means algorithm, employing a quantum circuit approach to compute the distance between centroids and data points for a heart disease dataset. Subroutines such as SwapTest and GroverOptim are integral to the proposed algorithm. The implementation was carried out using IBM’s Qiskit platform. A comparison between the classical and quantum k-means approaches was conducted to evaluate performance. The results indicate that the quantum k-means algorithm processes data faster than classical machines. Additionally, the quantum version outperforms its classical counterpart in terms of accuracy, precision, sensitivity, specificity, F1-score, and processing time when predicting heart disease.	Heart disease detection	$O\left(LNK\right)$
DiAdamo et al. [57]	A general, competitive, and parallelized version of the quantum k-means clustering algorithm is proposed to address challenges posed by noisy quantum hardware. This approach is applied to a real-world energy grid clustering scenario using real data from the German electricity grid. The new method significantly enhances performance, improving the balanced accuracy of the standard quantum k-means clustering by 67.8% compared to the labeling of the classical algorithm. The algorithm includes key subroutines such as SwapTest and GroverOptim, and is implemented using IBM’s Qiskit platform.	Energy grid classification	$O\left(\mathrm{poly}\right(n\left)\right)$
K. Benlamine et al. [58]	This work presents a comprehensive analysis of three different methods for estimating distance in quantum prototype-based clustering algorithms. The proposed algorithm is adaptable to all three methods. The results indicate that while the classical version of k-means operates in polynomial time, the quantum version achieves logarithmic time complexity, particularly for large datasets. The datasets utilized include Iris, Wine, and Breast Cancer from the UCI Machine Learning Repository. SwapTest and GroverOptim are essential components of this implementation. The platform used for implementation is not specified.	Clustering	$O(logn)$
H. Ohno [59]	This work introduces a quantum subroutine for the quantum k-means algorithm that leverages quantum entanglement and removes the need for explicit centroid calculations. Indeed, the subroutine estimates the Euclidean distance between the data points and the cluster centroids based on the cluster labels. The proposed k-means algorithm is evaluated on three datasets: Synthetic, Iris, and image. The algorithm is implemented using IBM’s Qiskit platform.	Image recognition	$O\left(M\sqrt{K}{log}^{2}K\right)$
Xiao Shi et al. [60]	The work presents a quantum-inspired k-means clustering algorithm that begins by mapping classical data into quantum states, which are represented as matrix product states. The algorithm then minimizes the loss function using the variational matrix product states method in an expanded space, leveraging the power of quantum-inspired techniques to efficiently handle the clustering process. This algorithm does not rely on Lloyd’s algorithm, with key components including SwapTest and GroverOptim. The proposed algorithm is applied to the Breast, Ionosphere, Wine, Yeast, and E. coli datasets, demonstrating higher prediction accuracies compared to the classical k-means algorithm. The platform used for implementation is not specified.	Clustering	Not mentioned
J. Chen, X. Qi, L. Chen et al. [61]	This work proposes a k-means algorithm called QALO-K, which combines k-means with a quantum-inspired ant lion optimization approach. It was tested on several standard datasets from the UCI Machine Learning Repository, including Iris, Glass, Wine, Cancer, Vowel, CMC, and Vehicle. The experimental results demonstrate that the detection rate and accuracy of QALO-K are superior to the classical k-means algorithm. The platform used for implementation is MATLAB.	Intrusion detection	$O\left(N^5\right)$

contains an overview of the applications of the quantum k-means algorithm.

4.2.3. Quantum Principal Component Analysis

Principal Component Analysis (PCA) is a method for reducing the dimensionality of data. It works by taking N-dimensional feature vectors (which may be correlated) from a training dataset, applying an orthonormal transformation, and compressing them to R-dimensional data. This lower-dimensional representational representation retains most of the important information and can be used in other machine learning algorithms. The advantage is that it allows similar conclusions to be drawn as with the full dataset, but with much faster execution, especially when $R\ll N$.

The quantum version of PCA (qPCA) was proposed by Lloyd, Mohseni and Rebentrost [62]. It offers and exponential speedup over the classical PCA algorithm by leveraging quantum computing techniques, potentially enabling much faster processing of large datasets.

The qPCA can be implemented using quantum phase estimation subroutine. A detailed description of each algorithm’s step is described below.

• Demean and normalization of classical data
  Firstly, the N-dimensional vectors should be demeaned. This can be expressed mathematically by the following equation:

  $$\begin{array}{cc}\hfill x\left(i\right)& \to x\left(i\right)-\overline{x},\overline{x}={\displaystyle \frac{1}{M}}\sum _{i=1}^{M}x\left(i\right)\hfill \end{array}$$

  (241)
  Next, the items should be normalized. This can be expressed mathematically by the following equation:

  $$\begin{array}{c}\hfill x\left(i\right)\to {\displaystyle \frac{x\left(i\right)}{\parallel x\parallel }},\parallel x\parallel =\sqrt{\sum _{k=1}^N{x}_k^2}\end{array}$$

  (242)
• Data encoding
  Classical data should be converted into quantum data as described previously.

  $$x\to |x\rangle =\sum _{k=1}^N{x}_k|k\rangle$$

  (243)
• Covariance/correlation matrix
  The density matrix can be described by the following equation:

  $$\rho ={\displaystyle \frac{1}{M}}\sum _{i=1}^M|x\left(i\right)\rangle \langle x\left(i\right)|$$

  (244)
  The tensor product $|x(i)\rangle \langle x(i)|$ is written as

  $$|x\left(i\right)\rangle \langle x\left(i\right)|=\sum _{k=1}^N\sum _{m=1}^N{x}_k^{\left(i\right)}{x}_m^{\left(i\right)}|k\rangle \langle m|$$

  (245)

  which, in matrix notation, is represented by

  $$|x\left(i\right)\rangle \langle x\left(i\right)|=\left[\begin{array}{cccc}{x}_1^{\left(i\right)}{x}_1^{\left(i\right)}& x_1^{\left(i\right)}{x}_2^{\left(i\right)}& \dots & x_1^{\left(i\right)}{x}_N^{\left(i\right)}\\ x_2^{\left(i\right)}{x}_1^{\left(i\right)}& x_2^{\left(i\right)}{x}_2^{\left(i\right)}& \dots & x_2^{\left(i\right)}{x}_N^{\left(i\right)}\\ ⋮& ⋮& \ddots & ⋮\\ x_N^{\left(i\right)}{x}_1^{\left(i\right)}& x_N^{\left(i\right)}{x}_2^{\left(i\right)}& \dots & x_N^{\left(i\right)}{x}_N^{\left(i\right)}\end{array}\right]$$

  (246)
  Thus, the sum over training examples produces the following matrix:

  $${\displaystyle \frac{1}{M}}\sum _{i=1}^M|x\left(i\right)\rangle \langle x\left(i\right)|={\displaystyle \frac{1}{M}}\left[\begin{array}{cccc}\sum _i{x}_1^{\left(i\right)}{x}_1^{\left(i\right)}& \sum _i{x}_1^{\left(i\right)}{x}_2^{\left(i\right)}& \dots & \sum _i{x}_1^{\left(i\right)}{x}_N^{\left(i\right)}\\ \sum _i{x}_2^{\left(i\right)}{x}_1^{\left(i\right)}& \sum _i{x}_2^{\left(i\right)}{x}_2^{\left(i\right)}& \dots & \sum _i{x}_2^{\left(i\right)}{x}_N^{\left(i\right)}\\ ⋮& ⋮& \ddots & ⋮\\ \sum _i{x}_N^{\left(i\right)}{x}_1^{\left(i\right)}& \sum _i{x}_N^{\left(i\right)}{x}_2^{\left(i\right)}& \dots & \sum _i{x}_N^{\left(i\right)}{x}_N^{\left(i\right)}\end{array}\right]$$

  (247)
  The representation of demeaned data is equivalent to covariance matrix.
• Exponential of density matrix
  QPE can be applied to efficiently obtain the eigenvalues and eigenvectors of density matrix. As mentioned before the QPE requires a unitary operation U. It is known that $U=e^{iH}$ is unitary for any Hermitian matrix H. The density matrix $\rho$ is Hermitian by definition. Therefore, the gate $U=e^{i\rho t}$ should be calculated in order to apply QPE subroutine. It should be noted that the eigenvectors of $\rho$ are also eigenvectors of $e^{i\rho t}$ and the eigenvalues $\lambda$ of $\rho$ are $e^{i\lambda t}$
• Eigendecomposition of density matrix
  The qPCA uses a slight modification of a QPE subroutine by applying the U to the density matrix and not to a eigenvector. For simplicity, let us apply U to the state $|x(i)\rangle$.

  $$\begin{array}{cc}{e}^{-i\rho t}|x\left(i\right)\rangle \hfill & ={\displaystyle \sum _{j=1}^M}{e}^{-i\lambda \left(j\right)t}|\varphi \left(j\right)\rangle \langle \varphi \left(j\right)|x\left(i\right)\rangle \hfill \\ \hfill & ={\displaystyle \sum _{j=1}^M}{e}^{-i\lambda \left(j\right)t}\langle \varphi \left(j\right)|x\left(i\right)\rangle |\varphi \left(j\right)\rangle \hfill \\ \hfill & ={\displaystyle \sum _{j=1}^M}c\left(ij\right)|\varphi \left(j\right)\rangle ,c\left(ij\right)=e^{-i\lambda \left(j\right)t}\langle \varphi \left(j\right)|x\left(i\right)\rangle \hfill \end{array}$$

  (248)
  The output of QPE is as follows:

  $${|0\rangle }_n|x\left(i\right)\rangle \to {\displaystyle \sum _{j=1}^M}c\left(ij\right)|\tilde{\lambda }\left(j\right)\rangle |\varphi \left(j\right)\rangle$$

  (249)
  The output can also be presented as density matrix representation as

  $$\eta \left(i\right)={\displaystyle \sum _{j=1}^M}{|c\left(ij\right)|}^2|\tilde{\lambda }\left(j\right)\rangle \langle \tilde{\lambda }\left(j\right)|\otimes |\varphi \left(j\right)\rangle \langle \varphi \left(j\right)|$$

  (250)
  As mentioned before, the QPE is applied to $\rho$ in qPCA. Therefore,

  $$\begin{array}{cc}\eta \hfill & ={\displaystyle \sum _{j=1}^M}{\displaystyle \sum _{i=1}^M}{\displaystyle \frac{1}{M}}{|c\left(ij\right)|}^2|\tilde{\lambda }\left(j\right)\rangle \langle \tilde{\lambda }\left(j\right)|\otimes |\varphi \left(j\right)\rangle \langle \varphi \left(j\right)|\hfill \\ \hfill & ={\displaystyle \sum _{j=1}^M}\rho \left(j\right)|\tilde{\lambda }\left(j\right)\rangle \langle \tilde{\lambda }\left(j\right)|\otimes |\varphi \left(j\right)\rangle \langle \varphi \left(j\right)|\hfill \end{array}$$

  (251)
  The $\lambda \left(j\right)$ coefficient is derived as follows:

  $$\begin{array}{cc}{\displaystyle \sum _{i=1}^M}{\displaystyle \frac{1}{M}}{|c\left(ij\right)|}^2\hfill & ={\displaystyle \sum _{i=1}^M}{\displaystyle \frac{1}{M}}{e}^{-i\lambda \left(j\right)t}\langle \varphi \left(j\right)|x\left(i\right)\rangle \langle x\left(i\right)|\varphi \left(j\right)\rangle e^{i\lambda \left(j\right)t}\hfill \\ \hfill & =\langle \varphi \left(j\right)|{\displaystyle \sum _{i=1}^M}{\displaystyle \frac{1}{M}}|x\left(i\right)\rangle \langle x\left(i\right)||\varphi \left(j\right)\rangle \hfill \\ \hfill & =\langle \varphi \left(j\right)|\rho |\varphi \left(j\right)\rangle =\lambda \left(j\right)\hfill \end{array}$$

  (252)
• Sampling
  The final step involves sampling from the final quantum state to obtain features of eigenvectors.

The qPCA offers an exponential speedup over its classical counterpart.

Table 9. Overview of qPCA variants.

Author	Description	Application	Complexity
Martin et al. [63]	The proposed quantum PCA introduces a model for pricing interest rate financial derivatives. It incorporates the QPE algorithm as a quantum subroutine. This algorithm is implemented using IBM’s Qiskit platform.	Finance	Not mentioned
Dri et al. [64]	The proposed quantum PCA is an end-to-end implementation of the algorithm designed for managing interest rate risk. It incorporates the QPE algorithm as a quantum subroutine. This algorithm is implemented using IBM’s Qiskit platform.	Finance	Not mentioned
Salari et al. [65]	The proposed quantum PCA is used for pattern recognition. The proposed algorithm is based on the QPE algorithm. The platform used for implementation is not specified.	Pattern recognition	$O(NlogN)$
Zidong Lin et al. [66]	The proposed quantum PCA is designed for classifying thoracic CT images from COVID-19 patients. The proposed algorithm is based on the QPE algorithm. This algorithm is implemented using an NMR quantum processor.	Classification of thoracic CT images from COVID-19 patients	$O\left({(logd)}^2\right)$
Max Hunter Gordon et al. [67]	The proposed quantum PCA is designed for quantum datasets and is applied to a set of molecular ground states corresponding to different interatomic distances. The algorithm accurately compresses these molecular ground states into a low-dimensional subspace. It is based on the QPE algorithm. However, this algorithm has not yet been implemented on real quantum hardware.	Dimensionality reduction	$O\left(N^2\right)$

contains an overview of the applications of the qPCA.

5. Quantum Deep Learning

As described above, various QML algorithms offer exponential or quadratic speedup over their classical counterparts. Researchers are also exploring the potential quantum versions of neural networks (NNs) in comparison with their classical versions. The potential advantages of quantum versions of NNs include exponential memory capacity, fewer hidden neurons with higher performance, faster learning and processing speed, as well as smaller scale and higher stability [19].

A quantum neural network (qNN) consists of four important components: the quantum input layer, quantum hidden layer, measurement layer, and a classical optimizer. The general structure of the quantum circuit for a qNN is shown in Figure 26.

The quantum input layer refers to the process of encoding classical data into quantum states. This process was described previously. Once the data is encoded into qubits, a unitary transformation is applied to the input, similar to how the weight vector functions in classical neural networks. The exact functionality of the unitary operator U depends on the specific problem. Finally, the output is obtained by measuring the output qubits [2]. The general mathematical form can be described by the following equation:

$$|f\rangle =U\sum _{n=0}^{N-1}{\theta }_n|x_n\rangle$$

(253)

where $|f\rangle$ represents the output quantum state, U the unitary operator, ${\theta }_n$ the weight associated with each input quantum state, and $|x_n\rangle$ the input quantum state.

Similar to classical NNs, the training of qNNs involves optimizing the parameters of the unitary operator U to minimize a loss function.

The combination of deep learning and quantum computing is in its early stages.

Table 10. Overview of quantum deep learning variants.

Author	Description
Zhao et al. [68]	The proposed work introduces a quantum feedforward neural network for classification purposes. It incorporates the swap test as a quantum subroutine. The platform used for implementation was not specified.
Tacchino F. et al.: [14]	The proposed work introduces a quantum version of a perceptron to classify simple patterns, such as distinguishing vertical or horizontal lines among various possible inputs. This algorithm is implemented using IBM’s Qiskit platform.
X-F Niu and W-P Ma [69]	The proposed work introduces a quantum neural network based on a multi-layer activation function, designed for lie detection. This algorithm is implemented using MATLAB.
Cong et al. [70]	The proposed work introduces a quantum convolutional neural network for quantum phase recognition. The algorithm is based on quantum circuits and unitary transformations (quantum gates). Additionally, the work presents a protocol for implementing the algorithm using neutral Rydberg atoms.
Henderson et al. [71]	The proposed work introduces a quantum convolutional neural network for image classification. The algorithm is based on quantum circuits and unitary transformations (quantum gates). This algorithm is implemented using the QxBranch Quantum Computer Simulation System.
Zhao et al. [72]	The proposed work introduces a quantum version of the Bayesian technique, incorporating quantum matrix inversion as a quantum subroutine. This algorithm is implemented using IBM’s and Rigetti’s platforms.
Wiebe et al. [73]	The proposed work explores the integration of quantum computing into deep learning tasks. It introduces quantum algorithms for accelerating training processes, particularly focusing on the use of quantum Boltzmann machines for unsupervised learning and quantum-enhanced optimization techniques for deep neural networks. The paper suggests that quantum speedups can improve efficiency in gradient descent and other optimization methods. The implementation platform is not explicitly mentioned in the paper.

provides an overview of the applications of qNNs.

It should be noted that the applications of quantum neural networks are currently limited due to the constraints of existing quantum hardware. However, as quantum hardware capabilities improve, it will become possible to apply quantum architectures of QNNs to larger datasets and demonstrate quantum advantage.

6. Real-World Applications of QML

There is an exponential growth of interest among researchers in applying QML techniques to real-world problems. The most common fields of application include healthcare, biology, finance, high-energy physics, pattern recognition and classification, image processing and analysis, wireless communication and more.

In healthcare, QML can be applied to medical imaging, biosignal analysis and medical health records to enable more precise medicine, facilitate early cancer diagnosis and predict different stages of diabetes. In [74], two distinct approaches were employed for medical image classification. The first approach involved integrating quantum circuits into the training process of classical neural networks, while the second focused on designing and training quantum orthogonal neural networks. These methods were applied to retinal color fundus images and chest X-rays. The algorithms were evaluated using IBM quantum hardware with configurations of 5, 7, and 16 qubits. A more comprehensive summary of the state of the art of quantum computing for healthcare applications is presented in [1,75].

In the biomedical domain, QML can achieve groundbreaking advancements in genomic sequence analysis, a field commonly referred to as the “omics” domain. The term “omics” encompasses data derived from genetics, such as DNA sequences and proteins, with the goal of developing effective and personalized treatments. QML has the potential to perform various tasks, including analyzing protein–DNA interactions, predicting gene expression, and conducting genomic sequencing analysis. Additionally, the categorization of cancer-causing genes to enable early cancer detection remains an area of ongoing research. For example, transcription factors regulate gene expression, but the mechanisms by which these proteins recognize and specifically bind to their DNA targets remain a topic of debate. In [76], a QML algorithm was implemented to predict binding specificity. The experiments were conducted using a quantum annealer to rank transcription factor binding. Additionally, in [77], a quantum-hybrid deep neural network was utilized to predict protein structures. A more comprehensive summary of the state of the art of quantum computing for omics study is presented in [1].

In finance, QML can be applied to portfolio optimization, fraud detection, market prediction and trading, pricing and risk management. In [78], a novel quantum reservoir computing (QRC) method was introduced and applied to the foreign exchange market. This approach effectively captured the stochastic dynamics of exchange rates, achieving significantly greater accuracy compared to classical reservoir computing techniques. Furthermore, in [79], a QML algorithm was employed for feature selection in fraud detection. The results obtained using an IBM Quantum computer were promising. A more comprehensive summary of the state of the art of quantum computing for finance applications is presented in [80,81].

High-energy physics (HEP) explores the fundamental nature of matter and the universe. While the standard model serves as a robust framework for explaining many physical phenomena, it does not address critical questions such as the source of dark matter or the properties of neutrino mass. QML offers exciting opportunities in HEP, including applications like quantum system simulations, nuclear physics computations (such as neutrino–nucleus scattering cross-sections), insights into quantum gravity and the development of quantum sensors to detect new physics beyond the standard model. The study by [82] demonstrates the use of QML for quantum simulations in high-energy physics. A more comprehensive summary of the state of the art of quantum computing for HEP applications is presented in [83].

QML has shown great potential in pattern recognition and classification tasks. The work presented in [84] introduces a quantum kNN algorithm that outperforms its classical equivalent in terms of time complexity. Additionally, the findings suggest that the quantum approach delivers insights that go beyond the capabilities of traditional methods.

In addition, QML holds significant potential in image processing. Quantum computing could enable major advancements in areas such as quantum image representation, geometric transformations, image protection, edge detection, image segmentation, filtering and compression [85]. In [86], a qSVM was implemented for cloud detection in satellite cloud images. The algorithm was developed using the PennyLane Python package and the experiments were conducted on a quantum simulator. In [87], a quantum approach to tomosynthesis is presented by implementing the 2D radon transform using the QFT and its inverse with the quantum 3D FFT, demonstrating the process through fundamental quantum gates. In [88], the quantum 3D FFT is further utilized for velocity filtering with a short execution time, serving as an important technical tool for isolating objects moving at speeds within certain limits. Both works were implemented using MATLAB 2022b. A more comprehensive summary of the state of the art of quantum computing for image processing is presented in [85,89]. Another emerging area is the wireless communication, where a QML-based framework for 6G communication network was proposed in [90]. This framework explores the potential of quantum algorithms to enhance data transmission, signal processing and network optimization in next generation wireless systems.

7. Future Directions in Quantum Machine Learning and Deep Learning

As quantum hardware continues to advance and software frameworks for quantum programming mature, QML and QDL are poised to evolve rapidly. However, several key challenges remain unresolved, and identifying promising research directions is crucial for unlocking the full potential of quantum-enhanced learning systems. This section outlines emerging areas of interest and critical open problems in the field.

7.1. Scalability and Quantum Advantage

One of the primary challenges is demonstrating a clear quantum advantage for practical machine learning tasks. While theoretical speedups exist for selected problems [45], most current QML models rely on hybrid approaches whose scaling behavior on real-world data is still poorly understood. Future work should explore concrete benchmarks comparing quantum models with classical baselines [21], and hardware-aware algorithm design to optimize circuit depth, qubit connectivity, and measurement schemes [91].

7.2. Barren Plateaus and Trainability

Variational quantum circuits (VQCs), central to many QML algorithms, often suffer from barren plateaus—regions in parameter space where gradients vanish exponentially [92]. This presents a major obstacle to training quantum models efficiently. Promising directions include novel cost function design [93], local cost functions and entanglement-aware ansatz structures [94], and layer-wise training and noise-aware optimization [95].

7.3. Quantum Data Representations

The way classical data is embedded into quantum states (quantum feature maps) significantly affects the performance and expressivity of QML models. Important lines of research are data encoding strategies with theoretical guarantees [96], expressibility vs. trainability trade-offs [97], and cost-efficient state preparation algorithms [98].

7.4. Model Expressivity and Generalization

Theoretical understanding of expressivity and generalization in quantum neural networks is still developing. Future work includes generalization bounds for variational quantum models [99], the relationship between expressivity, entanglement, and overfitting [100], and complexity theory perspectives on learnability [17].

7.5. Quantum Natural Language Processing (QNLP)

QNLP leverages quantum tensor structures to model grammatical and semantic relations. Although still emerging, the field holds potential for language understanding and semantic parsing [101]. Key directions are ccaling categorical QNLP models to larger corpora, hybrid QNLP pipelines using pre-trained classical language models, and noise robustness in compositional circuits.

7.6. Integration with Classical ML and Federated Architectures

Hybrid Quantum–Classical architectures offer a realistic near-term path. Examples include quantum kernel methods in support vector machines [49], quantum data encryption in federated learning [102], and decentralized optimization over quantum-secured communication channels.

7.7. Domain-Specific Applications and Benchmarks

Real-world adoption of QML depends on application-driven success stories in fields such as healthcare (drug discovery, patient stratification [103], finance (portfolio optimization and risk analysis [104], and bioinformatics (quantum-enhanced genomic analysis [76]. Future work must focus on the following:

• Domain-aligned datasets and reproducible QML benchmarks.
• Interpretability and robustness of quantum predictions.
• Integration into existing ML pipelines with domain constraints.

In summary, while current QML and QDL systems remain in a nascent stage, the research community is actively exploring numerous directions with transformative potential. Progress in quantum hardware, algorithm design, and theoretical understanding will jointly determine the trajectory of quantum machine learning in the coming decade.

8. Conclusions

This paper provides a comprehensive introduction to QC, specifically designed for beginners. It offers an overview of the fundamental concepts and tools that form the foundation of QC, such as qubits, superposition, entanglement, quantum gates and quantum algorithms. The paper also explores the connection between quantum algorithms and QML as well as QDL. Additionally, it examines their potential applications in various fields such as bioinformatics, finance and HEP. By offering a clear and accessible explanation of these key ideas, the paper seeks to provide readers with a solid understanding of both the theory and practical implications of quantum computing in the modern technological landscape.

The fundamental knowledge of quantum physics, linear algebra and electronics is essential for studying the field of QC. By presenting the QPE algorithm [4], the usefulness of this method becomes apparent, particularly in one of the most groundbreaking quantum algorithms to date, Shor’s algorithm [3]. Shor’s algorithm provides an efficient solution to the factoring problem that is currently difficult for classical computers. Moreover, another groundbreaking algorithm, Grover’s algorithm [5], can be applied as a black box, providing a quadratic improvement over classical algorithms.

With the exponential growth of data generation and rapid technological advancements in recent years, classical machine learning algorithms may face challenges in addressing complex real-world problems. QML, leveraging the principles of quantum computing such as superposition and entanglement, is well-positioned to tackle the machine learning challenges of the future. Quantum algorithms can be integrated with machine learning to develop QML algorithms. Quantum subroutines have already been implemented and form the foundation of QML algorithms, as presented in this work. The quantum SVM can be implemented using both Grover’s algorithm [11] and the HHL algorithm [49]. The quantum version of the k-means algorithm can be implemented using Grover’s algorithm [54], while the quantum version of PCA can be implemented using the QPE subroutine [62].

Researchers are also working on finding real-world applications for these algorithms. This work presents multiple applications. In [50], a quantum SVM is introduced, aimed at predicting solar irradiation based on the HHL algorithm. In [56], a quantum k-means algorithm based on Grover’s algorithm is applied to a heart disease dataset, where the quantum version outperforms its classical counterpart in terms of accuracy, precision, sensitivity, specificity and F1-score. In [63], quantum PCA is presented as an end-to-end implementation designed for managing interest rate risk, based on QPE.

Although these algorithms hold promise, they are not yet capable of fully replacing classical algorithms due to existing challenges. The first major challenge is state preparation, which involves converting classical data into quantum data. The second challenge lies in hardware limitations, as current quantum devices are not yet capable of handling large datasets effectively. Overcoming these barriers is essential to achieving true quantum supremacy in machine learning.

Looking ahead, future opportunities include the development of more effective quantum algorithms designed for practical and meaningful tasks. Additionally, considerations of time efficiency and algorithmic complexity will be crucial.

In summary, this work aims to provide a tutorial for beginners entering the field of QML by thoroughly studying the mathematics behind quantum algorithms and QML algorithms. Additionally, real-world applications are presented to illustrate the practical use of these concepts. The collective insights contribute to the expanding body of knowledge in quantum computing and bring us closer to their realization, paving the way for the implementation of these algorithms in real-world applications with practical use.