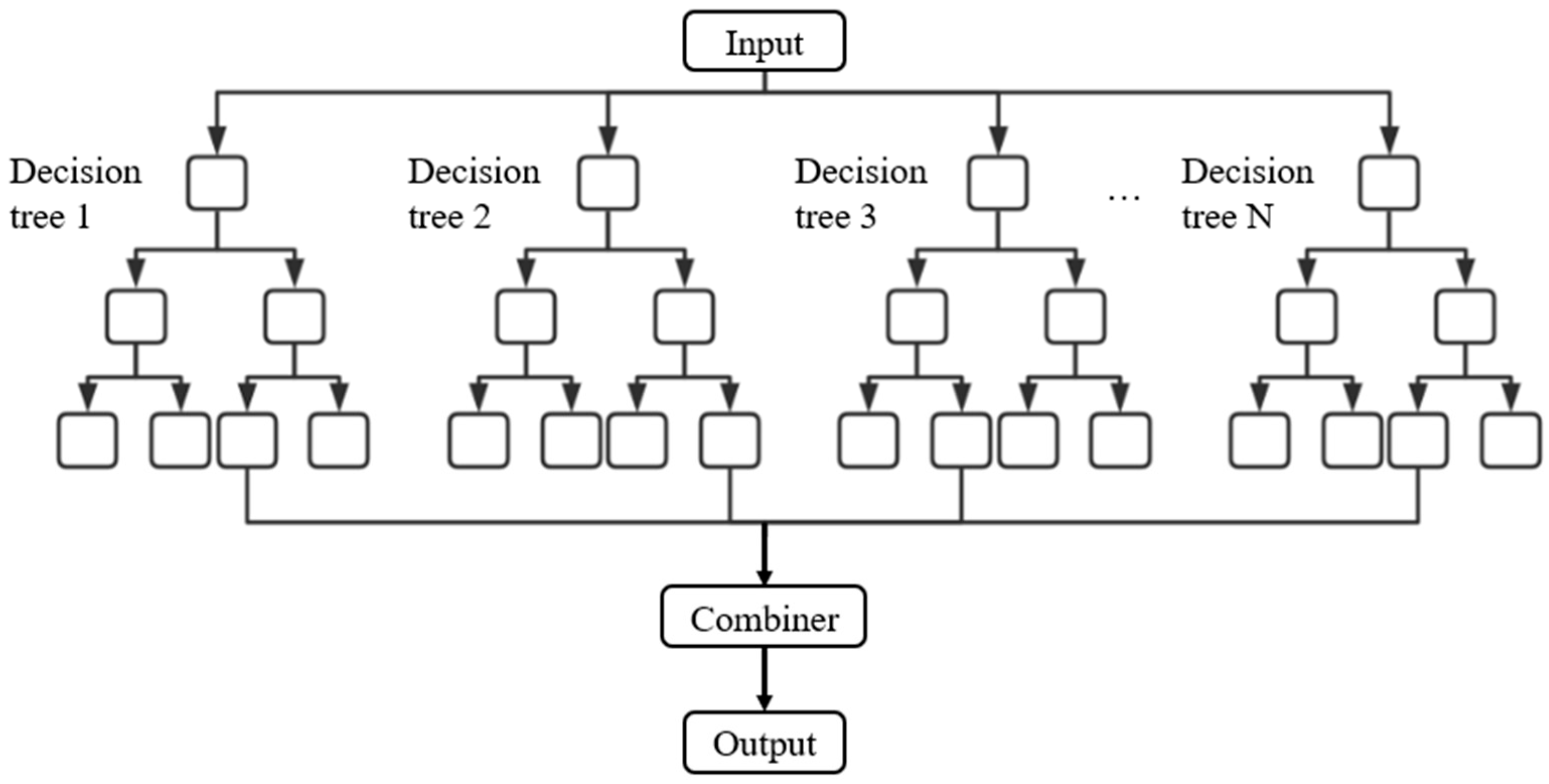
The trained models based on the three machine learning algorithms, random forest (RF), artificial neural networks (ANNs), and support vector machines (SVMs), were applied to perform predictive analysis of bearing layer depth. Two experimental cases were defined based on the set of explanatory variables used:
In both cases, the target variable was the depth of the bearing layer.
Input features were selected based on their availability in the borehole dataset and their relevance to the subsurface stratigraphy. In Case 2, stratigraphic classification was incorporated into a set of binary variables (0/1) indicating the presence or absence of a particular dominant soil type (e.g., clay, sand, or gravel) in each borehole record. This coding approach was adopted because detailed lithologic descriptions were inconsistent across the dataset, making more fine-grained or ordinal coding impractical. While richer categorical descriptors such as lithologic codes or depositional environments could provide additional insights, these data are not complete or standardized. We acknowledge that this is a limitation, and future research may explore the use of one-hot encoding or embedded categorical features.
5.1. Evaluation of Prediction Accuracy
For performance evaluation, the trained models were used to predict the bearing layer depth at 10 randomly selected locations in Tokyo. The predictions were compared against actual measured data at these sites, and the prediction errors were computed.
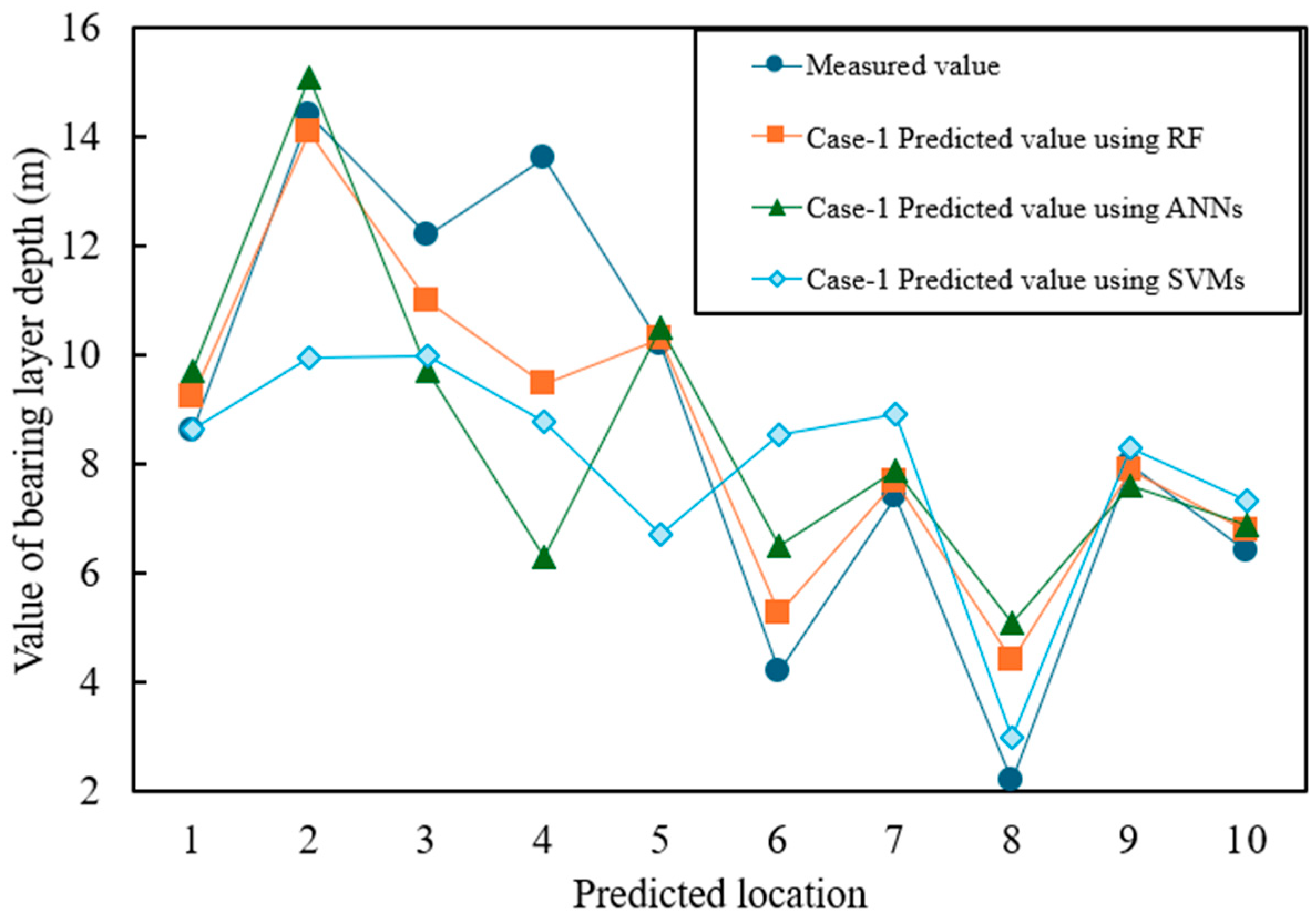
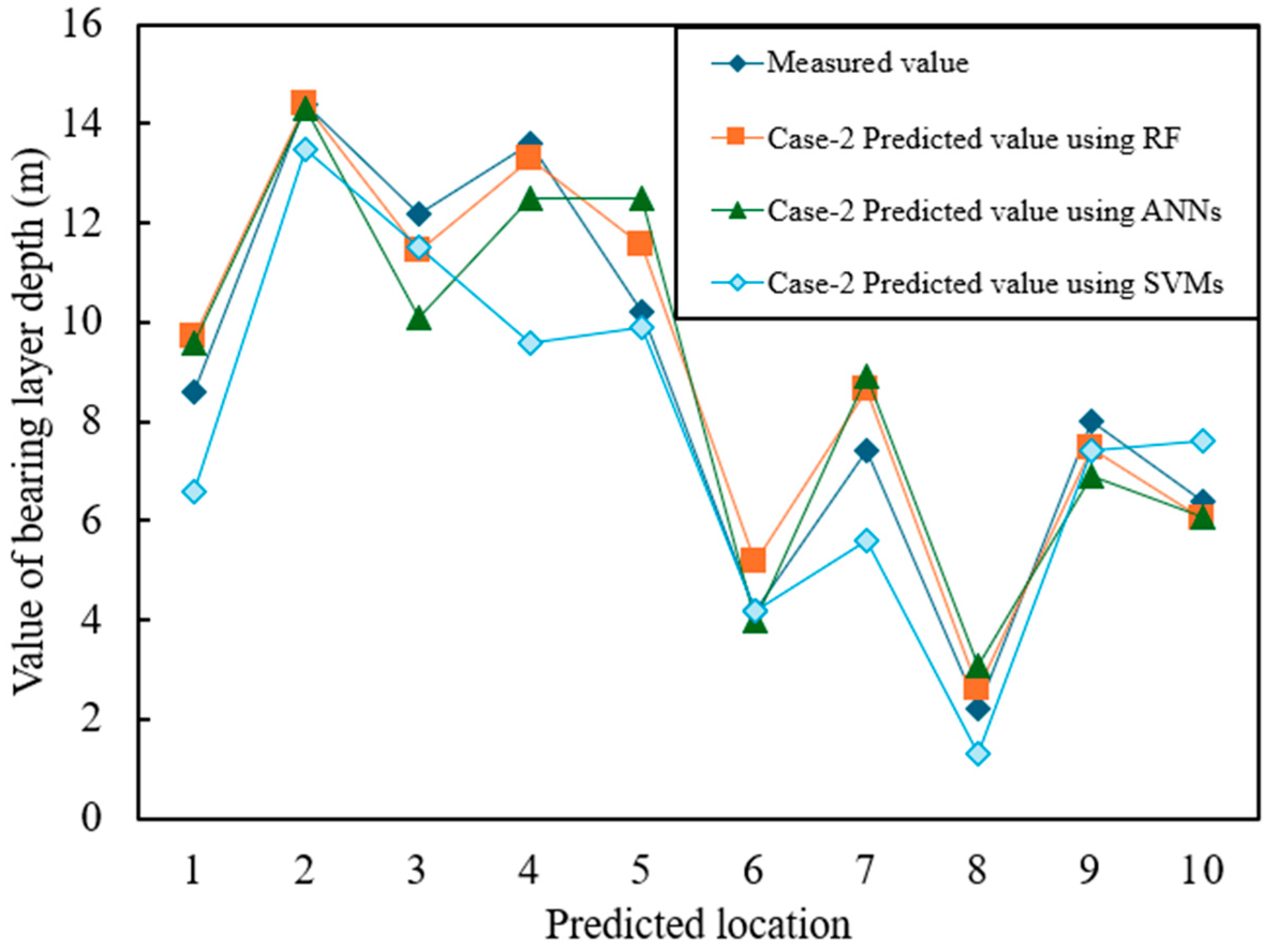
Figure 7 and
Figure 8 show the prediction results for Case-1 and Case-2, respectively, where the horizontal axis represents the predicted values and the vertical axis represents the measured values. The numerical results are summarized in
Table 6, which presents three widely used error metrics:
Mean absolute error (MAE): The average of the absolute differences between predicted and actual values;
Mean squared error (MSE): The average of the squared differences between predicted and actual values. Lower MSE values indicate a better model fit;
Root mean squared error (RMSE): The square root of MSE. Larger RMSE values suggest a greater overall error.
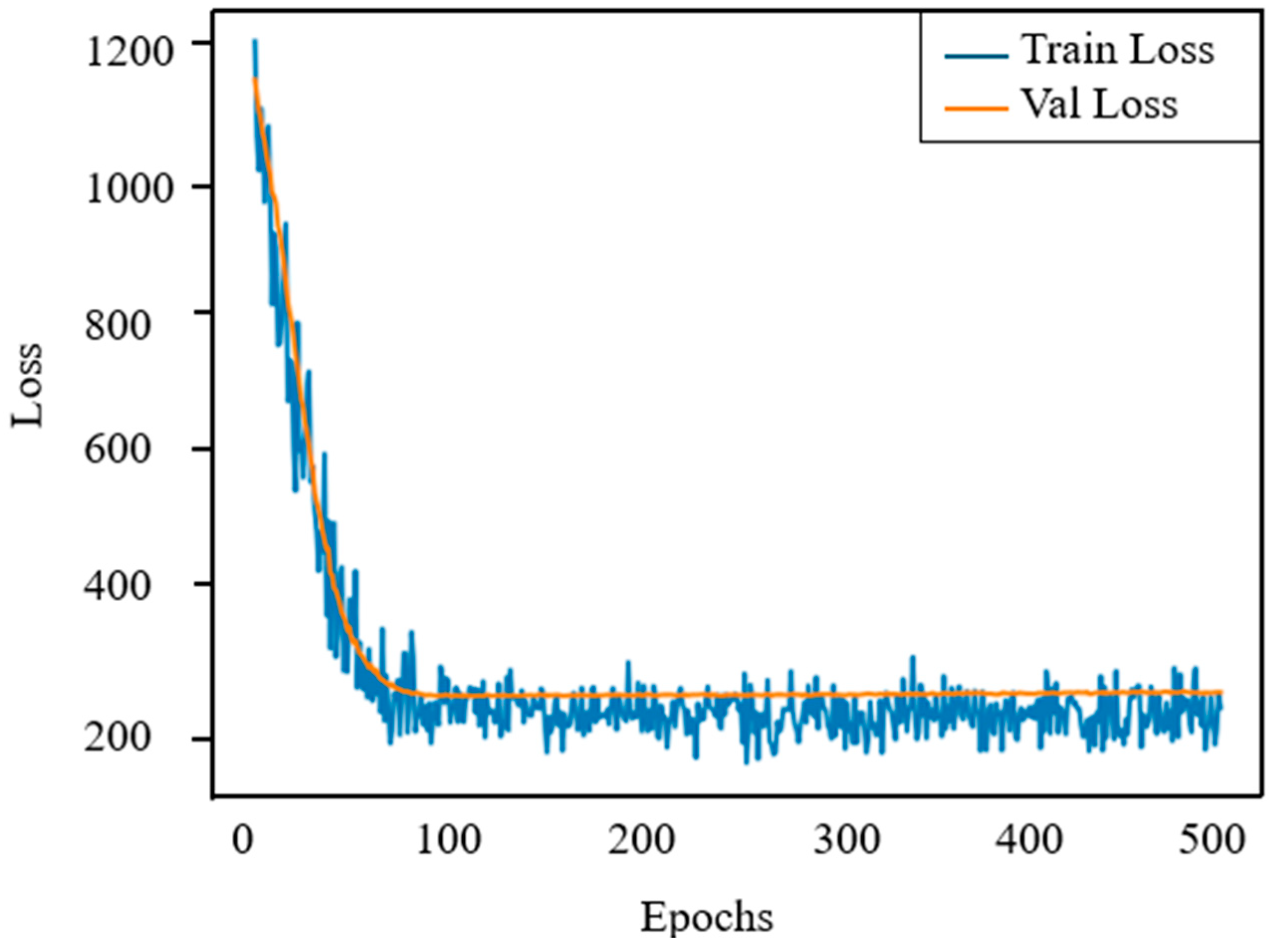
In terms of model performance, random forests consistently outperform ANNs and SVMs in terms of accuracy and robustness. However, to better understand the training behavior of ANNs and address overfitting, we plotted the training and validation loss curves, as shown in
Figure 9. The figure shows that both losses drop rapidly within the first 100 epochs, indicating fast convergence. After about 120 epochs, the curves stabilize and remain closely aligned, with a small gap between the two. This indicates that the model has good generalization capabilities to unseen data and no significant signs of overfitting. The observed stability confirms the effectiveness of the selected network architecture and training settings, including learning rate, batch normalization, and batch size. Overall, while ANNs are more sensitive to hyperparameter settings than random forests (RFs), the loss curve analysis provides quantitative evidence that the network has been properly regularized and maintains strong generalization capabilities.
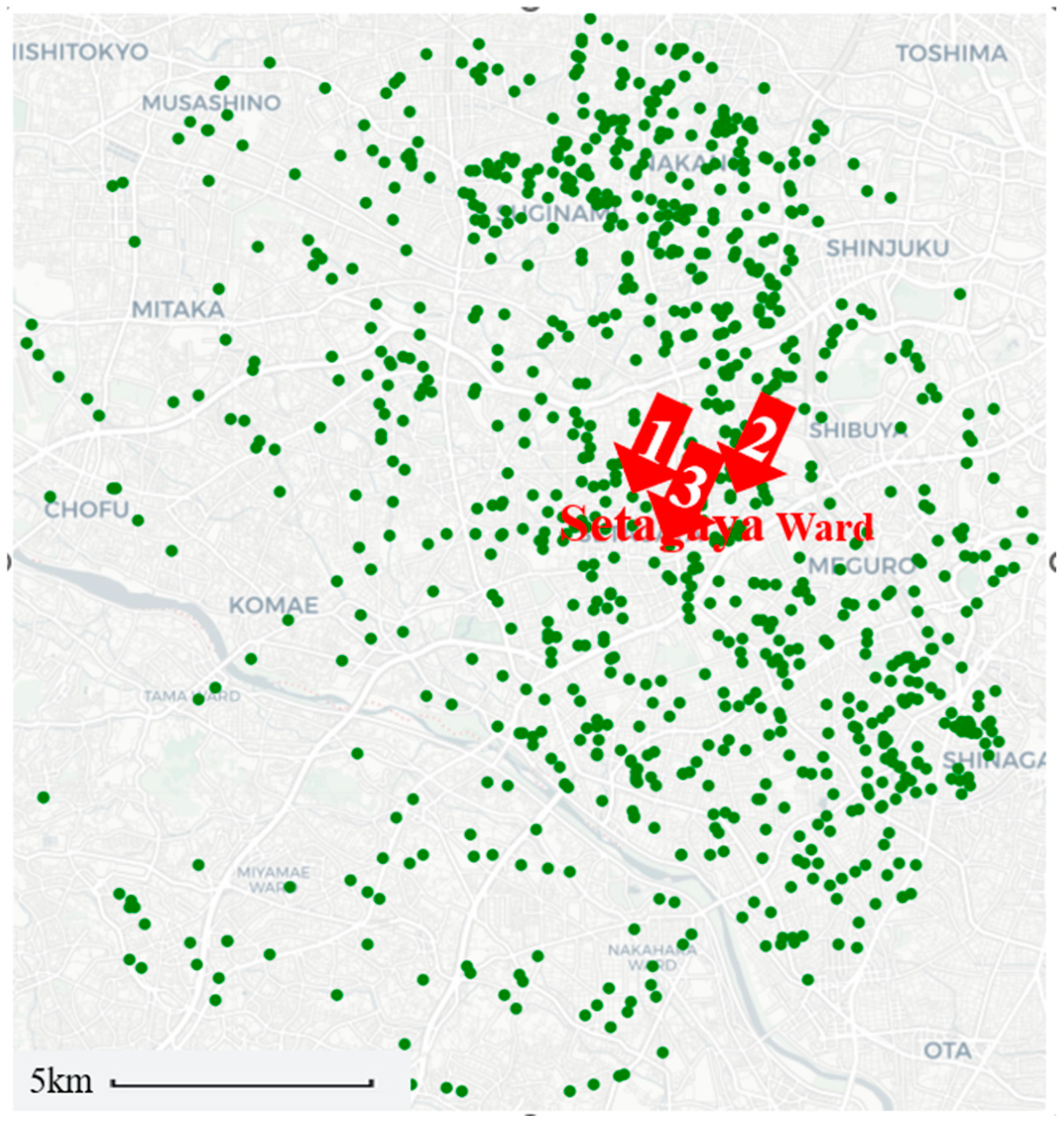
Table 7 presents the detailed prediction outcomes for the three representative locations highlighted in
Figure 3.
The results indicate that random forest consistently outperformed ANNs and SVMs in both cases. This superior performance is attributed to the robustness of RF, which is relatively insensitive to hyperparameter tuning and less prone to overfitting. In contrast, the performance of ANNs and SVMs exhibited greater variability, likely due to challenges in identifying optimal parameters, particularly under the influence of discretized feature spaces and limited data.
In terms of model-specific limitations, support vector machines (SVMs) are highly sensitive to kernel function and parameter selection and are computationally expensive for large datasets. Artificial neural networks (ANNs) require large amounts of training data to avoid overfitting, and their performance is affected by the choice of initialization strategy and learning rate. Random forest (RF) models, while robust, can suffer from feature selection bias in high-dimensional or sparse input spaces, and their ensemble nature reduces model interpretability.
Moreover, the inclusion of additional explanatory variables, as in Case-2, led to improved prediction accuracy across all models. This can be explained by two main factors:
- (1)
Enhanced Data Representation: The inclusion of stratigraphic classification as an additional feature enabled the models to better capture geological characteristics and underlying patterns relevant to bearing layer depth.
- (2)
Feature Interactions: Additional features increase the potential for discovering meaningful interactions among variables, allowing the models to build more accurate and expressive predictive functions.
However, while increasing the number of explanatory variables can enhance predictive performance, it may also increase the risk of overfitting, especially when irrelevant or redundant features are included. Therefore, careful feature selection is essential to balance model complexity and generalization ability.
For the random forest (RF) model, we evaluated the impact of varying the number of estimators (n_estimators) and the number of features considered at each split (max_features). The number of trees tested ranged from 10 to 150, increasing in increments of 10. The results show that the model performance improves rapidly when the number of trees reaches about 90, after which the improvement levels off, indicating diminishing returns. Similarly, max_features ranged from 1 to 5. The best results were observed when max_features was set to 5, meaning that the best performance was achieved using all input features at each node split. Overall, the RF model showed relatively low sensitivity to changes in hyperparameters, demonstrating its robustness.
For artificial neural networks (ANNs), we performed sensitivity analyses on the number of neurons in the hidden layer and the learning rate, two key hyperparameters that directly impact model complexity and training dynamics. We varied the number of neurons in the first hidden layer from 32 to 512 and tested learning rates ranging from 0.00001 to 0.01. Results show that both parameters significantly impact model performance. Specifically, a learning rate of 0.0001 consistently achieves stable convergence with the lowest error across multiple configurations. Too small a learning rate results in slow convergence, while too large a learning rate leads to instability and divergence during training. Similarly, too few neurons limits the capacity of the model, while too many leads to overfitting. These findings highlight the need to carefully tune ANN models.
To evaluate the sensitivity of the support vector machine (SVM) model, we investigated the impact of the kernel coefficient γ. This coefficient plays a crucial role in determining the shape of the decision boundary when using the radial basis function (RBF) kernel. The value of γ was varied from 0.001 to 1.0 in increments of 0.1, while the regularization parameter C was fixed to 1. The results show that the model performance fluctuates significantly within this range. Specifically, γ values between 0.2 and 0.4 produce the lowest RMSE and MAE, while values outside this range lead to increased prediction errors due to overfitting (larger γ) or underfitting (smaller γ). This shows that the SVM model is highly sensitive to the choice of kernel parameters.
In order to enhance the interpretability and reliability of the model in practical engineering, this study introduces a prediction uncertainty quantification method based on the traditional error assessment metrics (MAE, MSE, and RMSE) to provide a more comprehensive basis for model evaluation.
For the RF model, we used the Quantile Regression Forests (QRF) method to obtain the 95% prediction interval (PI) corresponding to each predicted value. This method can effectively estimate the upper and lower confidence bounds based on the distribution information of the nodes in the tree model.
For the SVM and ANN models, since they do not have built-in confidence outputs, we estimate the model uncertainty by the bootstrap resampling technique. This is carried out by resampling the training set multiple independent models, predicting the test set, and constructing empirical confidence intervals by counting the distribution of results for each prediction sample.
Therefore, the representative test samples were analyzed, and the results show that most of the actual values fall within the prediction intervals, reflecting that the models have good stability and robustness. In addition, the statistical results show that the average width of the prediction intervals of the models is controlled within a reasonable range and the coverage of the intervals is high, which further validates their potential to be applicable to engineering risk assessment.
In summary, the prediction uncertainty analysis in this study provides theoretical basis and data support for foundation design and risk assessment in seismic zones or sites with complex geological conditions.
5.2. Effects of Data Density on Prediction Accuracy
To investigate the impact of data density on prediction performance, we conducted an analysis using the random forest (RF) model developed in Case-2. Specifically, we examined how varying spatial data density influences model accuracy, with a focus on localized prediction performance.
Using Point 1 in
Figure 3 as the reference center, we generated six data subsets with different spatial densities: 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0 points/km
2. For instance, a density of 0.5 points/km
2 corresponds to a circular region with a radius of 10 km centered at Point 1, from which 157 data points were extracted [0.5 = 157/(π × 10
2)]. In total, six test cases were constructed based on these density levels. The composition of each dataset is illustrated in
Figure 10. To ensure a fair comparison between density conditions, all experiments use the same random forest model architecture and hyperparameter settings to ensure that changes in prediction performance only come from differences in the amount of spatial data, rather than changes in the model configuration itself.
In addition, data points under each density condition are selected by random sampling, and the experiment is repeated five times with different random seeds to reduce sampling bias. The prediction results for each density level reported in this article are the average of multiple experiments, which are representative and robust.
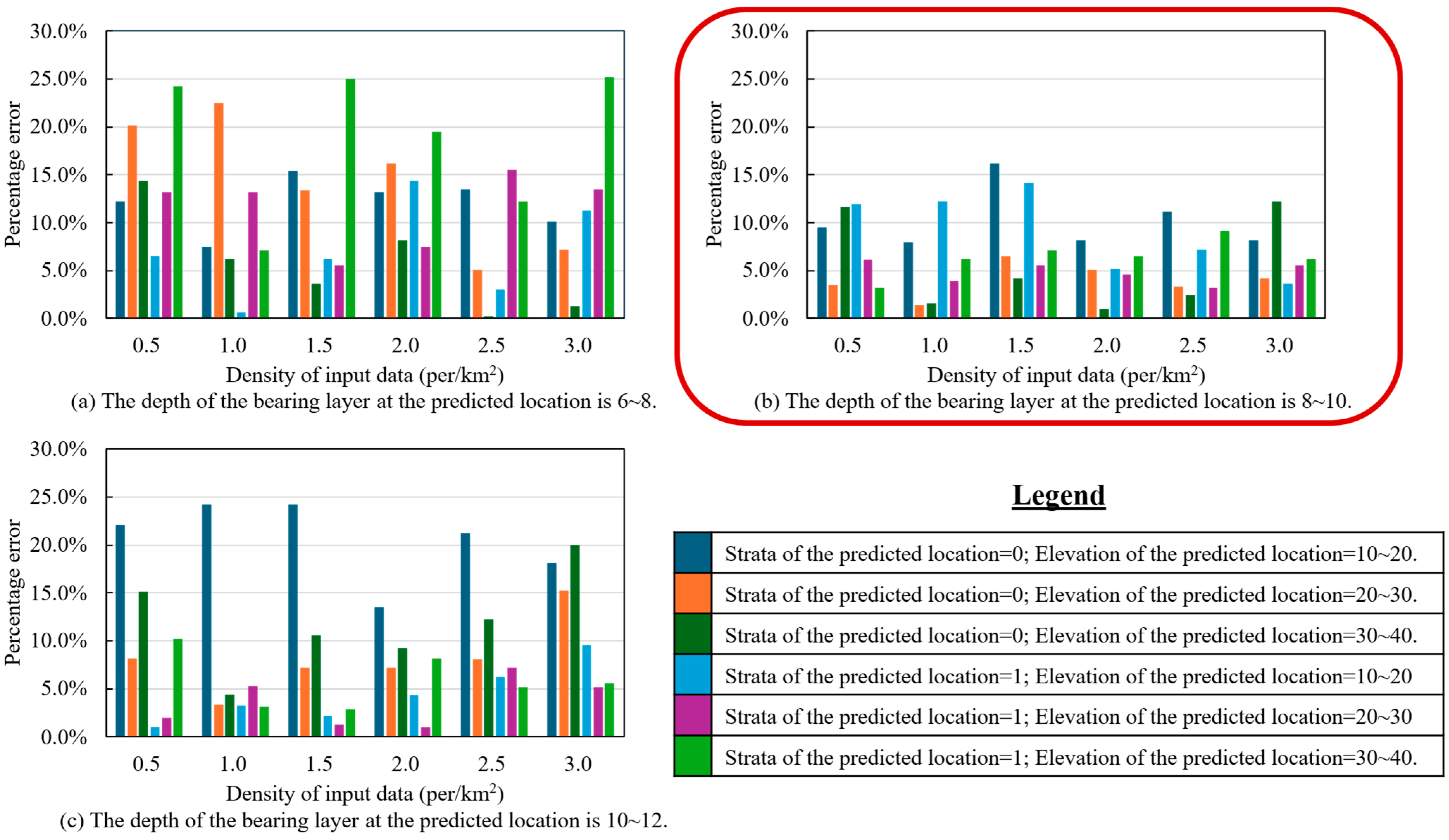
To ensure meaningful analysis, the evaluation was limited to data points within typical value ranges: bearing layer depth between 6 and 12 m, and elevation between 20 and 50 m. Predictions were then performed for each subset, and the results are shown in
Figure 11. Prediction accuracy was assessed using percentage error (
PE), defined by Equation (6):
A lower percentage error indicates higher prediction accuracy. To facilitate visual interpretation, color gradients were applied, with lighter shades representing lower error and hence better performance.
The results demonstrate that prediction accuracy improves with increasing data density, particularly when the bearing layer depth is in the range of 8 to 10 m. This suggests that spatially denser datasets enable the model to better capture local geotechnical variations, leading to more accurate predictions.
In general, complex machine learning models require more data to achieve stable and accurate predictions. As supported by prior studies [
54,
55], larger training datasets typically lead to better model generalization, with performance improvements often increasing logarithmically with data volume. The findings of this study support this trend, confirming the robustness and high potential of the random forest algorithm for geological prediction tasks.
However, the RF model is not without limitations. A key concern is overfitting, where the model performs well on training data but fails to generalize to unseen samples. Since random forests achieve flexibility by combining multiple deep decision trees, they may capture noise as signal in high-density scenarios. Therefore, mitigating overfitting is an important avenue for future research.
Two directions are proposed for improvement:
- (1)
Integrating regularization techniques within the RF framework to reduce overfitting while maintaining predictive performance.
- (2)
Exploring alternative machine learning algorithms and conducting comparative evaluations to identify models with superior generalization under varying geological conditions.
In addition, the training and testing data in this study are from the Tokyo region of Japan, which has a strong regional focus. Cross-regional cross-validation has not been performed under the current research framework, and the spatial generalization ability of the model still needs to be further explored. The significant differences in stratigraphic structure, and in water table and soil properties’ distribution in different regions may lead to unstable model migration effects. In the future, datasets from other regions (e.g., Kansai or Chubu region in Japan) will be introduced in the follow-up work, and attempts will be made to incorporate migration learning, regional adaptive modeling, and other methods to improve the applicability and robustness of the model in a wider geological context.
5.3. Practical Applications
The prediction model proposed in this study shows strong potential for practical applications. A promising future direction is to integrate it into geotechnical mapping tools based on geographic information systems (GIS), thereby enabling prediction of the spatial distribution of bearing layer depth over a wide area. In addition, the model can be deployed on a web-based platform to provide engineers and planners with preliminary remote estimates of subsurface conditions, potentially reducing the need for extensive field surveys in the early planning stages.
In addition, the model has potential applications in disaster risk management. For example, it can be integrated into hazard assessment frameworks to identify geotechnically vulnerable areas, such as those prone to liquefaction in earthquake-prone areas. These insights may help infrastructure planning and early warning strategies. Although these applications are currently at a conceptual stage, they represent important directions for future research and development.
Currently, most practical applications are still limited to the visualization of discrete measurement points on geospatial maps. Based on the results of this study, future work will focus on the development of a comprehensive software platform that can perform real-time subsurface predictions, update the output results to a central database, and integrate dynamic environmental indicators such as soil erosion or groundwater contamination.
Widespread access to detailed geotechnical information through smart digital tools has great potential to overcome the urban development challenges posed by subsurface uncertainty. Ultimately, this research can not only support safer and more resilient infrastructure but also promote more sustainable urban planning and improve the quality of life in growing cities.