Optimisation-Based Feature Selection for Regression Neural Networks Towards Explainability
Abstract
1. Introduction
- How can mathematical programming be applied to identify the most important features in a trained ReLU neural network for regression tasks?
- How does the proposed MILP-based feature selection method compare to existing feature selection approaches in terms of predictive performance?
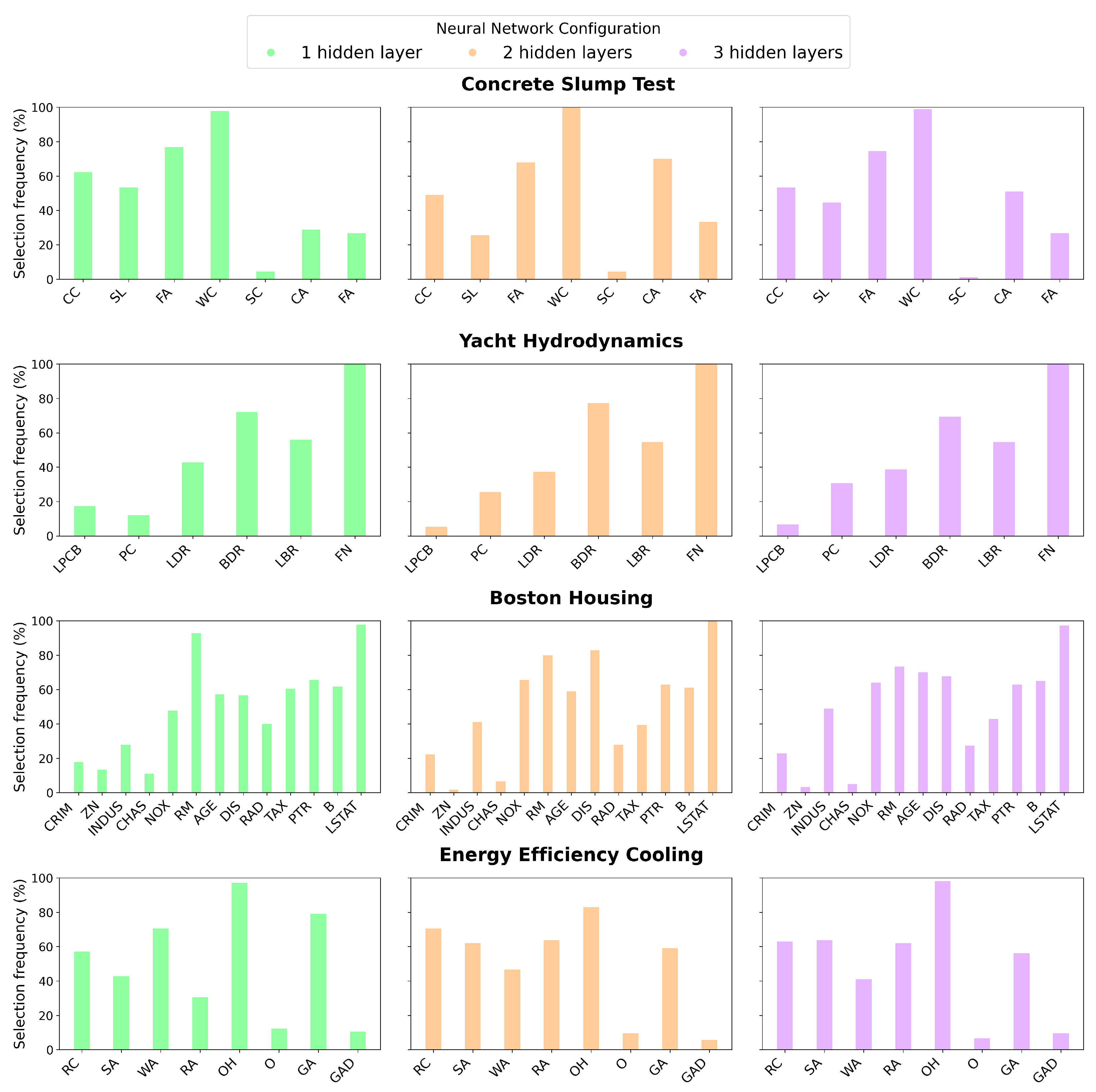
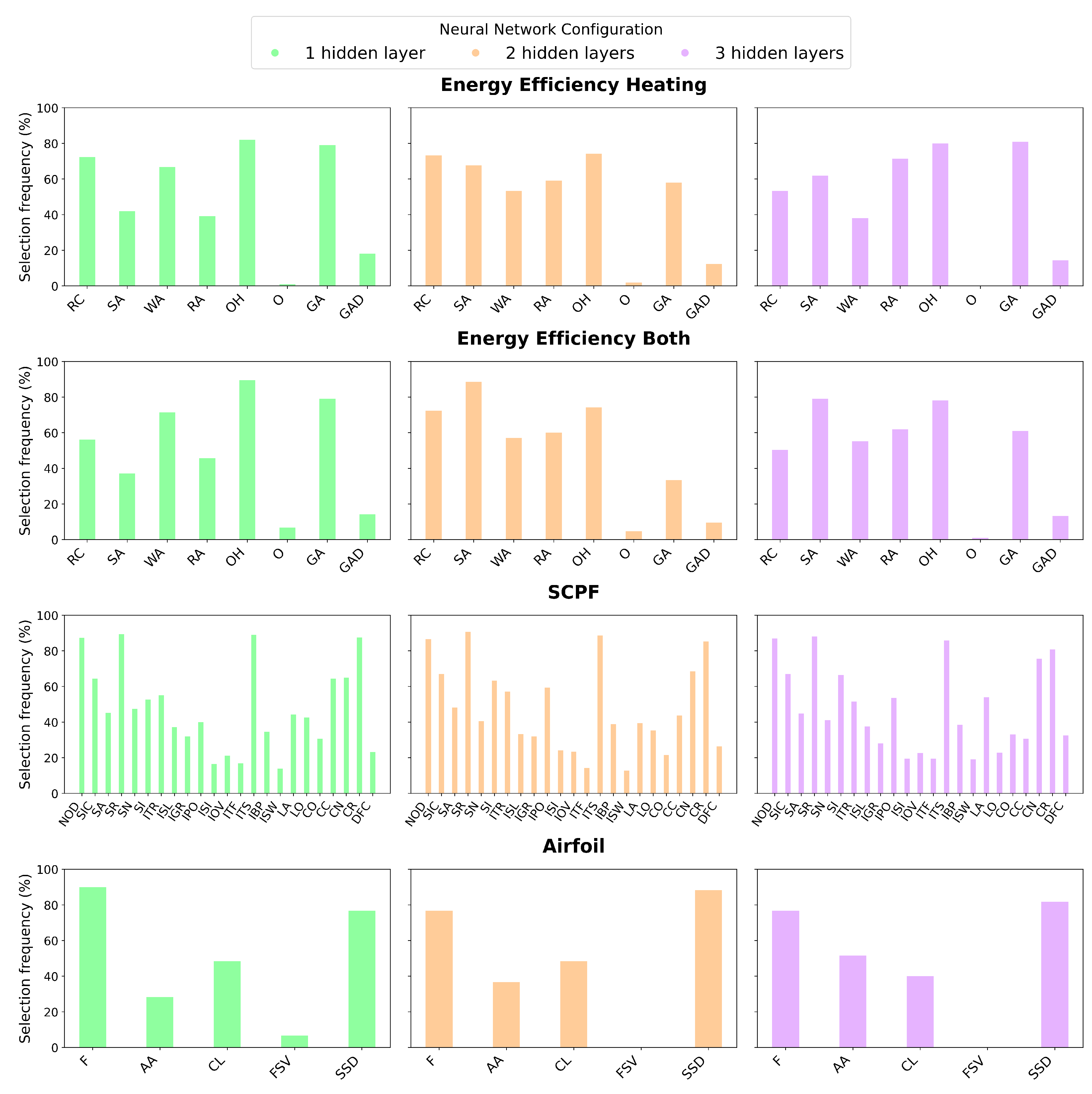
- What insights can be gained regarding feature importance across the examined datasets?
- The proposed approach identifies the most significant features in a regression dataset using a trained ReLU neural network.
- The neural network is mathematically formulated, with the weights and biases of the first hidden layer treated as variables.
- The mathematical formulation is versatile enough to be applied to a deep neural network and can address multi-output regression datasets.
- Scalability is ensured by incorporating a clustering step to aggregate samples, enabling the approach to handle large datasets effectively.
- A specialised solution procedure is described, consisting of (i) clustering; (ii) mathematical programming; (iii) neural network training. This pipeline is employed in a recursive feature elimination manner.
- A thorough computational comparison is performed against four other approaches, utilising eight datasets.
2. Methodology
2.1. Problem Statement
- The input values of C cluster centres with M features;
- The output values of C cluster centres;
- Determined weights and biases by the pre-trained neural network for all layers, l, from node i to node ;
- The number of features, , that the selected subset should contain.
- Weights and biases for the first hidden layer from node i to node ;
- Selected features.
- Minimise the summation of cluster centre errors, weighted by the percentage of samples in each cluster.
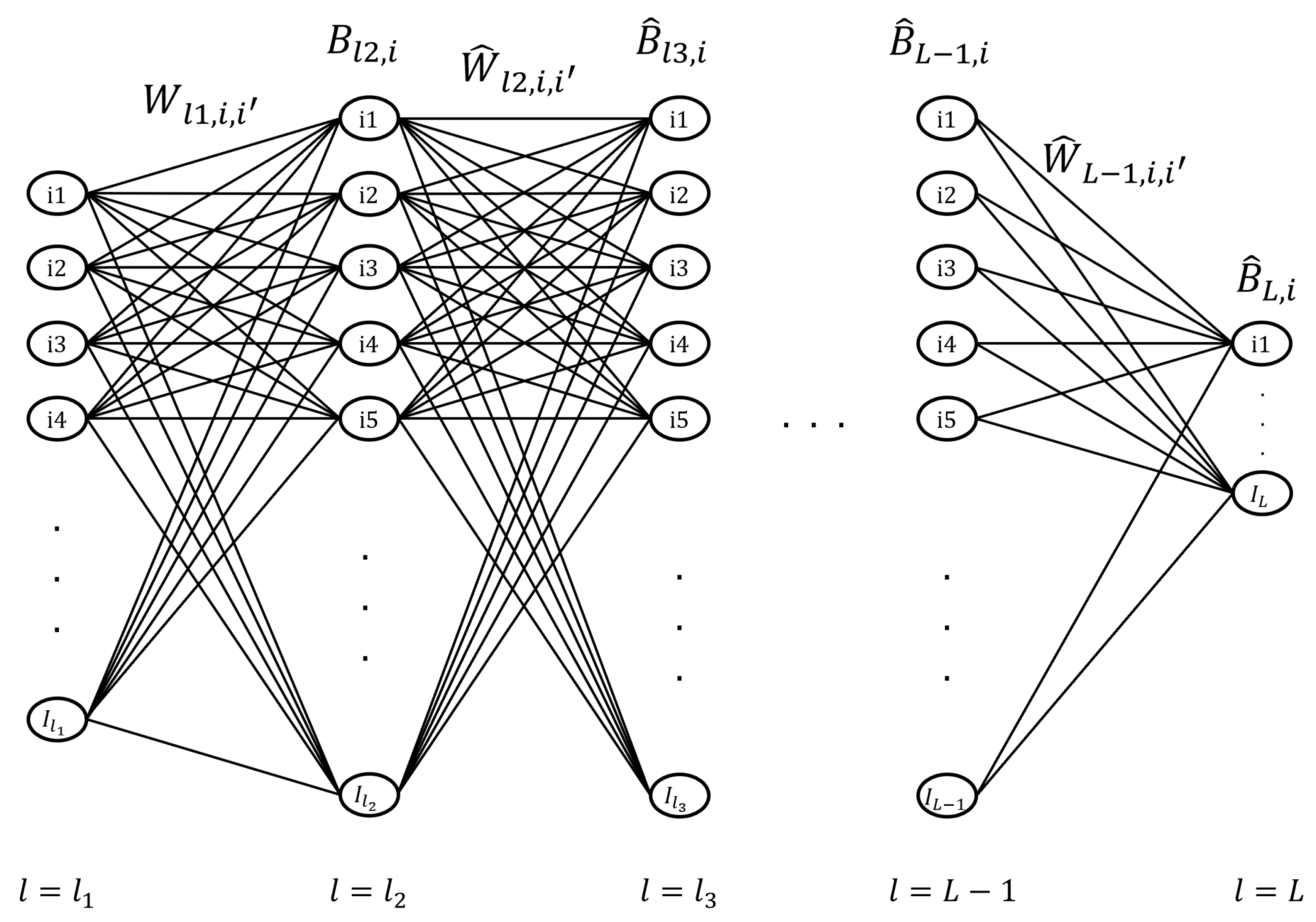
2.2. Mathematical Formulation
| Indices | |
| m | Feature |
| l | Layer |
| Node | |
| c | Cluster centre |
| Sets | |
| Set of nodes that belong to layer l | |
| Feature mapped to node i of input layer | |
| Parameters | |
| Pre-trained weight of layer l between node i and node | |
| Lower bound of weight in layer l between node i and node | |
| Upper bound of weight in layer l between node i and node | |
| Pre-trained bias in layer l for node i | |
| Lower bound of bias in layer l for node i | |
| Upper bound of bias in layer l for node i | |
| Feature value of cluster centre c for input node i of first layer | |
| Lower bound of input value for cluster centre c in layer l for node i | |
| Upper bound of input value for cluster centre c in layer l for node i | |
| Number of selected features | |
| Coefficient of cluster centre c, representing percentage of samples in it | |
| Value of cluster centre c at output node i | |
| Binary variables | |
| 1, if input of cluster centre c in layer l for node i is positive; otherwise 0 | |
| 1, if feature m is selected; otherwise 0 | |
| Continuous variables | |
| Output of cluster centre c in layer l for node i | |
| Error for cluster centre c at output node i | |
| Weight of layer l between node i and node | |
| Bias in layer l for node i |
3. Computational Methodology
3.1. Sample Clustering
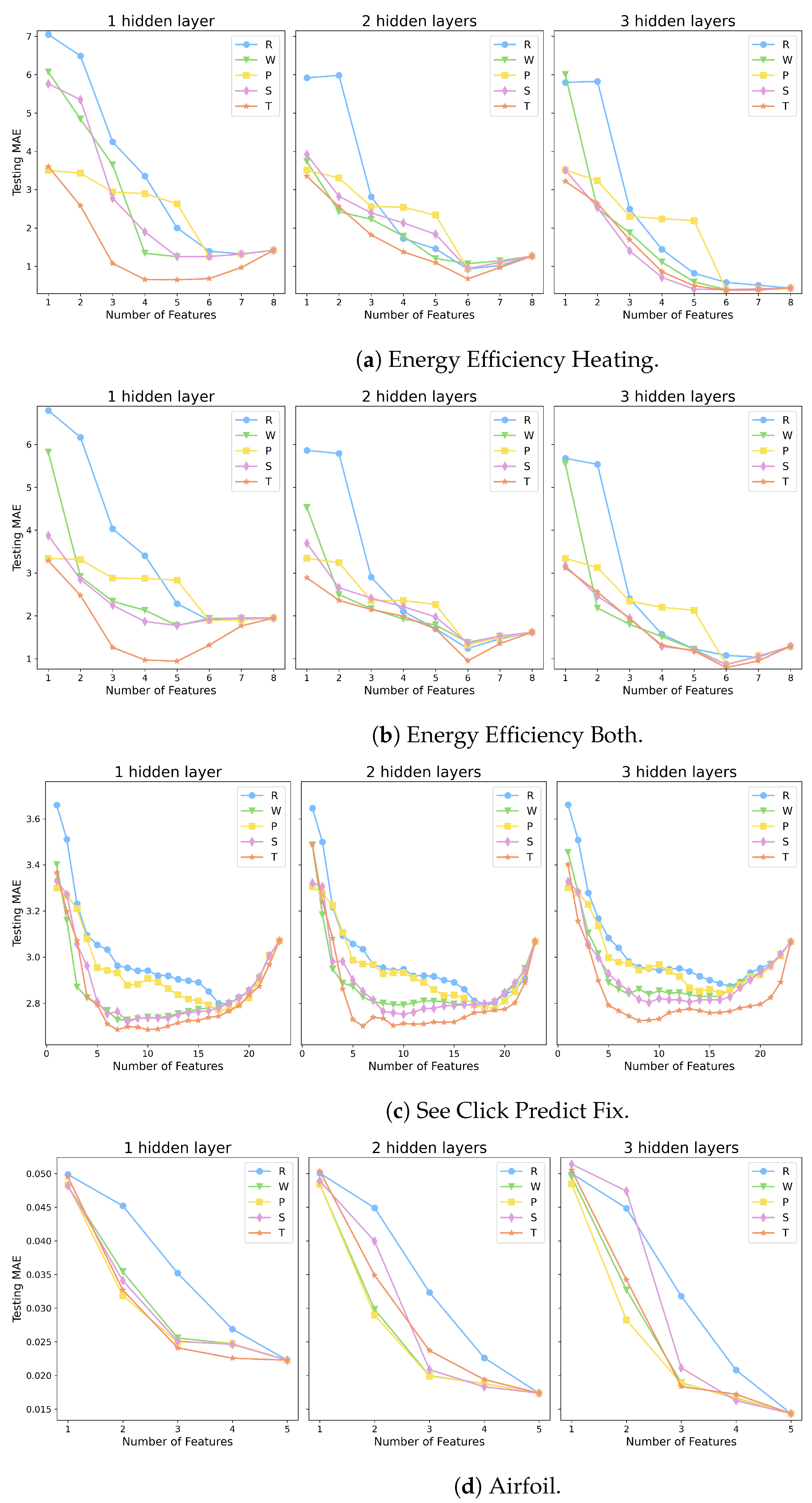
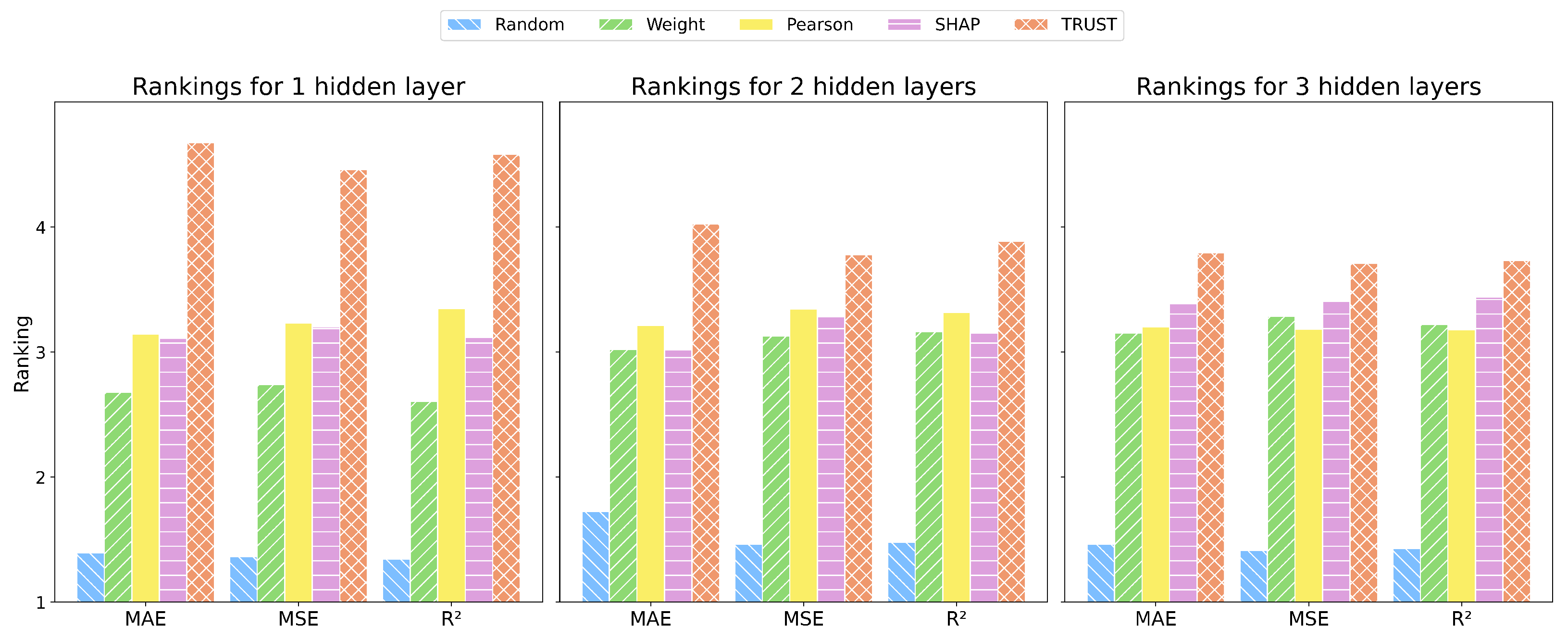
3.2. Computational Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Clustering Metrics
Appendix B. Sample Reduction
| Dataset | Training Samples | Average Clusters |
|---|---|---|
| Yacht Hydrodynamics | 247 | 124.0 |
| Boston Housing | 405 | 126.0 |
| Energy Efficiency Cooling | 615 | 106.3 |
| Energy Efficiency Heating | 615 | 106.3 |
| Energy Efficiency Both | 615 | 103.0 |
| See Click Predict Fix | 910 | 96.0 |
| Airfoil | 1203 | 104.3 |
Appendix C. Clustering Effect
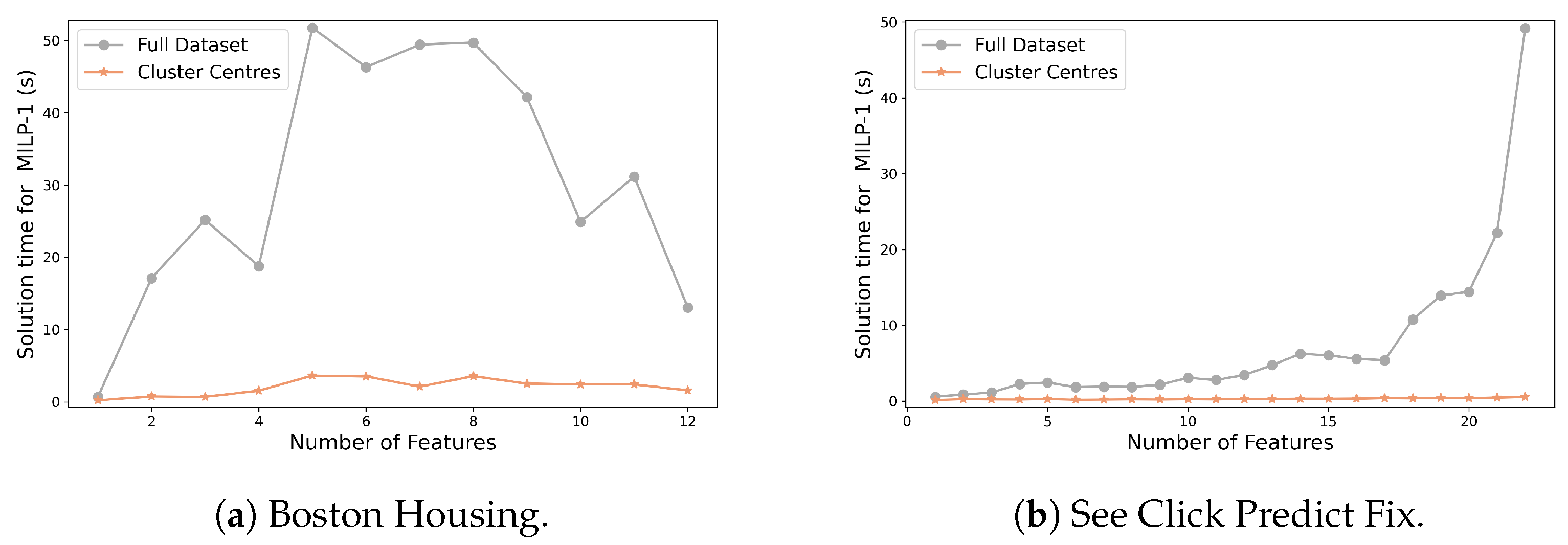
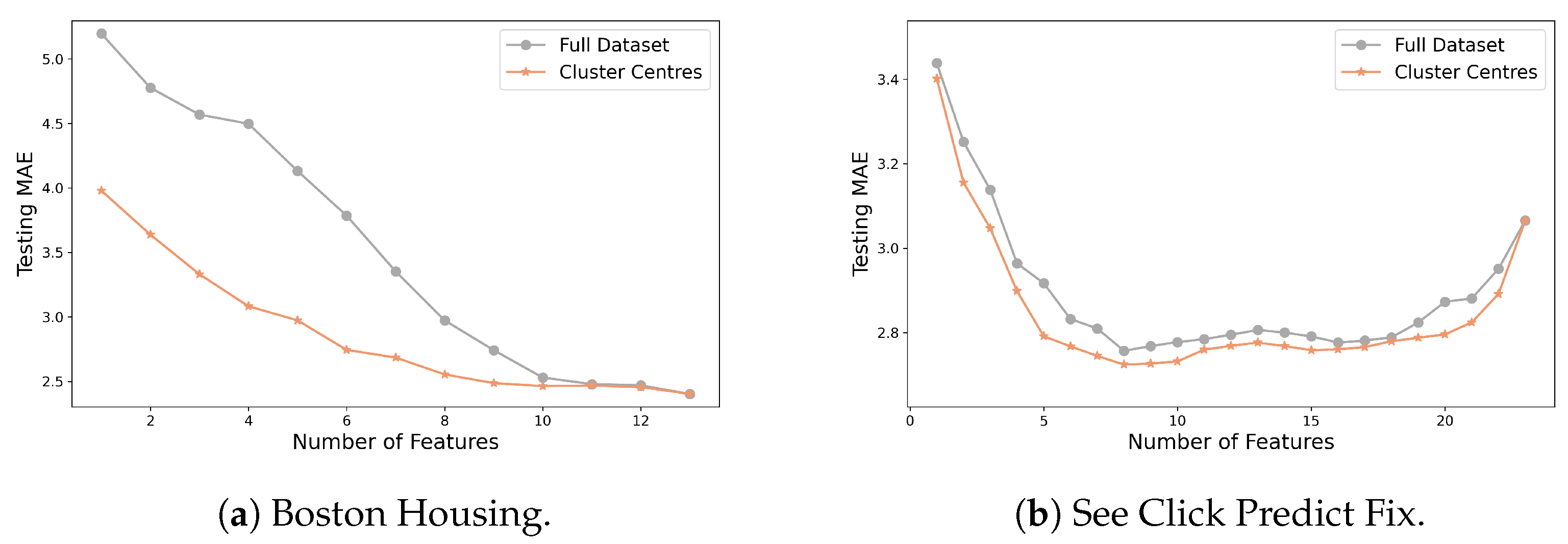
Appendix D. Feature Names
| Dataset | Feature | Abbreviation |
|---|---|---|
| CST | Cement (kg in a m3 mixture) | CC |
| CST | Slag (kg in a m3 mixture) | SL |
| CST | Fly ash (kg in a m3 mixture) | FA |
| CST | Water (kg in a m3 mixture) | WC |
| CST | Superplasticiser (kg in a m3 mixture) | SC |
| CST | Coarse aggregate (kg in a m3 mixture) | CA |
| CST | Fine aggregate (kg in a m3 mixture) | FA |
| YH | Longitudinal position of centre of buoyancy | LPCB |
| YH | Prismatic coefficient | PC |
| YH | Length–displacement ratio | LDR |
| YH | Beam–draught ratio | BDR |
| YH | Length–beam ratio | LBR |
| YH | Froude number | FN |
| BH | Per capita crime rate by town | CRIM |
| BH | Proportion of residential land zoned for lots over 25,000 sq.ft. | ZN |
| BH | Proportion of non-retail business acres per town | INDUS |
| BH | Charles River dummy variable | CHAS |
| BH | Nitric oxide concentration (parts per 10 million) | NOX |
| BH | Average number of rooms per dwelling | RM |
| BH | Proportion of owner-occupied units built prior 1940 | AGE |
| BH | Weighted distances to five Boston employment centres | DIS |
| BH | Index of accessibility to radial highways | RAD |
| BH | Full-value property-tax rate per $10,000 | TAX |
| BH | Pupil–teacher ratio by town | PTR |
| BH | where Bk is proportion of black people by town | B |
| BH | % Lower status of population | LSTAT |
| EEC, EEB, EEH | Relative compactness | RC |
| EEC, EEB, EEH | Surface area | SA |
| EEC, EEB, EEH | Wall area | WA |
| EEC, EEB, EEH | Roof area | RA |
| EEC, EEB, EEH | Overall height | OH |
| EEC, EEB, EEH | Orientation | O |
| EEC, EEB, EEH | Glazing area | GA |
| EEC, EEB, EEH | Glazing area distribution | GAD |
| SCPF | Number of days that issue stayed online | NOD |
| SCPF | Source = initiated city | SIC |
| SCPF | Source = android | SA |
| SCPF | Source = remote API created | SR |
| SCPF | Source = new map widget | SN |
| SCPF | Source = iPhone | SI |
| SCPF | Issue = tree | ITR |
| SCPF | Issue = street light | ISL |
| SCPF | Issue = graffiti | IGR |
| SCPF | Issue = pothole | IPO |
| SCPF | Issue = signs | ISI |
| SCPF | Issue = overgrowth | IOV |
| SCPF | Issue = traffic | ITF |
| SCPF | Issue = trash | ITS |
| SCPF | Issue = blighted property | IBP |
| SCPF | Issue = sidewalk | ISW |
| SCPF | Latitude | LA |
| SCPF | Longitude | LO |
| SCPF | City = Oakland | CO |
| SCPF | City = Chicago | CC |
| SCPF | City = NH | CN |
| SCPF | City = Richmond | CR |
| SCPF | Distance from city centre | DFC |
| AF | Frequency | F |
| AF | Attack angle | AA |
| AF | Chord length | CL |
| AF | Free stream velocity | FSV |
| AF | Suction side displacement thickness | SSD |
References
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Taylor & Francis: New York, NY, USA, 1984. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V.; Saitta, L. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Rio-Chanona, E.A.D.; Wagner, J.L.; Ali, H.; Fiorelli, F.; Zhang, D.; Hellgardt, K. Deep learning-based surrogate modeling and optimization for microalgal biofuel production and photobioreactor design. AIChE J. 2019, 65, 915–923. [Google Scholar] [CrossRef]
- Panerati, J.; Schnellmann, M.A.; Patience, C.; Beltrame, G.; Patience, G.S. Experimental methods in chemical engineering: Artificial neural networks—ANNs. Can. J. Chem. Eng. 2019, 97, 2372–2382. [Google Scholar] [CrossRef]
- Sildir, H.; Aydin, E. A Mixed-Integer linear programming based training and feature selection method for artificial neural networks using piece-wise linear approximations. Chem. Eng. Sci. 2022, 249, 117273. [Google Scholar] [CrossRef]
- Shah, V.; Konda, S.R. Neural Networks and Explainable AI: Bridging the Gap between Models and Interpretability. Int. J. Comput. Sci. Technol. 2021, 5, 2. [Google Scholar] [CrossRef]
- Camburu, O.M. Explaining Deep Neural Networks. arXiv 2020, arXiv:2010.01496. [Google Scholar]
- Bienefeld, N.; Boss, J.M.; Lüthy, R.; Brodbeck, D.; Azzati, J.; Blaser, M.; Willms, J.; Keller, E. Solving the explainable AI conundrum by bridging clinicians’ needs and developers’ goals. Digit. Med. 2023, 6, 94. [Google Scholar] [CrossRef]
- Chaddad, A.; Peng, J.; Xu, J.; Bouridane, A. Survey of Explainable AI Techniques in Healthcare. Sensors 2023, 23, 634. [Google Scholar] [CrossRef]
- Li, Y.; Cardoso-Silva, J.; Kelly, J.M.; Delves, M.J.; Furnham, N.; Papageorgiou, L.G.; Tsoka, S. Optimisation-based modelling for explainable lead discovery in malaria. Artif. Intell. Med. 2024, 147, 102700. [Google Scholar] [CrossRef]
- Alghamdi, F.A.; Almanaseer, H.; Jaradat, G.; Jaradat, A.; Alsmadi, M.K.; Jawarneh, S.; Almurayh, A.S.; Alqurni, J.; Alfagham, H. Multilayer Perceptron Neural Network with Arithmetic Optimization Algorithm-Based Feature Selection for Cardiovascular Disease Prediction. Mach. Learn. Knowl. Extr. 2024, 6, 987–1008. [Google Scholar] [CrossRef]
- Papadopoulos, S.; Kontokosta, C.E. Grading buildings on energy performance using city benchmarking data. Appl. Energy 2019, 233, 244–253. [Google Scholar] [CrossRef]
- Letzgus, S.; Wagner, P.; Lederer, J.; Samek, W.; Muller, K.R.; Montavon, G. Toward Explainable Artificial Intelligence for Regression Models: A methodological perspective. IEEE Signal Process. Mag. 2022, 39, 40–58. [Google Scholar] [CrossRef]
- Wheeler, A.P.; Steenbeek, W. Mapping the Risk Terrain for Crime Using Machine Learning. J. Quant. Criminol. 2021, 37, 445–480. [Google Scholar] [CrossRef]
- Marcinkevičs, R.; Vogt, J.E. Interpretable and explainable machine learning: A methods-centric overview with concrete examples. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2023, 13, e1493. [Google Scholar] [CrossRef]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
- Goerigk, M.; Hartisch, M. A framework for inherently interpretable optimization models. Eur. J. Oper. Res. 2023, 310, 1312–1324. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Why Should I Trust You? In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Janzing, D.; Minorics, L.; Blöbaum, P. Feature relevance quantification in explainable AI: A causality problem. arXiv 2019, arXiv:1910.13413. [Google Scholar]
- Jiménez-Luna, J.; Grisoni, F.; Schneider, G. Drug discovery with explainable artificial intelligence. Nat. Mach. Intell. 2020, 2, 573–584. [Google Scholar] [CrossRef]
- Zafar, M.R.; Khan, N. Deterministic Local Interpretable Model-Agnostic Explanations for Stable Explainability. Mach. Learn. Knowl. Extr. 2021, 3, 525–541. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature Selection. ACM Comput. Surv. 2018, 50, 1–45. [Google Scholar] [CrossRef]
- Clautiaux, F.; Ljubić, I. Last fifty years of integer linear programming: A focus on recent practical advances. Eur. J. Oper. Res. 2024. [Google Scholar] [CrossRef]
- Huchette, J.; Muñoz, G.; Serra, T.; Tsay, C. When Deep Learning Meets Polyhedral Theory: A Survey. arXiv 2023, arXiv:2305.00241. [Google Scholar]
- Fischetti, M.; Jo, J. Deep neural networks and mixed integer linear optimization. Constraints 2018, 23, 296–309. [Google Scholar] [CrossRef]
- Tjeng, V.; Xiao, K.; Tedrake, R. Evaluating Robustness of Neural Networks with Mixed Integer Programming. arXiv 2019, arXiv:1711.07356. [Google Scholar]
- Dias, L.S.; Ierapetritou, M.G. Data-driven feasibility analysis for the integration of planning and scheduling problems. Optim. Eng. 2019, 20, 1029–1066. [Google Scholar] [CrossRef]
- Dias, L.S.; Ierapetritou, M.G. Integration of planning, scheduling and control problems using data-driven feasibility analysis and surrogate models. Comput. Chem. Eng. 2020, 134, 106714. [Google Scholar] [CrossRef]
- Triantafyllou, N.; Papathanasiou, M.M. Deep learning enhanced mixed integer optimization: Learning to reduce model dimensionality. Comput. Chem. Eng. 2024, 187, 108725. [Google Scholar] [CrossRef]
- López-Flores, F.J.; Lira-Barragán, L.F.; Rubio-Castro, E.; El-Halwagi, M.M.; Ponce-Ortega, J.M. Hybrid Machine Learning-Mathematical Programming Approach for Optimizing Gas Production and Water Management in Shale Gas Fields. ACS Sustain. Chem. Eng. 2023, 11, 6043–6056. [Google Scholar] [CrossRef]
- Zhao, S.; Tsay, C.; Kronqvist, J. Model-based feature selection for neural networks: A mixed-integer programming approach. arXiv 2023, arXiv:2302.10344. [Google Scholar]
- Carrizosa, E.; Ramírez-Ayerbe, J.; Romero Morales, D. Mathematical optimization modelling for group counterfactual explanations. Eur. J. Oper. Res. 2024, 319, 399–412. [Google Scholar] [CrossRef]
- Lodi, A.; Ramírez-Ayerbe, J. One-for-many Counterfactual Explanations by Column Generation. arXiv 2024, arXiv:2402.09473. [Google Scholar]
- Bertsimas, D.; Dunn, J. Optimal classification trees. Mach. Learn. 2017, 106, 1039–1082. [Google Scholar] [CrossRef]
- Verwer, S.; Zhang, Y.; Ye, Q.C. Auction optimization using regression trees and linear models as integer programs. Artif. Intell. 2017, 244, 368–395. [Google Scholar] [CrossRef]
- Gkioulekas, I.; Papageorgiou, L.G. Tree regression models using statistical testing and mixed integer programming. Comput. Ind. Eng. 2021, 153, 107059. [Google Scholar] [CrossRef]
- Liapis, G.I.; Papageorgiou, L.G. Optimisation-Based Classification Tree: A Game Theoretic Approach to Group Fairness. Commun. Comput. Inf. Sci. 2025, 2311, 28–40. [Google Scholar] [CrossRef]
- Carrizosa, E.; Martin-Barragan, B. Two-group classification via a biobjective margin maximization model. Eur. J. Oper. Res. 2006, 173, 746–761. [Google Scholar] [CrossRef]
- Carrizosa, E.; Morales, D.R. Supervised classification and mathematical optimization. Comput. Oper. Res. 2013, 40, 150–165. [Google Scholar] [CrossRef]
- Blanco, V.; Japón, A.; Puerto, J. A mathematical programming approach to SVM-based classification with label noise. Comput. Ind. Eng. 2022, 172, 108611. [Google Scholar] [CrossRef]
- Liapis, G.I.; Papageorgiou, L.G. Hyper-box Classification Model Using Mathematical Programming. Lect. Notes Comput. Sci. 2023, 14286, 16–30. [Google Scholar] [CrossRef]
- Liapis, G.I.; Tsoka, S.; Papageorgiou, L.G. Interpretable optimisation-based approach for hyper-box classification. Mach. Learn. 2025, 114, 51. [Google Scholar] [CrossRef]
- Rosenberg, G.; Brubaker, J.K.; Schuetz, M.J.A.; Salton, G.; Zhu, Z.; Zhu, E.Y.; Kadıoğlu, S.; Borujeni, S.E.; Katzgraber, H.G. Explainable Artificial Intelligence Using Expressive Boolean Formulas. Mach. Learn. Knowl. Extr. 2023, 5, 1760–1795. [Google Scholar] [CrossRef]
- Toro Icarte, R.; Illanes, L.; Castro, M.P.; Cire, A.A.; McIlraith, S.A.; Beck, J.C. Training Binarized Neural Networks Using MIP and CP. In Proceedings of the Principles and Practice of Constraint Programming, Stamford, CT, USA, 30 September–4 October 2019; Springer International Publishing: Cham, Switzerland, 2019; pp. 401–417. [Google Scholar]
- Thorbjarnarson, T.; Yorke-Smith, N. Optimal training of integer-valued neural networks with mixed integer programming. PLoS ONE 2023, 18, e0261029. [Google Scholar] [CrossRef]
- Dua, V. A mixed-integer programming approach for optimal configuration of artificial neural networks. Chem. Eng. Res. Des. 2010, 88, 55–60. [Google Scholar] [CrossRef]
- Park, H.S.; Jun, C.H. A simple and fast algorithm for K-medoids clustering. Expert Syst. Appl. 2009, 36, 3336–3341. [Google Scholar] [CrossRef]
- Cheng, C.H.; Nührenberg, G.; Ruess, H. Maximum Resilience of Artificial Neural Networks. arXiv 2017, arXiv:1705.01040. [Google Scholar]
- Tsay, C.; Kronqvist, J.; Thebelt, A.; Misener, R. Partition-based formulations for mixed-integer optimization of trained ReLU neural networks. arXiv 2021, arXiv:2102.04373. [Google Scholar]
- Madhulatha, T.S. Comparison between K-Means and K-Medoids Clustering Algorithms. In Proceedings of the Advances in Computing and Information Technology, Chennai, India, 15–17 July 2011; pp. 472–481. [Google Scholar] [CrossRef]
- Arora, P.; Deepali; Varshney, S. Analysis of K-Means and K-Medoids Algorithm For Big Data. Procedia Comput. Sci. 2016, 78, 507–512. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: http://tensorflow.org (accessed on 1 February 2025).
- GAMS Development Corporation. General Algebraic Model System (GAMS); Release 46.1.0; GAMS Development Corporation: Washington, DC, USA, 2024. [Google Scholar]
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual. 2024. Available online: https://www.gurobi.com (accessed on 1 February 2025).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Vlachos, P. StatLib—Statistical Datasets. 2005. Available online: http://lib.stat.cmu.edu/datasets/ (accessed on 1 February 2025).
- Tsoumakas, G.; Spyromitros-Xioufis, E.; Vilcek, J.; Vlahavas, I. Mulan: A Java Library for Multi-Label Learning. J. Mach. Learn. Res. 2011, 12, 2411–2414. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2017. Available online: http://archive.ics.uci.edu/ml/index.php (accessed on 1 February 2025).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Herding, R.; Ross, E.; Jones, W.R.; Endler, E.; Charitopoulos, V.M.; Papageorgiou, L.G. Risk-aware microgrid operation and participation in the day-ahead electricity market. Adv. Appl. Energy 2024, 15, 100180. [Google Scholar] [CrossRef]


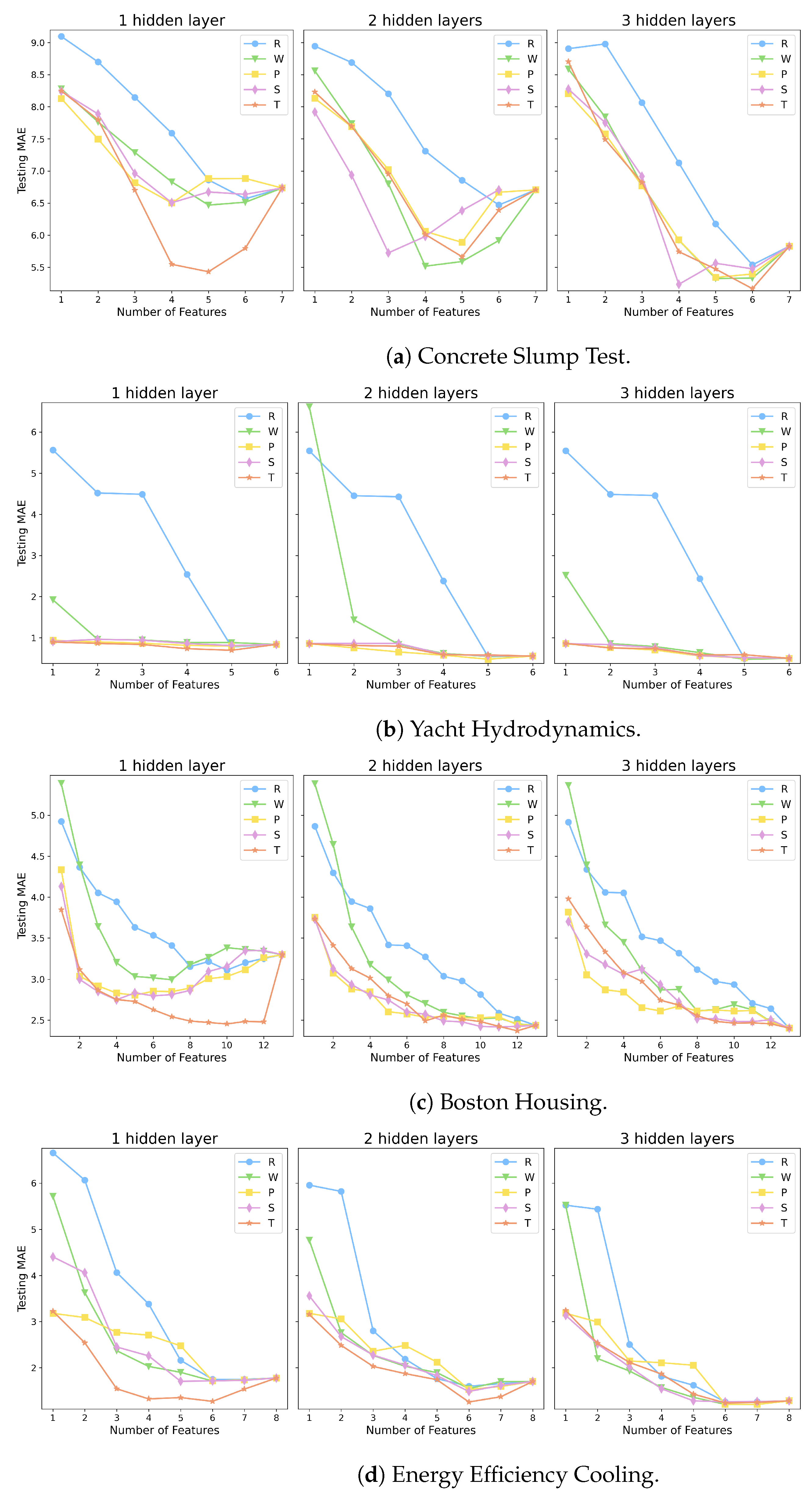
| Dataset | Abbreviation | Samples | Features | Outputs |
|---|---|---|---|---|
| Concrete Slump Test | CST | 103 | 7 | 3 |
| Yacht Hydrodynamics | YH | 308 | 6 | 1 |
| Boston Housing | BH | 506 | 13 | 1 |
| Energy Efficiency Cooling | EEC | 768 | 8 | 1 |
| Energy Efficiency Heating | EEH | 768 | 8 | 1 |
| Energy Efficiency Both | EEB | 768 | 8 | 2 |
| See Click Predict Fix | SCPF | 1137 | 23 | 3 |
| Airfoil | AF | 1503 | 5 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liapis, G.I.; Tsoka, S.; Papageorgiou, L.G. Optimisation-Based Feature Selection for Regression Neural Networks Towards Explainability. Mach. Learn. Knowl. Extr. 2025, 7, 33. https://doi.org/10.3390/make7020033
Liapis GI, Tsoka S, Papageorgiou LG. Optimisation-Based Feature Selection for Regression Neural Networks Towards Explainability. Machine Learning and Knowledge Extraction. 2025; 7(2):33. https://doi.org/10.3390/make7020033
Chicago/Turabian StyleLiapis, Georgios I., Sophia Tsoka, and Lazaros G. Papageorgiou. 2025. "Optimisation-Based Feature Selection for Regression Neural Networks Towards Explainability" Machine Learning and Knowledge Extraction 7, no. 2: 33. https://doi.org/10.3390/make7020033
APA StyleLiapis, G. I., Tsoka, S., & Papageorgiou, L. G. (2025). Optimisation-Based Feature Selection for Regression Neural Networks Towards Explainability. Machine Learning and Knowledge Extraction, 7(2), 33. https://doi.org/10.3390/make7020033






