Abstract
In today’s rapidly evolving transportation infrastructure, developing long-lasting, high-performance pavement materials remains a significant priority. Integrating machine learning (ML) techniques provides a transformative approach to optimizing asphalt mix design and performance prediction. This study investigates the use of waste plastics, including Polyethylene Terephthalate (PET), High-Density Polyethylene (HDPE), and Polyvinyl Chloride (PVC), as modifiers in asphalt concrete to enhance durability and mechanical performance. A predictive modeling approach was employed to estimate the bulk-specific gravity (Gmb) of asphalt concrete using various ML techniques, including Artificial Neural Networks (ANNs), Support Vector Machines (SVMs), Gaussian Processes (GPs), and Reduced Error Pruning (REP) Tree. The accuracy of each model was evaluated using statistical performance metrics, including the correlation coefficient (CC), scatter index (SI), mean absolute error (MAE), and root mean square error (RMSE). The results demonstrate that the ANN model outperformed all other ML techniques, achieving the highest correlation (CC = 0.9996 for training, 0.9999 for testing) and the lowest error values (MAE = 0.0004, RMSE = 0.0006, SI = 0.00026). A comparative analysis between actual and predicted Gmb values confirmed the reliability of the proposed ANN model, with minimal error margins and superior accuracy. Additionally, sensitivity analysis identified bitumen content (BC) and volume of bitumen (Vb) as the most influential parameters affecting Gmb, emphasizing the need for precise parameter optimization in asphalt mix design. This study demonstrates the effectiveness of machine learning-driven predictive modeling in optimizing sustainable asphalt mix design, offering a cost-effective, time-efficient, and highly accurate alternative to traditional experimental methods.
1. Introduction
Road construction and maintenance agencies frequently employ performance measures to evaluate asphalt mixes before they are used in construction. These index-based tests are being enhanced and integrated into performance-based frameworks, such as a balanced mix design or performance–engineered mixture design. Regardless of the performance metric used to evaluate mix performance, determining an ideal mix design involves modifying several mix design factors. Even if a mix design fits all the required criteria, there is no guarantee that it cannot be improved further within the solution space of all viable mix designs that meet the criteria. It is necessary to forecast mixture performance precisely using the elements intrinsic to the mix design process and impact performance to determine the best mix design [1].
Over 4 million miles of roads and highways, or 96% of all roadways, are built with an asphalt mixture. The qualities of the asphalt mixture significantly impact the strength and lifespan of asphalt pavements. The characteristics of an asphalt mixture, which is composed of asphalt, aggregates, and additives, are determined by the amounts of each component. The process used to determine the optimum proportion of aggregates to asphalt required to meet volumetric and mechanical requirements is known as the asphalt mix design. The asphalt mix design is a critical first step toward achieving optimal asphalt pavement performance. This technique involves several laboratory processes to determine the most appropriate and cost-effective bituminous mixes, ensuring aggregate gradation, and asphalt concentration [2,3]. Volumetric properties are fundamental to asphalt design approaches and are influenced by various factors such as aggregate grain size, mineralogy, absorption, asphalt content, mineral filler quantity, and compaction efforts [4]. The bulk-specific gravity (Gmb) of an asphalt mix is an important volumetric parameter for determining its optimum asphalt content. It represents the mix’s bulk-specific gravity, eliminating air spaces. The test process for measuring Gmb is now established in ASTM D2041 [5] standards. Ideally, an average Gmb value should be calculated for each trial combination during the design process to test other volumetric parameters and, finally, identify the optimal asphalt content of the planned mixture [6].
Previous investigations on the performance of asphalt mixtures, including industrial waste materials, found that using marble as a filler resulted in the highest stability [7]. Furthermore, adding hydrated lime filler significantly increased the asphalt mixture’s resistance to moisture damage, dynamic modulus, and flow number [8]. Moreover, waste marble was discovered to improve moisture damage resistance in terms of tensile strength ratio and loss of stability. Furthermore, the unbound foundation layer features were discovered as essential elements influencing the performance of flexible pavements, with results differing according to climate conditions, construction quality, material supply, traffic level, and pavement structure [9].
Nonetheless, the traditional sample preparation process for the Gmb test takes considerable time, ranging from 3 to 8 h. Furthermore, the vacuum process uses electric energy and produces waste asphalt mixes weighing 15,000 and 50,000 g per mix design [10]. Alternative testing methods, such as vacuum sealing (CoreLok) and pressure meter processes, have already been offered to overcome these issues. However, researchers have not widely adopted these methodologies because of their inherent limitations. As stated earlier, the characteristics of component materials and mixtures—such as the type and concentration of the additives, the source and gradation of the aggregate, the grade and content of the asphalt binder, and more—have a substantial influence on the performance of the mixture against different distresses. A limited number of samples and variables are used in many research attempts to model these attributes’ impact because of issues with raw material availability and constituent mechanism comprehension. Data-driven machine learning (ML) techniques provide helpful answers when no full mechanistic models are available. This is because they use several variables and datasets [11].
Numerous ML technologies have been widely used for data analysis and prediction model creation across various engineering applications in recent years. This development is driven mainly by their ability to produce accurate prediction models [12,13]. In the field of asphalt engineering, the volumetric properties of asphalt mixes have been extensively used in several studies to forecast various qualities and characteristics of bituminous mixtures. This method helps to reduce the time, material waste, and energy consumption associated with typical laboratory experimentation [14]. The purpose of this study was to present different ML models for predicting the design features of bulk-specific gravity mixtures. These ML model inputs include volume of bitumen (Vb), volume of voids (Vv), voids in mineral aggregate (VMA), voids filled with binder (VFB), and bitumen content. Over the last decade, pavement researchers have widely used Artificial Neural Networks (ANNs) in various applications. ANNs are successful at predicting or backcalculating pavement modulus. Researchers train ANNs using deflection data from falling weight deflectometers [15].
Tarefder et al. [16] used ANNs to predict the permeability of asphalt mixtures. They fed mixture factors such as air voids, particle size, saturation, and effective asphalt-to-dust ratio into the ANN model. Furthermore, ANN-based approaches have been used for pavement construction activities. For example, an intelligent asphalt compaction analyzer based on ANNs was created as a Quality Assurance/Quality Control (QA/QC) tool. This equipment is intended to determine the density of the asphalt mixture under the roller during the compaction process. Random forests were used in reference [17] to investigate how structural characteristics and the asphalt mixture affect pavement performance. These characteristics included pavement thickness, age, viscosity and content of the asphalt binder, air voids, bulk specific gravity, and aggregate gradation. The Long-Term Pavement Performance (LTPP) program’s data from 78 sections were used to examine pavement performance, with rutting, cracking, and roughness receiving particular attention [17]. The Mechanistic-Empirical Design Guide (ME-PDG), specifically the Reflection Cracking Design program, employs ANNs as a sub-algorithm within the software. Reference [18] illustrated how using ANNs makes it easier to calculate fracture growth through an overlay. Additionally, ANNs have been used in image analysis jobs. For example, Kim et al. [19] developed an automated quality assessment technique for aggregate production. This program classifies aggregation sizes using laser imagery and ANN approaches.
Saif et al. [20] used a support vector machine (SVM) and a traditional back-propagation neural network (BPNN) to evaluate the sustainability of asphaltic concrete mixtures. The results indicate that SVM outperforms BPNN in predicting the stability of asphaltic concrete mixes. SVM, multilayer perceptron artificial neural networks (MLP-ANN), M5Prime model tree approach (M5P), and Random Forest models were used by Cook et al. [21] to compare the hybrid Random Forest–Firefly Algorithm model (RF-FFA) model performance to that of frequently used solo ML models. Based on prediction accuracy, the results show that the hybrid RF-FFA model consistently outperforms solo ML models. Previous research has highlighted the widespread usage of ANNs as an ML method for calculating the Gmb value of asphalt mixtures. While ANNs excel at building high-accuracy predictive models, their inherent structure as computer codes makes mathematical implementation difficult [22].
As a result, it is critical to investigate an alternate ML approach capable of producing a simple and accurate mathematical equation for forecasting the Gmb values of asphalt mixes. This study aims to create a direct mathematical predictive model for Gmb of asphalt mixes using the GP, SVR, and REP Tree. The model will prioritize Vb, Vv, VMA, VFB, and BC as primary predictors and other characteristics that naturally influence Gmb readings. The objectives of this study are as follows:
- To create a practical and straightforward model for estimating the Gmb of asphalt mixes;
- To employ key input parameters such as Vb, Vv, VMA, BC, and VFB to predict the Gmb of asphalt mixes and
- To develop a direct empirical equation for predicting Gmb. This equation aims to streamline the process, reduce experimental efforts, and offer applicability for asphalt mix design and quality control purposes.
While it is known that blending various plastics with bitumen has been explored in prior research, the novelty of our study extends beyond the mere selection and proportioning of plastics. Instead, our research focuses on optimizing the performance of asphalt mixtures by carefully tailoring the proportions of PET (Polyethylene Terephthalate), HDPE (High-Density Polyethylene), and PVC (Polyvinyl Chloride) plastics to achieve specific performance objectives. Unlike previous studies that explored a wider variety of plastic types and proportions, our research focuses on achieving an optimal balance of the selected plastics to enhance specific performance metrics, including improved fatigue resistance, higher rutting resistance, and superior moisture sensitivity. Furthermore, our study explores the synergistic effects of combining these plastics at unique proportions, thereby unlocking potential benefits that may not have been realized in previous research endeavors. Through careful experimentation and analysis, we aim to identify the optimal blend ratios that maintain the structural integrity of the asphalt mixture and enhance its overall sustainability and longevity.
In essence, the novelty of our study lies not only in the selection of plastics and their proportions but also in our deliberate pursuit of specific performance enhancements through finely tuned compositions. By elucidating the intricacies of these tailored blends, we contribute to advancing the understanding of sustainable and high-performance asphalt technologies in pavement engineering.
2. Machine Learning
2.1. Gaussian Processes
Carl Friedrich Gauss is credited with developing the notion of Gaussian Processes (GP) and is best known for his work on normal distribution. GP can occur in infinite dimensions and are essentially multivariate normal distributions. This approach uses the Gaussian distribution as a foundational idea and is applied in machine learning. GP is an essential tool for using kernels to interpret models. They offer a valuable method for learning kernel machines and shed light on the connections and patterns found in the data. A Gaussian process encompasses a set of random variables that follow a joint Gaussian distribution. Each regression problem aims to uncover the relationship between two sets of parameters: the dependent variable (r) and the predictor variables (si). The dependent variable can be associated with an underlying regression function j(s), with the inclusion of independent identically distributed Gaussian noise (p), as depicted in Equation (1).
The noise, denoted by p, has a mean of zero and a variance of Rn2, indicating ε~T (0, Rn2).
In this context, GP represents the Gaussian process, where q(s) represents the mean value, v(s, s′) is the covariance function, and “i” denotes the identity matrix.
2.2. Support Vector Machine
Developed by Cortes and Vapnik in 1995 [23], the SVM has established itself as a formidable asset in machine learning, particularly in binary classification tasks. It operates by ingeniously addressing nonlinear problems through the strategic employment of kernel functions. These kernel functions are pivotal in reshaping the original data spaces, elevating them to higher-dimensional feature spaces. This transformation enables SVM to effectively handle complex data patterns, overcoming the limitations of linear approaches. This innovative transformation empowers SVM to discern nuanced global solutions with remarkable precision, unfettered by the proliferation of local minima that can impede other methodologies [24].
SVM analysis can be approached in two distinct ways. Firstly, an optimal margin classifier, which acts as a linear separator to delineate the decision surface, is utilized. Alternatively, one can opt for the kernel function approach, which involves computing the inner product of two vectors. This method begins by mapping the input data into an n-dimensional feature space. Subsequently, a nonlinear kernel function is employed to establish a fitting in the high-dimensional space via a predefined mapping process. When the kernel mapping is applied to the original data, it effectively separates the information linearly across the high-dimensional feature space without altering the input space [25]. This approach ensures that the input space remains unchanged while achieving a linear data separation of the transformed feature space [26]. Because kernel variables significantly impact the SVM solution’s accuracy and complexity, choosing the correct variable is crucial. Since the effectiveness of SVMs depends on the kernel function used, each application scenario requires careful consideration when selecting the proper kernel function and parameters. It is essential to give this considerable thought to achieve outstanding results and best practices for SVM-based analysis [27].
2.3. Artificial Neural Network
An artificial neural network (ANN) is a computational model comprising multiple interconnected nodes. These nodes function similarly to neurons, enabling signal transmission and simulating how information is processed in the brain. ANN is designed as a processing unit with input and output layers as well as hidden layers positioned in between [28]. This architecture often includes input, hidden, and output layers, as shown in Figure 1. Neural network techniques can be utilized to build fatigue life prediction models for asphalt mixtures while considering the interaction of several components. For this, an MLP-ANN, a type of artificial neural network trained using back-propagation, is frequently used [29]. An input layer with neurons representing input variables, one or more hierarchical hidden layers with computational neurons in charge of combining and transmitting information from earlier layers, and an output layer with a computation node in charge of producing the final prediction are the typical components of this network architecture [24]. The ANN model is trained using a training dataset and evaluated using a separate testing dataset. This method aids in quickly addressing complex problems and appropriately computing outcomes. Back-propagation in ANNs refers to a set of learning principles that regulate error propagation in reverse. This technique evaluates the weight-related error function, increasing the model’s reliability [30].
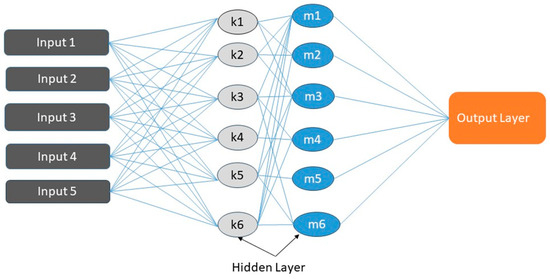
Figure 1.
Architecture of an Artificial Neural Network.
2.4. Reduced Error Pruning Tree
The REP Tree, which stands for Reduced Error Pruning Tree, is a rapid and efficient approach for constructing decision trees. This method generates decision trees by utilizing information gain or reduction in variance criteria. As a decision tree splitter and pruner, the REP Tree employs information gain as its primary criterion for splitting and pruning decision or regression trees. In detail, the REP Tree algorithm evaluates the potential splits within the dataset based on their ability to reduce error or increase information gain. This entails identifying the feature that best separates the data into distinct classes or reduces variance in the case of regression tasks. Subsequently, the algorithm recursively partitions the dataset into subsets based on the selected features until a stopping criterion is met, such as reaching a maximum depth or a minimum number of instances per leaf node [31]. The REP Tree represents a streamlined version of decision tree learners. Within this framework, depending on the nature of the problem, either a regression tree or a decision tree is constructed, with information gain as the primary criterion for splitting. Notably, the model undergoes pruning via Reduced Error Pruning techniques, ensuring the optimization of tree structure. A one-time sorting process handles numeric attributes while missing values are effectively managed by segmenting related instances [32].
3. Materials and Methodology
The utilization of various materials in asphalt mixtures has been the subject of extensive research to enhance the performance and sustainability of pavements. This study focuses on incorporating different proportions of PET, HDPE, and PVC in asphalt mixtures and traditional materials such as aggregate, marble powder, and bitumen VG 30. Figure 2 provides a clear overview of the methodology used in the study. The objective is to assess the impact of these additives on the mechanical properties, durability, and sustainability of the asphalt mixtures. The details of the materials are given in the subsequent sections.
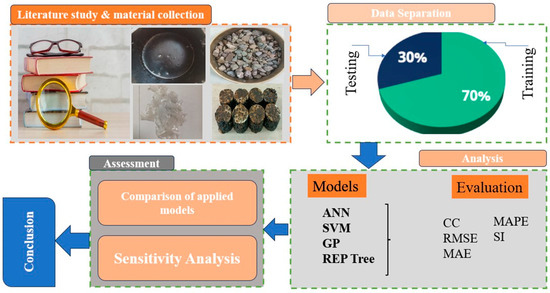
Figure 2.
Flowchart of the present study.
3.1. Aggregate
The selection of appropriate aggregates is crucial in asphalt mixture design as it significantly influences the mechanical properties and performance of pavements. In this study, locally sourced 20 mm aggregate obtained from the vicinity of Shoolini University is utilized as a primary component in asphalt mixtures. The aim is to investigate the suitability and performance of this aggregate in asphalt pavements, considering factors such as gradation, particle shape, and durability. The mechanical characteristics of the aggregates are listed in Table 1.

Table 1.
Physical characteristics of aggregates.
3.2. Bitumen
This research explores the vital role of bitumen in asphalt mixtures for constructing durable pavements, emphasizing its binding properties crucial for pavement integrity. Specifically, the study focuses on VG30-grade bitumen sourced from S.D. Bitumen & Allied Products in Haryana, India. The objective is to evaluate the feasibility and performance implications of incorporating different plastic additives into this bitumen. The investigation spans various content of varying plastic additives, ranging from 4.5% to 6%, to understand their potential impact comprehensively. By assessing the compatibility of plastic additives with bitumen and analyzing their effects on the mixture, the research seeks to provide insights into optimizing asphalt mixtures for enhanced durability and performance in pavement construction. The physical properties of the bitumen are presented in Table 2.

Table 2.
Bitumen characteristics.
3.3. Marble Powder
A filler is strategically introduced to enhance its overall consistency and performance to achieve the necessary uniformity within the asphalt mixture. This filler takes the form of marble powder, added in a proportion equivalent to 10% of the weight of the coarse aggregate. This careful incorporation of marble powder serves a dual purpose: Firstly, it promotes uniformity within the asphalt mixture, ensuring the composition meets stringent standards. Secondly, it contributes to optimizing the asphalt mixture, bolstering its durability and suitability for construction applications.
The asphalt composition undergoes refinement by precisely integrating marble powder as a filler, leading to a well-balanced, robust, and enduring mixture. This approach aligns with industry specifications and underscores the commitment to delivering high-quality asphalt solutions tailored to construction needs.
3.4. Waste Plastic
Our ongoing research explores the intricate interplay of three distinct types of plastic materials: PET, HDPE, and PVC. These materials are carefully combined in diverse proportions, forming the cornerstone of our experimental framework to unravel their complex properties and interactions. The primary objective of our study is to gain profound insights into the collective impact of PET, HDPE, and PVC on the targeted properties and outcomes, all achieved through the deliberate manipulation of their respective ratios. Both control and modified asphalt samples contained plastic additives in varied quantities ranging from 0% to 15%. To investigate their impacts on the asphalt mixture, PET, HDPE, and PVC combinations were used in ratios of 100:0:0, 50:50:0, 25:25:50, 0:100:0, 0:50:50, 50:25:25, 0:0:100, 50:0:50, and 25:50:25.
What sets our research apart is the careful selection of these plastics and their proportions and our purposeful endeavor to engineer specific performance enhancements through precisely calibrated compositions. By exploring a wide spectrum of blending ratios, we aim to unlock novel synergies and clarify the nuanced effects that arise from the unique combination of these materials. Through our endeavors, we strive to push the boundaries of understanding in polymer science, offering valuable contributions to the field’s knowledge base. Our research endeavors unveil the intricate dynamics between PET, HDPE, and PVC, providing a deeper understanding of their interactions. Additionally, these insights pave the way for developing advanced materials with tailored properties and enhanced functionalities, addressing pressing challenges and fostering innovation across various industries.
3.5. Asphalt Sample Preparation
In our experimental procedure, we conducted assessments to gauge the performance of asphalt mixes. These evaluations encompassed both modified and unmodified specimens. The modified samples underwent a transformation facilitated by incorporating waste plastic compositions with varying bitumen content compositions. To commence the experimentation, cylindrical specimens measuring 101.6 mm in diameter and 63.5 mm in height were utilized as the foundation. The aggregates were subjected to heating within the 170 to 190 °C range; subsequently, waste plastic materials were introduced in differing proportions. Following this, heated bitumen at a temperature of 160 °C was introduced to facilitate the formation of the asphalt mix. The prepared asphalt samples underwent a compaction process, subjected to 75 blows on both sides, utilizing a 4.5 kg compaction device. This rigorous compaction process was instrumental in ensuring the homogeneity and integrity of the asphalt samples, laying the groundwork for subsequent performance evaluations.
In asphalt mix design, volumetric parameters such as VMA, Vv, VFB, and Vb play a critical role in determining mix performance. Since our study predicts Gmb as the output, we must estimate these parameters using independent inputs such as BC, aggregate gradation, and material-specific gravity values without relying on direct Gmb measurements. The parameters are estimated using the empirical relationships presented in Equations (3)–(6).
where
BC = bitumen content, Gsb = bulk specific gravity of the aggregate, and Gb = specific gravity of bitumen
Through these experimental procedures, we aimed to clarify the influence of waste plastic composition variations on the properties and performance characteristics of the asphalt mixes. Such insights are crucial for advancing sustainable practices in asphalt construction while concurrently addressing environmental concerns associated with plastic waste disposal.
4. Data Collection
In this study, 539 observations were gathered from experiments conducted at the Shoolini University laboratory, focusing on the utilization of waste plastic. Subsequently, the dataset was split into training and testing subsets in a 70/30 ratio, resulting in 377 observations for training and 162 for testing. The range and sizes of these datasets are summarized in Table 3. Four ML techniques, ANN, GP, REP Tree, and SVM, were implemented to predict the Gmb of modified asphalt mixture using Weka 3.9.5 software. The input parameters considered for prediction included BC, Vb, Vv, VFB, and VMA. Statistical characteristics of these input parameters are presented in Table 4, and Histograms depicting the datasets are presented in Figure 3.

Table 3.
Range of experimental work dataset.

Table 4.
Statistical characteristics of the input parameters.
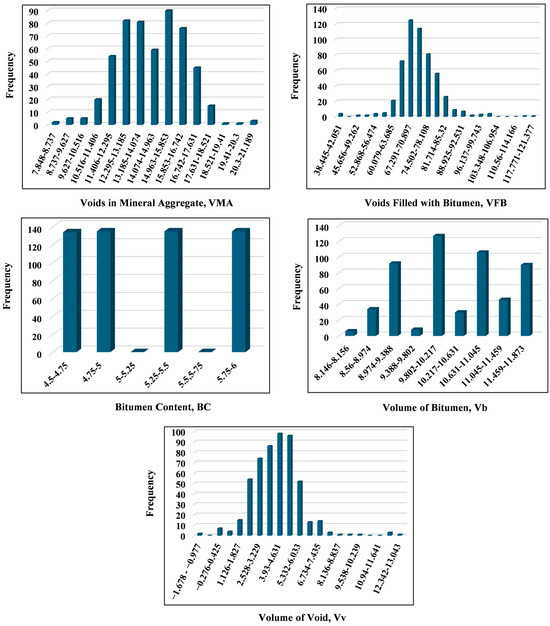
Figure 3.
Histogram of the input parameters.
Performance evaluation of the predictive models was conducted using various metrics outlined in Table 5. This assessment aimed to determine the accuracy and generalization abilities of the ML techniques employed. The study endeavors to enhance the understanding and prediction of hybrid asphalt concrete properties, thereby contributing to developing more sustainable and resilient infrastructure materials.

Table 5.
Evaluation metrics for performance assessment.
Performance Evaluation Parameters
In the assessment of predicting the Gmb of the asphalt concrete, various evaluation parameters were employed to gauge the accuracy and reliability of the predictions. These parameters included correlation coefficient (CC), root mean square error (RMSE), mean absolute error (MAE), and scatter index (SI).
CC is a metric that ranges from −1 to 1, where a higher CC value indicates a stronger correlation between predicted and actual values. A CC value closer to 1 signifies a more accurate prediction. RMSE and MAE are indicators of the average prediction error. Lower values of RMSE and MAE are desirable as they indicate a minor discrepancy between predicted and actual values, thus reflecting better prediction accuracy. SI provides insights into the dispersion of predicted values around the line of best fit. A lower SI value signifies better prediction accuracy, indicating less scatter or variability in the predictions. Equations (7)–(10) were used to calculate these evaluation parameters.
where
- = observed value;
- = predicted value;
- = average observed value;
- n = number of observations.
The evaluation results of these parameters are presented in Table 5, where the performance of the predictive models is assessed based on these metrics. The aim is to identify the model that yields the highest CC value and the lowest RMSE, MAE, and SI values, indicating superior predictive capability and accuracy in estimating the Gmb of asphalt concrete.
5. Results
5.1. GP Model Predictions
The GP model demonstrated outstanding predictive prowess, as evidenced by its remarkable performance across various metrics. Notably, the model attained exceptionally high CC values of 0.9935 and 0.9846 for the training and testing datasets. This indicates a robust linear relationship between the predicted and actual values, affirming the model’s ability to capture the underlying patterns in the data accurately. Furthermore, the GP model exhibited minimal MAE values of 0.0017 for training and 0.0028 for testing. These low MAE values indicate that, on average, the GP model’s predictions deviate by a very small margin from the actual values, emphasizing its precision and reliability. Similarly, RMSE values of 0.0058 for training and 0.0101 for testing further highlight the model’s accuracy and consistency. These values suggest that the model’s predictions have low variability and are close to the actual values, as shown in Figure 4, indicating its robust performance in predicting the Gmb of asphalt concrete.
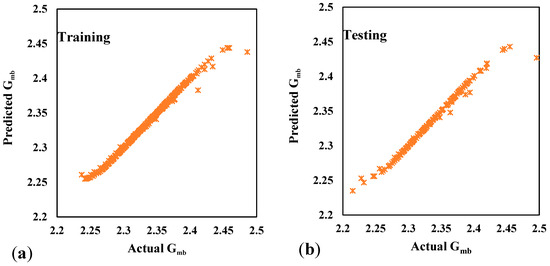
Figure 4.
Comparison of actual and predicted values for the GP model in training and testing.
Overall, these findings underscore the effectiveness and reliability of the GP model in accurately predicting Gmb values for training and testing datasets. Its ability to achieve high CC, low MAE, and RMSE values demonstrates its robustness and suitability for practical applications in asphalt concrete prediction.
5.2. SVM Model Predictions
SVM is a robust machine learning algorithm that is particularly effective for classification and regression tasks. It works by finding the optimal hyperplane that separates data points into different classes or predicts continuous target values in the case of regression. SVM achieves this by maximizing the margin between different classes or minimizing the error between predicted and actual values, depending on the task. The SVM model exhibits exceptional predictive performance, as demonstrated by the extremely high CC values of 0.9995 for training and 0.9989 for testing. The model achieves impressively low MAE values of 0.0004 for training and 0.0007 for testing. These values suggest that, on average, the SVM model’s predictions deviate by an incredibly small margin from the actual values, underscoring its precision and accuracy (Figure 5). Similarly, the RMSE values of 0.0015 for training and 0.0024 for testing indicate that the model’s predictions have minimal variability and are very close to the actual values overall.
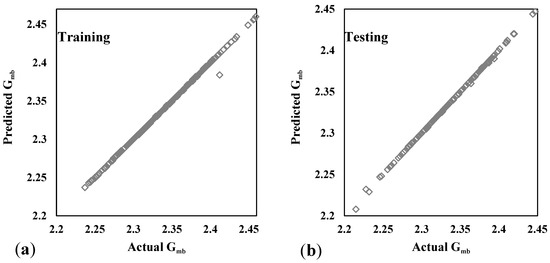
Figure 5.
Comparison of actual and predicted values for the SVM model in training and testing.
The extremely high CC values and the low MAE and RMSE values indicate that the SVM model effectively captures the complex relationships between input features and Gmb values, resulting in highly accurate predictions for training and testing datasets. These results highlight the SVM model’s exceptional performance and potential as a reliable predictive tool for asphalt concrete properties.
5.3. ANN Model Predictions
The results indicate that the ANN model outperforms all other models used in this study, with CC values of 0.9996 for training and an even higher value of 0.9999 for testing. The model achieves impressively low MAE values of 0.0004 for training and testing datasets. Similarly, the RMSE values of 0.0013 for training and an even lower value of 0.0006 for testing indicate that the model’s predictions have minimal variability and are extremely close to the actual values overall. The hidden layers consist of nine neurons, as shown in Figure 6, with a momentum of 0.2 and a learning rate of 0.2.
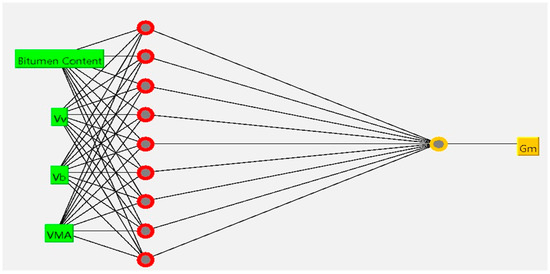
Figure 6.
Architecture of the optimal ANN model.
The ANN model demonstrates exceptional accuracy and robustness in predicting the Gmb of asphalt concrete. Its ability to achieve such high CC values, along with low MAE and RMSE values, as depicted in Figure 7, confirms its effectiveness as a reliable predictive tool in this context. Compared to the findings of [9], who applied ANN to predict the theoretical maximum specific gravity of asphalt concrete and obtained lower accuracy, this study exhibits a significant improvement in precision and reliability. Additionally, reference [10] explored the impact of aggregate gradation and asphalt mix volumetrics on the thermal properties of asphalt mixtures. However, their study did not incorporate machine learning techniques for predictive modeling. The present research extends the application of machine learning by utilizing multiple input parameters to optimize Gmb, thereby enhancing the mix design process.
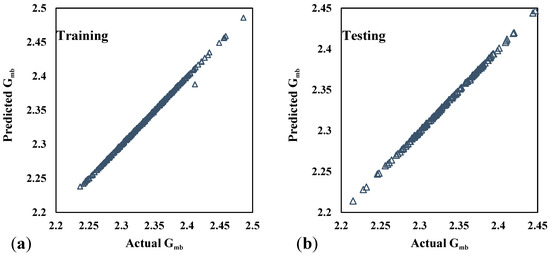
Figure 7.
Comparison of actual and predicted values for the ANN model in training and testing.
5.4. REP Tree Model Predictions
The results from the REP Tree model indicate a strong but comparatively lower predictive performance compared to other models used in the study. The CC values of 0.9551 for training and 0.9772 for testing demonstrate a substantial linear relationship between the predicted and actual values. While slightly lower than those achieved by other models like ANN, GP, and SVM, these CC values still suggest a reasonably good level of prediction accuracy. However, when considering the MAE and RMSE values, it becomes evident that the REP Tree model exhibits higher prediction errors compared to models like ANN, GP, and SVM. Specifically, the REP Tree model has MAE values of 0.0006 for training and 0.0038 for testing, indicating notable prediction deviations. Similarly, its RMSE value of 0.0153 for training and 0.0098 for testing further highlights the model’s greater error than the actual values. Figure 8 illustrates the comparison between actual and predicted values for the REP Tree model.
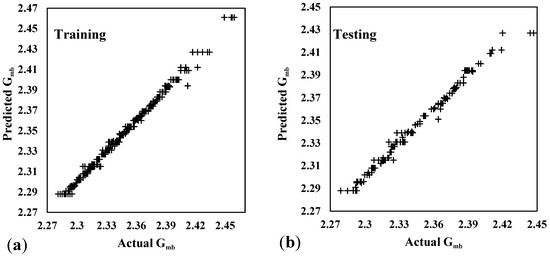
Figure 8.
Comparison of actual and predicted values for the REP Tree model in training and testing.
Despite these higher errors, the REP Tree model’s performance is still deemed acceptable within the context of the study. While it may not achieve the same level of predictive accuracy as ANN or SVM, it still provides reasonably accurate predictions for the Gmb of asphalt concrete. In practical terms, these results suggest that the REP Tree model can still be a valuable tool for prediction tasks in civil engineering and materials science, especially considering its simplicity and ease of interpretation compared to more complex models like ANN and SVM.
5.5. Comparison of All the Applied Models
In comparing all applied models, the ANN model emerges as the top performer, exhibiting unparalleled predictive accuracy and robustness. The exceptionally high CC values of 0.9996 for training and 0.9999 for testing signify a powerful linear relationship between the predicted and actual values. This suggests that the ANN model adeptly captures the underlying patterns in the data, outperforming all other models. Figure 9 illustrates the ANN model’s superior predictive performance with minimal deviation between predicted and actual values.
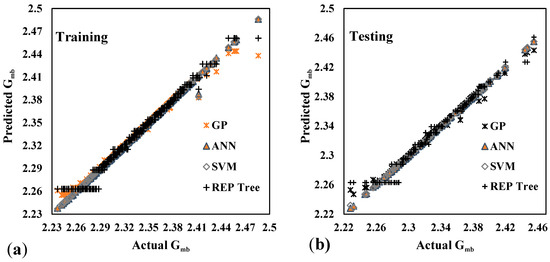
Figure 9.
Comparison of actual and predicted values for all the models in training and testing.
Furthermore, the remarkably low MAE values of 0.0004 for training and testing datasets indicate minimal average deviation between the ANN model’s predictions and the actual values. Similarly, the RMSE values of 0.0013 for training and 0.0006 for testing demonstrate minimal variability and closeness of predictions to actual values overall.
In summary, while SVM, GP, and REP Tree models exhibit strong predictive capabilities, the ANN model stands out as the clear frontrunner regarding predictive accuracy, precision, and robustness. Its exceptional performance underscores its effectiveness as a reliable predictive tool for predicting the Gmb of asphalt concrete, making it the preferred choice among all models evaluated in this study. Figure 10 illustrates the SI, providing additional evidence to support the superior performance of the ANN model during model evaluation.
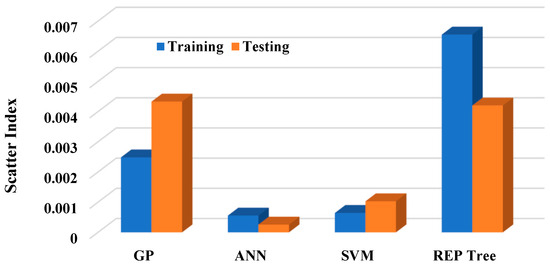
Figure 10.
Scatter index plot comparing models across training and testing phases.
5.6. Correlation Analysis of Input Parameters and Bulk-Specific Gravity
Our investigation explored how input parameters relate to Gmb and their influence on asphalt mixture properties. A significant trend emerged: an increase in the volume of VFB corresponded to higher Gmb values. This positive correlation indicates that a greater binder volume contributes to increased compactness and density in the mixture. Conversely, a contrasting trend emerged when analyzing other input parameters such as BC, VMA, Vv, and Vb. As these parameters increased, Gmb tended to decrease, as depicted in Figure 11. This inverse relationship implies that higher bitumen content, increased void space, or larger air void volumes result in lower overall density and reduced Gmb values [42,43].
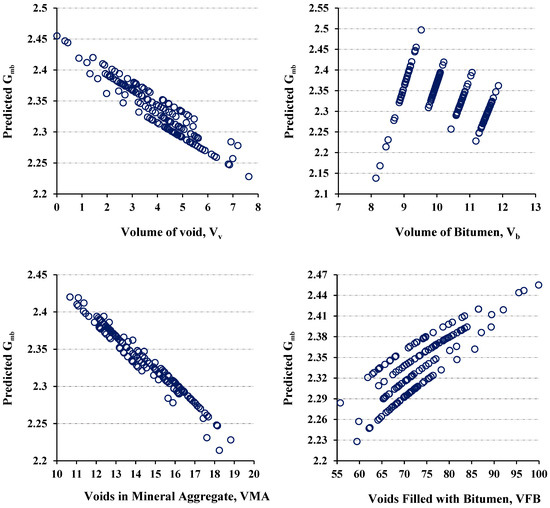
Figure 11.
Predicted Gmb vs. input parameters.
These findings align with fundamental principles in asphalt mixture design, emphasizing the pivotal role of binder content and void characteristics in determining pavement properties. It underscores the necessity of carefully managing binder content and void characteristics during mixture design to achieve desired performance attributes. Furthermore, these insights offer valuable direction for optimizing asphalt mixture compositions to meet specific project objectives, such as attaining target densities and enhancing long-term performance. By comprehending the connections between input parameters and Gmb, engineers can make informed decisions throughout the design and construction phases, advancing more sustainable and durable asphalt pavements.
The predictive performance of the developed models in this study demonstrates superior accuracy compared to previous research. While the Gene expression programming (GEP)-based model by reference [44] achieved a coefficient of determination (R2) of 97.6% and an RMSE of 0.0119, the ANN model in this study outperforms it with a CC of 0.9999 for testing and significantly MAE = 0.0004, RMSE = 0.0006. This higher precision underscores the efficacy of ANN in capturing complex relationships between input variables and Gmb values, particularly for modified asphalt mixtures incorporating PET, HDPE, and PVC. Additionally, while [44] model emphasizes aggregate absorption (Ab%), Gmb, and filler content (F%) as primary predictors, our study identifies BC and Vb as the most influential parameters. This distinction reflects a more comprehensive understanding of material-property interactions, especially in sustainable asphalt mixtures utilizing plastic waste. The superior predictive accuracy and broader input scope make the proposed model a robust and practical tool for optimizing asphalt mix design and quality control applications.
5.7. Sensitivity Analysis
The sensitivity analysis conducted for the best model, which in this study is the ANN, provides valuable insights into the influence of individual input parameters on the prediction of Gmb of asphalt concrete. By systematically removing one input parameter at a time and observing the resulting changes in model performance, we can discern the relative importance of each parameter. In this analysis, it becomes evident that BC and the percentage of volume of bitumen are the most influential parameters. When these parameters are removed from the model, its predictive accuracy and performance are notably affected. This suggests that BC and Vb play pivotal roles in determining the Gmb of asphalt concrete.
BC is a crucial component in asphalt concrete mixtures, serving as the binding agent that holds the aggregate particles together. Variations in BC can significantly affect the overall composition and properties of the asphalt mixture, including its density and compatibility. Therefore, changes in BC can substantially influence the resulting Gmb of asphalt concrete. Similarly, the percentage of the volume of bitumen is a key parameter that directly affects the volume of bitumen within the asphalt mixture. This parameter influences bitumen distribution throughout the mixture and can impact its density and compactness. Consequently, alterations in the percentage of bitumen volume can significantly affect the Gmb of asphalt concrete. The outcomes of the sensitivity analysis are presented in Table 6.

Table 6.
Sensitivity analysis of the ANN model.
6. Conclusions and Future Scope
This study demonstrates the effectiveness of machine learning in predicting the Gmb of asphalt mixtures modified with waste plastics. This study uniquely integrates machine learning models—ANN, SVM, GP, and REP Tree—to predict the Gmb of asphalt mixtures modified with waste plastics (PET, HDPE, and PVC). The proposed models provide a reliable and efficient alternative to traditional experimental methods, offering significant time and resource savings. ANN exhibited superior accuracy among the evaluated models, making it the most suitable predictive tool for asphalt mix design optimization. The key findings of this research are summarized as follows:
- Advanced predictive modeling offers a data-driven alternative to traditional experimental approaches, significantly reducing time and resource consumption.
- The comparative analysis confirms the reliability of ML models in replicating laboratory test results with high precision.
- ANN demonstrated the highest accuracy among all tested models, with a CC of 0.9999 and the lowest error metrics (MAE = 0.0004, RMSE = 0.0006). This highlights the ANN’s potential as the most reliable predictive tool for estimating Gmb in modified asphalt mixes.
- The ANN model exhibited minimal deviation between predicted and actual Gmb values, proving its robustness in accurately capturing the nonlinear relationships among input parameters.
- Sensitivity analysis revealed that bitumen content (BC) and volume of bitumen (Vb) are the most influential parameters affecting the prediction of Gmb.
- Machine learning models offer a scalable solution for optimizing asphalt mix design, reducing dependence on extensive laboratory testing.
- The study validates the use of waste plastic-modified asphalt as a viable approach to enhancing pavement performance and supporting sustainability efforts.
- While the findings of this study highlight the potential of ML models in asphalt mix design, some limitations remain:
- The reliance on VMA and VFA as input parameters may pose practical challenges, as they depend on preliminary Gmb measurements.
- The study is based on a specific dataset; the generalizability of the models needs validation with a larger dataset from diverse sources.
Future research should focus on developing predictive models that eliminate the reliance on preliminary Gmb values for estimating VMA and VFA, by integrating both empirical and ML-based estimation techniques to enhance model applicability in real-world asphalt mix design. Moreover, since volumetric properties alone do not ensure optimal performance, future studies will incorporate performance-based parameters such as rutting resistance, fatigue life, and moisture susceptibility, thereby expanding the scope of ML models in Balanced Mix Design (BMD) and performance-driven optimization. In addition, exploring hybrid ML models that combine deep learning with optimization algorithms is expected to yield enhanced prediction accuracy, while extending model validation to diverse climatic conditions and traffic load variations will further improve the generalizability of these approaches.
Author Contributions
Conceptualization: B.K.; methodology: B.K. and N.K.; formal analysis and investigation: B.K.; writing—original draft preparation: B.K. and N.K.; writing—review and editing: R.R. and V.S.; resources: B.K.; supervision: N.K., R.R. and V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Some data or models used during the study are available from the corresponding author by request.
Acknowledgments
The authors gratefully acknowledge the School of Core Engineering, Shoolini University Solan, for providing the necessary facilities related to the study.
Conflicts of Interest
On behalf of all authors, the corresponding author states that there is no conflicts of interest.
References
- Rahman, S.; Bhasin, A.; Smit, A. Exploring the use of machine learning to predict metrics related to asphalt mixture performance. Constr. Build. Mater. 2021, 295, 123585. [Google Scholar] [CrossRef]
- Roberts, F.L.; Kandhal, P.S.; Brown, E.R.; Lee, D.Y.; Kim, Y.R.; Kennedy, T.W. Hot Mix Asphalt Materials, Mixture Design and Construction, 3rd ed.; National Asphalt Pavement Association Education Foundation: Lanham, MD, USA, 2009; ISBN 978-0-692-78646-8. [Google Scholar]
- Kumar, B.; Kumar, N. Enhancing asphalt mixture performance through waste plastic modification: A comprehensive analysis of optimal compositions and volumetric properties. J. Struct. Integr. Maint. 2024, 9, 2376804. [Google Scholar] [CrossRef]
- Garcia, J.; Hansen, K. HMA Pavement Mix Type Selection Guide; National Asphalt Pavement Association (NAPA): Greenbelt, MD, USA, 2001. [Google Scholar]
- ASTM D 2041; Standard Test Method for Theoretical Maximum Specific Gravity and Density of Bituminous Paving Mixtures. ASTM International: West Conshohocken, PA, USA, 2003.
- Roberts, F.L.; Kandhal, P.S.; Lee, D.-Y.; Kennedy, T.W. Hot Mix Asphalt Materials, Mixture Design and Construction, 2nd ed.; National Asphalt Pavement Association Education Foundation: Lanham, MD, USA, 1996; ISBN 978-0914313014. [Google Scholar]
- Khan, D.; Khan, R.; Khan, M.T.; Alam, M.; Hassan, T. Performance of hot-mix asphalt using polymer-modified bitumen and marble dust as a filler. J. Traffic Transp. Eng. (Engl. Ed.) 2023, 10, 385–398. [Google Scholar] [CrossRef]
- Liang, Y.; Bai, T.; Zhou, X.; Wu, F.; Chenxin, C.; Peng, C.; Fuentes, L.; Walubita, L.F.; Li, W.; Wang, X. Assessing the Effects of Different Fillers and Moisture on Asphalt Mixtures’ Mechanical Properties and Performance. Coatings 2023, 13, 288. [Google Scholar] [CrossRef]
- Khasawneh, M.A.; Sawalha, A.A.; Aljarrah, M.T.; Alsheyab, M.A. Effect of aggregate gradation and asphalt mix volumetrics on the thermal properties of asphalt concrete. Case Stud. Constr. Mater. 2023, 18, e01725. [Google Scholar] [CrossRef]
- Dalhat, M.A.; Osman, S.A. Artificial Neural Network Modeling of Theoretical Maximum Specific Gravity for Asphalt Concrete Mix. Int. J. Pavement Res. Technol. 2024, 17, 406–422. [Google Scholar] [CrossRef]
- Reich, Y. Machine Learning Techniques for Civil Engineering Problems. Comput.-Aided Civ. Infrastruct. Eng. 1997, 12, 295–310. [Google Scholar] [CrossRef]
- Murad, Y.Z. Predictive model for bidirectional shear strength of reinforced concrete columns subjected to biaxial cyclic loading. Eng. Struct. 2021, 244, 112781. [Google Scholar] [CrossRef]
- Kumar, B.; Kumar, N.; Kashyap, V. Soft computing-based optimization of plastic waste utilization in flexible pavement construction. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 3087–3098. [Google Scholar] [CrossRef]
- Jweihan, Y.S.; Alawadi, R.J.; Momani, Y.S.; Tarawneh, A.N. Prediction of Marshall Test Results for Dense Glasphalt Mixtures Using Artificial Neural Networks. Front. Built Environ. 2022, 8, 949167. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, Y.R. Prediction of layer moduli from falling weight deflectometer and surface wave measurements using artificial neural network. Transp. Res. Rec. 1998, 1639, 53–61. [Google Scholar] [CrossRef]
- Tarefder, R.A.; White, L.; Zaman, M. Neural Network Model for Asphalt Concrete Permeability. J. Mater. Civ. Eng. 2005, 17, 19–27. [Google Scholar] [CrossRef]
- Gong, H.; Sun, Y.; Hu, W.; Polaczyk, P.A.; Huang, B. Investigating impacts of asphalt mixture properties on pavement performance using LTPP data through random forests. Constr. Build. Mater. 2019, 204, 203–212. [Google Scholar] [CrossRef]
- Zhou, F.; Lytton, R.L.; Hu, S.; Luo, R.; Tsai, F.-L.; Lee, S.I. Models for Predicting Reflection Cracking of Hot-Mix Asphalt Overlays; National Academies Press: Washington, DC, USA, 2010. [Google Scholar]
- Kim, H.; Rauch, A.F.; Haas, C.T. Automated Quality Assessment of Stone Aggregates Based on Laser Imaging and a Neural Network. J. Comput. Civ. Eng. 2004, 18, 58–64. [Google Scholar] [CrossRef]
- Saif, M.A.; El-Bisy, M.S.; Alawi, M.H. Application of Soft Computing Techniques to Predict the Stability of Asphaltic Concrete Mixes. In Proceedings of the Twelfth International Conference on Civil, Structural and Environmental Engineering Computing, Dubrovnik, Croatia, 4–7 September 2012; Topping, B.H.V., Costa Neves, L.F., Barros, R.C., Eds.; Civil-Comp Press: Stirlingshire, UK, 2013. [Google Scholar]
- Cook, R.; Lapeyre, J.; Ma, H.; Kumar, A. Prediction of Compressive Strength of Concrete: Critical Comparison of Performance of a Hybrid Machine Learning Model with Standalone Models. J. Mater. Civ. Eng. 2019, 31, 04019255. [Google Scholar] [CrossRef]
- Tarawneh, A.; Saleh, E.; Almasabha, G.; Alghossoon, A. Hybrid Data-Driven Machine Learning Framework for Determining Prestressed Concrete Losses. Arab. J. Sci. Eng. 2023, 48, 13179–13193. [Google Scholar] [CrossRef]
- Park, J.Y.; Yoon, Y.G.; Oh, T.K. Prediction of Concrete Strength with P-, S-, R-Wave Velocities by Support Vector Machine (SVM) and Artificial Neural Network (ANN). Appl. Sci. 2019, 9, 4053. [Google Scholar] [CrossRef]
- Angelaki, A.; Singh Nain, S.; Singh, V.; Sihag, P. Estimation of models for cumulative infiltration of soil using machine learning methods. ISH J. Hydraul. Eng. 2021, 27, 162–169. [Google Scholar] [CrossRef]
- Kumar, B.; Kumar, N. Forecasting Marshall stability of waste plastic reinforced concrete using SVM, ANN, and tree-based techniques. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 4569–4587. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Goh, S.H. Support vector machines: Their use in geotechnical engineering as illustrated using seismic liquefaction data. Comput. Geotech. 2007, 34, 410–421. [Google Scholar] [CrossRef]
- Suthar, M. Applying several machine learning approaches for prediction of unconfined compressive strength of stabilized pond ashes. Neural Comput. Appl. 2020, 32, 9019–9028. [Google Scholar] [CrossRef]
- Thakur, M.S.; Pandhiani, S.M.; Kashyap, V.; Upadhya, A.; Sihag, P. Predicting Bond Strength of FRP Bars in Concrete Using Soft Computing Techniques. Arab. J. Sci. Eng. 2021, 46, 4951–4969. [Google Scholar] [CrossRef]
- Kumar, B.; Kumar, N.; Mehta, V. Evaluation of soft computing techniques for predicting Marshall Stability of waste plastic-reinforced asphalt concrete. J. Struct. Integr. Maint. 2024, 9, 2371038. [Google Scholar] [CrossRef]
- Yang, G.; Yu, W.; Li, Q.J.; Wang, K.; Peng, Y.; Zhang, A. Random Forest–Based Pavement Surface Friction Prediction Using High-Resolution 3D Image Data. J. Test. Eval. 2021, 49, 1141–1152. [Google Scholar] [CrossRef]
- Kumar, A.R.S.; Goyal, M.K.; Ojha, C.S.P.; Singh, R.D.; Swamee, P.K.; Nema, R.K. Application of ANN, Fuzzy Logic and Decision Tree Algorithms for the Development of Reservoir Operating Rules. Water Resour. Manag. 2013, 27, 911–925. [Google Scholar] [CrossRef]
- Dhakate, P.P.; Patil, S.; Rajeswari, K.; Abin, D. Preprocessing and classifcation in WEKA using diferent classifers. Int. J. Eng. Res. Appl. 2014, 4, 91–93. [Google Scholar]
- ASTM C 128; Standard Test Method for Density, Relative Density (Specific Gravity) and Absorption of Fine Aggregate. ASTM International: West Conshohocken, PA, USA, 1992.
- ASTM C127; Standard Test Method for Density, Relative Density (Specific Gravity) and Absorption of Coarse Aggregate. ASTM International: West Conshohocken, PA, USA, 1992.
- ASTM C131/C131M; Standard Test Method for Resistance to Degradation of Small-Size Coarse Aggregate by Abrasion and Impact in the Los Angeles Machine. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D4791-10; Standard Test Method for Flat Particles, Elongated Particles, or Flat and Elongated Particles in Coarse Aggregate. ASTM International: West Conshohocken, PA, USA, 2010.
- ASTM D792-13; Standard Test Methods for Density and Specific Gravity (Relative Density) of Plastics by Displacement. ASTM International: West Conshohocken, PA, USA, 2013.
- ASTM D92–16; Standard Test Method for Flash and Fire Points by Cleveland Open Cup Tester. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM D5-97; Standard Test Method for Penetration of Bituminous Materials. ASTM International: West Conshohocken, PA, USA, 1998.
- ASTM D36; Standard Test Method for Softening Point of Bitumen (Ring and Ball Apparatus). ASTM International: West Conshohocken, PA, USA, 1995.
- ASTM D70; Standard Test Method for Specific Gravity and Density of Semi-Solid Bituminous Materials (Pycnometer Method). ASTM International: West Conshohocken, PA, USA, 1997.
- Aboufoul, M.; Garcia, A. Influence of air voids characteristics on the hydraulic conductivity of asphalt mixture. Road Mater. Pavement Des. 2017, 18, 39–49. [Google Scholar] [CrossRef]
- Russo, F.; Biancardo, S.A.; Formisano, A.; Dell’Acqua, G. Predicting percent air voids content in compacted bituminous hot mixture specimens by varying the energy laboratory compaction and the bulk density assessment method. Constr. Build. Mater. 2018, 164, 508–524. [Google Scholar] [CrossRef]
- Jweihan, Y.S. Predictive model of asphalt mixes’ theoretical maximum specific gravity using gene expression programming. Results Eng. 2023, 19, 101242. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).