1. Introduction
In the context of knowledge distillation, the SoftMax function is used to convert the raw output scores of a model into a probability distribution over classes. The SoftMax function was initially proposed for shallow neural networks [
1] in an attempt to treat the outputs of the neural network as probabilities of pattern classes conditioned on the inputs [
2]. However, a long period of time and various formulations of SoftMax were needed before it was accepted as a default solution for multi-class classification problems. The traditional deep neural networks, including AlexNet, GoogLeNet, ResNet, VGG etc. [
3], as well as the modern transformer-based architectures, append a SoftMax layer in their fully connected classification part.
At first, Ba and Caruana [
4], and later Hinton et al. [
5], trained a student network by matching the logits of the student network and a pre-trained teacher network. The stimulating model compression method proposed by Hinton et al. was coined as knowledge distillation, and by dividing the logits used in the SoftMax layer by a temperature parameter other than 1, the dark knowledge has been revealed in the form of soft targets. Therefore, dark knowledge explicitly refers to the remaining outputs of the SoftMax layer that are different from the highest one. These values represent the hidden knowledge used in the training by distillation from a teacher model to a smaller student model. As such, the softer distribution of SoftMax consists of the introduction of a temperature parameter
T whose value is
for classical SoftMax and is empirically varied between
and
in the temperature scaling version of the function. While no formal proof for the choice of the right temperature for a target task is given, one could heuristically observe that raising the temperature leads to the appearance of a classification plateau. Consequently, the learning benefit due to SoftMax relaxation is gradually reduced until it disappears for a large
T value due to the occurrence of deep informational entropy [
6]. The problem tackled in this research is how to non-heuristically determine an optimal temperature for a given classification task to maximally benefit from the knowledge distillation method.
2. Related Works
The knowledge distillation method [
7] was quickly embraced in many application fields of machine learning like speech recognition, machine translation or computer vision [
8] etc., but in our paper, the knowledge distillation method is considered for practical testing and demonstration purposes in the context of class incremental learning [
9]. A wide majority of the mainstream class incremental methods like Learning without Forgetting (LwF) [
10], Incremental Classifier and Representation Learning (iCaRL) [
11], or more recently, FOSTER: Feature Boosting and Compression for Class-Incremental Learning [
12] exploit knowledge distillation; see also [
13] or [
14] for other models. Even though other newer models for incremental learning already outperform the iCaRL method, iCaRL has been chosen for the practical demonstration of our theoretical method due to its simplicity, which makes it suitable to understand how things work in practice.
Novel knowledge distillation methods have been proposed for different image classification tasks, e.g., for hyperspectral image classification [
15], for remote sensing image scene classification [
16] or for cervical cell image classification [
17]. The combination of transfer learning and knowledge distillation, proposed in the paper [
17], effectively improved the classification of cervical cell images.
In the paper [
18], the authors introduced an online knowledge distillation framework, which makes use of an attention mechanism to combine the predictions of a cohort of lightweight networks into a powerful ensemble with the purpose of enhancing the distillation effect. Moreover, in the paper [
19], an improved residual neural network (ResNet)-based algorithm for concrete dam crack detection using a dynamic knowledge distillation approach is presented.
The knowledge distillation components proved to be helpful when only a few labeled samples are available, like in the papers [
15] or [
16], but no specific optimal values for the temperature parameters were proposed in those papers, as we propose in our work. In the class-incremental learning setting, our method effectively mitigates the issue of catastrophic forgetting by computing optimal temperature parameters for the models proposed in the papers [
10,
11,
12]. Moreover, our algorithm is model agnostic so it can be directly applied to any class-incremental architectures using temperature-varying SoftMax.
3. Materials and Methods
The transformation of the neural network outputs
to the probabilities
y in the last layer is usually conducted with the application of a normalized exponential function called SoftMax:
This function has a parameter T called temperature that is usually set to 1. According to Hinton et al. [
5], using a higher value for T produces a softer probability distribution over classes, thus mitigating through a proper loss the effects of catastrophic forgetting in incremental learning.
Incremental learning (IL) [
20] refers to a class of machine learning algorithms in which the learning process goes through a continuous model adaptation based on a constantly arriving data stream [
21].
A common approach to incremental learning is to initialize the new model with the same weights as the pre-trained model and then to add a corresponding SoftMax layer by removing the last layer of the previous model. After that, the model is trained starting from the point where the pre-trained model had been extended for a faster convergence. If the previous model is large, it is not necessary to update the weights for its previous layers by marking them as un-trainable. Only the weights of the extra layers were updated by using fine tuning. But this is not enough to deal with the effects of catastrophic forgetting and exploiting the dark knowledge through knowledge distillation turned out to be very helpful to increase the overall accuracy of incremental learning; see [
10] or [
11].
Catastrophic forgetting [
22] reflects the tendency of deep networks to forget past information when new data are incorporated. As said above, catastrophic forgetting is classically mitigated through the use of a knowledge distillation component because it is assumed to offer a good balance between stability and plasticity in incremental deep models.
The experiments start by varying the temperature T of the temperature scaling SoftMax to check the dependence of the classes and temperatures for intra-class separability during distillation. The data
are considered for each incremental step
t and
K the memory size, i.e., number of classes kept in the memory, given the cross entropy loss, defined as:
where
is the indicator function and
p stands for the predictive probabilities of the corresponding class, e.g., the SoftMax output.
The distillation loss is defined as:
where
y is the temperature scaling SoftMax applied on the raw scores predicted by the network.
The final loss now is:
where
provides the weight of the distillation loss.
can be set to the fraction between old classes number over the sum of old classes number plus new classes number.
The main objective of our research is to propose a recipe to control the dark knowledge transference by clustering its values according to their relevance and by pushing the limits of SoftMax classification possibilities with the use of a decision tree. As such, an inductive proof is first provided to set the temperature variations in machine learning models that use distillation in a non-heuristic way. At the same time, one can argue that the temperature problem in multi-class classification, studied in existing related works like [
10], is useful but not sufficient for a thorough study of SoftMax classification capacity. As a complement to the temperature setting, our focus is on controlling the behavior of the temperature scaling SoftMax function in its operating temperature limits [
23].
The setting for our experiments starts from the iCaRL incremental learning algorithm that saves
K exemplars from previously seen classes and uses distillation loss in a way similar to
Learning without Forgetting [
11] to retain the knowledge of previous classes. Also, the iCaRL uses a nearest-mean-of-exemplars classification strategy. It has been modified to use a SoftMax output layer for classification.
Hinton et al. [
5] gave results for temperatures ranging from 1 to 20 only for different datasets, one of them being the classical MNIST dataset, probably because they found just plateau values for higher temperatures. However, they provide no formal result along this line and that was one of the initial motivations for our contribution.
Given the statistical distribution of the output, there will always be some large values on top of the Gaussian curve and the standard SoftMax can find a hard threshold for them. After that, the temperature scaling SoftMax was included and it was tested for temperature values. The results were as expected: at T = 1, there is always a hard label; at T = 20, there is always a plateau of values; and as the number of classes increases, the values of probabilities decrease so that they sum up to 1. The contribution of this paper is to provide the optimal Tmax between 2 and 20 that gives the optimal knowledge distillation effect for a given precision set by the user. In the next section, an inductive proof of the SoftMax capacity is provided that allows us to set the optimal Tmax value.
4. SoftMax Distillation Capacity
The experiments start by varying the number of classes and clustering the results of SoftMax. For example, for 100 classes and T = 2, as in Hinton’s paper, it finds the relevant cluster with not just two but around eight large values, i.e.,
So, for 100 classes, by varying the temperature T from 1 to 2, the number of relevant values for learning increases with an exponential factor of 3 from to .
But if the number of classes becomes 1000, then already for T = 9, the relevant cluster contains 30 values, making it irrelevant for learning without forgetting through the distillation.
Our experiments are gathered in
Table 1 for our modification of ICaRL, explained in detail in the ablation study from the numerical section. The table displays the results obtained by increasing the temperature while keeping the number of classes constant K = 100, and
Table 2 shows the experiments for 10, 100 and 1000 classes and with temperature increments of T = 1, T = 2 and T = 20. ImageNet ILSVRC was used as the dataset (for 1000 classes), as will be presented in detail in the numerical experiments section. Our interest is in separating past and new classes by using the temperature scaling SoftMax but also in knowing in a non-heuristic way the number of classes we can incrementally learn by penalizing or relaxing the SoftMax layer. We observed that for a large number of classes, e.g., 1000, the main cluster contains 30 values, which is useless for separating the classes, and therefore, the distillation reaches its limit.
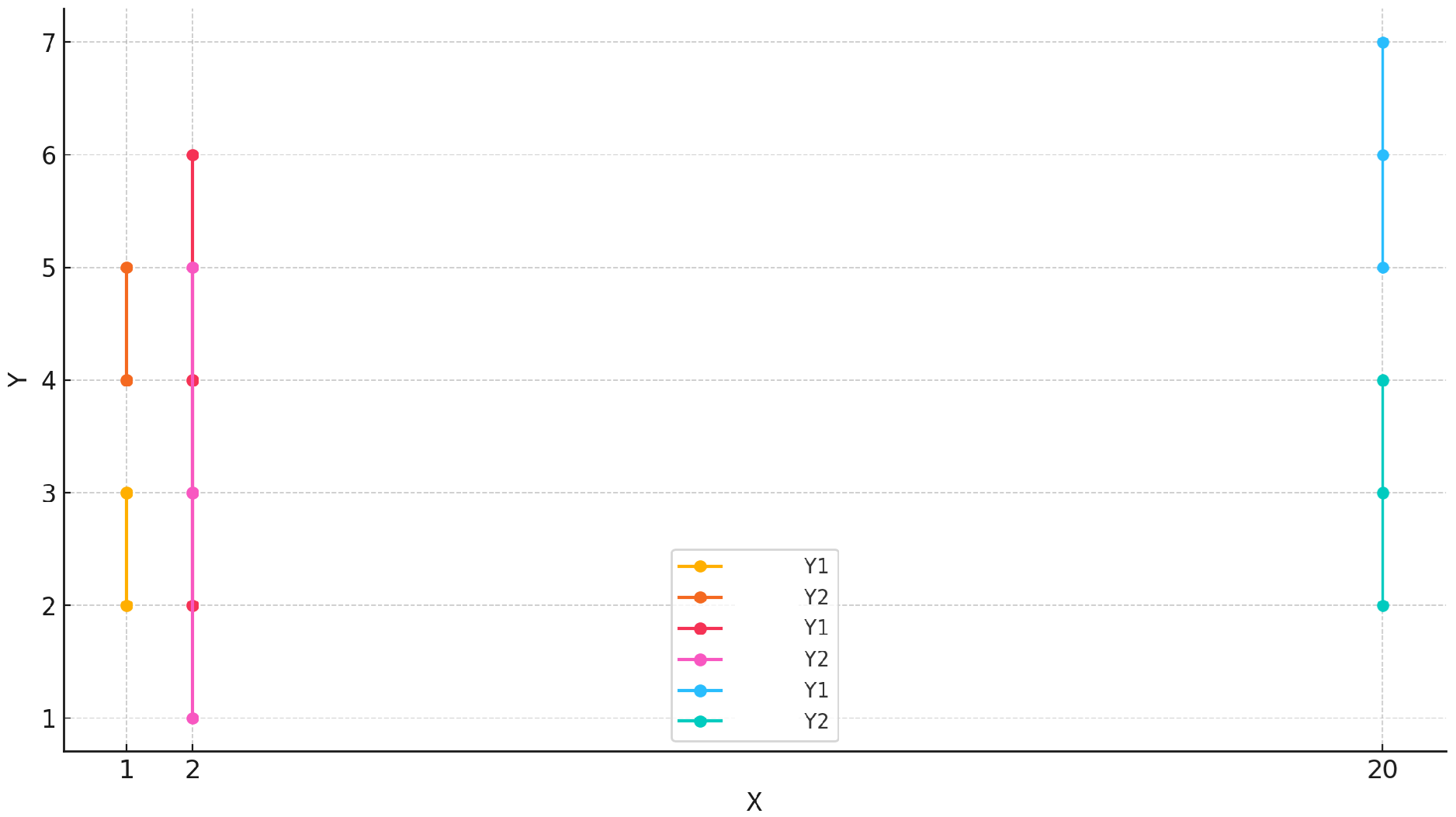
A visualization of the elements from
Table 2 for 10 classes is given in
Figure 1. One can observe that for temperatures T = 2 and T = 20, one obtains 6 possible values clustered for distillation.
Note that the number of clusters is set up dynamically by calculating the MeanShift and estimating the bandwidth [
24].
The number of clusters depends directly on the temperature setting. In this context, the last cluster means the highest probability values and the largest index given by the MeanShift clustering algorithm. This algorithm is a centroid-based algorithm, which works by updating candidates for centroids to be the mean of the points within a given region. In this context,
Table 1 reads as follows: in our experiments, for temperature T = 1, three clusters were obtained, i.e., cluster 1, cluster 2 and cluster 3 which has only two large values that are easily separable. For T = 2, two clusters we obtained, and the softer distributions within cluster 2 have eight values that are still separable. Finally, for the other temperature settings, the MeanShift algorithm applied to the output values of the network provided us with just one cluster with all values in it, making it hard to distinguish from the plateau and hence not so relevant for dark knowledge transference. Consequently,
Table 2 reads as follows: for the setting T = 1 and 100 classes, three clusters were obtained, and cluster 3 has only two values in it that will be considered relevant.
Inductive proof of the SoftMax capacity: Inspired by our dark-knowledge-clustering experiments, a constructive proof was designed for the temperature scaling SoftMax classification capacity while varying the number of classes and the temperature parameters. As far as we are aware, this is one of the largest experiments that took place for a specific learning algorithm and it involved documenting the SoftMax classification limits as we vary the temperature parameters in range from 1 to 20 and the number of classes in range of 10 to 1000.
Let us start with the first part of our inductive proof: the verification of the hypothesis for two classes. It is considered that before the classification layer, the values obtained are
and
. It is proven that one can choose an
for arbitrary values with small variations so a rank
exists such that
The maximum value for T is attained when the equality is satisfied. Since the denominator is common, the equation can be considered without loss of the generality:
Next, the natural logarithm
is applied and one can consequently obtain
which provides us for the considered class classification margin
with the following estimation for the Tmax
meaning that all values can be distinguished with up to
precision limits below the temperature setting Tmax. As an example for values 1 and 9, one can obtain by the formula and upper round a Tmax of 9 with, for example, an epsilon of 0.4. The values of the SoftMax for this example are [0.29133917 0.70866083]. Now, the inductive step is performed to generalize our formula for a number of
K classes. The hypotheses now read:
which is consequently reduced to
By summing up and reducing the inner terms, one can obtain
where
is equal to the sum of logarithmic variations meaning that
. Since
is sub-unitary, the overall variation
is only becoming smaller in the limit for the k considered classes.
A similar example for iCaRL for K = 100 classes with SoftMax temperature again T = 9 and overall
precision = 0.008 is presented in
Figure 2. Please note that ICaRL uses sigmoids as activation functions for the classes so the output values are sub-unitary, which is probably the reason why they employed the nearest-mean-of-exemplars instead of the SoftMax, as was carried out in our algorithm adaptation.
One can conclude now that the classification capacity is not bounded by the temperature parameters as one can compute a specific Tmax such that for K classes we can still have separability as long as the considered temperature is less than Tmax. Since this is now clear, we turn to another problem of SoftMax for incremental learning which in our opinion is the additional characterization of the minimal oscillating values as the number of classes grows. In the next step, the focus will be on further pushing the limits of knowledge distillation and the introduction of a model-agnostic distillation algorithm.
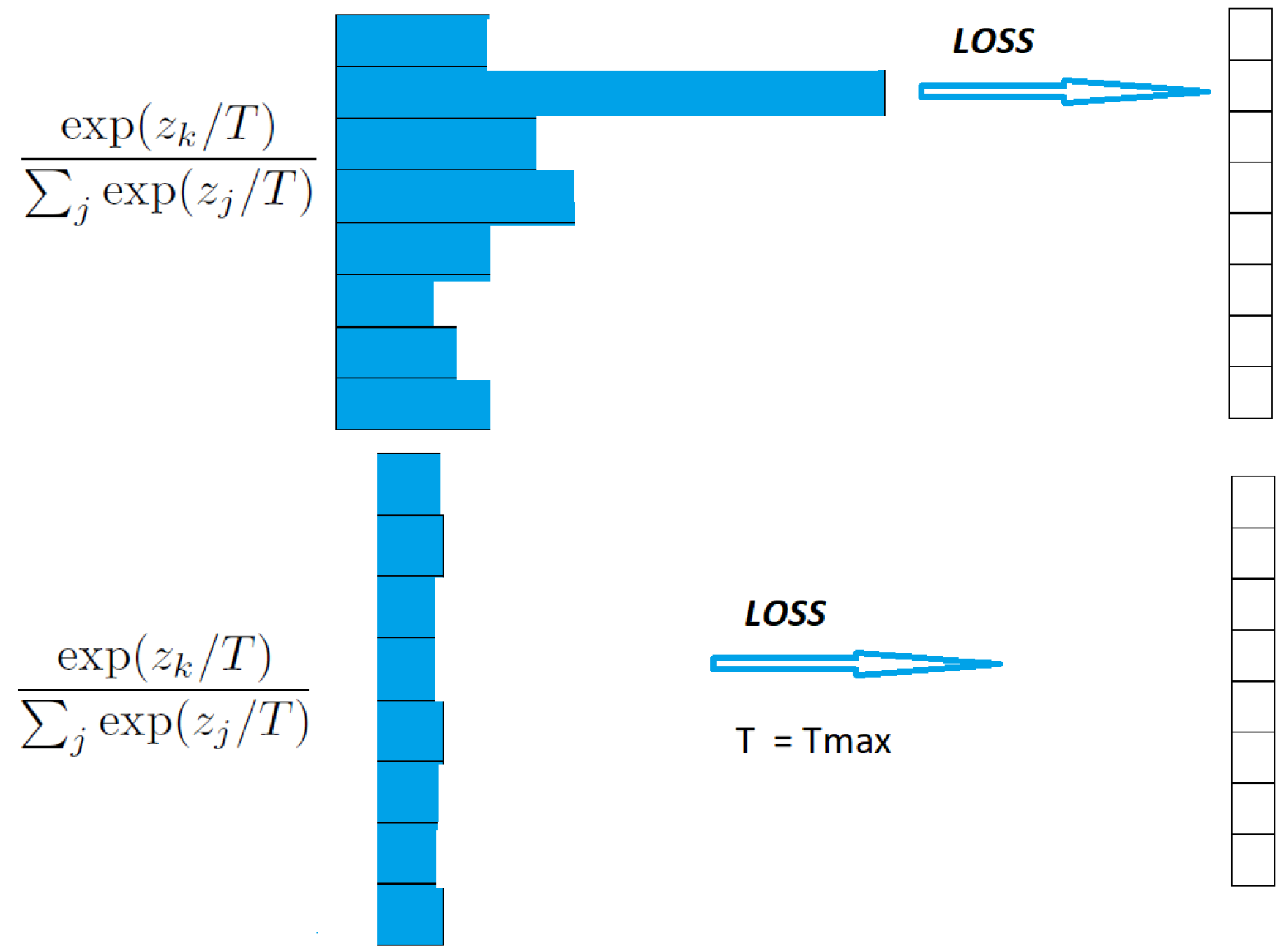
5. Balancing the Number of Classes and the Temperature
Having determined the Tmax for a given number of classes K and a requested
precision, the interest now is in the balance between the number of classes K and the temperature T, such that we can push the limits of the SoftMax classification. The situation at this point can be observed graphically in
Figure 3.
Since the new classes keep streaming and there is no gain in further increasing the temperature above Tmax, an incremental decision tree with information gain splitting was designed to try to classify the incoming classes. In the classical situation, one could compute the loss between the SoftMax output and the corresponding label. Now, one needs to compute the corresponding training loss between all the class outputs and their training labels in order to distinguish a class with the highest probability.
Note that the Kullback–Leibler (KL) [
25] divergence or relative entropy is the difference between the cross-entropy and the entropy. In this view, even if it is asymmetrical, the KL divergence can be viewed as a measure of the distance between two probability distributions on a random variable. As the divergence is a convex function on the domain of probability distributions, an alternative approach would be to use differentiation in order to obtain a maximum on the number of classes and the temperature. In both cases, the overall purpose is to avoid extreme disorder due to the fact that there is no majority value, no matter how much one exponentially magnifies the outputs. One can use an incremental learning tree or start from the values obtained with Tmax, and one can start incorporating classes until the information gain is zero. Our decision tree was built by testing the information gain contained in the SoftMax clusters used to compute the distillation loss.
Information gain (IG) is the reduction in entropy or surprise by transforming a dataset and it can be used as a splitting rule in decision trees. The information gain of a random variable X obtained from an observation of a random variable A taking
is defined as
and therefore it is the Kullback–Leibler divergence of the prior distribution and the posterior distribution with
I being mutual information.
Information gain is calculated by comparing the entropy of the dataset before and after a transformation. For our tree, the two distributions produced for a specific stream by the convolutional neural network at a specific time were considered. Information gain is, in this context, a statistical property that measures how well a given attribute separates the training examples according to their target classification. To construct the tree, one can use the Hoeffding tree, which is an incremental decision tree learner for large data streams [
26,
27]. Since the purpose is to squeeze information out of the SoftMax function as the number of classes increases, one can assume that the overall data distribution is not changing over time as in the case of the original convolutional neural network (CNN is here ResNet32) algorithm where fine-tuning and weight normalization must be performed. The main splitting iteration reads as in
Figure 4.
Our decision tree was built to determine exactly which number of streamed classes one can still theoretically classify. We begin with T = Tmax and for the batch of the data streams on which the Tmax was computed. It was continued with the second stream of new classes and then we checked the information gain. Depending on the maximum information gain, one can continue on one branch or another until and one can add classes until the information gain is zero or all the values corresponding to our classes are classified. In this way, one can exactly determine the number of classes and can still incorporate with the same Tmax as the number of classes K continues to increase without lowering the Tmax, which means that the limits of SoftMax classification have been pushed up to a situation where the original incremental algorithm will no longer learn to classify new classes. For the previous example at hand, with T = 9 and K = 100 classes, we managed to continuously incorporate the classification of another 83 classes without having to vary the temperature.
We are now able to provide the model-agnostic, dark-knowledge-clustering Algorithm 1 below in a straightforward implementation format.
| Algorithm 1: Model-agnostic distillation algorithm |
![Make 06 00094 i001]() |
The next two sections are dedicated to present our numerical experiments and to practically validate our theoretical findings.
6. Numerical Experiments in a Class-Incremental Learning Framework
For the numerical experiments, a class-incremental learning model has been used that relies on the SoftMax function and knowledge distillation at its core.
Even though there exists a large body of related work, most of the authors considered only the heuristic scenarios like in the papers [
20,
28,
29] or focused only on optimizing temperature parameters for the SoftMax function like in the papers [
30,
31,
32] when dealing with the catastrophic forgetting problem. We take a different approach and we use our method to push the classification limits of the model non-heuristically.
The iCaRL algorithm, proposed by Rebuffi et al. in [
10], is a model largely adopted by the community as the algorithm has the theoretical capacity to continuously learn in an infinite number of states. Also, it is able to get close to the accuracy obtained in the classical batch mode, which can handle a limited number of classes, all available at the same time and not incrementally. Based on three main components, the iCaRL engine is powered by a
convolutional neural network (CNN), more specifically a ResNet18 architecture, which offers an incremental class learning solution. These three components of the iCaRL algorithm are as follows: classification by a nearest-mean-of-exemplars rule, prioritized exemplar selection based on herding and representation learning using knowledge distillation and prototype rehearsal. For the purpose of our experiments, the focus will only be on the first component, because our work is oriented towards the improvement of this layer.
Ablation study for testing the method with the ICaRL algorithm: iCaRL uses a nearest-mean-of-exemplars classification strategy. Instead of this, for our ablation study, we have used for the classification layer, a temperature scaling SoftMax function with variable temperature parameter T.
Instead of searching in the range of 1 to 20 for the
T parameter, as was heuristically proposed by Hinton et al. in [
5], one can use our method to determine the Tmax and the relevant clusters for controlling the distillation effect up to a sort of doubling the amount of relevant dark knowledge transferred. Of course, the increased distillation effect will not be directly reflected in the model accuracy which will not scale in the same manner but it will overall slightly improve, and in incremental learning any small gain is significant.
Our method has been implemented using the Tensorflow framework in an online Python development environment and we have considered the ILSVRC 2012 dataset available at the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) [
3].
As previously mentioned, in the last layer of classification, the iCaRL algorithm uses a normal NCM (nearest class mean) and approximated mean with mean-of-exemplars for computing theoretical class means. For our test scenario, which is merely an ablation study, we changed the mean-of-exemplars with SoftMax and we tested this novel configuration over 100 classes (115,873 images) grouped into 10 classes per batch.
Because our goal was to avoid catastrophic forgetting vs. accuracy as a trade off, the accuracy parameter was only used for comparison between batches. Thus, we noticed that in the beginning, we obtained better accuracy in the case of the first classes. Moreover, we can also observe that in the case of iCaRL-ST1 (iCaRL with SoftMax Temperature 1) and iCaRL-ST20 (iCaRL with SoftMax Temperature 20), the difference in accuracy between the first classes is smaller than in the original algorithm case.
From this point on, we pushed the SoftMax limit and we replaced the NCM method with it. Moreover, we increased the number of classes to 1000 (1,281,167 images) but we kept the number of classes per batch at 10. In this way, we obtained 90 more iterations. This type of experiment has not been performed by the authors of iCaRL because they stopped at iteration 10, choosing to increase the number of classes per iteration to 100 classes per iteration.
During the tests, the use of RAM remained bounded without following a growth trend. The maximum limit did not exceed the range of 4 GB–6 GB of RAM, as in the case of the unmodified algorithm.
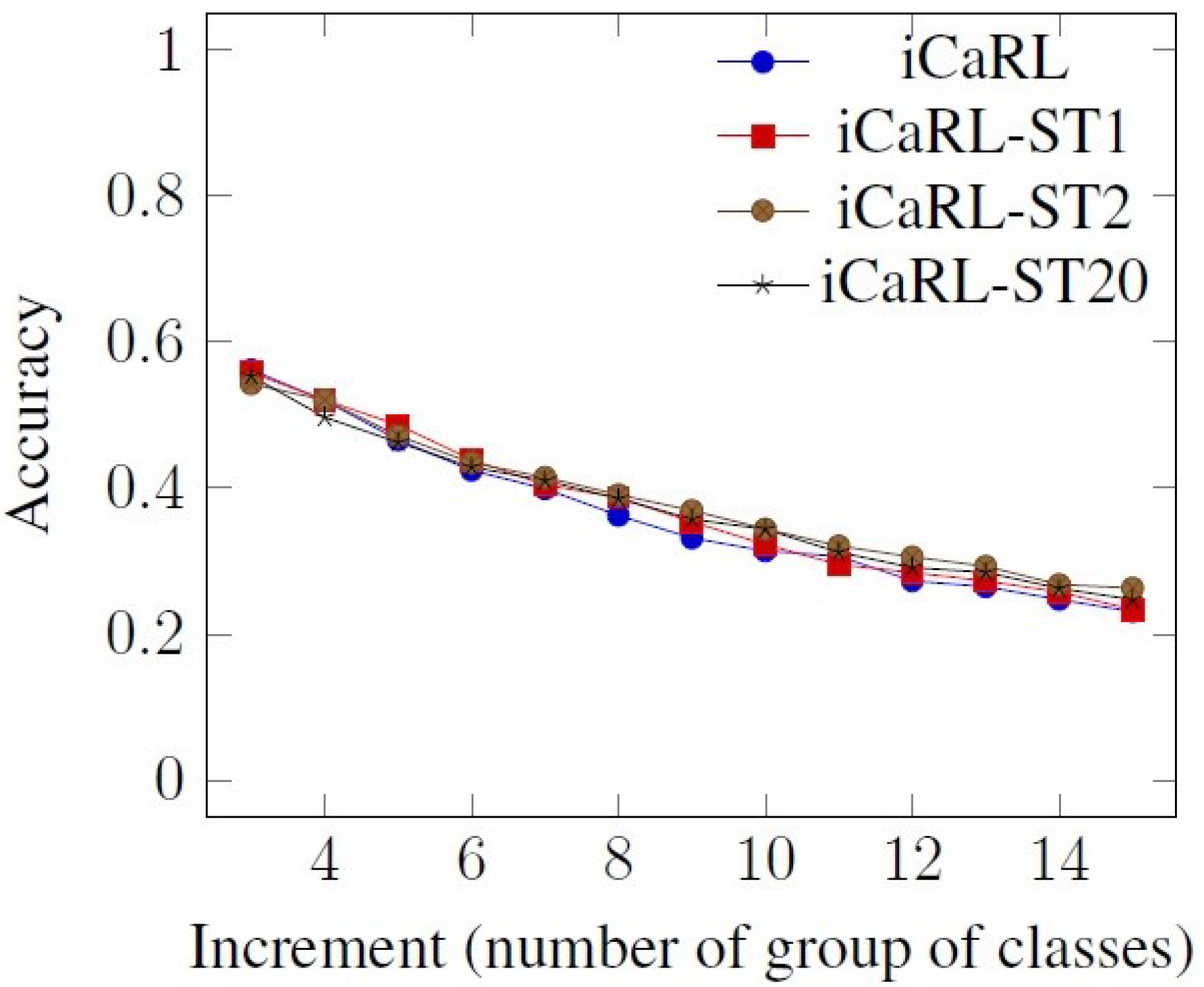
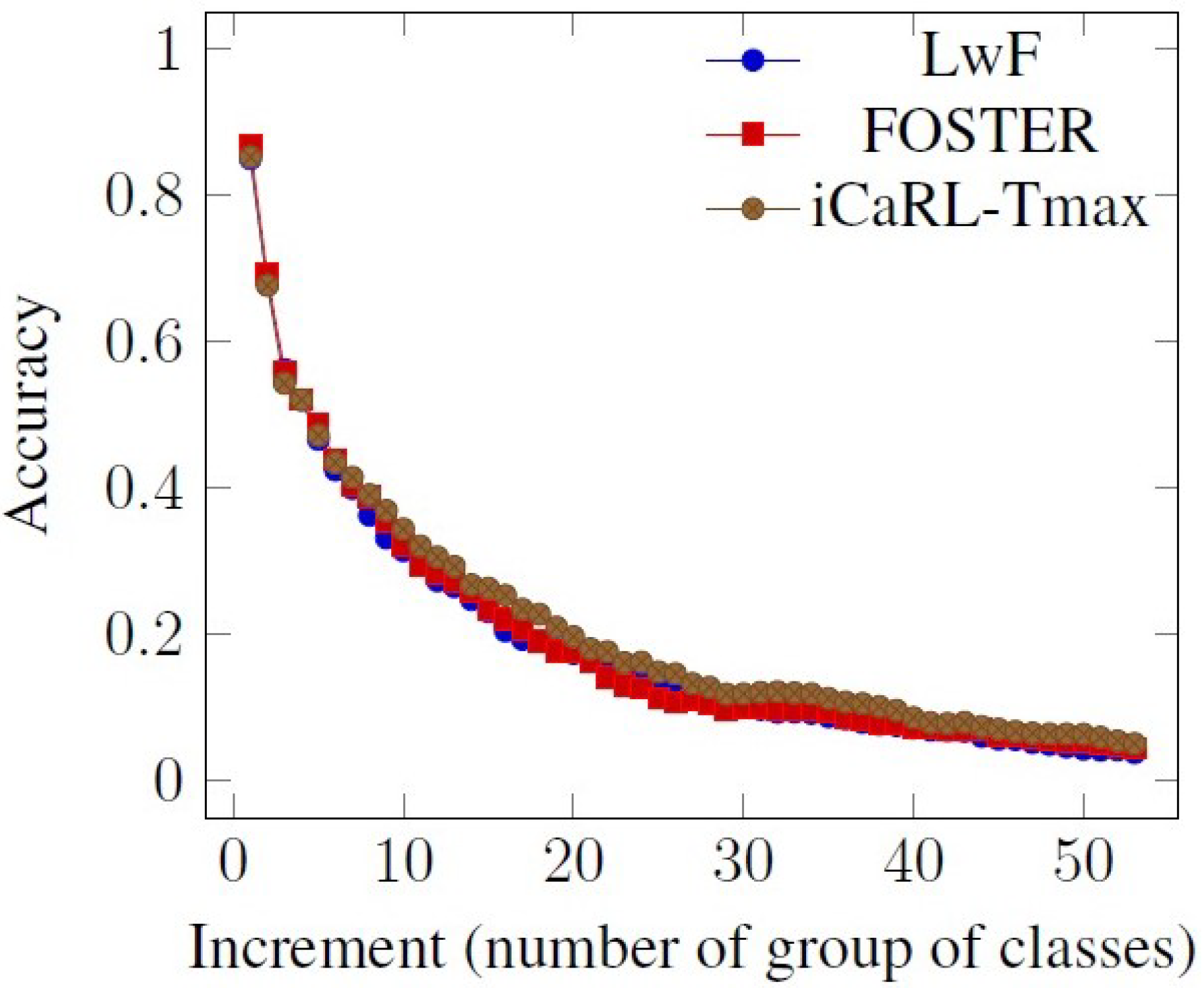
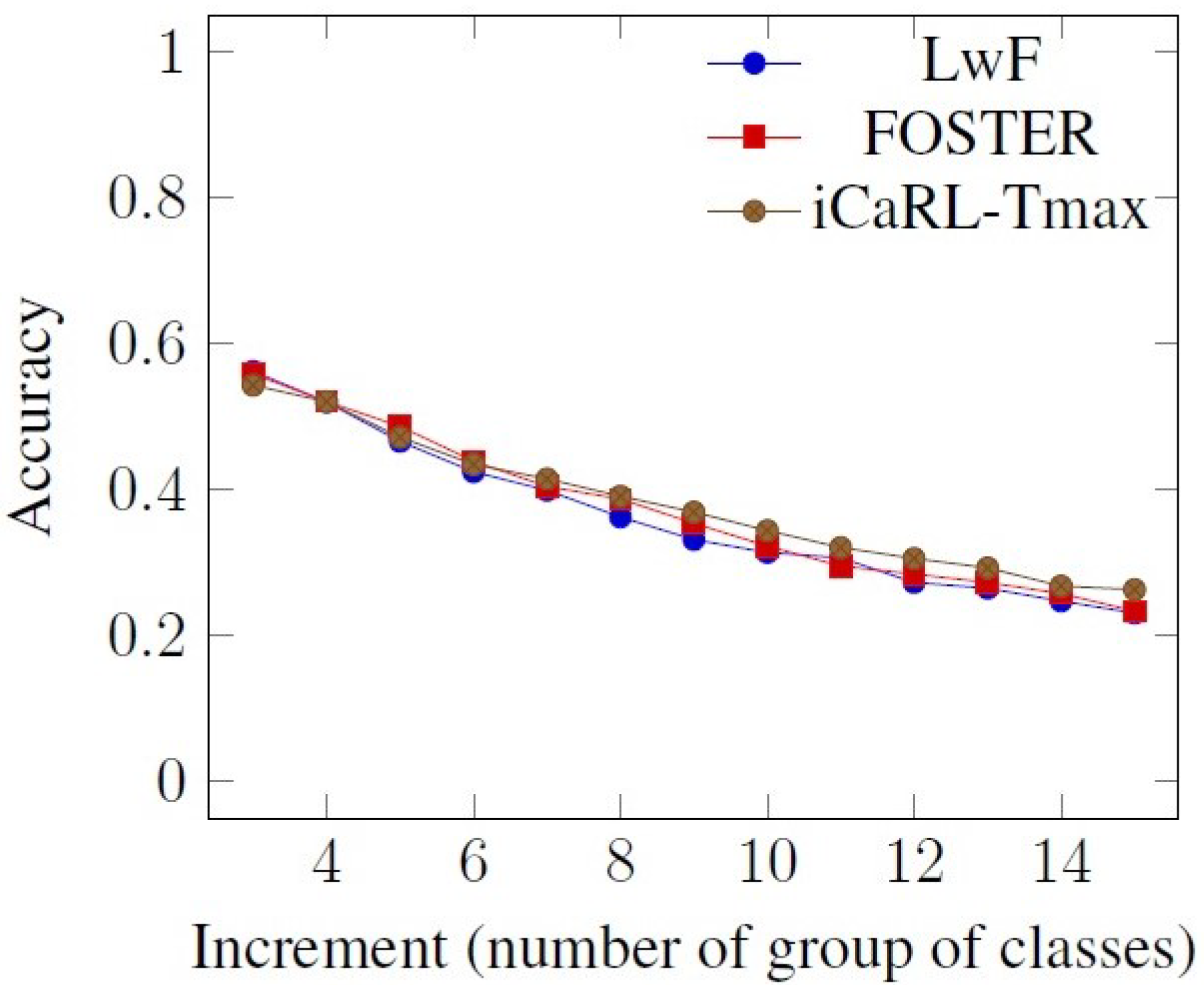
One can observe from
Figure 5,
Figure 6 and
Figure 7 (cropped results for better viewing), that by controlling the dark knowledge transference by setting the temperature parameter to the value provided as relevant by our method, the results obtained are slightly better.
In order to determine a score for the accuracy comparison and improvement, the original iCaRL accuracy results were considered as a benchmark and the differences between the reference model and the modified models, iCaRL-ST1, iCaRL-ST2 and iCaRL-ST20, when the number of classes increases were computed. We then computed the minimum and the maximum of the accuracy differences for each incremental step. For our modified models, starting from the second group of classes, we obtained a minimum of 0.012 and a maximum of 0.035 accuracy improvement, meaning that our models are always degrading the accuracy with the arrival of new classes slower than the reference model.
However, another interesting behavior was observed. In the case of iCaRL-ST2 (iCaRL with SoftMax Temperature 2), even if in the case of the first classes the accuracy is close or slightly lower than in the case of the original algorithm, in the following iterations, the performance follows an increasing trend.
7. Further Experimental Tests
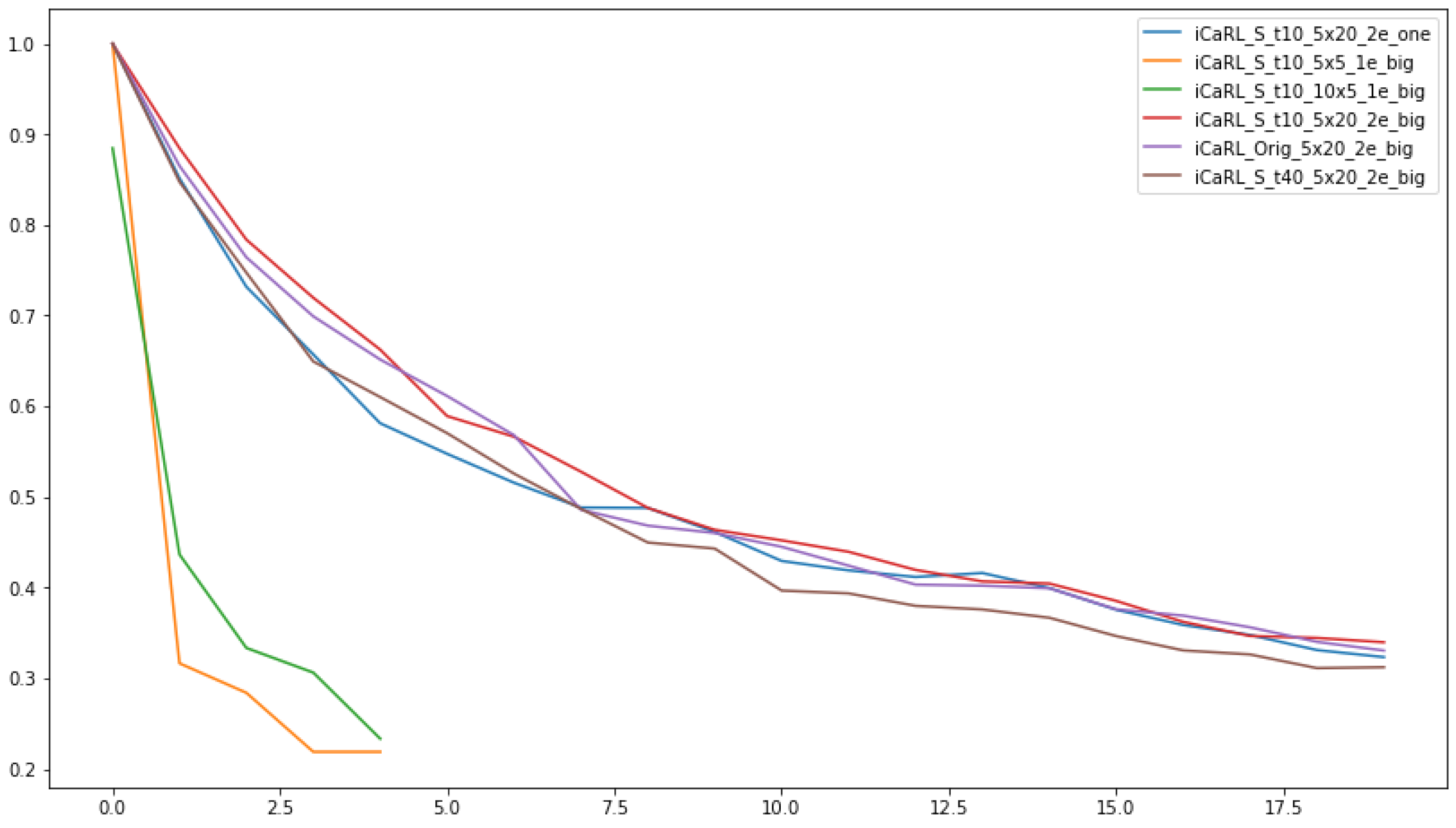
The following two types of experimental tests were further performed: we varied the number of classes and the number of batches sent to the network and we changed the temperature of SoftMax and the number of epochs while the classes were randomly selected from a limited number of classes but also from the entire data set.
The classifier saves the exemplars and weights after each increment. We evaluated and compared the performance after each class increment using Top 5 accuracy. We gather the results in
Figure 8.
7.1. Testing the Difference between 2 and 60 Epochs
The following settings were generally used: 5 classes, 20 increments (batches), a batch size of 64 (128 batch size was used in the original work), and 2 and 60 epochs (60 epochs were used in the original work); from the large set of 1000 classes, 100 were randomly chosen.
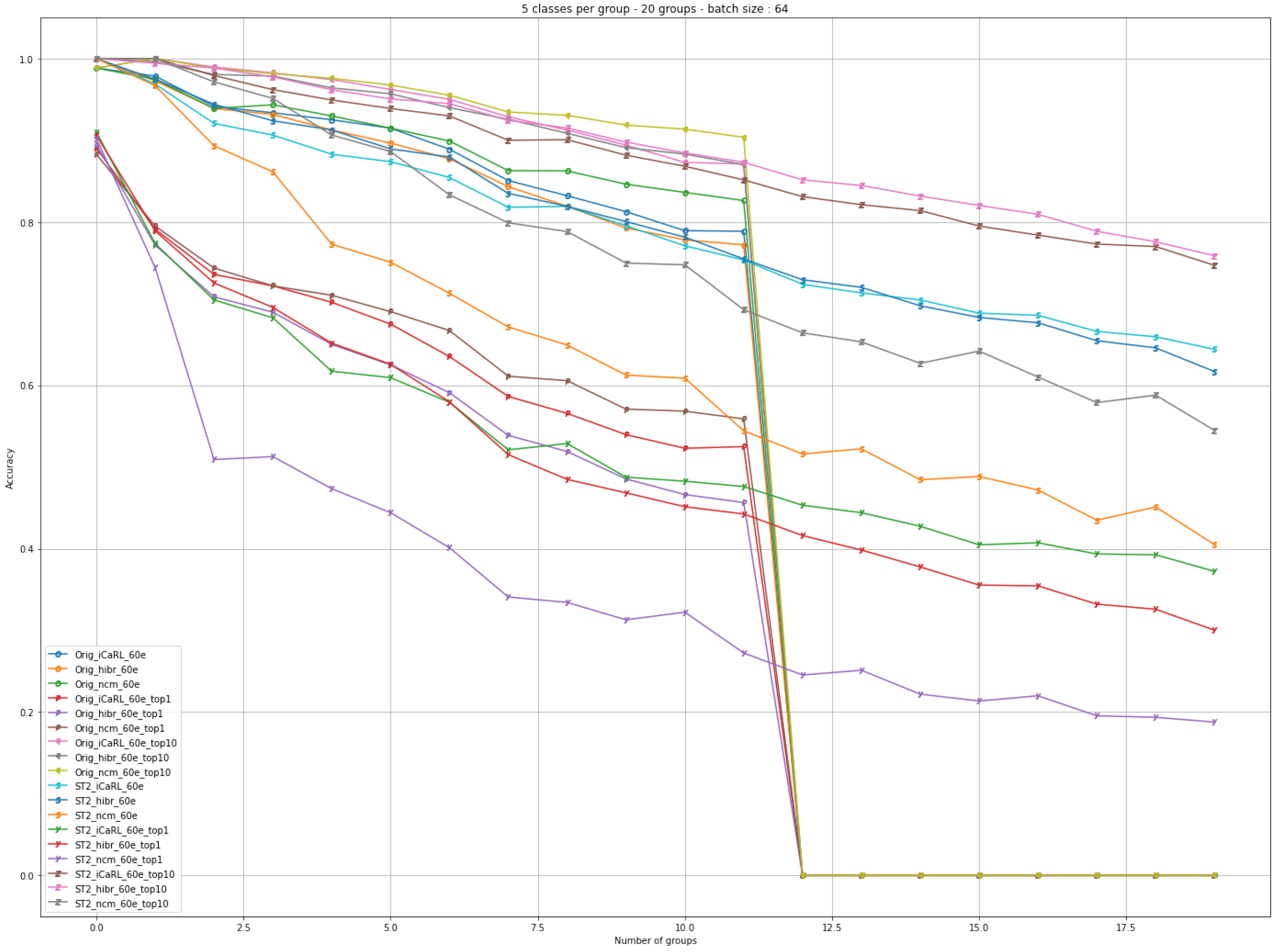
This time the evaluation also checked the performance of the network in the cases: iCaRL, Hybrid and the theoretical case of NCM. The original and SoftMax modification had a temperature of 2. Note that in the case of the unmodified algorithm with 60 epochs, at iteration 12, catastrophic forgetting occurred.
The first observation, is represented by the fact that by running several epochs, the performance of the model increases. One can observe in the upper part of the graph, that after 60 epochs, with one small outlier in the case of changing the temperature to the value 2 in the NCM - ST2_ncm_60e, the results are are all following a similar trend.
The behavior in the case of the hybrid combination is also interesting to watch. If the performance is very good when running 60 epochs (Orig_hibr_60e), the performance for running only 2 epochs (Orig_hibr_2e) is extremely different.
In the case of using SoftMax with modified temperature, we can see better performance compared to the initial algorithm and this was achieved by running only 2 epochs. See Orig_iCaRL_2e and Orig_hibr_2e compared to ST2_iCaRL_2e and ST2_hibr_2e.
The learning curve along the batches of classes, if we discuss the difference between the number of epochs, is much higher in the case of the original algorithm and lower in the case of SoftMax. For example, Orig_iCaRL_60e compared to Orig_iCaRL_2e and ST2_iCaRL_60e compared to ST2_iCaRL_2e.
If we are referring to a practical application, we could make a reference to autonomous driving. In this scenario, computing power and the network to transmit data streams are limited [
33]. On the other hand, a rapid adaptation of the model and incorporation of new features in a short time is required [
34].
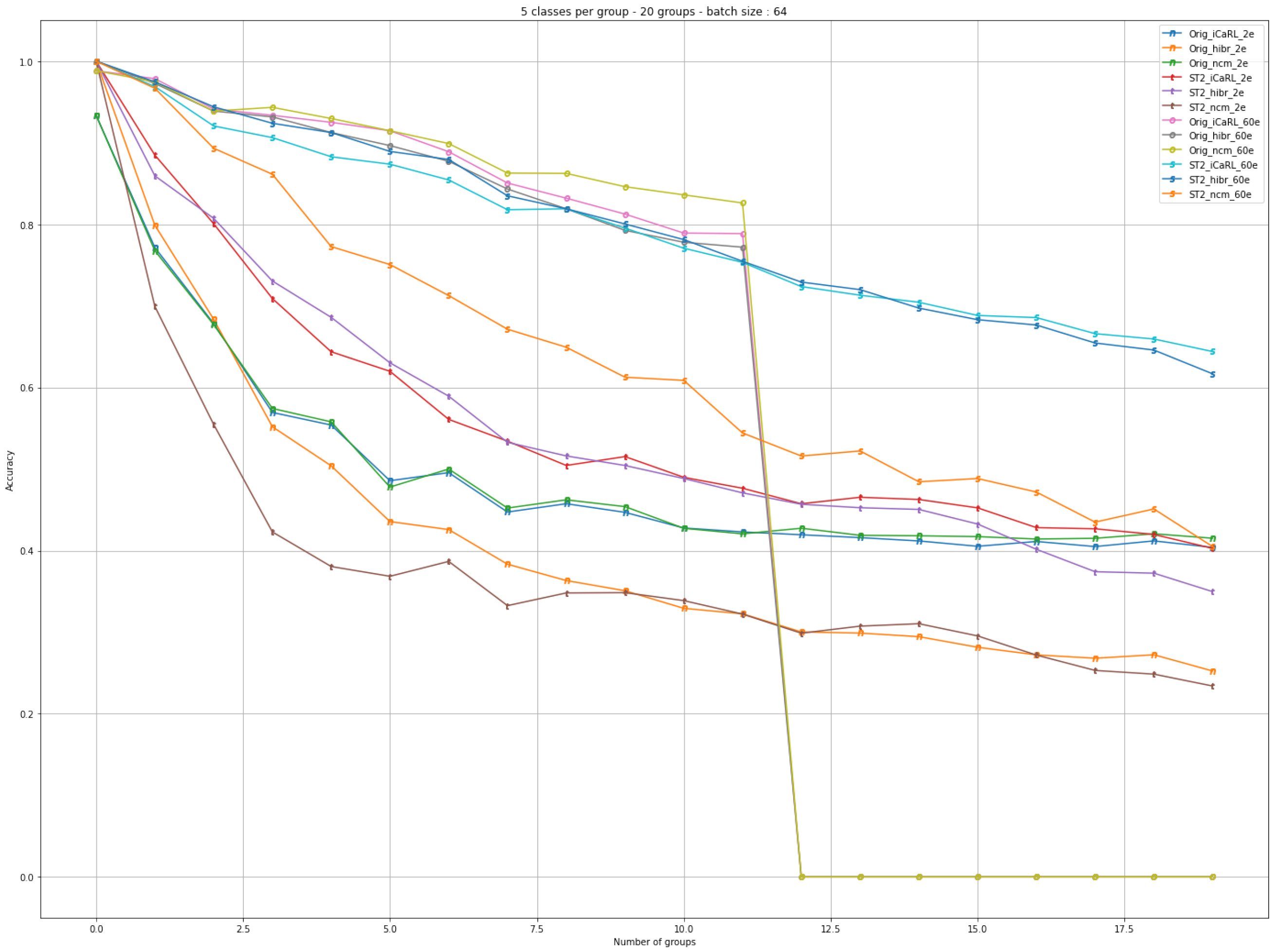
7.2. Testing 60 Epochs for Top 1 and Top 10
For an overview, the Top 5 accuracy (in the sense that any of the answers with the highest probability of model 5 must match the expected answer), the Top 1 accuracy (conventional accuracy: the model answer, i.e., the one with the highest probability, must be exactly the expected answer) and the Top 10 accuracy (in the sense that any of the answers with the highest probability of model 10 must match the expected answer) have been added for the 60 epochs tests.
In
Figure 9, it can be seen that the temperature obtains a better accuracy in the case of a smaller number of epochs. In the case of running two epochs and changing the temperature by a value of 2, the results are considerably better. Even the drop in accuracy between the first and second iterations is not very sharp. If the number of epochs increases, the difference in accuracy is not very large.
An interesting aspect can also be observed in
Figure 10. The very big difference is found between Top 1 accuracy and Top 5 accuracy. After this accuracy, the results are not considerable. Specifically, between the Top 5 accuracy and the Top 10 accuracy, the difference is very small.
In the case of the Top 1 accuracy, it starts somewhere around 0.9 and drops sharply after the second batch below 0.8, while in the case of the Top 5 accuracy, it remains above the value of 9.5 for the next 4 batches. Moreover, in the case of the Top 10 accuracy, this trend is maintained for the next 8 batches.
Overall, our method is model agnostic and the same procedure as above could be applied to other models such as LwF [
11] or FOSTER [
12]. In
Table 3, we gather the results obtained by setting the temperature for the standard case
for a softer distribution with
and for the calculated
with the same
separability. As datasets, we used CIFAR-100 for 100 classes and ImageNet ILSVRC for 1000 classes. In
Figure 6 and
Figure 7 (cropped results for better viewing), we easily observe a better Top 1 accuracy when using the calculated Tmax. This result is in line with the one from
Table 3 and shows the advantages of analytically determining a Tmax value.