Balancing Results from AI-Based Geostatistics versus Fuzzy Inference by Game Theory Bargaining to Improve a Groundwater Monitoring Network
Abstract
1. Introduction
2. Materials and Methods
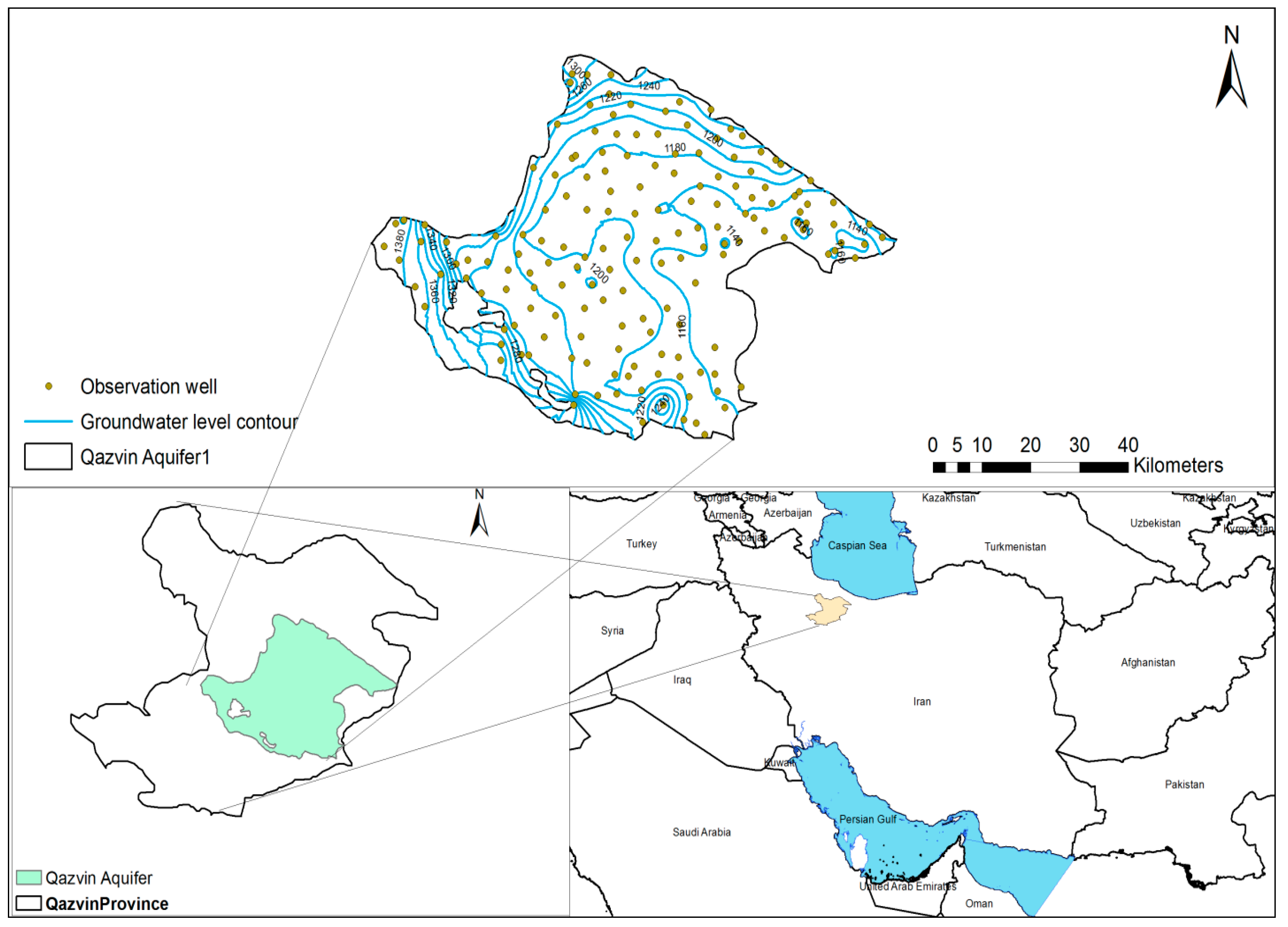
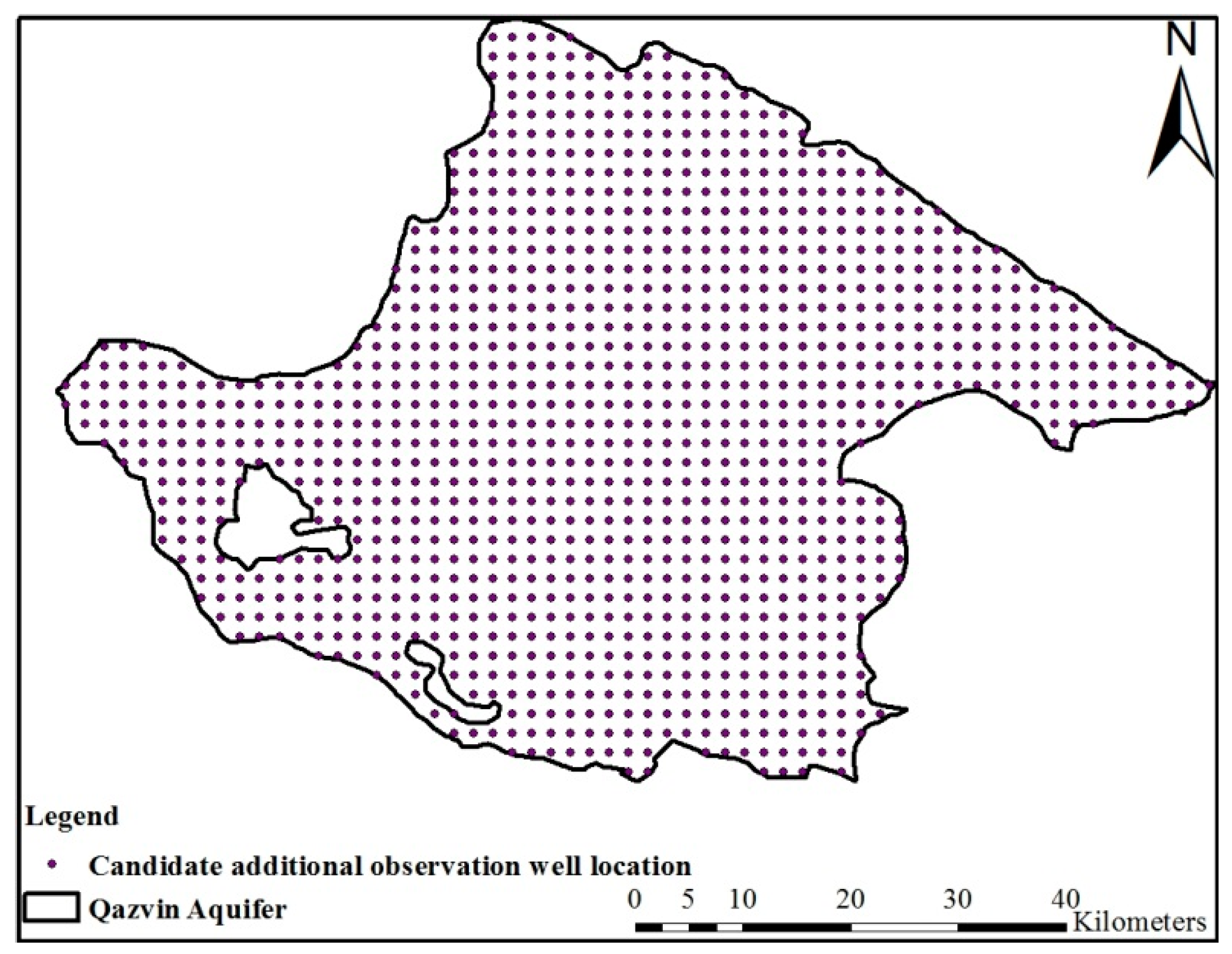
2.1. Study Area
2.2. Comparison of Groundwater Surface Mapping Methods for the Study Area
2.2.1. Kriging
2.2.2. Inverse Distance Weighting (IDW)
2.2.3. Spline
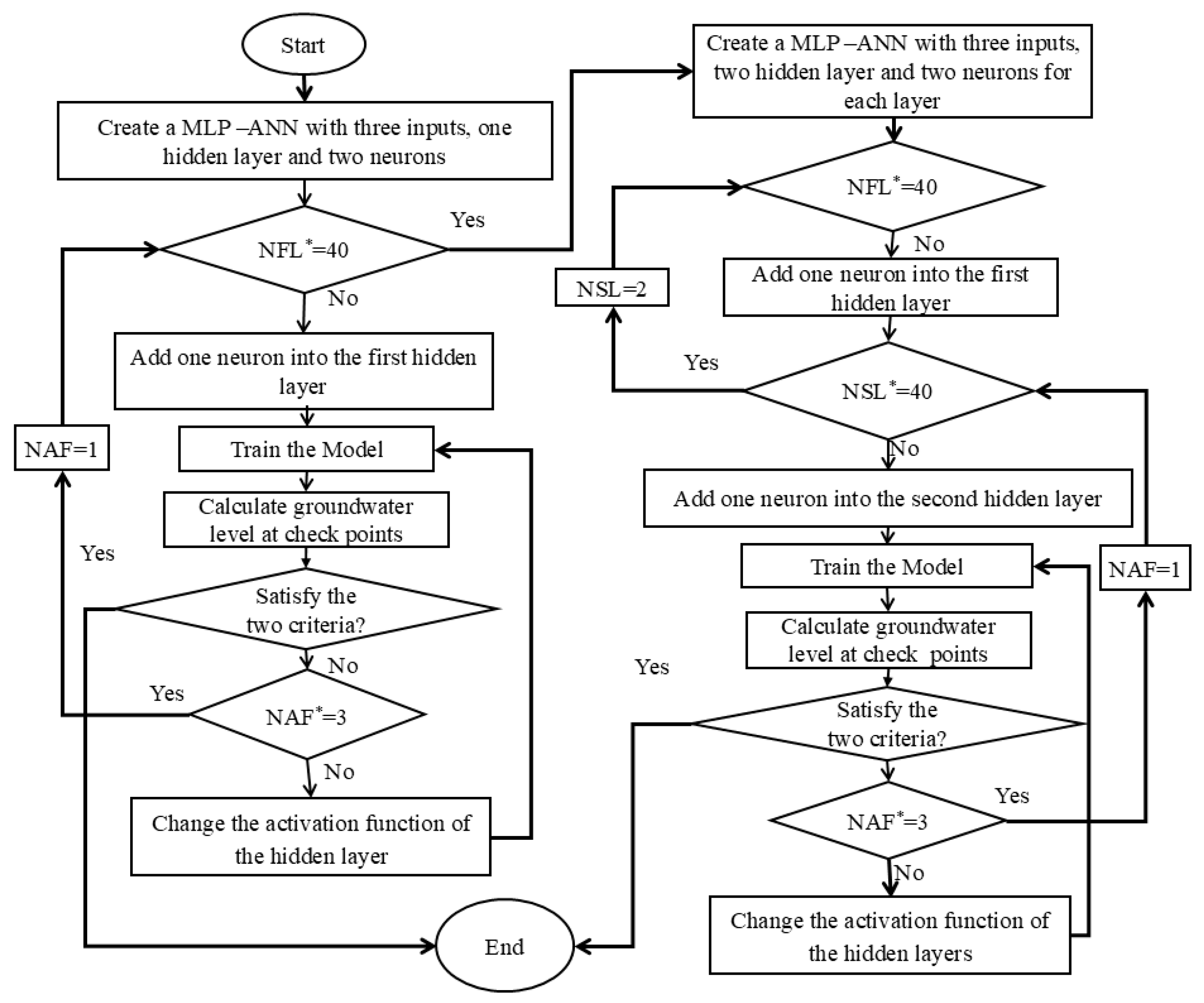
2.2.4. Artificial Neural Network (ANN)
2.2.5. Cross-Validation for Evaluation of Surface Fitting Methods
2.3. Designed Methodology and Model
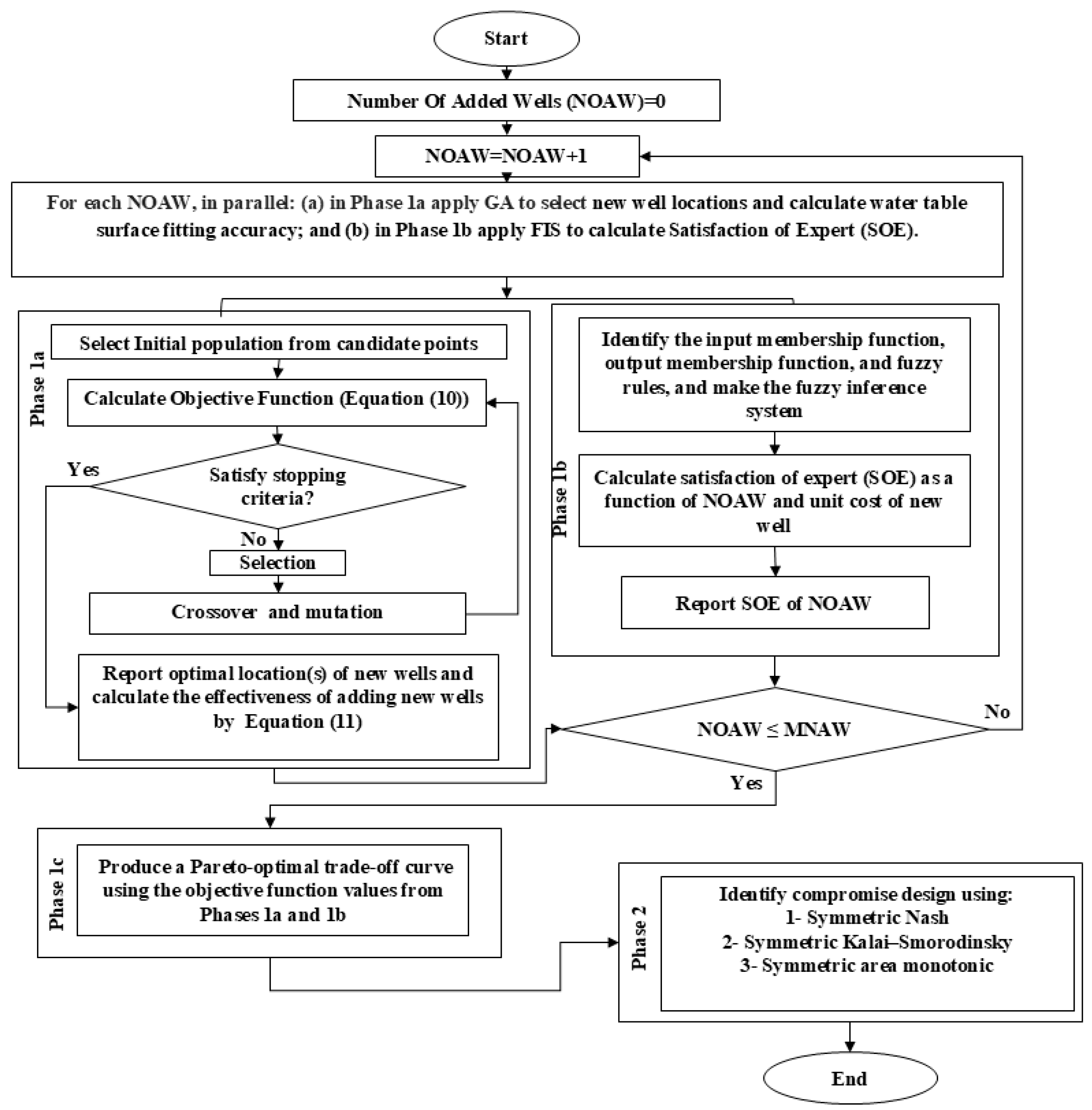
- Phase 1: This phase is executed MNAW times to construct a Pareto optimum trade-off curve. It is further subdivided as follows:
- ○
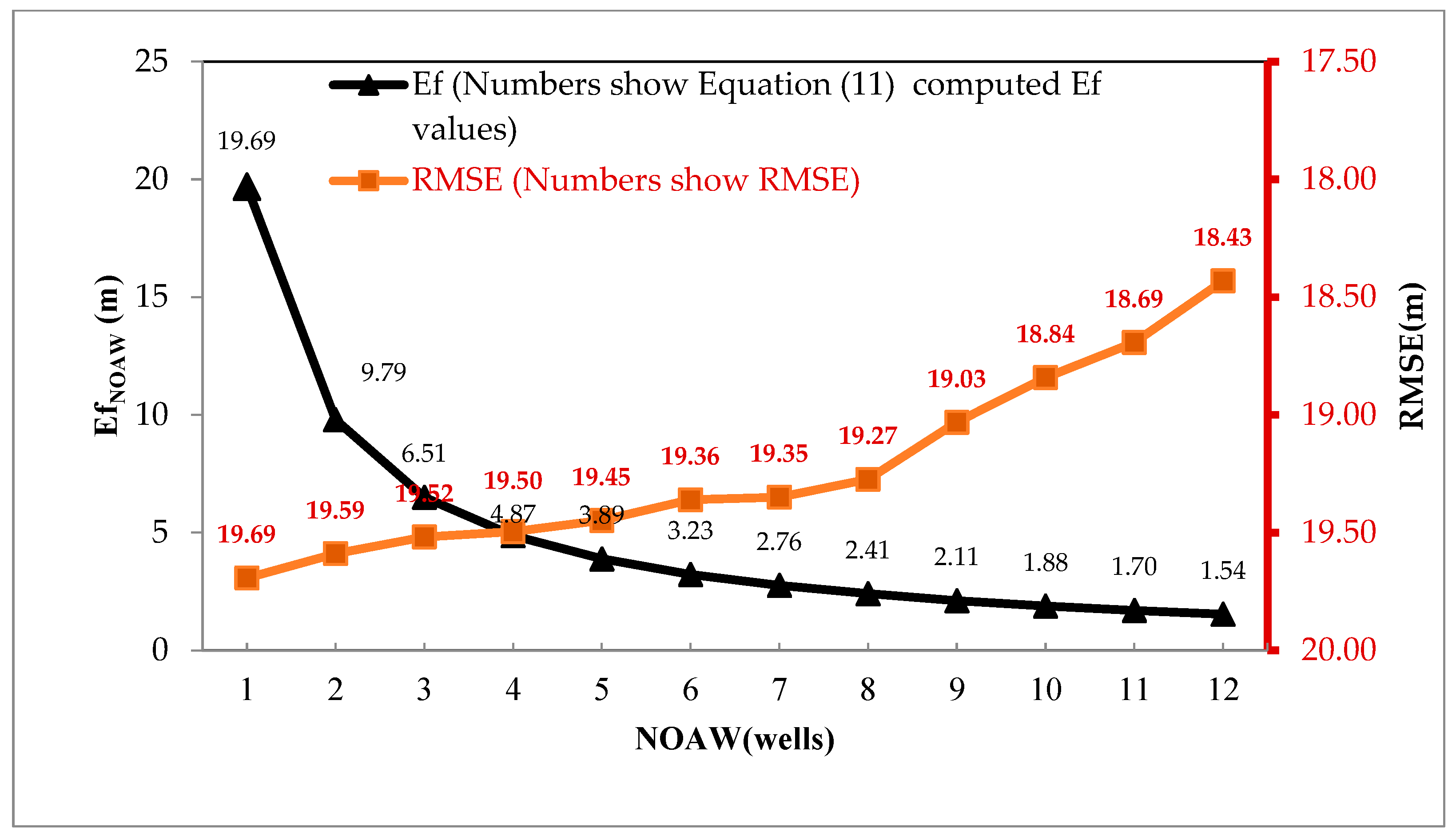
- Phase 1a: For each specified Number of Additional Wells (NOAWs) (ranging from 1 to MNAW), the model employs kriged groundwater level, the most accurate interpolation method, combined with a heuristic optimization algorithm. This phase aims to identify new well location(s) that will maximize the improvement in water level representation achieved through the kriging method.
- ○
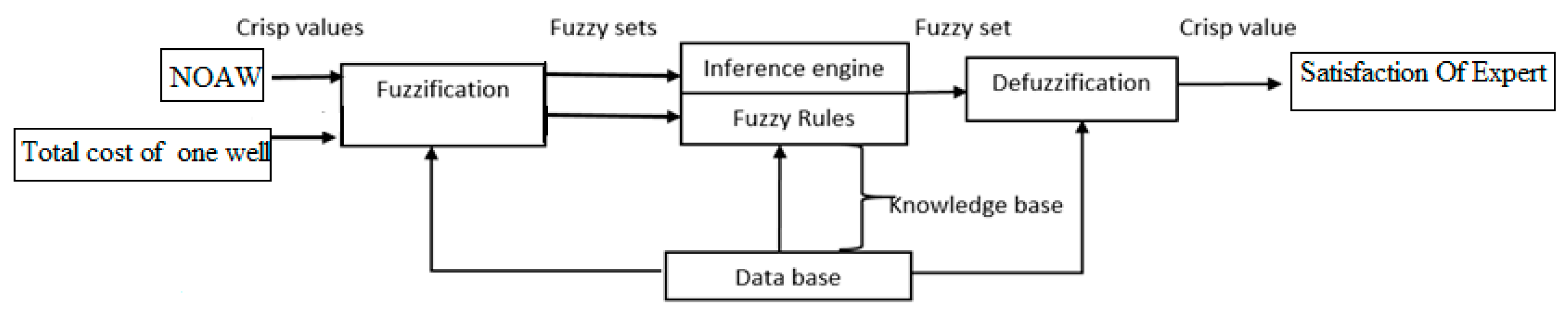
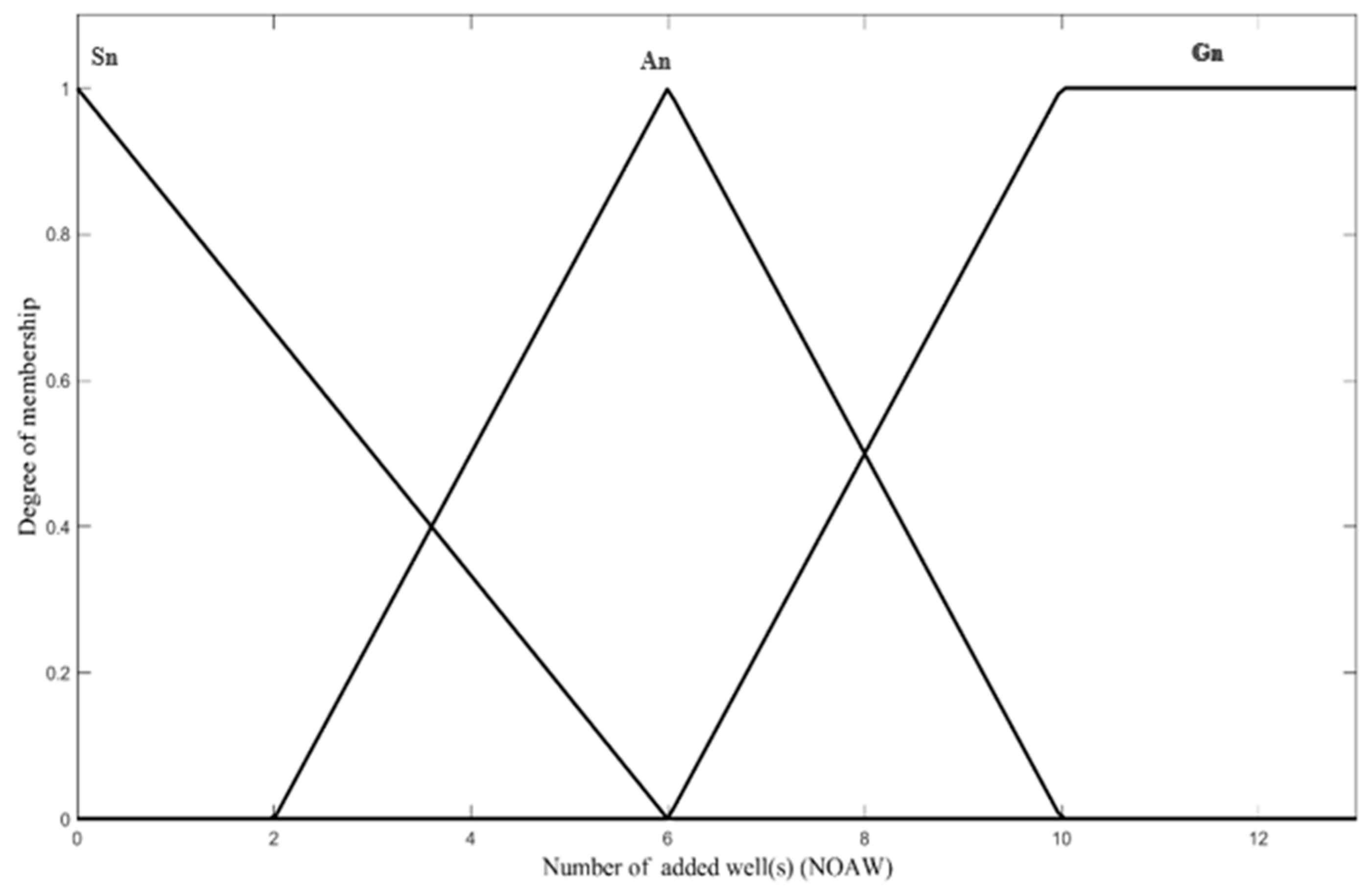
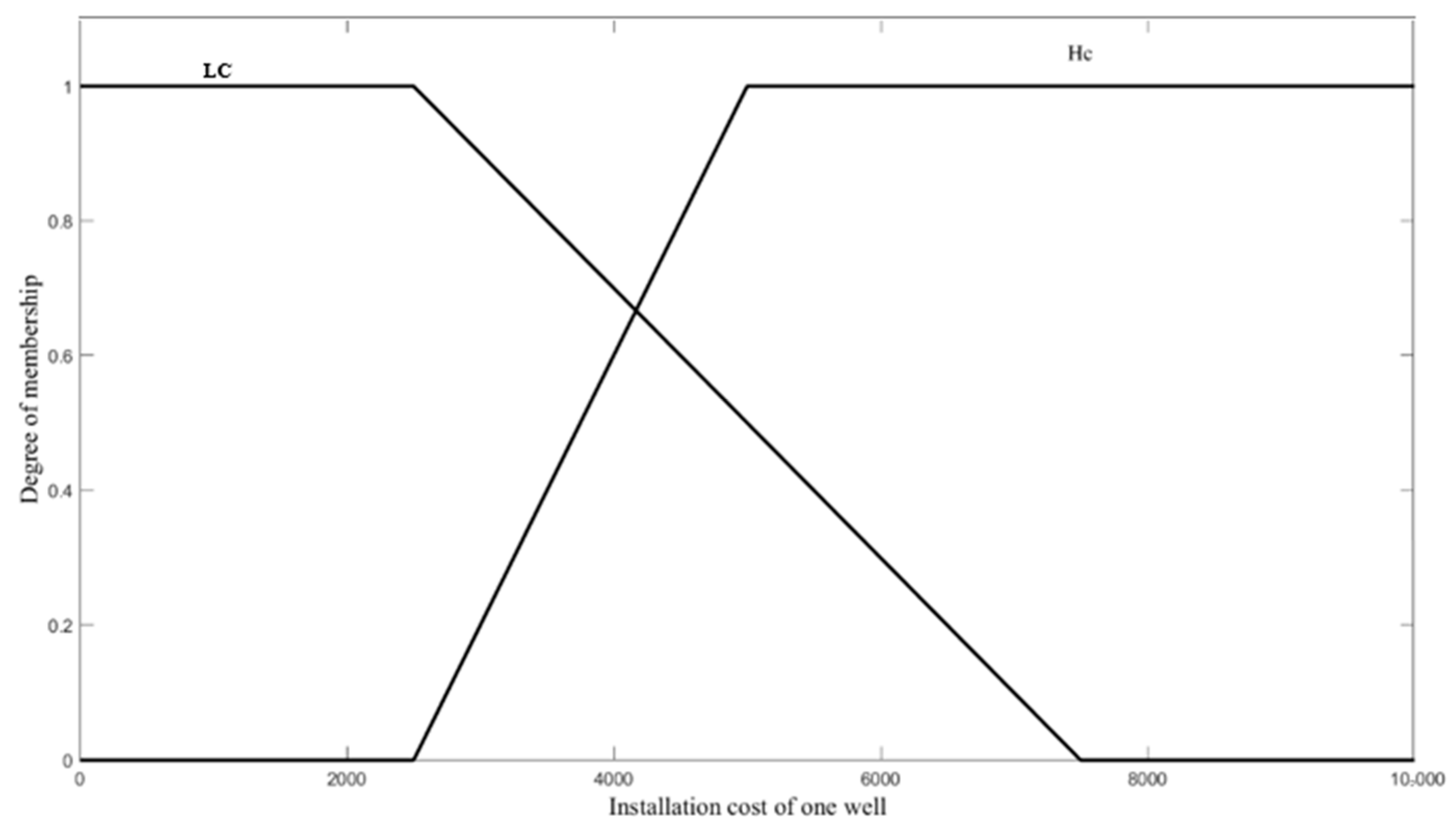
- Phase 1b: This phase utilizes an FIS to incorporate local expert opinions regarding the preferred number of a new well(s) and the unit cost of a new well.
- ○
- Phase 1c: After executing phases 1a and 1b MNAW times, phase 1c constructs the Pareto optimum curve. This curve visualizes the trade-off between accuracy improvement from phase 1a vs. the expert opinion from phase 1b. It provides a comprehensive view of potential conflicts and compromises between numerical optimization and experiential input.
- Phase 2: In this phase, three game theory techniques are applied to the Pareto optimum curve to identify equilibrium strategies. By applying these game theory techniques, the model identifies the most balanced and effective strategies for well placement, considering both numerical accuracy and expert opinions. These strategies help ensure that the final decision on the number and location of new wells is both optimal and equitable.
2.3.1. Phase 1 (Produce Heuristic and Experiential Solutions)
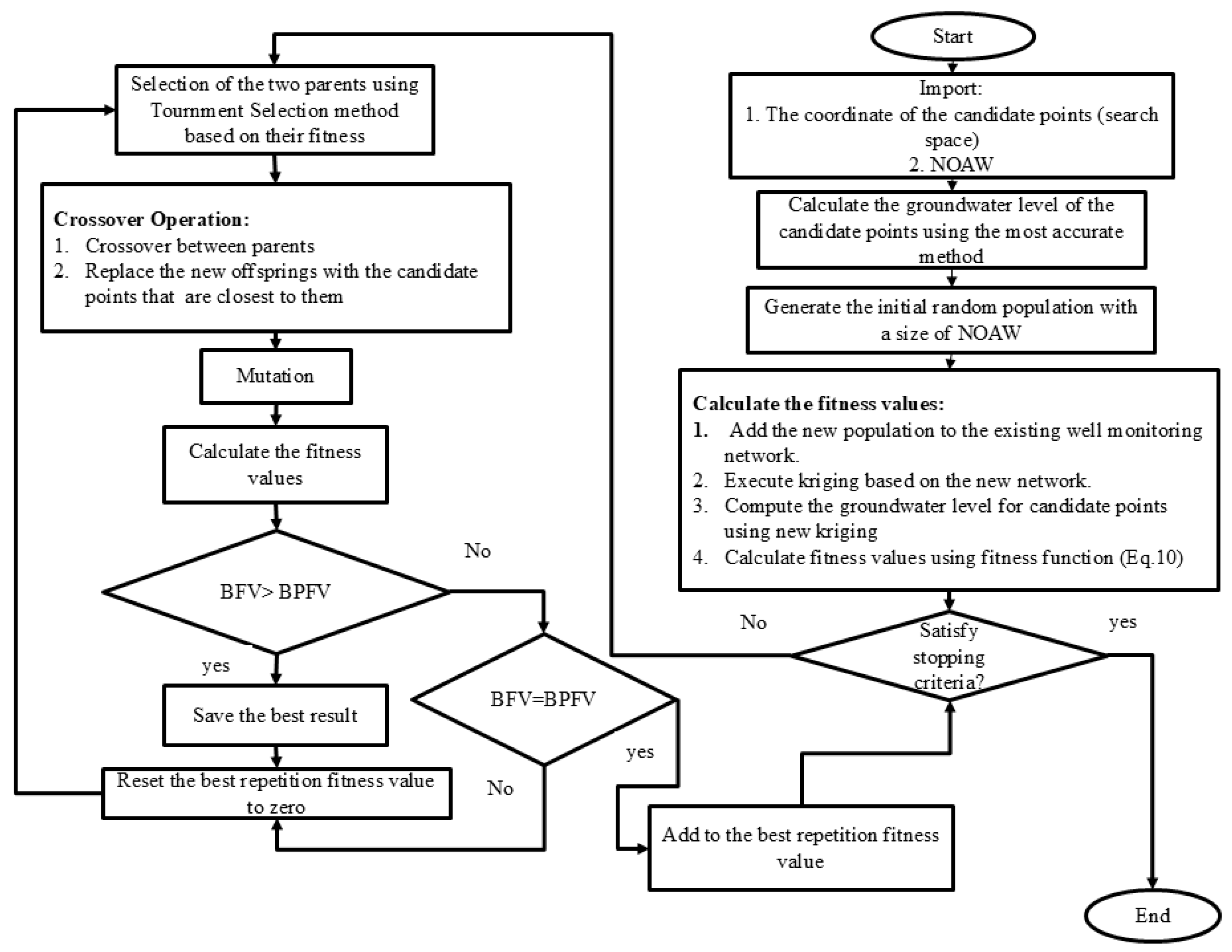
Phase 1a (Produce and Apply Genetic Algorithm (GA))
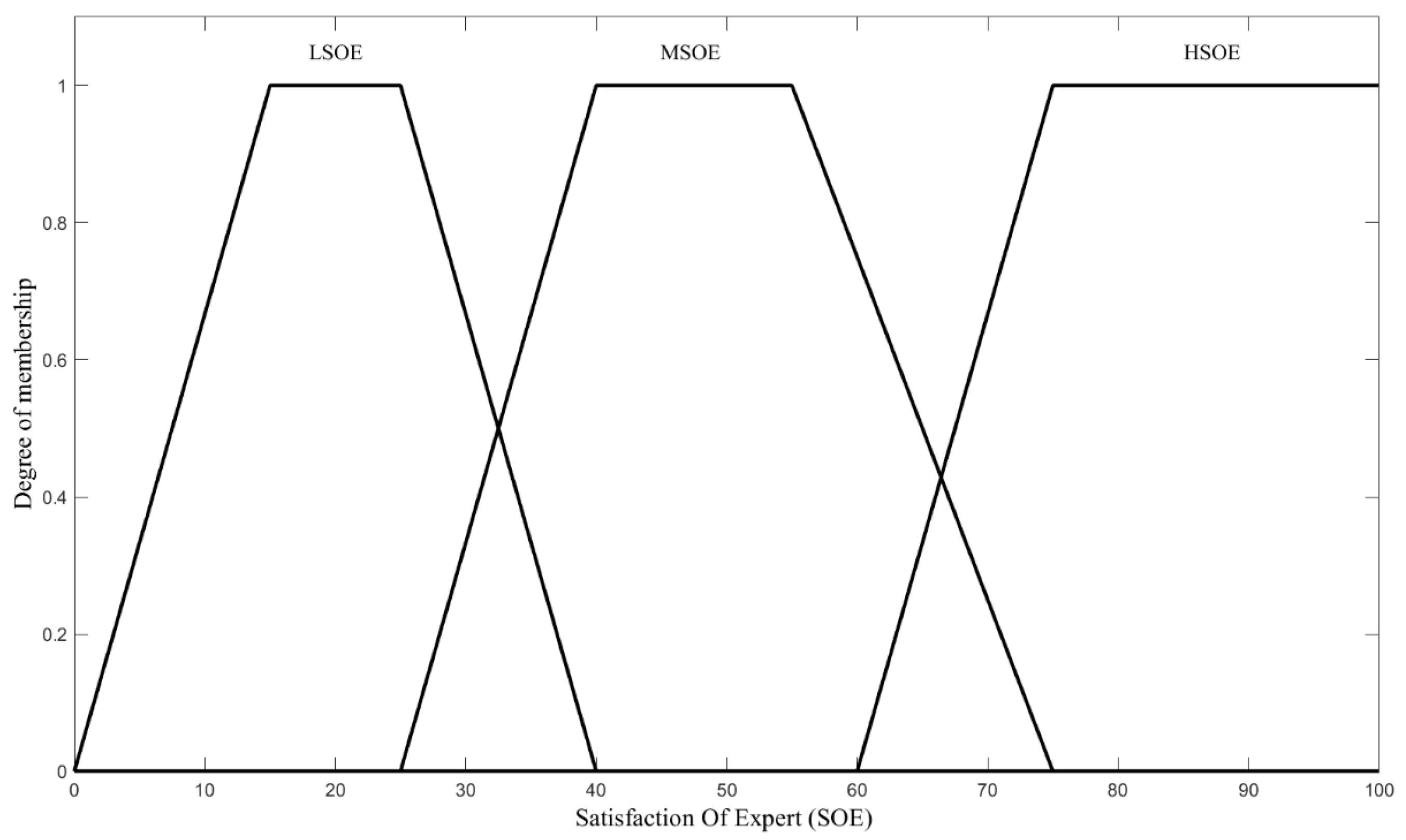
Phase 1b (Produce and Apply Fuzzy Inference System, FIS)
Phase 1c (Normalized Pareto Curve Production and Application)
2.3.2. Phase 2 (Produce and Use Symmetric Conflict Resolution Methods)
- Method 1: Nash solution
- Method 2: Kalai—Smorodinsky solution
- Method 3: symmetric area monotonic solution
3. Results
3.1. Water Table Estimation
3.2. Phase 1a (GA Application)
3.3. Phase 1b (FIS Application)
3.4. Phase 1c (Pareto Curve Production)
3.5. Phase 2
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rajaee, T.; Ebrahimi, H.; Nourani, V. A Review of the Artificial Intelligence Methods in Groundwater Level Modeling. J. Hydrol. 2019, 572, 336–351. [Google Scholar] [CrossRef]
- Amiri, S.; Rajabi, A.; Shabanlou, S.; Yosefvand, F.; Izadbakhsh, M.A. Prediction of Groundwater Level Variations Using Deep Learning Methods and GMS Numerical Model. Earth Sci. Inform. 2023, 16, 3227–3241. [Google Scholar] [CrossRef]
- Todd, D.K.; Mays, L.W. Groundwater Hydrology; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 0471452548. [Google Scholar]
- Narany, T.S.; Ramli, M.F.; Aris, A.Z.; Sulaiman, W.N.A.; Fakharian, K. Spatial Assessment of Groundwater Quality Monitoring Wells Using Indicator Kriging and Risk Mapping, Amol-Babol Plain, Iran. Water 2014, 6, 68–85. [Google Scholar] [CrossRef]
- Kavusi, M.; Khashei Siuki, A.; Dastourani, M. Optimal Design of Groundwater Monitoring Network Using the Combined Election-Kriging Method. Water Resour. Manag. 2020, 34, 2503–2516. [Google Scholar] [CrossRef]
- Tavassoli, A.; Waghei, Y.; Nazemi, A. Comparison of Kriging and Artificial Neural Network Models for the Prediction of Spatial Data. J. Stat. Comput. Simul. 2022, 92, 352–369. [Google Scholar] [CrossRef]
- Majedi-Asl, M.; Fuladipanah, M.; Mahmoudpour, H.; Ebrahimpour, E.; Kisi, O. Optimization Design of Quality Monitoring Network of Urmia Plain Using Genetic Algorithm and Vulnerability Map. Geocarto Int. 2023, 38, 2152492. [Google Scholar] [CrossRef]
- Abdi, E.; Ali, M.; Santos, C.A.G.; Olusola, A.; Ghorbani, M.A. Enhancing Groundwater Level Prediction Accuracy Using Interpolation Techniques in Deep Learning Models. Groundw. Sustain. Dev. 2024, 26, 101213. [Google Scholar] [CrossRef]
- Uyan, M.; Cay, T. Spatial Analyses of Groundwater Level Differences Using Geostatistical Modeling. Environ. Ecol. Stat. 2013, 20, 633–646. [Google Scholar] [CrossRef]
- Rabah, F.K.J.; Ghabayen, S.M.; Salha, A.A. Effect of GIS Interpolation Techniques on the Accuracy of the Spatial Representation of Groundwater Monitoring Data in Gaza Strip. J. Environ. Sci. Technol. 2011, 4, 579–589. [Google Scholar] [CrossRef]
- Amini, H.; Ashrafzadeh, A.; Khaledian, M. Enhancing Groundwater Salinity Estimation through Integrated GMDH and Geostatistical Techniques to Minimize Kriging Interpolation Error. Earth Sci. Inform. 2024, 17, 283–297. [Google Scholar] [CrossRef]
- Jithendra, T.; Basha, S.S. Analyzing Groundwater Level with Hybrid ANN and ANFIS Using Metaheuristic Optimization. Earth Sci. Inform. 2023, 16, 3323–3353. [Google Scholar] [CrossRef]
- Hashemi, M.; Sepaskhah, A.R. Evaluation of Artificial Neural Network and Penman–Monteith Equation for the Prediction of Barley Standard Evapotranspiration in a Semi-Arid Region. Theor. Appl. Climatol. 2020, 139, 275–285. [Google Scholar] [CrossRef]
- Tirol Kirçiçek, N.; Baba, A.; Koçbay, A.; Toklu, M.M. Evaluation of GIS-Based Spatial Interpolation Methods for Groundwater Level: A Case Study of Türkiye. Turk. J. Earth Sci. 2024, 33, 576–591. [Google Scholar] [CrossRef]
- Aceves-De-Alba, J.; ENRIQUE Júnez, H.; González-Trinidad, J.; Cardona-Benavides, A.; Bautista-Capetillo, C. Methodology for the Optimization of Groundwater Quality Monitoring Networks Oriented to Satisfy a Specific Spatial Coverage. Appl. Ecol. Environ. Res. 2019, 17, 10861–10882. [Google Scholar] [CrossRef]
- Nunes, L.M.; Cunha, M.C.; Ribeiro, L. Groundwater Monitoring Network Optimization with Redundancy Reduction. J. Water Resour. Plan. Manag. 2004, 130, 33–43. [Google Scholar] [CrossRef]
- Ohmer, M.; Liesch, T.; Wunsch, A. Spatiotemporal Optimization of Groundwater Monitoring Networks Using Data-Driven Sparse Sensing Methods. Hydrol. Earth Syst. Sci. 2022, 26, 4033–4053. [Google Scholar] [CrossRef]
- Abedian, H.; Mohammadi, K.; Rafiee, R. Optimizing Monitoring Network of Water Table by Geostatistical Methods. J. Geol. Min. Res. 2013, 5, 223–231. [Google Scholar] [CrossRef][Green Version]
- Teimoori, S.; Olya, M.H.; Miller, C.J. Groundwater Level Monitoring Network Design with Machine Learning Methods. J. Hydrol. 2023, 625, 130145. [Google Scholar] [CrossRef]
- Mirzaie-Nodoushan, F.; Bozorg-Haddad, O.; Loaíciga, H.A. Optimal Design of Groundwater-Level Monitoring Networks. J. Hydroinform. 2017, 19, 920–929. [Google Scholar] [CrossRef]
- Ayvaz, M.T.; Elçi, A. Identification of the Optimum Groundwater Quality Monitoring Network Using a Genetic Algorithm Based Optimization Approach. J. Hydrol. 2018, 563, 1078–1091. [Google Scholar] [CrossRef]
- Hosseini, M.; Kerachian, R. A Data Fusion-Based Methodology for Optimal Redesign of Groundwater Monitoring Networks. J. Hydrol. 2017, 552, 267–282. [Google Scholar] [CrossRef]
- Amiri, H.; Azadi, S.; Javadpour, S.; Naghavi, A.A.; Boczkaj, G. Selecting Wells for an Optimal Design of Groundwater Monitoring Network Based on Monitoring Priority Map: A Kish Island Case Study. Water Resour. Ind. 2022, 27, 100172. [Google Scholar] [CrossRef]
- Rosen, M.R. Groundwater monitoring networks, in Groundwater. In Encyclopedia of Life Support Systems (EOLSS); Silveira, L., Ed.; Eolss Publishers: Oxford, UK, 2003; Available online: https://www.eolss.net/ebooklib/bookinfo/groundwater.aspx#chapters (accessed on 15 May 2024).
- Kraft, B.; Jung, M.; Körner, M.; Reichstein, M. Hybrid Modeling: Fusion of a Deep Approach and Physics-Based Model for Global Hydrological Modeling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 1537–1544. [Google Scholar] [CrossRef]
- Fisher, J. Optimization of Water-Level Monitoring Networks in the Eastern Snake River Plain Aquifer Using a Kriging-Based Genetic Algorithm Method; Scientific Investigations Report 2013-5120; US Geological Survey: Reston, VA, USA, 2013. [Google Scholar]
- Firat, M.; Turan, M.E.; Yurdusev, M.A. Comparative Analysis of Fuzzy Inference Systems for Water Consumption Time Series Prediction. J. Hydrol. 2009, 374, 235–241. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An Experiment in Linguistic Synthesis with a Fuzzy Logic Controller. Int. J. Hum. Comput. Stud. 1973, 51, 135–147. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Trans. Syst. Man Cybern. 1985, 1, 116–132. [Google Scholar] [CrossRef]
- Dhar, A.; Patil, R.S. Multiobjective Design of Groundwater Monitoring Network Under Epistemic Uncertainty. Water Resour. Manag. 2012, 26, 1809–1825. [Google Scholar] [CrossRef]
- Masoumi, Z.; Rezaei, A.; Maleki, J. Improvement of Water Table Interpolation and Groundwater Storage Volume Using Fuzzy Computations. Environ. Monit. Assess. 2019, 191, 401. [Google Scholar] [CrossRef]
- Nourani, V.; Maleki, S.; Najafi, H.; Baghanam, A.H. A Fuzzy Logic-Based Approach for Groundwater Vulnerability Assessment. Environ. Sci. Pollut. Res. 2024, 31, 18010–18029. [Google Scholar] [CrossRef]
- Noori, R.; Maghrebi, M.; Mirchi, A.; Tang, Q.; Bhattarai, R.; Sadegh, M.; Noury, M.; Haghighi, A.T.; Kløve, B.; Madani, K. Anthropogenic Depletion of Iran’s Aquifers. Proc. Natl. Acad. Sci. USA 2021, 118, e2024221118. [Google Scholar] [CrossRef]
- Moridi, A. State of Water Resources in Iran. Int. J. Hydrol. 2017, 1, 111–114. [Google Scholar] [CrossRef]
- Hashemi, M.; Zadeh, H.M.; Zarghami, M.; Demeke, B.W.; Delgarm, R.T. An Analysis of Why Rehabilitation and Balancing Programs for Aquifers Do Not Meet Water Organizations’ Targets (a Case Study of the Qazvin Aquifer in Iran). Agric. Water Manag. 2023, 281, 108258. [Google Scholar] [CrossRef]
- Yao, L.; Huo, Z.; Feng, S.; Mao, X.; Kang, S.; Chen, J.; Xu, J.; Steenhuis, T.S. Evaluation of Spatial Interpolation Methods for Groundwater Level in an Arid Inland Oasis, Northwest China. Environ. Earth Sci. 2014, 71, 1911–1924. [Google Scholar] [CrossRef]
- Mair, A.; Fares, A. Comparison of Rainfall Interpolation Methods in a Mountainous Region of a Tropical Island. J. Hydrol. Eng. 2011, 16, 371–383. [Google Scholar] [CrossRef]
- Ohmer, M.; Liesch, T.; Goeppert, N.; Goldscheider, N. On the Optimal Selection of Interpolation Methods for Groundwater Contouring: An Example of Propagation of Uncertainty Regarding Inter-Aquifer Exchange. Adv. Water Resour. 2017, 109, 121–132. [Google Scholar] [CrossRef]
- Boumpoulis, V.; Michalopoulou, M.; Depountis, N. Comparison between Different Spatial Interpolation Methods for the Development of Sediment Distribution Maps in Coastal Areas. Earth Sci. Inform. 2023, 16, 2069–2087. [Google Scholar] [CrossRef]
- Franke, R. Smooth Interpolation of Scattered Data by Local Thin Plate Splines. Comput. Math. Appl. 1982, 8, 273–281. [Google Scholar] [CrossRef]
- Mitáš, L.; Mitášová, H. General Variational Approach to the Interpolation Problem. Comput. Math. Appl. 1988, 16, 983–992. [Google Scholar] [CrossRef]
- Safavi, H.R.; Ahmadi, K.M. Prediction and Assessment of Drought Effects on Surface Water Quality Using Artificial Neural Networks: Case Study of Zayandehrud River, Iran. J. Environ. Health Sci. Eng. 2015, 13, 68. [Google Scholar] [CrossRef]
- Lophaven, S.N.; Nielsen, H.B.; Sondergaard, J.; Dace, A. A Matlab Kriging Toolbox; Technical Report No. IMM-TR-2002-12; Technical University of Denmark: Copenhagen, Denmark, 2002. [Google Scholar]
- Tomassi, A.; Trippetta, F.; de Franco, R.; Ruggieri, R. From Petrophysical Properties to Forward-Seismic Modeling of Facies Heterogeneity in the Carbonate Realm (Majella Massif, Central Italy). J. Pet. Sci. Eng. 2022, 211, 110242. [Google Scholar] [CrossRef]
- Shexo, A.H.M.; Abdullah, T.H. Robust Estimation Based on Lognormal Kriging Technique for Some Soil Data. Math. Model. Eng. Probl. 2024, 11, 5. [Google Scholar] [CrossRef]
- Rajabi, F.; Faraji, N.; Hashemi, M. An Efficient Video-Based Rainfall Intensity Estimation Employing Different Recurrent Neural Network Models. Earth Sci. Inform. 2024, 17, 2367–2380. [Google Scholar] [CrossRef]
- Shadkani, S.; Hashemi, S.; Pak, A.; Lahijan, A.B. Random Forest and Multilayer Perceptron Hybrid Models Integrated with the Genetic Algorithm for Predicting Pan Evaporation of Target Site Using a Limited Set of Neighboring Reference Station Data. Earth Sci. Inform. 2024, 17, 1261–1280. [Google Scholar] [CrossRef]
- Mirarabi, A.; Nassery, H.R.; Nakhaei, M.; Adamowski, J.; Akbarzadeh, A.H.; Alijani, F. Evaluation of Data-Driven Models (SVR and ANN) for Groundwater-Level Prediction in Confined and Unconfined Systems. Environ. Earth. Sci. 2019, 78, 489. [Google Scholar] [CrossRef]
- Magalhães-Mendes, J. A Comparative Study of Crossover Operators for Genetic Algorithms to Solve the Job Shop Scheduling Problem. WSEAS Trans. Comput. 2013, 12, 164–173. [Google Scholar]
- Mahmoudpour, H.; Janatrostami, S.; Ashrafzadeh, A. Optimal Design of Groundwater Quality Monitoring Network Using Aquifer Vulnerability Map. Water Resour. Manag. 2023, 37, 797–818. [Google Scholar] [CrossRef]
- Hashemi, M.; Mazandarani Zadeh, H.; Daneshkare Arasteh, P.; Zarghami, M. Economic and Environmental Impacts of Cropping Pattern Elements Using Systems Dynamics. Civ. Eng. J. 2019, 5, 1020–1032. [Google Scholar] [CrossRef]
- Gladish, D.W.; Pagendam, D.E.; Janardhanan, S.; Gonzalez, D. Geostatistical Based Optimization of Groundwater Monitoring Well Network Design. Front. Earth Sci. 2023, 11, 1188316. [Google Scholar] [CrossRef]
- Loganathan, S.; Ramakrishnan, D.; Sathiyamoorthy, M.; Azamathulla, H.M. Assessment of Irrigational Suitability of Groundwater in Thanjavur District, Southern India Using Mamdani Fuzzy Inference System. Results Eng. 2024, 21, 101789. [Google Scholar] [CrossRef]
- Kambalimath, S.; Deka, P.C. A Basic Review of Fuzzy Logic Applications in Hydrology and Water Resources. Appl. Water Sci. 2020, 10, 191. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Nash, J.F. The Bargaining Problem. Econometrica 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Kalai, E.; Smorodinsky, M. Other Solutions to Nash’s Bargaining Problem. Econometrica 1975, 43, 513–518. [Google Scholar] [CrossRef]
- Salazar, R.; Szidarovszky, F.; Coppola, E.; Rojano, A. Application of Game Theory for a Groundwater Conflict in Mexico. J. Environ. Manag. 2007, 84, 560–571. [Google Scholar] [CrossRef]
- Chitsazan, M.; Rahmani, G.; Neyamadpour, A. Groundwater Level Simulation Using Artificial Neural Network: A Case Study from Aghili Plain, Urban Area of Gotvand, South-West Iran. Geopersia 2013, 3, 35–46. [Google Scholar]
- Dewana, B.R.; Prasetyo, S.Y.J.; Hartomo, K.D. Comparison of IDW and Kriging Interpolation Methods Using Geoelectric Data to Determine the Depth of the Aquifer in Semarang, Indonesia. J. Ilm. Tek. Elektro Komput. Dan Inform. 2022, 8, 215. [Google Scholar] [CrossRef]
- Njeban, H.S. Comparison and Evaluation of GIS-Based Spatial Interpolation Methods for Estimation Groundwater Level in AL-Salman District—Southwest Iraq. J. Geogr. Inf. Syst. 2018, 10, 362–380. [Google Scholar] [CrossRef]
- Arkoc, O. Modeling of Spatiotemporal Variations of Groundwater Levels Using Different Interpolation Methods with the Aid of GIS, Case Study from Ergene Basin, Turkey. Model. Earth Syst. Environ. 2022, 8, 967–976. [Google Scholar] [CrossRef]
- Noori, S.; Ebrahimi, K.; Liaghat, A.-M.; Hoorfar, A.-H. Comparison of Different Geostatistical Methods to Estimate Groundwater Level at Different Climatic Periods. Water Environ. J. 2013, 27, 10–19. [Google Scholar] [CrossRef]
- Hashemi Tameh, M.A.; Mazandarani Zadeh, H.; Arasteh Daneshkar, P. A Novel Solution to Define the Optimum Number and Location of New Wells to Improve Groundwater Level Map. Procedia Eng. 2016, 154, 252–259. [Google Scholar] [CrossRef]
- Chang, L.-C.; Chu, H.-J.; Chen, Y.-W. A Fuzzy Inference System for the Conjunctive Use of Surface and Subsurface Water. Adv. Fuzzy Syst. 2013, 2013, 128393. [Google Scholar] [CrossRef]
- Isazade, V.; Qasimi, A.B.; Toomanian, A.; Isazade, E. The Effect of Drought Phenomenon on the Surface of Groundwater Aquifer in Qazvin Plain in Iran. J. Appl. Sci. Technol. Trends 2023, 4, 80–85. [Google Scholar] [CrossRef]

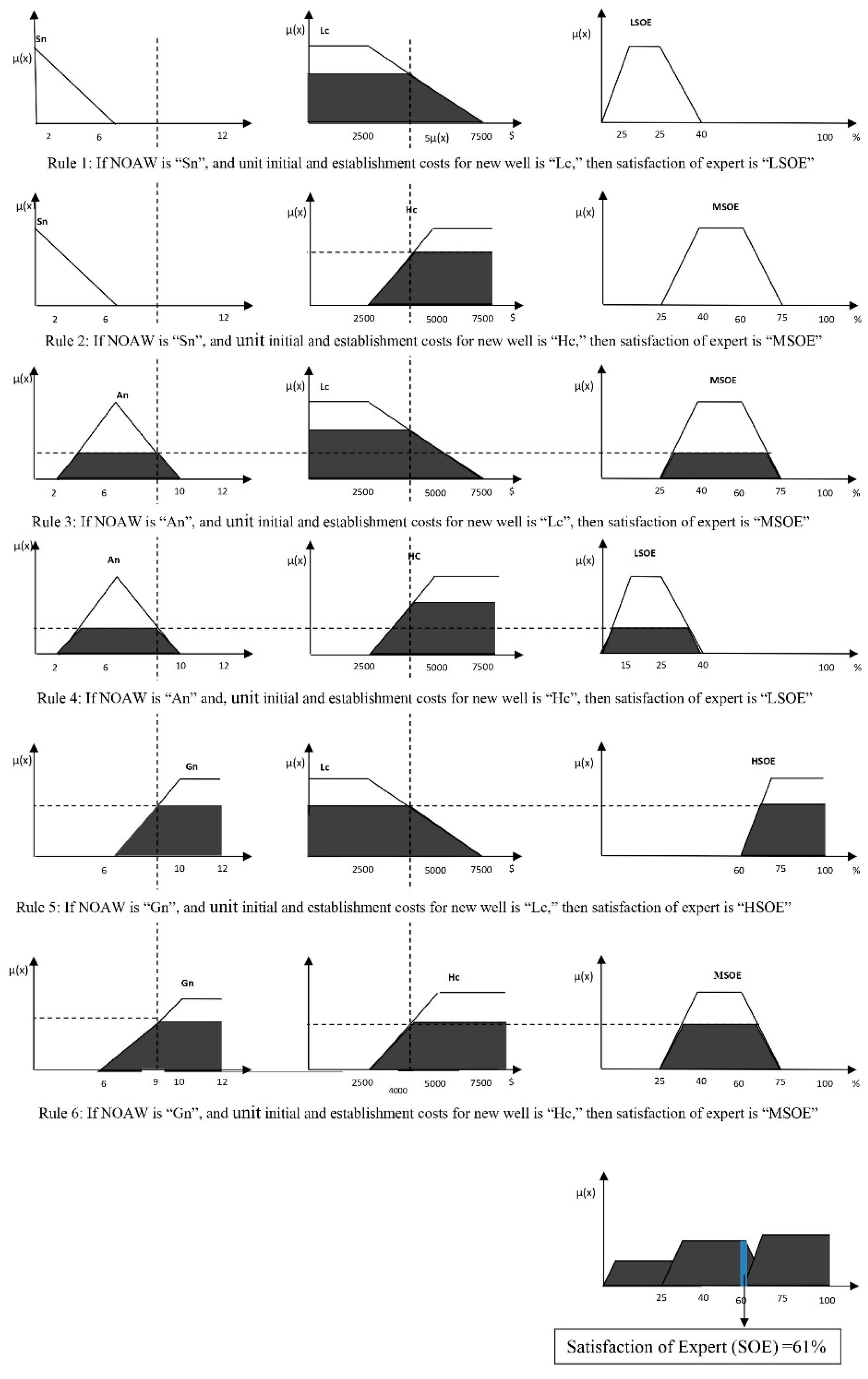


| Unit Cost of New Well | NOAW | |||
| Small | Average | Great | ||
| Low cost | LSOE | MSOE | HSOE | |
| High cost | MSOE | LSOE | LSOE | |
| Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| Statistical Parameter | IDW | Kriging | MLP-ANN | Spline | ||||
| Train | Test | Train | Test | Train | Test | Train | Test | |
| R2 | 1.00 | 0.75 | 1.00 | 0.81 | 0.97 | 0.93 | 1.00 | 0.79 |
| RMSE | 0.09 | 26.80 | 0.00 | 24.53 | 10.77 | 13.70 | 0.04 | 26.52 |
| MAE | 0.04 | 13.44 | 0.00 | 11.93 | 4.50 | 6.62 | 0.02 | 12.10 |
| RMSLE | 0.000 | 0.009 | 0.000 | 0.009 | 0.004 | 0.005 | 0.000 | 0.009 |
| ARE | 0.001 | 0.496 | 0.000 | 0.423 | 0.155 | 0.279 | 0.001 | 0.457 |
| Number of Additional Wells (NOAWs) | Satisfaction of the Expert (SOE) for USD 4000/Well | Satisfaction of the Expert (SOE) for USD 6000/Well | Satisfaction of the Expert (SOE) for USD 8000/Well |
|---|---|---|---|
| 1 | 35 | 44 | 49 |
| 2 | 36 | 44 | 49 |
| 3 | 37 | 42 | 43 |
| 4 | 37 | 31 | 31 |
| 5 | 39 | 27 | 24 |
| 6 | 39 | 25 | 20 |
| 7 | 44 | 27 | 20 |
| 8 | 52 | 30 | 20 |
| 9 | 61 | 27 | 20 |
| 10 | 68 | 25 | 20 |
| 11 | 68 | 25 | 20 |
| 12 | 68 | 25 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hashemi, M.; Peralta, R.C.; Yost, M. Balancing Results from AI-Based Geostatistics versus Fuzzy Inference by Game Theory Bargaining to Improve a Groundwater Monitoring Network. Mach. Learn. Knowl. Extr. 2024, 6, 1871-1893. https://doi.org/10.3390/make6030092
Hashemi M, Peralta RC, Yost M. Balancing Results from AI-Based Geostatistics versus Fuzzy Inference by Game Theory Bargaining to Improve a Groundwater Monitoring Network. Machine Learning and Knowledge Extraction. 2024; 6(3):1871-1893. https://doi.org/10.3390/make6030092
Chicago/Turabian StyleHashemi, Masoumeh, Richard C. Peralta, and Matt Yost. 2024. "Balancing Results from AI-Based Geostatistics versus Fuzzy Inference by Game Theory Bargaining to Improve a Groundwater Monitoring Network" Machine Learning and Knowledge Extraction 6, no. 3: 1871-1893. https://doi.org/10.3390/make6030092
APA StyleHashemi, M., Peralta, R. C., & Yost, M. (2024). Balancing Results from AI-Based Geostatistics versus Fuzzy Inference by Game Theory Bargaining to Improve a Groundwater Monitoring Network. Machine Learning and Knowledge Extraction, 6(3), 1871-1893. https://doi.org/10.3390/make6030092









