A Novel Integration of Data-Driven Rule Generation and Computational Argumentation for Enhanced Explainable AI
Abstract
1. Introduction
2. Related Work
2.1. Rule-Based Explainable Artificial Intelligence
2.2. Argument-Based XAI and Defeasible Reasoning
2.3. Argument-Based XAI
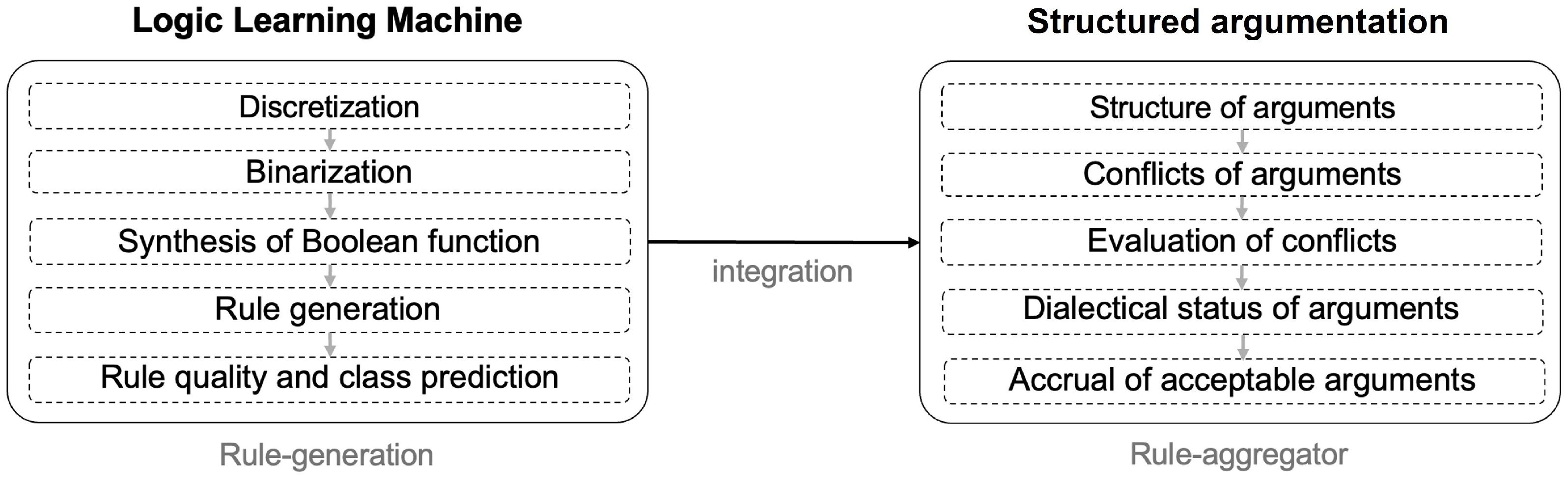
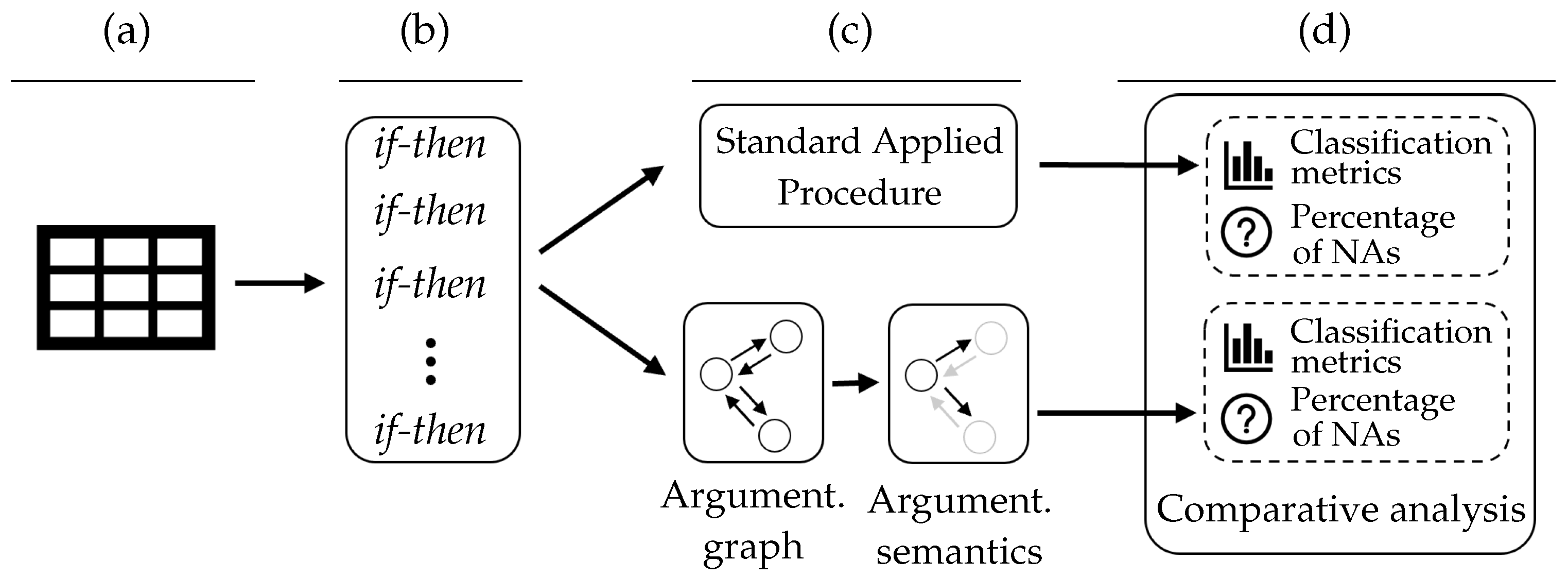
3. Integration of the Logic Learning Machine and Structured Argumentation
3.1. Rule Generator: The Logic Learning Machine
3.1.1. Discretization
- The sets including examples separated by the cutoff :
- The counter that counts the number of examples separated in a determinant way by :
- The value that measures the total effective distance between examples belonging to different classes that are separated in a determinant way by :
3.1.2. Binarization
3.1.3. Synthesis of the Boolean Function
- Each Boolean function can be written with operators AND, OR, and NOT that constitute the Boolean algebra; if NOT is not considered, then a simpler structure, called a Boolean lattice, is obtained. From now on, only the Boolean lattice is considered.
- The sum (OR) and product (AND) of m terms can be denoted as follows:
- A logical product is called an implicant of a function f if the following relation holds: , where each element is called a literal.
3.1.4. Rule Generation
- If for each , then no condition relative to is added to the rule.
- If is nominal, then a condition is added to the rule, where V is the set of values associated with each .
- If is ordered, then a condition is added to the rule, where V is the union of the intervals associated with each .
- the number of rules for each class; it affects the total number of generated rules;
- the maximum number of conditions in a rule; it forces the number of premises of each rule not to exceed a certain threshold;
- the maximum error (in %) that a rule can score.
3.1.5. Rules Aggregator Logic: Standard Applied Procedure
- is the number of training set examples that satisfy both the premise and the consequence of the rule r;
- is the number of training set examples that satisfy the premise but do not satisfy the consequence of the rule r;
- is the number of training set examples that do not satisfy either the premise or the consequence of the rule r;
- is the number of training set examples that do not satisfy the premise and satisfy the consequence of the rule r.
- Covering: ,
- Error: .
3.2. Rules Aggregator Logic: Computational Argumentation
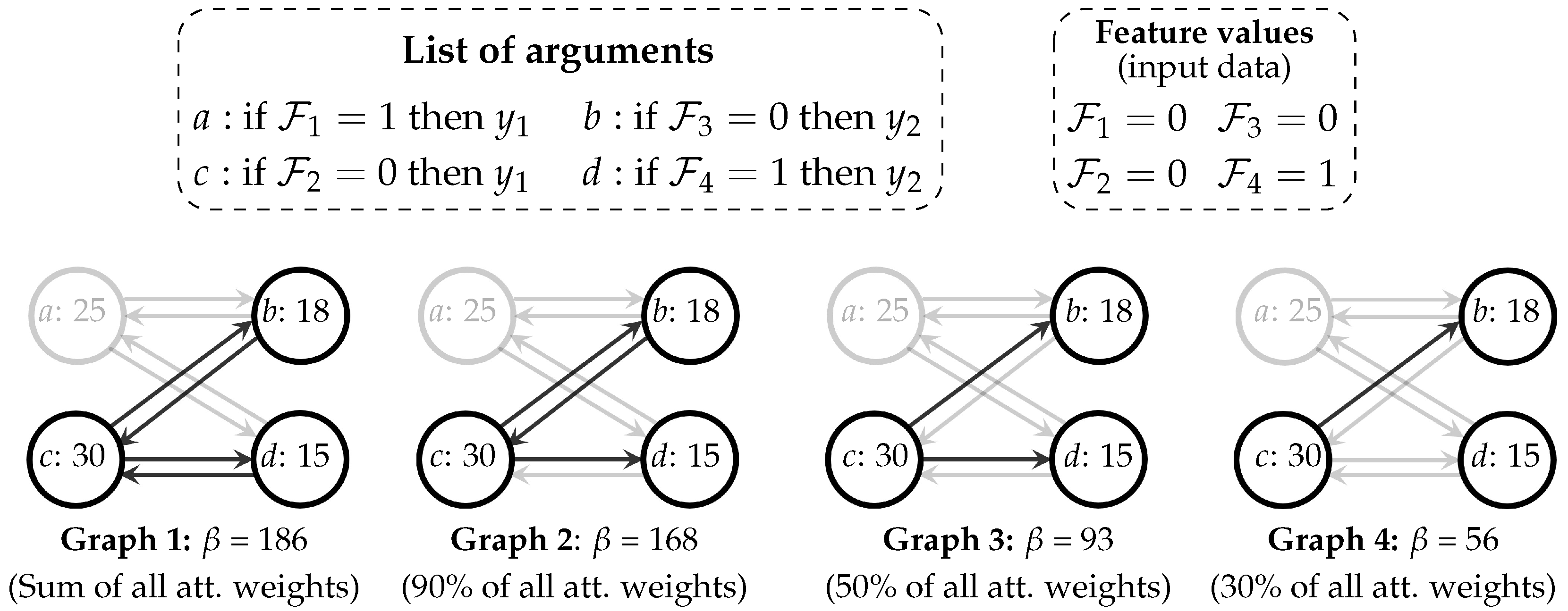
3.2.1. Creation of the Structure of Arguments
3.2.2. Conflicts of Arguments
3.2.3. Evaluation of Conflicts
- P1: Rebuttal attacks.
- P2: Attack with smaller weight.
- P3: In cases of equal weights, the attack whose source argument has the smallest weight.
3.2.4. Dialectical Status of Arguments
Extension-Based Semantics
- •
- as .
- •
- as for some .
- •
- as .
- •
- as for some .
- defends and
- defends
- •
- is admissible if .
- •
- is a complete extension if .
- •
- is a grounded extension if is maximal, or is minimal, or is minimal.
- •
- is a preferred extension if is maximal or is maximal.
Ranking-Based Semantics
3.2.5. Accrual of Acceptable Arguments and Final Inference
- Extension-based semantics:
- -
- An extension containing arguments that support different claims is not employed for the final decision, as it does not provide a single, justifiable point of view. This suggests that the inconsistency budget was set too small. Therefore, the final inference is undecided on whether any extension can be accepted.
- -
- When multiple acceptable extensions are produced, their credibility is determined by the number of accepted arguments in each extension, disregarding argument weights since they have already been used to define the attack weights. This is a limited, simplistic approach to reduce the number of undecided situations after applying semantics, like the preferred one, that could yield multiple extensions. Eventually, the defeasible reasoning process ends undecided if all extensions have the same number of arguments.
- Ranking-based semantics:
- -
- The inference is left undecided if the ranking-based semantics produces a tie between top-ranked arguments supporting different claims.
4. Design and Methods
5. Results and Discussion
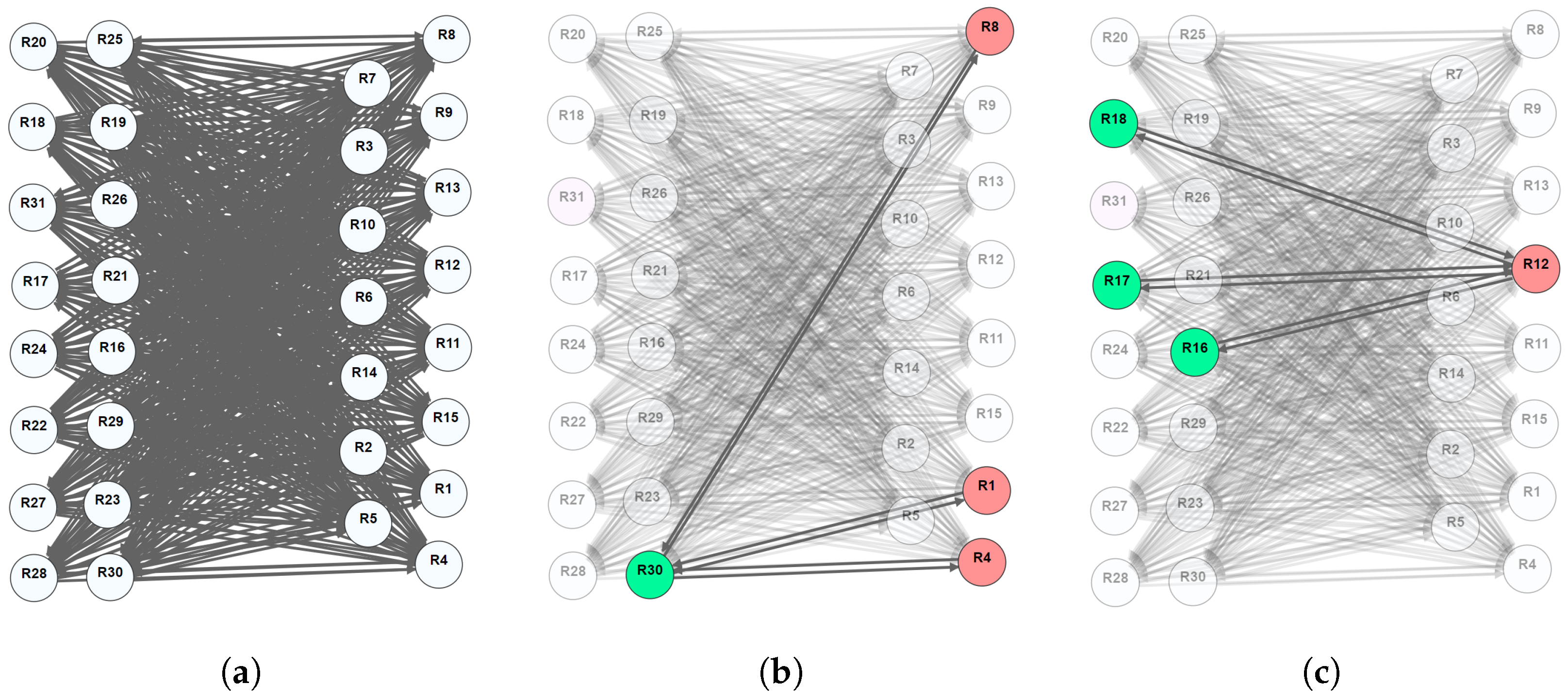
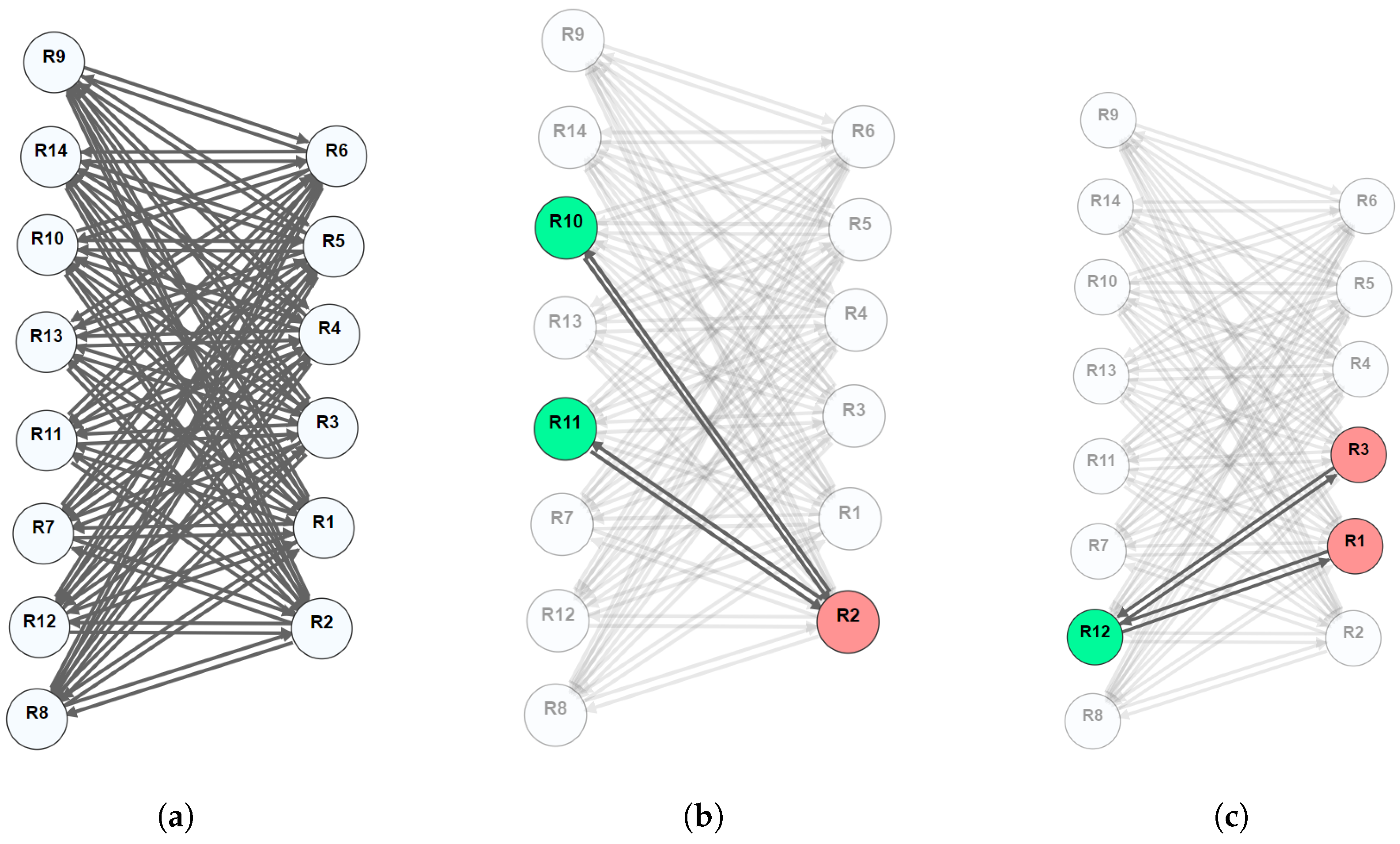
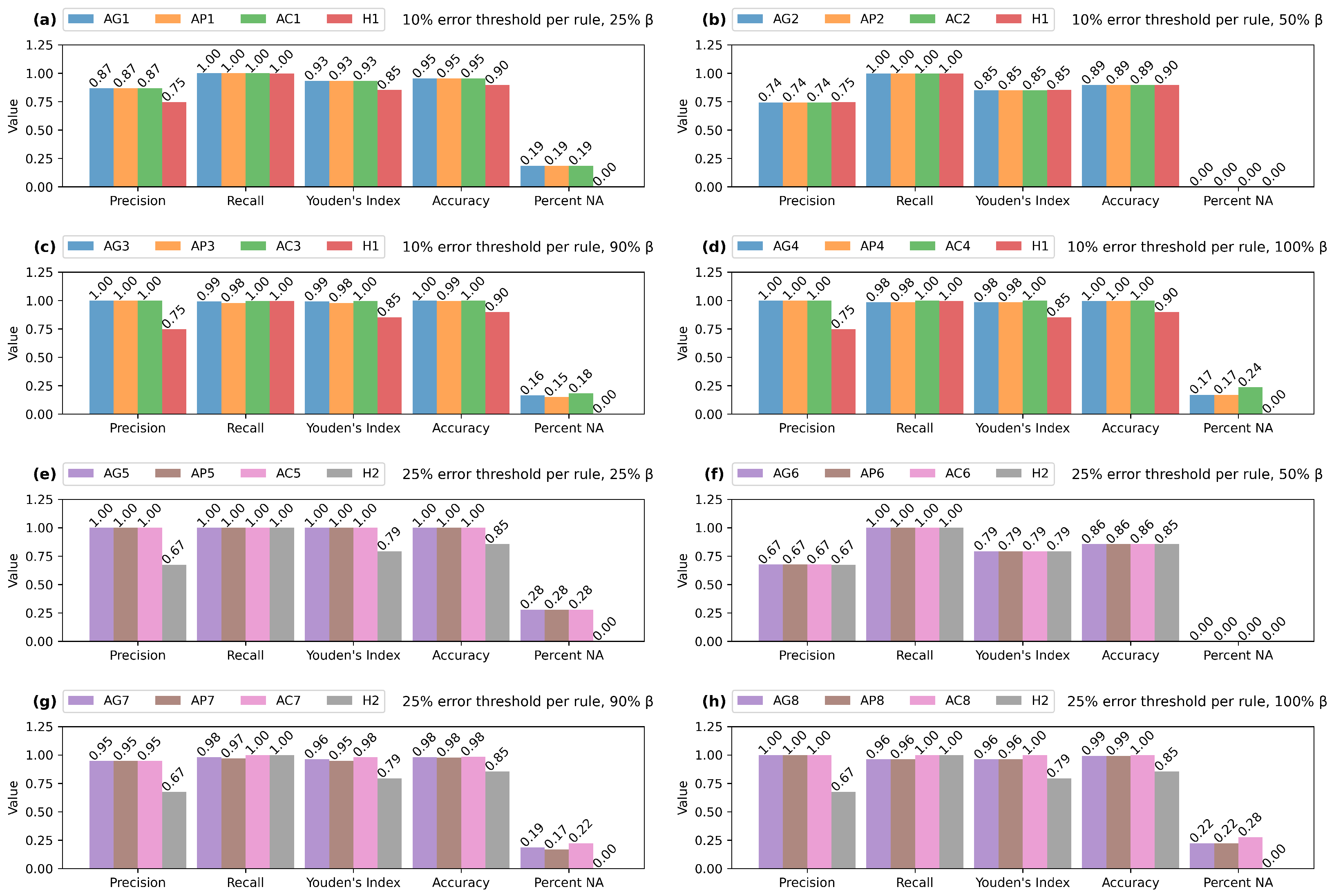
5.1. CARS Dataset
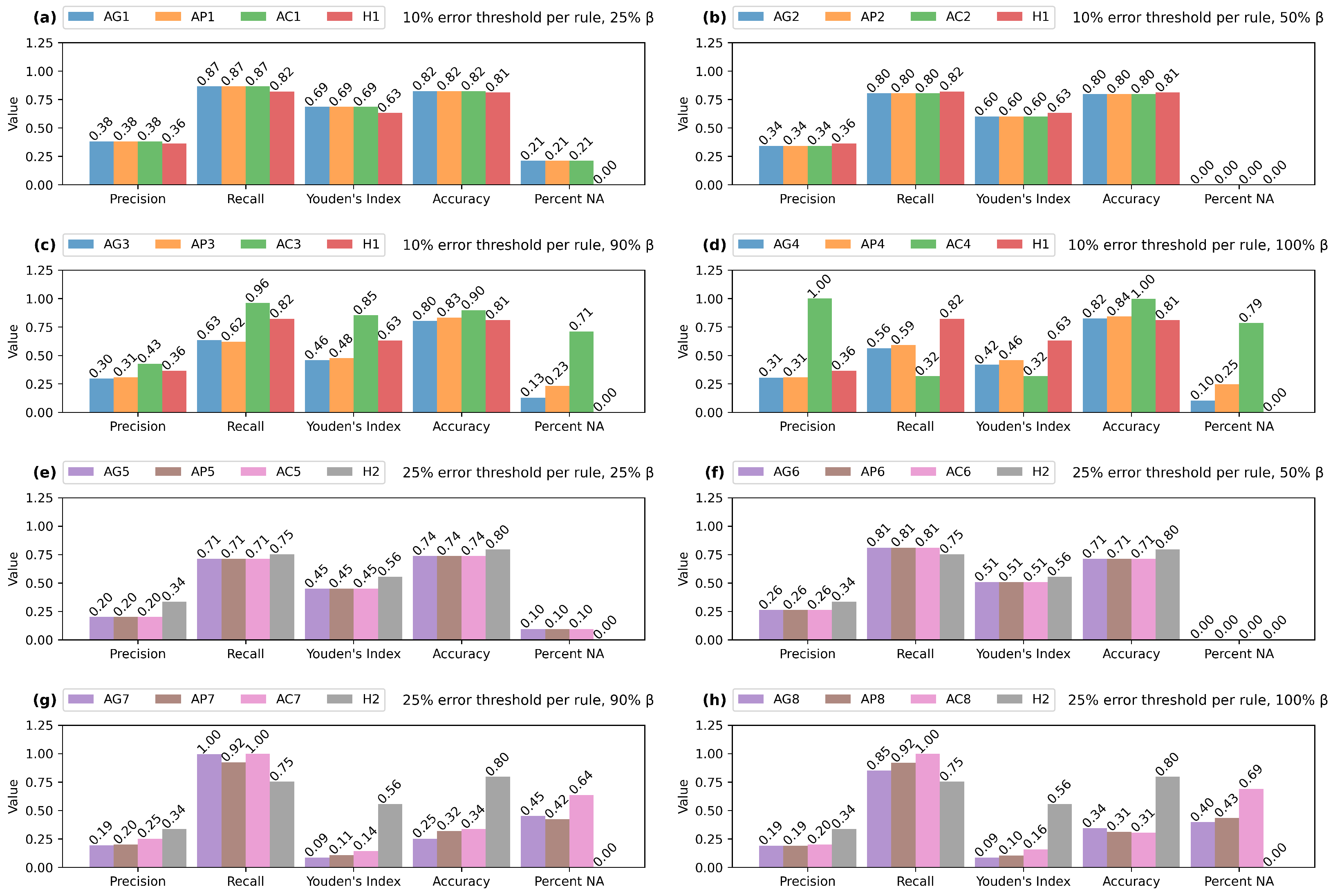
5.2. CENSUS Dataset
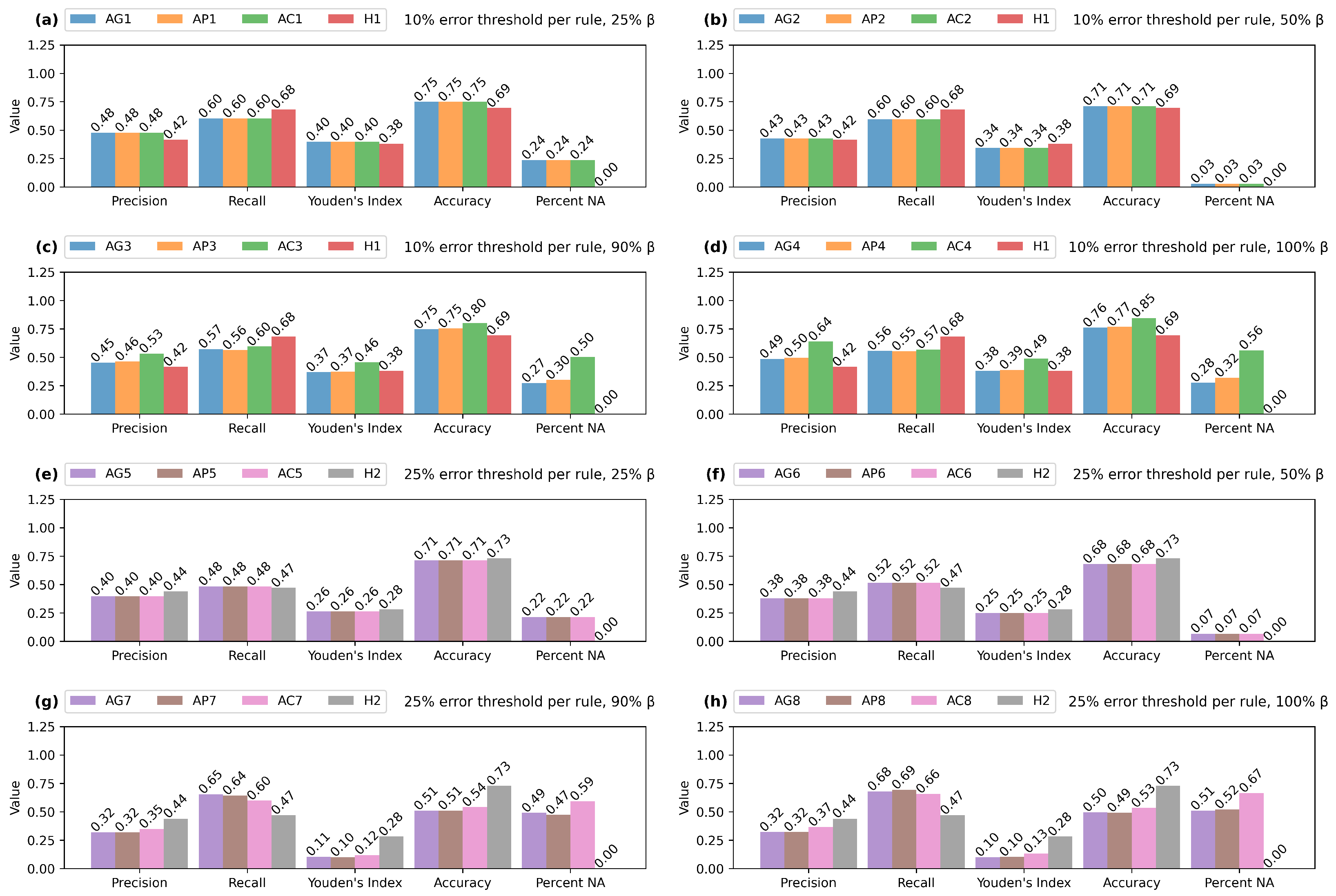
5.3. BANK Dataset
5.4. MYOCARDIAL Dataset
5.5. Summary and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Ali, S.; Abuhmed, T.; El-Sappagh, S.; Muhammad, K.; Alonso-Moral, J.M.; Confalonieri, R.; Guidotti, R.; Del Ser, J.; Díaz-Rodríguez, N.; Herrera, F. Explainable Artificial Intelligence (XAI): What we know and what is left to attain Trustworthy Artificial Intelligence. Inf. Fusion 2023, 99, 101805. [Google Scholar] [CrossRef]
- Markus, A.F.; Kors, J.A.; Rijnbeek, P.R. The role of explainability in creating trustworthy artificial intelligence for health care: A comprehensive survey of the terminology, design choices, and evaluation strategies. J. Biomed. Inform. 2021, 113, 103655. [Google Scholar] [CrossRef] [PubMed]
- van der Waa, J.; Nieuwburg, E.; Cremers, A.; Neerincx, M. Evaluating XAI: A comparison of rule-based and example-based explanations. Artif. Intell. 2021, 291, 103404. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Cao, J.; Zhou, T.; Zhi, S.; Lam, S.; Ren, G.; Zhang, Y.; Wang, Y.; Dong, Y.; Cai, J. Fuzzy inference system with interpretable fuzzy rules: Advancing explainable artificial intelligence for disease diagnosis—A comprehensive review. Inf. Sci. 2024, 662, 120212. [Google Scholar] [CrossRef]
- Miller, T. Contrastive explanation: A structural-model approach. Knowl. Eng. Rev. 2021, 36, e14. [Google Scholar] [CrossRef]
- Besnard, P.; Garcia, A.; Hunter, A.; Modgil, S.; Prakken, H.; Simari, G.; Toni, F. Introduction to structured argumentation. Argum. Comput. 2014, 5, 1–4. [Google Scholar] [CrossRef]
- Atkinson, K.; Baroni, P.; Giacomin, M.; Hunter, A.; Prakken, H.; Reed, C.; Simari, G.; Thimm, M.; Villata, S. Towards artificial argumentation. AI Mag. 2017, 38, 25–36. [Google Scholar] [CrossRef]
- Tompits, H. A survey of non-monotonic reasoning. Open Syst. Inf. Dyn. 1995, 3, 369–395. [Google Scholar] [CrossRef]
- Lindström, S. A semantic approach to nonmonotonic reasoning: Inference operations and choice. Theoria 2022, 88, 494–528. [Google Scholar] [CrossRef]
- Brewka, G. Nonmonotonic Reasoning: Logical Foundations of Commonsense; Cambridge University Press: Cambridge, UK, 1991; Volume 12. [Google Scholar]
- Sklar, E.I.; Azhar, M.Q. Explanation through Argumentation. In Proceedings of the 6th International Conference on Human-Agent Interaction, New York, NY, USA, 15–18 December 2018; HAI ’18. [Google Scholar] [CrossRef]
- Vassiliades, A.; Bassiliades, N.; Patkos, T. Argumentation and explainable artificial intelligence: A survey. Knowl. Eng. Rev. 2021, 36, e5. [Google Scholar] [CrossRef]
- Rizzo, L.; Longo, L. Comparing and extending the use of defeasible argumentation with quantitative data in real-world contexts. Inf. Fusion 2023, 89, 537–566. [Google Scholar] [CrossRef]
- Vilone, G.; Longo, L. A Quantitative Evaluation of Global, Rule-Based Explanations of Post-Hoc, Model Agnostic Methods. Front. Artif. Intell. 2021, 4, 160. [Google Scholar] [CrossRef] [PubMed]
- Muselli, M.; Ferrari, E. Coupling logical analysis of data and shadow clustering for partially defined positive Boolean function reconstruction. IEEE Trans. Knowl. Data Eng. 2009, 23, 37–50. [Google Scholar] [CrossRef]
- Bennetot, A.; Franchi, G.; Ser, J.D.; Chatila, R.; Díaz-Rodríguez, N. Greybox XAI: A Neural-Symbolic learning framework to produce interpretable predictions for image classification. Knowl.-Based Syst. 2022, 258, 109947. [Google Scholar] [CrossRef]
- Rizzo, L. A Novel Structured Argumentation Framework for Improved Explainability of Classification Tasks. In Proceedings of the Explainable Artificial Intelligence; Longo, L., Ed.; Springer Nature: Cham, Switzerland, 2023; pp. 399–414. [Google Scholar]
- Ferrari, E.; Verda, D.; Pinna, N.; Muselli, M. A Novel Rule-Based Modeling and Control Approach for the Optimization of Complex Water Distribution Networks. In Proceedings of the Advances in System-Integrated Intelligence; Valle, M., Lehmhus, D., Gianoglio, C., Ragusa, E., Seminara, L., Bosse, S., Ibrahim, A., Thoben, K.D., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 33–42. [Google Scholar]
- Nicoletta, M.; Zilich, R.; Masi, D.; Baccetti, F.; Nreu, B.; Giorda, C.B.; Guaita, G.; Morviducci, L.; Muselli, M.; Ozzello, A.; et al. Overcoming Therapeutic Inertia in Type 2 Diabetes: Exploring Machine Learning-Based Scenario Simulation for Improving Short-Term Glycemic Control. Mach. Learn. Knowl. Extr. 2024, 6, 420–434. [Google Scholar] [CrossRef]
- Parodi, S.; Manneschi, C.; Verda, D.; Ferrari, E.; Muselli, M. Logic Learning Machine and standard supervised methods for Hodgkin’s lymphoma prognosis using gene expression data and clinical variables. Health Inform. J. 2018, 24, 54–65. [Google Scholar] [CrossRef]
- Verda, D.; Parodi, S.; Ferrari, E.; Muselli, M. Analyzing gene expression data for pediatric and adult cancer diagnosis using logic learning machine and standard supervised methods. BMC Bioinform. 2019, 20, 390. [Google Scholar] [CrossRef]
- Gerussi, A.; Verda, D.; Cappadona, C.; Cristoferi, L.; Bernasconi, D.P.; Bottaro, S.; Carbone, M.; Muselli, M.; Invernizzi, P.; Asselta, R.; et al. LLM-PBC: Logic Learning Machine-Based Explainable Rules Accurately Stratify the Genetic Risk of Primary Biliary Cholangitis. J. Pers. Med. 2022, 12, 1587. [Google Scholar] [CrossRef]
- Lindgren, T. Methods for rule conflict resolution. In Proceedings of the European Conference on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2004; pp. 262–273. [Google Scholar]
- Clark, P.; Boswell, R. Rule induction with CN2: Some recent improvements. In Proceedings of the Machine Learning—EWSL-91: European Working Session on Learning, Porto, Portugal, 6–8 March 1991; Proceedings 5. Springer: Berlin/Heidelberg, Germany, 1991; pp. 151–163. [Google Scholar]
- Doe, J.; Smith, J. A Survey of the Role of Voting Mechanisms in Explainable Artificial Intelligence (XAI). J. Artif. Intell. Res. 2022, 59, 123–145. [Google Scholar]
- Nössig, A.; Hell, T.; Moser, G. A Voting Approach for Explainable Classification with Rule Learning. In Proceedings of the IFIP International Conference on Artificial Intelligence Applications and Innovations; Springer: Berlin/Heidelberg, Germany, 2024; pp. 155–169. [Google Scholar]
- Lindgren, T.; Boström, H. Classification with intersecting rules. In Proceedings of the Algorithmic Learning Theory: 13th International Conference, ALT 2002, Lübeck, Germany, 24–26 November 2002; Proceedings 13. Springer: Berlin/Heidelberg, Germany, 2002; pp. 395–402. [Google Scholar]
- Lindgren, T.; Boström, H. Resolving rule conflicts with double induction. Intell. Data Anal. 2004, 8, 457–468. [Google Scholar] [CrossRef]
- Kitson, N.K.; Constantinou, A.C.; Guo, Z.; Liu, Y.; Chobtham, K. A survey of Bayesian Network structure learning. Artif. Intell. Rev. 2023, 56, 8721–8814. [Google Scholar] [CrossRef]
- Čyras, K.; Rago, A.; Albini, E.; Baroni, P.; Toni, F. Argumentative XAI: A survey. arXiv 2021, arXiv:2105.11266. [Google Scholar]
- Espinoza, M.M.; Possebom, A.T.; Tacla, C.A. Argumentation-based agents that explain their decisions. In Proceedings of the 2019 8th IEEE Brazilian Conference on Intelligent Systems (BRACIS), Salvador, Brazil, 15–18 October 2019; pp. 467–472. [Google Scholar]
- Caroprese, L.; Vocaturo, E.; Zumpano, E. Argumentation approaches for explanaible AI in medical informatics. Intell. Syst. Appl. 2022, 16, 200109. [Google Scholar] [CrossRef]
- Governatori, G.; Maher, M.J.; Antoniou, G.; Billington, D. Argumentation semantics for defeasible logic. J. Log. Comput. 2004, 14, 675–702. [Google Scholar] [CrossRef]
- Baroni, P.; Giacomin, M. On principle-based evaluation of extension-based argumentation semantics. Artif. Intell. 2007, 171, 675–700. [Google Scholar] [CrossRef]
- Wu, Y.; Caminada, M.; Podlaszewski, M. A labelling-based justification status of arguments. Stud. Log. 2010, 3, 12–29. [Google Scholar]
- Caminada, M. Argumentation semantics as formal discussion. Handb. Form. Argum. 2017, 1, 487–518. [Google Scholar]
- Rizzo, L. ArgFrame: A multi-layer, web, argument-based framework for quantitative reasoning. Softw. Impacts 2023, 17, 100547. [Google Scholar] [CrossRef]
- Baroni, P.; Caminada, M.; Giacomin, M. An introduction to argumentation semantics. Knowl. Eng. Rev. 2011, 26, 365–410. [Google Scholar] [CrossRef]
- Longo, L. Defeasible reasoning and argument-based systems in medical fields: An informal overview. In Proceedings of the 2014 IEEE 27th International Symposium on Computer-Based Medical Systems, New York, NY, USA, 27–29 May 2014; pp. 376–381. [Google Scholar]
- Cocarascu, O.; Stylianou, A.; Čyras, K.; Toni, F. Data-empowered argumentation for dialectically explainable predictions. In ECAI 2020; IOS Press: Amsterdam, The Netherlands, 2020; pp. 2449–2456. [Google Scholar]
- Castagna, F.; McBurney, P.; Parsons, S. Explanation–Question–Response dialogue: An argumentative tool for explainable AI. Argum. Comput. 2024, 1–23, preprint. [Google Scholar] [CrossRef]
- Ferrari, E.; Muselli, M. Maximizing pattern separation in discretizing continuous features for classification purposes. In Proceedings of the The 2010 IEEE International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010. [Google Scholar]
- Cangelosi, D.; Muselli, M.; Parodi, S.; Blengio, F.; Becherini, P.; Versteeg, R.; Conte, M.; Varesio, L. Use of Attribute Driven Incremental Discretization and Logic Learning Machine to build a prognostic classifier for neuroblastoma patients. BMC Bioinform. 2014, 15, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, E.; Verda, D.; Pinna, N.; Muselli, M. Optimizing Water Distribution through Explainable AI and Rule-Based Control. Computers 2023, 12, 123. [Google Scholar] [CrossRef]
- Muselli, M.; Quarati, A. Reconstructing positive Boolean functions with shadow clustering. In Proceedings of the 2005 IEEE European Conference on Circuit Theory and Design, Cork, Ireland, 2 September 2005; Volume 3. [Google Scholar]
- Walton, D.; Reed, C.; Macagno, F. Attack, Rebuttal, and Refutation. In Argumentation Schemes; Cambridge University Press: Cambridge, UK, 2008; pp. 220–274. [Google Scholar]
- Baumann, R.; Spanring, C. A Study of Unrestricted Abstract Argumentation Frameworks. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence (IJCAI-17), Melbourne, Australia, 19–25 August 2017; Volume 17, pp. 807–813. [Google Scholar]
- Dunne, P.E.; Hunter, A.; McBurney, P.; Parsons, S.; Wooldridge, M.J. Inconsistency tolerance in weighted argument systems. In Proceedings of the AAMAS (2), Budapest, Hungary, 10–15 May 2009; pp. 851–858. [Google Scholar]
- Dunne, P.E.; Hunter, A.; McBurney, P.; Parsons, S.; Wooldridge, M. Weighted argument systems: Basic definitions, algorithms, and complexity results. Artif. Intell. 2011, 175, 457–486. [Google Scholar] [CrossRef]
- Bistarelli, S.; Santini, F. Conarg: A constraint-based computational framework for argumentation systems. In Proceedings of the 2011 IEEE 23rd International Conference on Tools with Artificial Intelligence, Boca Raton, FL, USA, 7–9 November 2011; pp. 605–612. [Google Scholar]
- Pazienza, A.; Ferilli, S.; Esposito, F.; Bistarelli, S.; Giacomin, M. Constructing and Evaluating Bipolar Weighted Argumentation Frameworks for Online Debating Systems. In Proceedings of the AI3@ AI* IA, Bari, Italy, 14–17 November 2017; pp. 111–125. [Google Scholar]
- Vilone, G.; Longo, L. An Examination of the Effect of the Inconsistency Budget in Weighted Argumentation Frameworks and their Impact on the Interpretation of Deep Neural Networks. In Proceedings of the Joint Proceedings of the xAI-2023 Late-breaking Work, Demos and Doctoral Consortium Co-Located with the 1st World Conference on eXplainable Artificial Intelligence (xAI-2023), Lisbon, Portugal, 26–28 July 2023; Longo, L., Ed.; CEUR Workshop Proceedings: Tenerife, Spain, 2023; Volume 3554, pp. 53–58. Available online: https://CEUR-WS.org (accessed on 6 June 2024).
- Dung, P.M. On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n-person games. Artif. Intell. 1995, 77, 321–357. [Google Scholar] [CrossRef]
- Bonzon, E.; Delobelle, J.; Konieczny, S.; Maudet, N. A comparative study of ranking-based semantics for abstract argumentation. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Caminada, M.W.; Gabbay, D.M. A logical account of formal argumentation. Stud. Log. 2009, 93, 109. [Google Scholar] [CrossRef]
- Caminada, M. On the issue of reinstatement in argumentation. In Proceedings of the European Workshop on Logics in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2006; pp. 111–123. [Google Scholar]
- Besnard, P.; Hunter, A. A logic-based theory of deductive arguments. Artif. Intell. 2001, 128, 203–235. [Google Scholar] [CrossRef]
- Vilone, G.; Longo, L. Development of a Human-Centred Psychometric Test for the Evaluation of Explanations Produced by XAI Methods. In Proceedings of the Explainable Artificial Intelligence; Longo, L., Ed.; Springer Nature: Cham, Switzerland, 2023; pp. 205–232. [Google Scholar]
- Lv, G.; Chen, L.; Cao, C.C. On glocal explainability of graph neural networks. In Proceedings of the International Conference on Database Systems for Advanced Applications; Springer: Cham, Switzerland, 2022; pp. 648–664. [Google Scholar]


| Datasets | ||||
|---|---|---|---|---|
| CARS | CENSUS | BANK | MYOCARDIAL | |
| Features | 6 | 14 | 16 | 59 |
| Records | 1728 | 30162 | 45211 | 1436 |
| Class distribution (positive-negative) | 30–70% | 25–75% | 29–71% | 24–76% |
| Feature types | Numerical, categorical | Numerical, categorical | Numerical, categorical | Numerical, categorical |
| Target feature | Class | Income | y | ZSN |
| Model | Error Threshold per Rule | Max. Premises per Rule | Conflict Resolution |
|---|---|---|---|
| 10% | 4 | Standard Applied Procedure | |
| 25% | 4 | Standard Applied Procedure |
| Model | Input Rules | Semantics | Inc. Budget |
|---|---|---|---|
| // | Same as | Grounded/Preferred/Categoriser | 25% |
| // | Same as | Grounded/Preferred/Categoriser | 50% |
| // | Same as | Grounded/Preferred/Categoriser | 90% |
| // | Same as | Grounded/Preferred/Categoriser | 100% |
| // | Same as | Grounded/Preferred/Categoriser | 25% |
| // | Same as | Grounded/Preferred/Categoriser | 50% |
| // | Same as | Grounded/Preferred/Categoriser | 90% |
| // | Same as | Grounded/Preferred/Categoriser | 100% |
| Error Threshold per Rule | # Rules | Average # Premises | # Attacks | |||
|---|---|---|---|---|---|---|
| 25% | 50% | 90% | 100% | |||
| 10% | 9 | 2 | 6 | 17 | 29 | 36 |
| 25% | 6 | 1.5 | 2 | 4 | 8 | 10 |
| Error Threshold per Rule | # Rules | Average # Premises | # Attacks | |||
|---|---|---|---|---|---|---|
| 25% | 50% | 90% | 100% | |||
| 10% | 31 | 2.74 | 54 | 240 | 357 | 480 |
| 25% | 14 | 2.14 | 12 | 48 | 74 | 96 |
| Error Threshold per Rule | # Rules | Average # Premises | # Attacks | |||
|---|---|---|---|---|---|---|
| 25% | 50% | 90% | 100% | |||
| 10% | 31 | 2.74 | 61 | 234 | 367 | 468 |
| 25% | 15 | 2.85 | 13 | 56 | 86 | 112 |
| Error Threshold per Rule | # Rules | Average # Premises | # Attacks | |||
|---|---|---|---|---|---|---|
| 25% | 50% | 90% | 100% | |||
| 10% | 33 | 2.57 | 102 | 270 | 458 | 540 |
| 25% | 14 | 1.71 | 16 | 49 | 81 | 98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rizzo, L.; Verda, D.; Berretta, S.; Longo, L. A Novel Integration of Data-Driven Rule Generation and Computational Argumentation for Enhanced Explainable AI. Mach. Learn. Knowl. Extr. 2024, 6, 2049-2073. https://doi.org/10.3390/make6030101
Rizzo L, Verda D, Berretta S, Longo L. A Novel Integration of Data-Driven Rule Generation and Computational Argumentation for Enhanced Explainable AI. Machine Learning and Knowledge Extraction. 2024; 6(3):2049-2073. https://doi.org/10.3390/make6030101
Chicago/Turabian StyleRizzo, Lucas, Damiano Verda, Serena Berretta, and Luca Longo. 2024. "A Novel Integration of Data-Driven Rule Generation and Computational Argumentation for Enhanced Explainable AI" Machine Learning and Knowledge Extraction 6, no. 3: 2049-2073. https://doi.org/10.3390/make6030101
APA StyleRizzo, L., Verda, D., Berretta, S., & Longo, L. (2024). A Novel Integration of Data-Driven Rule Generation and Computational Argumentation for Enhanced Explainable AI. Machine Learning and Knowledge Extraction, 6(3), 2049-2073. https://doi.org/10.3390/make6030101







