A New and Lightweight R-Peak Detector Using the TEDA Evolving Algorithm

Abstract

The literature on ECG delineation algorithms has seen significant growth in recent decades. However, several challenges still need to be addressed. This work aims to propose a lightweight R-peak-detection algorithm that does not require pre-setting and performs classification on a sample-by-sample basis. The novelty of the proposed approach lies in the utilization of the typicality eccentricity detection anomaly (TEDA) algorithm for R-peak detection. The proposed method for R-peak detection consists of three phases. Firstly, the ECG signal is preprocessed by calculating the signal’s slope and applying filtering techniques. Next, the preprocessed signal is inputted into the TEDA algorithm for R-peak estimation. Finally, in the third and last step, the R-peak identification is carried out. To evaluate the effectiveness of the proposed technique, experiments were conducted on the MIT-BIH arrhythmia database (MIT-AD) for R-peak detection and validation. The results of the study demonstrated that the proposed evolutive algorithm achieved a sensitivity (Se in %), positive predictivity (+P in %), and accuracy (ACC in %) of 95.45%, 99.61%, and 95.09%, respectively, with a tolerance (TOL) of 100 milliseconds. One key advantage of the proposed technique is its low computational complexity, as it is based on a statistical framework calculated recursively. It employs the concepts of typicity and eccentricity to determine whether a given sample is normal or abnormal within the dataset. Unlike most traditional methods, it does not require signal buffering or windowing. Furthermore, the proposed technique employs simple decision rules rather than heuristic approaches, further contributing to its computational efficiency.

1. Introduction

Cardiovascular diseases (CVDs) are among the greatest concerns for public health and humanity. The World Health Organization (WHO) reported that 17.9 million people died due to CVDs in 2019, meaning 32% of all global deaths [1]. Electrocardiogram (ECG) analysis is a powerful method for analyzing cardiac health. It can be an ally to saving many lives by rapid and accurate identification of CVDs, like arrhythmias, for example, [2].

The ECG signal is the electrical activity of different cardiac tissues obtained from a patient’s skin, providing a graphic pattern that represents the heart muscle’s function [3]. Sequential waves represent the cardiac cycle. Each wave part is associated with one physiological heart activity [4]. It is a powerful non-invasive method, and analyses of them can determine cardiac health [5]. The signal amplitude and intervals, defined by fiducial points, supply the most helpful information [5,6]. The main feature of arrhythmia detection is an accurate R-peak detection, which is critical for heart rate measurement. Different ventricular arrhythmias can be classified by detecting and examining QRS complexes and determining the R–R interval [7,8].

Different works in the literature have presented several automated algorithms for QRS and R-peak detection techniques [9]. However, implementations of the proposed algorithms are still challenging for ECG signal analysis in the real world [3,6]. Some proposed ECG detectors have very high accuracy but use several complex steps under specific conditions [3,10,11]. Undoubtedly, a computational technique to analyze the ECG signal with higher accuracy in streaming applications is still required. Since data flows continuously from data streams at high speed, traditional data management systems do not support the continuous queries required by streaming applications [10]. Instead, new techniques must be defined, or adapted methods should appear for ECG streaming settings [12,13].

Applications of medical services in healthcare in the Internet of Medical Things (IOMT) context will increase greatly in the coming years. Traditional methods cannot collect, analyze, query and store data within a reasonable time frame [14] for processing real-time data streams. In this new paradigm, a large amount of multimodal information comes from multiple resources, sensors, or other biomedical acquisition systems. The IOMT system needs low power consumption, low memory usage, and low CPU resource usage to deal with the continuous data volume from all the other streaming frames to maintain performance [15].

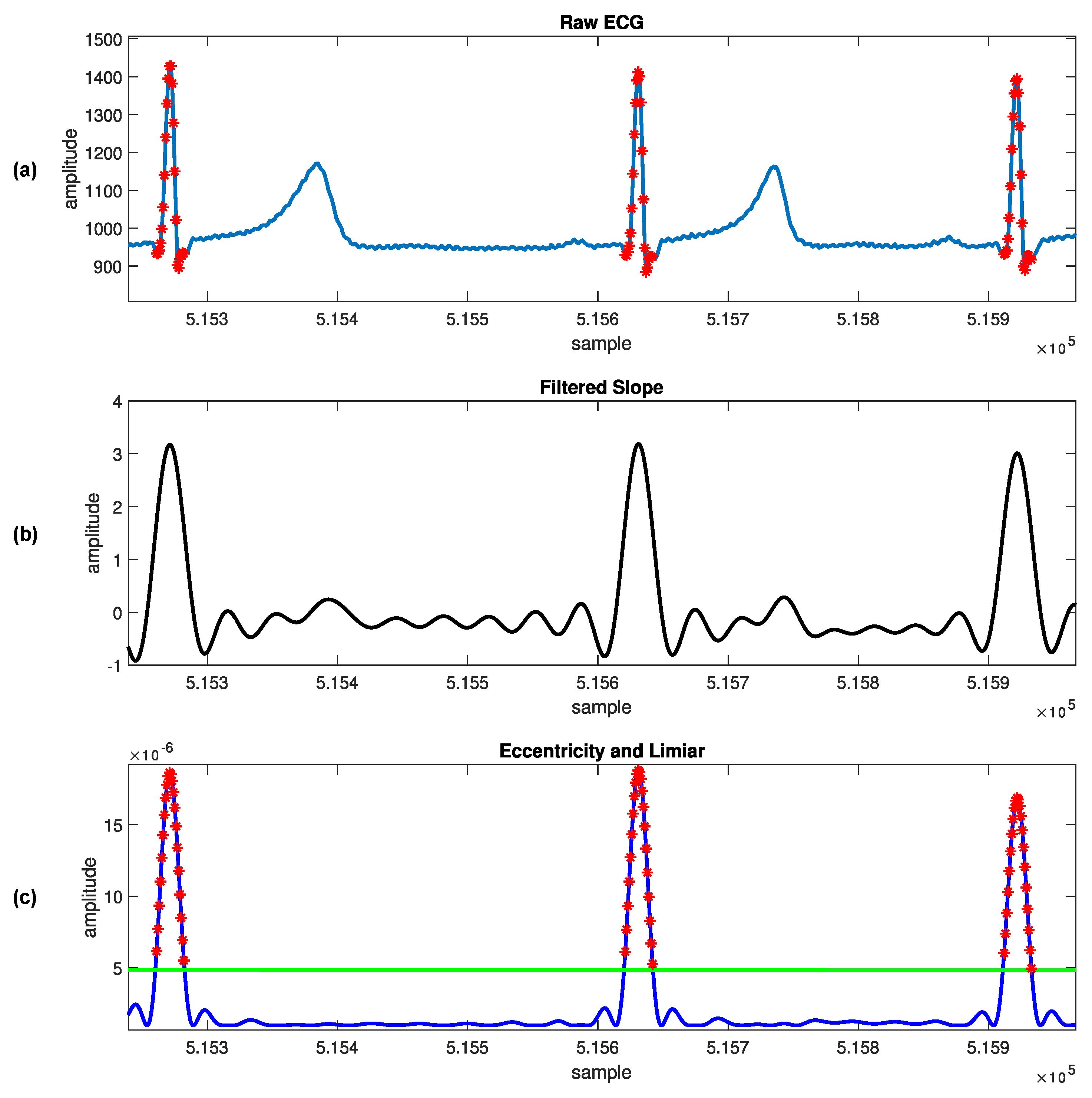
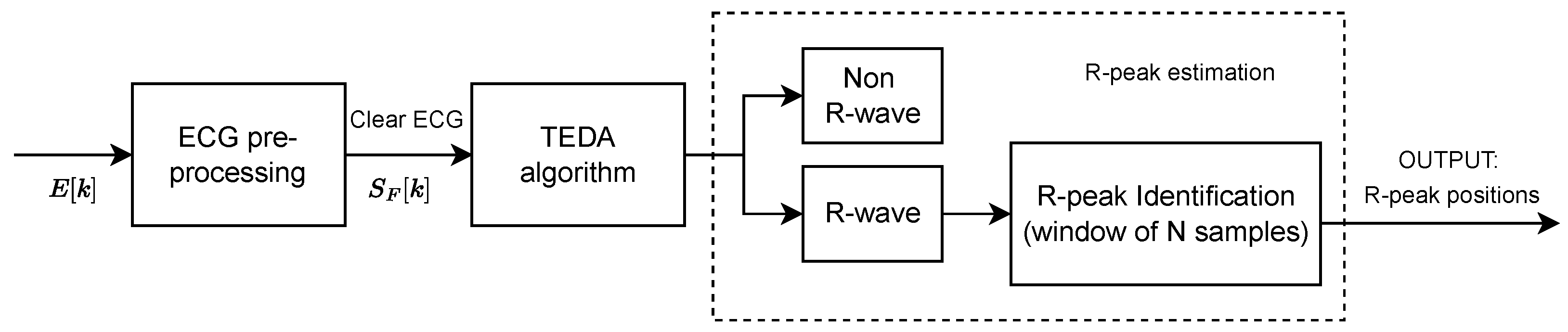
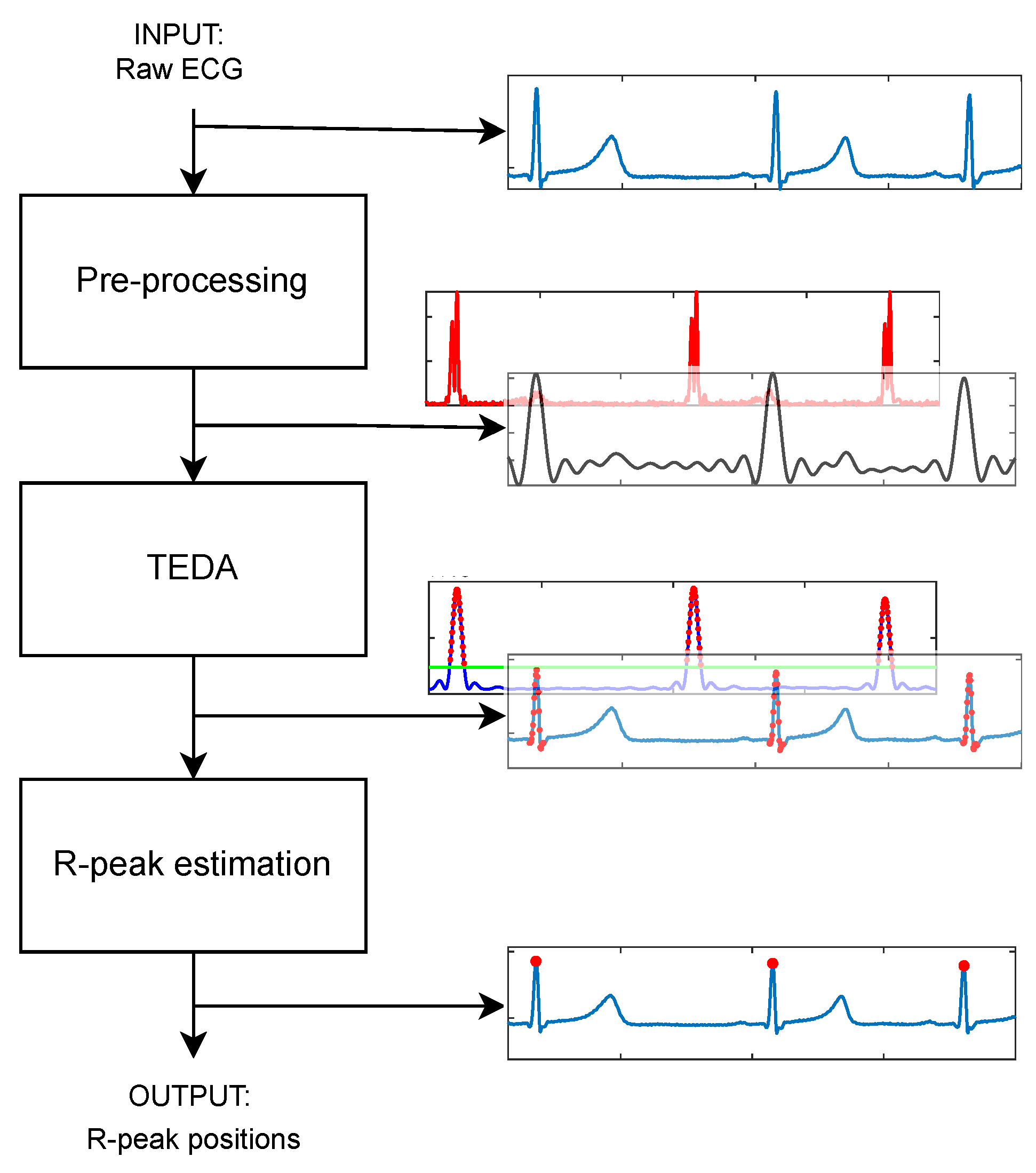
We can find in the literature a constant search for novel and more efficient ways to reduce computing costs so that the technique can be implementable in practice [16]. Our approach uses the typicality eccentricity detection anomaly (TEDA) algorithm recursively to minimize storage and time consumption, so that agents with lower computational complexity, such as portable and smart devices, could use it. TEDA is a recursive method designed to detect industrial signal anomalies in streaming applications. The R-peak wave portion is interpreted as an anomaly by TEDA because it is a very eccentric portion when compared to the rest of the ECG wave. Because of this, we infer the position of the R peak. In the literature, few algorithms are recursive in their analysis of the ECG signal.

TEDA can be an alternative to a statistical framework. New metrics are the TEDA’s foundation, all based on the similarity/proximity of data in the data space, not on density or entropy, as per traditional methods. TEDA is suitable for data streams because it is lightweight and recursive, so signals can be analyzed as they are generated and it can interpret large amounts of data, such as physiological data recorded continuously in an ICU. ECG signals are streaming data, and detections are needed continuously to aid in diagnosing heart disease, for example. An accurate streaming ECG analysis approach requires continuous adaptation. However, streaming data can be infinite, so algorithms that store the entire data for analysis are unsuitable. Instead, detectors should process data in real time and constantly update the model directly from the input stream [10,17].

This work proposes a novel automated ECG feature extraction algorithm based on the TEDA algorithm with a light preprocessing step, designed to detect R peaks by verifying their eccentricity in relation to the other waveform points. Its simplicity and low computational complexity make it a potential candidate for real-time and streaming ECG applications.

The highlights of this study can be summarized as follows:

• The proposed method is much lighter in terms of computational complexity.
• For the first time, the approach uses the TEDA algorithm for physiological signals, more specifically, for electrocardiogram signals.
• The method achieves a sensitivity (Se), positive predictivity (+P), and accuracy (ACC) of $95.45\%$, $99.61\%$, and $95.09\%$ for a 100 ms tolerance (TOL).
• The proposed technique can be performed online without pre-setting.
• The method shows a reduced and efficient pipeline compared to other studies in the literature.

2. Materials and Methods

The proposed method for R-peak detection is composed of three phases that are executed sequentially. First, we preprocess the ECG signal, applying slope calculation of the ECG raw signal and filtering. Next, we follow the preprocessed signal into the TEDA algorithm for R-peak estimation and then, in the third and last step, we carry out the R-peak identification. Figure 1 and Figure 2 illustrate the method’s flow process and introduce fundamental notation that will be used consistently throughout the paper.

2.1. Dataset

The Massachusetts Institute of Technology’s Beth Israel Hospital Arrhythmia Database (MIT-AD) is a public database available at PhysioNet [18]. It provides us with a good resource to test the effectiveness of the proposed method. MIT-BIH-AD is a popular database that consists of 48 half-hour ECG recordings from two channels. The ECG signals are from 47 subjects recorded at Boston’s Beth Israel Hospital between 1975 and 1979. Of 47 subjects, 25 subjects were men, aged 32 to 89, and 22 subjects were women, aged 23 to 89. Of these recordings, 60% of the records are from inpatients, and 40% are from outpatients. The sampling frequency is 360 samples per second [19].

2.2. Preprocessing

By applying the raw ECG signal directly to the TEDA algorithm, we have already achieved an accuracy of around 60% in R-peak detection when using the MIT-AD dataset. To improve this result, considering that a big part of the detection problem was related to the signal fluctuation in the baseline and noise [20], we made simple preprocessing steps to achieve satisfactory accuracy when implementing the R-peak detection using the TEDA algorithm. Accurate detection of R peaks in an electrocardiogram (ECG) is challenging due to their duration and various sources of noise, such as powerline interference, motion artifacts, and baseline, which can alter signal characteristics [3].

Figure 3 shows the preprocessing flowchart. An ECG is sampled at a fixed frequency and stored as a vector, so that $E\left[k\right]$ denotes the value of the k-th sample. First, we calculated the signal’s slope ($S\left[k\right]$) to verify the signal’s abrupt modification caused at the moment of the R-wave upward defection. The slope is the average absolute value of the amplitude difference between the following sample $E_{k+1}$ and the actual $E_k$, and between the $E_k$ and the last sample $E_{k-1}$. Equation (1) presents the slope definition [6].

$$S\left[k\right]=\left\{\begin{array}{cc}|E_{k+1}-E_k|\hfill & k=1,\hfill \\ \left(\right|E_{k+1}-E_k|+|E_k-E_{k-1}\left|\right)/2\hfill & 1<k<n,\hfill \\ |E_k-E_{k-1}|\hfill & k=n.\hfill \end{array}\right.$$

(1)

We filtered this new signal to remove noise to surpass the non-peak detection caused by powerline interference, motion artifacts, and baseline. As the maximum heartbeat is at most 220 beats per minute (bpm), corresponding to a frequency of less than 4 Hz [3], the filter chosen is a band-pass with 1 and 10 Hz cutoff frequencies. Figure 4 illustrates an example of signal preprocessing (record 113). The curve at the top is the raw ECG signal, the curve in the middle of the figure is the ECG slope, and the curve at the bottom is the slope signal after being filtered.

2.3. TEDA Algorithm

After calculating and filtering the slope, the preprocessed signal, $S_F\left[k\right]$, is the input of the TEDA algorithm. TEDA was presented by [21] as a statistical framework influenced by recursive density estimation algorithms. It employs concepts of typicity and eccentricity to infer whether a given sample is normal or abnormal to the dataset, instead of the data density used in more traditional statistical algorithms [22]. The typicality of TEDA is the similarity of a presented sample to the rest of the dataset. Eccentricity is the contrary, showing the sample’s difference to other samples.

The R wave is the upward deflection with the largest amplitude in the peak in the ECG wave. However, evaluating the signal regarding the slope is particularly important in not considering the T peak as an R peak. The T-peak amplitude can sometimes be higher than the R peak, but the T-wave slope is relatively slow compared to the R-peak slope [6]. Consequently, the eccentricity of the R wave’s slope is more significant than that of the other samples, which would not necessarily occur if we only considered the amplitude. Therefore, we can define the R-wave sequence as the samples with high eccentricity and low typicality.

TEDA employs the sum of the geometric distance between actual and past samples in the set to calculate the eccentricity. Thus, the higher the value, the lower the typicality of the sample. The eccentricity is a recursive calculation and was expressed by [23] as

$${\xi }_k\left(S_F\right)=\frac{1}{k}+\frac{{({\mu }_k^S-S_F\left[k\right])}^T({\mu }_k^S-S_F\left[k\right])}{k{\left[{\sigma }^2\right]}_k^S},{\left[{\sigma }^2\right]}_k^S>0,$$

(2)

where k is the discretization instant; $S_F\left[k\right]$ is the filtered slope in the k-th iteration; ${\mu }_k^S$ is the average of $S_F\left[k\right]$ in the k-th iteration; and ${\left[{\sigma }^2\right]}_k^S$ is the variance in $S_F\left[k\right]$ in the k-th iteration. The calculation of ${\mu }_k^S$ and ${\left[{\sigma }^2\right]}_k^S$ are also recursive calculations represented by Equations (3) and (4), respectively.

$${\mu }_k^S=\frac{(k-1)}{k}{\mu }_{k-1}^S+\frac{1}{k}{S}_F\left[k\right],k\ge 1,{\mu }_0^S=0,$$

(3)

$${\left[{\sigma }^2\right]}_k^S=\frac{(k-1)}{k}{\left[{\sigma }^2\right]}_{k-1}^S+\frac{1}{k}{∥S_F\left[k\right]-{\mu }_k^S∥}^2,k\ge 1,{\left[{\sigma }^2\right]}_0^S=0.$$

(4)

Equation (5) illustrates the typicality of a sample, $S_F\left[k\right]$, at the k-th iteration. It is the eccentricity complement. The normalized eccentricity can be seen in Equation (6).

$${\tau }_k\left(S_F\right)=1-{\xi }_k\left(S_F\right),$$

(5)

$${\zeta }_k\left(S_F\right)=\frac{{\xi }_k\left(S_F\right)}{2},\sum _{i=1}^k{\xi }_k\left(S_F\right)=1,k\ge 2.$$

(6)

It is necessary to separate R-wave samples from non-R-wave samples, as shown in Figure 1. For that, we define a comparison threshold, expressed as

$${\zeta }_k>\frac{m^2+1}{2k},m>0,$$

(7)

where m is a constant and k corresponds to the discretization instant [21].

Algorithm 1 presents an overview of all the TEDA steps based on the above-mentioned equations. The input of Algorithm 1 is the preprocessed ECG data samples, $S_F\left[k\right]$, and a comparison threshold constant, m. The output for each input, $S_F\left[k\right]$, indicates the sample’s classification as an R-wave or non-R-wave sample. Figure 5 shows an example of the eccentricity value and its comparison with the threshold (record 113). The top of Figure 5 illustrates the raw ECG signal, $E\left[k\right]$, and the positions of the detected points corresponding to the R wave. In the middle, just for comparison, we can see the signal after preprocessing, $S_F\left[k\right]$. At the bottom, we can see the eccentricity, the threshold and the R wave, which are the points with eccentricity above the threshold.

Algorithm 1: TEDA.

2.4. R-Peak Estimation

Once TEDA determines the samples with higher eccentricity, we need to find this sequence’s highest absolute amplitude value to determine the R peak. Figure 6a illustrates three R-wave sequences. We consider the point with the highest eccentricity, within a TOL interval, as the sequence’s R peak, as illustrated in Figure 6b.

3. Results

To demonstrate the effectiveness of the proposed method, we carried out a set of tests.

Table 1. Accuracy and precision evaluation for R-peak detection on MIT-AD.

Record	TB	TP	FP	FN	Se (%)	+P (%)	F1 Score (%)	ACC (%)
100	2273	2273	0	0	100	100	100	100
101	1865	1862	5	3	99.84	99.73	99.79	99.57
102	2187	2163	1	24	98.90	99.95	99.43	98.86
103	2084	2080	2	4	99.81	99.90	99.86	99.71
104	2229	2212	41	17	99.24	98.18	98.71	97.44
105	2572	2548	26	24	99.07	98.99	99.03	98.08
106	2027	1549	2	478	76.42	99.87	86.58	76.34
107	2137	2108	0	29	98.64	100	99.32	98.64
108	1763	1528	49	235	86.67	96.89	91.50	84.33
109	2532	2486	0	46	98.18	100	99.08	98.18
111	2124	2120	2	4	99.81	99.91	99.86	99.72
112	2539	2539	2	0	100	99.92	99.96	99.92
113	1795	1795	1	0	100	99.94	99.97	99.94
114	1879	1876	8	3	99.84	99.58	99.71	99.42
115	1953	1951	1	2	99.90	99.95	99.92	99.85
116	2412	2314	2	98	95.94	99.91	97.88	95.86
117	1535	1535	1	0	100	99.93	99.97	99.93
118	2278	2275	2	3	99.87	99.91	99.89	99.78
119	1987	1598	2	389	80.42	99.88	89.10	80.34
121	1863	1859	6	4	99.79	99.68	99.73	99.46
122	2476	2476	0	0	100	100	100	100
123	1518	1515	0	3	99.80	100	99.90	99.80
124	1619	1591	3	28	98.27	99.81	99.04	98.09
200	2601	2572	16	29	98.89	99.38	99.13	98.28
201	1963	1861	1	102	94.80	99.95	97.31	94.76
202	2136	2111	1	25	98.83	99.95	99.39	98.78
203	2980	2486	65	494	83.42	97.46	89.89	81.64
205	2656	2595	1	61	97.70	99.96	98.82	97.67
207	1860	1687	95	173	90.70	94.67	92.64	86.29
208	2955	1969	10	986	66.63	99.49	79.81	66.41
209	3055	2987	1	18	99.40	99.97	99.68	99.37
210	2650	2432	9	218	91.77	99.63	95.54	91.46
212	2748	2738	2	10	99.64	99.93	99.78	99.56
213	3251	3003	0	248	92.37	100	96.03	92.37
214	2262	2245	1	17	99.25	99.96	99.60	99.20
215	3363	3328	3	35	98.96	99.91	99.43	98.87
217	2208	2179	2	29	98.69	99.91	99.29	98.60
219	2154	2117	2	37	98.28	99.91	99.09	98.19
220	2048	2047	0	1	99.95	100	99.98	99.95
221	2427	2030	1	397	83.64	99.95	91.07	83.61
222	2483	2263	1	220	91.14	99.96	95.34	91.10
223	2605	2243	1	362	86.10	99.96	92.51	86.07
228	2053	1990	37	63	96.93	98.17	97.55	95.22
230	2256	2255	0	1	99.96	100	99.98	99.96
231	1571	1567	1	4	99.75	99.94	99.84	99.68
232	1780	1776	7	4	99.78	99.61	99.69	99.38
233	3079	3036	0	43	98.60	100	99.30	98.60
234	2753	2741	1	12	99.56	99.96	99.76	99.53
Total	109,494	104,511	414	4983	95.45	99.61	97.48	95.09

presents the evaluation results for each ECG record in terms of sensitivity (Se in %), positive predictivity (+P in %), and accuracy (ACC in %).

Identifying a type of wave in an ECG sequence does not mean that the identified points should appear at the exact annotation or particular time. Instead, the difference in timing between the identified point and the annotation should be inferior to a TOL. Table 1 presents results for a 100 ms TOL. Traditional values adopted for TOL are 150, 70, or 40 ms [24].

Aside from the Se, +P, and ACC, we calculated the averaged timing difference ${\mu }_t$ and the associated standard deviation ${\sigma }_t$ of the correctly labeled points concerning the annotation. Equations (8) and (9) illustrate the averaged timing difference ${\mu }_t$ and the associated standard deviation ${\sigma }_t$, respectively.

$${\mu }_t=\frac{1}{N},\sum _{i=1}^N(n_i^{\prime }-n_i).$$

(8)

$${\sigma }_t=\sqrt{\frac{1}{N},\sum _{i=1}^N{(n_i^{\prime }-{\mu }_i)}^2}.$$

(9)

where N is the number of samples labeled correctly as an R peak within the tolerance TOL, and $n^{\prime }$ and n are the time stamps of the detected peak inferred by this approach and annotated by specialists, respectively.

Table 2. Accuracy and precision evaluation for R-peak detection on MIT-AD.

TOL (ms)	${\mathit{\mu }}_{\mathit{t}}\pm \mathit{\sigma }$ (ms)	Se (%)	+P (%)	F1 Score (%)	ACC (%)
40	$5.9\pm 3.2$	$95.12$	$98.77$	$96.91$	$94.00$
70	$6.0\pm 3.7$	$95.38$	$99.38$	$97.34$	$94.82$
100	$6.1\pm 4.0$	$95.45$	$99.61$	$97.48$	$95.09$
150	$6.2\pm 4.8$	$95.44$	$99.75$	$97.55$	$95.21$

presents the averaged timing difference and the associated standard deviation or different TOLs. We also verify the proposal’s effectiveness by presenting typical metrics used to validate classification performance, such as positive prediction, sensitivity, F1 score, and accuracy.

4. Discussion

The literature on ECG delineation algorithms has been increasing over the last decades. R-peak detection applications use methods ranging from traditional processing methods to machine learning and its subbranches, such as deep learning [2]. The conventionally used methods often focus on the frequency aspect, using complex mathematical functions, transforms, and optimization techniques that need substantial computational resources [12].

Among the different techniques developed for ECG analysis, time-domain analysis, frequency-domain analysis, and wavelet transform are the predominant approaches. Many ECG R-peak detection methods utilizing transforms [25] primarily use Hilbert (HT) [26,27,28], Pan–Tompkins (PT) [29,30], and wavelet transforms [31,32,33]. Transform-based methods often require buffering of multiple samples before detection. In contrast, streaming algorithms like TEDA perform detection sample by sample. Transform-based techniques often require multiple preprocessing steps and complex signal processing operations.

The work presented in [5] introduces a P, QRS, and T-peaks detector that utilizes adaptive thresholding and a template waveform. In the initial stage, an adaptive thresholding process is employed for QRS complex detection, followed by threshold initialization. Additionally, false-positive QRS complexes are effectively removed using kurtosis coefficient computation. The method further includes the detection of Q and S points through clustering and the identification of P and T peaks using min–max techniques. Detailed explanations of the detection of Q, S, P, and T points are beyond the scope of our study. Their proposed technique for R-peak detection offers reduced computational complexity compared to conventional methods, as it relies on simple decision rules rather than heuristic or optimization approaches. However, it involves a multi-step process flow. The method involves preprocessing the ECG, employing adaptive thresholding to detect R peaks, and applying post-processing based on the kurtosis coefficient to eliminate false R peaks and enhance accuracy. To initialize the threshold, baseline estimation and RMS value calculation of the ECG from a 3-second buffer are required. This is in contrast to our proposed approach, where classification is performed sample by sample without pre-setting.

The work presented in [6] employed hierarchical clustering and discrete wavelet transform (DWT) for ECG analysis. They initially identified a template of the single ECG beat and then detected all R peaks using hierarchical clustering. Subsequently, T-wave boundaries were delineated based on template morphology. The T-wave peaks were determined using modulus maxima analysis (MMA) of the DWT coefficients. Throughout the analysis, a sliding window of 1.2 s was utilized at each step.

Our work shares similarities with this approach. We also perform preprocessing and utilize similarity-based metrics to classify the R wave. In their work, the signals are preprocessed through filtering and normalization. Next, hierarchical clustering with the linkage algorithm and Euclidean distance is applied to determine R-clusters and non-R-clusters. Once the R-wave clusters are identified, the corresponding R-wave ECG sample sequences are extracted. In addition, a post-processing step is incorporated to remove false R peaks. Although the subsequent stages of their method involve T-wave peak detection, we will not discuss the methods employed for this step in our work.

It is relevant to note that the aforementioned approach involves signal windowing and relies on prior knowledge of the signal. For instance, their proposed preprocessing step of signal normalization requires prior knowledge of the signal, which implies a pre-setting requirement. This limitation could restrict the applicability of their technique in streaming applications. In contrast, our proposed approach performs classification sample by sample, without any pre-setting requirements.

Overall, our approach aligns with certain aspects of the work presented in [6], but it distinguishes itself by enabling sample-by-sample classification without the need for pre-setting and avoiding signal windowing. These characteristics make our approach particularly suitable for streaming applications.

The study presented in [24] proposes a refined post-processing ECG delineation method that classifies each sample point in the ECG recording using 1D-UNet and determines the boundaries of the waveforms. The ECG signals are divided into segments of a single heartbeat cycle before being inputted into 1D-UNet. These segments allow the network to accurately extract the characteristics of different waveforms. A post-processing algorithm, utilizing the morphological information, eliminates the influence of misclassified data points. Tests conducted on public ECG databases demonstrate satisfactory delineation performance with sensitivities of 99.88% and 99.48%, respectively. However, the 1D-UNet, due to its 1D convolutional operations along the temporal axis, coupled with the post-processing, is computationally complex and not suitable for online real-time performance.

Although some studies have achieved slightly higher accuracy, their complex nature and computational demands limit their practical use. In comparison, our method offers a simplified and efficient R-peak detection approach suitable for streaming applications. It is important to note that the calculation of eccentricity in the TEDA algorithm involves summing the geometric distances between current and past samples, enhancing the algorithm’s ability to identify samples with high eccentricity and low typicality as R peaks. This methodology efficiently separates R peaks from noise and other components of the ECG waveform without requiring the complete dataset for analysis, allowing detectors to process data directly from the input stream in real time. The adaptability and efficiency of TEDA in handling noise significantly improve the accuracy and reliability of R-peak detection, making it a robust solution for continuous ECG monitoring and analysis in various clinical contexts.

5. Comparison with the State of the Art

The article presented in [34] introduces an advanced method for detecting QRS complexes in ECG signals, aiming to improve the automatic diagnosis of cardiovascular diseases. The proposed technique is based on a sophisticated preprocessing process that includes band-pass filtering, differentiation, squaring, and integration, followed by peak detection and an adaptive threshold approach to identify QRS complexes accurately. This methodology demonstrates an ACC of $99.41\%$, Se of $99.72\%$, and P+ of $99.69\%$ on the MIT-AD. The total complexity of the algorithm can be expressed by $O\left(NM\right)$, where N is the number of ECG signal samples and M is the dimension of the applied filters. The other steps add linear complexity $O\left(N\right)$, leading to a total approximate complexity of $O\left(N\right(M+3\left)\right)$. The method involves multiple preprocessing steps, including band-pass filtering, differentiation, squaring, and integration, each contributing to the total computational load. The implementation of filters and the sequence of operations might be computationally intensive.

The article in [5] is outlined in two main stages: initially, an FIR filter in the 5–20 Hz band is used for preprocessing, followed by a cubing operation to enhance the R peaks and adaptive thresholding for effective QRS complex detection. Subsequently, a clustering process is employed to generate a template waveform of the ECG segment between the S and Q wave points, followed by a conditional thresholding method based on the morphology of the template to detect P and T peaks. This approach demonstrates precision in detection, as validated on standard databases such as MIT-AD. Applied to the MIT-AD, the final results were an Se of $99.81\%$, +P of $99.85\%$, and an ACC of $99.66\%$. The size of the analysis windows mainly influences the complexity of the technique, the order of the FIR filter, and the total number of samples processed, with $O\left(N\right)$ being linear relative to the number of samples for operations such as filtering, normalization, and thresholding. However, despite the technique exhibiting linear complexity $O\left(N\right)$, it requires multiple processing steps, including FIR filtering, cubing, adaptive thresholding, and clustering processes for template waveform generation. The complexity of clustering processes can range significantly based on the algorithm chosen: from $O(NlogN)$ for optimized DBSCAN, up to $O\left(N^2\right)$ or even $O\left(N^3\right)$ for hierarchical clustering or spectral clustering, respectively. Hence, the computational burden of the clustering step could substantially impact the method’s feasibility on devices with limited processing and storage capacities, particularly without optimizations.

The article presented in [6] introduces a methodology for automatically detecting R and T peaks in ECG signals, combining hierarchical clustering techniques and discrete wavelet transform (DWT). The process begins with the ECG signal being filtered using a fourth-order Butterworth filter to eliminate noise, followed by the normalization of the data. The detection of R peaks is performed through hierarchical clustering, which analyzes the similarity between samples based on Euclidean distance. In contrast, T peaks are identified by analyzing the modulus maxima of the DWT coefficients. This method achieved impressive results on the MIT-AD: an Se of $99.89\%$, a +P of $99.97\%$, and an ACC of $99.83\%$. The complexity of hierarchical clustering varies with the specific approach used but is generally considered high compared to other clustering methods. Agglomerative hierarchical clustering, one of the most common methods, has a typical computational complexity of $O\left(N^3\right)$ in the general case. This is due to repeatedly calculating distances between all pairs of clusters, and then, combining the two closest clusters at each step.

The work presented in [35] proposes an advanced approach for detecting the QRS complex in ECG signals. The method begins with preprocessing the ECG signal, including band-pass filtering to remove noise, differentiation to highlight rapid changes indicative of the QRS complex, and application of the Hilbert transform to form the signal envelope. The crucial step is the application of a modified adaptive threshold, using two thresholds (upper and lower) that are dynamically adjusted based on the statistical analysis of the signal within each analysis window. This process allows for accurate detection of the QRS complex, adapting to the variable characteristics of the ECG signal. The efficacy of the method was validated on 48 recordings from the MIT-AD, achieving an Se of $99.62$%, a +P of $99.88\%$, and an ACC of $99.51\%$ for QRS complex detection, highlighting the precision and adaptability of the proposed approach for detecting QRS complexes under different signal conditions. The complexity of this method can be estimated by considering the primary operations described in the article, where filtering with a sixth-order Butterworth filter and differentiation have essentially linear complexities concerning the number of samples N, implying an $O\left(N\right)$ complexity for these stages. However, the application of the Hilbert transform raises the overall complexity of the method to $O(NlogN)$ due to the use of FFT and IFFT. The modified adaptive threshold step, though based on statistical analysis and dynamic adjustments of thresholds, likely maintains a linear complexity $O\left(N\right)$, given the nature of its processing.

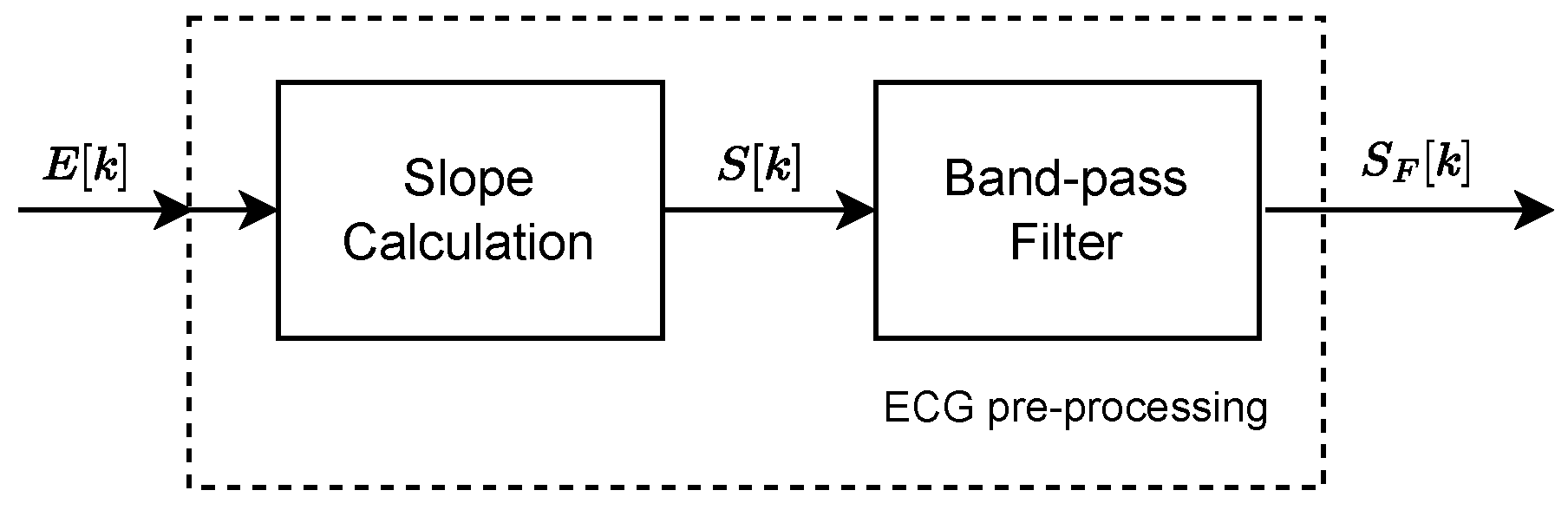
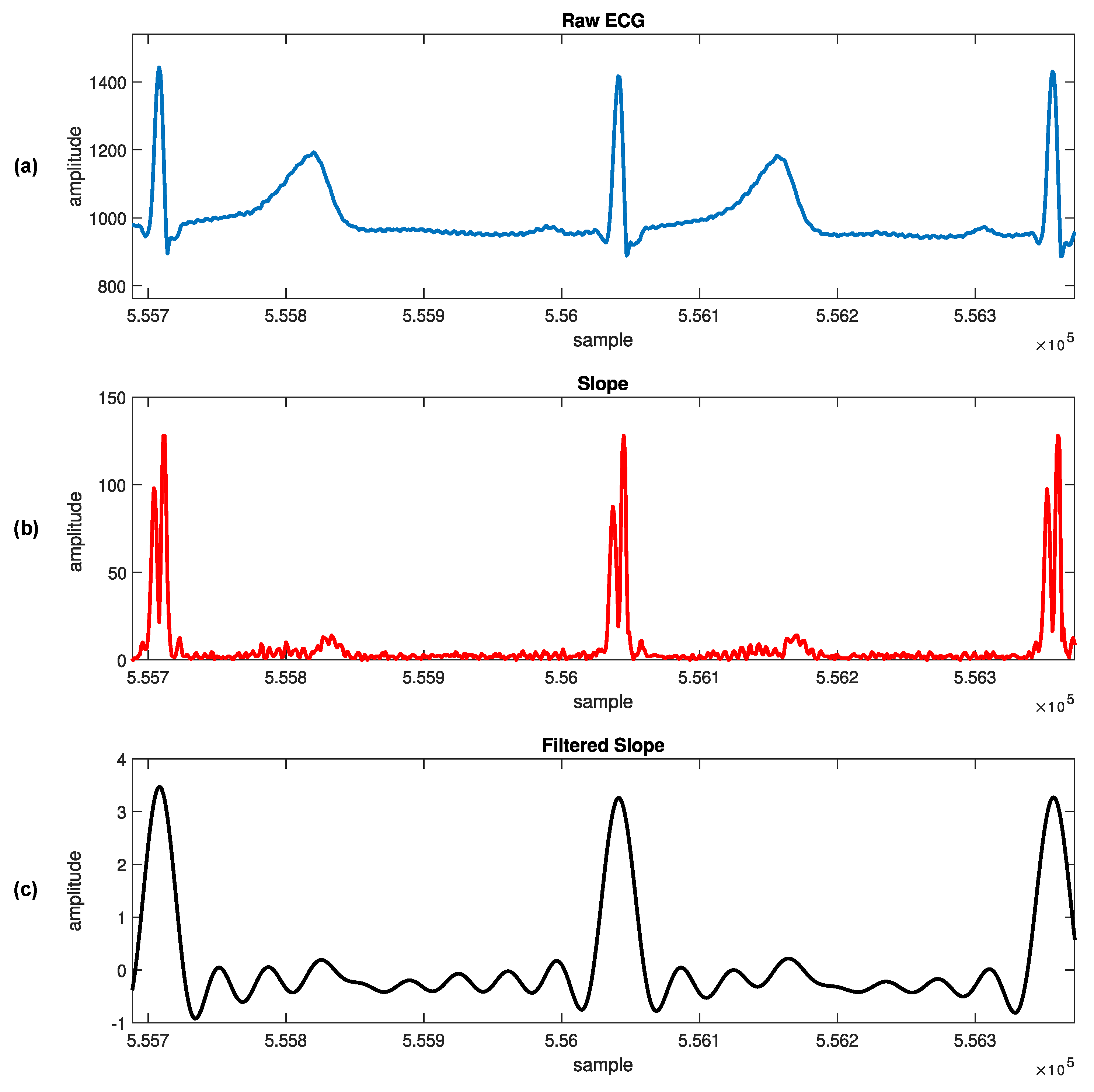
The method proposed in this work includes preprocessing with slope calculation and FIR filtering, followed by the TEDA algorithm and the estimation of the R peak. The computational complexity presents essential nuances. The preprocessing step with the FIR filter has a complexity of $O\left(NM\right)$, where N is the number of signal samples and M is the order of the filter, indicating an operation that scales linearly with the size of the signal but also depends on the chosen filter order. The slope calculation and the TEDA algorithm, which analyzes each sample individually, contribute an additional linear complexity $O\left(N\right)$. Finally, determining the R peak among the samples selected by TEDA maintains linear complexity $O\left(M\right)$, where M is the number of R-peak candidates. Therefore, the total complexity of the method is predominantly influenced by the FIR filtering stage and can be characterized as $O\left(NM\right)$, assuming that M is not significantly large relative to N.

Table 3. Comparison of R-peak detection techniques.

Reference	Se	P+	ACC	Estimated Complexity
[34]	$99.72\%$	$99.69\%$	$99.41\%$	$O\left(N\right(M+3\left)\right)$
[5]	$99.81\%$	$99.85\%$	$99.66\%$	$O(NlogN)$, $O\left(N^2\right)$ or $O\left(N^3\right)$
[6]	$99.89\%$	$99.97\%$	$99.83\%$	$O\left(N^3\right)$
[35]	$99.62$%	$99.88\%$	$99.51\%$	$O(NlogN)$
Our work	$95.45$%	$99.61\%$	$97.48\%$	$O\left(NM\right)$

summarizes the comparison between the techniques presented here.

The comparison between different R-peak detection techniques in ECG signals reveals that, although the Se and ACC of our proposal are slightly lower than those of other methods, the P+ is significantly higher. This factor is crucial in clinical practice because it indicates a low rate of false positives, ensuring that almost all detected R peaks are accurate. This characteristic is precious in continuous monitoring applications, where reliability in identifying actual cardiac events is a priority. Even though slightly lower sensitivity and accuracy might suggest a more conservative detection of R peaks, the high predictive positivity ensures the clinical relevance of the detections, minimizing interruptions or false alarms in monitoring systems.

Our proposal also stands out for its reduced computational complexity, estimated at $O\left(NM\right)$, making it particularly attractive for implementation in embedded systems and wearable devices. In contexts where the conservation of computational and energy resources is essential, the algorithm’s efficiency becomes critical. The lower complexity translates into lower energy consumption and processing capacity, facilitating integration into portable cardiac monitoring devices that operate continuously and autonomously. This feature allows our technique to be implemented more viably and sustainably in terms of resources compared to more complex methods, paving the way for broader applications in mobile health and remote patient monitoring.

Finally, using the TEDA algorithm in our approach offers a distinctive advantage, allowing for adaptive and intelligent analysis of ECG signals. By focusing on the eccentricity and typicality of the samples, TEDA effectively identifies QRS complexes, even under challenging signal conditions, such as in the presence of noise or pathological variations. This adaptability ensures that our proposal is technically feasible for a wide range of applications, including wearable devices and embedded systems, and robust in different clinical contexts. Thus, by balancing efficiency, precision, and adaptability, our technique represents a promising advancement in R-peak detection, promoting more reliable and accessible cardiac monitoring.

6. Conclusions

The proposed technique was performed in three steps. In the first step, the ECG signals were preprocessed, which involved slope calculation and filtering. The second step involved the application of the TEDA algorithm, where eccentricity was recursively calculated. Finally, the R-peak estimation was determined as the point with the highest eccentricity. To evaluate the effectiveness of the technique we used the traditional MIT-AD. The results demonstrated that the technique achieved an Se, +P, and ACC of $95.45\%$, $99.61\%$, and $95.09\%$, respectively, with a TOL of 100 ms. One significant advantage of the proposed technique is its low computational complexity. Unlike complex traditional approaches that involve signal transformation, buffering, windowing, or complex mathematical functions, the proposed technique relies on an evolutive recursive algorithm. In conclusion, the proposed technique presents a novel approach to R-peak detection in ECG signals. The combination of preprocessing, the TEDA algorithm, and R-peak estimation results in a robust performance. Furthermore, the technique’s low computational complexity makes it well suited for real-time and streaming applications. Future research could explore the application of this technique to the analysis of other physiological signals or investigate potential enhancements to further improve its performance.

This research showed that the proposed technique exhibited an Se and ACC around $95\%$ on the MIT-AD, with specific experiments demonstrating values below $99\%$ for these metrics. This observation is not exclusive to this study; as noted in the literature, other works also report variable performances, with individual experiments showing an Se and ACC below the $99\%$ threshold. This highlights the inherent complexity in processing ECG signals and detecting QRS complexes, especially considering the diversity of arrhythmias and signal variations among subjects. The necessity for ongoing enhancement of the approach is recognized, and future work will involve a more detailed investigation into cases where the current technique underperformed. The focus will be on fine-tuning and adding refinement steps for specific scenarios, a prevalent strategy in existing proposals in the literature. Such endeavors aim to increase the robustness and adaptability of the method, ensuring high rates of Se and ACC generally and enhancing effectiveness in challenging conditions. This approach will contribute to further developing automatic tools for diagnosing cardiovascular diseases.

Finally, TEDA also exhibits the potential for adaptation to detecting other waves in ECG signals, such as T and P waves. Given the algorithm’s flexibility in distinguishing signal characteristics based on eccentricity and typicality, there is significant promise for exploring its application beyond R peaks in future work by adjusting its parameters to capture the nuances of these specific waves.