Defining a Digital Twin: A Data Science-Based Unification

Abstract

The concept of a digital twin (DT) has gained significant attention in academia and industry because of its perceived potential to address critical global challenges, such as climate change, healthcare, and economic crises. Originally introduced in manufacturing, many attempts have been made to present proper definitions of this concept. Unfortunately, there remains a great deal of confusion surrounding the underlying concept, with many scientists still uncertain about the distinction between a simulation, a mathematical model and a DT. The aim of this paper is to propose a formal definition of a digital twin. To achieve this goal, we utilize a data science framework that facilitates a functional representation of a DT and other components that can be combined together to form a larger entity we refer to as a digital twin system (DTS). In our framework, a DT is an open dynamical system with an updating mechanism, also referred to as complex adaptive system (CAS). Its primary function is to generate data via simulations, ideally, indistinguishable from its physical counterpart. On the other hand, a DTS provides techniques for analyzing data and decision-making based on the generated data. Interestingly, we find that a DTS shares similarities to the principles of general systems theory. This multi-faceted view of a DTS explains its versatility in adapting to a wide range of problems in various application domains such as engineering, manufacturing, urban planning, and personalized medicine.

1. Introduction

It is a rarity for a subject matter in academia to capture the attention of all academic disciplines. Nonetheless, the notion of a digital twin appears to be a singular instance of such widespread interest. This can be seen from the large number of articles published over the last few years addressing problems in a wide range of application domains including manufacturing, health, economics and climate science [1,2,3,4]. The idea of a digital twin can be loosely stated as follows: A digital twin is a digital representation of a real-world object that is essentially indistinguishable of its real-world counterpart. Here digital representation means that a digital twin is a software implementation and a real-world object could be either a system or process that has a physical representation, e.g., an engine, a biological cell or a manufactural process. For a collection of further but similar definitions see [5].

Despite the considerable interest in digital twin research, there remains a great deal of confusion surrounding this concept. This relates not only to its implementation and application but even to the meaning of the term “digital twin” itself [6,7,8]. The fact that the digital twin concept was originally introduced in manufacturing [9], but is now being used in various fields, could be a contributing factor to the confusion. As a consequence, many attempts have been made for filling this gap, however, without reaching a satisfying definition of the concept. This lack in clarity could become a major obstacle in the further deployment of the concept, especially, considering its cross-disciplinary potential to address humanity’s most complex issues such as climate change, healthcare and economic crises [3,10,11].

The main purpose of this paper is to introduce a formal definition of a digital twin (DT). In order to obtain such a definition, we assume a data science framework. This allows us to perceive the overall problem from a data-centric perspective that enables a functional definition between all key components which are integrated into a wider unit we call digital twin system (DTS). Upon examining the framework presented by data science, it becomes evident that the primary function of a DT is to generate data via simulations. On the other hand, a DTS provides techniques that enable the effective analysis of data and decision-making based on the data generated from a DT, and potentially from other sources as well. Overall, our framework is theory-driven whereas previous approaches are application- and technology-driven. This allow us to obtain an abstract and formal definition of the digital twin concept providing a standardized language that simplifies the information transfer across different fields. Additionally, our digital twin framework provides significant benefits for the overall study design by offering systematic guidance for its implementation.

This paper is organized as follows. We will start our discussion by first reviewing the origins of a digital twin and related concepts in detail. This will allow us to identify shortcomings of previous definitions of the digital twin concept. Then we will provide a comparison with physical theories and show they can become a special case thereof. Next, we introduce formal definitions for a digital twin (DT) and a digital twin system (DTS) and provide an in-depth discussion of its building components, special cases and interpretations. This is followed by a comprehensive discussion of our framework, its components and relations to the literature. Finally, we present an outlook to open problems and a summary.

2. Grant Vision of DT and Derived Application

We start our discussion by providing background information about the origins of the digital twin concept.

The book Mirror Worlds: or the Day Software Puts the Universe in a Shoebox…How It Will Happen and What It Will Mean by David Gelernter [12], published in 1991, is widely credited as the first appearance of the idea of a digital twin. Despite the fact that the book does not use the term “digital twin” but “mirror world” it provides an intriguing vision of the underlying idea and a description of a “mirror world” that can be found in similar form in recent publications [13]. For example, the prologue starts as follows [12]:

“This book describes an event that will happen someday soon: You will look into a computer screen and see reality. Some part of your world the town you live in, the company you work for, your school system, the city hospital… This Mirror World you are looking at is fed by a steady rush of new data pouring in through cables.”

It is noteworthy that Gelernter realized that a mirror world is not “ordinary” but needs to be different in some sense. This is expressed in the following quote.

“Mirror Worlds aren’t ordinary programs. They are software ensembles, glued-together out of many separate programs all chattering at once.”

From this follows that the resulting mirror world needs to be a rather complex object to perform an envisioned task and he considers an “ensemble” to plays a key role. This is further emphasized by the following quote:

“Consider Darwin’s twin processes of speciation and evolution. Ensembles evolve: ensembles develop species. Individuals don’t.”

In modern terms and with some benevolence, one can summarize the key components of a digital twin and describe it as adaptive, real-time, ensemble system. Aside from describing a mirror world, Gelernter’s book discusses also some examples for the practical application of a mirror world, including aircrafts, hospitals, cities, companies and manufacturing processes. The book finishes with a grant vision which is presented in the form of a question:

“why not capture an entire country?”

This reminds of the metaverse and shows the farsighted vision of Gelernter even beyond a digital twin. Despite this bird’s eye perspective one can see why its presentation inspired many follow-up studies and it is widely seen as grant vision for a digital twin.

It is also worth to note that David Gelernter was involved in the foundation of the company Mirror Worlds Technologies, Inc. which had the goal to translate ideas from his book into practise. The company provided a software, called Scopeware, for organizing user files as a time-based stream and for making data easily accessible across platforms. Unfortunately, the company no longer exists. Irrespective of this outcome, the provided capabilites of Scopeware, which was offered in the early 2000s, are certainly indicative of technological constraints in general and a reminder that there is always a gap between a grant vision and its practical realization. In the case of Scopeware, it is obvious that its envisioned capabilities are very modest compared to the outlined perspectives in his book [12].

Even Earlier Visions

For reasons of completeness, we would like to mention that Gelernter’s book was by no means the first outlining the idea of a digital twin. For instance, in [14] the “Digital simulation of an aerospace vehicle” was presented in 1967. An extension of this can be found in [15] published in 1970. This demonstrates that similar ideas can be found much earlier than the 1990s, although, their scope is less comprehensive and their description much more focused on particular application problems.

3. What Is a Digital Twin: A Literature Survey

If one wants to use a digital twin for an application, one needs to define it. However, as we have seen above, Gelernter did not provide a detailed definition of a digital twin (or mirror world) but rather outlined components and implications he considered key.

Michael Grieves is widely recognized as the first to describe the concept of a digital twin in more technical terms [9], although he also did not provide a formal definition. Subsequently, numerous publications have attempted to bridge this gap by providing more comprehensive explanations. In the following, we present a collection of various characterizations of the term “digital twin” one can find in the literature, arranged in chronological order.

• “The Digital Twin is an integrated multiphysics, multiscale, probabilistic simulation of an as-built vehicle or system that uses the best available physical models, sensor updates, fleet history, etc., to mirror the life of its corresponding flying twin” [16].
• “The Digital Twin is a set of virtual information constructs that fully describes a potential or actual physical manufactured product from the micro atomic level to the macro geometrical level. At its optimum, any information that could be obtained from inspecting a physical manufactured product can be obtained from its Digital Twin” [17].
• “Digital twin is an integrated multi-physics, multi-scale, probabilistic simulation of a complex product and uses the best available physical models, sensor updates, etc., to mirror the life of its corresponding twin. Meanwhile, digital twin consists of three parts: physical product, virtual product, and connected data that tie the physical and virtual product” [18].
• “A complete DT should include five dimensions: physical part, virtual part, connection, data, and service” [18]
• “The digital twin is composed of three components, which are the physical entities in the physical world, the virtual models in the virtual world, and the connected data that tie the two worlds” [19].
• “Digital twin is a virtual, dynamic model in the virtual world that is fully consistent with its corresponding physical entity in the real world and can simulate its physical counterpart’s characteristics, behavior, life, and performance in a timely fashion” [20].
• “A Digital Twin is a virtual instance of a physical system (twin) that is continually updated with the latter’s performance, maintenance, and health status data throughout the physical system’s life cycle” [21].
• “The digital twin is actually a living model of the physical asset or system, which continually adapts to operational changes based on the collected online data and information, and can forecast the future of the corresponding physical counterpart” [22].
• “A digital twin is defined as a virtual representation of a physical asset enabled through data and simulators for real-time prediction, optimization, monitoring, control- ling, and improved decision making” [23].
• “In health care, the ‘digital twin’ denotes the vision of a comprehensive, virtual tool that integrates coherently and dynamically the clinical data acquired over time for an individual using mechanistic and statistical models. This borrows but expands the concept of ‘digital twin’ used in engineering industries, where in silico representations of a physical system, such as an engine or a wind farm, are used to optimize design or control processes, with a real-time connection between the physical system and the model” [2].
• “A Digital Twin is a dynamic and self-evolving digital/virtual model or simulation of a real-life subject or object (part, machine, process, human, etc.) representing the exact state of its physical twin at any given point of time via exchanging the real-time data as well as keeping the historical data. It is not just the Digital Twin which mimics its physical twin but any changes in the Digital Twin are mimicked by the physical twin too” [6].

From these characterizations one obtains the following impressions. First, many of the different contributions given above share various aspects. For instance, the term “virtual X” where X stands for information constructs, part, models, instance, representation or tool, is used in almost all descriptions and if it is not used then it is replaced by a phrase conveying a similar meaning, e.g., “mirror the life of its corresponding flying twin” or “living model of the physical asset or system”. Other omnipresent terms one can find are “simulation” and “model”. Second, the above characterizations list components and properties considered important for realizing a digital twin. That means all contributions provide a parts list of what should constitute a digital twin corresponding to a bottom-up approach. In contrast, a top-down approach would provide a higher-level description for the functioning of a digital twin. We will return to this point in Section 5 when we present a data science perspective.

The third observation is related to the previous one. To be specific, a descriptive list is needed because a digital twin is not a monolithic unit but a structured system [24]. This point is also connected to the usage of the term “digital twin” itself. Some authors use this term to indicate the entire system including the virtual representation of a physical object, see, e.g., [18], while others reserve the term DT only for the latter. In this case different terms are used as name for the embedding system, for instance, in [25] this is called “digital twin system” (system-of-systems), in [17] “digital twin model” and in [26] “digital twin framework”. Unfortunately, often no clear distinction between a digital twin (DT) and a digital twin system (DTS) is made which leads to confusions because of an overuse of the term which does not allow a clear differentiation between different aspects. In this paper, we avoid such a confusion by reserving the term “digital twin” for the virtual representation of a physical object and indicate by “digital twin system” the entire system that includes a digital twin. In Section 5 both terms will be defined in detail.

We would like to add that another advantage one gains from distinguishing between a DT and a DTS can be seen when looking at the description by [17] given above, stating “At its optimum, any information that could be obtained from inspecting a physical manufactured product can be obtained from its Digital Twin”. This mean, ideally, the available information from a digital twin is indistinguishable from its physical counterpart. However, this means also that this information is not yet analyzed but only available in the form of data produced by the digital twin. Hence, a DT alone is merely a mechanism to generate data. For analyzing such data, additional methods need to be used which allow then a decision-making. Importantly, methods for decision-making are also needed when instead of a digital twin the actual physical object is used, e.g., by measuring data via sensors. We return to this point in Section 5 when discussion a special case of a digital twin system.

In our view, the reason why numerous characterizations of a digital twin have been published (with our list being far from exhaustive) is that none of them offers a comprehensive and formal definition. This becomes evident upon comparing these characterizations with one another. Others have also acknowledged this incompleteness and have attempted to address these shortcomings by proposing improvements. Unfortunately, the approach to defining a digital twin appears to be uniform across all attempts, and can be summarized as follows: First, a specific problem, such as one from engineering, manufacturing, or healthcare, is identified, and then analyzed by deconstructing it into its main properties. However, given the distinct nature of the initial problems, such as engineering versus manufacturing versus healthcare, which are vastly dissimilar from one another, the characterizations of these issues are correspondingly disparate. As a result, any possible commonalities are obscured by problem- and application-specific considerations, leading to significantly different characterizations of a digital twin.

For this reason, in this paper, we choose a different strategy. Specifically, we will elevate the concept of a DT by embedding it within a data science framework. As a consequence this will lead to different definitions of a DT and a DTS that are theory-driven. However, before we can start with this we need one further discussion and this is about physical theories. Interestingly later we will see that within our framework those are special cases of digital twins.

4. Comparison with Physical Theories

In the following, we will examine several properties of a digital twin (DT) in the context of physical theories. By doing so, we will demonstrate that a physical theory can be seen as a particular instance of a digital twin. As example, let’s say our physical object of interest is a falling stone and we will use this example to discuss the following properties.

4.1. Adaptive System

In general, an adaptive system is a system that has the ability to adjust or modify its behavior, structure, or parameters in response to changes in its environment or internal conditions. For this, it possesses certain mechanisms that enable the system to adapt. A physical theory can be seen as a special case thereof.

Every physical theory has parameters that cannot be derived from the theory itself. For instance, Newtonian mechanics is based on the gravitational constant and quantum mechanics requires the Planck constant. Without knowing the values of such parameters, a theory is not functional because it is incomplete. This implies that no predictions can be derived from such a theory.

As the parameters in a physical theory cannot be derived, they must be estimated from experimental data. This property makes physical theories a special type of an adaptive system where the estimation of the parameters occurres before an analysis. Assuming the parameters are constant (over time) and $t=0$ marks the beginning of an analysis, then the parameters, $\alpha$, need to be measured before $t=0$. Since the parameters are constant, the time of the measurement is irrelevant as long as it occurs before $t=0$. Formally, all such measurements give the same value of the parameters, i.e., $\alpha (t=0)=\alpha (t\le 0)$. Overall, this make a physical theory a special case of an adaptive system because it requires the adaptation of its parameters via a measurement.

4.2. Real-Time System

Every entity in reality has a life time. For instance, a yeast cell “lives” for about 90 min before it divides, an average human life expectancy in the US is about 80 years, the Roman empire lasted for 500 years, and the life time of stars with a mass like the Sun is about 10 billion years. Nothing lasts forever nor can a time span be shorter than the Planck time (${10}^{-43}$ s)—which is the time it would take a photon travelling at the speed of light to cross a distance equal to one Planck length. Furthermore, the life time is not universal but problem dependent. For instance, when we are interested in studying a falling stone its real-time system starts at the moment the stone is dropped and it ends when it hits the ground. There is nothing before nor is there anything after. Furthermore, time intervals on which noticeable changes occur are in the millisecond (ms) range rather than on the scale of the Planck time.

There is no doubt that Newtonian mechanics gives us all information we need to describe, e.g., a falling stone. Also the numerical solution via simulations (see below) with the help of modern computers is even faster than real-time events of the stone that means the actual observations take longer than the calculation of the mathematical results. Hence, in this case Newtonian mechanics can be seen as a real-time system of a falling stone because the calculations can be slowed down to the actual time of the phenomenon.

4.3. Data Stream

Physical theories that are based on differential equations are defined by the following three components.

• Evolution equations (or dynamical system)
• Parameters
• Initial conditions

Initial conditions are different from parameters in providing information about the value of variables of the system at a certain time. For the stone example, this corresponds to the position and velocity of the stone at time zero. In general, measurements about system’s variables at $t=0$ to determine the initial conditions of the model can be seen as a special case for utilizing a data stream. For the stone example this means that data at $t=0$ are used to measure the position and velocity.

While it is certainly possible to measure such variables also at other times, for physical theories, this is not necessary. Hence, the data stream is limited to one time point at $t=0$.

4.4. Simulations

Since every physical theory is a mathematical model there are two ways to solve the underlying equations. The first would be an analytical solution and the second a numerical solution. An analytical solution means that the solution of a mathematical model can be found in closed form which could be an analytical expression in the form of a function that depends on the system variables and parameters. This is the preferred and most elegant form of a solution. However, if an analytical solution cannot be found then numerical approaches need to be used and one way is via simulations [27,28,29,30]. Hence, in general, simulations refer to a numerical approach for obtaining a solution of a mathematical model, typically, executed with the help of computers. Interestingly, it is also possible to find solutions via simulations in cases when an analytical solution is known.

4.5. Special Case of a Digital Twin: Physical Theory

Taking together, we can see that a stone is a physical object and instead of performing an experiment by dropping the stone and observing it fall one can use Newtonian mechanics to describe it. This establishes Newtonian mechanics as a special case of digital twin for a falling stone. We would like to note that this special case may be the most simple example of a digital twin.

This argument can be generalized to other basic physical objects which are by definition described by physical theories. Therefore, in general, a physical theory can be seen as a special case of digital twin where the central focus is the physical object itself. This statement will become fully transparent in the next section when we formally introduce a DT and a DTS.

5. Defining Digital Twin and Digital Twin System

Now we are in a position to introduce a definition for a digital twin (DT) and a digital twin system (DTS). Both entities are related with each other but we need to define a DT first because the DT will be an integral part of the DTS.

5.1. Digital Twin

From the preceding discussions, we can find one abstract commonality one can extract from all the different characterizations of a digital twin.

Remark 1.

Every digital twin is a mathematical model but not every mathematical model is a digital twin. This can be formally expressed as follows:

$$\begin{array}{c}\hfill DT⟹mathematical model\end{array}$$

(1)

Importantly, a mathematical model of a physical theory has the connotation of being interpretable because its components allow a connection to the real/physical-entity to be modeled. For this reason, it seem plausible to demand the same property for a general digital twin. That means any digital twin should be an interpretable mathematical model. However, we would like to highlight that this property is optional and not obligatory.

There is, however, another property of a mathematical model a digital twin must have and that is a digital twin needs to be a generative model [31,32]. Generative model means that a model has the ability to generate data on its own similar to the process the model aims to describe.

Given the preceding discussion, one finds that there is one key property a mathematical model needs to possess upon which our definition of a digital twin is based.

Definition 1 (Digital twin).

A digital twin (DT) is a mathematical model with an updating mechanism that generates data which are indistinguishable from its physical counterpart.

First, we would like to note that in the complexity science community a mathematical model with an updating mechanism is called a complex adaptive system (CAS) [33,34,35]. We will defer a detailed discussion thereof to Section 6 because this mechanism can only be understood when a DT is put into action. However, this requires a DT to be a part of the DTS. Only in this context the deeper meaning of this component will be unveiled since it addresses a dynamical property that is absent in a static configuration.

The second part of Definition 1 provides guidance on how to determine whether a mathematical model can be classified as a digital twin. For this we need a measure, e.g., a similarity measure or distance measure, to compare data from a DT with data from its physical counterpart, we call physical object (PO), because only if both are similar the mathematical model becomes a digital twin of the physical object. We call data experimentally measured from the physical object $D_{EX}$ and data measured from the mathematical model D. This can be formulated as follows.

Definition 2 (Identification of a digital twin).

Given a distance measure d, data $D_{EX}$ measured from a physical object and data D measured from a mathematical model, e.g., via simulations. If

$$\begin{array}{c}\hfill d(D_{EX},D)<\theta \end{array}$$

(2)

where $\theta \in \mathbb{R}$ is a threshold, then the mathematical model is called digital twin of the physical object and we write $D_{DT}=D$.

The selection of a distance measure depends on the application but possible choices are a Kolmogorov-Smirnov test [36] for comparing the distribution of $D_{EX}$ and D or the mean-squared error (MSE) for comparing measurements from sensors. Since the Kolmogorov-Smirnov test is a hypothesis test, the selection of a significance level will determine the corresponding threshold $\theta$ [37]. In contrast, for the mean-squared error the value of the threshold $\theta$ needs to be determined in a problem-specific manner.

In general, the identification of a digital twin does not need to be based on one feature only but can be multidimensional. For instance, for engineering problems a number of different features can be measured by sensors or for medical problems different molecular units, e.g., gene expression, methylation or protein expression can be measured. In such a case, Equation (2) is replaced by multiple equations, each one for a feature and all inequalities should hold, at least in the most stringent case.

5.2. Digital Twin System

Having defined a digital twin in the preceding section, allows us now to provide a definition for a digital twin system which includes a DT as a component. The following definition places a DTS into a data science framework.

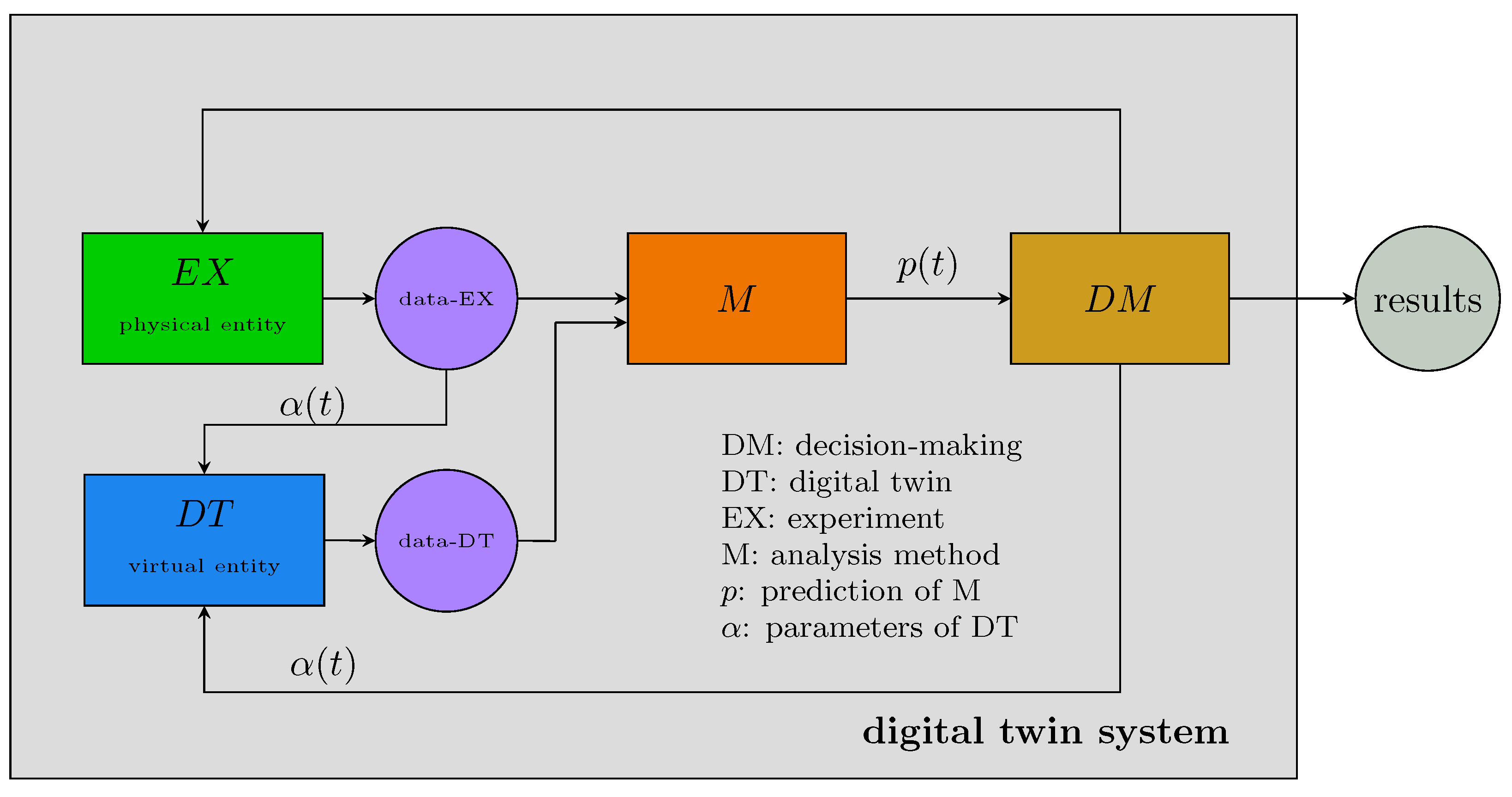
Definition 3 (Digital twin system).

A digital twin system (DTS) is a structured system that processes data from an experiment (EX) and a digital twin (DT) via analysis methods (M) and decision-making (DM). Hence, on the highest abstraction level a digital twin system (DTS) is a decision-making system. The functional interrelations among the units of a DTS are explicated in Figure 1.

As one can see, our definition of a DTS does not provide a list of properties, similar to the ones presented in Section 3, but the definition provides functional relations among the structural components of a DTS, detailed in Figure 1. In this figure, the digital twin (DT) receives input from the experiment (EX) (about the physical counterpart) and the decision making unit (DM) allowing to adjust its parameters, indicated by $\alpha \left(t\right)$. The dependency on the time, t, indicates that this can be an iterative process allowing a continuous updating to experimental data and the quality of predictions, $p\left(t\right)$, from analysis methods (M). It is also noteworthy that there is feedback from the decision-making unit (DM) to the experiment (EX) allowing full control over the entire range of possible experiments. Overall, all these interactions among the units of a DTS allow the iterative integration of data from an experiment and a digital twin for decision-making.

We would like to highlight that the DTS in Figure 1 is a minimal system that means it can be extended in many ways, e.g., by allowing multiple experiments of multiple physical objects requiring multiple digital twins, one for each physical object. Also the units M and DM can have an internal structure, i.e., they can consist of multiple analysis methods. As an example for a DTS in health having such a structure, we refer to [24].

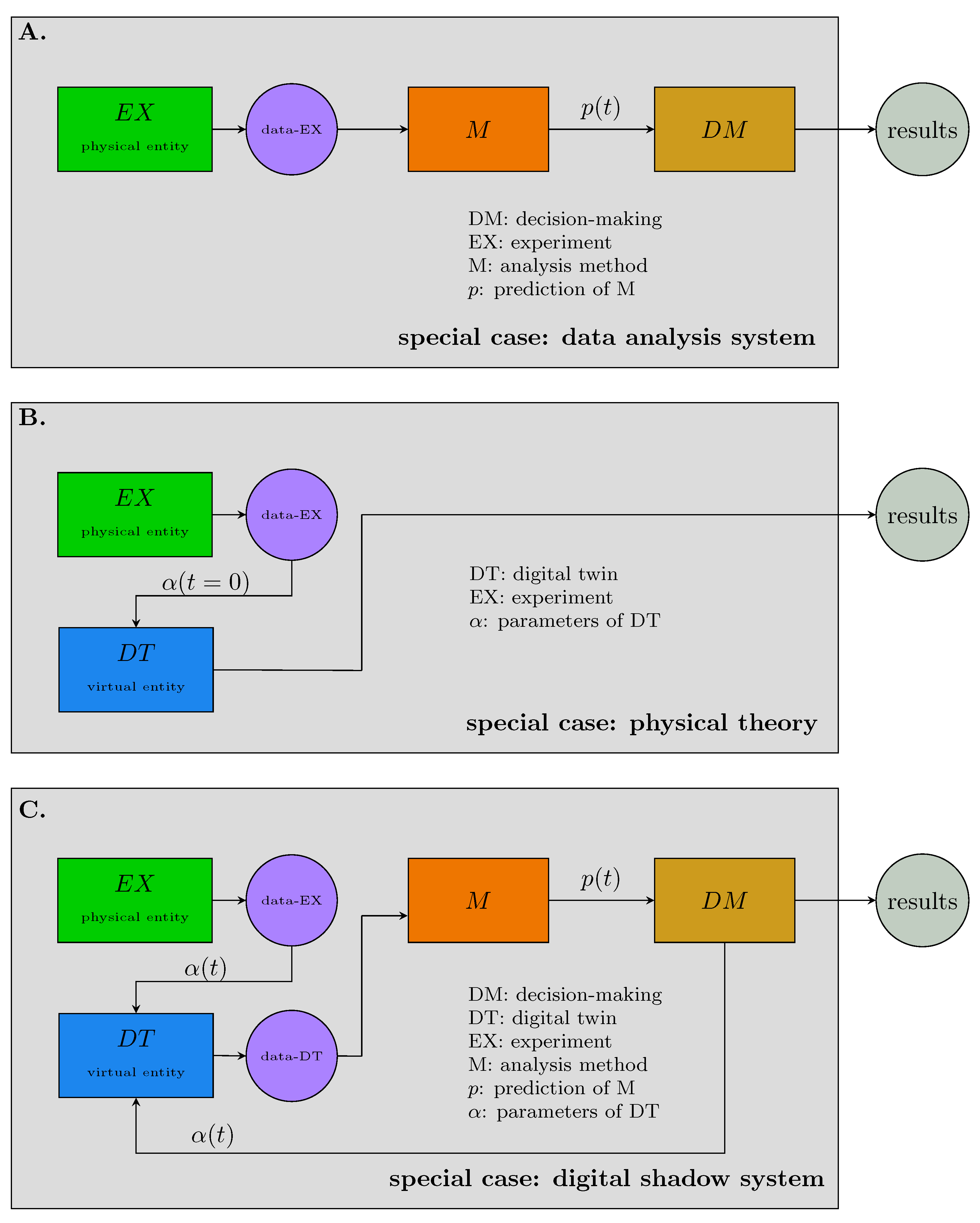
To obtain a better understanding of the DTS in Figure 1, let’s discuss a number of special cases that follow directly from the definition of a DTS. The first special case is obtained by deleting the digital twin (DT) and its connections. The resulting system, shown in Figure 2A, gives a (ordinary) data analysis system. That means irrespective of whether one studies problems in machine learning, artificial intelligence, or statistics the underling data analysis system assumes the form shown Figure 2A. This similarity between the DTS depicted in Figure 1 and the data analysis system shown in Figure 2A is the basis for calling Definition 3 data science-based, as the core of the DTS performs a (ordinary) data analysis.

Figure 2B shows the next special case of the DTS when deleting the units M and DM. In this case, the remaining system assumes the form of a physical theory; see the discussion above. This implies that the resulting data (data-DT) from the model correspond to information because of the nature of the underlying mathematical model corresponding to a physical theory. For this reason, also the unit data-DT has been deleted. We would like to highlight that there is another important change and this effects the parameters $\alpha (t=0)$ of the DT. Specifically, the parameters of physical theories are not updated but specified at the beginning (indicated by $t=0$) and remain fixed thereafter. This may seems a small change but it is the ultimate novelty of a DT and the reason why a physical theory is just a special case of a DT. We will return to this point in Section 6.

Finally, in Figure 2C, we show a system that is very similar to the DTS in Figure 1, however, with two important differences. The first difference consists in the deletion of the connection between the data from the experiment (data-EX) to the analysis method (M) and the second in deleting the feedback between decision-making (DM) and the experiment (EX). The structure and the connections of the remaining system are identical to Figure 1. The reason, why this special case deserves attention is that many of the current DTS discussed in the literature are of the form shown in Figure 2C. That means the DTS becomes a chain starting from experiment (EX) going over DT, M to DM. Examples in the literature from health and medicine that describe such a linear chain can be found in [2,38,39]. Similar examples can be found for DTS in climate science [40]. Herefor, it is quite clear that the connection between DM and EX is missing either because the time-scale which could lead to an observable effect could take centuries, or due to the fact that forecasts are made about future climate or earth states which are not accessible in the presence. For problems in engineering and manufacturing the special case shown in Figure 2C is sometimes called digital shadow [41] and examples can be found in [42,43]. Since the literature does usually not discriminate between a DT and a DTS the system in Figure 2C would be more correctly called digital shadow system (DSS) because it refers to the entire decision-making system.

6. Discussion

From our presentation in the preceding sections, it becomes clear that a DTS is a multi-component model with an intricate inner structure. Due to this complexity the most important conceptual contribution of a DT, which is part of a DTS, is often overlooked. This conceptual contribution is related to the question regarding the difference between a (mathematical) model and a DT [44]. In the following, we provide a discussion of this difference which also highlights the main contribution of a DT.

6.1. Characteristics of a DT

The traditional idea of a (mathematical) model describing a problem, e.g., in the form of a physical theory, is that the model is fully specified at the beginning (usually indicated by $t=0$) and then evolves over time providing a description of desired aspects of a problem. In case a model is given by differential equations, fully specified means its parameters, initial conditions and connectivities among the variables need to be specified. Similarly, for agent-based models, one needs to specify its parameters, initial conditions and the rules of interactions between the components of the model. In contrast to this, a DT is very different. To understand this important difference the following quote is helpful: “The virtual models update themselves based on the data from the physical world, to keep abreast of the changes” [19].

In this paper, we call such a model update an updating mechanism. Typically, this means a DT is updated at various time points based on data from the physical object (PO). In our definition of a DTS this is indicated by the time dependent parameters, $\alpha \left(t\right)$, forming the input to a DT; see Figure 1. To be clear, we would like to highlight that this is in fact not limited to the parameters of a DT but could effect any aspect including the structure of the model itself. As an extreme example, theoretically, this could even mean an agent-based model is exchanged with a mechanistic model or vice versa.

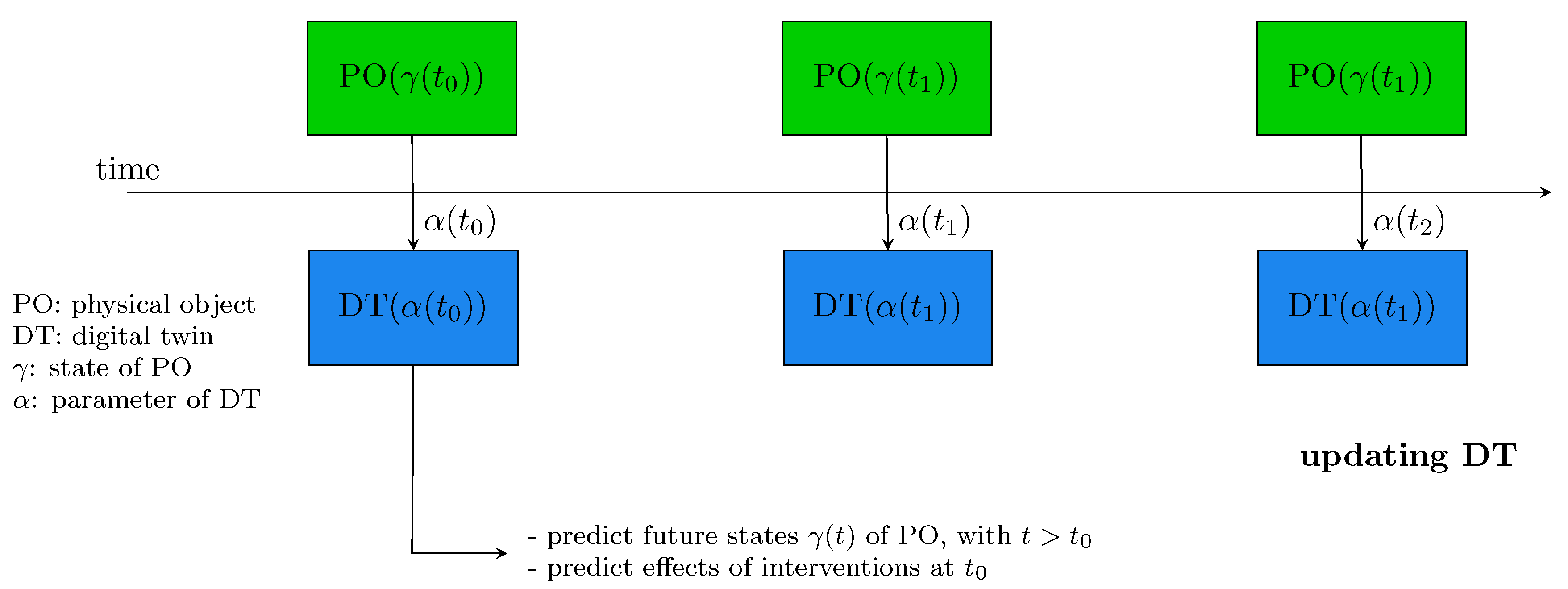
The next question is how many updates of the DT are needed? While, practically, we could be limited to a few updates since every update requires data from the physical object, which may be associated with costs, theoretically, a continuous updating could be ideal. This would establish the DT as a real-time system providing a perfect synchronization with the associated physical object (PO). In Figure 3, we show such a synchronization for three updates occurring at $t_0,t_2$ and $t_2$. At each update time point, the parameters of the DT are updated indicated by $\alpha \left(t_i\right)$ with $i\in \{1,2,3\}$. Such an update is necessary because the state of the physical object (PO), indicated by $\gamma \left(t\right)$, changes over time.

We would like to note that, theoretically, it would be most desirable to have a continuous update of a DT, however, practically, this may not be feasible. An example for such a restriction is a health DT corresponding to a patient. The problem in such a case is that the measurement could be based on a biopsy of a patient in order to achieve such a synchronization. However, for medical and ethical reasons the number of biopsies a patient can undergo is very limited because each procedure is accompanied by risk and discomfort. Hence, in such a medical context a DT cannot be continuously updated. Instead, a rather small but optimal number of update time points needs to be identified to obtained a good approximation of such a system.

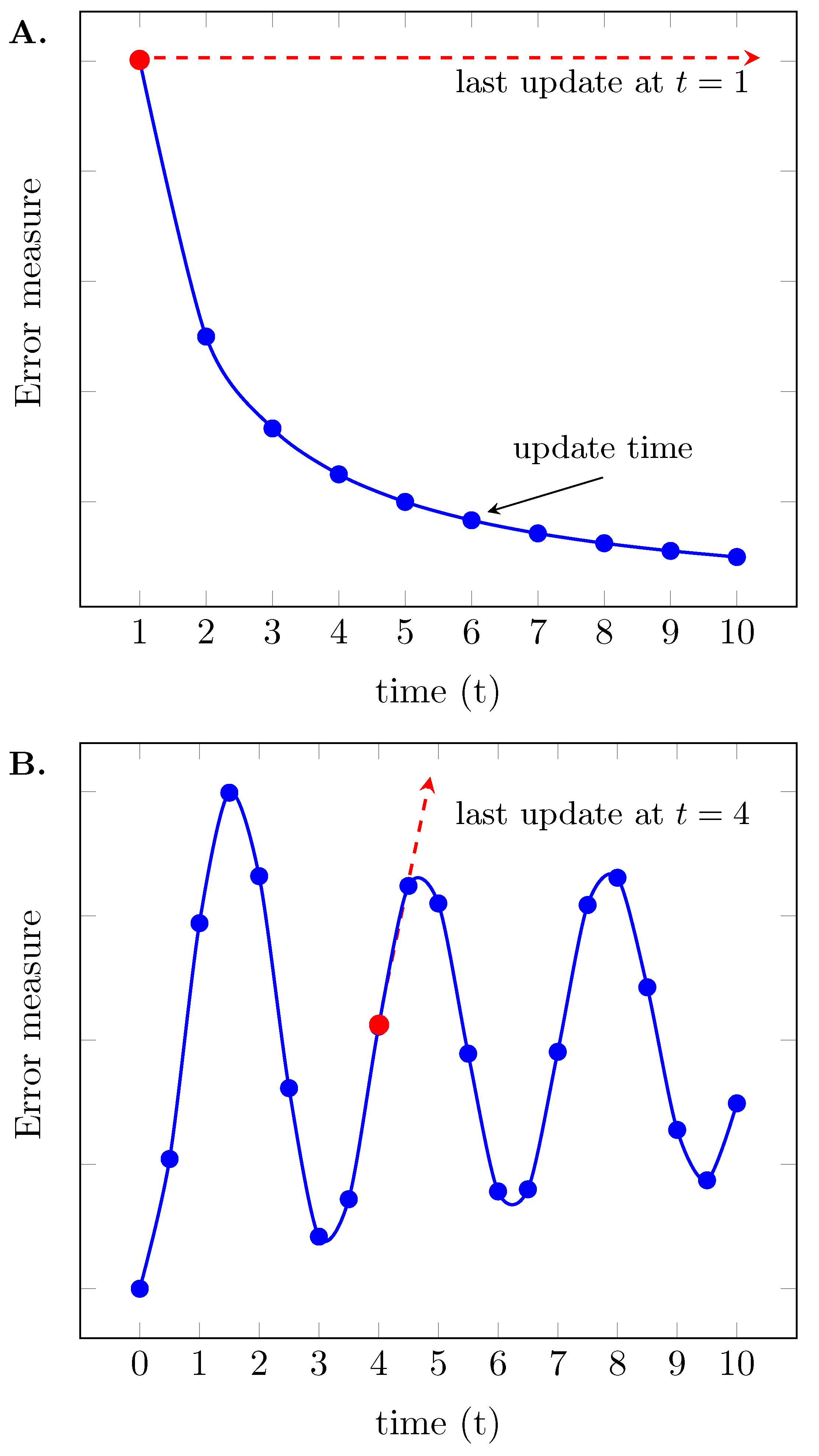
Another point to consider is the effect of an update. In general, an update can have two effects: (A) Improvement of the performance and (B) stabilization of the performance. In Figure 4, we show examples for both cases. In Figure 4A, the blue curve shows an error measure over time that quantifies the performance of a DT. The update times are highlighted by dots indicating discrete update times. Typically, after each update the performance of a DT should improve corresponding to an decreasing error until convergence is eventually reached. The horizontal dashed line in red correspond to the performance of the DT when the last update would occurs at $t=1$. Hence, this reference line corresponds to an ordinary simulation model without update.

The second possible effect of an update is visualized in Figure 4B. Here we observe an oscillatory behavior of the performance. That means updates lead to a stabilization of the behavior of the DT around a limit cycle preventing its drifting toward a worse performance. This situation is indicated by the red point. Specifically, when the updating would stop at $t=4$ the performance of the DT would deteriorate toward higher errors following the dashed line in red. Again this would corresponds to an ordinary simulation model without update. Both cases demonstrate the advantages of a DT’s updating mechanism compared to a simulation model lacking such capability.

In summary, one can say that the novel conceptual idea of a DT is not the introduction of a new (mathematical) model but to use an existing model in combination with an updating mechanism. This makes a DT a data-driven model because the updating is based on data.

6.2. Types of DT Models

When choosing a model for a DT there are different options. On the highest categorization level one can distinguish between two types of DT models.

• Physics-based models
• Data-driven models

Physics-based models, also known as mechanistic models, use fundamental laws and equations from physics to represent the behavior of the physical system being modeled [45,46]. These models are particularly useful when the physical properties and interactions of the system are well understood and can accurately predict the system’s response under different conditions. Such models can be seen as theory-driven.

In contrast, where fundamental laws are not available such models need to be approximated. Such an approximation can be provided by data-driven models that use machine learning and statistical techniques to learn from available data for making predictions and to gain insights. These models are driven by the data itself, and their effectiveness depends on the quality, quantity, and representativeness of the data used for training and testing. Data-driven models are widely used in various fields, including finance, medicine, and many other fields. Examples for data-driven models of a DT are regression models, Markov models or neural networks [47,48].

That means a DT model can be either theory-driven or data-driven, however, both models include in addition an update mechanism, as discussed above. Due to the fact that the update mechanism is always data-based this makes the theory-driven DT model a hybrid-model.

6.3. Connections to CAS and GST

When defining a digital twin in Section 5, we have seen that a DT has the form of a complex adaptive system (CAS). It is noteworthy that every complex adaptive system is an open system, which means that it has a channel for interacting with the environment. In general, an open system is characterized by its ability to exchange either matter, energy, or information with the external environment through the boundary of the system [49,50]. In our case, a DT is an open system because it has an updating mechanism allowing to exchange information. It is well-established that open systems are more powerful and flexible than closed systems, but they are also more challenging to work with. Furthermore, in contrast to closed systems, solutions for open systems can usually not be found analytically and often require simulation methods.

At a broader conceptual level, the interdisciplinary applications of a digital twin system (DTS) show resemblances to general systems theory (GST) [51,52,53]. GST is a conceptual framework that offers a holistic approach to studying systems across various domains. Its main objective is to explore the general principles and characteristics that apply universally to all types of systems, regardless of their specific components or nature. GST emphasizes the significance of interconnectedness, interactions, and emergent properties in systems. It advocates the analysis of systems as wholes, as understanding the properties and behaviors of the entire system cannot be fully achieved by analyzing individual components in isolation (i.e., in a reductionistic manner). Therefore, recognizing the relationships and interactions among the elements of a system is crucial. Moreover, a complex adaptive system (CAS) is a specific type of system that falls under the broader scope of GST [54]. This establishes a connection to our problem, where a digital twin functions as a CAS. This association between a DTS and the principles of general systems theory is not only appealing but also intuitively clear, particularly since many of the issues addressed by DTs involve open systems [55,56,57].

As a side note, we want to add that GST struggled in a similar way to digital twin research in finding a proper definition for the field [58]. This may not come as a surprise since its scope is very wide and its approach can be considered a top-down approach. In a top-down approach, the analysis or understanding of a system starts with examining the overall structure, behavior, and properties of the system as a whole, and then progresses to the examination of its individual components and their interactions. This comes usually in a more abstract form because only the individual components of a system have a practical interpretation but not its overarching theoretical structure. In the context of GST, the theory emphasizes the study of the general principles and characteristics that apply to all types of systems, regardless of their specific nature or components which takes a holistic perspective, considering the interactions, relationships, and emergent properties of the entire system.

As a consequence thereof, the theory of GST but also DTS appears quite abstract despite the fact that a practical application of both theories can assume a simple form. In our opinion, this is a major problem of previous definition attempts of a DT, as discussed in Section 3. All of these definition attempts start from the practical perspective of a DT and build upon this the overall system. Hence, such approaches follow a bottom-up approach. In contrast, both GST and DTS are formulated as a top-down approach. An implication of this is that numerical cases of a DTS do not enhance insights of such a formulation because they provide merely instances that appear similar to the many existing applications. Instead, the actual benefit is the holistic perspective offered that should translate in a more efficient and systematic design of a study.

6.4. What-If Scenarios

In order to prevent false impressions, we would like to discuss next an important implication for the operational mode of a DT. One may wonder why a continuous updating of a DT will not lead to a trivial prediction problem since in such a case the DT is perfectly synchronized to the physical object. The reason therefor is that the predictions made by a DT do not aim to forecast the current state of the physical object (PO) but to its response upon interventions. In other words, a DT should allow to investigate “what if” questions. To be specific, let’s consider three examples: (A) operation of an engine in a particular setting, (B) administration of a medication to a patient and (C) implementation of a governmental policy to regulate CO2 emission. Potential questions of interest one would like to answer are: (A) what is the failure state of the engine if operated in a specific setting (B) what is the health state of a patient if administered a medication and (C) what is the earth climate if a governmental policy is adopted? All of these questions ask about states of the physical object (failure state of engine/health of patient/climate of earth) at some time in the future about which, currently, no information is available. Furthermore, all three examples involve interventions which are changes in the state of the physical object. These two factors (prediction about the future and intervention of the system) ensure that a DTS needs to make non-trivial predictions because they require predictions of future states of the physical object which are not directly given by the current data used for the update of a DT. Hence, the DT itself, including updates, needs to be a “good” model of the physical object which is still very difficult to realize for the three examples discussed.

6.5. Differences to Previous Definitions of DT

At the beginning of this article in Section 3, we provided a literature survey of previous attempts to define a digital twin. In the following, we want to summarize the most important differences between our proposed framework and those studies.

Application-driven approach: From the literature one can see that many attempts to define a digital twin approach the problem from an application-driven perspective. This means that a problem, usually from manufacturing or engineering, is identified and then discussed by utilizing expert knowledge. Unfortunately, this makes the information transfer to other fields challenging for scientists lacking domain-specific knowledge from the underlying field of such studies. Considering the fact that digital twin research is of interdisciplinary interest [59] this is a severe issue.

Technology-driven approach: Other studies approach the problem in a technology-driven manner. This means they focus on the implementation and realization of various parts of a digital twin discussing algorithmic or technological difficulties. Frequently, this is done in combination with an application-driven discussion. One major drawback of such approaches is their tendency to be cumbersome and overloaded with non-essential details, making it difficult to grasp the core concepts of the barebone theory. In this context, it is worth reflecting on our previous discussion about physical theories in Section 4, where we observed that physical theories do not establish a direct connection to their technological implementation. Rather, they concentrate solely on providing a theoretical description of phenomena. This observation inspired our approach.

Theory-driven approach: In order to avoid the above problems, we assumed a theory-driven approach to define our digital twin framework. This helps avoiding problems from application-driven presentations defying a simple information transfer to other fields and problems from technology-driven studies providing cumbersome presentations. As a consequence, our theory-driven framework is not only more abstract and formal but also more general.

An immediate benefit of our theoretical presentation is that the roles of a DT (see Definition 1) and a DTS (see Definition 3) are clearly defined. This allows to avoid confusion because often no clear distinction between a digital twin (DT) and a digital twin system (DTS) is made which leads to an overuse of the term “digital twin” without a clear context-specific differentiation.

6.6. Application Benefits of Our Framework

In addition to the theoretical advantages discussed above, our framework offers significant benefits for practical applications. One of the most crucial advantages is its impact on study design. Rather than approaching a problem with an application-driven or technology-driven focus, our framework provides systematic guidance for a theory-driven approach.

To begin, it allow to establish clear definitions for a DT (see Definition 1) and a DTS (see Definition 3). These definitions serve as a foundation for realizing DTs and DTSs while considering the specific needs of the application and technology involved in the problem. Moreover, the functional relationships between all components, as depicted in Figure 1, facilitate seamless connections between a DT and a DTS. This systematic guidance ensures that any digital twin research can be realized effectively, simplifying also the exchange of information among researchers from diverse application domains. Overall, our framework offers a straightforward and effective approach for digital twin implementations and fosters collaboration across different research areas.

6.7. Interpretations of DT and DTS

Based on our preceding discussion, we provide in the following answers to some frequently asked questions. This provides further clarity about the meaning of a DT and a DTS.

• What is the difference between a digital twin and a digital twin system? A digital twin is a mathematical model that has measureable characteristics that are indistinguishable from its physical counterpart. Hence, a DT is just a mechanism for generating data that are practically almost identical to data generated by its physical counterpart. The DT is part of a digital twin system which outlines a decision-making framework. That means a DTS processes the data generated by a DT, converts it into information and translate the latter into decisions.
• Does the definition of a DTS as given in this paper, or any other characterization of DT from the literature, tell you how to specify a digital twin? No, it assumes you have a mathematical model for a DT that is sufficient to serve as virtual representation of a physical entity.
• Does the definition of a DTS as given in this paper provide general standards? Yes, our definition provides a flexible functional framework that allows to see a digital twin as part of a wider process for analyzing data. Here the standards are set for the connectivity of the involved components.
• Does the definition of a DTS as given in this paper provide specifications for what technologies should be used? No, this information can only be provided by addressing a particular problem. Hence, such an answer is not generic but application domain-specific. In contrast, the data science-based definition of our digital twin system is application domain-independent.
• Why do physical theories not require updates? Because mathematical models that deserve to be called “theory” provide faithful descriptions of (physical) problems. That means they are “good” even without an update mechanism. Put differently, mathematical models used for problems in engineering, manufacturing, health, medicine or climate science are much more complex than physical problems and, currently, no theories are known that would be comparable in quality to their physical theory counterparts. Hence, the need for introducing mathematical models in such areas with an updating mechanism—which we called a DT—is due to quality deficits of the current models in these areas.
• Is a DTS a jack of all trades? No, because of two reasons. First, the underlying problem is very difficult and no (single) mathematical model is known to provide a model with sufficient quality. Second, the predictions of a DTS refer to (A) future states of the physical object and (B) involve interventions of it; see Figure 3. That means a DTS aims to answer “what if” questions requiring the underlying system (corresponding to PO) to go through significant changes.

At the beginning of this article, we mentioned that the concept of a digital twin originated in manufacturing [9]. However, as we have shown in the preceding sections, it is beneficial to place a digital twin into the wider context of data science [60]. This allows the interpretation of a DTS as a general decision-making system whereas a DT is a key component thereof allowing to generate simulated data in an adaptive manner. The latter is enabled by the updating mechanism of the DT. Overall, this means we converted the application-specific idea of a DT into an application-independent form amenable for theoretical definitions. Hence, despite emerging first in applied form a DTS is a theoretical concept for analyzing data. This explains also its widespread usage across many academic fields and industries. For general applications of this concept, we suggest starting from its theoretical formulation given in Section 5, and then moving toward application-specific realizations. This will enable a common denominator and improve the communication among seemingly distinct fields.

Finally, we want to note that in our opinion it has been recognized before that an application-independent formulation of a DT is needed to reach a more comprehensive understanding. For instance, in [17] a complex systems-based approach has been presented. While a DT can certainly be seen as complex adaptive system (CAS) [33], as discussed in this paper, a CAS falls short in providing means for analyzing data and decision-making. For this reason we embedded a DT into a DTS providing such an overarching framework by data science. It is worth noting that while complex adaptive systems are primarily used for the modeling of phenomena, a CAS can also be seen as a data generator. In fact, there is no inherent difference between the two when placed in a broader context that utilizes the resulting information/data for decision-making.

In summary, a DT and a DTS are multi-faceted objects that can be viewed from various angles. In our opinion, data science provides a framework that is wide enough for accommodating any form of application while also providing a solid theoretical foundation. It is the latter aspect that was the focus of this paper.

7. Outlook

In the preceding discussion, we mentioned that updating a DT could also involve the change of the entire model structure itself. However, we did not answer the question how such a new model could be selected. As an outlook, we would like to add that this could be realized via data-driven models that learn their structure during the course of updating events. Candidates for such data-driven models could be based on deep learning. In the literature, approaches dealing with such problems are generally summarized under the term neural architecture search (NAS) [61,62].

Furthermore, we would like to remark that in the case of continuous updating of the DT, in combination with an architecture learning model, the DTS could perform online learning (OL) [63]. OL is a learning paradigm from machine learning that is characterized by learning a model in a sequential order, as opposed to batch learning which learns a model from the entire (training) data set at once or in one step which is the standard way of most machine learning paradigms [64]. Overall, this would result in the most powerful DTS one could envision that continuously improves over (possibly a long) time to provide solutions to problems currently beyond our reach. Finally, another learning paradigm that could be of relevance is meta-learning as shown by results in [65].

8. Conclusions

In this paper, we propose a definition of a digital twin concept. This concept has stirred up attention due to its anticipated potential to address some of the most urgent issues faced by humanity, including climate change, healthcare, and economic crises. Unlike many other attempts, we utilize a data science framework that facilitates a functional representation of a DT as part of a larger entity, we call a digital twin system (DTS). We show that in our framework, a DT can be interpreted as an open dynamical system with an updating mechanism, also referred to as complex adaptive system (CAS). Its primary function is the generation of data via simulations that are ideally indistinguishable from its physical counterpart. In contrast, a DTS provides techniques for analyzing data and decision-making. Interestingly, we find and discuss a connection between a DTS and the principles of general systems theory (GST), which explains its versatility in adapting to a wide range of problems in various application domains and highlights its potential.

We believe that one factor contributing to the delayed definition of the digital twin concept is the Babylonian confusion of tongues resulting from its interdisciplinary nature and origins in manufacturing. To overcome this problem, we have elevated the concept by embedding it within a data science framework. On the one hand, this approach allows for theory-driven considerations to reach a solid foundation while on the other hand, it provides enough flexibility to guide practical implementations for domain-specific problems.