Improving Spiking Neural Network Performance with Auxiliary Learning
Abstract
1. Introduction
- We utilized AL for training SNN and experimentally demonstrated that using one or more auxiliary tasks increases the performance.
- We performed an analysis of different auxiliary task learning setups and analyzed their influence on performance.
- We compared the results with state-of-the-art SNN solutions and showed that using AL improves their accuracy.
2. Related Work
2.1. Spiking Neural Networks
2.2. Auxiliary Learning
2.3. Input Data Augmentation
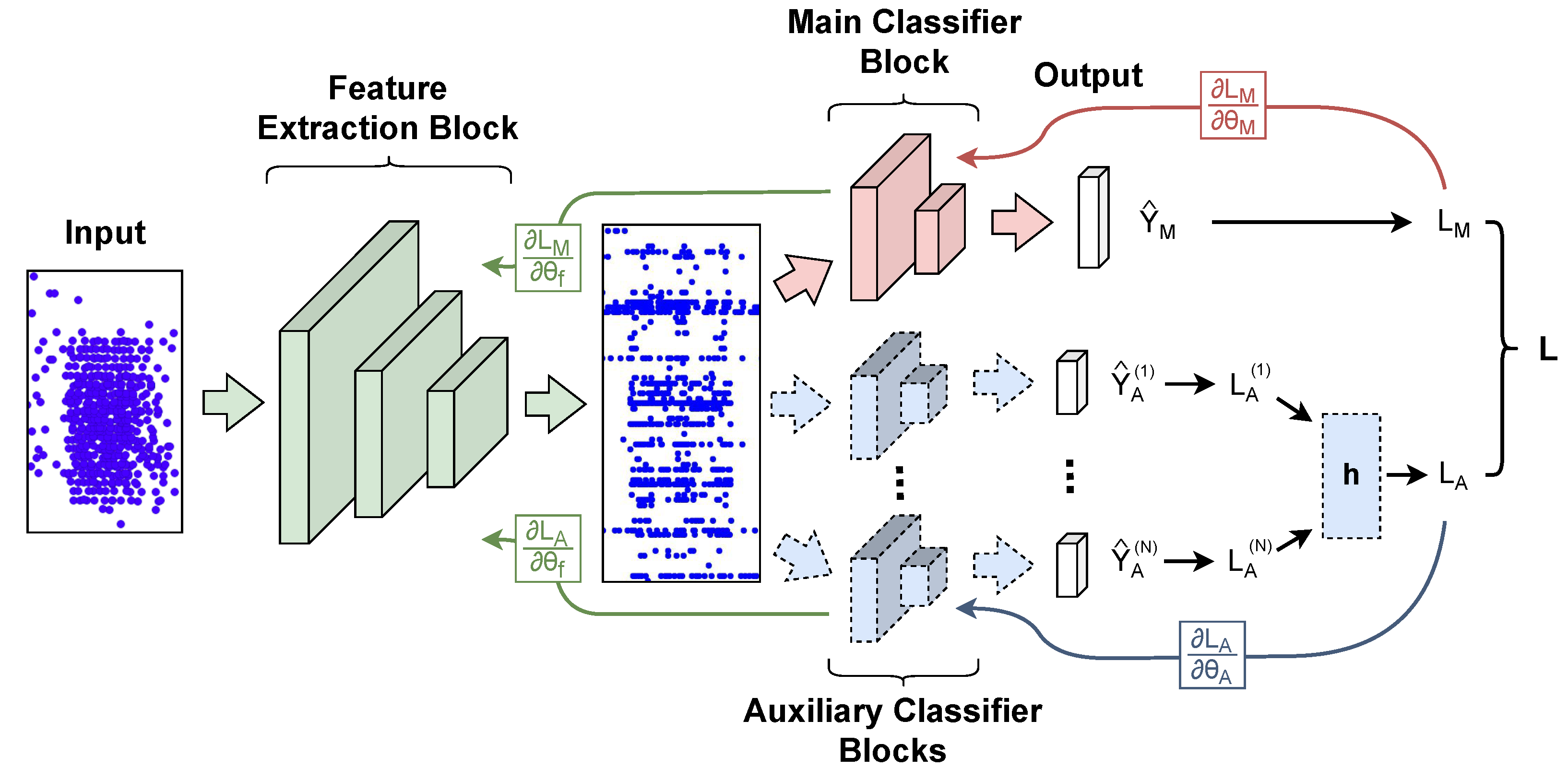
3. Methods
3.1. Problem Definition
3.2. Architecture
3.3. Training and Testing
3.4. Implementation
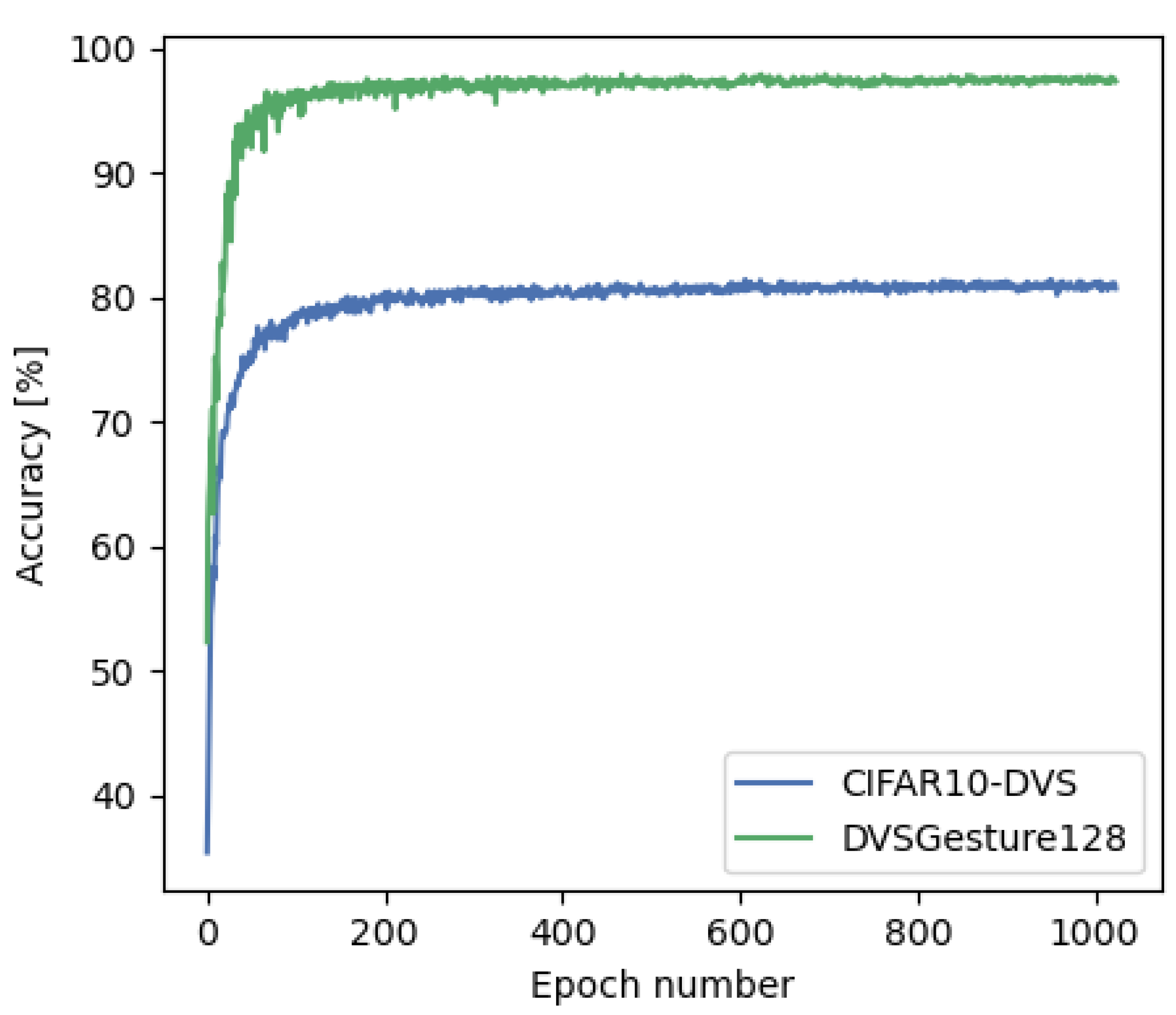
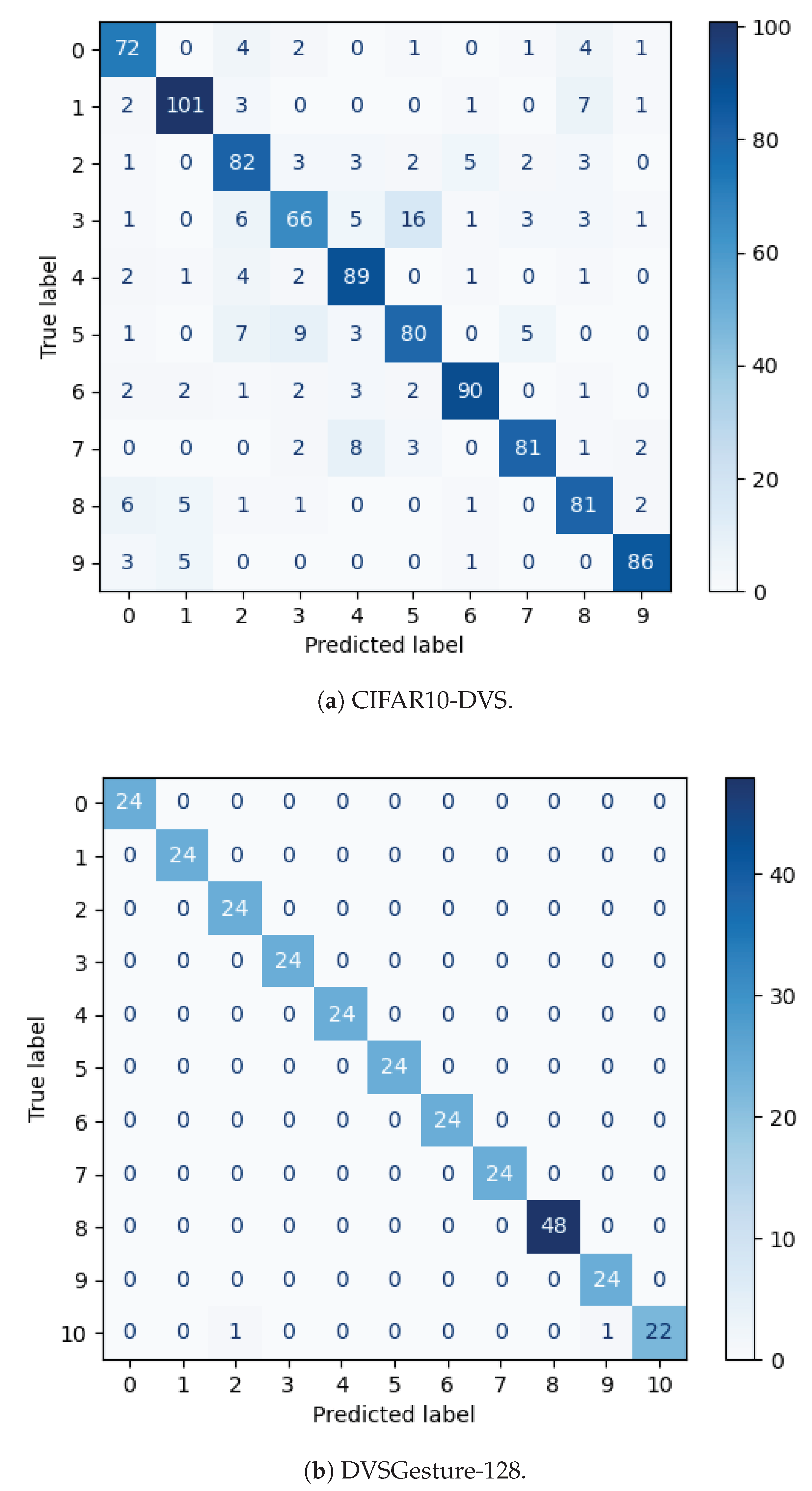
4. Experiments and Results
4.1. Training with One Auxiliary Task
4.2. Training with More Than One Auxiliary Task
4.3. Using Implicit Differentiation
4.4. Comparison with State-of-the-Art SNNs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AL | Auxiliary learning |
| ANNs | Artificial neural networks |
| BPTT | Backpropagation through time |
| LIF | Leaky integrate and fire |
| MTL | Multitask learning |
| PLIF | Parametric leaky integrate and fire |
| SBP | Spike-based backpropagation |
| SGD | Stochastic gradient descent |
| SNNs | Spiking neural networks |
| STDP | Spike-timing-dependent plasticity |
References
- Ghosh-Dastidar, S.; Adeli, H. Spiking Neural Networks. Int. J. Neural Syst. 2009, 19, 295–308. [Google Scholar] [CrossRef] [PubMed]
- Gerstner, W.; Kistler, W.M. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Maass, W. Networks of spiking neurons: The third generation of neural network models. Neural Netw. 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Emmert-Streib, F.; Yang, Z.; Feng, H.; Tripathi, S.; Dehmer, M. An Introductory Review of Deep Learning for Prediction Models with Big Data. Front. Artif. Intell. 2020, 3, 4. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Orchard, G.; Frady, E.P.; Rubin, D.B.D.; Sanborn, S.; Shrestha, S.B.; Sommer, F.T.; Davies, M. Efficient Neuromorphic Signal Processing with Loihi 2. In Proceedings of the 2021 IEEE Workshop on Signal Processing Systems (SiPS), Coimbra, Portugal, 19–21 October 2021. [Google Scholar]
- Davies, M.; Wild, A.; Orchard, G.; Sandamirskaya, Y.; Guerra, G.A.F.; Joshi, P.; Plank, P.; Risbud, S.R. Advancing Neuromorphic Computing with Loihi: A Survey of Results and Outlook. Proc. IEEE 2021, 109, 911–934. [Google Scholar] [CrossRef]
- Mohammadi, M.; Chandarana, P.; Seekings, J.; Hendrix, S.; Zand, R. Static hand gesture recognition for American sign language using neuromorphic hardware. Neuromorphic Comput. Eng. 2022, 2, 044005. [Google Scholar] [CrossRef]
- Ceolini, E.; Frenkel, C.; Shrestha, S.B.; Taverni, G.; Khacef, L.; Payvand, M.; Donati, E. Hand-Gesture Recognition Based on EMG and Event-Based Camera Sensor Fusion: A Benchmark in Neuromorphic Computing. Front. Neurosci. 2020, 14, 637. [Google Scholar] [CrossRef]
- Buettner, K.; George, A.D. Heartbeat Classification with Spiking Neural Networks on the Loihi Neuromorphic Processor. In Proceedings of the 2021 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Tampa, FL, USA, 7–9 July 2021; pp. 138–143. [Google Scholar] [CrossRef]
- Hajizada, E.; Berggold, P.; Iacono, M.; Glover, A.; Sandamirskaya, Y. Interactive Continual Learning for Robots: A Neuromorphic Approach. In Proceedings of the International Conference on Neuromorphic Systems, Knoxville, TN, USA, 27–29 July 2022; Association for Computing Machinery: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Smith, J.D.; Severa, W.; Hill, A.J.; Reeder, L.; Franke, B.; Lehoucq, R.B.; Parekh, O.D.; Aimone, J.B. Solving a Steady-State PDE Using Spiking Networks and Neuromorphic Hardware. In Proceedings of the International Conference on Neuromorphic Systems, Oak Ridge, TN, USA, 28–30 July 2020; Association for Computing Machinery: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Li, Y.; Kim, Y.; Park, H.; Geller, T.; Panda, P. Neuromorphic Data Augmentation for Training Spiking Neural Networks. In Proceedings of the Computer Vision—ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer Nature: Cham, Switzerland, 2022; pp. 631–649. [Google Scholar]
- Yin, B.; Corradi, F.; Bohté, S.M. Effective and Efficient Computation with Multiple-timescale Spiking Recurrent Neural Networks. In Proceedings of the International Conference on Neuromorphic Systems, Oak Ridge, TN, USA, 28–30 July 2020. [Google Scholar] [CrossRef]
- Kugele, A.; Pfeil, T.; Pfeiffer, M.; Chicca, E. Efficient Processing of Spatio-Temporal Data Streams With Spiking Neural Networks. Front. Neurosci. 2020, 14, 439. [Google Scholar] [CrossRef]
- Khalifa, N.E.; Loey, M.; Mirjalili, S. A comprehensive survey of recent trends in deep learning for digital images augmentation. Artif. Intell. Rev. 2022, 55, 2351–2377. [Google Scholar] [CrossRef] [PubMed]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Shi, B.; Hoffman, J.; Saenko, K.; Darrell, T.; Xu, H. Auxiliary Task Reweighting for Minimum-data Learning. Adv. Neural Inf. Process. Syst. 2020, 33, 7148–7160. [Google Scholar] [CrossRef]
- Liu, S.; Davison, A.; Johns, E. Self-Supervised Generalisation with Meta Auxiliary Learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2019; Volume 32. [Google Scholar]
- Du, Y.; Czarnecki, W.M.; Jayakumar, S.M.; Farajtabar, M.; Pascanu, R.; Lakshminarayanan, B. Adapting Auxiliary Losses Using Gradient Similarity. arXiv 2018, arXiv:1812.02224. [Google Scholar] [CrossRef]
- Fang, W.; Yu, Z.; Chen, Y.; Masquelier, T.; Huang, T.; Tian, Y. Incorporating Learnable Membrane Time Constant to Enhance Learning of Spiking Neural Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seattle, WA, USA, 13–19 June 2020. [Google Scholar] [CrossRef]
- Schröder, F.; Biemann, C. Estimating the influence of auxiliary tasks for multi-task learning of sequence tagging tasks. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Virtual Event, 5–10 July 2020; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 2971–2985. [Google Scholar] [CrossRef]
- Eshraghian, J.K.; Ward, M.; Neftci, E.; Wang, X.; Lenz, G.; Dwivedi, G.; Bennamoun, M.; Jeong, D.S.; Lu, W.D. Training Spiking Neural Networks Using Lessons From Deep Learning. arXiv 2021, arXiv:2109.12894. [Google Scholar] [CrossRef]
- Tavanaei, A.; Ghodrati, M.; Kheradpisheh, S.R.; Masquelier, T.; Maida, A. Deep learning in spiking neural networks. Neural Netw. 2019, 111, 47–63. [Google Scholar] [CrossRef]
- Wu, Y.; Deng, L.; Li, G.; Zhu, J.; Xie, Y.; Shi, L. Direct Training for Spiking Neural Networks: Faster, Larger, Better. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, Honolulu, HW, USA, 27 January–1 February 2019; AAAI Press: Washington, DC, USA, 2019. [Google Scholar] [CrossRef]
- Lee, J.H.; Delbruck, T.; Pfeiffer, M. Training Deep Spiking Neural Networks Using Backpropagation. Front. Neurosci. 2016, 10, 508. [Google Scholar] [CrossRef] [PubMed]
- Gerstner, W.; Kistler, W.M. Mathematical formulations of Hebbian learning. Biol. Cybern. 2002, 87, 404–415. [Google Scholar] [CrossRef] [PubMed]
- Hebb, D.O. The Organization of Behavior: A Neuropsychological Theory; Wiley: Hoboken, NJ, USA, 1949. [Google Scholar]
- Konorski, J. Conditioned Reflexes and Neuron Organization; Cambridge University Press: Cambridge, UK, 1948. [Google Scholar]
- Frémaux, N.; Sprekeler, H.; Gerstner, W. Functional requirements for reward-modulated spike-timing-dependent plasticity. J. Neurosci. 2010, 30, 13326–13337. [Google Scholar] [CrossRef]
- Legenstein, R.; Pecevski, D.; Maass, W. A Learning Theory for Reward-Modulated Spike-Timing-Dependent Plasticity with Application to Biofeedback. PLoS Comput. Biol. 2008, 4, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, J.; Mostafa, H.; Neftci, E. Synaptic Plasticity Dynamics for Deep Continuous Local Learning (DECOLLE). Front. Neurosci. 2020, 14, 424. [Google Scholar] [CrossRef] [PubMed]
- Neftci, E.O.; Mostafa, H.; Zenke, F. Surrogate Gradient Learning in Spiking Neural Networks: Bringing the Power of Gradient-Based Optimization to Spiking Neural Networks. IEEE Signal Process. Mag. 2019, 36, 51–63. [Google Scholar] [CrossRef]
- Shrestha, S.B.; Orchard, G. SLAYER: Spike Layer Error Reassignment in Time. arXiv 2018, arXiv:1810.08646. [Google Scholar] [CrossRef]
- Ponulak, F.; Kasiński, A. Supervised Learning in Spiking Neural Networks with ReSuMe: Sequence Learning, Classification, and Spike Shifting. Neural Comput. 2010, 22, 467–510. [Google Scholar] [CrossRef] [PubMed]
- Nski, A.; Ponulak, F.F. Comparison of supervised learning methods for spike time coding in spiking neural networks. Int. J. Appl. Math. Comput. Sci. 2006, 16, 101–113. [Google Scholar]
- Mozer, M.C. A Focused Backpropagation Algorithm for Temporal Pattern Recognition. Complex Syst. 1989, 3, 348–381. [Google Scholar]
- Wang, Z.; Dai, Z.; Póczos, B.; Carbonell, J. Characterizing and Avoiding Negative Transfer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar] [CrossRef]
- Standley, T.; Zamir, A.R.; Chen, D.; Guibas, L.; Malik, J.; Savarese, S. Which Tasks Should Be Learned Together in Multi-task Learning? In Proceedings of the 37th International Conference on Machine Learning, Virtual Event, 12–18 July 2020; Volume 119, pp. 9120–9132. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W.M.; Naud, R.; Paninski, L. Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Kandel, E.R.; Schwartz, J.H.; Jessell, T.M.; Siegelbaum, S.; Hudspeth, A. Principles of Neural Science; McGraw-hill: New York, NY, USA, 2013; Volume 5. [Google Scholar]
- Navon, A.; Achituve, I.; Maron, H.; Chechik, G.; Fetaya, E. Auxiliary Learning by Implicit Differentiation. arXiv 2020, arXiv:2007.02693. [Google Scholar]
- Fang, W.; Chen, Y.; Ding, J.; Chen, D.; Yu, Z.; Zhou, H.; Masquelier, T.; Tian, Y. SpikingJelly. 2020. Available online: https://github.com/fangwei123456/spikingjelly (accessed on 8 July 2023).
- Li, H.; Liu, H.; Ji, X.; Li, G.; Shi, L. CIFAR10-DVS: An Event-Stream Dataset for Object Classification. Front. Neurosci. 2017, 11, 309. [Google Scholar] [CrossRef]
- Amir, A.; Taba, B.; Berg, D.; Melano, T.; McKinstry, J.; Di Nolfo, C.; Nayak, T.; Andreopoulos, A.; Garreau, G.; Mendoza, M.; et al. A Low Power, Fully Event-Based Gesture Recognition System. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 7388–7397. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar] [CrossRef]
- Zheng, H.; Wu, Y.; Deng, L.; Hu, Y.; Li, G. Going Deeper With Directly-Trained Larger Spiking Neural Networks. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Li, Y.; Guo, Y.; Zhang, S.; Deng, S.; Hai, Y.; Gu, S. Differentiable Spike: Rethinking Gradient-Descent for Training Spiking Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Virtual Event, 6–14 December 2021; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2021; Volume 34, pp. 23426–23439. [Google Scholar]
- Na, B.; Mok, J.; Park, S.; Lee, D.; Choe, H.; Yoon, S. AutoSNN: Towards Energy-Efficient Spiking Neural Networks. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022. [Google Scholar]
- Guo, Y.; Tong, X.; Chen, Y.; Zhang, L.; Liu, X.; Ma, Z.; Huang, X. RecDis-SNN: Rectifying Membrane Potential Distribution for Directly Training Spiking Neural Networks. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 326–335. [Google Scholar] [CrossRef]
- Meng, Q.; Xiao, M.; Yan, S.; Wang, Y.; Lin, Z.; Luo, Z.Q. Training High-Performance Low-Latency Spiking Neural Networks by Differentiation on Spike Representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–24 June 2023. [Google Scholar]
- Zhou, Z.; Zhu, Y.; He, C.; Wang, Y.; YAN, S.; Tian, Y.; Yuan, L. Spikformer: When Spiking Neural Network Meets Transformer. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Shen, H.; Luo, Y.; Cao, X.; Zhang, L.; Xiao, J.; Wang, T. Training Stronger Spiking Neural Networks with Biomimetic Adaptive Internal Association Neurons. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
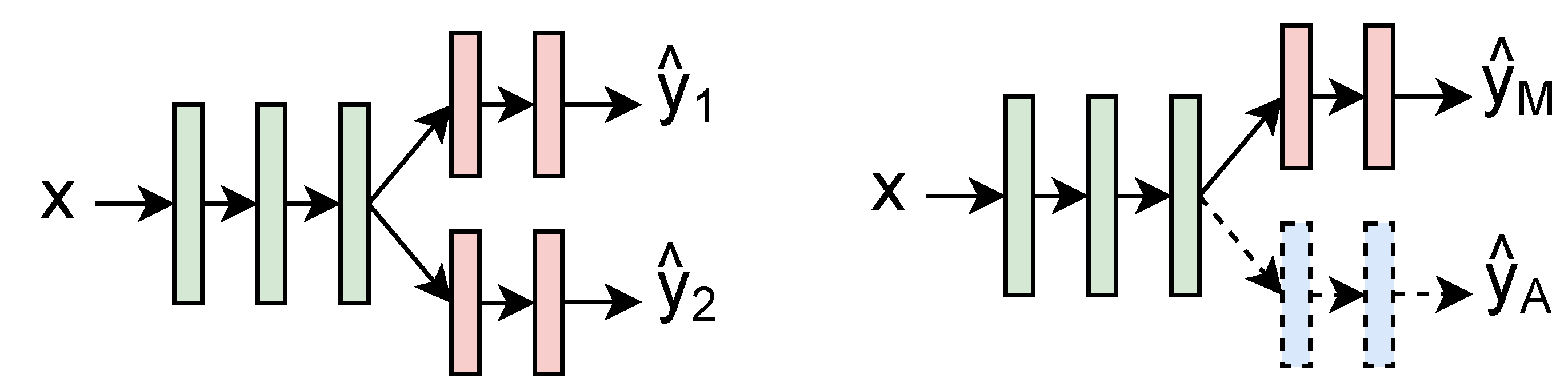
| Dataset | Number of Layers per Block | |
|---|---|---|
| Feature Extraction | Main/Auxiliary Classifier | |
| DVS-CIFAR10 | 4 | 2 |
| DVS128-Gesture | 5 | 2 |
| CIFAR10-DVS | DVS128-Gesture | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Class | M | A1 | A2 | A3 | Class | M | A1 | A2 | A3 |
| Airplane | 0 | 0 | 0 | 0 | Hand clapping | 0 | 0 | 1 | 0 |
| Automobile | 1 | 1 | 0 | 1 | Right hand wave | 1 | 1 | 3 | 1 |
| Bird | 2 | 2 | 1 | 2 | Left hand wave | 2 | 2 | 2 | 2 |
| Cat | 3 | 3 | 1 | 3 | Right arm clockwise | 3 | 3 | 3 | 1 |
| Deer | 4 | 4 | 1 | 4 | Right arm counter clock | 4 | 4 | 3 | 1 |
| Dog | 5 | 5 | 1 | 3 | Left arm clockwise | 5 | 5 | 2 | 2 |
| Frog | 6 | 6 | 1 | 5 | Left arm counter clock | 6 | 6 | 2 | 2 |
| Horse | 7 | 7 | 1 | 4 | Arm roll | 7 | 7 | 0 | 0 |
| Ship | 8 | 8 | 0 | 0 | Air drums | 8 | 8 | 0 | 0 |
| Truck | 9 | 9 | 0 | 1 | Air guitar | 9 | 9 | 4 | 3 |
| Other gestures | 10 | 10 | 5 | 4 | |||||
| Model | Validation Accuracy after 250 Epochs (%) | |||||
|---|---|---|---|---|---|---|
| CIFAR10-DVS | DVSGesture128 | |||||
| A1 | A2 | A3 | A1 | A2 | A3 | |
| ST-SNN | 72.24 ± 0.35 | 72.24 ± 0.35 | 72.24 ± 0.35 | 96.07 ± 0.27 | 96.07 ± 0.27 | 96.07 ± 0.27 |
| ST-SNN + aug | 80.83 ± 0.70 | 80.83 ± 0.70 | 80.83 ± 0.70 | 98.32 ± 0.31 | 98.32 ± 0.31 | 98.32 ± 0.31 |
| AL-SNN + aug + = 0.1 | 80.98 ± 0.38 | 81.00 ± 0.40 | 80.78 ± 0.31 | 98.50 ± 0.33 | 98.55 ± 0.37 | 98.44 ± 0.28 |
| AL-SNN + aug + = 0.2 | 81.60 ± 0.55 | 80.35 ± 0.71 | 81.02 ± 0.67 | 98.50 ± 0.26 | 98.50 ± 0.33 | 98.61 ± 0.28 |
| AL-SNN + aug + = 0.3 | 81.38 ± 0.47 | 79.45 ± 0.70 | 81.13 ± 0.58 | 98.67 ± 0.37 | 98.73 ± 0.26 | 98.61 ± 0.17 |
| AL-SNN + aug + = 0.4 | 81.00 ± 0.49 | 78.90 ± 0.39 | 81.05 ± 0.42 | 98.44 ± 0.33 | 98.61 ± 0.20 | 98.32 ± 0.13 |
| AL-SNN + aug + = 0.5 | 81.75 ± 0.33 | 78.72 ± 0.44 | 80.85 ± 0.81 | 98.67 ± 0.13 | 98.38 ± 0.16 | 98.55 ± 0.31 |
| Model | Validation Accuracy after 250 Epochs (%) | |
|---|---|---|
| CIFAR10-DVS | DVSGesture128 | |
| ST-SNN | 72.24 ± 0.35 | 96.07 ± 0.48 |
| ST-SNN + aug | 80.83 ± 0.70 | 98.32 ± 0.31 |
| AL-SNN + aug | 81.75 ± 0.33 | 98.73 ± 0.26 |
| AL-SNN-2T + aug | 80.22 ± 0.64 | 98.38 ± 0.31 |
| AL-SNN-3T + aug | 80.67 ± 0.24 | 98.67 ± 0.24 |
| AL-SNN-4T + aug | 80.77 ± 0.54 | 98.73 ± 0.33 |
| Model | Validation Accuracy after 250 Epochs (%) | |
|---|---|---|
| CIFAR10-DVS | DVSGesture128 | |
| ST-SNN | 72.24 ± 0.35 | 96.07 ± 0.48 |
| ST-SNN + aug | 80.83 ± 0.70 | 98.32 ± 0.31 |
| AL-SNN + aug | 81.75 ± 0.33 | 98.73 ± 0.26 |
| AL-SNN-IDL-4T + aug | 81.15 ± 0.27 | 98.67 ± 0.24 |
| AL-SNN-IDNL-4T + aug | 81.69 ± 0.34 | 98.84 ± 0.39 |
| Dataset | Model | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|---|
| CIFAR10-DVS | AL-SNN + aug + = 0.5 | 82.80 | 0.829 | 0.828 | 0.827 |
| DVSGesture128 | AL-SNN-IDNL-4T + aug | 99.31 | 0.993 | 0.993 | 0.993 |
| Model | Reference | CIFAR10-DVS | DVSGesture-128 |
|---|---|---|---|
| STBP [48] | AAAI 2021 | 67.80 | 96.87 |
| PLIF [22] | ICCV 2021 | 74.80 | 97.57 |
| Dspike [49] | NeurIPS 2021 | 75.40 | - |
| AutoSNN [50] | ICML 2022 | 72.50 | 96.53 |
| RecDis [51] | CVPR 2022 | 72.42 | - |
| DSR [52] | CVPR 2022 | 77.27 | - |
| NDA [14] | ECCV 2022 | 81.70 | - |
| SpikeFormer [53] | ICLR 2023 | 80.90 | 98.30 |
| AIA [54] | ICASSP 2023 | 83.90 | - |
| AL-SNN (ours) | - | 82.80 | 99.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cachi, P.G.; Ventura, S.; Cios, K.J. Improving Spiking Neural Network Performance with Auxiliary Learning. Mach. Learn. Knowl. Extr. 2023, 5, 1010-1022. https://doi.org/10.3390/make5030052
Cachi PG, Ventura S, Cios KJ. Improving Spiking Neural Network Performance with Auxiliary Learning. Machine Learning and Knowledge Extraction. 2023; 5(3):1010-1022. https://doi.org/10.3390/make5030052
Chicago/Turabian StyleCachi, Paolo G., Sebastián Ventura, and Krzysztof J. Cios. 2023. "Improving Spiking Neural Network Performance with Auxiliary Learning" Machine Learning and Knowledge Extraction 5, no. 3: 1010-1022. https://doi.org/10.3390/make5030052
APA StyleCachi, P. G., Ventura, S., & Cios, K. J. (2023). Improving Spiking Neural Network Performance with Auxiliary Learning. Machine Learning and Knowledge Extraction, 5(3), 1010-1022. https://doi.org/10.3390/make5030052








