What about the Latent Space? The Need for Latent Feature Saliency Detection in Deep Time Series Classification
Abstract
1. Introduction
- 1.
- We provide an extension of our study of prominent time series saliency methods on top of six classification methods by incorporating two additional classifiers (temporal convolutional network, input-cell attention LSTM). As a byproduct of this extension, we contribute to the discussion of “attention as explanation” by identifying the input-cell attention mechanism [6] as a suitable saliency method for time series classification. We provide evidence for the vanishing saliency problem in recurrent neural networks and compare the functionality of two solutions proposed in the literature.
- 2.
- We empirically investigate the problem of latent feature saliency using an experimental framework of simulated and real-world datasets. This framework includes an architecture for simulation studies, visual investigation of saliency maps, and quantitative validation of the methods. To simulate natural and realistic time series, we employ the popular Fourier series latent model. According to the Fourier theorem, any given signal can be expressed as the sum of Fourier sinusoidal components. Hence, this framework can also be applied to other latent models which are not covered in this paper.
- 3.
- Based on the results of the experiments, we compile a list of recommendations for more effective utilization of the investigated time series saliency methods. Furthermore, we identify effective candidate methods for tackling the problem of latent feature saliency detection.
- Problem definition: First, we discuss the distinction between shapelet- and latent space-related classification problems. We posit the argument of the ideal saliency methods for latent features and suggest a framework for extending the current methods (Section 1.1).
- Empirical evidence: To evaluate multiple state-of-the-art post hoc saliency methods, we extend the experiments in [5] on simulated time series data with patterns in both temporal and latent spaces. Through visual and quantitative evaluations, we demonstrate their lack of interpretable outputs when the informative pattern originates from the latent space rather than the temporal domain. Additionally, we run similar experiments using a real-world predictive maintenance dataset (Section 3 and Section 4).
- Recommendations for use of saliency methods: Finally, we provide a list of recommendations for utilizing common saliency methods in time series problems and identify potential candidate methods for the development of a latent feature saliency detection method (Section 5).
1.1. Problem Formulation
2. Literature Review on Post Hoc Saliency Methods
3. Materials and Methods
3.1. Classification Models and Saliency Methods
3.2. Synthetic Data Generation
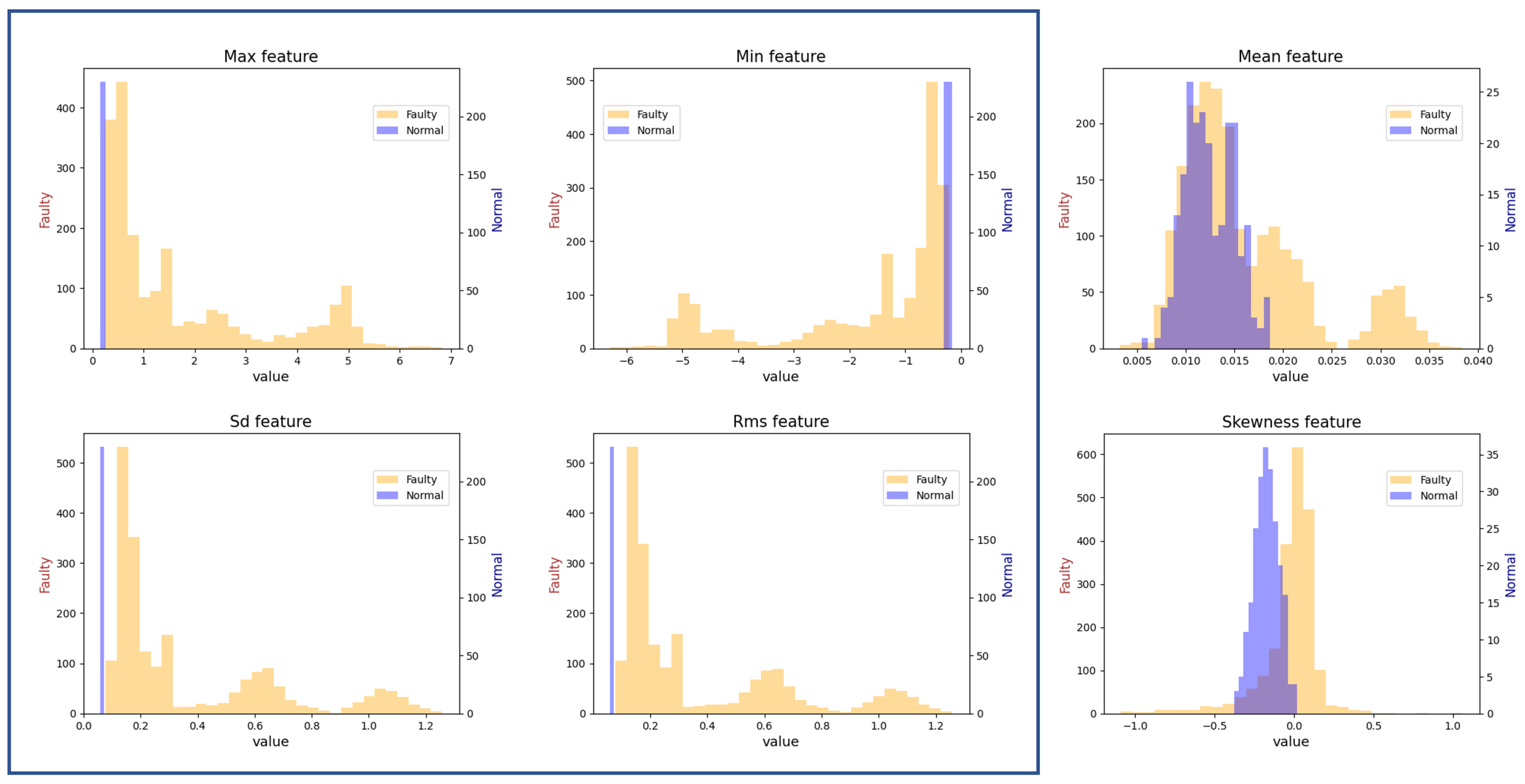
3.3. Real-World Dataset
3.4. Quantitative Evaluation
4. Results
4.1. Classification Performance
4.2. Saliency Method Evaluation in Simulation Experiments
4.3. Saliency Method Evaluation on the CWRU Dataset
5. Discussion
5.1. Classification Performance–Explainability Relation
5.2. Effectiveness of the Tested Saliency Methods
5.3. Need for Development of Methods Able to Detect Latent Feature Saliency for Time Series Classification
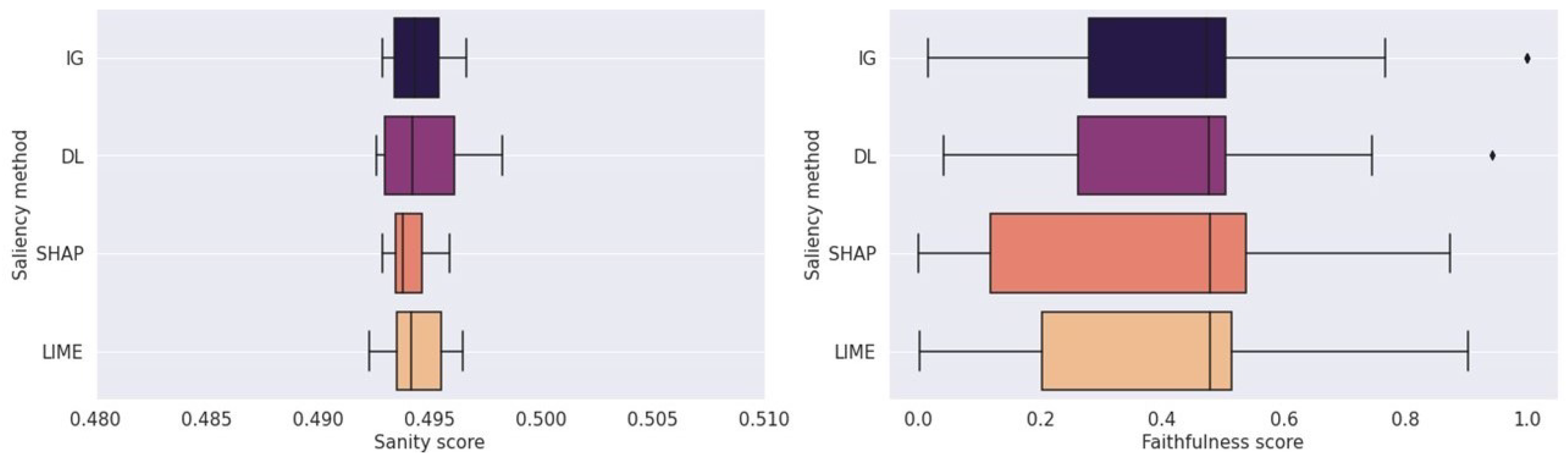
5.4. Note on Sanity and Faithfulness Evaluation
5.5. Recommendations
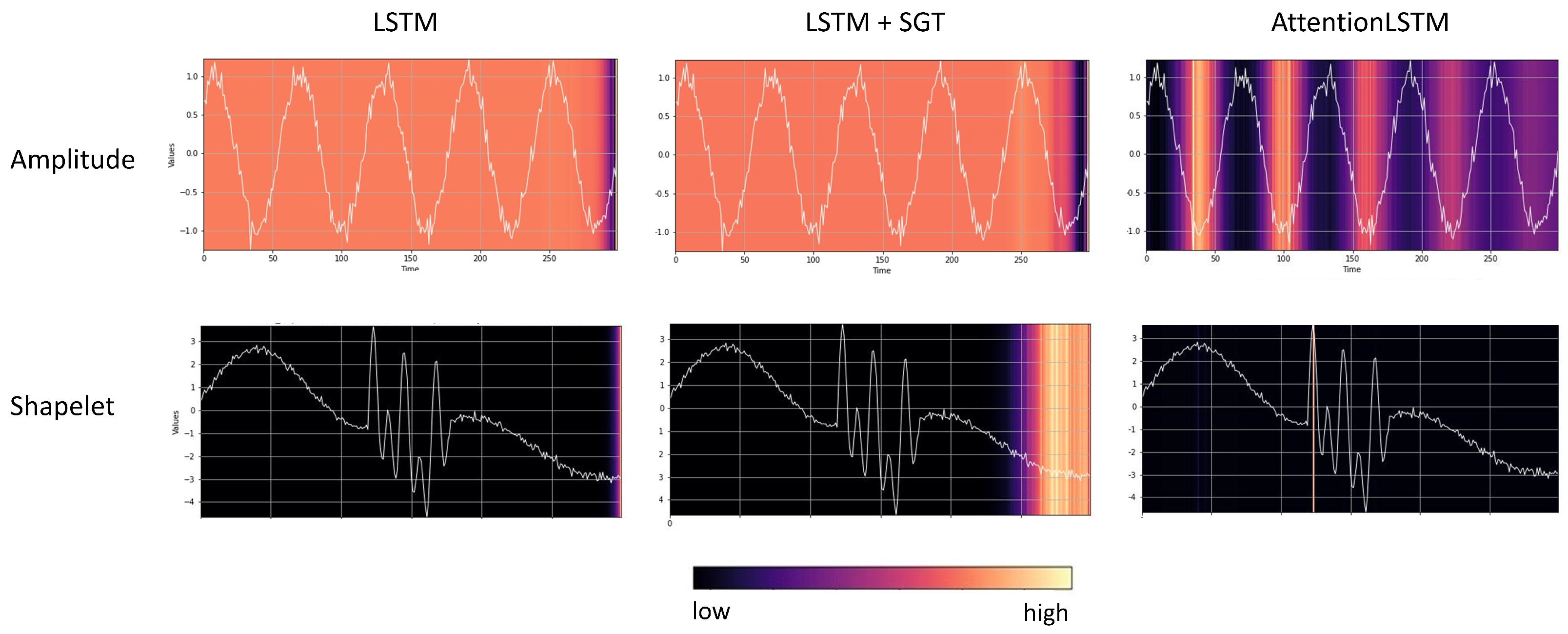
- Step 0: Vanishing saliency problem in RNNs. This work supports the findings of Bai et al. [36] and Cui et al. [45] regarding the inefficiency of LSTM models for time series classification. CNN and TCN models exhibit more reliable performance throughout the experiments. The vanishing saliency problem should be considered when employing recurrent neural networks, as Figure 5 depicts how gradient-based methods might not yield desired results.
- Step 1: Visual evaluation of multiple saliency methods. Even though some saliency methods outperformed the counterparts on average, we still observed varying scores throughout the experiments. Thus, we recommend utilizing different methods from different subcategories (e.g., gradient-based, model-agnostic) to capture different aspects of feature importance. A visual evaluation of the provided heat maps gives the first intuition on the salient domain, i.e., the time domain or latent space. If only a specific segment is highlighted as important, the methods will likely highlight the importance of a distinctive shapelet. If the heat maps are not interpretable, we recommend employing counterfactual methods.As discussed in Section 3, for a given sample, counterfactual methods identify a similar but counterclass sample to compare and thus visually depict the important and class-distinctive features of the time series. Figure 12 presents examples of Native Guide’s outputs in amplitude- and phase-shift-related experiments. As depicted, counterfactual samples (orange) correctly depict the difference in the peak for amplitude and phase shift difference. Upon visual inspection, counterfactual explanation methods might provide more insights than feature attribution methods.
- Step 2: Quantitative evaluation. For an effective evaluation of the saliency maps’ trustworthiness, we encourage using the faithfulness score. Furthermore, when evaluating the methods by sanity scores, we hypothesize that focusing on the structural similarity only will represent this property of time series more precisely than the complete structural similarity index, since the other similarity components are data-type-specific and only meaningful for image data. The proposed similarity measure then iswhere represent the standard deviations of two normalized time series X and , is the correlation coefficient, and c is a constant, added to prevent numerical difficulties.
- Step 3: Usage of ante hoc explainable methods. Suppose the saliency methods achieve low faithfulness and sanity scores and their results remain uninformative after employing multiple methods and counterfactual explanations. In that case, we recommend considering the use of ante hoc methods. In particular, we found AttentionLSTM results to be consistently reliable throughout the experiments.
- Step 4: Feature engineering. Suppose the prior knowledge about the classification problem implies a specific latent model. In that case, an alternative solution is to utilize the prior knowledge directly by a preprocessing feature extraction step based on the latent model. The resulting engineered features should be employed instead of the raw time series. This way, saliency scores for the output of the feature extraction layer can be analyzed, and thus explainability is achieved. This approach is studied and advocated in time series literature for many latent models [46,47,48,49].
5.6. Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Implementation Details
Appendix A.2. Synthetic Data Generation
- Scenario 1: Label based on the presence of a shapelet
- Scenario 2: Label based on differences in the latent features
- 1.
- Two normal distributions with different means (based on Table A1) were selected for classes 0 and 1. For positive parameters, the distributions were log-normal.
- 2.
- Per each class, Fourier parameters were sampled from the given distributions.
- 3.
- The rest of the parameters were sampled from the same distribution for both classes.
- 4.
- Sampled parameters were given to the deterministic Fourier series in Equation (A1) to generate the temporal samples. Rows were then labeled with the associated class, from the corresponding distribution of which the informative parameters were sampled.
| Exp. | Number of Sines | Freq. Low | Freq. High | Phase Low | Phase High | Dominant Amplitude | Decay Rate | Noise Ratio |
|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 0.3 | 0.1 | ||||
| 2 | 10 | 1 | 0.3 | 0.1 | ||||
| 3 | 10 | 1 | 0.3 | 0.1 | ||||
| 4 | 10 | 1 | 0.3 | 0.1 | ||||
| 5 | 10/10 | / | / | / | / | 1/1 | 0.3/0.3 | 0.1/0.1 |
| 6 | 1/1 | / | / | / | / | 1/1 | 0.3/0.3 | 0.1/0.1 |
| 7 | 1/1 | / | / | 0/ | / | 1/1 | 0.3/0.3 | 0.1/0.1 |
| 8 | 10/10 | / | / | 0/ | / | 1/1 | 0.3/0.3 | 0.1/0.1 |
| 9 | 10/10 | / | / | 0/ | / | 1/3 | 0.3/0.3 | 0.1/0.1 |
| 10 | 1/1 | / | / | / | / | 1/3 | 0.3/0.3 | 0.1/0.1 |
| Experiment | Label Feature | Description of Shapelet |
|---|---|---|
| 1 | Shapelet | Random position, |
| window length of 0.2 × sequence length | ||
| 2 | Shapelet | Fixed position, |
| last 0.2 × sequence length time steps | ||
| 3 | Shapelet | Fixed position, |
| starting at time step 0.4 × sequence length | ||
| with window length 0.2 × sequence length | ||
| 4 | Shapelet | Fixed position, |
| first 0.2 × sequence length time steps | ||
| 5 | Frequency | Overlapping frequency ranges |
| 6 | Frequency | Overlapping frequency ranges |
| 7 | Phase shift | Nonoverlapping phase shift ranges |
| 8 | Phase shift | Nonoverlapping phase shift ranges |
| 9 | Amplitude | Different dominant amplitude |
| 10 | Amplitude | Different dominant amplitude |
References
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A Survey of Methods for Explaining Black Box Models. ACM Comput. Surv. 2018, 51, 1–42. [Google Scholar] [CrossRef]
- Ismail, A.A.; Gunady, M.K.; Corrada Bravo, H.; Feizi, S. Benchmarking Deep Learning Interpretability in Time Series Predictions. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS), Online, 6–12 December 2020; pp. 6441–6452. [Google Scholar]
- Loeffler, C.; Lai, W.C.; Eskofier, B.; Zanca, D.; Schmidt, L.; Mutschler, C. Don’t Get Me Wrong: How to apply Deep Visual Interpretations to Time Series. arXiv 2022, arXiv:2203.07861. [Google Scholar] [CrossRef]
- Schlegel, U.; Oelke, D.; Keim, D.A.; El-Assady, M. An Empirical Study of Explainable AI Techniques on Deep Learning Models For Time Series Tasks. In Proceedings of the Pre-Registration Workshop NeurIPS (2020), Vancouver, BC, Canada, 11 December 2020. [Google Scholar]
- Schröder, M.; Zamanian, A.; Ahmidi, N. Post-hoc Saliency Methods Fail to Capture Latent Feature Importance in Time Series Data. In Proceedings of the ICLR 2023 Workshop on Trustworthy Machine Learning for Healthcare, Online, 4 May 2023. [Google Scholar]
- Ismail, A.A.; Gunady, M.; Pessoa, L.; Corrada Bravo, H.; Feizi, S. Input-Cell Attention Reduces Vanishing Saliency of Recurrent Neural Networks. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Ye, L.; Keogh, E. Time series shapelets: A new primitive for data mining. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD09), Paris, France, 28 June–1 July 2009; pp. 947–956. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps. arXiv 2014, arXiv:1312.6034. [Google Scholar] [CrossRef]
- Shrikumar, A.; Greenside, P.; Shcherbina, A.; Kundaje, A. Not Just a Black Box: Learning Important Features through Propagating Activation Differences. In Proceedings of the 33rd International Conference on Machine Learning (ICML’16), New York, NY, USA, 19–24 June 2016; Volume 48. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the Computer Vision (ECCV 2014), Zurich, Switzerland, 6–12 September 2014; pp. 818–833. [Google Scholar]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M.A. Striving for Simplicity: The All Convolutional Net. arXiv 2015, arXiv:1412.6806. [Google Scholar] [CrossRef]
- Smilkov, D.; Thorat, N.; Kim, B.; Kim, B.; Viégas, F.B.; Wattenberg, M. SmoothGrad: Removing noise by adding noise. arXiv 2017, arXiv:1706.03825. [Google Scholar] [CrossRef]
- Fong, R.; Patrick, M.; Vedaldi, A. Understanding Deep Networks via Extremal Perturbations and Smooth Masks. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 Ocotber–2 November 2019; pp. 2950–2958. [Google Scholar]
- Shrikumar, A.; Greenside, P.; Kundaje, A. Learning Important Features Through Propagating Activation Differences. In Proceedings of the 34th International Conference on Machine Learning (ICML’17), Sydney, Australia, 6–11 August 2017; Volume 70. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic Attribution for Deep Networks. In Proceedings of the 34th International Conference on Machine Learning (ICML’17), Sydney, Australia, 11–15 August 2017; Volume 70, pp. 3319–3328. [Google Scholar]
- Bastings, J.; Filippova, K. The elephant in the interpretability room: Why use attention as explanation when we have saliency methods? In Proceedings of the 2020 EMNLP Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP, Online, 11–12 November 2020. [Google Scholar]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.; Wojciech, S. On Pixel-Wise Explanations for Non-Linear Classifier Decisions by Layer-Wise Relevance Propagation. PLoS ONE 2015, 10, e130140. [Google Scholar] [CrossRef] [PubMed]
- Montavon, G.; Lapuschkin, S.; Binder, A.; Samek, W.; Müller, K.R. Explaining Nonlinear Classification Decisions with Deep Taylor Decomposition. Pattern Recognit. 2017, 65, 211–222. [Google Scholar] [CrossRef]
- Carrillo, A.; Cantú, L.F.; Noriega, A. Individual Explanations in Machine Learning Models: A Survey for Practitioners. arXiv 2021, arXiv:2104.04144. [Google Scholar] [CrossRef]
- Petsiuk, V.; Das, A.; Saenko, K. RISE: Randomized Input Sampling for Explanation of Black-box Models. In Proceedings of the 29th British Machine Vision Conference (BMVC), Newcastle, UK, 3–6 September 2018. [Google Scholar]
- Fong, R.C.; Vedaldi, A. Interpretable Explanations of Black Boxes by Meaningful Perturbation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 3449–3457. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?” Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 16), New York, NY, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Datta, A.; Sen, S.; Zick, Y. Algorithmic Transparency via Quantitative Input Influence: Theory and Experiments with Learning Systems. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 23–26 May 2016; pp. 598–617. [Google Scholar]
- Lipovetsky, S.; Conklin, M. Analysis of regression in game theory approach. Appl. Stoch. Model. Bus. Ind. 2001, 17, 319–330. [Google Scholar] [CrossRef]
- Štrumbelj, E.; Kononenko, I. Explaining Prediction Models and Individual Predictions with Feature Contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Shapley, L.S. A value for n-person games. In Contributions to the Theory of Games II; Princeton University Press: Princeton, NJ, USA, 1953; pp. 307–317. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Guidotti, R.; Monreale, A.; Spinnato, F.; Pedreschi, D.; Giannotti, F. Explaining Any Time Series Classifier. In Proceedings of the 2020 IEEE Second International Conference on Cognitive Machine Intelligence (CogMI), Atlanta, GA, USA, 28–31 October 2020; pp. 167–176. [Google Scholar]
- Karlsson, I.; Rebane, J.; Papapetrou, P.; Gionis, A. Locally and Globally Explainable Time Series Tweaking. Knowl. Inf. Syst. 2020, 62, 1671–1700. [Google Scholar] [CrossRef]
- Wang, Z.; Samsten, I.; Mochaourab, R.; Papapetrou, P. Learning Time Series Counterfactuals via Latent Space Representations. In Proceedings of the 24th International Conference on Discovery Science (DS 2021), Halifax, NS, Canada, 11–13 October 2021; pp. 369–384. [Google Scholar]
- Ates, E.; Aksar, B.; Leung, V.J.; Coskun, A.K. Counterfactual Explanations for Multivariate Time Series. In Proceedings of the 2021 International Conference on Applied Artificial Intelligence (ICAPAI), Halden, Norway, 19–21 May 2021; pp. 1–8. [Google Scholar]
- Delaney, E.; Greene, D.; Keane, M.T. Instance-Based Counterfactual Explanations for Time Series Classification. In Proceedings of the Case-Based Reasoning Research and Development: 29th International Conference (ICCBR 2021), Salamanca, Spain, 13–16 September 2021; pp. 32–47. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Le Cun, Y.; Jackel, L.; Boser, B.; Denker, J.; Graf, H.; Guyon, I.; Henderson, D.; Howard, R.; Hubbard, W. Handwritten digit recognition: Applications of neural network chips and automatic learning. IEEE Commun. Mag. 1989, 27, 41–46. [Google Scholar] [CrossRef]
- Ismail, A.A.; Corrada Bravo, H.; Feizi, S. Improving Deep Learning Interpretability by Saliency Guided Training. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS2021), Online, 6–14 December 2021; pp. 26726–26739. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- CWRU Bearing Dataset. Available online: https://engineering.case.edu/bearingdatacenter/download-data-file (accessed on 10 October 2022).
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Neely, M.; Schouten, S.F.; Bleeker, M.J.R.; Lucic, A. Order in the Court: Explainable AI Methods Prone to Disagreement. In Proceedings of the ICML Workshop on Theoretic Foundation, Criticism, and Application Trend of Explainable AI, Virtual Event, 23 July 2021. [Google Scholar]
- Parvatharaju, P.S.; Doddaiah, R.; Hartvigsen, T.; Rundensteiner, E.A. Learning Saliency Maps to Explain Deep Time Series Classifiers. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Virtual Event, 1–5 November 2021; pp. 1406–1415. [Google Scholar]
- Schlegel, U.; Keim, D.A. Time Series Model Attribution Visualizations as Explanations. In Proceedings of the 2021 IEEE Workshop on TRust and EXpertise in Visual Analytics (TREX), New Orleans, LA, USA, 24–25 October 2021; pp. 27–31. [Google Scholar]
- Wiegreffe, S.; Pinter, Y. Attention is not Explanation. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, 3–7 November 2019; pp. 11–20. [Google Scholar]
- Jain, S.; Wallace, B.C. Attention is not Explanation. In Proceedings of the 2019 Annual Conference of the North American Chapter of the Association for Computational Linguistics, Minneapolis, MN, USA, 2–7 June 2019. [Google Scholar]
- Lim, B.; Arik, S.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Cui, Z.; Chen, W.; Chen, Y. Multi-scale convolutional neural networks for time series classification. arXiv 2016, arXiv:1603.06995. [Google Scholar] [CrossRef]
- Bagnall, A.; Lines, J.; Hills, J.; Bostrom, A. Time-series classification with COTE: The collective of transformation-based ensembles. IEEE Trans. Knowl. Data Eng. 2015, 27, 2522–2535. [Google Scholar] [CrossRef]
- Tseng, A.; Shrikumar, A.; Kundaje, A. Fourier-transform-based attribution priors improve the interpretability and stability of deep learning models for genomics. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Online, 6–12 December 2020; pp. 1913–1923. [Google Scholar]
- Kazemi, S.M.; Goel, R.; Eghbali, S.; Ramanan, J.; Sahota, J.; Thakur, S.; Wu, S.; Smyth, C.; Poupart, P.; Brubaker, M. Time2vec: Learning a vector representation of time. arXiv 2019, arXiv:1907.05321. [Google Scholar] [CrossRef]
- Rangapuram, S.S.; Seeger, M.W.; Gasthaus, J.; Stella, L.; Wang, Y.; Januschowski, T. Deep state space models for time series forecasting. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; pp. 8024–8035. [Google Scholar]
- Falcon, W. PyTorch Lightning. Available online: https://github.com/Lightning-AI/lightning (accessed on 5 June 2022).
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25st ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’19), Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Kokhlikyan, N.; Miglani, V.; Martin, M.; Wang, E.; Alsallakh, B.; Reynolds, J.; Melnikov, A.; Kliushkina, N.; Araya, C.; Yan, S.; et al. Captum: A unified and generic model interpretability library for PyTorch. arXiv 2020, arXiv:2009.07896. [Google Scholar] [CrossRef]









| Model | Remarks |
|---|---|
| Time series classifiers | |
| LSTM | |
| LSTM + SGT | Trained via the saliency-guided training procedure |
| AttentionLSTM | Input-cell attention mechanism combined with LSTM |
| CNN | |
| CNN + SGT | Trained via the saliency-guided training procedure |
| TCN | |
| Saliency methods | |
| Integrated Gradients | Gradient-based |
| Deep-Lift | Gradient-based |
| LIME | Model-agnostic |
| Kernel SHAP | Model-agnostic |
| Input-cell attention | Ante hoc method (with LSTM classifier) |
| Experiment | Label Associated with | Remarks |
|---|---|---|
| 1–4 | Shapelet | The label depends on existence of a shapelet, appearing at the beginning, middle, or end of the time series, or a random position (4 scenarios). |
| 5, 6 | Frequency | The labels depend on the frequency of the dominant sine wave in the Fourier series. The experiments differ in the number of sines waves, thus rendered as simple or complex (2 scenarios). |
| 7, 8 | Phase shift | Similar to the experiments 5, 6, except for the deciding latent parameter which is the phase shift of the Fourier series. |
| 9, 10 | Amplitude | Similar to the experiments 5, 6, except for the deciding latent parameter which is the maximum amplitude of the Fourier series. |
| Classifier | Shapelet | Frequency | Phase Shift | Amplitude | ||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | F1 | Accuracy | F1 | Accuracy | F1 | Accuracy | F1 | |
| LSTM | 0.8535 | 0.8466 | 0.9749 | 0.9470 | 0.5157 | 0.4914 | 0.9981 | 0.9981 |
| LSTM + SGT | 0.8242 | 0.8417 | 0.9082 | 0.9117 | 0.5352 | 0.4145 | 0.9160 | 0.9230 |
| CNN | 0.6221 | 0.7439 | 0.9610 | 0.9633 | 0.9629 | 0.9625 | 0.9981 | 0.9981 |
| CNN + SGT | 0.8721 | 0.9138 | 0.9610 | 0.9633 | 0.9649 | 0.9634 | 1.0000 | 1.0000 |
| TCN | 0.7442 | 0.8275 | 0.9610 | 0.9633 | 0.9844 | 0.9842 | 0.9981 | 0.9981 |
| AttentionLSTM | 0.9307 | 0.9361 | 0.9375 | 0.9406 | 0.9507 | 0.8985 | 1.0000 | 1.0000 |
| Classifier | Accuracy | F1 | Balanced Accuracy |
|---|---|---|---|
| AttentionLSTM | 0.9816 | 0.9896 | 0.9613 |
| TCN | 0.9990 | 0.9994 | 0.9994 |
| CNN + SGT | 0.9928 | 0.9960 | 0.9798 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schröder, M.; Zamanian, A.; Ahmidi, N. What about the Latent Space? The Need for Latent Feature Saliency Detection in Deep Time Series Classification. Mach. Learn. Knowl. Extr. 2023, 5, 539-559. https://doi.org/10.3390/make5020032
Schröder M, Zamanian A, Ahmidi N. What about the Latent Space? The Need for Latent Feature Saliency Detection in Deep Time Series Classification. Machine Learning and Knowledge Extraction. 2023; 5(2):539-559. https://doi.org/10.3390/make5020032
Chicago/Turabian StyleSchröder, Maresa, Alireza Zamanian, and Narges Ahmidi. 2023. "What about the Latent Space? The Need for Latent Feature Saliency Detection in Deep Time Series Classification" Machine Learning and Knowledge Extraction 5, no. 2: 539-559. https://doi.org/10.3390/make5020032
APA StyleSchröder, M., Zamanian, A., & Ahmidi, N. (2023). What about the Latent Space? The Need for Latent Feature Saliency Detection in Deep Time Series Classification. Machine Learning and Knowledge Extraction, 5(2), 539-559. https://doi.org/10.3390/make5020032





