Biologically Inspired Self-Organizing Computational Model to Mimic Infant Learning
Abstract
1. Introduction
1.1. Infant Learning
1.2. Need for Self-Organization in Assistive Robots
1.3. SOM Models for Assistive Robots
1.4. Structure
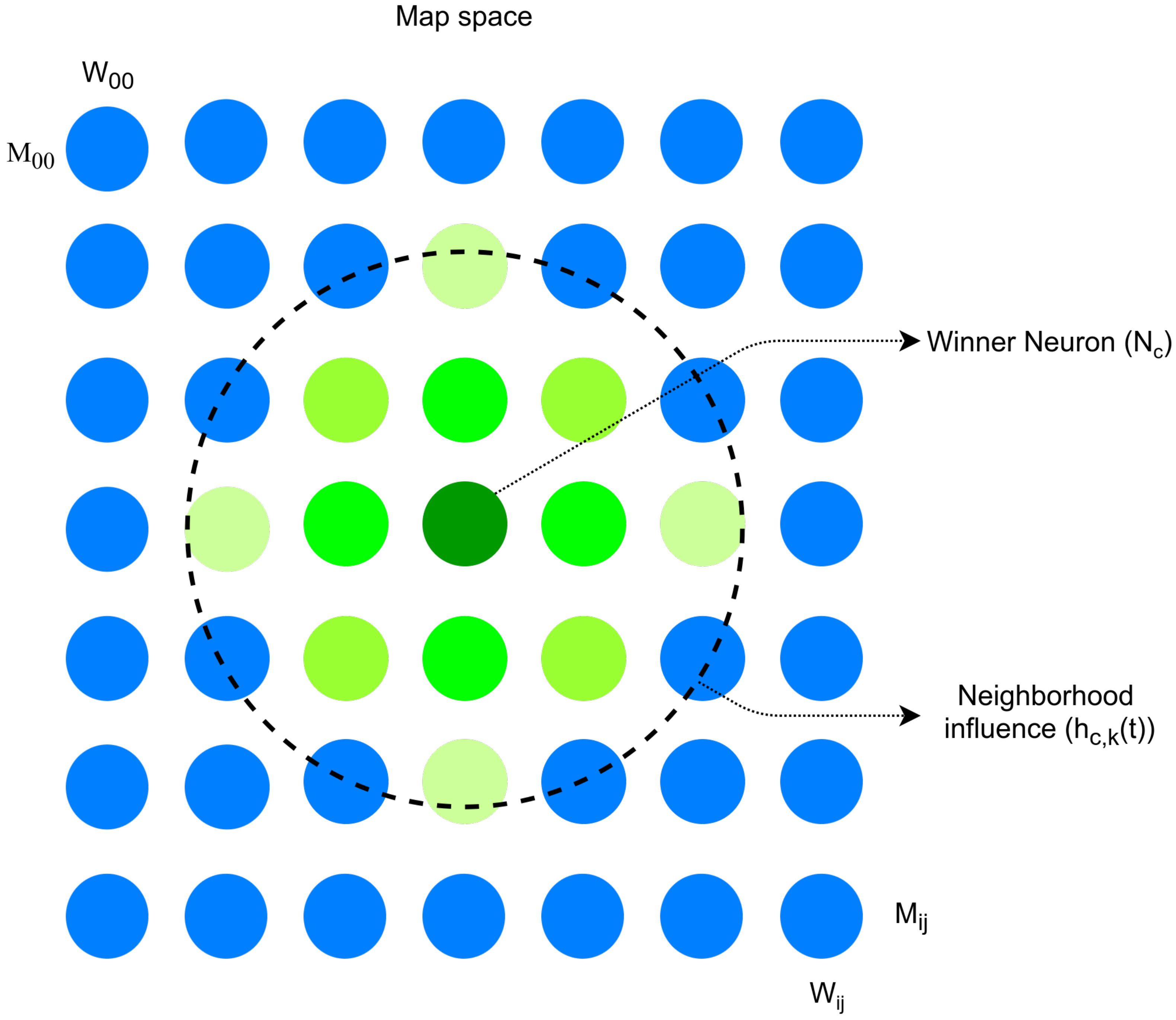
2. Self-Organizing Map
| Algorithm 1 Self-Organizing Map |
| INIT Map Size, |
| SET ∀ Weight Vectors, Random values between 0 and 1 |
| SET Learning rate, |
| SET Neighborhood radius, |
| SET Maximum iteration, |
| while do |
| random input vector |
| Winner Neuron |
| end while |
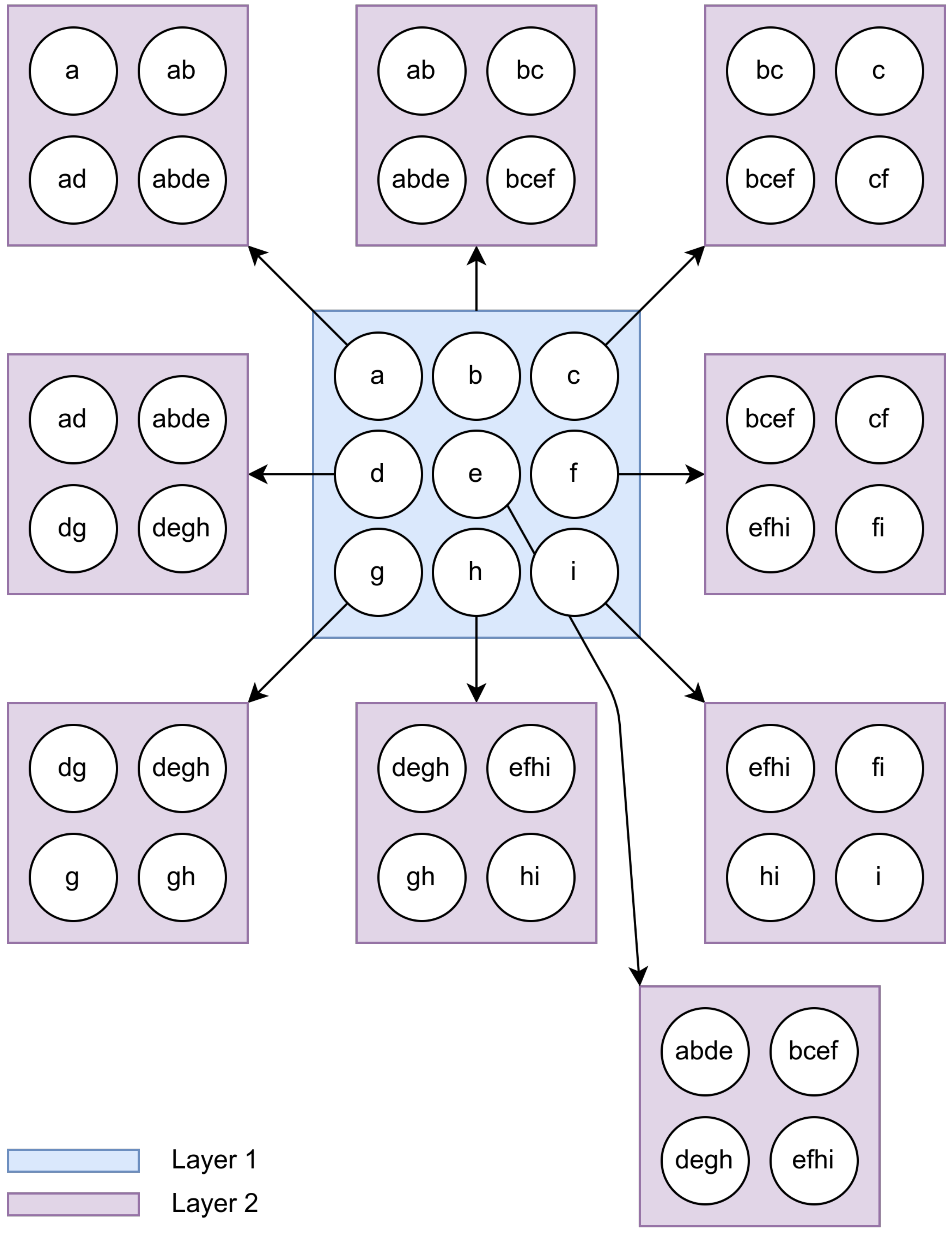
2.1. Growing Hierarchical Self-Organizing Map
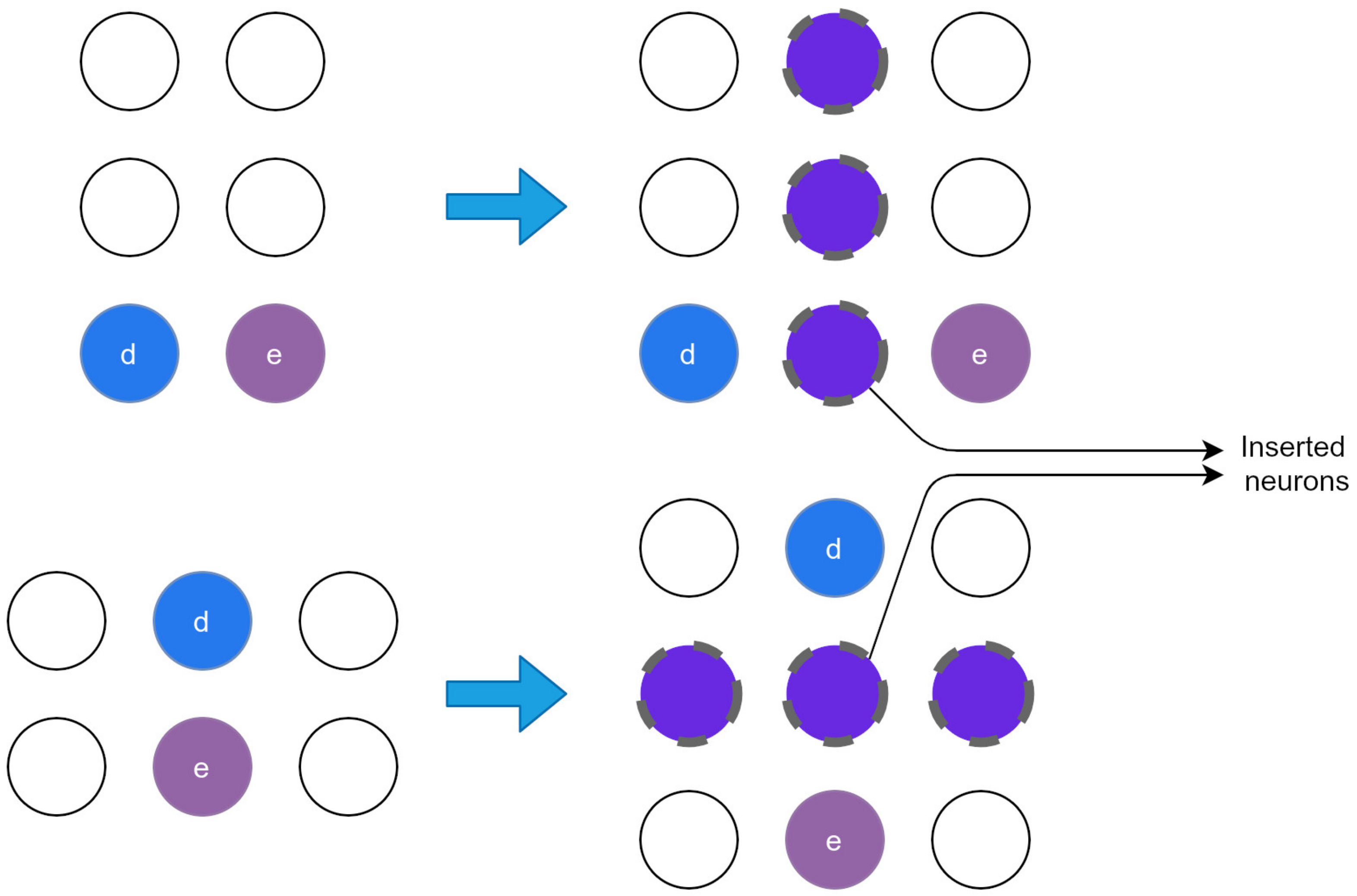
2.2. Parameter-Less Growing Hierarchical Self-Organizing Map
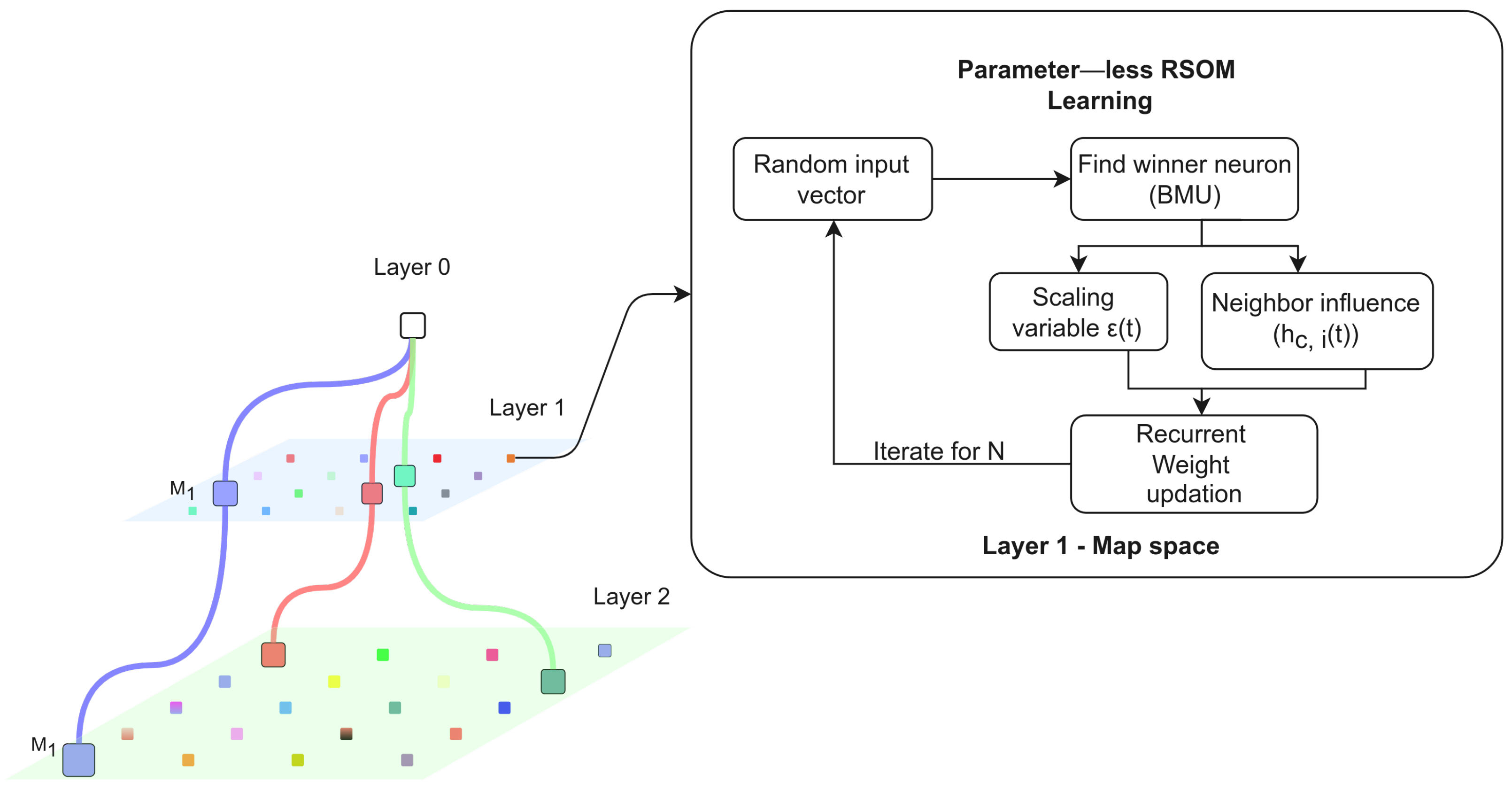
2.3. Recurrent Self-Organizing Map
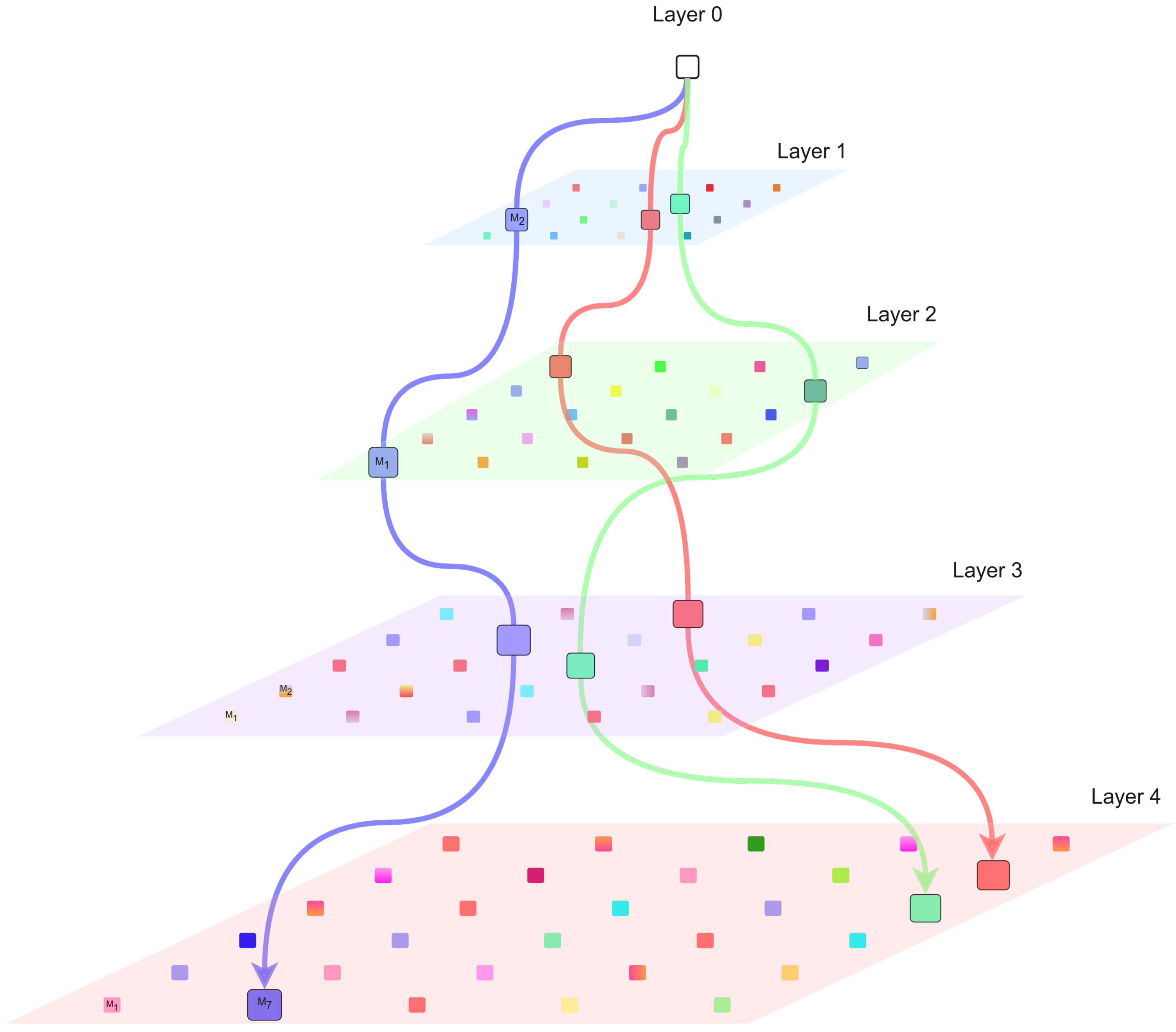
2.4. Parameter-Less Growing Hierarchical Recurrent Self-Organizing Map
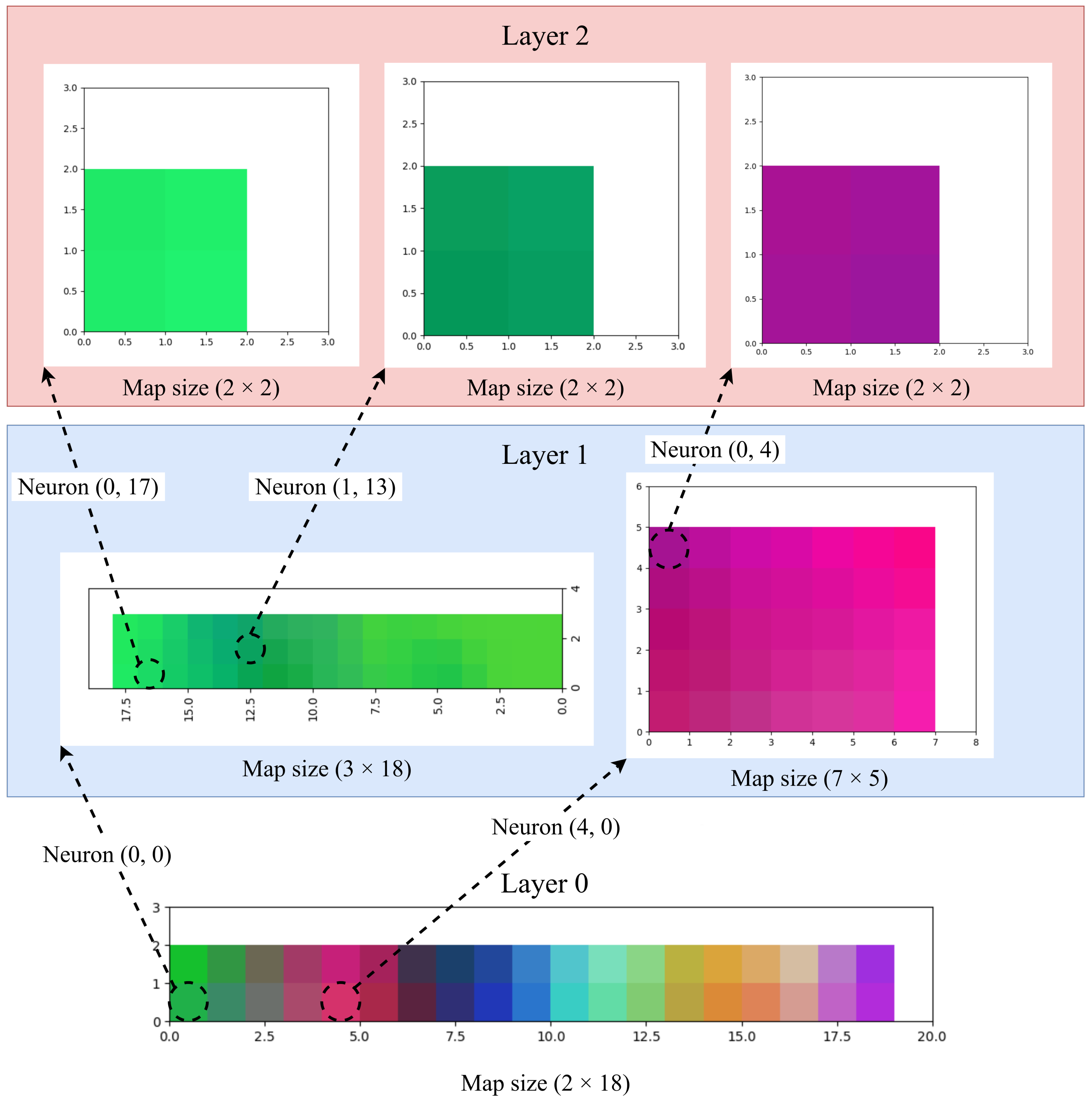
3. Testing and Evaluation
- Compute the mean vector of each map in the hierarchy (Equation (18)).
- Compare the test image with the maps in the hierarchy.
- Find the map with the closest mean vector for the test image.
3.1. Color Clustering
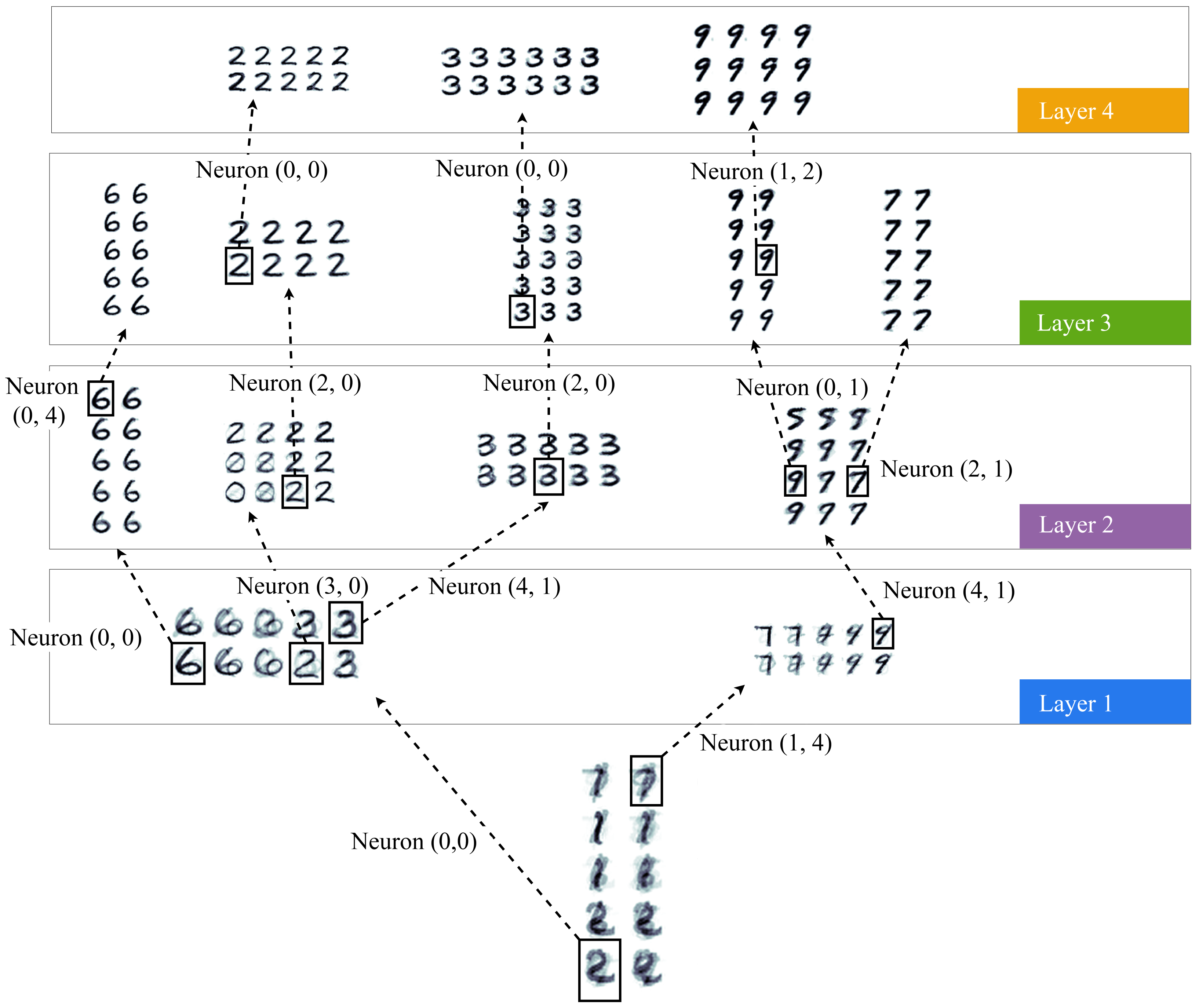
3.2. Handwritten Digits Clustering
3.3. Finger Identification
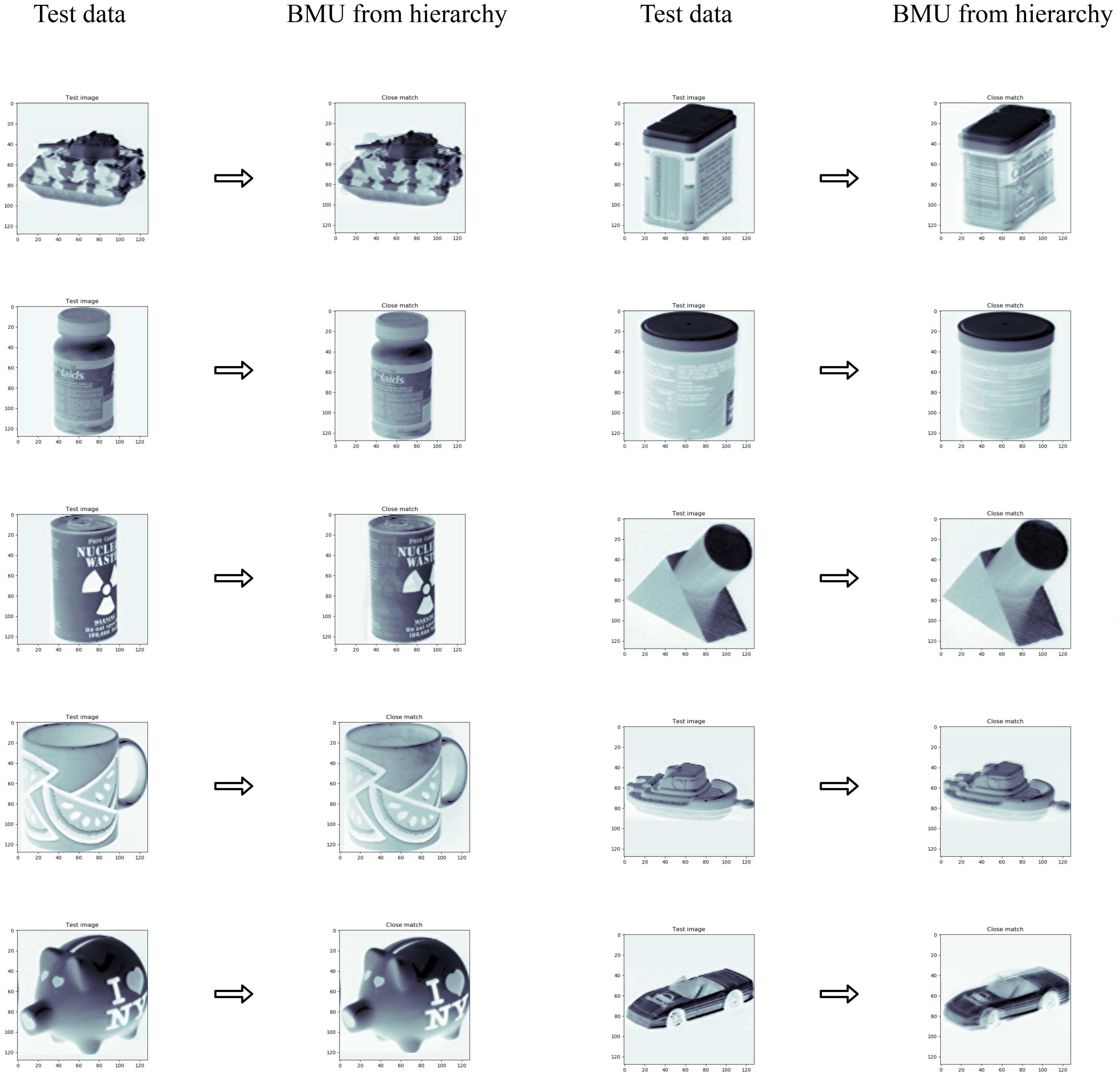
3.4. Object Classification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Johnson, D.O.; Cuijpers, R.H.; Juola, J.F.; Torta, E.; Simonov, M.; Frisiello, A.; Bazzani, M.; Yan, W.; Weber, C.; Wermter, S.; et al. Socially Assistive Robots: A Comprehensive Approach to Extending Independent Living. Int. J. Soc. Robot. 2014, 6, 195–211. [Google Scholar] [CrossRef]
- Matarić, M.J.; Scassellati, B. Socially assistive robotics. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1973–1994. [Google Scholar]
- Maslach, C.; Leiter, M.P. Understanding burnout: New models. In The Handbook of Stress and Health: A Guide to Research and Practice; John Wiley & Sons Ltd.: West Sussex, UK, 2017; pp. 36–56. [Google Scholar]
- Bianchi, R.; Boffy, C.; Hingray, C.; Truchot, D.; Laurent, E. Comparative symptomatology of burnout and depression. J. Health Psychol. 2013, 18, 782–787. [Google Scholar] [CrossRef] [PubMed]
- Bemelmans, R.; Gelderblom, G.J.; Jonker, P.; de Witte, L. Socially Assistive Robots in Elderly Care: A Systematic Review into Effects and Effectiveness. J. Am. Med Dir. Assoc. 2012, 13, 114–120.e1. [Google Scholar] [CrossRef]
- Dickstein-Fischer, L.A.; Crone-Todd, D.E.; Chapman, I.M.; Fathima, A.T.; Fischer, G.S. Socially assistive robots: Current status and future prospects for autism interventions. Innov. Entrep. Health 2018, 5, 15–25. [Google Scholar] [CrossRef]
- Ingrand, F. Deliberation for autonomous robots: A survey. Artificial Intell. 2017, 247, 10–44. [Google Scholar] [CrossRef]
- Feng, F.; Chan, R.H.; Shi, X.; Zhang, Y.; She, Q. Challenges in task incremental learning for assistive robotics. IEEE Access 2019, 8, 3434–3441. [Google Scholar] [CrossRef]
- Santhanaraj, K.K.; Ramya, M.M.; Dinakaran, D. A survey of assistive robots and systems for elderly care. J. Enabling Technol. 2021, 15, 66–72. [Google Scholar] [CrossRef]
- Bousquet-Jette, C.; Achiche, S.; Beaini, D.; Cio, Y.L.K.; Leblond-Ménard, C.; Raison, M. Fast scene analysis using vision and artificial intelligence for object prehension by an assistive robot. Eng. Appl. Artif. Intell. 2017, 63, 33–44. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Montaño-Serrano, V.M.; Jacinto-Villegas, J.M.; Vilchis-González, A.H.; Portillo-Rodríguez, O. Artificial Vision Algorithms for Socially Assistive Robot Applications: A Review of the Literature. Sensors 2021, 21, 5728. [Google Scholar] [CrossRef]
- Panek, P.; Mayer, P. Challenges in adopting speech control for assistive robots. In Ambient Assisted Living; Springer: Berlin/Heidelberg, Germany, 2015; pp. 3–14. [Google Scholar]
- Li, J. Recent Advances in End-to-End Automatic Speech Recognition. APSIPA Trans. Signal Inf. Process. 2022, 11, e8. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Xie, L. Intensity-slam: Intensity assisted localization and mapping for large scale environment. IEEE Robot. Autom. Lett. 2021, 6, 1715–1721. [Google Scholar] [CrossRef]
- Ali, A.J.B.; Kouroshli, M.; Semenova, S.; Hashemifar, Z.S.; Ko, S.Y.; Dantu, K. Edge-SLAM: Edge-assisted visual simultaneous localization and mapping. ACM Trans. Embed. Comput. Syst. 2022, 22, 1–31. [Google Scholar] [CrossRef]
- Elshaw, M.; Moore, R.K.; Klein, M. Hierarchical Recurrent Self-Organising Memory (H-RSOM) Architecture for an Emergent Speech Representation towards Robot Grounding. Available online: http://lands.let.ru.nl/acorns/documents/publications/NCAF_paper_2009.pdf (accessed on 8 May 2023).
- Zhang, T.; Zeng, Y.; Pan, R.; Shi, M.; Lu, E. Brain-Inspired Active Learning Architecture for Procedural Knowledge Understanding Based on Human-Robot Interaction. Cogn. Comput. 2021, 13, 381–393. [Google Scholar] [CrossRef]
- Gergely, G. What should a robot learn from an infant? Mechanisms of action interpretation and observational learning in infancy. Connect. Sci. 2003, 15, 191–209. [Google Scholar] [CrossRef]
- Anderson, J.R.; Matessa, M.; Lebiere, C. ACT-R: A theory of higher level cognition and its relation to visual attention. Human–Comput. Interact. 1997, 12, 439–462. [Google Scholar] [CrossRef]
- Ritter, F.E.; Tehranchi, F.; Oury, J.D. ACT-R: A cognitive architecture for modeling cognition. WIREs Cogn. Sci. 2019, 10, e1488. [Google Scholar] [CrossRef]
- Rosenbloom, P.S. The Sigma cognitive architecture and system. AISB Q. 2013, 136, 4–13. [Google Scholar]
- Ustun, V.; Rosenbloom, P.S.; Sajjadi, S.; Nuttall, J. Controlling Synthetic Characters in Simulations: A Case for Cognitive Architectures and Sigma. arXiv 2021, arXiv:2101.02231. [Google Scholar]
- Rosenbloom, P.S.; Ustun, V. An architectural integration of Temporal Motivation Theory for decision making. In Proceedings of the 17th Annual Meeting of the International Conference on Cognitive Modeling, Montreal, QC, Canada, 19–22 July 2019. [Google Scholar]
- Singer, W. The brain as a self-organizing system. Eur. Arch. Psychiatry Neurol. Sci. 1986, 236, 4–9. [Google Scholar] [CrossRef]
- Singer, W. The Brain, a Complex Self-organizing System. Eur. Rev. 2009, 17, 321–329. [Google Scholar] [CrossRef]
- Van Orden, G.C.; Holden, J.G.; Turvey, M.T. Self-organization of cognitive performance. J. Exp. Psychol. Gen. 2003, 132, 331–350. [Google Scholar] [CrossRef] [PubMed]
- Dresp-Langley, B. Seven Properties of Self-Organization in the Human Brain. Big Data Cogn. Comput. 2020, 4, 10. [Google Scholar] [CrossRef]
- Patel, M.; Miro, J.V.; Dissanayake, G. A hierarchical hidden markov model to support activities of daily living with an assistive robotic walker. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; IEEE: Manhattan, NY, USA, 2012; pp. 1071–1076. [Google Scholar]
- Zhou, X.; Bai, T.; Gao, Y.; Han, Y. Vision-Based Robot Navigation through Combining Unsupervised Learning and Hierarchical Reinforcement Learning. Sensors 2019, 19, 1576. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Ahn, M.; Levine, S.; Kumar, V.; Hausman, K.; Gu, S. Emergent real-world robotic skills via unsupervised off-policy reinforcement learning. arXiv 2020, arXiv:2004.12974. [Google Scholar]
- Wang, C.; Qiu, Y.; Wang, W.; Hu, Y.; Kim, S.; Scherer, S. Unsupervised online learning for robotic interestingness with visual memory. IEEE Trans. Robot. 2021, 38, 2446–2461. [Google Scholar] [CrossRef]
- Yates, T.S.; Ellis, C.T.; Turk-Browne, N.B. Emergence and organization of adult brain function throughout child development. NeuroImage 2021, 226, 117606. [Google Scholar] [CrossRef]
- Haken, H. Synergetics of brain function. Int. J. Psychophysiol. 2006, 60, 110–124. [Google Scholar] [CrossRef]
- Chersi, F.; Ferro, M.; Pezzulo, G.; Pirrelli, V. Topological Self-Organization and Prediction Learning Support Both Action and Lexical Chains in the Brain. Top. Cogn. Sci. 2014, 6, 476–491. [Google Scholar] [CrossRef]
- Fingelkurts, A.A.; Fingelkurts, A.A.; Neves, C.F. Consciousness as a phenomenon in the operational architectonics of brain organization: Criticality and self-organization considerations. Chaos Solitons Fractals 2013, 55, 13–31. [Google Scholar] [CrossRef]
- Lloyd, R. Self-organized cognitive maps. Prof. Geogr. 2000, 52, 517–531. [Google Scholar] [CrossRef]
- Doniec, M.W.; Scassellati, B.; Miranker, W.L. Emergence of Language-Specific Phoneme Classifiers in Self-Organized Maps. In Proceedings of the 2007 International Joint Conference on Neural Networks, Orlando, FL, USA, 12–17 August 2007; pp. 2081–2086, ISSN 1098-7576. [Google Scholar] [CrossRef]
- Huang, K.; Ma, X.; Song, R.; Rong, X.; Tian, X.; Li, Y. An autonomous developmental cognitive architecture based on incremental associative neural network with dynamic audiovisual fusion. IEEE Access 2019, 7, 8789–8807. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Alahakoon, D.; Halgamuge, S.; Srinivasan, B. Dynamic self-organizing maps with controlled growth for knowledge discovery. IEEE Trans. Neural Netw. 2000, 11, 601–614. [Google Scholar] [CrossRef] [PubMed]
- Dittenbach, M.; Merkl, D.; Rauber, A. The growing hierarchical self-organizing map. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27–27 July 2000; IEEE: Manhattan, NY, USA, 2000; Volume 6, pp. 15–19. [Google Scholar]
- Walker, A.; Hallam, J.; Willshaw, D. Bee-havior in a mobile robot: The construction of a self-organized cognitive map and its use in robot navigation within a complex, natural environment. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; pp. 1451–1456. [Google Scholar] [CrossRef]
- Huang, K.; Ma, X.; Song, R.; Rong, X.; Tian, X.; Li, Y. A self-organizing developmental cognitive architecture with interactive reinforcement learning. Neurocomputing 2020, 377, 269–285. [Google Scholar] [CrossRef]
- Huang, K.; Ma, X.; Song, R.; Rong, X.; Li, Y. Autonomous cognition development with lifelong learning: A self-organizing and reflecting cognitive network. Neurocomputing 2021, 421, 66–83. [Google Scholar] [CrossRef]
- Gliozzi, V.; Madeddu, M. A visual auditory model based on Growing Self-Organizing Maps to analyze the taxonomic response in early childhood. Cogn. Syst. Res. 2018, 52, 668–677. [Google Scholar] [CrossRef]
- Mici, L.; Parisi, G.I.; Wermter, S. An Incremental Self-Organizing Architecture for Sensorimotor Learning and Prediction. IEEE Trans. Cogn. Dev. Syst. 2018, 10, 918–928. [Google Scholar] [CrossRef]
- Zhu, D.; Cao, X.; Sun, B.; Luo, C. Biologically Inspired Self-Organizing Map Applied to Task Assignment and Path Planning of an AUV System. IEEE Trans. Cogn. Dev. Syst. 2018, 10, 304–313. [Google Scholar] [CrossRef]
- Jitviriya, W.; Hayashi, E. Design of emotion generation model and action selection for robots using a Self Organizing Map. In Proceedings of the 2014 11th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Nakhon Ratchasima, Thailand, 14–17 May 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Jitviriya, W.; Koike, M.; Hayashi, E. Emotional Model for Robotic System Using a Self-Organizing Map Combined with Markovian Model. J. Robot. Mechatronics 2015, 27, 563–570. [Google Scholar] [CrossRef]
- Johnsson, M.; Balkenius, C. Sense of touch in robots with self-organizing maps. IEEE Trans. Robot. 2011, 27, 498–507. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Nene, S.A.; Nayar, S.K.; Murase, H. Columbia Object Image Library (Coil-100); Citeseer: State College, PA, USA, 1996. [Google Scholar]
- Rauber, A.; Merkl, D.; Dittenbach, M. The growing hierarchical self-organizing map: Exploratory analysis of high-dimensional data. IEEE Trans. Neural Netw. 2002, 13, 1331–1341. [Google Scholar] [CrossRef] [PubMed]
- Dittenbach, M.; Rauber, A.; Merkl, D. Recent advances with the growing hierarchical self-organizing map. In Advances in Self-Organising Maps; Springer: Berlin/Heidelberg, Germany, 2001; pp. 140–145. [Google Scholar]
- Berglund, E.; Sitte, J. The parameterless self-organizing map algorithm. IEEE Trans. Neural Netw. 2006, 17, 12. [Google Scholar] [CrossRef] [PubMed]
- Kuremoto, T.; Komoto, T.; Kobayashi, K.; Obayashi, M. Parameterless-Growing-SOM and Its Application to a Voice Instruction Learning System. J. Robot. 2010, 2010, 307293. [Google Scholar] [CrossRef]
- Varsta, M.; Heikkonen, J.; Millan, J.d.R. Context Learning with the Self-Organizing Map; Helsinki University of Technology: Espoo, Finland, 1997. [Google Scholar]
- Angelovič, P. Time series prediction using RSOM and local models. In Proceedings of IIT.SRC 2005, Bratislava, Slovakia, 23 April 2015; Citeseer: State College, PA, USA, 2005; pp. 27–34. [Google Scholar]
- Sá, J.; Rocha, B.; Almeida, A.; Souza, J.R. Recurrent self-organizing map for severe weather patterns recognition. Recurr. Neural Netw. Solf Comput. 2012, 8, 151–175. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Johnsson, M.; Balkenius, C.; Hesslow, G. Associative self-organizing map. In Proceedings of the International Conference on Neural Computation, Tianjin, China, 14–16 August 2009; SCITEPRESS: Setúbal, Portugal, 2009; Volume 2, pp. 363–370. [Google Scholar]




| Test Type | GHSOM | GHRSOM | PL-GHSOM | PL-GHRSOM |
|---|---|---|---|---|
| Color Clustering | 96.12% | 96.03% | 95.87% | 95.98% |
| Handwritten Digits Clustering | 92.62% | 94.52% | 95.09% | 95.06% |
| Finger Identification | 97.96% | 97.89% | 97.86% | 97.84% |
| Image Classification | 91.03% | 91.06% | 90.89% | 90.69% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santhanaraj, K.K.; Devaraj, D.; MM, R.; Dhanraj, J.A.; Ramanathan, K.C. Biologically Inspired Self-Organizing Computational Model to Mimic Infant Learning. Mach. Learn. Knowl. Extr. 2023, 5, 491-511. https://doi.org/10.3390/make5020030
Santhanaraj KK, Devaraj D, MM R, Dhanraj JA, Ramanathan KC. Biologically Inspired Self-Organizing Computational Model to Mimic Infant Learning. Machine Learning and Knowledge Extraction. 2023; 5(2):491-511. https://doi.org/10.3390/make5020030
Chicago/Turabian StyleSanthanaraj, Karthik Kumar, Dinakaran Devaraj, Ramya MM, Joshuva Arockia Dhanraj, and Kuppan Chetty Ramanathan. 2023. "Biologically Inspired Self-Organizing Computational Model to Mimic Infant Learning" Machine Learning and Knowledge Extraction 5, no. 2: 491-511. https://doi.org/10.3390/make5020030
APA StyleSanthanaraj, K. K., Devaraj, D., MM, R., Dhanraj, J. A., & Ramanathan, K. C. (2023). Biologically Inspired Self-Organizing Computational Model to Mimic Infant Learning. Machine Learning and Knowledge Extraction, 5(2), 491-511. https://doi.org/10.3390/make5020030







