1. Introduction
Energy pricing and electric consumption are two of the most important factors that affect the functioning of modern societies [
1]. The energy sector is constantly evolving, and it is essential to have accurate predictions of energy prices and consumption to ensure stability and affordability [
2]. In recent years, artificial intelligence (AI) has emerged as a powerful tool for making predictions in various fields, including energy [
3].
There are several factors that can contribute to an increase in electricity prices, such as fuel costs, supply and demand, infrastructure investment, government policies, or natural disasters [
4,
5,
6]. The energy industry is currently facing several difficulties, including the need to address climate change by reducing greenhouse gas emissions and transitioning to clean energy sources, which can affect energy costs; government regulations that can greatly impact electricity prices, leading to conflicting opinions on the best course of action; and geopolitical conflict that can also have a major impact on both energy pricing and supply [
7]. A report by Fitch Rations [
8] states that the 2023 electricity forward prices are about three times higher compared to the historical average of Europe in most Western European countries. The report also expects gas and electricity prices to remain much higher than historical levels in 2023 and 2024. Another report conducted by Ember [
9] highlights the proposed 45% renewable energy goal for 2030, which would see 69% of the EU’s electricity generated from renewables by that year. It also mentions that EU electricity generation is still heavily reliant on fossil fuels. These challenges highlight the importance of continued innovation and investment in the energy sector to ensure a reliable and affordable energy supply.
From December 2020 to the present, wholesale electricity prices have experienced a substantial increase, reaching double their previous levels. This increase is largely attributed to European Union policies regarding the reduction of CO
2 emissions, the significant appreciation of natural gas prices, and the current conflict in Ukraine as of February 2022 [
10,
11].
The ongoing conflict between Russia and Ukraine has highlighted the need for increased stability in the energy markets and the importance of ensuring a consistent and affordable energy supply. In this context, the use of AI models to predict energy pricing and electric consumption is particularly relevant [
12,
13]. The prediction of real-time prices has been previously proposed as a potential solution for enhancing the efficiency of electric planning, budget preparation, and network performance [
14,
15].
In the current energy market situation in Spain, which is characterized by high levels of renewable energy penetration and price volatility, there is a need for accurate and reliable models to predict electricity prices and consumption. In this context, our study aims to address this need by evaluating the performance of various machine learning algorithms for electricity price and consumption modeling in the Spanish market. Specifically, we analyze and compare the performance of linear regression, random forest, XGBoost, LSTM, and GRU algorithms using real-life data on Spanish electricity consumption and prices from 1 January 2014 to 30 April 2022. Our study provides valuable insights for the energy market in Spain. Firstly, our analysis indicates that using advanced methods, specifically LSTM and GRU artificial neural networks, can significantly enhance the accuracy and reliability of electricity price modeling. This finding can inform the development of more effective pricing strategies for electricity in Spain. Secondly, our study highlights the importance of having access to high-quality data for electricity demand and price modeling, emphasizing the need for policymakers to prioritize the development of reliable and up-to-date Spanish energy data systems. Finally, our comparison of machine learning algorithms for electricity consumption modeling suggests that XGBoost occasionally obtains the most accurate method for forecasting energy demand in Spain. This information can be used to improve energy demand forecasting and inform decision-making in the Spanish energy market.
We would like to point out that while day-ahead markets are crucial in determining electricity prices in advance, intraday markets also play a crucial role in the electricity market, offering flexibility to market participants to adjust their positions in response to changing demand and supply conditions within the same day. These markets enable electricity traders to manage their risks and optimize their profits by providing real-time price signals that reflect the current market conditions. Intraday markets are particularly important in this context, for energy resources can introduce greater volatility and uncertainty in the supply of electricity [
16]. By allowing for short-term adjustments to supply and demand, intraday markets can help ensure the stability and reliability of the power system. The use of advanced forecasting methods to predict intraday electricity prices is becoming increasingly important, as it can provide market participants with valuable information for their trading strategies [
17]. Nevertheless, intraday electricity market data prediction is a topic that has been little explored in the literature. The majority of studies focus on daily, weekly, or even monthly forecasting. There is limited research on hourly electricity prices and consumption predictions. Our study fills this gap in the literature by using hourly data, which provides a more detailed analysis of intraday market behavior.
Our study makes several original contributions to the field of intraday electricity market data prediction. Firstly, we focus on the prediction of hourly electricity prices and consumption, which has been a relatively unexplored area in the literature. Using this level of detail, we provide a more comprehensive analysis of intraday market behavior. Secondly, we compare the performance of different machine learning algorithms for this purpose. Our results provide insights into the strengths and weaknesses of these algorithms for this specific task. Finally, we use real-life data on Spanish electricity consumption and prices on an hourly basis, which has not been previously analyzed in the literature. Overall, our study contributes to the understanding of intraday electricity market data prediction and provides valuable insights for energy policymakers and industry practitioners. Our study contributes to the literature by addressing the gaps in existing research on electricity price and consumption modeling in the Spanish market and providing valuable insights into the potential of AI to improve energy efficiency and inform policy decisions related to energy in Spain.
Related Works
Countless authors acknowledge the challenges associated with predicting electricity prices, including its volatility and uncertainty [
18,
19] and the difficulties in applying it at a large scale within the electric market [
20,
21]. Electric demand is influenced by various factors, such as local meteorological conditions, the intensity of commercial and daily activities, energy supply and distribution strategies, and the variability of renewable energy production [
18,
20,
22].
According to Lu et al. [
20], the goals of electricity price prediction can be divided into two categories: point predictions and probabilistic predictions. Probabilistic predictions assign a probability to each possible forecast outcome. When the output variable is not discrete, the forecast is usually made using intervals. On the other hand, point predictions are deterministic estimates that provide an exact result, for example, the electricity price at every 30-minute interval for the next 24 h, resulting in 48 data points. The authors assert that most studies in this field [
23,
24,
25,
26] focus on point predictions and use evaluation metrics such as root mean squared error (RMSE) and mean absolute error (MAE) to assess the accuracy of their predictions [
27,
28].
An important reference to consider is the study conducted by [
29], which reviews the state-of-the-art algorithms and best practices for forecasting day-ahead electricity prices and proposes an open-access benchmark for the evaluation of new predictive algorithms. Assessing the accuracy of electricity price forecasting models is crucial, but it is equally important to determine whether any difference in accuracy is statistically significant. This is crucial to ensuring that the difference in accuracy is not due to chance variations between the forecasts. However, statistical testing is often overlooked in the literature on electricity price forecasting [
18]. Many studies focus solely on comparing the accuracy of models based on error metrics and do not evaluate the statistical significance of differences in accuracy. This approach should be revised to ensure that forecasting methods are compared with the necessary statistical rigor. Lenha et al. [
30] report that more than two-thirds of studies on electricity price prediction make use of time series techniques, artificial neural networks (ANNs), or a combination of both. According to the authors in [
10], autoregressive models are the most commonly used models for electricity price forecasting. In [
31], a method for predicting next-day electricity prices using ARIMA models was presented, with results from both mainland Spain and California markets. A day-ahead electricity price forecasting model in the Denmark-West region using ARIMA and ANNs was presented in [
32]. Keles et al. [
33] analyzed a predictive system using ANNs to estimate electricity prices on a daily basis. Similarly, Panapakidis and Dagoumas [
34] proposed diverse ANN topologies based on clustering algorithms to make their predictions. Many other techniques can be found in the literature for the same purpose [
35]; some examples are deep learning [
25,
36], fuzzy logic [
37], and tree-based [
38] solutions. In [
39], the authors presented a hybrid model called EA-XGB for building energy prediction and compared its performance with ARIMA and XGB models. The experiment showed that the EA-XGB hybrid model performed best in forecasting building energy consumption using the dataset provided by the US National Renewable Energy Laboratory. The study [
40] introduces a deep learning framework for building energy consumption forecasts that combines convolutional neural networks (CNN) and long short-term memory (LSTM) networks. The proposed framework was tested on two datasets and showed better performance than traditional machine learning models. Additionally, in [
41], the authors proposed a multi-energy load forecasting method based on parallel architecture CNN-GRU and transfer learning for data-deficient integrated energy systems. The proposed method was tested on two datasets and showed better performance than other traditional machine learning models.
In this study, we aimed to provide a comprehensive comparison of different machine learning techniques and their performance in predicting Spanish energy pricing and consumption. To achieve this, we include several machine learning techniques in our analysis, such as linear regression [
42], random forests [
43], XGBoost [
39,
44], LSTM [
45], and GRU [
46]. The inclusion of these models allowed us to evaluate their strengths and weaknesses and identify the most suitable approach for our problem. By including a range of models with varying levels of complexity, we were able to provide a more complete picture of the performance of different machine learning approaches in the context of Spanish energy pricing and consumption.
Our study differs from previous research in several ways. Firstly, while most papers in this area use daily or monthly data, our analysis is based on hourly data. This level of granularity provides a more accurate representation of energy consumption patterns and allows for a more precise analysis of the relationship between consumption and prices. Furthermore, our study is unique because it examines the relationship between energy consumption and prices simultaneously, whereas previous research typically focused on either consumption or prices alone. This approach allows for a more comprehensive understanding of the factors that influence energy consumption in the Spanish market. Therefore, our study contributes to the literature by providing a more detailed analysis of energy consumption patterns and their relationship with prices, which can help inform energy policies and improve energy efficiency in Spain.
The rest of the document is structured as follows: The proposed methodology is detailed in
Section 2.
Section 3 introduces the experiments conducted.
Section 4 presents the main results. Finally, the conclusions are gathered in
Section 5.
2. Methodology
This section outlines the methodology adopted in this study, including the data description, pre-processing, and evaluation of the predictive models.
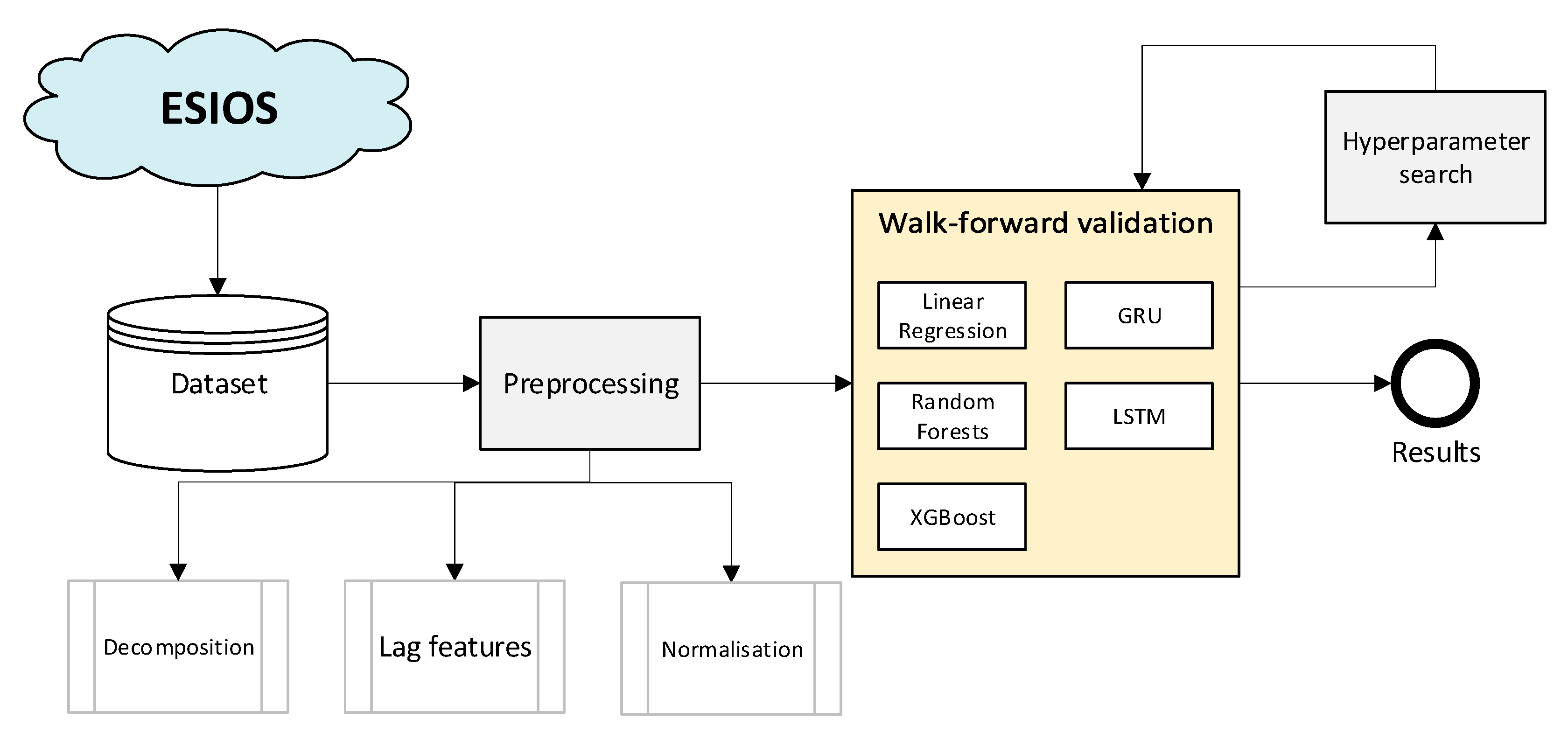
Figure 1 illustrates the overall procedure followed in our study. The flowchart outlines the different stages involved in data collection, processing, and analysis. First, the dataset is downloaded from the ESIOS API and stored locally. Next, the data are pre-processed, which includes adding the decomposition of the time series, lag features, and normalizing the data. Thirdly, the walk-forward validation method is employed to evaluate the performance of the models. Fourthly, an experimental hyperparameter search is iteratively performed to identify the optimal hyperparameters for each model. Finally, the results are obtained and analyzed.
2.1. Dataset
In this study, data were obtained from the Spanish Electricity Network (SEN) through the REData and Esios APIs. The SEN website provides various tools for extracting information, including a calendar to select specific days, a graph for visualizing daily demand, a data table for numerical information, accumulated demand from different energy sources, and the option to display different electrical systems. We gathered data covering the period from 1 January 2014 to 30 April 2022, at hourly intervals, resulting in a total of 73.119 observations. While the data used in our study are publicly available on the official website, we suggest using the dataset we utilized for future studies and comparisons. It can be downloaded from [
47].
The decision to focus solely on Spain in our study was intentional, as we wanted to investigate the unique context of the Spanish energy market and consumption trends. Furthermore, the lack of updated public datasets in the literature made it challenging to compare our results with those of other research studies in different countries. Therefore, in this study, we focused on Spain, where we were able to obtain the required data. We recommend other researchers use our dataset to address this issue for future studies and enable better comparisons across different research projects.
While our study is primarily focused on Spain, we believe that the presented approach and methodology can be applicable to other regions as well. Nonetheless, it is important to note that the success of our approach in other regions may depend on various factors, including the similarities in energy market structure and regulations as well as the availability and quality of relevant data.
2.2. Preprocessing
The first step of our data preparation was to decompose the original time series into trend, season, and residual. This process allows us to separate the underlying patterns of the data from the random fluctuations, providing a more accurate representation of the time series. The trend component represents the long-term behavior of the series and captures any upward or downward trend over time. The seasonal component provides the recurring patterns in the data. The residual component captures the unexplained variability or noise in the time-series that is not registered by the other two components. As an example,
Figure 2 illustrates the decomposition of the electricity price time series, including the trend, seasonal, and residual components. It is important to note that these components were solely used for analytical purposes and not incorporated into the models presented in this study, which utilize the original time series data.
As opposed to other problems, time series observations are not independent of each other. Hence, we will not split the data randomly. Instead, the data will be divided chronologically into three parts: a training set, a validation set, and a test set, to preserve the temporal relationship between observations. To improve the performance of supervised learning models, lag features may be created by adding columns that represent previous time stamps
to the dataset in order to provide additional information for the current time stamp
. In time series analysis, «lag feature» refers to a variable that is delayed or shifted in time relative to another variable. That is to say, it is the value of a variable at a previous time step that is included as a predictor in a model to capture temporal dependencies and autocorrelation in the data. The creation of lag features in time series data is a commonly used preprocessing step in predictive modeling. The idea behind this is that past samples of a time series contain information that can be useful for predicting future values. By adding columns to the dataset that represent the values of previous time stamps, the model can use this information to make better estimates. The assumption is that the relationship between past and future values is not completely random and that past patterns can be used to inform predictions about forthcoming values [
48].
After creating the lag features, the next step in the preprocessing stage is normalizing the data. Data normalization is important in order to ensure that all the features have the same scale, which helps the predictors perform better. In this study, normalization was performed between
, which is a common range used in machine learning. We used the following equation to this end:
where
is the normalized value,
is the value of the series, and max and min are the maximum and minimum of the time series. Following Nielsen’s recommendations [
49], we normalized the data for each feature individually, scaling the values so that they fall within the range
. This method is useful when each feature has a different scale and units, as it allows them to be compared and processed on a similar basis.
2.3. Techniques
The current section briefly introduces the models used in this research. We implemented linear regression (LR), random forest (RF), extreme gradient boosting (XGB), long short-term memory (LSTM), and gated recurrent unit (GRU) algorithms.
LR is a commonly used statistical model for predictive tasks. It assumes a linear relationship between the dependent and independent variables and aims to fit a line or a hyperplane to the data. The goal is to use the relationship established by the fitted model to make predictions about the dependent variable based on the values of the explanatory variables. LR is simple to implement and interpret, making it a popular choice for many regression problems [
50,
51].
RF is a type of ensemble machine learning algorithm that combines the predictions of multiple decision trees to make a final prediction. It was introduced by Breiman [
52] as an improvement over traditional decision trees. RF algorithms are known for their ability to generalize well, reduce overfitting, and capture a wider variety of patterns in the data, making them suitable for both regression and classification problems [
53].
The XGB was the third algorithm implemented in this study. XGB is a gradient-boosting tree method that combines decision trees in an ensemble model, where the prediction of one tree serves as input for the next tree. This sequential learning process can lead to improved predictions compared to single decision trees. The algorithm has been successful in both regression and classification problems [
38,
39] and is known for its ability to handle a large number of features and its ability to capture non-linear relationships in data.
Two neural network-based models were implemented in this study, LSTM and GRU. LSTM networks are a type of recurrent neural network (RNN) designed to handle the issue of vanishing gradients in traditional RNNs. LSTMs are well suited for tasks involving sequences of data, such as time series prediction, language translation, and speech recognition [
24,
30,
45]. The LSTM architecture allows them to remember important information from the past for an extended period of time, making them ideal for long-term dependencies in time series data.
GRUs are another type of RNN, similar in concept to LSTM. Both use gate mechanisms to control the flow of information. The main difference between these two is how information is retained over time. While LSTMs use three gates: an input, output, and forget gate, GRUs use two gates: an update gate and a reset gate. This makes GRU faster and computationally more efficient compared to LSTM. Nevertheless, GRU may not perform as well as LSTM on very long sequences, as they may struggle to retain information over extended periods [
54,
55].
The machine learning algorithms employed in this study were chosen for their ability to handle complex nonlinear relationships and temporal dependencies in the data. Linear regression was included as a baseline model to provide a benchmark for comparison with the more advanced machine learning algorithms. Random forest and XGBoost were chosen for their ability to capture complex interactions between variables and handle large feature spaces. LSTM and GRU were chosen for their ability to model time series data with long-term dependencies, which are characteristic of electricity price and consumption data. The inclusion of lagged variables in the models allowed us to capture the persistence of electricity prices and consumption over time and to account for seasonality and other temporal effects. Therefore, all the models, including LSTM and GRU, will make use of the delayed inputs. As mentioned, the use of lagged inputs can capture the dependencies of past observations on future values, which is important in the forecasting task at hand.
3. Experiments
In this section, we describe the experiments carried out to evaluate the performance of the implemented models for predicting electricity consumption and electricity prices.
To ensure the reproducibility of our experiments, we provide details on the technologies used in our study. We conducted our experiments on a machine with an Intel(R) Core (TM) i7-10750H CPU @ 2.60GHz, 2592 MHz, 6 processors, and 12 logic processors. The operating system used was Microsoft Windows 10 Home version 21H2. The machine had 32 GB of RAM memory and a 1 TB HDD (model SAMSUNG MZVLB1T0HBLR-000H1). Additionally, the machine had a dedicated NVIDIA GeForce RTX 2060 GPU and integrated Intel(R) UHD Graphics. For our data processing, we used Python 3.9.7, Numpy, Pandas, and JSON. To visualize our results, we used Matplotlib and Seaborn. For traditional machine learning, we used Scikit-learn, while for neural networks, we used Tensorflow and Keras.
For the simpler models, LR, RF, and XGB, we conducted a series of experiments to evaluate their performance. In these experiments, we tested different configurations of the models, with a focus on the number of lags used in the features, as this is usually an important factor in the performance of time series models. For the LR, we conducted experiments to evaluate the intercept parameter, the number of jobs, and the sign of the coefficients. In the case of the RF, we tested several hyperparameters, including the number of estimators, the Gini, entropy, and log loss criterion, the maximum depth of the tree, and the minimum number of samples required to split an internal node. We also conducted experiments to test the XGB model using similar hyperparameters to the RF, with a particular focus on the number of estimators. However, due to space limitations, we only report the most important results in the paper. For the LSTM and GRU, we conducted a more extensive hyperparameter search, including the number of epochs, patience, learning rate, batch size, and number of neurons. We evaluated the impact of these hyperparameters on the predictive performance of the models. Due to limited space, we could not include all the results, though we present a summary of the most significant outcomes in the next section. In summary, we conducted a basic grid search to optimize our models. Specifically, we calculated the model intercept for the LR algorithm and utilized all available processors, constraining the coefficients to be positive and not using intercept in calculations. Regarding the RF algorithm, we employed 500 estimators and the squared error criterion. The maximum tree depth was 7, and we set the maximum number of features to 0.8 and the maximum number of samples to 0.6. XGB employed 500 estimators too; the learning rate used to weight each model was 0.4, with a maximum depth of 5, and the number of samples used in each tree was 0.7. The remaining two models’ parameters were described in more detail in the following section.
In order to evaluate the predictions made by the models, it is important to consider certain relevant elements. These elements will help determine the accuracy and performance of the models.
Firstly, the evaluation of the models’ estimates was conducted using the walk-forward validation method. This method consists of dividing the time series into several folds, training the model with a portion of the data, and then evaluating the performance on a validation set. A sliding window approach was used to select the different subsets of data for validation. The time series was divided into multiple windows, and for each window, the previous windows were used for training and the current window was used for validation. This process is repeated several times, each time using a different subset of the data as validation and the remaining data as training. In doing so, we can assess the models’ ability to generalize to new unseen data, making them particularly appropriate for time series forecasting. This approach ensures that the model is tested on different time periods and reduces the risk of overfitting to a specific period.
The accuracy of the predictions made by the models is assessed by comparing the estimated values with the actual values. To evaluate the performance of the models, three metrics were used: the mean absolute error (MAE):
The root mean squared error (RMSE):
Additionally, the mean absolute percentage error (MAPE):
where
is the actual value,
is the estimation, and
n is the number of samples. These three metrics provide different perspectives on the performance of the models and help to understand the accuracy of the predictions.
4. Results
In the following section, we present the evaluation of the prediction performance of our implemented models, LR, RF, XGB, LSTM, and GRU. The prediction of electricity prices and electricity consumption is evaluated using different evaluation metrics: MAE, RMSE, and MAPE. For each model, we provide two tables to showcase the forecasting results: one for the electricity pricing estimation and another for the prediction of electricity consumption. The metrics were calculated with the denormalized values of the data, providing a comprehensive assessment of the prediction’s performance.
Table 1 presents the performance of the electricity price and consumption predictions obtained using LR. Each row shows the results for a different number of lags used as input. The input delays in our models are sequential. For instance, when we set the lag to be 4, the input features used in the models will be
and
. This means that we consider the values of the variable in the previous four-time steps as inputs to the model. The columns related to the price depict that the three errors (MAE, RMSE, and MAPE) remain consistent across different lag values, indicating that the model is stable. On the other hand, the consumption errors show some variation in lag values. For example, for lags 12 and 16, the MAE and RMSE are significantly higher compared to other lags. The minimum RMSE for price modeling is 28.70, which corresponds to a lag of 24. Similarly, the best RMSE for consumption was obtained with 24 lags. However, for the remaining two errors, the optimal parameter is obtained with fewer lags, specifically with 2 and 4. It should be noted that there does not appear to be a clear trend in the errors for either the price or consumption models.
The results of the electricity price and consumption forecasting using RF are shown in
Table 2. The results of the analysis indicate a clear increasing trend in the errors for both the price and consumption models, suggesting that as the number of lags increases, the models tend to perform worse. Interestingly, the RF model shows better performance with fewer lags. It is important to note that hyperparameters can have a significant impact on the results. The performance of a model is highly dependent on the choice of hyperparameters, and therefore it is essential to carefully tune them to achieve the best performance. In fact, the results indicate that RF with fewer lags has even better errors than LR. This highlights the importance of selecting an appropriate number of lags when using this model. Furthermore, it is noteworthy that the behavior of the errors is similar for both the price and consumption models. This may suggest that there are underlying factors influencing both variables in a similar way and that the models are capturing these factors to some extent.
Table 3 shows the results of the electricity price and consumption prediction using XGB. The results of the analysis show that the XGB model exhibits more variability in errors compared to the previous models. Additionally, the results indicate that, in most cases, XGB performs worse with fewer lags. Surprisingly, increasing the number of lags up to 12 tends to enhance the error, but beyond this point, the errors tend to become worse. This may be caused by overfitting in the model. These findings suggest that careful consideration should be given to the selection of appropriate parameters when using XGB in order to avoid overfitting and obtain more reliable results.
The following
Table 4 shows the prediction results of electricity prices using LSTM with various hyperparameter settings. In this case, the hyperparameters are the number of epochs, patience, learning rate, batch size, and number of neurons. Upon examination of this table, there does not seem to be a clear pattern or trend in the performance of the prediction with different hyperparameters. In this case, the best configuration was found with 100 epochs, 20 patience, a 0.001 learning rate, 16 batch sizes, and 8 neurons, with a MAE of 9.17, a RMSE of 12.83, and a MAPE of 4.73.
The corresponding table for electricity consumption using LSTM can be seen in
Table 5. Based on the results, it appears that increasing the number of epochs generally leads to improvement in prediction, with the lowest MAE and MAPE being achieved when the number of epochs is between 400 and 600. Regarding other parameters, it is not possible to draw a clear pattern. The best number of neurons and batch size, as well as the optimal learning rate and patience values, vary and seem to depend on other parameters as well.
Finally, we evaluated the performance of GRU, as can be seen in
Table 6. Based on the data presented in the table, it can be concluded that there is no clear pattern in the prediction of electricity prices using GRU. Nevertheless, some observations can be made. The number of epochs, patience, and learning rate do not appear to have a significant impact on the prediction. The batch size and the number of neurons seem to have some effect; the lowest values of MAE and MAPE were achieved with a batch size of 64 and 4 neurons, respectively.
The last table,
Table 7, displays the prediction performance of the GRU model for electricity consumption. In this case, the results suggest a consistent pattern of lower prediction error with smaller batch sizes and a higher number of neurons. Specifically, the best configuration according to the lowest MAE and MAPE values was achieved with a batch size of 16 and a number of neurons equal to 8 when using 700 epochs with 150 patience and a learning rate of 0.001.
Finally, we gathered all the best results in
Table 8 in order to determine which one presented the best results. After further analysis, it can be observed that the performance of the models varied depending on the evaluation metric used. For the price modeling task, the LSTM model showed the best performance according to both the MAE and RMSE metrics. However, when considering the MAPE metric, the best results were obtained with the GRU model. Additionally, it is worth noting that although both LSTM and GRU models showed similar and good results for price modeling, XGB was able to achieve even better results for the consumption task. This suggests that different models may perform better for different tasks and that careful consideration should be given to selecting the most appropriate model for the specific application at hand. Overall, these findings demonstrate the utility of using multiple models and evaluation metrics to gain a comprehensive understanding of the performance of different time series prediction models.
We compared the performance of these five different models on our task using a two-tailed
t-test. We computed the
p-value for each pair of models and set a significance level of 0.05 using the RMSE metric. The results of
Table 9 show that for both price and consumption prediction, the statistical tests indicated that LR and XGB were not significant. RF and XGB were not significant in predicting the differences between the actual and predicted values of price and consumption. Furthermore, LSTM and GRU also did not show significant differences in their performance in predicting both price and consumption. However, the statistical tests revealed that the rest of the models were significant in their performance for both price and consumption prediction.
It is worth noting that XGB achieved the best results in consumption prediction, which is an interesting finding. However, the statistical tests showed that there was no significant difference between the performance of RF and XGB in both price and consumption prediction. This is an important result, as it suggests that RF, which is a more interpretable model than XGB, may be a good alternative to XGB in some applications. It is also worth mentioning that the tests showed that LSTM and GRU performed significantly better than the other models in either price or consumption prediction. Therefore, these results provide valuable insights into the strengths and weaknesses of different machine learning algorithms for intraday electricity price and consumption prediction, which can inform the development of more effective energy policies and pricing strategies.
Figure 3 illustrates a comparison of price and consumption predictions from five different models.
Figure 3a depicts the predicted values of all models against the actual price values for future time points
, and
h.
Figure 3b shows the same comparison but for the consumption data. The figure provides a visual representation of the performance of each model and its ability to capture the dynamics of the underlying data. The comparison allows us to identify the models that performed best in terms of accuracy and precision. This figure illustrates a useful summary of the model predictions and their ability to forecast the future values of the two different time series.
As a final remark, it is worth noting that pricing and consumption of electricity are not independent variables. Rather, they are closely related and can influence each other in various ways. For instance, when electricity prices are high, consumers may adjust their behavior to reduce their costs, which can lead to a decrease in energy consumption. Furthermore, electricity suppliers often offer different price ranges at different times of the day, which can encourage consumers to use electricity during off-peak hours, resulting in a reduction in total energy consumption. Therefore, investigating the relationship between pricing and consumption can provide insights into the drivers of electricity demand and inform policies aimed at promoting energy efficiency and reducing energy consumption.
5. Conclusions
In this study, we evaluated the performance of various machine learning methods for predicting electricity consumption and electricity prices. The models included LR, RF, XGB, LSTM, and GRU. Our results showed that LSTM and GRU were the best models for predicting electricity prices, with similar performance and high accuracy, suggesting that they are well-suited for this task. However, for electricity consumption modeling, XGB achieved the best results, indicating that it is a strong contender for this application. Despite these differences, the results of all three models (LSTM, GRU, and XGB) were relatively close, with low error rates and high accuracy, highlighting the potential of machine learning methods for predicting electricity consumption and pricing. In contrast, the LR model had significantly worse performance than the other models, with a relatively high error rate.
In conclusion, this research highlights the importance of using machine learning techniques for the prediction of electricity prices and consumption and the superior performance of XGB, LSTM, and GRU models compared to other machine learning methods. It stresses the potential of these models for real-world applications and provides a foundation for future research in the energy field. Future work can focus on exploring new methods, such as fuzzy neural networks, to efficiently handle uncertainty in prediction tasks. Additionally, the proposed methodology might be tested and applied to other regions with similar characteristics. A more exhaustive hyperparameter search can also be performed to improve model performance.
Finally, we suggest including additional performance measures that provide information about the behavior of the predicted model in the tails. It may be used with the Kupiec test or other tail tests to assess the model’s performance beyond the mean. These measures can provide valuable insights into the model’s behavior, especially in cases where the tails of the prediction error distribution are of interest.