Robust Reinforcement Learning: A Review of Foundations and Recent Advances
Abstract
:1. Introduction
2. Preliminaries
2.1. Optimization
2.2. Optimal Control
Hamilton-JACOBI-Bellman Equation
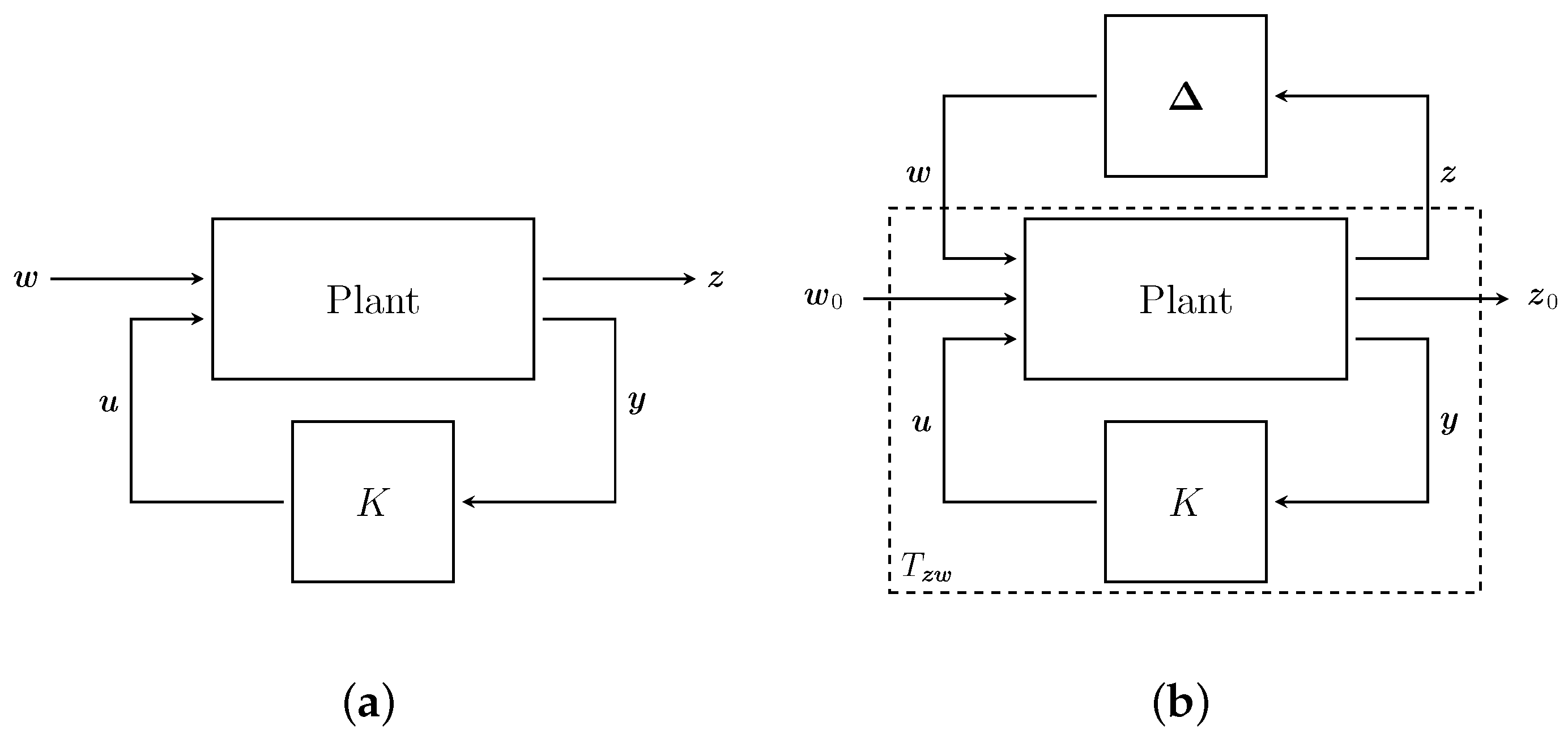
2.2.1. Robust Control
Relations to Game Theory
2.2.2. Differential Games
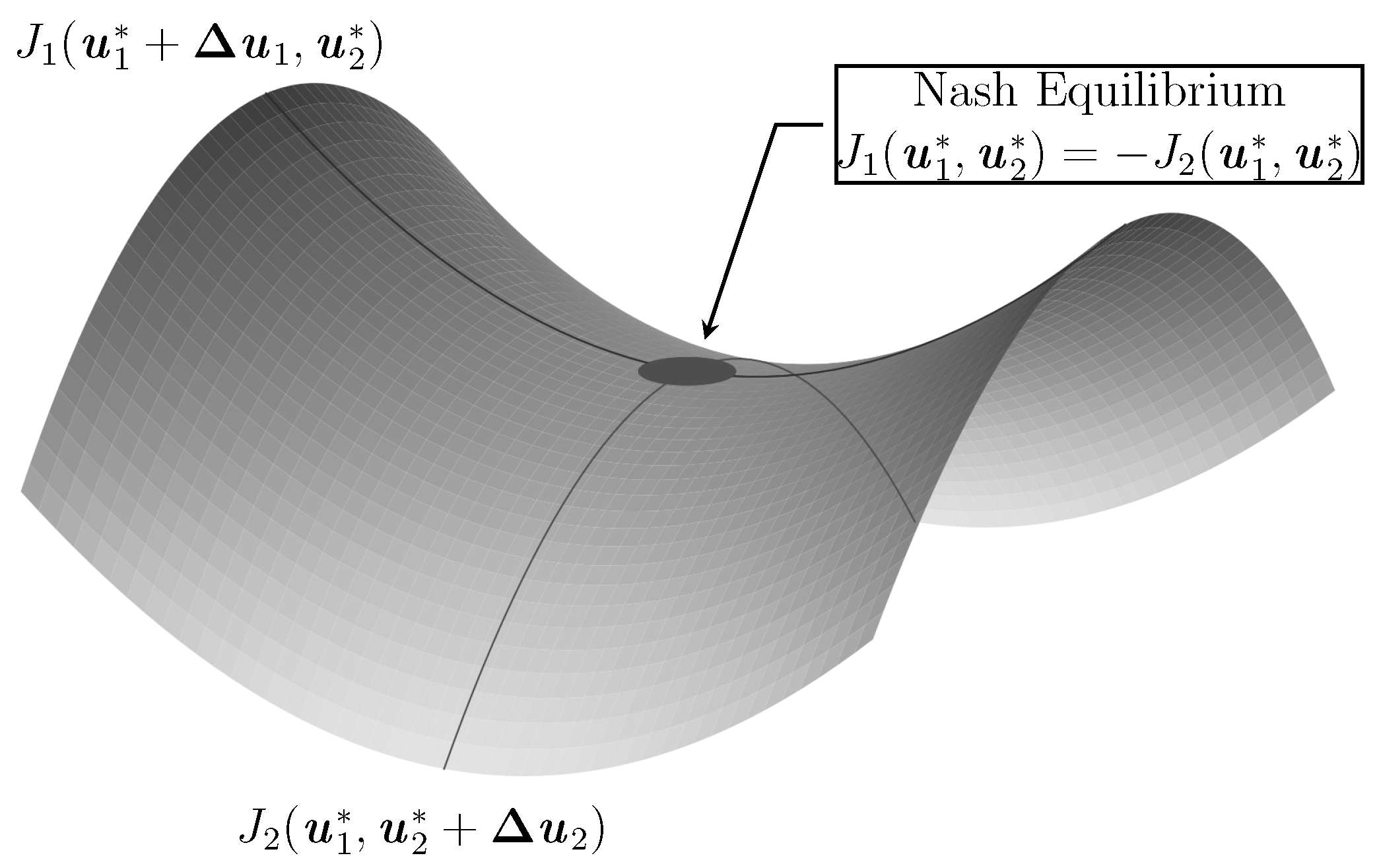
2.2.3. Nash Equilibrium
2.2.4. Two-Player Zero-Sum Game
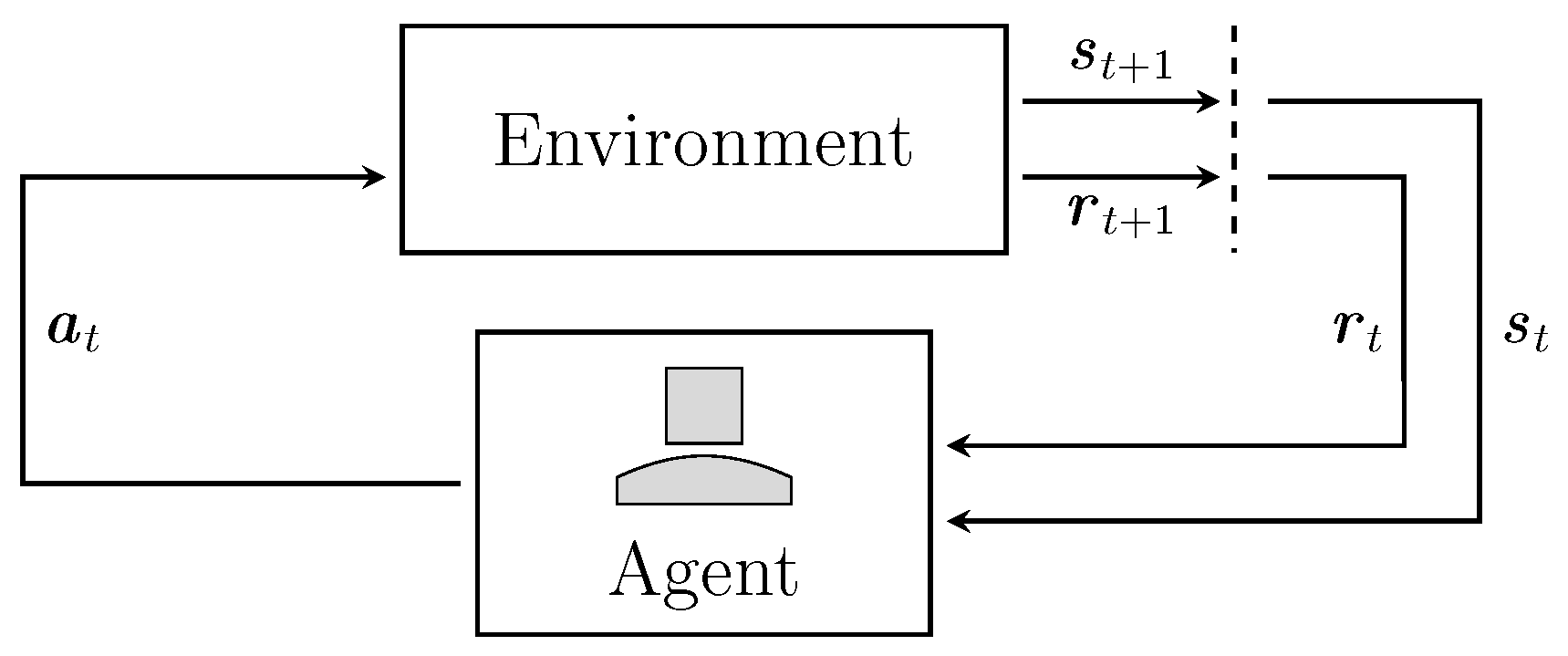
2.3. Reinforcement Learning
2.3.1. Single Agent Reinforcement Learning
2.3.2. Multi Agent Reinforcement Learning
3. Robustness in Reinforcement Learning
3.1. Transition and Reward Robust Designs
3.2. Disturbance Robust Designs
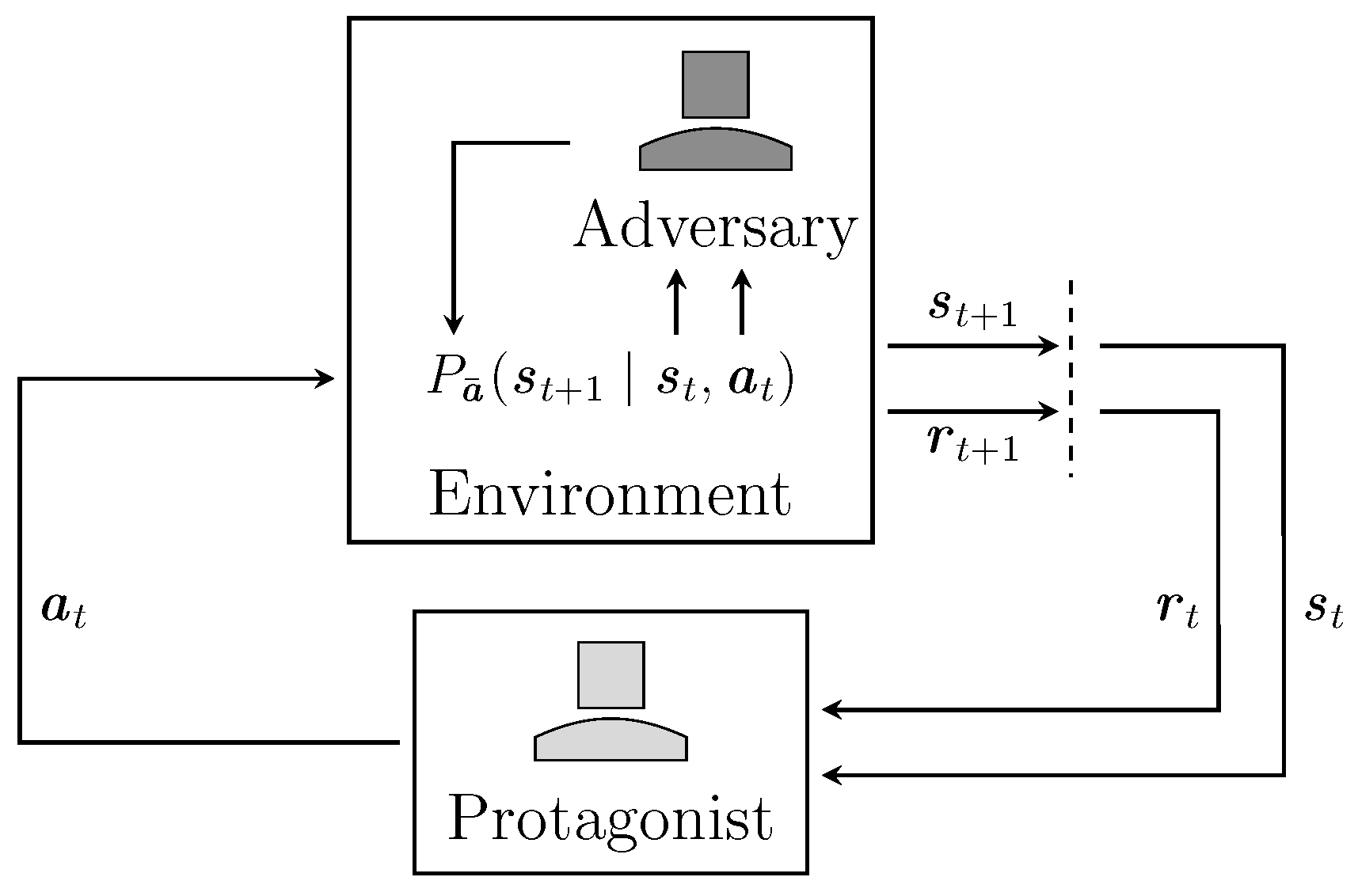
3.3. Action Robust Designs
3.4. Observation Robust Designs
3.5. Relations to Maximum Entropy RL and Risk Sensitivity
4. Conclusions
4.1. Summary
4.2. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A.; Powell, J.D. Feedback Control of Dynamic Systems; Addison-Wesley: Reading, MA, USA, 1994. [Google Scholar]
- Bennett, S. A brief history of automatic control. IEEE Control Syst. Mag. 1996, 16, 17–25. [Google Scholar]
- Bryson, A.E. Optimal control-1950 to 1985. IEEE Control Syst. Mag. 1996, 16, 26–33. [Google Scholar] [CrossRef]
- Kirk, D.E. Optimal Control Theory: An Introduction; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Morimoto, J.; Doya, K. Robust Reinforcement Learning. In Advances in Neural Information Processing Systems 13; Leen, T.K., Dietterich, T.G., Tresp, V., Eds.; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Pinto, L.; Davidson, J.; Gupta, A. Supervision via Competition: Robot Adversaries for Learning Tasks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar]
- Pinto, L.; Davidson, J.; Sukthankar, R.; Gupta, A. Robust Adversarial Reinforcement Learning. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Tamar, A.; Xu, H.; Mannor, S. Scaling up robust MDPs by reinforcement learning. arXiv 2013, arXiv:1306.6189. [Google Scholar]
- Tessler, C.; Efroni, Y.; Mannor, S. Action Robust Reinforcement Learning and Applications in Continuous Control. In Proceedings of the 36th International Conference on Machine Learning (ICML), PMLR, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Zhou, K.; Doyle, J.C. Essentials of Robust Control; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Hansen, L.P.; Sargent, T.J. Robustness; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Ben-Tal, A.; Nemirovski, A. Robust convex optimization. Math. Oper. Res. 1998, 23, 769–805. [Google Scholar] [CrossRef] [Green Version]
- Ben-Tal, A.; Nemirovski, A. Robust optimization–methodology and applications. Math. Program. 2002, 92, 453–480. [Google Scholar] [CrossRef]
- Safonov, M.G. Origins of robust control: Early history and future speculations. Annu. Rev. Control 2012, 26, 173–181. [Google Scholar] [CrossRef]
- Zames, G. Feedback and optimal sensitivity: Model reference transformations, multiplicative seminorms, and approximate inverses. IEEE Trans. Autom. Control 1981, 26, 301–320. [Google Scholar] [CrossRef]
- Doyle, J. Analysis of feedback systems with structured uncertainties. In IEE Proceedings D-Control Theory and Applications; IET: London, UK, 1982. [Google Scholar]
- Zames, G.; Francis, B. Feedback, minimax sensitivity, and optimal robustness. IEEE Trans. Autom. Control 1983, 28, 585–601. [Google Scholar] [CrossRef]
- Doyle, J.C.; Glover, K.; Khargonekar, P.P.; Francis, B.A. State-space solutions to standard H2 and H∞ control problems. IEEE Trans. Autom. Control 1989, 1691–1696. [Google Scholar] [CrossRef] [Green Version]
- Van Der Schaft, A.J. L 2-gain analysis of nonlinear systems and nonlinear state feedback H∞ control. IEEE Trans. Autom. Control 1992, 37, 770–784. [Google Scholar] [CrossRef] [Green Version]
- Bagnell, J.A.; Ng, A.Y.; Schneider, J.G. Solving Uncertain Markov Decision Processes; Carnegie Mellon University, the Robotics Institute: Pittsburgh, PA, USA, 2001. [Google Scholar]
- Nilim, A.; El Ghaoui, L. Robust control of Markov decision processes with uncertain transition matrices. Oper. Res. 2005, 53, 780–798. [Google Scholar] [CrossRef] [Green Version]
- Iyengar, G.N. Robust dynamic programming. Math. Oper. Res. 2005, 30, 257–280. [Google Scholar] [CrossRef] [Green Version]
- Glover, K.; Doyle, J.C. State-space formulae for all stabilizing controllers that satisfy an H(infinity)-norm bound and relations to risk sensitivity. Syst. Control Lett. 1988, 11, 167–172. [Google Scholar] [CrossRef]
- Basar, T.; Bernhard, P. H∞-Optimal Control and Related Minimax Design Problems: A Dynamic Game Approach; Birkháuser: Boston, MA, USA, 2008. [Google Scholar]
- Limebeer, D.J.N.; Anderson, B.D.O.; Khargonekar, P.P.; Green, M. A Game Theoretic Approach to H∞ Control for Time-varying Systems. SIAM J. Control Optim. 1992, 30, 262–283. [Google Scholar] [CrossRef]
- McEneaney, W.M. Robust control and differential games on a finite time horizon. Math. Control Signals Syst. 1995, 8, 138–166. [Google Scholar] [CrossRef]
- Isaacs, R. Differential Games I: Introduction; Technical Report; Rand Corp: Santa Monica, CA, USA, 1954. [Google Scholar]
- Owen, G. Game Theory; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Ho, Y.; Bryson, A.; Baron, S. Differential games and optimal pursuit-evasion strategies. IEEE Trans. Autom. Control 1965, 10, 385–389. [Google Scholar] [CrossRef]
- Starr, A.W.; Ho, Y.C. Nonzero-sum differential games. J. Optim. Theory Appl. 1969, 3, 184–206. [Google Scholar] [CrossRef]
- Littman, M.L. Value-function reinforcement learning in Markov games. Cogn. Syst. Res. 2001, 2, 55–66. [Google Scholar] [CrossRef] [Green Version]
- Uther, W.; Veloso, M. Adversarial Reinforcement Learning; Carnegie Mellon University: Pittsburgh, PA, USA, 1997. [Google Scholar]
- Shoham, Y.; Leyton-Brown, K. Multiagent systems: Algorithmic, Game-Theoretic, and Logical Foundations; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- LaValle, S.M. Robot Motion Planning: A Game-Theoretic Foundation. Algorithmica 2000, 26, 430–465. [Google Scholar] [CrossRef]
- Charalambous, C.D.; Rezaei, F. Stochastic uncertain systems subject to relative entropy constraints: Induced norms and monotonicity properties of minimax games. IEEE Trans. Autom. Control 2007, 52, 647–663. [Google Scholar] [CrossRef]
- Xu, H.; Mannor, S. The robustness-performance tradeoff in Markov decision processes. In Advances in Neural Information Processing Systems (NIPS); MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Xu, H.; Mannor, S. Distributionally robust Markov decision processes. In Advances in Neural Information Processing Systems (NIPS); Curran Associates, Inc.: Red Hook, NY, USA, 2010. [Google Scholar]
- Delage, E.; Mannor, S. Percentile optimization for Markov decision processes with parameter uncertainty. Oper. Res. 2010, 58, 203–213. [Google Scholar] [CrossRef] [Green Version]
- Mannor, S.; Mebel, O.; Xu, H. Lightning does not strike twice: Robust MDPs with coupled uncertainty. arXiv 2012, arXiv:1206.4643. [Google Scholar]
- Hu, Z.; Hong, L.J. Kullback-Leibler Divergence Constrained Distributionally Robust Optimization. Available at Optimization Online. 2013. Available online: https://asset-pdf.scinapse.io/prod/2562747313/2562747313.pdf (accessed on 12 March 2022).
- Lim, S.H.; Xu, H.; Mannor, S. Reinforcement learning in robust markov decision processes. In Advances in Neural Information Processing Systems (NIPS); Curran Associates, Inc.: Red Hook, NY, USA, 2013. [Google Scholar]
- Wiesemann, W.; Kuhn, D.; Rustem, B. Robust Markov Decision Processes. Math. Oper. Res. 2013, 38, 153–183. [Google Scholar] [CrossRef] [Green Version]
- Yu, P.; Xu, H. Distributionally robust counterpart in Markov decision processes. IEEE Trans. Autom. Control 2015, 61, 2538–2543. [Google Scholar] [CrossRef] [Green Version]
- Mannor, S.; Mebel, O.; Xu, H. Robust MDPs with k-rectangular uncertainty. Math. Oper. Res. 2016, 41, 1484–1509. [Google Scholar] [CrossRef]
- Goyal, V.; Grand-Clement, J. Robust Markov Decision Process: Beyond Rectangularity. arXiv 2018, arXiv:1811.00215. [Google Scholar]
- Smirnova, E.; Dohmatob, E.; Mary, J. Distributionally robust reinforcement learning. arXiv 2019, arXiv:1902.08708. [Google Scholar]
- Coulson, J.; Lygeros, J.; Dörfler, F. Regularized and Distributionally Robust Data-Enabled Predictive Control. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019. [Google Scholar]
- Derman, E.; Mannor, S. Distributional robustness and regularization in reinforcement learning. arXiv 2020, arXiv:2003.02894. [Google Scholar]
- Turchetta, M.; Krause, A.; Trimpe, S. Robust model-free reinforcement learning with multi-objective Bayesian optimization. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Abdulsamad, H.; Dorau, T.; Belousov, B.; Zhu, J.J.; Peters, J. Distributionally Robust Trajectory Optimization Under Uncertain Dynamics via Relative-Entropy Trust Regions. arXiv 2021, arXiv:2103.15388. [Google Scholar]
- Yang, I. Wasserstein Distributionally Robust Stochastic Control: A Data-Driven Approach. IEEE Trans. Autom. Control 2021, 66, 3863–3870. [Google Scholar] [CrossRef]
- Klima, R.; Bloembergen, D.; Kaisers, M.; Tuyls, K. Robust temporal difference learning for critical domains. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems (AAMAS). International Foundation for Autonomous Agents and Multiagent Systems, Montreal, QC, Canada, 13–17 May 2019. [Google Scholar]
- Pan, X.; Seita, D.; Gao, Y.; Canny, J. Risk Averse Robust Adversarial Reinforcement Learning. arXiv 2019, arXiv:1901.08021. [Google Scholar]
- Tan, K.L.; Esfandiari, Y.; Lee, X.Y.; Sarkar, S. Robustifying reinforcement learning agents via action space adversarial training. In Proceedings of the 2020 American control conference (ACC), Denver, CO, USA, 1–3 July 2020. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Advances in Neural Information Processing Systems 27 (NIPS); Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Huang, S.; Papernot, N.; Goodfellow, I.; Duan, Y.; Abbeel, P. Adversarial Attacks on Neural Network Policies. arXiv 2017, arXiv:1702.02284. [Google Scholar]
- Mandlekar, A.; Zhu, Y.; Garg, A.; Fei-Fei, L.; Savarese, S. Adversarially robust policy learning: Active construction of physically-plausible perturbations. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Pattanaik, A.; Tang, Z.; Liu, S.; Bommannan, G.; Chowdhary, G. Robust Deep Reinforcement Learning with Adversarial Attacks. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems (AAMAS). International Foundation for Autonomous Agents and Multiagent Systems, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Gleave, A.; Dennis, M.; Kant, N.; Wild, C.; Levine, S.; Russell, S. Adversarial Policies: Attacking Deep Reinforcement Learning. arXiv 2019, arXiv:1905.10615. [Google Scholar]
- Zhang, H.; Chen, H.; Xiao, C.; Li, B.; Liu, M.; Boning, D.; Hsieh, C.J. Robust Deep Reinforcement Learning against Adversarial Perturbations on State Observations. arXiv 2020, arXiv:2003.08938. [Google Scholar]
- Lütjens, B.; Everett, M.; How, J.P. Certified adversarial robustness for deep reinforcement learning. In Proceedings of the Conference on Robot Learning (CoRL), Osaka, Japan, 30 October–1 November 2019. [Google Scholar]
- Grünwald, P.D.; Dawid, A.P. Game theory, maximum entropy, minimum discrepancy and robust Bayesian decision theory. Ann. Stat. 2004, 32, 1367–1433. [Google Scholar] [CrossRef] [Green Version]
- Osogami, T. Robustness and risk-sensitivity in Markov decision processes. In Advances in Neural Information Processing Systems (NIPS); Curran Associates, Inc.: Red Hook, NY, USA, 2012. [Google Scholar]
- Eysenbach, B.; Levine, S. If MaxEnt RL is the Answer, What is the Question? arXiv 2019, arXiv:1910.01913. [Google Scholar]
- Eysenbach, B.; Levine, S. Maximum entropy rl (provably) solves some robust rl problems. arXiv 2021, arXiv:2103.06257. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Papageorgiou, M.; Leibold, M.; Buss, M. Optimierung; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Kall, P.; Wallace, S.W.; Kall, P. Stochastic Programming; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Beyer, H.G.; Sendhoff, B. Robust optimization–A comprehensive survey. Comput. Methods Appl. Mech. Eng. 2007, 196, 3190–3218. [Google Scholar] [CrossRef]
- Xu, H.; Caramanis, C.; Mannor, S. A distributional interpretation of robust optimization. Math. Oper. Res. 2012, 37, 95–110. [Google Scholar] [CrossRef]
- Wiesemann, W.; Kuhn, D.; Sim, M. Distributionally robust convex optimization. Oper. Res. 2014, 62, 1358–1376. [Google Scholar] [CrossRef] [Green Version]
- Heger, M. Consideration of risk in reinforcement learning. In Machine Learning Proceedings 1994; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Scarf, H.E. A Min-Max Solution of an Inventory Problem; Technical Report; Rand Corp: Santa Monica, CA, USA, 1957. [Google Scholar]
- Bolza, O. Vorlesungen über Variationsrechnung; BG Teubner: Stuttgart, Germany, 1909; Available online: https://diglib.uibk.ac.at/ulbtirol/content/titleinfo/372088 (accessed on 12 March 2022).
- McShane, E.J. On multipliers for Lagrange problems. Am. J. Math. 1939, 61, 809–819. [Google Scholar] [CrossRef]
- Bliss, G.A. Lectures on the Calculus of Variations; University of Chicago Press: Chicago, IL, USA, 1946. [Google Scholar]
- Cicala, P. An Engineering Approach to the Calculus of Variations; Libreria Editrice Universitaria Levrotto & Bella: Turin, Italy, 1957. [Google Scholar]
- Pontryagin, L.S. Mathematical Theory of Optimal Processes; Routledge: London, UK, 2018. [Google Scholar]
- Bellman, R. The theory of dynamic programming. Bull. Am. Math. Soc. 1954, 60, 503–515. [Google Scholar] [CrossRef] [Green Version]
- Doya, K. Reinforcement Learning in Continuous Time and Space. Neural Comput. 2000, 12, 219–245. [Google Scholar] [CrossRef] [PubMed]
- Bellman, R. A Markovian decision process. J. Math. Mech. 1957, 6, 679–684. [Google Scholar] [CrossRef]
- Kalman, R.E. Contributions to the theory of optimal control. Bol. Soc. Mat. Mex. 1960, 5, 102–119. [Google Scholar]
- Kalman, R.E.; Bertram, J.E. Control system analysis and design via the “second method” of Lyapunov: I—Continuous-time systems. J. Basic Eng. 1960, 82, 371–393. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Isaacs, R. Differential Games: A Mathematical Theory with Applications to Warfare and Pursuit, Control and Optimization; Dover Publications: Mineola, NY, USA, 1999. [Google Scholar]
- Nash, J. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Awheda, M. On Multi-Agent Reinforcement Learning in Matrix, Stochastic and Differential Games. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2017. [Google Scholar]
- Bowling, M.H.; Veloso, M.M. An Analysis of Stochastic Game Theory for Multiagent Reinforcement Learning. 2000. Available online: https://apps.dtic.mil/sti/citations/ADA385122 (accessed on 12 March 2022).
- Howard, R.A. Dynamic Programming and Markov Processes. 1960. Available online: https://psycnet.apa.org/record/1961-01474-000 (accessed on 12 March 2022).
- Littman, M.L. Markov games as a framework for multi-agent reinforcement learning. In Machine Learning Proceedings 1994; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Sharma, R.; Gopal, M. A robust Markov game controller for nonlinear systems. Appl. Soft Comput. 2007, 7, 818–827. [Google Scholar] [CrossRef]
- Monahan, G.E. State of the art—A survey of partially observable Markov decision processes: Theory, models, and algorithms. Manag. Sci. 1982, 28, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Kaelbling, L.P.; Littman, M.L.; Cassandra, A.R. Planning and acting in partially observable stochastic domains. Artif. Intell. 1998, 101, 99–134. [Google Scholar] [CrossRef] [Green Version]
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. Adv. Neural Inf. Process. Syst. 1999, 12. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the 35th International Conference on Machine Learning PMLR, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef] [Green Version]
- Kakade, S.M. A natural policy gradient. In Advances in Neural Information Processing Systems; NIPS: Cambridge, MA, USA, 2001; Volume 14. [Google Scholar]
- Peters, J.; Schaal, S. Natural actor-critic. Neurocomputing 2008, 71, 1180–1190. [Google Scholar] [CrossRef]
- Peters, J.; Mulling, K.; Altun, Y. Relative entropy policy search. In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 7–9 July 2015. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Lanctot, M.; Zambaldi, V.; Gruslys, A.; Lazaridou, A.; Tuyls, K.; Perolat, J.; Silver, D.; Graepel, T. A Unified Game-Theoretic Approach to Multiagent Reinforcement Learning. In Advances in Neural Information Processing Systems; NIPS: Cambridge, MA, USA, 2017; Volume 30. [Google Scholar]
- Laurent, G.J.; Matignon, L.; Fort-Piat, L. The world of independent learners is not Markovian. Int. J.-Knowl.-Based Intell. Eng. Syst. 2011, 15, 55–64. [Google Scholar] [CrossRef] [Green Version]
- Claus, C.; Boutilier, C. The Dynamics of Reinforcement Learning in Cooperative Multiagent Systems. In Proceedings of the Fifteenth National/Tenth Conference on Artificial Intelligence/Innovative Applications of Artificial Intelligence. American Association for Artificial Intelligence, Madison, WI, USA, 26–30 July 1998. [Google Scholar]
- Shapley, L.S. Stochastic games. Proc. Natl. Acad. Sci. USA 1953, 39, 1095–1100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buşoniu, L.; Babuška, R.; Schutter, B.D. Multi-agent reinforcement learning: An overview. In Innovations in Multi-Agent Systems and Applications-1; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Gronauer, S.; Diepold, K. Multi-agent deep reinforcement learning: A survey. Artif. Intell. Rev. 2021, 55, 895–943. [Google Scholar] [CrossRef]
- Littman, M.L.; Szepesvári, C. A generalized reinforcement-learning model: Convergence and applications. ICML 1996, 96, 310–318. [Google Scholar]
- Szepesvári, C.; Littman, M.L. A unified analysis of value-function-based reinforcement-learning algorithms. Neural Comput. 1999, 11, 2017–2060. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Foerster, J.; Assael, I.A.; De Freitas, N.; Whiteson, S. Learning to communicate with deep multi-agent reinforcement learning. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Advances in Neural Information Processing Systems; NIPS: Cambridge, MA, USA, 2017; Volume 30. [Google Scholar]
- Foerster, J.; Farquhar, G.; Afouras, T.; Nardelli, N.; Whiteson, S. Counterfactual multi-agent policy gradients. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Rashid, T.; Samvelyan, M.; Schroeder, C.; Farquhar, G.; Foerster, J.; Whiteson, S. Qmix: Monotonic value function factorisation for deep multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning (ICML), PMLR, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Mahajan, A.; Rashid, T.; Samvelyan, M.; Whiteson, S. Maven: Multi-agent variational exploration. In Advances in Neural Information Processing Systems (NIPS); Curran Associates, Inc.: Red Hook, NY, USA, 2019. [Google Scholar]
- Son, K.; Kim, D.; Kang, W.J.; Hostallero, D.E.; Yi, Y. Qtran: Learning to factorize with transformation for cooperative multi-agent reinforcement learning. In Proceedings of the 36th International Conference on Machine Learning (ICML), PMLR, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Rashid, T.; Farquhar, G.; Peng, B.; Whiteson, S. Weighted qmix: Expanding monotonic value function factorisation for deep multi-agent reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 10199–10210. [Google Scholar]
- Zhu, Y.; Zhao, D. Online minimax Q network learning for two-player zero-sum Markov games. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 1228–1241. [Google Scholar] [CrossRef]
- Yu, C.; Velu, A.; Vinitsky, E.; Wang, Y.; Bayen, A.; Wu, Y. The Surprising Effectiveness of PPO in Cooperative, Multi-Agent Games. arXiv 2021, arXiv:2103.01955. [Google Scholar]
- Xu, H.; Mannor, S. Robustness and generalization. Mach. Learn. 2012, 86, 391–423. [Google Scholar] [CrossRef] [Green Version]
- Satia, J.K.; Lave Jr, R.E. Markovian decision processes with uncertain transition probabilities. Oper. Res. 1973, 21, 728–740. [Google Scholar] [CrossRef]
- Xiao, C.; Li, B.; Zhu, J.Y.; He, W.; Liu, M.; Song, D. Generating adversarial examples with adversarial networks. arXiv 2018, arXiv:1801.02610. [Google Scholar]
- White, C.C., III; Eldeib, H.K. Markov decision processes with imprecise transition probabilities. Oper. Res. 1994, 42, 739–749. [Google Scholar] [CrossRef]
- Givan, R.; Leach, S.; Dean, T. Bounded parameter Markov decision processes. In European Conference on Planning; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Littman, M.L. Memoryless policies: Theoretical limitations and practical results. In From Animals to Animats 3: Proceedings of the Third International Conference on Simulation of Adaptive Behavior; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Zhu, J.J.; Jitkrittum, W.; Diehl, M.; Schölkopf, B. Worst-Case Risk Quantification under Distributional Ambiguity using Kernel Mean Embedding in Moment Problem. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Korea, 14–18 December 2020. [Google Scholar]
- Gupta, V. Near-optimal Bayesian ambiguity sets for distributionally robust optimization. Manag. Sci. 2019, 65, 4242–4260. [Google Scholar] [CrossRef] [Green Version]
- Rahimian, H.; Mehrotra, S. Distributionally robust optimization: A review. arXiv 2019, arXiv:1908.05659. [Google Scholar]
- Badrinath, K.P.; Kalathil, D. Robust Reinforcement Learning using Least Squares Policy Iteration with Provable Performance Guarantees. In Proceedings of the International Conference on Machine Learning PMLR, Virtual, 18–24 July 2021. [Google Scholar]
- Abdullah, M.A.; Ren, H.; Ammar, H.B.; Milenkovic, V.; Luo, R.; Zhang, M.; Wang, J. Wasserstein robust reinforcement learning. arXiv 2019, arXiv:1907.13196. [Google Scholar]
- Todorov, E.; Erez, T.; Tassa, Y. Mujoco: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012. [Google Scholar]
- O’Donoghue, B.; Osband, I.; Munos, R.; Mnih, V. The uncertainty bellman equation and exploration. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Derman, E.; Mankowitz, D.; Mann, T.; Mannor, S. A Bayesian Approach to Robust Reinforcement Learning. In Proceedings of the Conference on Uncertainty in Artificial Intelligence (UAI), PMLR, Tel Aviv, Israel, 22–25 July 2019. [Google Scholar]
- Rajeswaran, A.; Ghotra, S.; Ravindran, B.; Levine, S. Epopt: Learning robust neural network policies using model ensembles. arXiv 2016, arXiv:1610.01283. [Google Scholar]
- Tamar, A.; Glassner, Y.; Mannor, S. Optimizing the CVaR via sampling. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Mankowitz, D.J.; Levine, N.; Jeong, R.; Shi, Y.; Kay, J.; Abdolmaleki, A.; Springenberg, J.T.; Mann, T.; Hester, T.; Riedmiller, M. Robust reinforcement learning for continuous control with model misspecification. arXiv 2019, arXiv:1906.07516. [Google Scholar]
- Lutter, M.; Mannor, S.; Peters, J.; Fox, D.; Garg, A. Robust Value Iteration for Continuous Control Tasks. arXiv 2021, arXiv:2105.12189. [Google Scholar]
- Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The limitations of deep learning in adversarial settings. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbruecken, Germany, 21–24 March 2016. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Welling, M.; Teh, Y.W. Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the 28th international conference on machine learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Salman, H.; Yang, G.; Zhang, H.; Hsieh, C.J.; Zhang, P. A convex relaxation barrier to tight robustness verification of neural networks. arXiv 2019, arXiv:1902.08722. [Google Scholar]
- Ziebart, B.D. Modeling Purposeful Adaptive Behavior with the Principle of Maximum Causal Entropy; Carnegie Mellon University: Pittsburgh, PA, USA, 2010. [Google Scholar]
- Howard, R.A.; Matheson, J.E. Risk-sensitive Markov decision processes. Manag. Sci. 1972, 18, 356–369. [Google Scholar] [CrossRef]
- Jaquette, S.C. A utility criterion for Markov decision processes. Manag. Sci. 1976, 23, 43–49. [Google Scholar] [CrossRef]
- Denardo, E.V.; Rothblum, U.G. Optimal stopping, exponential utility, and linear programming. Math. Program. 1979, 16, 228–244. [Google Scholar] [CrossRef]
- Patek, S.D. On terminating Markov decision processes with a risk-averse objective function. Automatica 2001, 37, 1379–1386. [Google Scholar] [CrossRef]
- Osogami, T. Iterated risk measures for risk-sensitive Markov decision processes with discounted cost. arXiv 2012, arXiv:1202.3755. [Google Scholar]
- Whittle, P. Risk-sensitive linear quadratic Gaussian control. Adv. Appl. Probab. 1981, 13, 764–777. [Google Scholar] [CrossRef]
- Whittle, P. Risk sensitivity, a strangely pervasive concept. Macroecon. Dyn. 2002, 6, 5–18. [Google Scholar] [CrossRef] [Green Version]
- Nass, D.; Belousov, B.; Peters, J. Entropic Risk Measure in Policy Search. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019. [Google Scholar]
- Petersen, I.; James, M.; Dupuis, P. Minimax optimal control of stochastic uncertain systems with relative entropy constraints. IEEE Trans. Autom. Control 2000, 45, 398–412. [Google Scholar] [CrossRef] [Green Version]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar]
- Papernot, N.; McDaniel, P.; Goodfellow, I.; Jha, S.; Celik, Z.B.; Swami, A. Practical black-box attacks against machine learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, Abu Dhabi, United Arab Emirates, 2–6 April 2017. [Google Scholar]



| Item | Definition |
|---|---|
| State | |
| Action | |
| Reward | r |
| Stochastic Transition Matrix | |
| Transition probability | |
| Horizon | T |
| Uncertainty | |
| Objective | |
| Bellman Operator | |
| History | |
| Parameter | |
| Value Function | V |
| Q Function | Q |
| Policy/Strategy | |
| Discount Factor | |
| Expectation | |
| Variance | |
| Identity Matrix | |
| Probability Distribution | |
| Learning Rate | |
| Adversary | A |
| Protagonist | P |
| Reinforcement Learning | Optimal Control |
|---|---|
| State | State |
| Action | Control |
| Reward r | Cost |
| Observations o | Measurements y |
| Transition | Dynamics |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moos, J.; Hansel, K.; Abdulsamad, H.; Stark, S.; Clever, D.; Peters, J. Robust Reinforcement Learning: A Review of Foundations and Recent Advances. Mach. Learn. Knowl. Extr. 2022, 4, 276-315. https://doi.org/10.3390/make4010013
Moos J, Hansel K, Abdulsamad H, Stark S, Clever D, Peters J. Robust Reinforcement Learning: A Review of Foundations and Recent Advances. Machine Learning and Knowledge Extraction. 2022; 4(1):276-315. https://doi.org/10.3390/make4010013
Chicago/Turabian StyleMoos, Janosch, Kay Hansel, Hany Abdulsamad, Svenja Stark, Debora Clever, and Jan Peters. 2022. "Robust Reinforcement Learning: A Review of Foundations and Recent Advances" Machine Learning and Knowledge Extraction 4, no. 1: 276-315. https://doi.org/10.3390/make4010013
APA StyleMoos, J., Hansel, K., Abdulsamad, H., Stark, S., Clever, D., & Peters, J. (2022). Robust Reinforcement Learning: A Review of Foundations and Recent Advances. Machine Learning and Knowledge Extraction, 4(1), 276-315. https://doi.org/10.3390/make4010013






