Explainable AI Framework for Multivariate Hydrochemical Time Series
Abstract
1. Introduction
- An open-source and application-oriented XAI framework through swiftly accessible and combinable modules is provided
- Every module can be evaluated and verified separately using robust methods
- From a domain expert’s perspective, the DDS-XAI provides more meaningful and relevant explanations than comparable XAIs
- Evaluation criteria of explainability are derived from well-founded principles: Grice’s maxims [11]
Related Works
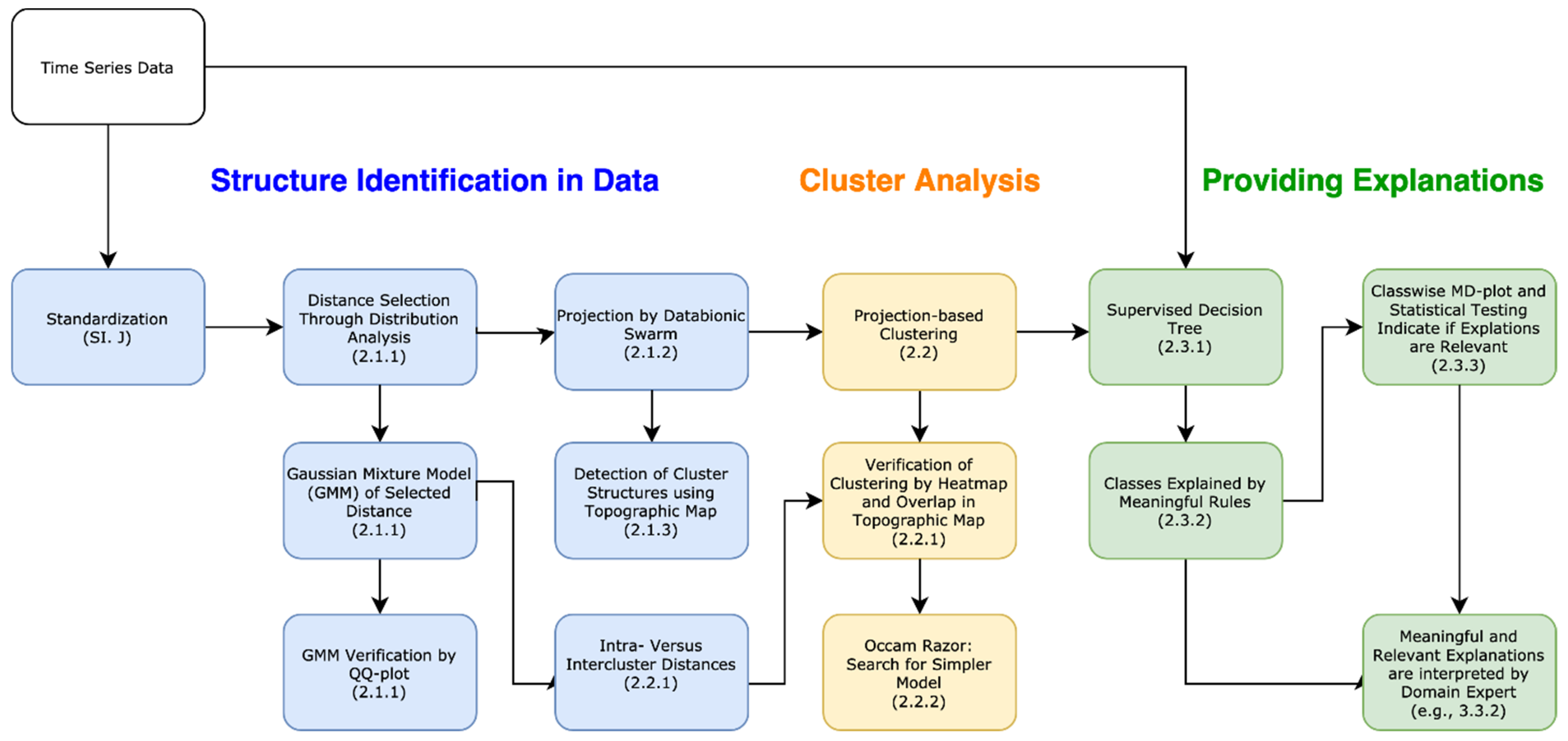
2. XAI Framework
2.1. Step I: Identification of Structures in the Data
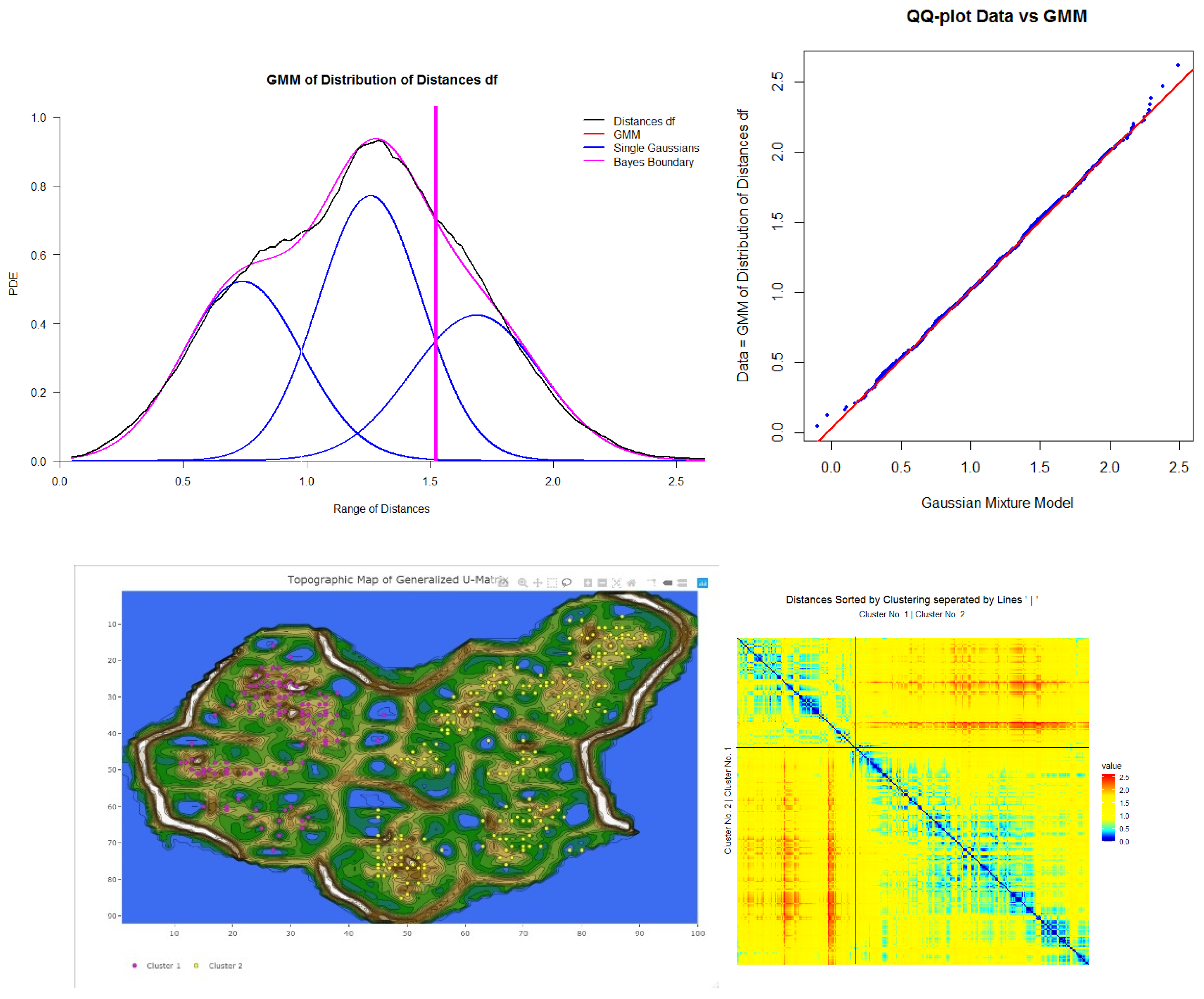
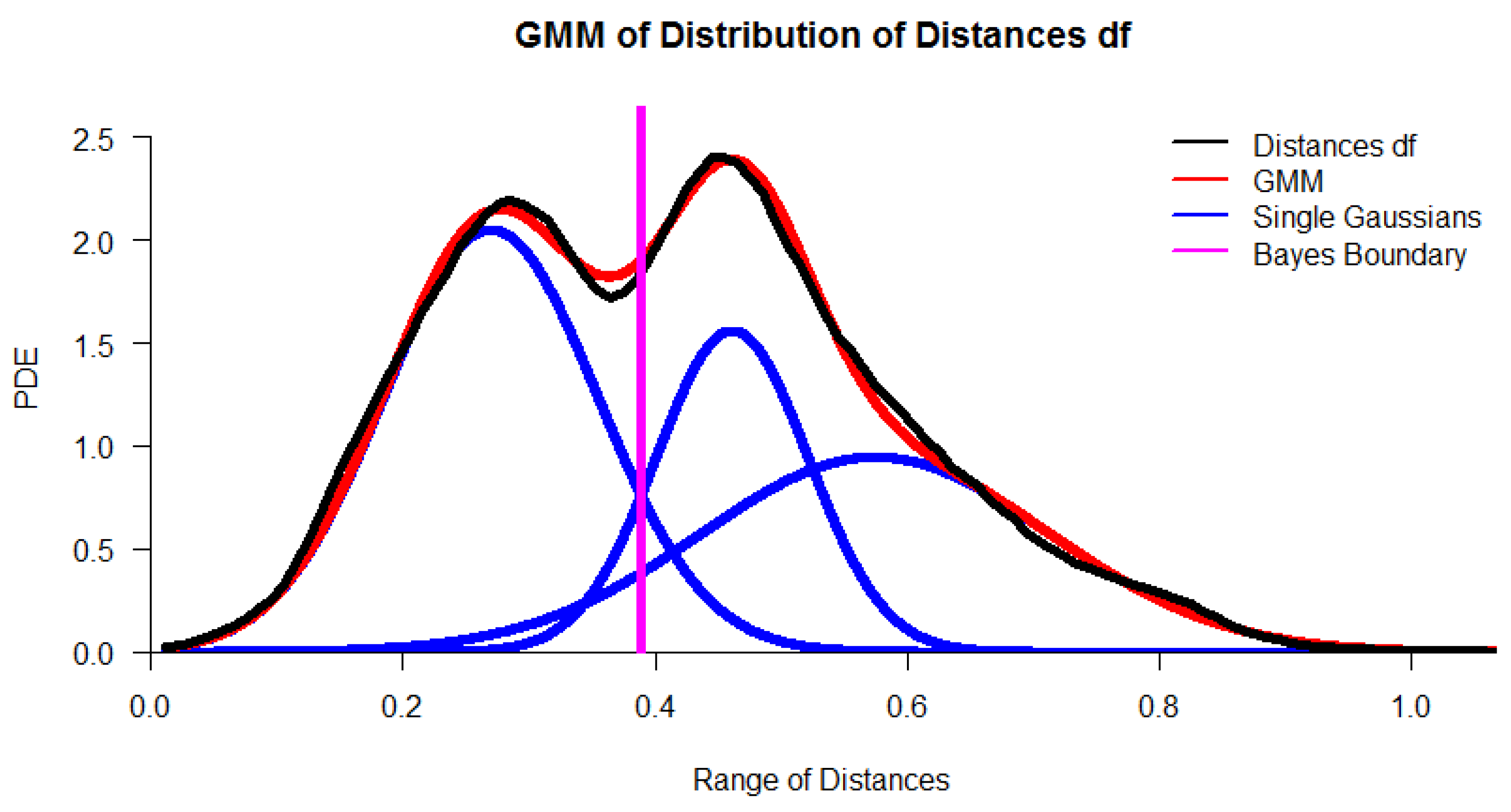
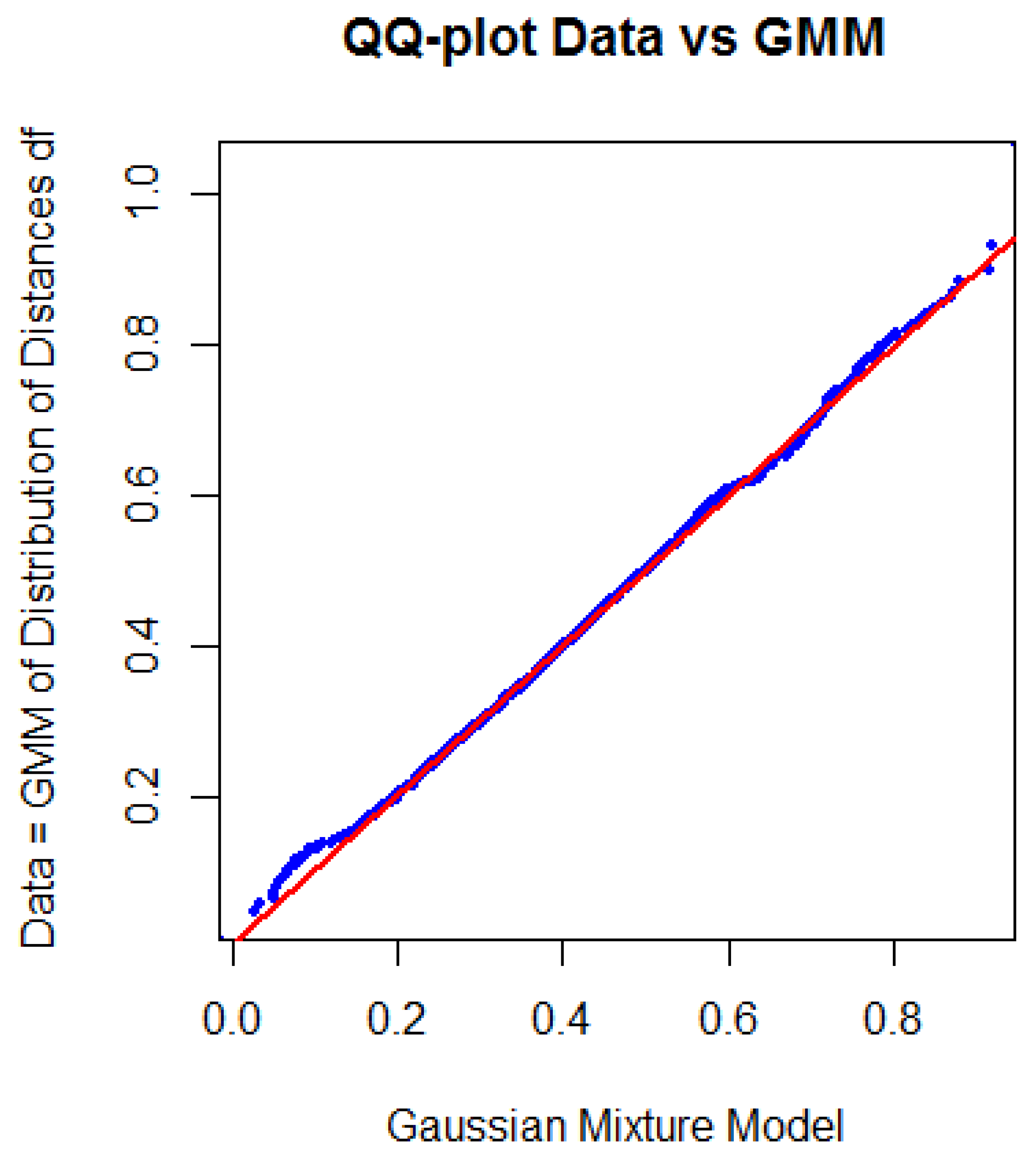
2.1.1. Distance Selection
2.1.2. Projection
2.1.3. Structure Visualization by Topographic Map
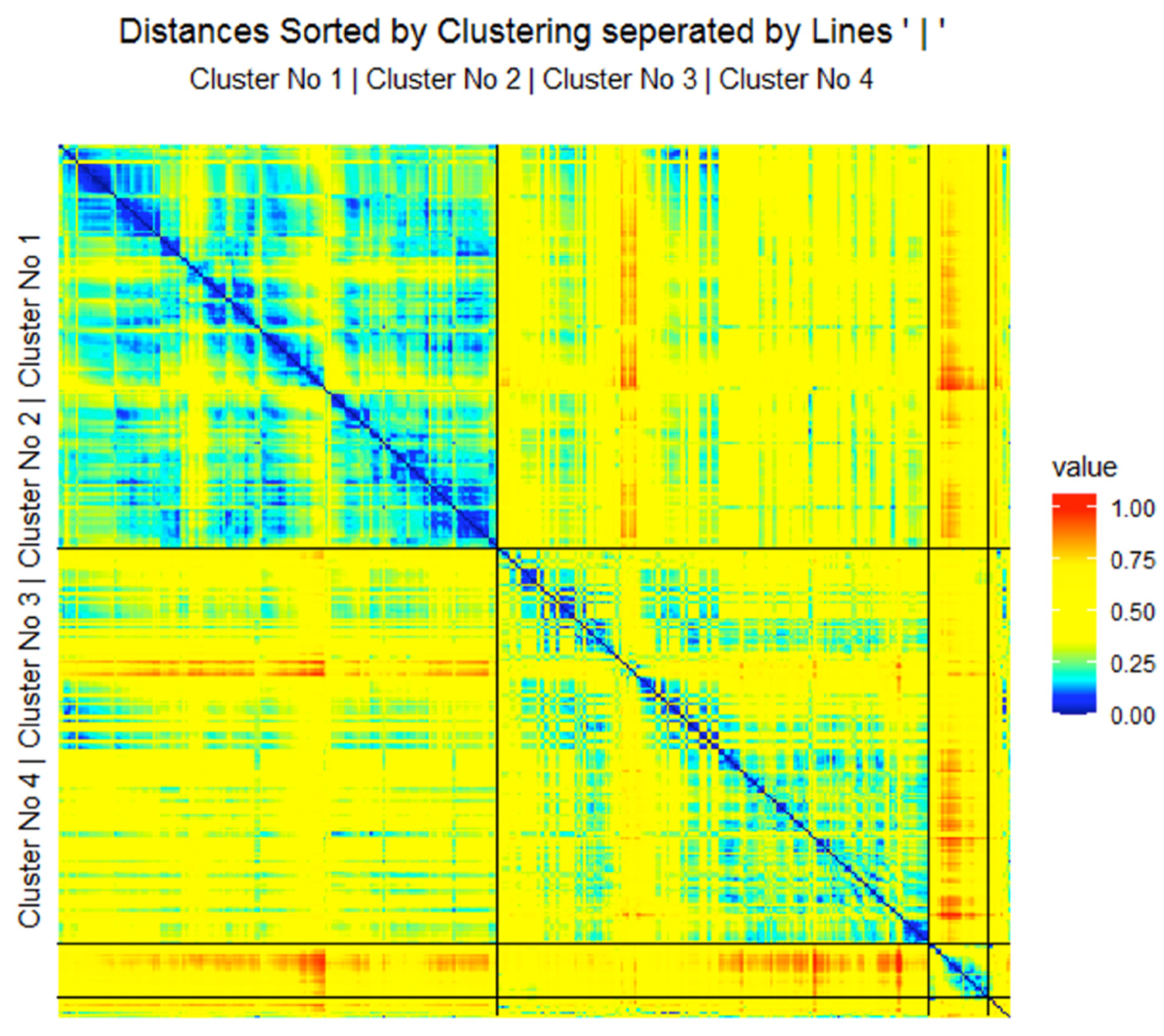
2.2. Step II: Cluster Analysis with Projection-Based Clustering (PBC)
2.2.1. Verification of a Clustering
2.2.2. Occam’s Razor
2.3. Step III: Providing Meaningful and Relevant Explanations
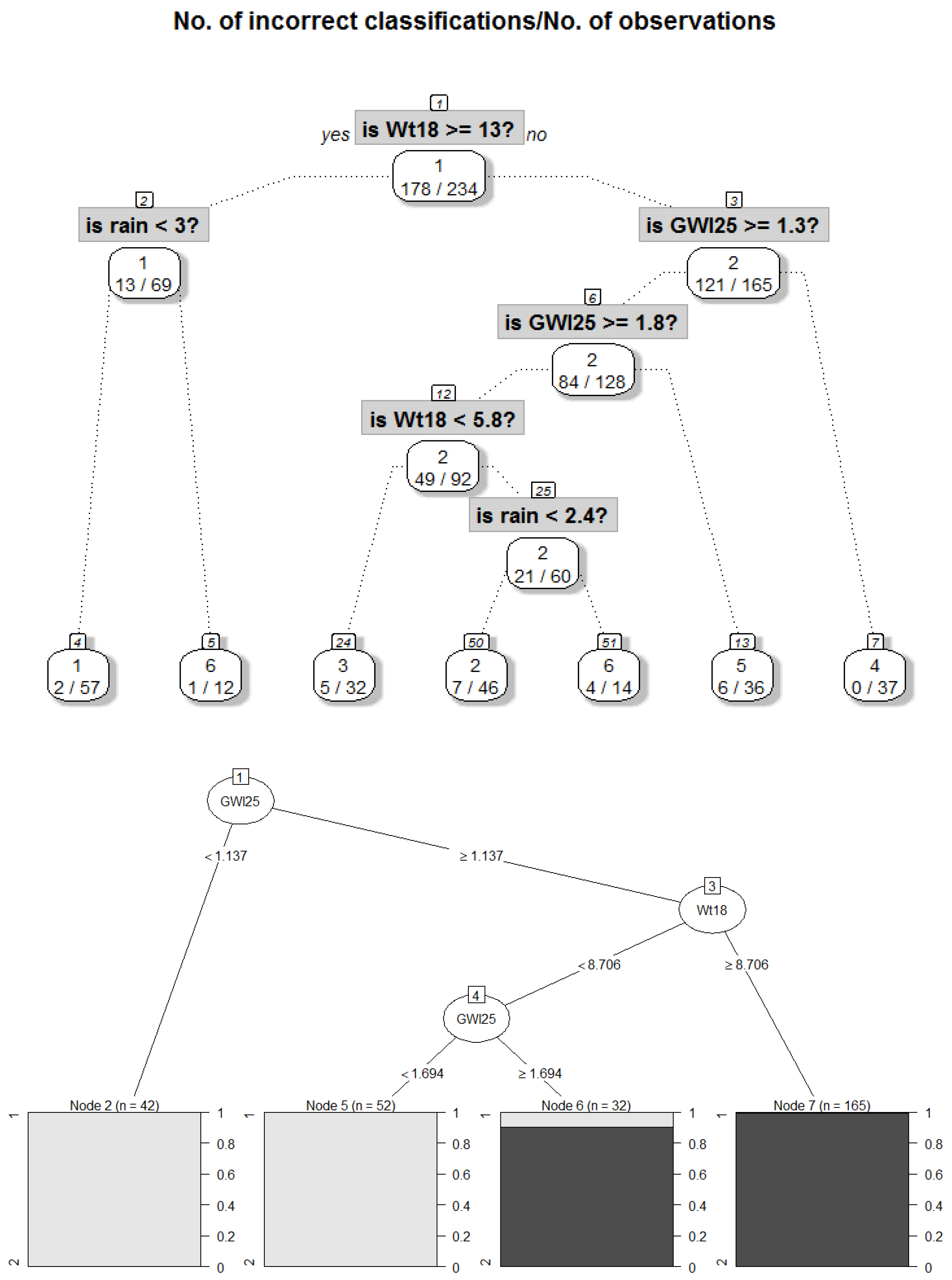
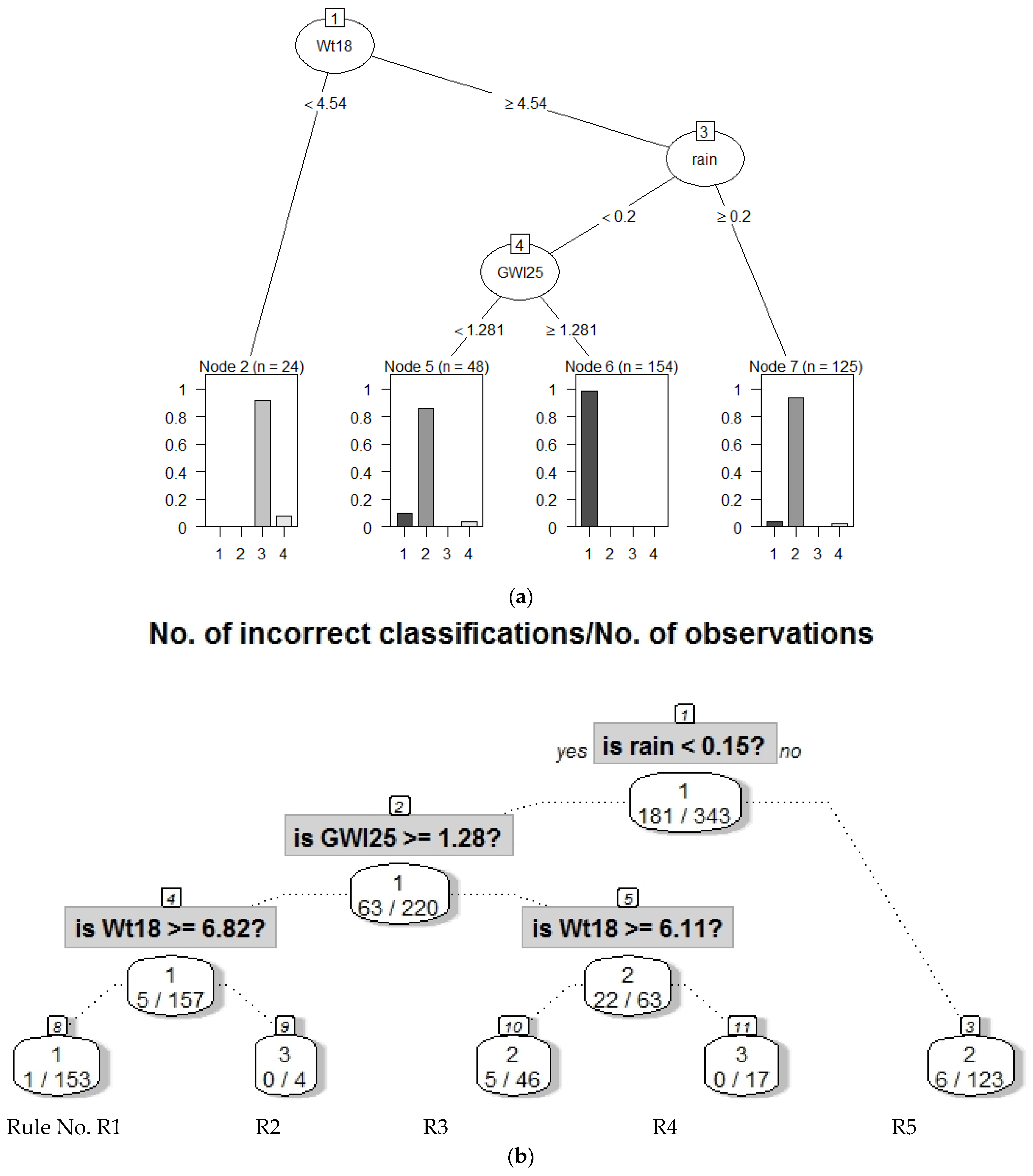
2.3.1. Decision Trees for Identified Structures in Data
2.3.2. Extracting Meaningful Explanations
2.3.3. Evaluating the Relevance of Explanations
3. Results
3.1. Step I: Structure Identification
3.2. Step II: Cluster Analysis
3.3. Step III: Providing Explanations
3.3.1. Evaluating the Relevance of DDS-XAI’s Explanations
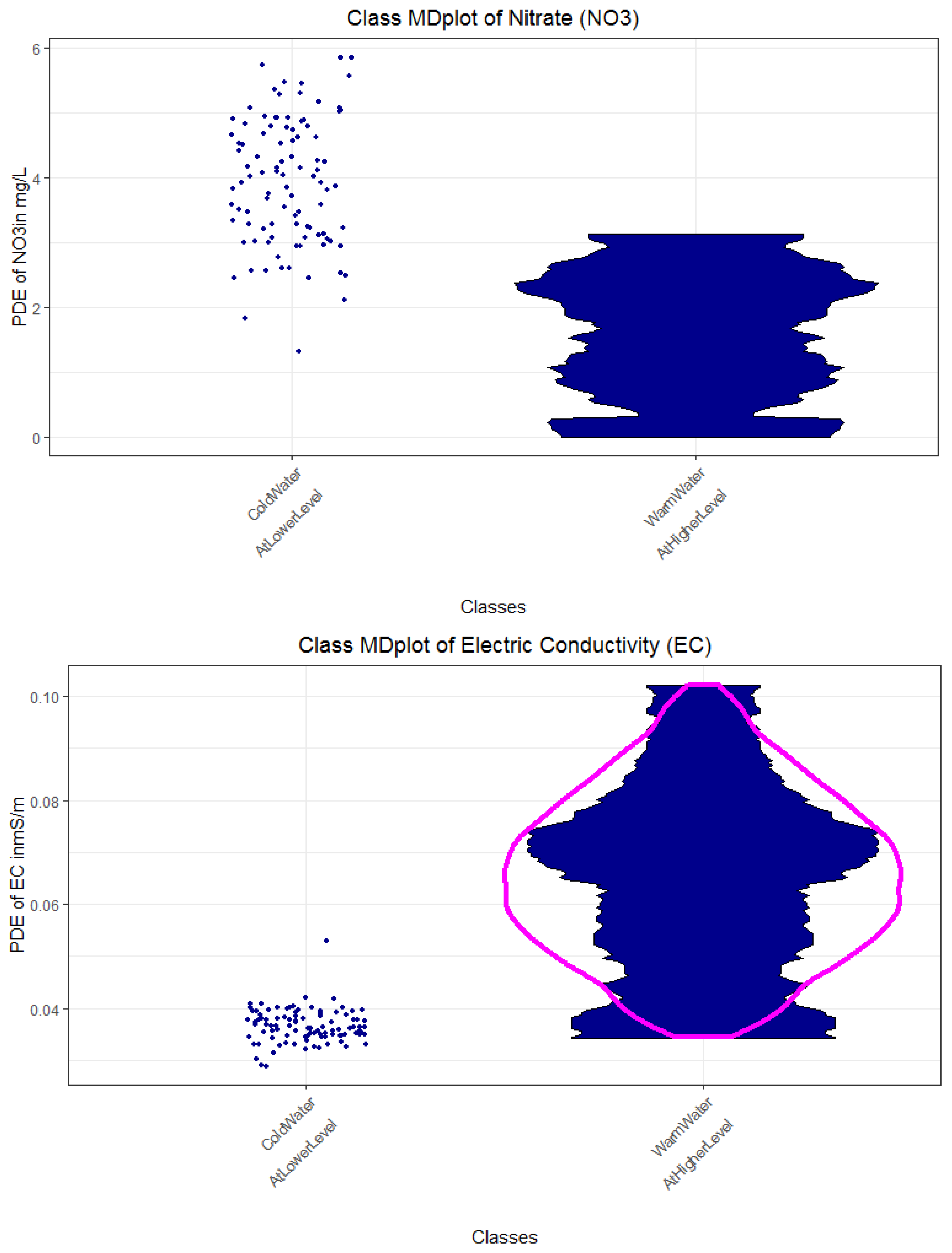
3.3.2. Interpreting Explanations
3.4. Comparison of DDS-XAI with eUD3.5 and IMM
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Features after Preprocessing
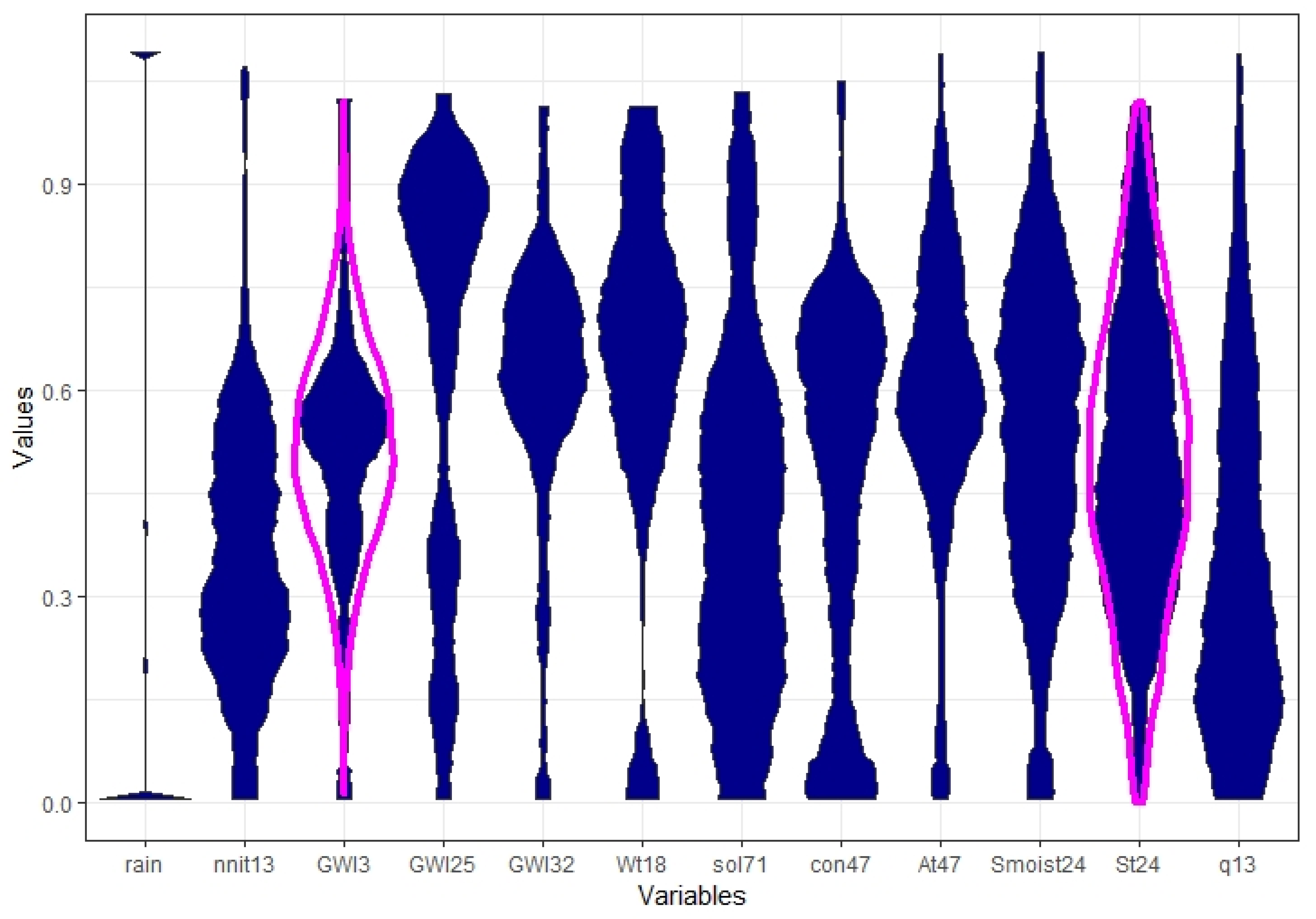
Appendix B. Comparison to the K-Means Clustering Approach
| PBC/k-Means | 1 | 2 | 3 | RowSum | RowPercentage |
|---|---|---|---|---|---|
| 1 | 24 | 77 | 61 | 162 | 47.23 |
| 2 | 28 | 65 | 66 | 159 | 46.36 |
| 3 | 0 | 8 | 14 | 22 | 6.41 |
| ColumnSum | 52 | 150 | 141 | 343 | 0 |
| ColPercentage | 15.16 | 43.73 | 41.11 | 0 | 100 |
| PBC/k-Means | 1 | 2 | 3 | 4 | 5 | 6 | RowSum | RowPercentage |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 3 | 4 | 19 | 30 | 56 | 24.45 |
| 2 | 32 | 0 | 12 | 0 | 0 | 0 | 44 | 19.21 |
| 3 | 0 | 0 | 10 | 26 | 3 | 3 | 39 | 17.03 |
| 4 | 10 | 22 | 4 | 1 | 0 | 0 | 37 | 16.16 |
| 5 | 30 | 0 | 0 | 0 | 0 | 0 | 30 | 13.10 |
| 6 | 10 | 1 | 4 | 5 | 3 | 2 | 23 | 10.04 |
| ColumnSum | 82 | 23 | 33 | 36 | 19 | 36 | 229 | 0 |
| ColPercentage | 35.81 | 10.04 | 14.41 | 15.72 | 8.3 | 15.72 | 0 | 100 |
Appendix C. Kolmogorov-Smirnov Tests of Clusters
| Cluster No. (Sample Size) | C2 (159) | C3 (22) |
|---|---|---|
| C1 (162) | D = 0.13429, p = 0.11 | D = 0.74074, p < 0.001 |
| C2 (159) | D = 0.84906, p < 0.001 |
| Cluster No. (Sample Size) | C2 (159) | C3 (22) |
|---|---|---|
| C1 (162) | D = 0.50769, p < 0.001 | D = 0.98765, p < 0.001 |
| C2 (159) | D = 0.83019, p < 0.001 |
Appendix D. Silhouette Plots

Appendix E. Distinction of Classes 1 and 2 in Regard to Rain and Water Temperature

Appendix F. Definitions for Distance Distributions
Appendix G. Linear Models

Appendix H. Class MDplots of eUD3.5 and k-Means
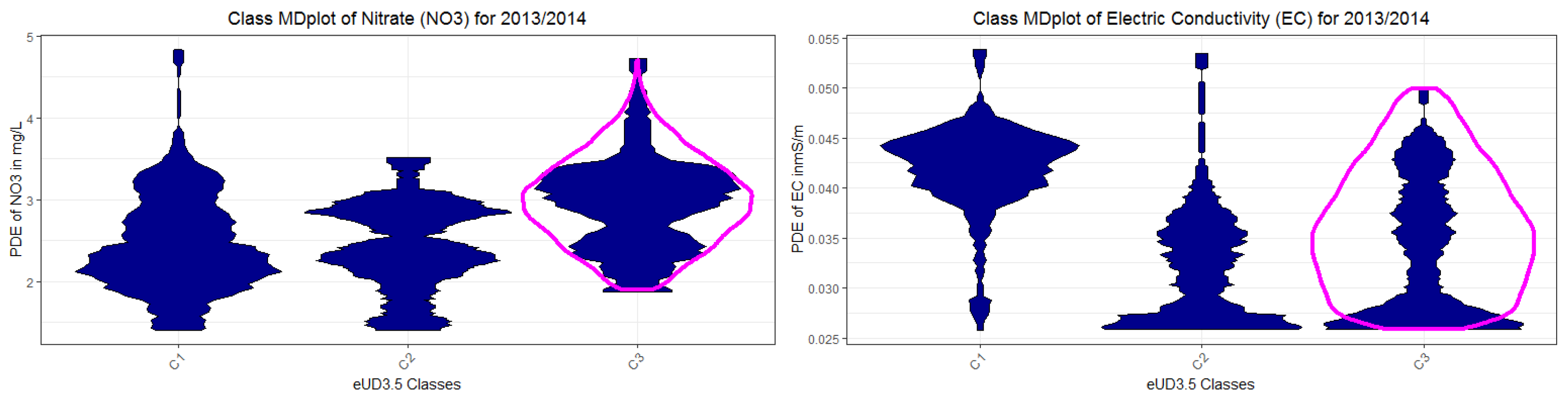

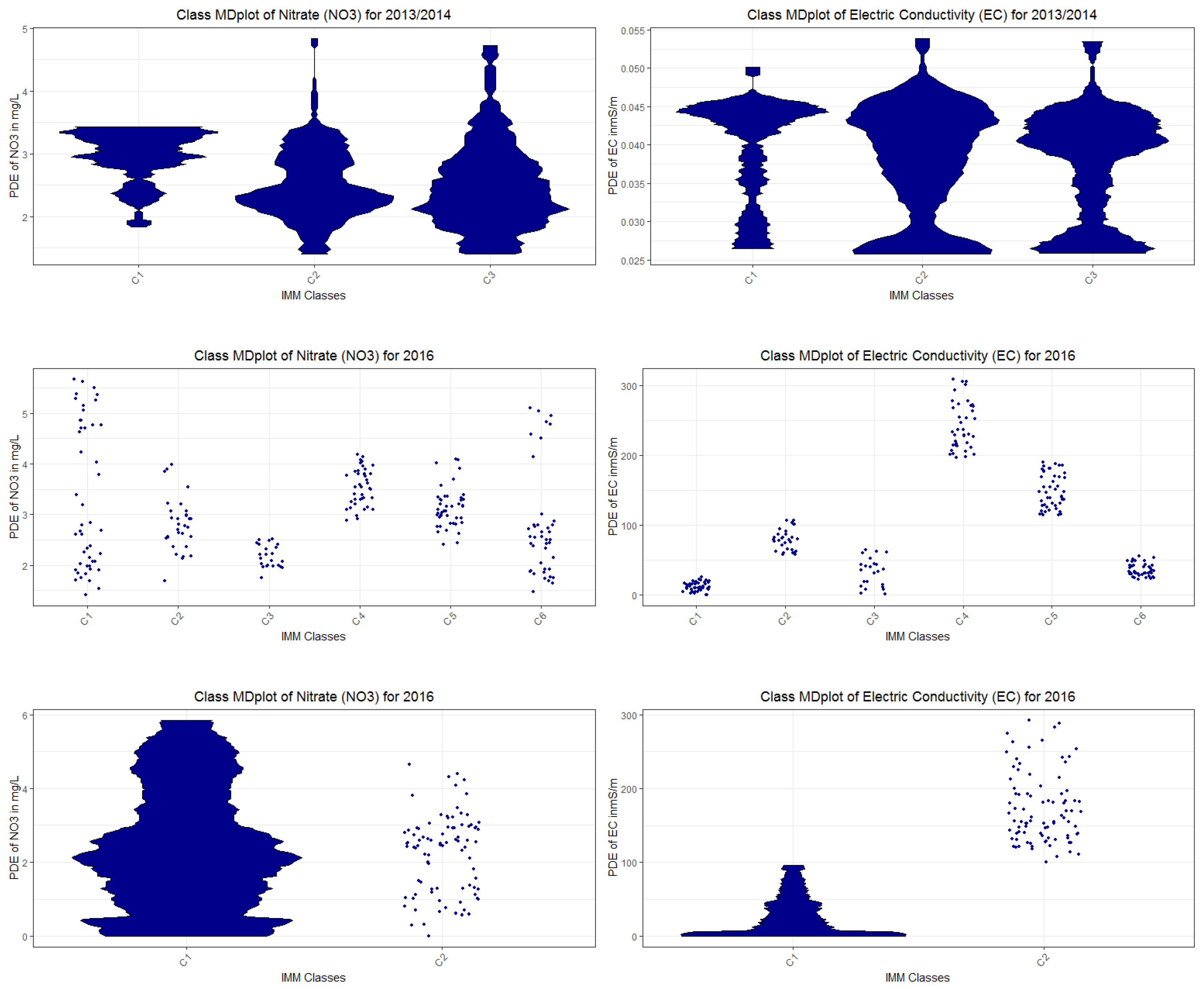
Appendix I. Used R Packages
| Name of Packag | Usage | Reference | Accessibility |
|---|---|---|---|
| ABCanalysis | Computed ABCanalysis for outlier detection | [95] | https://CRAN.R-project.org/package=ABCanalysis |
| DataVisualizations | Mirrored density plot (MD plot), density estimation, heatmap | [96] | https://CRAN.R-project.org/package=DataVisualizations |
| FCPS | 54 alternative clustering algorithms for specific cluster structures | [45] | https://CRAN.R-project.org/package=FCPS |
| DatabionicSwarm | Projection algorithm that finds a large variety of cluster structures and can cluster data as a special of Projection-based clustering. | [55,97] | https://CRAN.R-project.org/package=DatabionicSwarm |
| parallelDist | Distance computation for many distance metrics | [94] | https://CRAN.R-project.org/package=parallelDist |
| AdaptGauss | Gaussian Mixture Modelling (GMM), QQ plot for GMM | [46] | https://CRAN.R-project.org/package=AdaptGauss |
| rpart | Supervised Decision Tree | [79] | https://CRAN.R-project.org/package=rpart |
| evtree | Supervised Decision Tree | [68] | https://CRAN.R-project.org/package=evtree |
| GeneralizedUmatrix | Provides the topographic map, enables to visualize any projection method with it | [58] | https://CRAN.R-project.org/package=GeneralizedUmatrix |
| ProjectionBased Clustering | Provides projection-based clustering, interactive interfaces for cutting tiled topographic map into islands and for interactive clustering | [42,43] | https://CRAN.R-project.org/package=ProjectionBasedClustering |
| FeatureImpCluster | “Implements a novel approach for measuring feature importance in k-means clustering” | [40] | https://CRAN.R-project.org/package=FeatureImpCluster |
Appendix J. Collection and Preprocessing of Multivariate Time Series Data
Appendix K. DDS-XAI Results of 2015 and 2016 Data
| Rule No. Color | Class No. | No. of Days | Explanations | Short Description of Class for Subsequent Plots |
|---|---|---|---|---|
| R1 magenta | 1 | 55 | Wt18 >= 13.1 and rain < 3 =>Warm stream water without heavy rain intensity | WarmWater WithoutHeavyRain |
| R4, yellow | 2 | 39 | Wt18 < 13.1 and Wt18 ≥ 5.8 and GWl25 ≥ 1.8 and rain < 2.3 =>Intermediate stream water temperature and rain intensity with higher ground water levels | LightRain MildWater AtHighLevel |
| R3 black | 3 | 27 | GWl25 ≥ 1.8 and Wt18 < 5.8 => High ground water levels with cold water | ColdWaterAtHighLevel |
| R7 red | 4 | 37 | Wt18 < 13.1 and GWl25 < 1.3 => Low ground water levels with decreasing water temperature | CoolerWater AtLowLevel |
| R6 blue | 5 | 30 | Wt18 < 13.1 and GWl25 >= 1.3 and GWl25 < 1.8 => intermediate ground water level with decreasing water temperature | CoolerWater AtIntermediateLevel |
| R2 and R8 teal | 6 | 21 | Wt18 ≥ 13.1 and rain ≥ 3 OR Wt18 < 13.1 and Wt18 ≥ 5. and GWl25 ≥ 1.8 and rain ≥ 2.3 => high rain intensity with either warm water with or intermediate water temperature and high ground water levels | HighRainIntensityAt HighLevel |
| - | Unclassified | 5 | Excluded, because cannot be explained with decision trees | Outliers |
| Rule No. Color | Class No. | No. of Days | Explanations | Short Description of Class for Subsequent Plots |
|---|---|---|---|---|
| R1 and R2 magenta | 1 | 94 | GWl25 < 1.1 or GWl25< 1.7 and Wt18 < 8.7 => low stream water temperature temperature with lower groundwater levels | ColdWaterAtLowerLevel |
| R4, yellow | 2 | 165 | GWl25 ≥ 1.1 and Wt18 > 8.7 => Intermediate stream water temperature with high groundwater level | WarmWaterAtHigherLevel |
| R3 | 90% in 2 10% in 1 | 32 | GWl25 > 1.7 and Wt18 < 8.7 | IncorrectlyClassified |

References
- Durand, P.; Breuer, L.; Johnes, P.J. Nitrogen processes in aquatic ecosystems. In European Nitrogen Assessment (ENA); Sutton, M.A., Howard, C.M., Erisman, J.W., Billen, G., Bleeker, A., Grennfelt, P., van Grinsven, H., Grizzeti, B., Eds.; Cambridge University Press: Cambridge, UK, 2011; Chapter 7; pp. 126–146. [Google Scholar]
- Cirmo, C.P.; McDonnell, J.J. Linking the hydrologic and biogeochemical controls of nitrogen transport in near-stream zones of temperate-forested catchments: A review. J. Hydrol. 1997, 199, 88–120. [Google Scholar] [CrossRef]
- Diaz, R.J. Overview of hypoxia around the world. J. Environ. Qual. 2001, 30, 275–281. [Google Scholar] [CrossRef] [PubMed]
- Howarth, R.W.; Billen, G.; Swaney, D.; Townsend, A.; Jaworski, N.; Lajtha, K.; Downing, J.A.; Elmgren, R.; Caraco, N.; Jordan, T. Regional nitrogen budgets and riverine N & P fluxes for the drainages to the North Atlantic Ocean: Natural and human influences. In Nitrogen Cycling in the North Atlantic Ocean and Its Watersheds; Springer: Berlin, Germany, 1996; pp. 75–139. [Google Scholar]
- Rode, M.; Wade, A.J.; Cohen, M.J.; Hensley, R.T.; Bowes, M.J.; Kirchner, J.W.; Arhonditsis, G.B.; Jordan, P.; Kronvang, B.; Halliday, S.J.; et al. Sensors in the stream: The high-frequency wave of the present. Environ. Sci. Technol. 2016, 50, 19. [Google Scholar] [CrossRef]
- Aubert, A.H.; Thrun, M.C.; Breuer, L.; Ultsch, A. Knowledge discovery from high-frequency stream nitrate concentrations: Hydrology and biology contributions. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Aubert, A.H.; Breuer, L. New seasonal shift in in-stream diurnal nitrate cycles identified by mining high-frequency data. PLoS ONE 2016, 11, e0153138. [Google Scholar] [CrossRef] [PubMed]
- Miller, T.; Howe, P.; Sonenberg, L. Explainable AI: Beware of inmates running the asylum. In Proceedings of the International Joint Conference on Artificial Intelligence, Workshop on Explainable AI (XAI), Melbourne, Australia, 19–25 August 2017; pp. 36–42. [Google Scholar]
- Miller, T. Explanation in artificial intelligence: Insights from the social sciences. Artif. Intell. 2019, 267, 1–38. [Google Scholar] [CrossRef]
- Thrun, M.C.; Gehlert, T.; Ultsch, A. Analyzing the Fine Structure of Distributions. PLoS ONE 2020, 15, e0238835. [Google Scholar] [CrossRef]
- Grice, H.P. Logic and conversation. In Speech Acts; Brill: Leiden, The Netherlands, 1975; pp. 41–58. [Google Scholar]
- Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Pellerin, B.A.; Downing, B.D.; Kendall, C.; Dahlgren, R.A.; Kraus, T.E.; Saraceno, J.; Spencer, R.G.; Bergamaschi, B.A. Assessing the sources and magnitude of diurnal nitrate variability in the San Joaquin River (California) with an in situ optical nitrate sensor and dual nitrate isotopes. Freshw. Biol. 2009, 54, 376–387. [Google Scholar] [CrossRef]
- Ultsch, A. The integration of connectionist models with knowledge-based systems: Hybrid systems. In Proceedings of the 1998 IEEE International Conference on Systems, Man, and Cybernetics, San Diego, CA, USA, 14 October 1998; pp. 1530–1535. [Google Scholar]
- Ultsch, A.; Korus, D. Integration of neural networks and knowledge-based systems. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Biran, O.; Cotton, C. Explanation and justification in machine learning: A survey. In Proceedings of the IJCAI-17 Workshop on Explainable AI (XAI), Melbourne, Australia, 19–21 August 2017; pp. 8–13. [Google Scholar]
- Le, N.Q.K.; Do, D.T.; Chiu, F.-Y.; Yapp, E.K.Y.; Yeh, H.-Y.; Chen, C.-Y. XGBoost improves classification of MGMT promoter methylation status in IDH1 wildtype glioblastoma. J. Pers. Med. 2020, 10, 128. [Google Scholar] [CrossRef]
- Do, D.T.; Le, T.Q.T.; Le, N.Q.K. Using deep neural networks and biological subwords to detect protein S-sulfenylation sites. Brief. Bioinform. 2020. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should I trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4765–4774. [Google Scholar]
- Lipton, Z.C. The mythos of model interpretability. Queue 2018, 16, 31–57. [Google Scholar] [CrossRef]
- Ultsch, A.; Halmans, G.; Mantyk, R. CONKAT: A connectionist knowledge acquisition tool. In Proceedings of the 24th Annual Hawaii International Conference on System Sciences, Kauai, HI, USA, 8–11 January 1991; pp. 507–513. [Google Scholar]
- Ultsch, A.; Korus, D.; Kleine, T. Integration of neural networks and knowledge-based systems in medicine. In Proceedings of the Conference on Artificial Intelligence in Medicine in Europe, Pavia, Italy, 25–28 June 1995; pp. 425–426. [Google Scholar]
- Yoon, J.; Kim, D.-W. Classification based on predictive association rules of incomplete data. IEICE Trans. Inf. Syst. 2012, 95, 1531–1535. [Google Scholar] [CrossRef]
- Letham, B.; Rudin, C.; McCormick, T.H.; Madigan, D. An interpretable stroke prediction model using rules and Bayesian analysis. In Proceedings of the 27th AAAI Conference on Artificial Intelligence, Bellevue, WA, USA, 14–18 July 2013. [Google Scholar]
- Riid, A.; Sarv, M. Determination of regional variants in the versification of estonian folksongs using an interpretable fuzzy rule-based classifier. In Proceedings of the 8th Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT-13), Milan, Italy, 11–13 September 2013. [Google Scholar]
- Nauck, D.; Kruse, R. Obtaining interpretable fuzzy classification rules from medical data. Artif. Intell. Med. 1999, 16, 149–169. [Google Scholar] [CrossRef]
- Izonin, I.; Tkachenko, R.; Kryvinska, N.; Tkachenko, P. Multiple Linear Regression based on Coefficients Identification using Non-Iterative SGTM Neural-Like Structure. In Proceedings of the International Work-Conference on Artificial Neural Networks, Gran Canaria, Spain, 12–14 June 2019; pp. 467–479. [Google Scholar]
- Tkachenko, R.; Izonin, I. Model and principles for the implementation of neural-like structures based on geometric data transformations. In Proceedings of the International Conference on Computer Science, Engineering and Education Applications, Kiev, Ukraine, 18–20 January 2018; pp. 578–587. [Google Scholar]
- Larus-Stone, N.; Angelino, E.; Alabi, D.; Seltzer, M.; Kaxiras, V.; Saligrama, A.; Rudin, C. Systems optimizations for learning certifiably optimal rule lists. In Proceedings of the SysML Conference, Stanford, CA, USA, 15–16 February 2018; p. 16. [Google Scholar]
- Lakkaraju, H.; Bach, S.H.; Leskovec, J. Interpretable decision sets: A joint framework for description and prediction. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1675–1684. [Google Scholar]
- Hewett, R.; Leuchner, J. The power of second-order decision tables. In Proceedings of the 2002 SIAM International Conference on Data Mining, Chicago, IL, USA, 11–13 April 2002; pp. 384–399. [Google Scholar]
- Blockeel, H.; De Raedt, L.; Ramon, J. Top-down induction of clustering trees. In Proceedings of the 15th International Conference (ICML), San Francisco, CA, USA, 24–27 July 1998; pp. 55–63. [Google Scholar]
- Basak, J.; Krishnapuram, R. Interpretable hierarchical clustering by constructing an unsupervised decision tree. IEEE Trans. Knowl. Data Eng. 2005, 17, 121–132. [Google Scholar] [CrossRef]
- Kim, B.; Shah, J.A.; Doshi-Velez, F. Mind the gap: A generative approach to interpretable feature selection and extraction. In Proceedings of the Conference on Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2260–2268. [Google Scholar]
- Loyola-González, O.; Gutierrez-Rodríguez, A.E.; Medina-Pérez, M.A.; Monroy, R.; Martínez-Trinidad, J.F.; Carrasco-Ochoa, J.A.; García-Borroto, M. An Explainable Artificial Intelligence Model for Clustering Numerical Databases. IEEE Access 2020, 8, 52370–52384. [Google Scholar] [CrossRef]
- Dasgupta, S.; Frost, N.; Moshkovitz, M.; Rashtchian, C. Explainable k-Means and k-Medians Clustering. In Proceedings of the 37th International Conference on Machine Learning, Vienna, Austria, 12–18 July 2020. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Leisch, F. A toolbox for k-centroids cluster analysis. Comput. Stat. Data 2006, 51, 526–544. [Google Scholar] [CrossRef]
- Pfaffel, O. FeatureImpCluster: Feature Importance for Partitional Clustering. Available online: cran.r-project.org (accessed on 4 February 2021).
- Thrun, M.C.; Ultsch, A. Uncovering High-Dimensional Structures of Projections from Dimensionality Reduction Methods. MethodsX 2020, 7, 101093. [Google Scholar] [CrossRef]
- Thrun, M.C.; Ultsch, A. Using Projection based Clustering to Find Distance and Density based Clusters in High-Dimensional Data. J. Classif. 2020. [Google Scholar] [CrossRef]
- Thrun, M.C.; Pape, F.; Ultsch, A. Interactive Machine Learning Tool for Clustering in Visual Analytics. In Proceedings of the 7th IEEE International Conference on Data Science and Advanced Analytics (DSAA 2020), Sydney, Australia, 6–9 October 2020; pp. 672–680. [Google Scholar]
- Bouveyron, C.; Hammer, B.; Villmann, T. Recent developments in clustering algorithms. In Proceedings of the European Symposium on Artificial Neural Networks, Bruges, Belgium, 25–27 April 2012. [Google Scholar]
- Thrun, M.C.; Stier, Q. Fundamental Clustering Algorithms Suite. SoftwareX 2021, 13, 100642. [Google Scholar] [CrossRef]
- Ultsch, A.; Thrun, M.C.; Hansen-Goos, O.; Lötsch, J. Identification of Molecular Fingerprints in Human Heat Pain Thresholds by Use of an Interactive Mixture Model R Toolbox (AdaptGauss). Int. J. Mol. Sci. 2015, 16, 25897–25911. [Google Scholar] [CrossRef]
- Thrun, M.C. Projection Based Clustering Through Self-Organization and Swarm Intelligence; Ultsch, A., Hüllermeier, E., Eds.; Springer: Berlin, Germany, 2018. [Google Scholar]
- Setzu, M.; Guidotty, R.; Mionreale, A.; Turini, F.; Pedreschie, D.; Gianotti, F. GLocalX—From local to Global Explanations of Black Box AI Models. Artif. Intell. 2021, 103457. [Google Scholar] [CrossRef]
- Ultsch, A. Data mining and knowledge discovery with emergent self-organizing feature maps for multivariate time series. In Kohonen Maps, 1st ed.; Oja, E., Kaski, S., Eds.; Elsevier: Amsterdam, The Netherlands, 1999; pp. 33–46. [Google Scholar]
- Demartines, P.; Hérault, J. CCA: ”Curvilinear component analysis”. In Proceedings of the 15 Colloque sur le Traitement du Signal et des Images, Juan-Les-Pins, France, 18–21 September 1995. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Venna, J.; Peltonen, J.; Nybo, K.; Aidos, H.; Kaski, S. Information retrieval perspective to nonlinear dimensionality reduction for data visualization. J. Mach. Learn. Res. 2010, 11, 451–490. [Google Scholar]
- Ultsch, A. Clustering with DataBots. In Proceedings of the International Conference on Advances in Intelligent Systems: Theory and Applications (AISTA), Canberra, Australia, 2–4 February 2000; pp. 99–104. [Google Scholar]
- Nash, J.F. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef] [PubMed]
- Thrun, M.C.; Ultsch, A. Swarm Intelligence for Self-Organized Clustering. Artif. Intell. 2021, 290, 103237. [Google Scholar] [CrossRef]
- Nash, J.F. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Johnson, W.B.; Lindenstrauss, J. Extensions of Lipschitz mappings into a Hilbert space. Contemp. Math. 1984, 26, 189–206. [Google Scholar]
- Ultsch, A.; Thrun, M.C. Credible Visualizations for Planar Projections. In Proceedings of the 12th International Workshop on Self-Organizing Maps and Learning Vector Quantization, Clustering and Data Visualization (WSOM), Nany, France, 28–30 June 2017; pp. 1–5. [Google Scholar]
- Thrun, M.C.; Lerch, F.; Lötsch, J.; Ultsch, A. Visualization and 3D Printing of Multivariate Data of Biomarkers. In Proceedings of the International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision (WSCG), Plzen, Czech Republic, 30 May–3 June 2016; pp. 7–16. [Google Scholar]
- Bonner, R.E. On Some Clustering Technique. IBM J. Res. Dev. 1964, 8, 22–32. [Google Scholar] [CrossRef]
- Hennig, C.; Meila, M.; Murtagh, F.; Rocci, R. Handbook of Cluster Analysis; Chapman&Hall/CRC Press: New York, NY, USA, 2015; p. 730. [Google Scholar]
- Mörchen, F.; Ultsch, A. Efficient mining of understandable patterns from multivariate interval time series. Data Min. Knowl. Disc. 2007, 15, 181–215. [Google Scholar] [CrossRef]
- Hintze, J.L.; Nelson, R.D. Violin plots: A box plot-density trace synergism. Am. Stat. 1998, 52, 181–184. [Google Scholar]
- Ultsch, A. Pareto density estimation: A density estimation for knowledge discovery. In Innovations in Classification, Data Science, and Information Systems; Baier, D., Werrnecke, K.D., Eds.; Springer: Berlin, Germany, 2005; Volume 27, pp. 91–100. [Google Scholar]
- Sober, E. Let’s Razor Ockham’s Razor. In Explanation and Its Limits; Knowles, D., Ed.; Cambridge University Press: Cambridge, UK, 1991; pp. 73–94. [Google Scholar]
- Breiman, L. Random forests. Mach Learn 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Grubinger, T.; Zeileis, A.; Pfeiffer, K.-P. Evtree: Evolutionary learning of globally optimal classification and regression trees in R. J. Stat. Softw. 2014, 61, 1–29. [Google Scholar] [CrossRef]
- Miller, G.A. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81. [Google Scholar] [CrossRef] [PubMed]
- Cowan, N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behav. Brain Sci. 2001, 24, 87–114. [Google Scholar] [CrossRef] [PubMed]
- Mörchen, F.; Ultsch, A.; Hoos, O. Extracting interpretable muscle activation patterns with time series knowledge mining. Int. J. Knowl. Based Intell. Eng. Syst. 2005, 9, 197–208. [Google Scholar] [CrossRef]
- Rao, C. Use of Hellinger distance in graphical displays. Multivariate statistics and matrices in statistics. In Proceedings of the 5th Tartu Conference, Pühajärve, Estonia, 23–28 May 1995; pp. 143–161. [Google Scholar]
- Hartigan, J.A.; Hartigan, P.M. The dip test of unimodality. Ann. Stat. 1985, 13, 70–84. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–22. [Google Scholar]
- Hofmeyr, D.; Pavlidis, N. Maximum clusterability divisive clustering. In Proceedings of the 2015 IEEE Symposium Series on Computational Intelligence, Cape Town, South Africa, 7–10 December 2015; pp. 780–786. [Google Scholar]
- Steinley, D.; Brusco, M.J.; Henson, R. Principal cluster axes: A projection pursuit index for the preservation of cluster structures in the presence of data reduction. Multivar. Behav. Res. 2012, 47, 463–492. [Google Scholar] [CrossRef]
- Ward, J.H., Jr. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Hierarchical clustering. In Cluster Analysis, 5th ed.; Wiley: Hoboken, NJ, USA, 2011; pp. 71–110. [Google Scholar]
- Therneau, T.; Atkinson, B.; Ripley, B.; Ripley, M.B. Package ‘Rpart’. Available online: https://cran.r-project.org/web/packages/rpart/rpart.pdf (accessed on 20 April 2016).
- Orlowski, N.; Lauer, F.; Kraft, P.; Frede, H.-G.; Breuer, L. Linking spatial patterns of groundwater table dynamics and streamflow generation processes in a small developed catchment. Water 2014, 6, 3085–3117. [Google Scholar] [CrossRef]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3319–3328. [Google Scholar]
- Mittelstadt, B.; Russell, C.; Wachter, S. Explaining explanations in AI. In Proceedings of the Conference on Fairness, Accountability, and Transparency, Atlanta, GA, USA, 29–31 January 2019; pp. 279–288. [Google Scholar]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. 2018, 51, 1–42. [Google Scholar] [CrossRef]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Aghabozorgi, S.; Shirkhorshidi, A.S.; Wah, T.Y. Time-series clustering–A decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Herrmann, L. Swarm-Organized Topographic Mapping. Ph.D. Thesis, Philipps-Universität Marburg, Marburg, Germany, 2011. [Google Scholar]
- Handl, J.; Knowles, J.; Kell, D.B. Computational cluster validation in post-genomic data analysis. Bioinformatics 2005, 21, 3201–3212. [Google Scholar] [CrossRef]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice Hall College Div: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Cormack, R.M. A review of classification. J. R. Stat. Soc. Ser. A 1971, 134, 321–367. [Google Scholar] [CrossRef]
- Conover, W.J. Practical Nonparametric Statistics; John Wiley & Sons: New York, NY, USA, 1971. [Google Scholar]
- Neumaier, A. Combinatorial Configurations in Terms of Distances; University of Vienna: Vienna, Austria, 1981. [Google Scholar]
- Legendre, P.; Gallagher, E.D. Ecologically meaningful transformations for ordination of species data. Oecologia 2001, 129, 271–280. [Google Scholar] [CrossRef]
- Conde, A.; Domínguez, J. Scaling the chord and Hellinger distances in the range [0, 1]: An option to consider. J. Asia Pac. Biodivers. 2018, 11, 161–166. [Google Scholar] [CrossRef]
- Eckert, A. ParallelDist: Parallel Distance Matrix Computation Using Multiple Threads, 0.2.4. Available online: https://cran.r-project.org/web/packages/parallelDist/parallelDist.pdf (accessed on 4 February 2021).
- Ultsch, A.; Lötsch, J. Computed ABC Analysis for Rational Selection of Most Informative Variables in Multivariate Data. PLoS ONE 2015, 10, e0129767. [Google Scholar] [CrossRef] [PubMed]
- Thrun, M.C.; Ultsch, A. Effects of the payout system of income taxes to municipalities in Germany. In Proceedings of the 12th Professor Aleksander Zelias International Conference on Modelling and Forecasting of Socio-Economic Phenomena, Cracow, Poland, 8–11 May 2018; pp. 533–542. [Google Scholar]
- Thrun, M.C.; Ultsch, A. Swarm Intelligence for Self-Organized Clustering (Extended Abstract). In Proceedings of the 29th International Joint Conference on Artificial Intelligence (IJCAI), Yokohama, Japan, 7–15 January 2021; pp. 5125–5129. [Google Scholar]
- Thrun, M.C.; Breuer, L.; Ultsch, A. Knowledge discovery from low-frequency stream nitrate concentrations: Hydrology and biology contributions. In Proceedings of the European Conference on Data Analysis (ECDA), Paderborn, Germany, 4–6 July 2018; pp. 46–47. [Google Scholar]
- Milligan, G.W.; Cooper, M.C. A study of standardization of variables in cluster analysis. J. Classif. 1988, 5, 181–204. [Google Scholar] [CrossRef]

| Variable | Abbreviation | International System of Units |
|---|---|---|
| Soil temperature | St24 | °C |
| Groundwater level 3 = lowland, 25 = hill slope, 32= upstream in riparian zone | GWl3 GWl25 GWl32 | m |
| Soil moisture | Smoist24 | m³/m³ |
| Rainfall | rain | mm/d |
| Discharge | q13 q18 | L/s |
| Electric conductivity (EC) | Con47 | mS/m |
| Solar radiation | Sol71 | W/m2 |
| Air temperature | At47 | °C |
| Streamwater temperature | Wt18 Wt13 | °C |
| Nitrate (NO3) | nnit13 | mg/L |
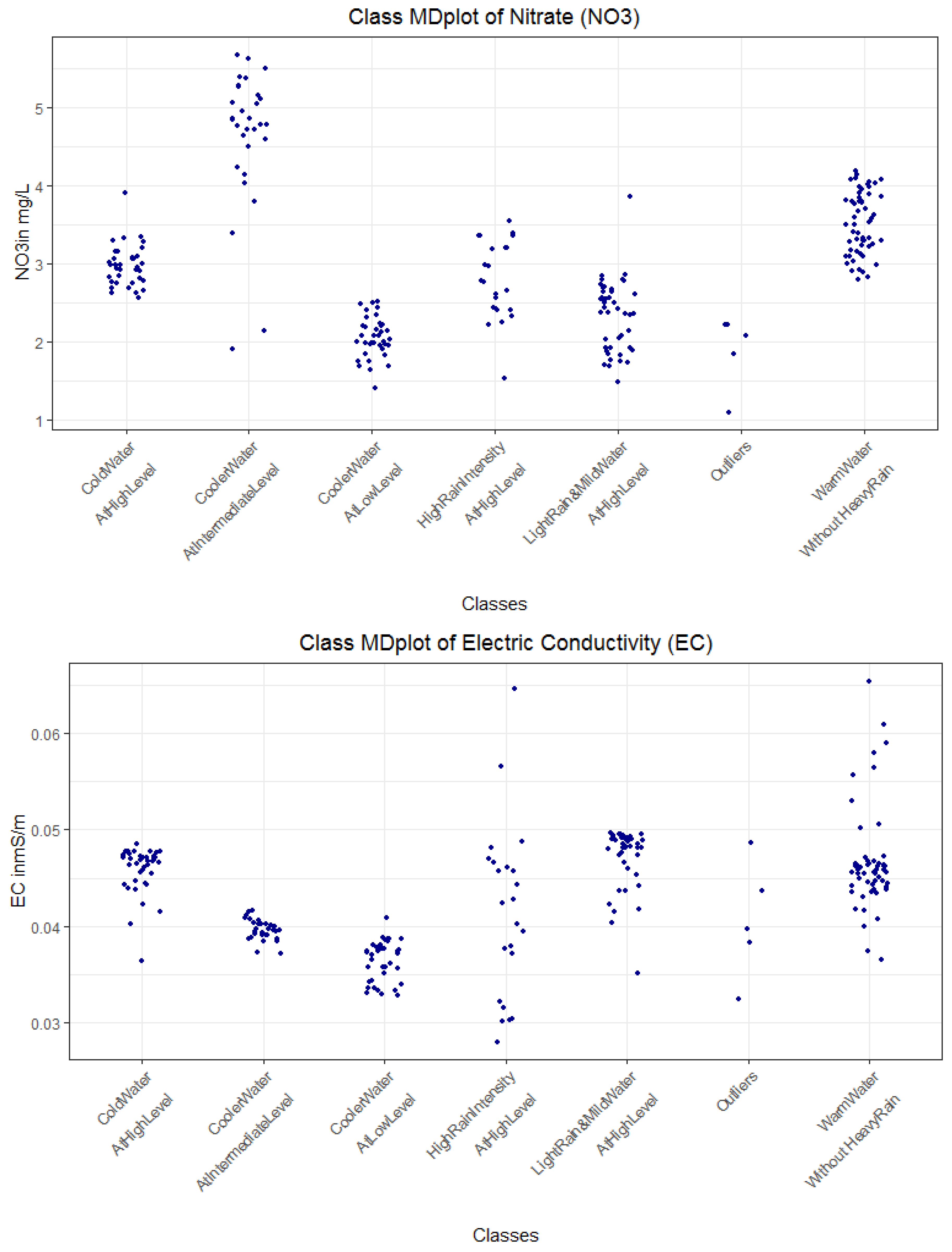
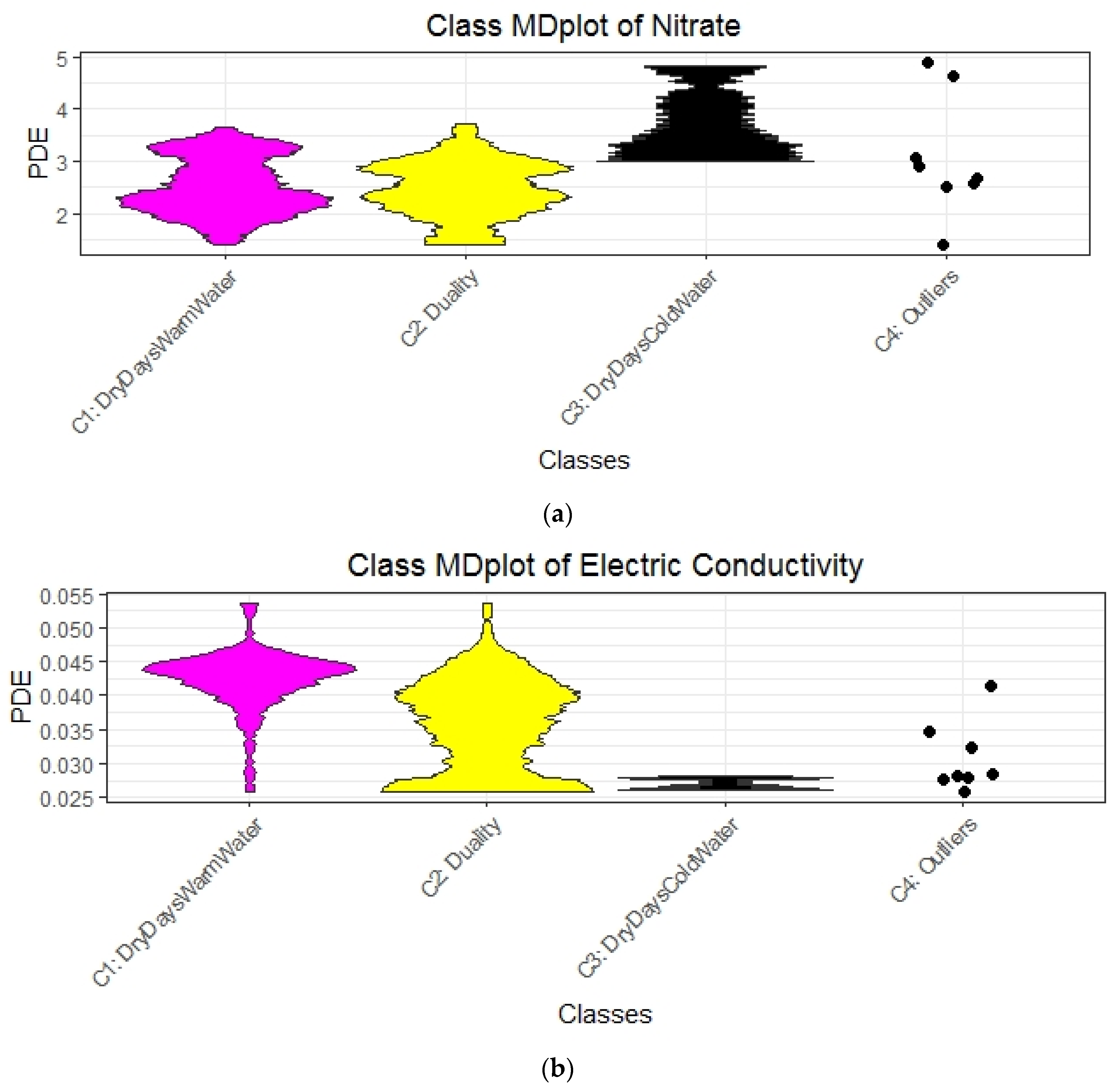
| Rule No. Color | Class No. | No. of Days | Explanations | Short Description of Class for Subsequent Plots |
|---|---|---|---|---|
| R1 magenta | 1 | 162 | rain < 0.15 and GWl25 ≥ 1.28 and Wt18 ≥ 6.86 => Dry days, increased stream water temperature and groundwater levels | DryDaysWarmWater |
| R3 and R5, Figure A3 yellow | 2 | 159 | rain < 0.15 and GWl25 < 1.28 and Wt18 ≥ 6.11 or rain ≥ 0.15 and Wt18 ≥ 6.11 => Intermediate stream water temperature with either dry days and low groundwater levels or rainy days with a high level of water | Duality |
| R2 and R4 black | 3 | 22 | rain < 0.15 and GWl25 ≥ 1.28 and Wt18 < 6.86 or rain < 0.15 and GWl25 < 1.28 and Wt18 < 6.11 => Dry days with colder stream water and variable groundwater levels | DryDaysColdWater |
| - | Unclassified | 7 | Excluded, because cannot be explained with decision trees | Outliers |
| Method | Data Coverage | Number of Explanations | Year of Data |
|---|---|---|---|
| IMM | 98 | 1 * | 2013/2014 |
| 98 | 1 * | 2015 | |
| 100 | 1 * | 2016 | |
| eUD3.5 | 98 | 541 | 2013/2014 |
| 98 | 503 | 2015 | |
| 100 | 552 | 2016 | |
| DDS-XAI | 96.5% | 5 | 2013/2014 |
| 89% | 7 | 2015 | |
| 89% | 4 | 2016 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thrun, M.C.; Ultsch, A.; Breuer, L. Explainable AI Framework for Multivariate Hydrochemical Time Series. Mach. Learn. Knowl. Extr. 2021, 3, 170-204. https://doi.org/10.3390/make3010009
Thrun MC, Ultsch A, Breuer L. Explainable AI Framework for Multivariate Hydrochemical Time Series. Machine Learning and Knowledge Extraction. 2021; 3(1):170-204. https://doi.org/10.3390/make3010009
Chicago/Turabian StyleThrun, Michael C., Alfred Ultsch, and Lutz Breuer. 2021. "Explainable AI Framework for Multivariate Hydrochemical Time Series" Machine Learning and Knowledge Extraction 3, no. 1: 170-204. https://doi.org/10.3390/make3010009
APA StyleThrun, M. C., Ultsch, A., & Breuer, L. (2021). Explainable AI Framework for Multivariate Hydrochemical Time Series. Machine Learning and Knowledge Extraction, 3(1), 170-204. https://doi.org/10.3390/make3010009





