Exploiting Weak Ties in Incomplete Network Datasets Using Simplified Graph Convolutional Neural Networks

Abstract

This paper explores the value of weak-ties in classifying academic literature with the use of graph convolutional neural networks. Our experiments look at the results of treating weak-ties as if they were strong-ties to determine if that assumption improves performance. This is done by applying the methodological framework of the Simplified Graph Convolutional Neural Network (SGC) to two academic publication datasets: Cora and Citeseer. The performance of SGC is compared to the original Graph Convolutional Network (GCN) framework. We also examine how node removal affects prediction accuracy by selecting nodes according to different centrality measures. These experiments provide insight for which nodes are most important for the performance of SGC. When removal is based on a more localized selection of nodes, augmenting the network with both strong-ties and weak-ties provides a benefit, indicating that SGC successfully leverages local information of network nodes.

1. Introduction

In addition to providing entertainment and social engagement, social networks also serve the important function of rapidly disseminating scientific information to the research community. Social media platforms such as ResearchGate and Academia.edu help authors rapidly find related work and supplement standard library searches. Twitter not only serves as an important purveyor of standard news [1] but also disseminates specialty news in fields such as neuroradiology [2]. Venerable academic societies such as the Royal Society (@royalsociety) now have official Twitter accounts. Shuai et al. [3] discuss the role of Twitter mentions within the scientific community and the citations that create a topological arrangement between scientific publications. Given that scientific articles possess the potential to change the landscape of technology, it is important to understand the information transference properties of academic networks: can techniques originally developed for social networks yield insights about scientific networks as well?

Pagerank [4] produced a revolution in the ability to search through the myriad of webpages by examining the network structure for relevance. This concept has been applied to citation networks in academic literature, which conceptually has many overlaps with the interlinking of websites, and Ding et al. [5] apply the Pagerank algorithm to citations. The same first author extends this work to investigate endorsement in the network as well [6]. Endorsement as a process produces an effect that not only allows readers to navigate essential information, relevant overlaps or apply appropriate credit but also amplifies readership which is a dynamic seen frequently in online social processes. These links are direct links and also referred to as strong-ties [7].

Indirect or weak-ties have also been identified as important in social networks, most notably in Granovetter’s seminal work: “The strength of weak ties” [8]. These indirect edges can be created through edges that span different communities (clusters of nodes) acting as ‘bridges’. They can also be the result of ‘triangulation’ where ‘friends-of-friends’ produce a link due to the common connection they share. Figure 1 shows an example of a weak-ties connection between nodes A-C with a dotted edge representing connectivity due to a shared connection with node B. It can be said that A-C are connected from friends-of-friends, or triangulation creating a weak-tie. The work of [9] applies this concept to predicting edge production in a social network of professional profiles and shows that the explicit modeling of this triangulation dynamic leads to improved performance.

For our study on academic connections, we used two datasets, Cora [10] and Citeseer [11], which are discussed in more detail in Section 3. In addition to network structure, these datasets contain class labels, relating to the publication venues, which can be used to test machine learning prediction algorithms. In datasets that exhibit homophily, utilizing the features of nodes within a topological arrangement (an adjacency matrix) produces improved classification performance over an instance only framework. Our investigation focuses on whether the explicit addition of weak ties will assist the inference process since they provide assistance in other network based processes. For instance, Roux et al. [12] investigate whether expertise within groups can cross the ‘boundaries’ from communities which are cohesive due to strong-tie connections. The work of [13] considers how differentiation of the edge types can improve the accuracy of social recommendations.

Determining the effect of interactions between nodes can be a time consuming process, which requires computational resources to analyze large networks. With the goal of understanding how node connections influence labels, various methodologies, such as [14], have been proposed where nodes iteratively propagate information throughout the network until convergence is achieved. A notable example of such is DeepWalk [15] which uses local information from truncated random walks to learn the latent variable representations. Relational neighbor classifiers such as Social Context Relational Neighbor (SCRN) have been shown to achieve good performance at inferring the labels of citation networks [14]. Graph Convolutional Networks (GCNs) [16] extended the methodology of Convolutional Neural Networks (CNNs) from images to graphs. GCNs, as CNNs, are constructed upon multiple layers of neural networks which makes them less amenable to interpretation [17,18,19].

This paper uses the approach of the Simplified Graph Convolutional Neural Networks (SGC) [20] to investigate the importance of strong vs. weak ties. The methodological framework, discussed in more detail in Section 4, provides a reduction in the complexity of the model and computation time required. It has an intuitive manner of producing feature projections and generating the non-linearity for different classes. Even though it is a deep learning approach that accounts for multiple-layers, the simplification allows a single parameter matrix to be produced that can more easily be interpreted if desired. An SGC implementation can be found in the DGL library [21,22].

The SGC uses the features of the nodes and the connectivity in the adjacency matrix to infer the class labels. In this paper we augment this adjacency matrix so that weak-ties are included as well. This produces a matrix in which the strong-ties and the weak-ties are treated equally at the start of the inference procedure. Results using this augmented adjacency matrix are compared to the label produced using the original adjacency matrix. Our experiments also consider the possibility of missing nodes. Obtaining complete datasets of networks is a challenge for a wide range of reasons; for instance, online platforms limit the API calls from developer accounts to reduce the website loads. It is then a crucial question as to whether the results of the investigation are sensitive to missing nodes [23]. Therefore, our experiments remove a range of pre-selected percentages of the network to compare the results. Nodes are ranked for removal based on three different centrality algorithms: betweenness, closeness, and VoteRank [24]. These algorithms sort the nodes in descending order and remove the top percentage chosen (e.g., 20%) so that the inference is performed without the influence of these nodes. We seek to answer the question: which gaps in the data are most likely to affect the SGC? The results help provide another piece of evidence towards the utility of weak-ties in sociological processes.

An added incentive for exploring the use of the SGC, is that it addresses an issue with the application of GCNs (graph convolutional neural networks) [16], where the increase in the number of layers beyond 2–3 can produce a degradation in the results. The number of layers employed by the GCN also corresponds to the $K^{th}$ order neighborhood used in the SGC, and the results will be compared between both methodologies in Section 5. Although the application with GCNs [16] displays the degradation with an increase in the number of layers, L (corresponding to the $K^{th}$ order neighborhood), the SGC does not display this degradation with an increase in K. The authors of [20] describe how the non-linearity for applications such as social networks may introduce unnecessary complexity.

The next section presents key work in the development of graph CNNs and other scientific explorations attesting to the power of weak-ties. Section 3 describes the datasets used in this study, and Section 4 outlines the methodology of the SGC. Then, in Section 5, we present results on the effects of augmenting the adjacency matrix with weak ties and removing nodes ranked on a selection of centrality measures. Within the results section is a subsection which compares the performance of the SGC with that of the GCN. Lastly, the conclusion is presented in Section 6, which summarizes the outcomes, outlines future work, and discusses the application to other datasets.

2. Related Work

This section presents an overview of related work on graph convolutional neural networks and weak ties.

2.1. Graph Convolutional Neural Networks

The work of [25] introduces how graph based methods can be used with convolutional neural networks (CNNs). These graph based methods are spectrally defined and their use within a spatial application utilizes recursive polynomials on the graph Laplacian. This enables spectrally motivated approaches to handle heterogeneous graphs. Convolutional neural networks [26] are employed as they allow for containing an efficient model architecture for extracting meaningful statistical patterns in high-dimensional datasets that can also be large (big data applications [27]). The application of CNNs to learn local stationary structures and apply them to hierarchical pattern searches has driven many advancements in ML tasks [28]. A key contribution of [25] is that the extension of the model to generalize to graphs is founded upon localized graph filters instead of the CNN localized convolution filter (or kernel). It presents a spectral graph formulation and how filters can be defined in respect to individual nodes in the graph with a certain number of ‘hops’ distance. An introduction to the field can be found in [29], where the reader can find a motivation for the fundamental analysis operations of signals from regular grids (lattice structures) to more general graphs. The authors of [30] build upon the work of signals on graphs and shows that a shift-invariant convolution filter can be formulated as a polynomial of adjacency matrices. These filters are defined as polynomials of functions of the graph adjacency matrix, which describes an intuitive spatial formulation of the graph convolutional neural network. The use of the adjacency matrix is utilized in the approach described in Section 4. The filter uses the adjacency matrix and defines the exponent of the matrix as the degree polynomial. Effectively these exponents in the polynomial represent the number of edges (’hops’) from any node.

The approach used here follows that of the work of [31], which relies on the adjacency matrix for filtering. It is noteworthy to emphasize that the graph based approach, which the authors provide code for, shows performance similar to the approach of CNNs the on CIFAR-10 and ImageNet datasets. This generalization could help understand how signals produced in the datasets can be collected whether they be image, document, sound based, brain region based, and more. Allowing for graph data that is heterogeneous is a flexibility which can produce more interesting applications. The model employed describes taking the single hop (defined edges) and the ‘2-hop’ edges to be filtered upon that allows an extended radius of feature influence to be introduced for classification. This concept of using the adjacency matrix powers is explored in Section 5 where the exponent is taken over a range of values which represents the number of ‘hops’. The authors of [16] also use this concept of the hop number that relies on the number of hidden-layers in the neural network and is the basis for the comparison approach employed in this work (described in Section 4).

Weak-Ties

After the publication of Granovetter’s seminal work on the importance of weak ties [8] there have been multiple follow-up studies exploring how social links affect a member’s ability to interact with others in the network and how different types of edges serve disparate roles in transmission and collaboration. Weak ties are important in many types of organizational structures; for instance, Patacchini et al. [32] studied the role of weak ties in criminal collusion. Since innovation requires teamwork and collaboration, organizations need to empower their workers to leverage their weak ties as described in [33]. The work of [34] looks at the effect of weak-ties on the job search process. Extracting information from the network of interactions is not a straightforward process and the work of [35] examines how this can be performed. Given recent evidence for increased social contention [36,37], the research of [38] considers the important question of how weak-ties can facilitate the increase of emotions such as anger on social media. Although weak-ties can be found to play a role in negative situations, there are other contexts where they play an important positive role, such as psychological well being where casual friendships add to happiness (strong ties plus weak ties) [39].

3. Data

Two datasets, Cora [10] and Citeseer [11], were used in this study. The Cora dataset is a citation network where the nodes refer to unique authors and the edges represent a weighted value for the mean citation relationship (from scientific publications). These scientific publications are classified and labeled into seven categories. The data were divided into a separate training and test set in order to provide consistent benchmarks between methodologies. The Citeseer dataset is another network dataset based upon citations where the nodes are also authors and edge values represent the mean citation relationship; it includes six different class labels. The SGC methodology described in Section 4 was used to infer the correct labels for a subset of the nodes in these datasets using both the original connectivity matrix and an augmented one.

Table 1. Summary statistics of the networks from the datasets used in this study: Cora [10] and Citeseer [11]. Each of these datasets has a set of classes used to identify groups of publications in Cora as well as with Citeseer.

	Cora	Citeseer
# of Nodes	2708	3327
# of Edges	10,556	9228
# of Classes	7	6
Average degree	3.8981	2.8109
Density	0.00143	0.00084
Triadic closure	0.0934	0.13006

provides an overview of some of the basic information of the datasets.

Figure 2 shows the degree distribution for the Cora dataset and how the distribution changes when different percentages of the network were removed. Those percentages of the network were removed according to different network centrality measures: betweenness in Figure 2a, closeness in Figure 2b, and VoteRank in Figure 2c. Figure 3 shows the same operation but using the Citeseer dataset. It is interesting to note how the Cora and Citeseer plots differ between their equivalent subfigures. The plots for the betweenness and the closeness change much more than VoteRank which provides evidence that it is more robust against choosing nodes with many edges as a measure of centrality in different datasets.

4. Methodology

For a graph $G=(V,\mathbf{A})$, $\mathcal{V}$ is the node within a set of N nodes $V=\{v_1,v_2,\dots ,v_N\}$, and the adjacency matrix is a symmetric matrix, $\mathbf{A}\in {\mathbb{R}}^{NxN}$. Each element of $\mathbf{A}$, $a_{i,j}$, holds the value of the weighted edge between two nodes $v_i$ and $v_j$ (an absence of an edge is represented by $a_{ij}=0$). The degree matrix $\mathbf{D}=\mathrm{diag}(d_1,d_2,\dots ,d_N)$ is a diagonal matrix of zero off diagonal entries and each diagonal entry is the row sum of the matrix $\mathbf{A}$; $d_i={\sum }_j{\mathbf{A}}_{ij}$. There is a feature vector, ${\mathbf{x}}_i$, for each node i so that the set of features in the network of nodes is a $n\times d$ matrix, $\mathbf{X}\in {\mathbb{R}}^{n\times d}$ where d is the dimensionality of the feature vector. Each node is assigned a class label from the set of classes C; for each node we wish to utilize both $\mathbf{A}$ and $\mathbf{X}$ to infer ${\mathbf{y}}_i\in {\{0,1\}}^C$. ${\mathbf{y}}_i\in {\{0,1\}}^C$ is ideally a one-hot encoded vector which can be supplied data to assist the parameter estimations.

The normalized adjacency matrix with included self-loops is defined as,

$$\mathbf{S}={\tilde{\mathbf{D}}}^{-\frac{1}{2}}\tilde{\mathbf{A}}{\tilde{\mathbf{D}}}^{-\frac{1}{2}},$$

(1)

and $\tilde{\mathbf{A}}=\mathbf{A}+\mathbf{I}$ and $\tilde{\mathbf{D}}=\mathrm{diag}\left(\tilde{\mathbf{A}}\right)$. The classifier employed by the SGC is:

$$\widehat{Y}=\mathrm{softmax}({\mathbf{S}}^K\mathbf{X}\mathbf{\Theta }).$$

(2)

Here, the softmax can be replaced with $\sigma$ as used in binary logistic regression when $C=2$, and for the softmax on multiple categories we have $\mathrm{softmax}\left(\mathbf{x}\right)=exp\left(\mathbf{x}\right)/{\sum }_{c=1}^{C}exp\left({\mathbf{x}}_c\right)$. The component $\mathbf{\Theta }$ is the matrix of parameter values for the projections of the feature vectors so that it is of dimensionality $d\times C$, $\mathbf{\Theta }\in {\mathbb{R}}^{d\times C}$. Intuitively this can be understood as the parameter matrix holding a single vector of parameters of length equal to that of the feature vector and as many of these vectors as there are class labels. This linearization derives from the general concept in deep learning for sequential affine transforms in layers which are subsequent stages,

$$\widehat{Y}=\mathrm{softmax}(\mathbf{S}\dots \mathbf{S}\mathbf{S}\mathbf{X}{\mathbf{\Theta }}^{\left(1\right)}{\mathbf{\Theta }}^{\left(2\right)}\dots {\mathbf{\Theta }}^{\left(K\right)}).$$

(3)

It can then be seen how the value of K chosen represents the number of layers in the network employed. More details can be found in [20] where the methodological derivation is elaborated upon. A key requirement in this framework is the setting of the parameter value k. This can be considered as a tuning parameter for varying of the number of propagation steps taken. This relates to the matrix powers of an adjacency matrix which produce in each entry the number of ‘walks’ between nodes [40,41].

From the adjacency matrix the matrix including weak-ties produced through ‘triangulation’ ([9]) can be found via the walks of length two with ${\mathbf{A}}^2$. The original adjacency matrix is said to contain the strong-ties and there is considerable sociological research into the value of each type of connectivity [8]. In this work we explore the use of an adjacency matrix which contains both the strong-ties and the weak-ties via;

$${\mathbf{A}}^{\prime }={\mathbf{A}}^2+\mathbf{A}.$$

(4)

Figure 4 demonstrates this, and it can be seen visually in the subfigures. Figure 4a shows a hypothetical network with 4 nodes connected in a chain and Figure 4b shows how those nodes are connected when ${\mathbf{A}}^{\prime }$ is produced from including both the strong-ties and the weak-ties.

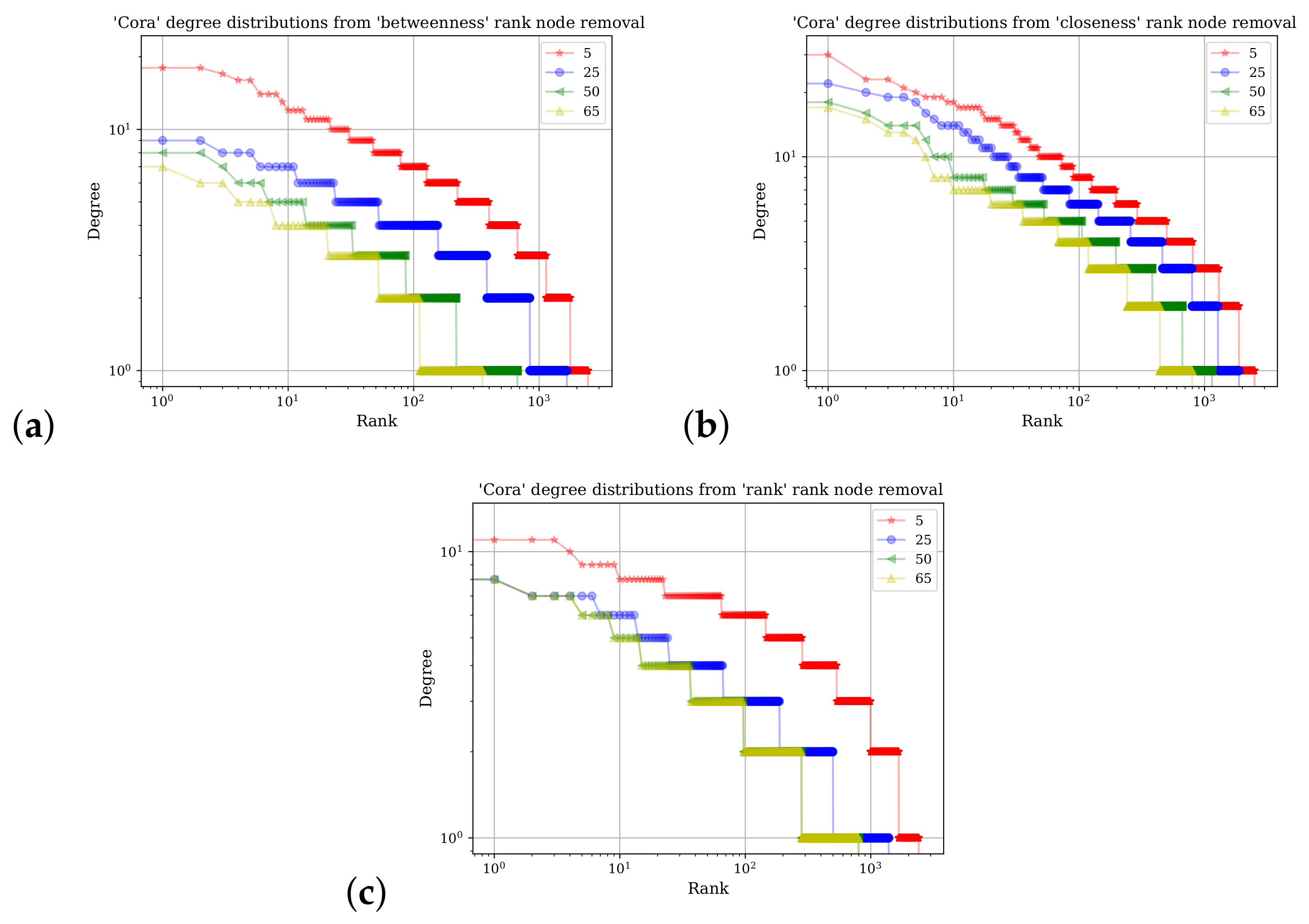
Figure 5 shows a demonstration of the SGC methodology in its ability to accurately predict class labels on the Cora and Citeseer datasets. To explore how robust the methodology is, different percentages of the network were removed; nodes were selected for removal based on their rank calculated from different centrality measures: betweenness, closeness, and VoteRank. Each network measure expresses different aspects of a node’s position in a network and therefore changes in the prediction accuracy, which assist in understanding empirically how node network placements contribute the most in correct label prediction. The VoteRank algorithm considers local node influences more than betweenness or closeness. Figure 5a shows results obtained from running the model on the Cora dataset, and the Citeseer results are shown in Figure 5b.

5. Results

This section explores how the class label prediction accuracy is affected by different removal strategies when the connectivity matrix contains both the links for the strong ties and the weak ties. These results show how the parameter k can affect the accuracy of the prediction of class labels. Section 4 explores how the Simplified Graph Convolutional Neural Network (SGC) methodology performs on the datasets of Cora and Citeseer when different percentages of the nodes are removed. The nodes are removed according to their rank in terms of network centrality positions: betweenness, closeness, and VoteRank. For example, if 20% are removed using closeness as a measure, the nodes were ordered according to the value of closeness from largest to smallest, and the top 20% of the nodes in that percentile of closeness are removed. The purpose of this manipulation is to explore how robust the methodology is to central node removals whose influence on class labels can extend beyond their immediate vicinity.

As shown in Figure 5, we explore how the accuracy is affected by the different network measures used to rank nodes for removal but with the modified adjacency matrix that defines the connectivity for each node. This modification incorporates direct edges (links) called ‘strong ties’, as well as links between nodes that have a common friend. These newly introduced edges are the ‘weak ties’ that are a result of ‘triangulation’ as shown in Figure 4. The changes in the results due to the inclusion of the weak-ties can assist in establishing their importance in people’s classification efforts in real life. A set of plots compare the accuracy of the SGC prediction of class labels with different network removal rankings given the addition of weak ties. The effect of the parameter value of k on accuracy is also explored to understand the sensitivity of the results to the only parameter that requires tuning in SGC.

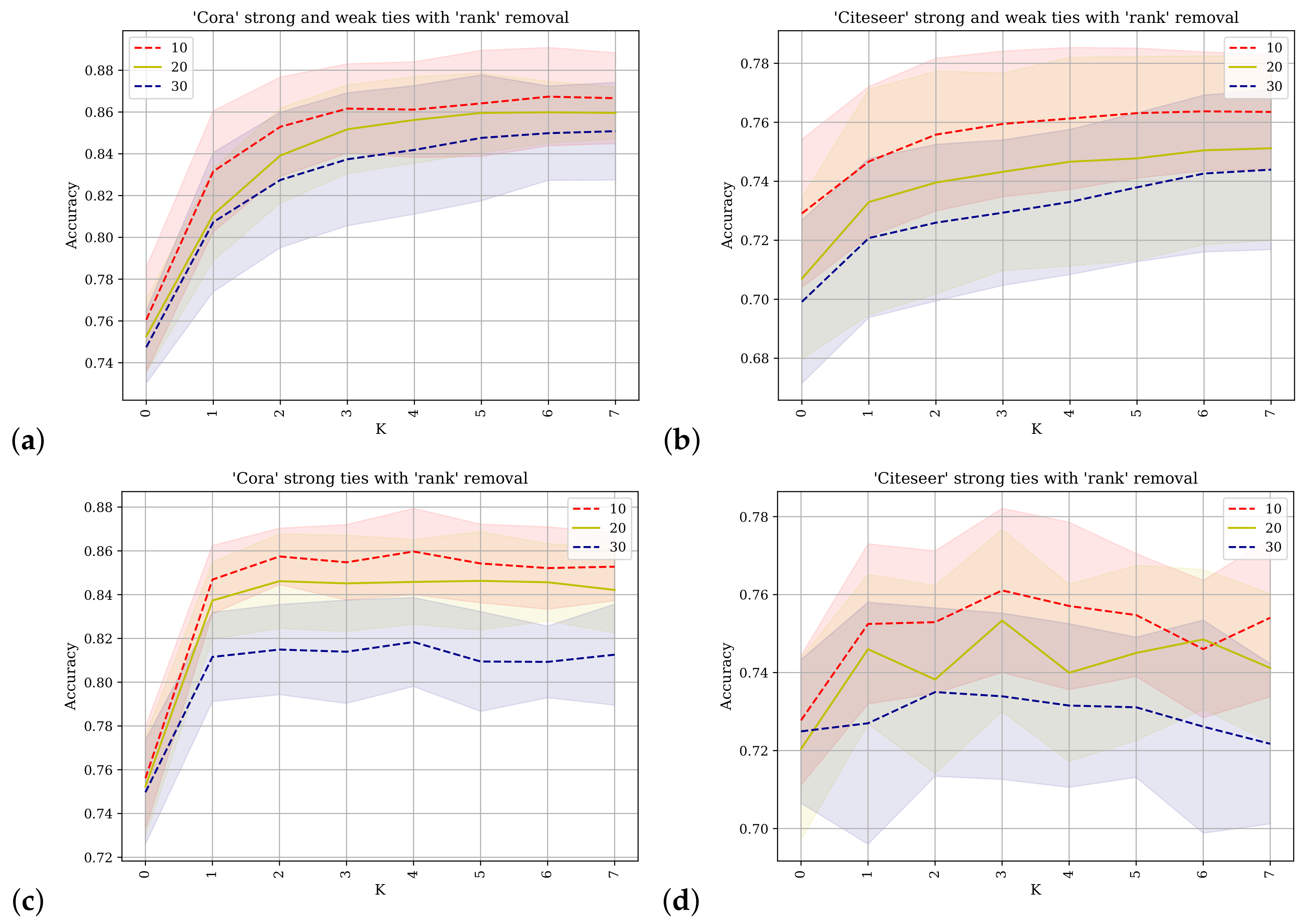
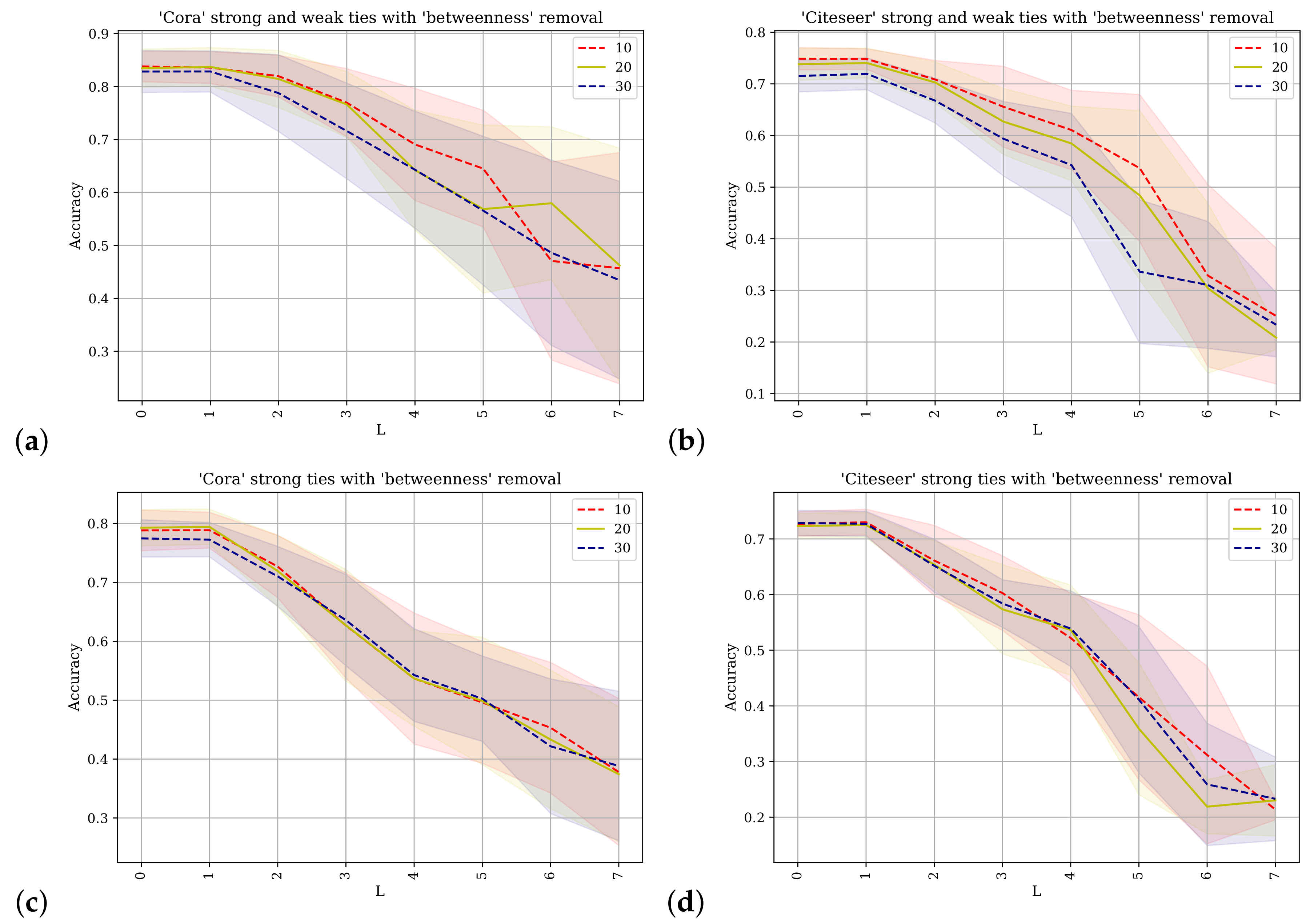
Figure 6 shows the results of applying the SGC with different values of k for predicting class labels. On the horizontal axis is the value of k and on the vertical axis the accuracy as a percentage of the test class labels predicted correctly. The betweenness metric is used to rank the nodes and different percentages of the network’s nodes are removed. The percentage values for each line are indicated in the legend. Figure 6a,b shows the results obtained from using the Cora and Citeseer datasets where the adjacency matrix used contains direct links between nodes and their strong-ties as well as their weak-ties as described in Section 4. Figure 6c,d shows the results when the original adjacency matrix containing only the strong-ties is used. For $k=0$ similar results are obtained and for the final k value, $k=7$, but the progression differs. The difference in progression is evident for the Cora dataset at $k=1$ and up to $k=4$ where the predictive accuracy for Figure 6a is reduced. This also applies to the Citeseer dataset, and especially to the scenario where 20% or 30% of the nodes have been removed. When $k=0$ the SGC operates effectively in a manner similar to logistic regression where the network information is not used and inference is conducted using only the features of the node in question. These results support the conclusion that the augmented network topology of the strong-ties and the weak-ties does not facilitate improved accuracy of label prediction.

Figure 7 also shows the results of applying the SGC with different values of k for predicting class labels. The value of k is shown on the horizontal axis and on the vertical axis the accuracy as a percentage of test class labels being predicted correctly. Here the closeness metric is used to rank the nodes for removal. The different percentages for the removal of network nodes for each line is shown in the plot legends. Figure 7a,b shows the results obtained from using the Cora and Citeseer datasets where the adjacency matrix used contains direct links between nodes and their immediate neighbors (strong-ties) as well as their weak-ties (edges obtained via triangulation) as described in Section 4. Figure 7c,d shows the results when the original adjacency matrix containing only the strong-ties is used. For $k=0$ similar results are obtained between the different pairs as the connectivity of the adjacency is not incorporated and node inference looks only at the features obtained from the node of concern. For $k=7$ similar values are obtained through the extended radius of the adjacency power, but the progression of the trace differs between pairs of the plots. The difference between the pairs of traces can be easily seen by inspection of the application to the Cora dataset at values $k=1$ and up to $k=4$ where the predictive accuracy for Figure 7a is reduced. This also applies to the Citeseer dataset, and is attenuated when 20% or 30% of the nodes have been removed. These results also support the conclusion that the augmented network topology of the strong-ties and the weak-ties does not facilitate improved accuracy of label prediction and that these conclusions are robust according to removal with a different network centrality ranking.

Figure 8 also shows the results of applying the SGC with different values of k for predicting class labels but uses the VoteRank centrality metric to rank the nodes for removal. The different percentages of node removal for each line are shown in the plot legends. Figure 8a,b shows the results obtained from the Cora and Citeseer datasets where the adjacency matrix used contains direct links between nodes and their immediate neighbors (strong-ties) as well as their weak-ties (edges obtained via triangulation) as described in Section 4. Figure 8c,d shows the results when the original adjacency matrix containing only the strong-ties is used. When $k=0$ similar results are obtained between the different pairs as the connectivity of the adjacency is not incorporated and node inference looks only at the features from the node of concern. The application of VoteRank changes the interpretation of the previous results where both applications to Cora and Citeseer have improved results for the augmented adjacency matrix (strong-ties and weak-ties) from $k=3$ and upwards.

The set of results show that for $k<3$ the adjacency matrix containing the set of original strong-ties edges suffices to produce the best results. For larger values of k the augmented adjacency, which contains both the strong-ties and the weak-ties, can show improved performance when nodes are removed according to the VoteRank algorithm and not according to betweenness or closeness. This emphasizes that there is a complex interplay between how node centrality is measured and the manner in which the inference methodology operates. It cannot be considered an a priori principle that weak-ties can provide an increased predictive power due to its support from the social science domain and its adherence to it. On the contrary, they induce a requirement for larger values of k to reach the maximum accuracy implying that the SGC requires more ‘layers’ which effectively aggregates information from more distant nodes in order to counter balance the introduction of weak-ties as strong-ties. This can provide anecdotal evidence that those two types of edges may require separate treatment. Further experiments conducted, working with a starting network of only the weak-ties, produced networks with an increased number of disconnected components.

These results also support the claims of the authors of ‘VoteRank’ when they state that the methodology identifies a set of decentralized spreaders as opposed to focusing on a group of spreaders which overlap in their sphere of influence. This is why the VoteRank targeted node removal was more effective in reducing the accurate label inference since more locally influential nodes for classification were identified; the weak-ties provided extra information about local labels in the absence of these essential strong-tie connected nodes.

Comparison to GCN

This section compares results from applying SGC [20] vs. using the original GCN framework [16]. Appendix B of [16] discusses the effect of adding more network layers on accuracy. It states that the best choice is 2–3 layers and that after 7 layers there is steep degradation of accuracy. The number of layers corresponds to the number of ‘K’ hops as explored with the SGC previously. The SGC methodology encapsulates the K hop neighborhood without the non-linearity and therefore avoids the degradation of accuracy with increased K or L. Figure 9, Figure 10 and Figure 11 present the results of applying the GCN in the same set of situations that we evaluated with SGC. The number of layers L is on the x-axis (corresponding analogously to the K in SGC) and the y-axis is the accuracy. In each of these figures, the Cora and Citeseer datasets are used when examining the strong with weak ties in an augmented network as well as using the original network containing only the strong ties. Each figure removes a percentage of the nodes based upon the rank of the nodes with the centrality measures of betweenness, closeness, and VoteRank respectively. The plots have three lines per plot where there are different percentages (10%, 20%, and 30%) of the nodes removed based upon the centrality measure. In each of the Figure 9, Figure 10 and Figure 11 it can be seen how the accuracy degrades after $L=1$ showing how the SGC is able to include more network information about each node without introducing unnecessary complexity which degrades accuracy. The degradation of the accuracy in relation to the choice of centrality measure is comparable between the results, showing that the GCN is less specific to the node network positions than the SGC is, which can be attributed to the non-linearity the GCN introduces via the layers.

In Appendix A, an additional set of tables are provided in order to see the comparison between the effectiveness of the SGC and the GCN over the values of K and L respectively. The two datasets and the centrality measures with the different edge sets are examined.

6. Conclusions

This paper explores the uses of the recently introduced methodology, the Simplified Graph Convolutional Neural Network (SGC); class label inferences are produced based on the network structure, represented by an adjacency matrix, in combination with node feature vectors. There is interest in exploring this model in more depth since it provides a succinct yet expressive formulation for describing how nodes can influence class label prediction within a network. Besides the parameters fitted in order to optimize the target label prediction, there is only a single parameter value k, which requires manual tuning. This parameter is related to the number of layers $S^k$ (described in Section 4).

The exploration conducted here investigates the degree to which the accurate prediction of class labels is reduced by removing percentages of the network ranked by centrality metrics. This provides evidence to the practitioner who collects data, that may contain gaps in the network, and needs to know if the conclusions can be drastically affected by missing data on key nodes as to whether the the SGC is sensitive to such issues. Three different network centrality measures are used to select removal nodes: betweenness, closeness, and VoteRank. We find that the methodology does manage to produce analogous predictions based upon different percentages of removal (10/20/30). The largest observed changes were when the nodes were selected for removal with the VoteRank algorithm and not with betweenness or closeness. This shows that the SGC label assignments are more sensitive to the local label information derived from the features of the local nodes than well connected groups of nodes in the center of the network. This also explains why it has displayed the ability to be robust in its predictions.

The other question explored is whether the results would change if the SGC was supplied an adjacency matrix that contained the ‘triangulated edges’ to begin with. The existing edges in the adjacency matrix can be referred to as strong-ties as they are direct links; the edges that connect friends-of-friends (produced from triangulation $A^2$), can be referred to as weak-ties. A matrix with both of these edge sets was supplied to the SGC to compare the accuracy predictions. There is considerable sociological literature discussing the importance of these edges in helping to discover important connections. Our results show a degraded outcome with the exception of when nodes were removed with the VoteRank algorithm. This indicates that the inclusion of the weak-ties provides a more robust edge set when important local nodes are removed. The results do not show an ability to improve the prediction of class labels for low removal percentages when weak-ties are included.

The datasets used in this study contained monolithic graphs, where every node is reachable from any other node. There are many datasets where the data contains disjoint graphs, and this can be particularly common when the observational capabilities are limited in comparison to the process. A notable example is with protein interaction graphs. Applying the investigation taken here with such data would alter the adjacency matrix but not in a way that would cause a failure in its ability to follow the procedures described. Since the exploration did not depend upon a small fraction of the number of nodes, the study could continue with such data as long as the distribution of the relative betweenness and closeness is not excessively skewed for the subgraphs. The investigation therefore can be conducted on a wide range of datasets to explore the role of weak ties in the networks. Corporate networks are an interesting avenue for extensions as the nodes would be more ‘complex’ entities which may rely on their network connections in different ways. A key aspect of the extendibility is the overhead of the approach. Since the parameter, feature and adjacency matrix are combined with linear operators with a non-nested set of intermediate features, inferences are relatively cheaper than other approaches that build deeper trees and introduce further non-linearities.