Multi-Label Classification with Optimal Thresholding for Multi-Composition Spectroscopic Analysis
Abstract
1. Introduction
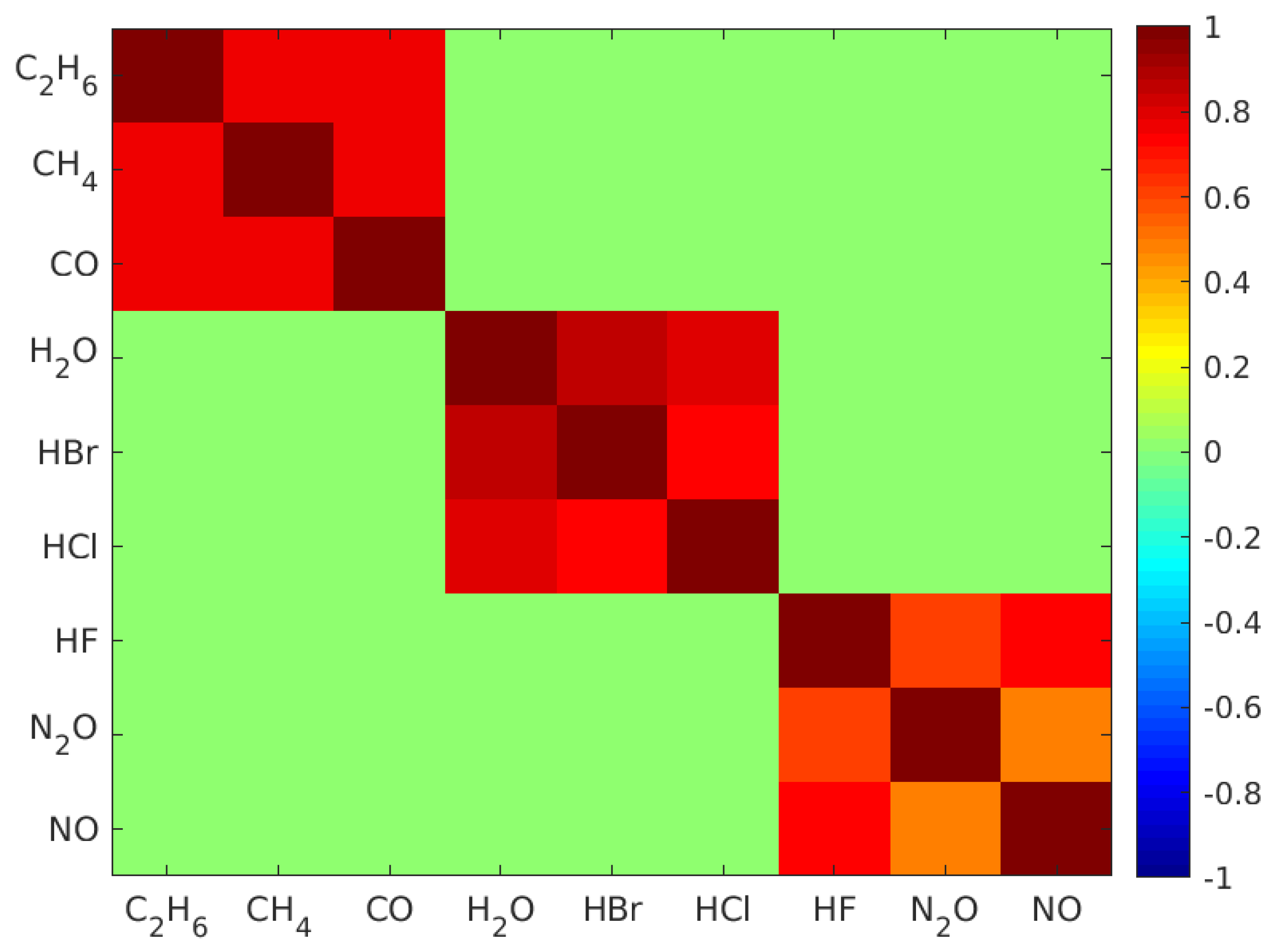
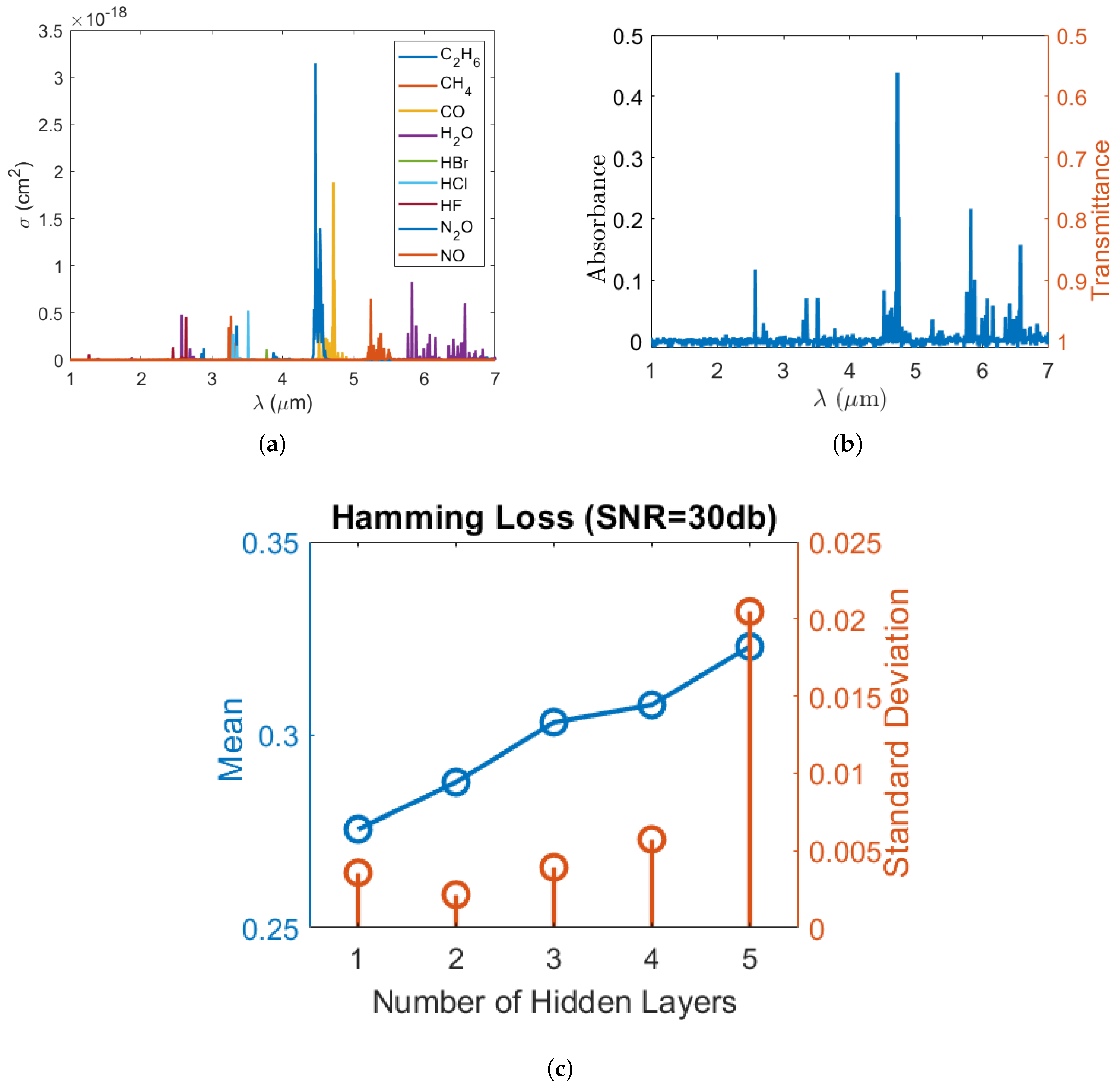
2. Dataset
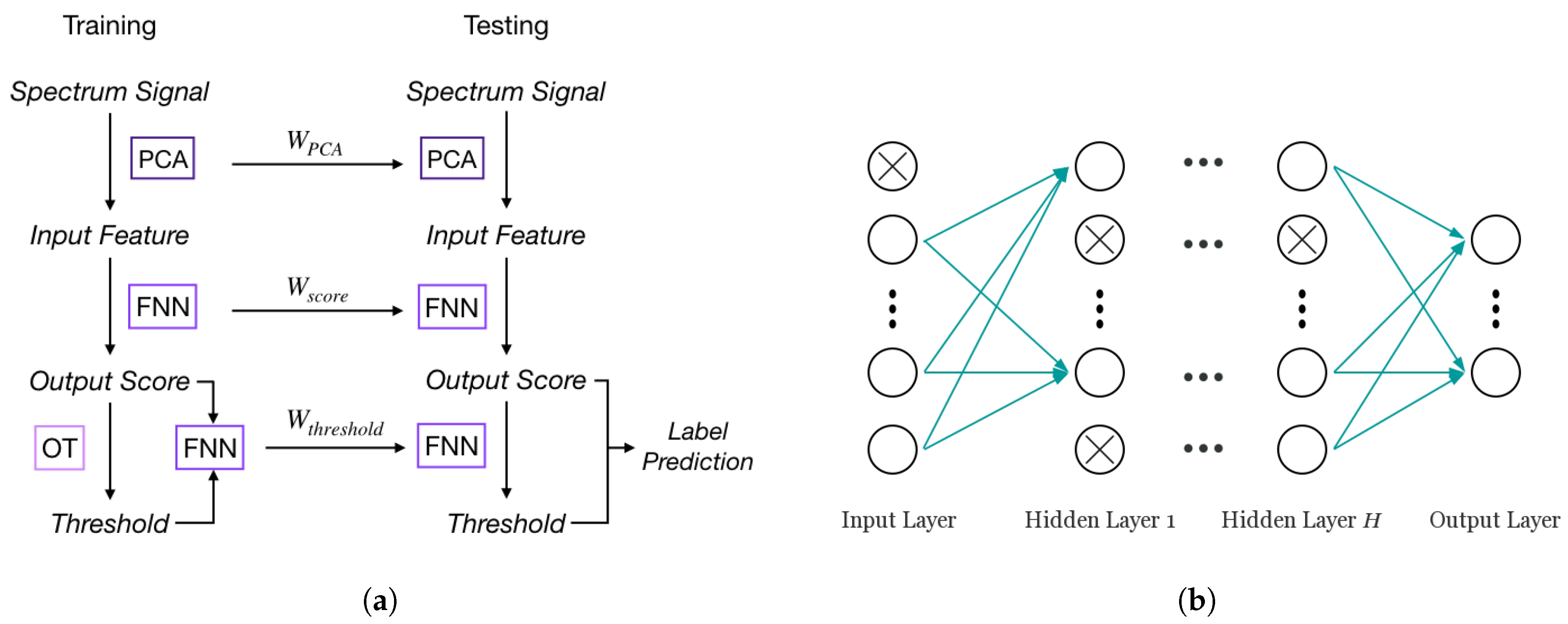
3. Algorithm
3.1. Feedforward Neural Networks
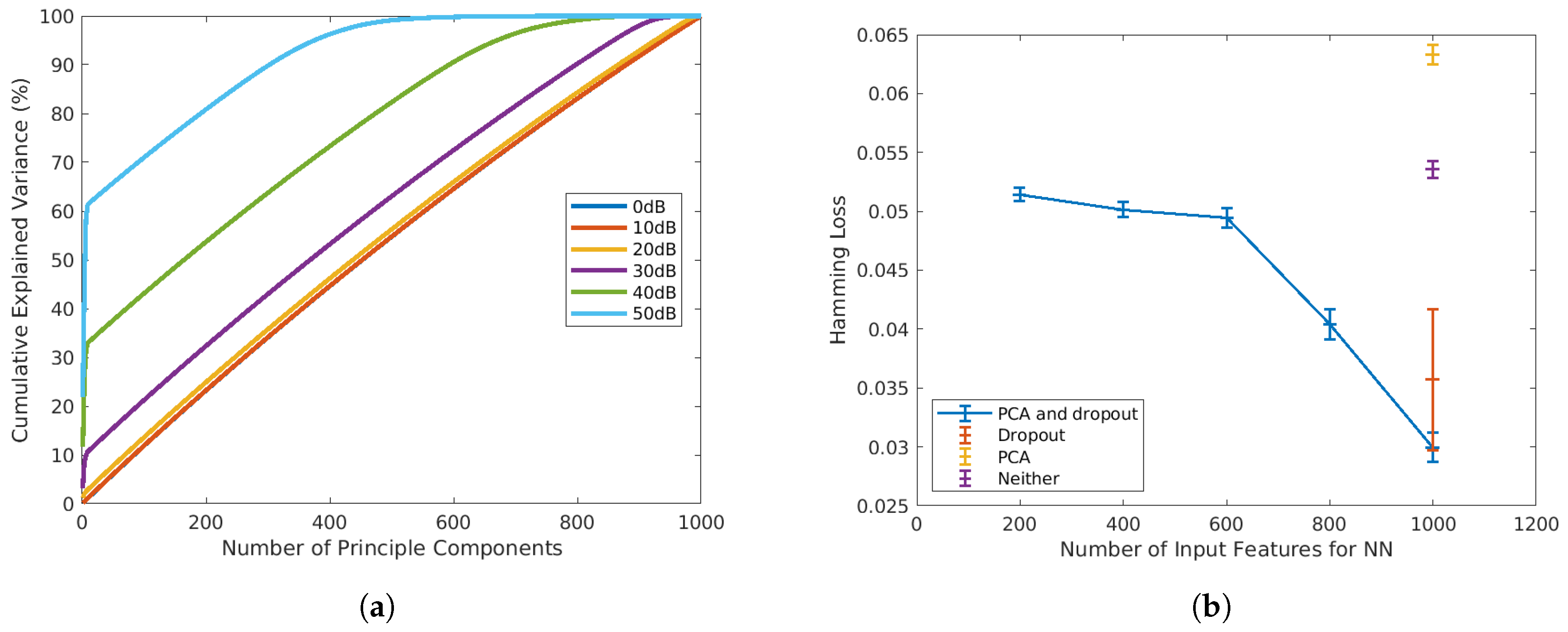
3.2. Principal Component Analysis
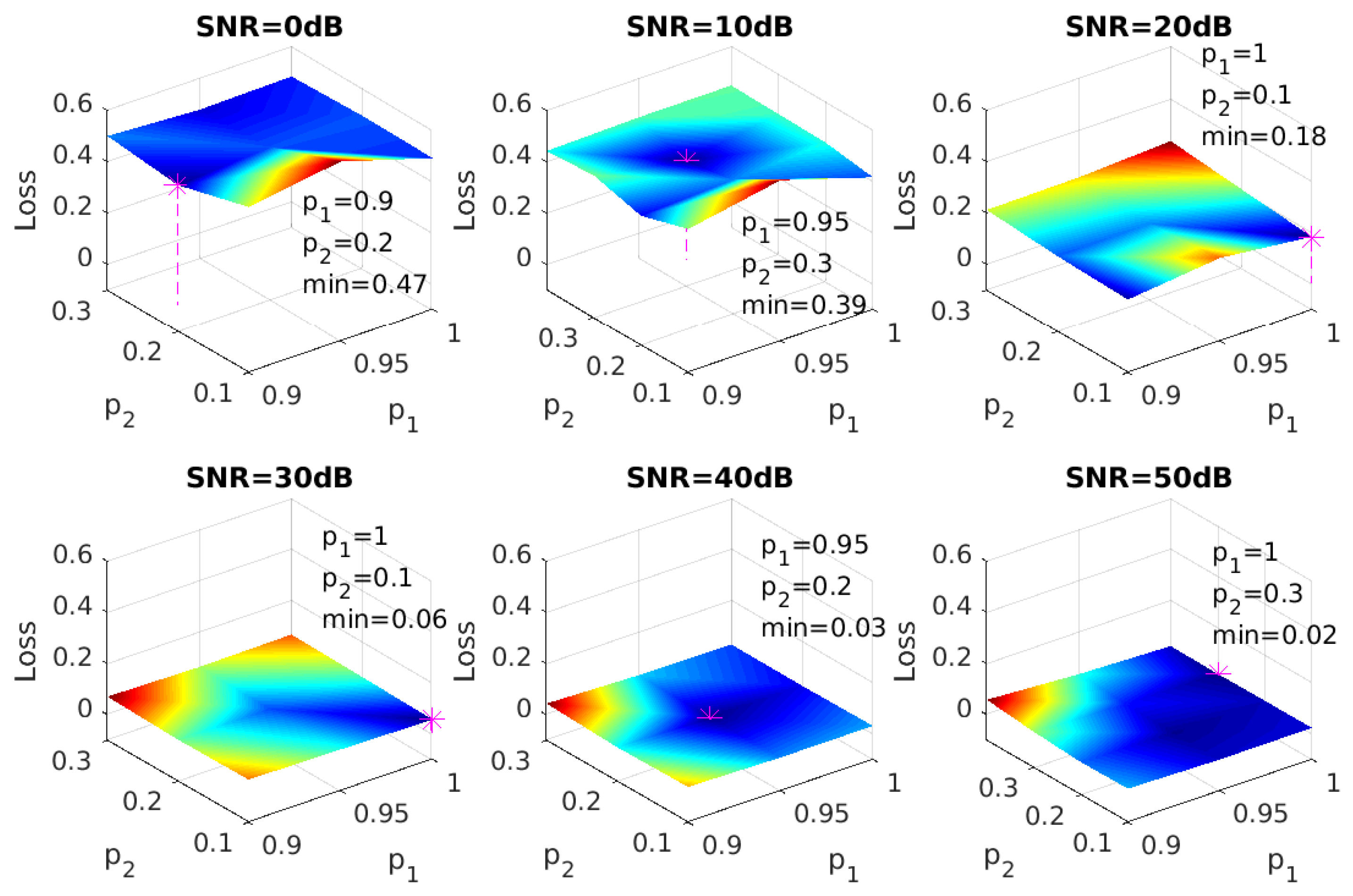
3.3. Optimal Thresholding
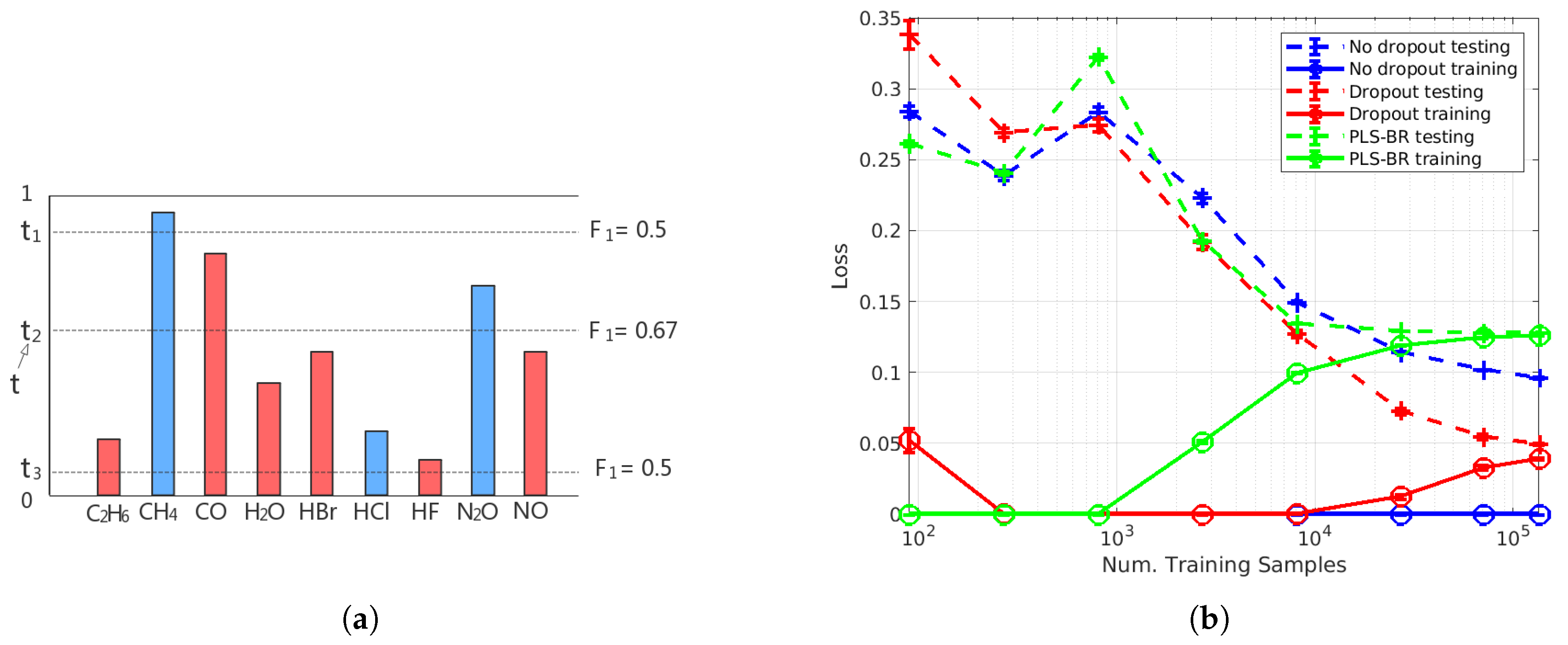
3.4. Evaluation Metrics
4. Results and Discussions
4.1. Hyper-Parameter Tuning
4.1.1. Dropout
4.1.2. Training Sample Size
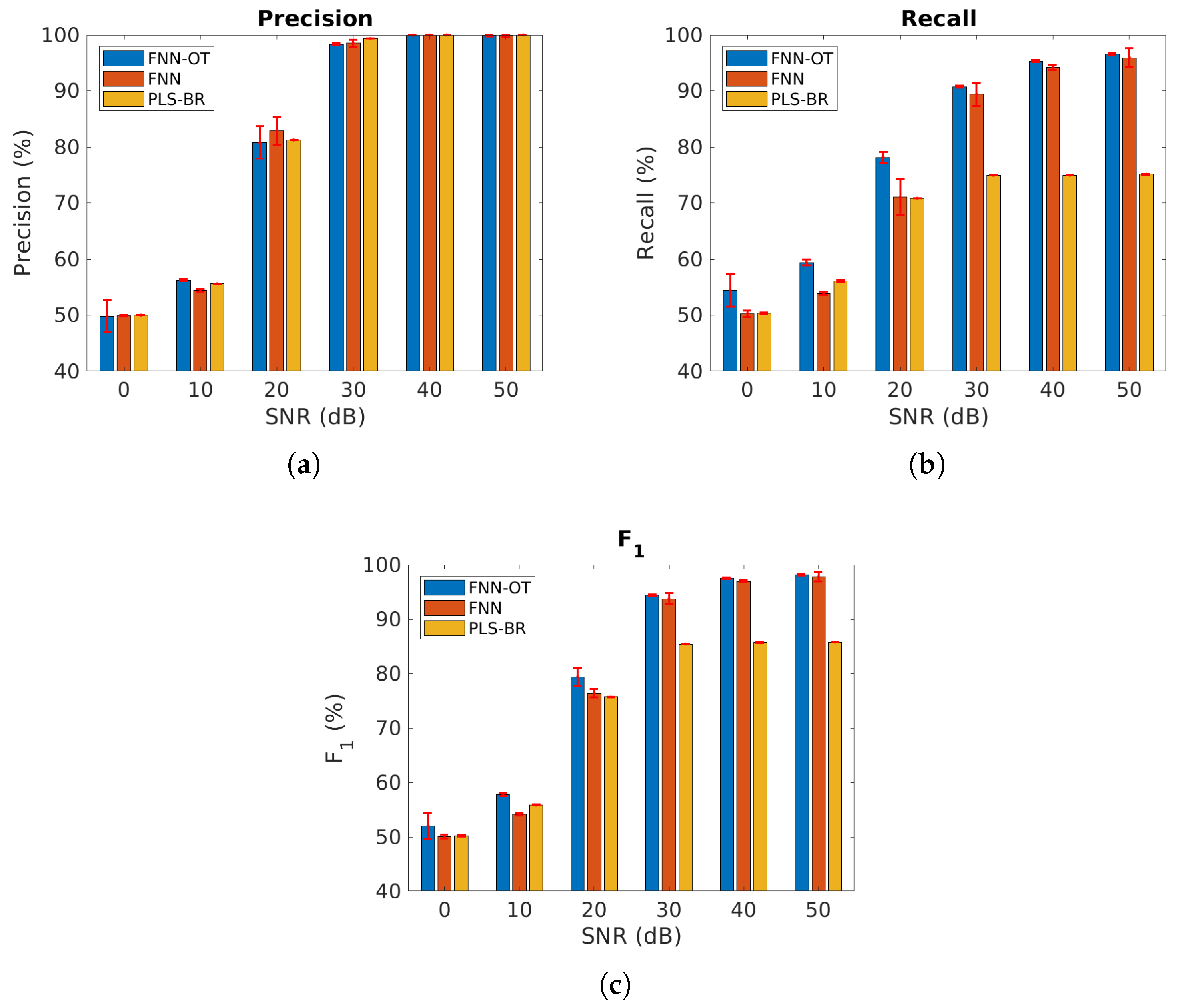
4.2. Performance Comparison of Mutually Independent Gas Data
4.3. Performance Comparison for Highly Correlated Gas Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Generation of Correlated Uniformly Distributed Random Variables
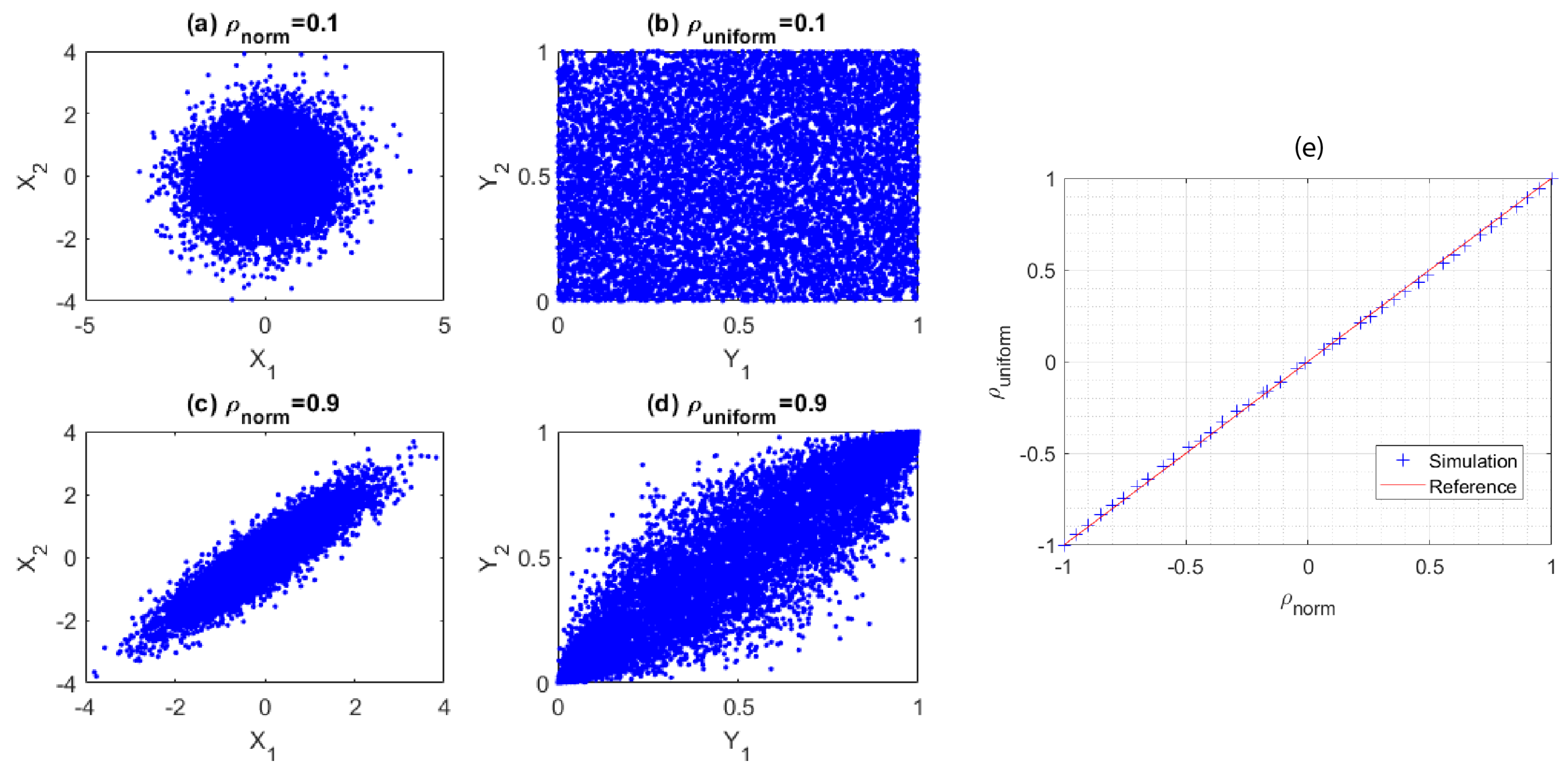
Appendix B. Partial Least Squares Method
References
- Gallagher, M.; Deacon, P. Neural networks and the classification of mineralogical samples using X-ray spectra. In Proceedings of the 2002 9th International Conference on Neural Information Processing (ICONIP’02), Singapore, 18–22 November 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 5, pp. 2683–2687. [Google Scholar]
- Jiang, J.; Zhao, M.; Ma, G.-M.; Song, H.-T.; Li, C.-R.; Han, X.; Zhang, C. Tdlas-based detection of dissolved methane in power transformer oil and field application. IEEE Sens. J. 2018, 18, 2318–2325. [Google Scholar] [CrossRef]
- Dong, D.; Jiao, L.; Li, C.; Zhao, C. Rapid and real-time analysis of volatile compounds released from food using infrared and laser spectroscopy. TrAC Trends Anal. Chem. 2019, 110, 410–416. [Google Scholar] [CrossRef]
- Christy, C.D. Real-time measurement of soil attributes using on-the-go near infrared reflectance spectroscopy. Comput. Electron. Agric. 2008, 61, 10–19. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, Y.; Liu, T.; Sun, T.; Grattan, K.T. Tdlas detection of propane/butane gas mixture by using reference gas absorption cells and partial least square approach. IEEE Sens. J. 2018, 18, 8587–8596. [Google Scholar] [CrossRef]
- Schumacher, W.; Kühnert, M.; Rösch, P.; Popp, J. Identification and classification of organic and inorganic components of particulate matter via raman spectroscopy and chemometric approaches. J. Raman Spectrosc. 2011, 42, 383–392. [Google Scholar] [CrossRef]
- Goodacre, R. Explanatory analysis of spectroscopic data using machine learning of simple, interpretable rules. Vib. Spectrosc. 2003, 32, 33–45. [Google Scholar] [CrossRef]
- Yang, Y. An evaluation of statistical approaches to text categorization. Inf. Retr. 1999, 1, 69–90. [Google Scholar] [CrossRef]
- Schapire, R.E.; Singer, Y. Boostexter: A boosting-based system for text categorization. Mach. Learn. 2000, 39, 135–168. [Google Scholar] [CrossRef]
- Tsoumakas, G.; Katakis, I. Multi-label classification: An overview. Int. J. Data Warehous. Min. 2006, 3, 1–13. [Google Scholar] [CrossRef]
- Gibaja, E.; Ventura, S. Multi-label learning: A review of the state of the art and ongoing research. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 411–444. [Google Scholar] [CrossRef]
- Zhang, Y.; Schneider, J. Maximum margin output coding. In Proceedings of the 29th International Coference on International Conference on Machine Learning (ICML’12), Edinburgh, UK, 26 June–1 July 2012; Omnipress: Madison, WI, USA, 2012; pp. 379–386. [Google Scholar]
- Zhang, M.; Wu, L. Lift: Multi-label learning with label-specific features. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 107–120. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.-L.; Zhang, K. Multi-label learning by exploiting label dependency. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’10), Washington, DC, USA, 25–28 July 2010; ACM: New York, NY, USA, 2010; pp. 999–1008. [Google Scholar] [CrossRef]
- Li, Q.; Xie, B.; You, J.; Bian, W.; Tao, D. Correlated logistic model with elastic net regularization for multilabel image classification. IEEE Trans. Image Process. 2016, 25, 3801–3813. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Qiao, M.; Bian, W.; Tao, D. Conditional graphical lasso for multi-label image classification. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2977–2986. [Google Scholar]
- Godbole, S.; Sarawagi, S. Discriminative Methods for Multi-Labeled Classification. In Advances in Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2004; pp. 22–30. [Google Scholar]
- Katakis, I.; Tsoumakas, G.; Vlahavas, I. Multilabel text classification for automated tag suggestion. In Proceedings of the ECML PKDD Discovery Challenge, Antwerp, Belgium, 15–19 September 2008; Volume 75. [Google Scholar]
- Tsoumakas, G.; Vlahavas, I. Random k-Labelsets: An Ensemble Method for Multilabel Classification. In European Conference on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2007; pp. 406–417. [Google Scholar]
- Read, J.; Pfahringer, B.; Holmes, G.; Frank, E. Classifier Chains for Multi-Label Classification. In Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Gemany, 2009; pp. 254–269. [Google Scholar]
- Huang, K.H.; Lin, H.T. Cost-sensitive label embedding for multi-label classification. Mach. Learn. 2017, 106, 1725–1746. [Google Scholar] [CrossRef]
- Szymański, P.; Kajdanowicz, T.; Chawla, N. LNEMLC: Label Network Embeddings for Multi-Label Classifiation. arXiv 2018, arXiv:1812.02956. [Google Scholar]
- Szymański, P.; Kajdanowicz, T.; Kersting, K. How is a data-driven approach better than random choice in label space division for multi-label classification? Entropy 2016, 18, 282. [Google Scholar] [CrossRef]
- Clare, A.; King, R.D. Knowledge Discovery in Multi-Label Phenotype Data. In European Conference on Principles of Data Mining and Knowledge Discovery; Springer: Berlin/Heidelberg, Germany, 2001; pp. 42–53. [Google Scholar]
- Zhang, M.-L.; Zhou, Z.-H. A k-nearest neighbor based algorithm for multi-label classification. In Proceedings of the 2005 IEEE International Conference on Granular Computing, Beijing, China, 25–27 July 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 2, pp. 718–721. [Google Scholar]
- Younes, Z.; Abdallah, F.; Denœux, T. Multi-label classification algorithm derived from k-nearest neighbor rule with label dependencies. In Proceedings of the 2008 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–5. [Google Scholar]
- Read, J.; Hollmén, J. Multi-label classification using labels as hidden nodes. arXiv 2015, arXiv:1503.09022. [Google Scholar]
- Zhang, M.-L.; Zhou, Z.-H. Multilabel neural networks with applications to functional genomics and text categorization. IEEE Trans. Knowl. Data Eng. 2006, 18, 1338–1351. [Google Scholar] [CrossRef]
- Nam, J.; Kim, J.; Mencía, E.L.; Gurevych, I.; Fürnkranz, J. Large-Scale Multi-Label Text Classification- Revisiting Neural Networks. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2014; pp. 437–452. [Google Scholar]
- Collobert, R.; Weston, J. A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; ACM: New York, NY, USA, 2008; pp. 160–167. [Google Scholar]
- Gong, Y.; Jia, Y.; Leung, T.; Toshev, A.; Ioffe, S. Deep convolutional ranking for multilabel image annotation. arXiv 2013, arXiv:1312.4894. [Google Scholar]
- Wang, J.; Yang, Y.; Mao, J.; Huang, Z.; Huang, C.; Xu, W. Cnn-rnn: A unified framework for multi-label image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2285–2294. [Google Scholar]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Benner, D.C.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R.; et al. The HITRAN 2012 Molecular Spectroscopic Database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Holland, S.M. Principal Components Analysis (PCA); Department of Geology, University of Georgia: Athens, GA, USA, 2008. [Google Scholar]
- Allred, C.S. Partially Correlated Uniformly Distributed Random Numbers. Available online: https://medium.com/capital-one-tech/partially-correlated-uniformly-distributed-random-numbers-5ce82486b68a (accessed on 1 November 2019).
- Luaces, O.; Díez, J.; Barranquero, J.; del Coz, J.J.; Bahamonde, A. Binary relevance efficacy for multilabel classification. Prog. Artif. Intell. 2012, 1, 303–313. [Google Scholar] [CrossRef]
- Madden, M.G.; Howley, T. A Machine Learning Application for Classification of Chemical Spectra. In Applications and Innovations in Intelligent Systems XVI; Springer: London, UK, 2009; pp. 77–90. [Google Scholar]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Elbassbasi, M.; Kzaiber, F.; Ragno, G.; Oussama, A. Classification of raw milk by infrared spectroscopy (ftir) and chemometric. J. Sci. Specul. Res. 2010, 1, 28–33. [Google Scholar]
- Hirri, A.; Bassbasi, M.; Oussama, A. Classification and quality control of lubricating oils by infrared spectroscopy and chemometric. Int. J. Adv. Technol. Eng. Res. 2013, 3, 59–62. [Google Scholar]
- Hirri, A.; Bassbasi, M.; Platikanov, S.; Tauler, R.; Oussama, A. Ftir spectroscopy and pls-da classification and prediction of four commercial grade virgin olive oils from morocco. Food Anal. Methods 2016, 9, 974–981. [Google Scholar] [CrossRef]

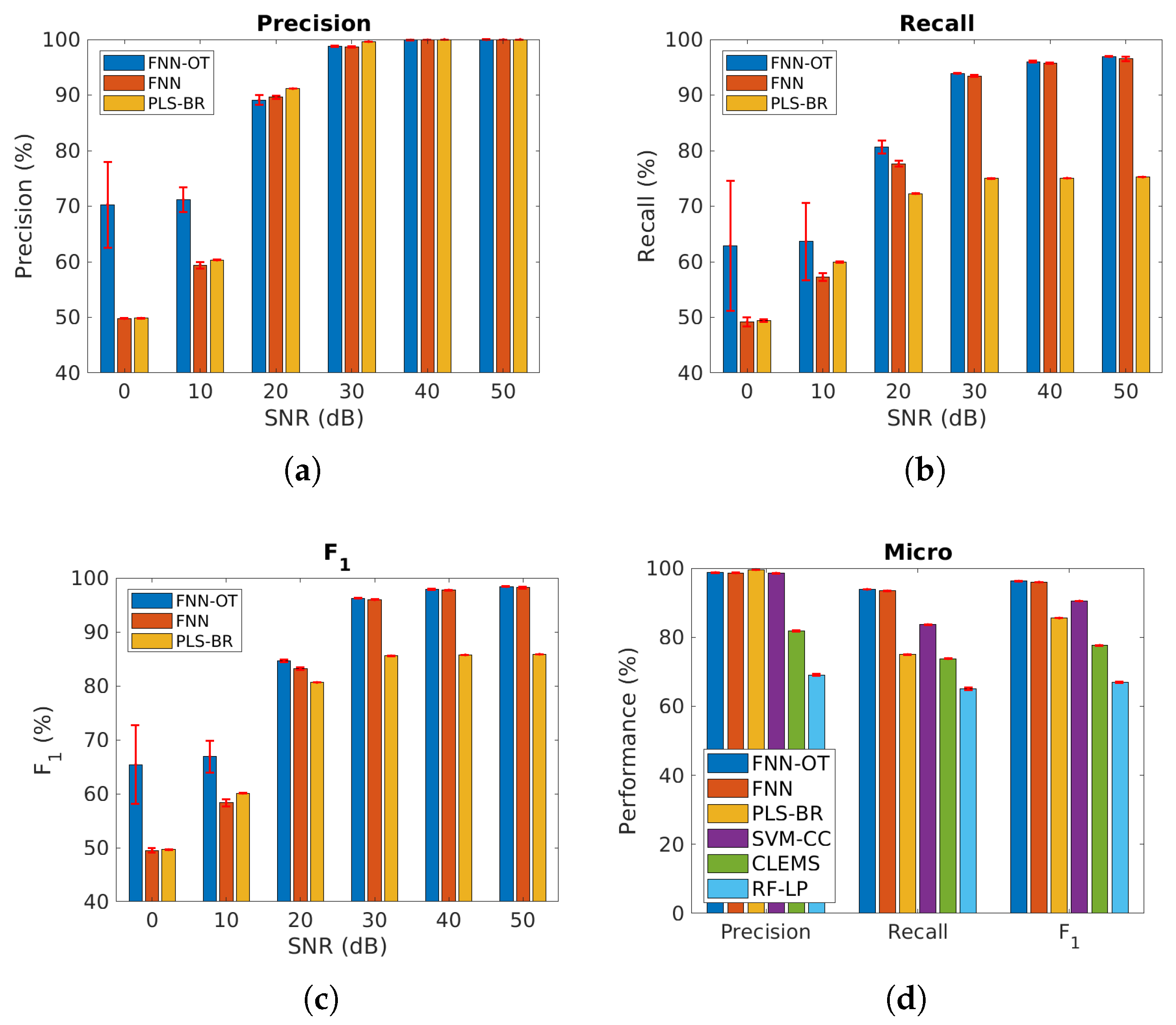
| Micro-Averaged Precision | |||
| FNN-OT | FNN | PLS-BR | |
| 0.50 ± 0.03 | 0.499 ± 0.001 | 0.4998 ± 0.0004 | |
| 0.562 ± 0.002 | 0.545 ± 0.003 | 0.5561 ± 0.0004 | |
| 0.81 ± 0.03 | 0.83 ± 0.02 | 0.8124 ± 0.0003 | |
| 0.983 ± 0.002 | 0.985 ± 0.006 | 0.9935 ± 0.0001 | |
| 0.9992 ± 0.0002 | 0.9996 ± 0.0001 | 1 ± 0 | |
| 0.998 ± 0.001 | 0.998 ± 0.002 | 1 ± 0 | |
| Micro-Averaged Recall | |||
| FNN-OT | FNN | PLS-BR | |
| 0.54 ± 0.03 | 0.502 ± 0.006 | 0.504 ± 0.001 | |
| 0.594 ± 0.005 | 0.539 ± 0.003 | 0.561 ± 0.001 | |
| 0.78 ± 0.01 | 0.71 ± 0.03 | 0.7083 ± 0.0003 | |
| 0.908 ± 0.002 | 0.89 ± 0.02 | 0.7488 ± 0.0002 | |
| 0.953 ± 0.002 | 0.942 ± 0.004 | 0.7492 ± 0.0003 | |
| 0.965 ± 0.003 | 0.96 ± 0.02 | 0.7507 ± 0.0002 | |
| Micro-AveragedScore | |||
| FNN-OT | FNN | PLS-BR | |
| 0.52 ± 0.02 | 0.501 ± 0.003 | 0.5017 ± 0.0007 | |
| 0.578 ± 0.003 | 0.542 ± 0.003 | 0.5587 ± 0.0008 | |
| 0.79 ± 0.02 | 0.764 ± 0.008 | 0.7568 ± 0.0003 | |
| 0.9439 ± 0.0007 | 0.94 ± 0.01 | 0.8539 ± 0.0002 | |
| 0.9755 ± 0.0009 | 0.970 ± 0.002 | 0.8566 ± 0.0002 | |
| 0.981 ± 0.002 | 0.978 ± 0.009 | 0.8576 ± 0.0001 | |
| Micro-Averaged Precision | |||
| FNN-OT | FNN | PLS-BR | |
| 0.70 ± 0.08 | 0.4979 ± 0.0008 | 0.498 ± 0.001 | |
| 0.71 ± 0.02 | 0.594 ± 0.006 | 0.6030 ± 0.0005 | |
| 0.89 ± 0.01 | 0.896 ± 0.003 | 0.9114 ± 0.0003 | |
| 0.987 ± 0.001 | 0.987 ± 0.001 | 0.9961 ± 0.0001 | |
| 0.9989 ± 0.0003 | 0.9991 ± 0.0002 | 1 ± 0 | |
| 0.9996 ± 0.0005 | 0.9998 ± 0.0001 | 0.9926 ± 0.0007 | |
| Micro-Averaged Recall | |||
| FNN-OT | FNN | PLS-BR | |
| 0.6 ± 0.1 | 0.492 ± 0.008 | 0.495 ± 0.002 | |
| 0.64 ± 0.07 | 0.573 ± 0.007 | 0.599 ± 0.001 | |
| 0.81 ± 0.01 | 0.777 ± 0.005 | 0.7232 ± 0.0004 | |
| 0.9388 ± 0.0007 | 0.934 ± 0.002 | 0.7497 ± 0.0003 | |
| 0.960 ± 0.002 | 0.957 ± 0.001 | 0.7505 ± 0.0002 | |
| 0.9692 ± 0.0007 | 0.965 ± 0.004 | 0.7497 ± 0.0002 | |
| Micro-AveragedScore | |||
| FNN-OT | FNN | PLS-BR | |
| 0.65 ± 0.07 | 0.495 ± 0.004 | 0.496 ± 0.001 | |
| 0.67 ± 0.03 | 0.583 ± 0.007 | 0.6011 ± 0.0007 | |
| 0.846 ± 0.003 | 0.832 ± 0.002 | 0.8064 ± 0.0002 | |
| 0.9625 ± 0.0004 | 0.9597 ± 0.0006 | 0.8555 ± 0.0002 | |
| 0.9791 ± 0.0009 | 0.9776 ± 0.0006 | 0.8575 ± 0.0002 | |
| 0.9841 ± 0.0004 | 0.9821 ± 0.0020 | 0.8542 ± 0.0004 | |
| Precision | Recall | Score | Computing Time | |
|---|---|---|---|---|
| FNN-OT | 0.987 ± 0.001 | 0.9388 ± 0.0007 | 0.9625 ± 0.0004 | 640 s |
| FNN | 0.987 ± 0.001 | 0.934 ± 0.002 | 0.9597 ± 0.0006 | 440 s |
| PLS-BR | 0.9961 ± 0.0001 | 0.7497 ± 0.0003 | 0.8555 ± 0.0002 | 100 s |
| SVM-CC | 0.9855 ± 0.0007 | 0.8365 ± 0.0009 | 0.9049 ± 0.0004 | 1440 s |
| CLEMS | 0.819 ± 0.002 | 0.738 ± 0.002 | 0.7765 ± 0.0008 | 12,000 s |
| RF-LP | 0.691 ± 0.002 | 0.650 ± 0.004 | 0.670 ± 0.002 | 720 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, L.; Yuen, B.; Lu, T. Multi-Label Classification with Optimal Thresholding for Multi-Composition Spectroscopic Analysis. Mach. Learn. Knowl. Extr. 2019, 1, 1084-1099. https://doi.org/10.3390/make1040061
Gan L, Yuen B, Lu T. Multi-Label Classification with Optimal Thresholding for Multi-Composition Spectroscopic Analysis. Machine Learning and Knowledge Extraction. 2019; 1(4):1084-1099. https://doi.org/10.3390/make1040061
Chicago/Turabian StyleGan, Luyun, Brosnan Yuen, and Tao Lu. 2019. "Multi-Label Classification with Optimal Thresholding for Multi-Composition Spectroscopic Analysis" Machine Learning and Knowledge Extraction 1, no. 4: 1084-1099. https://doi.org/10.3390/make1040061
APA StyleGan, L., Yuen, B., & Lu, T. (2019). Multi-Label Classification with Optimal Thresholding for Multi-Composition Spectroscopic Analysis. Machine Learning and Knowledge Extraction, 1(4), 1084-1099. https://doi.org/10.3390/make1040061






