Targeted Adaptable Sample for Accurate and Efficient Quantile Estimation in Non-Stationary Data Streams
Abstract
1. Introduction
- A more detailed description of the underlying theory and the derivation of all mathematical formulae,
- New experiments (double the amount) that illustrate further the behaviour of our algorithm and its advantages over the existing methodologies and
- More comprehensive analysis of the results and an in-depth discussion of new findings.
Previous Work
2. Proposed Algorithm
2.1. Quantiles
2.2. Challenges of Non-Stochasticity
2.3. Constraints: Key Theoretical Results
2.3.1. Streams with Repeated Datum Values
2.3.2. Emergent Algorithm Design Aims
- Aim 1:
- the buffer should store a list of monotonically-increasing stream values
- Aim 2:
- the position of the current quantile estimate should be as close to the centre of the buffer as possible
- Corollary:
- the buffer should slide “up” or “down” the empirical cumulative density function of stream data as the quantile estimate increases or decreases
- Aim 3:
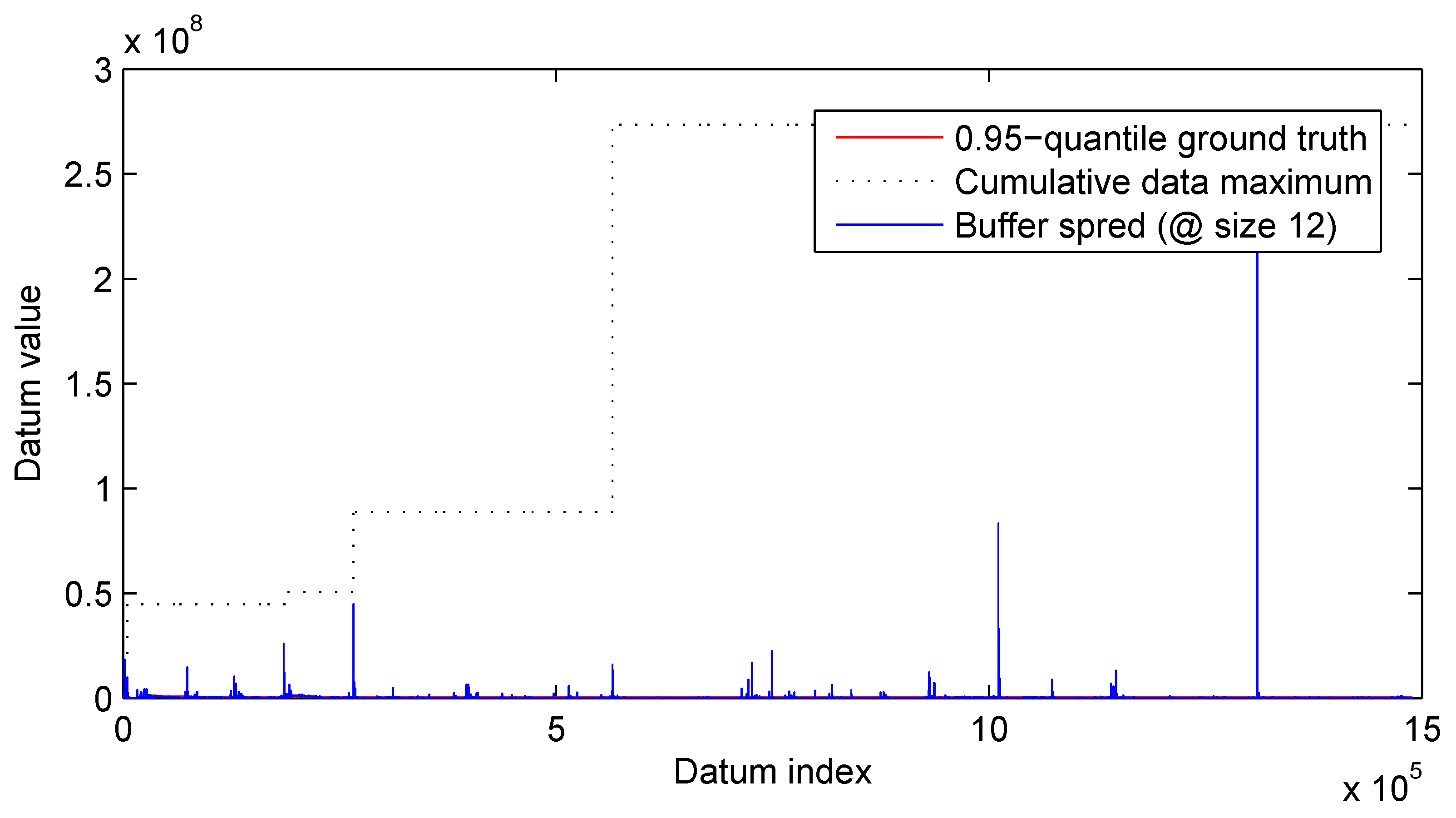
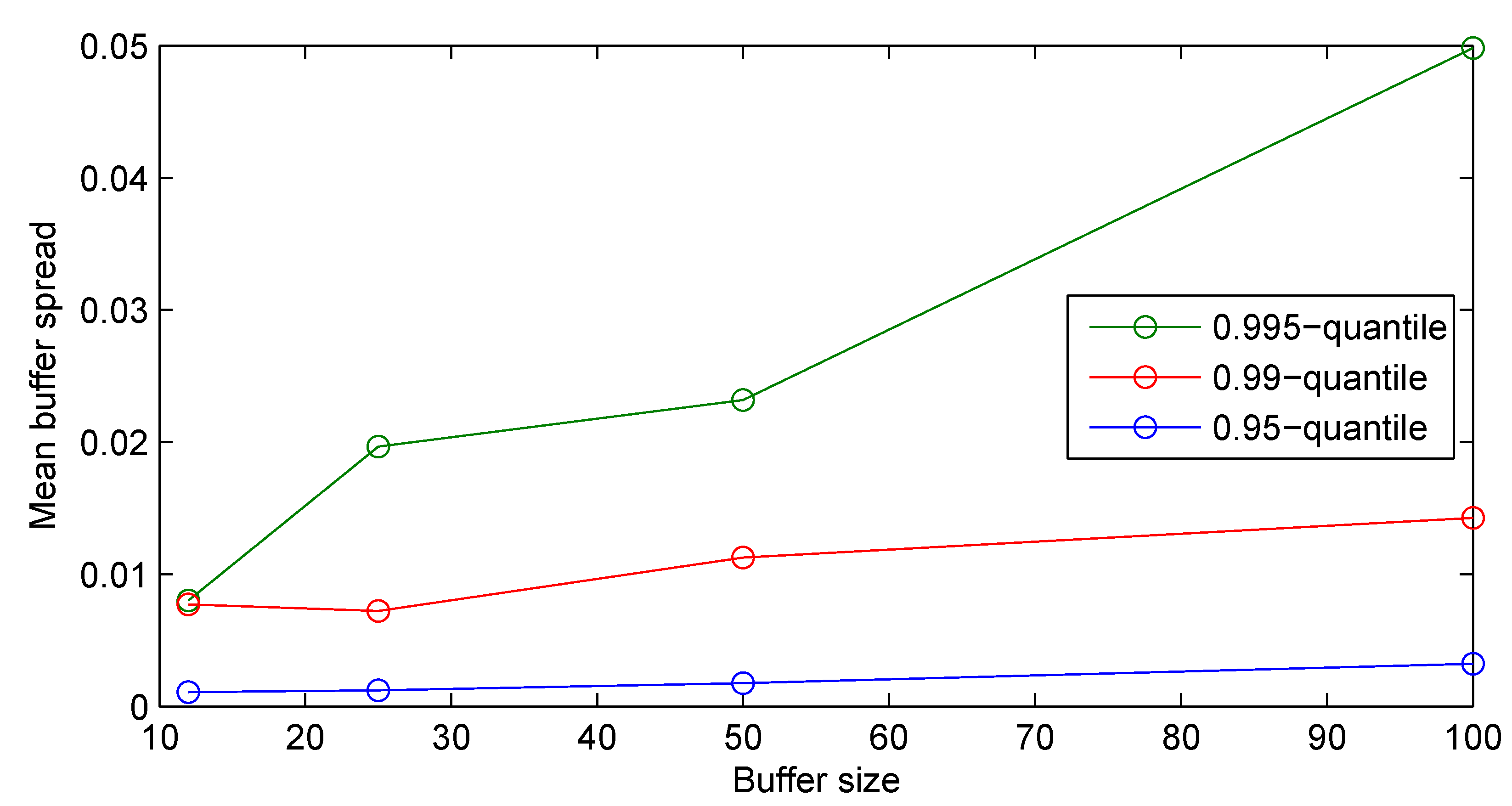
- the spread of values in the buffer (i.e., the difference between the highest and the lowest values in the buffer) should decrease in the periods when the quantile estimate is not changing
2.4. Targeted Adaptable Sample Algorithm
2.4.1. Initialization
2.4.2. Continuous Operation
3. Evaluation and Results
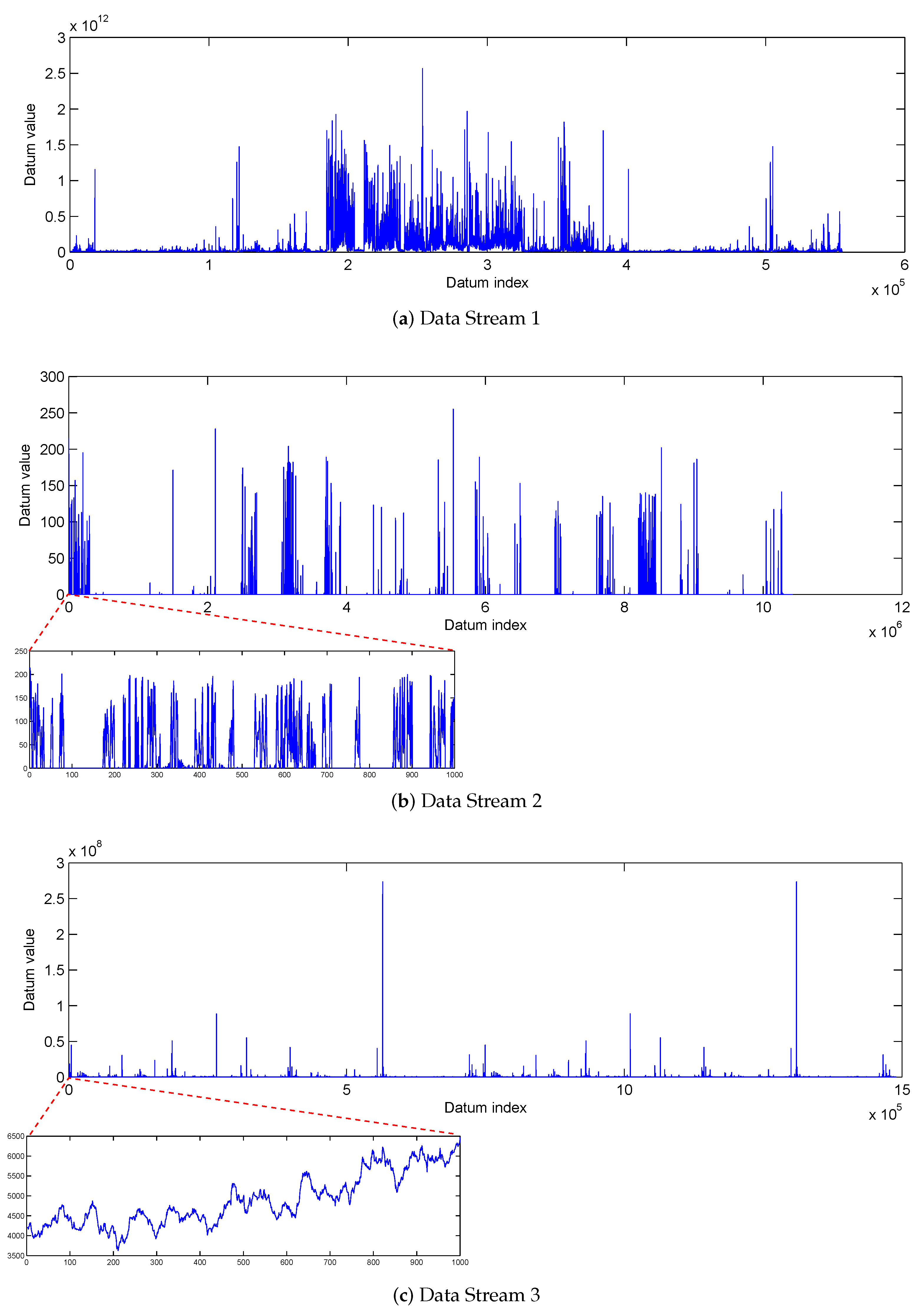
3.1. Evaluation Data
3.1.1. Synthetic Data
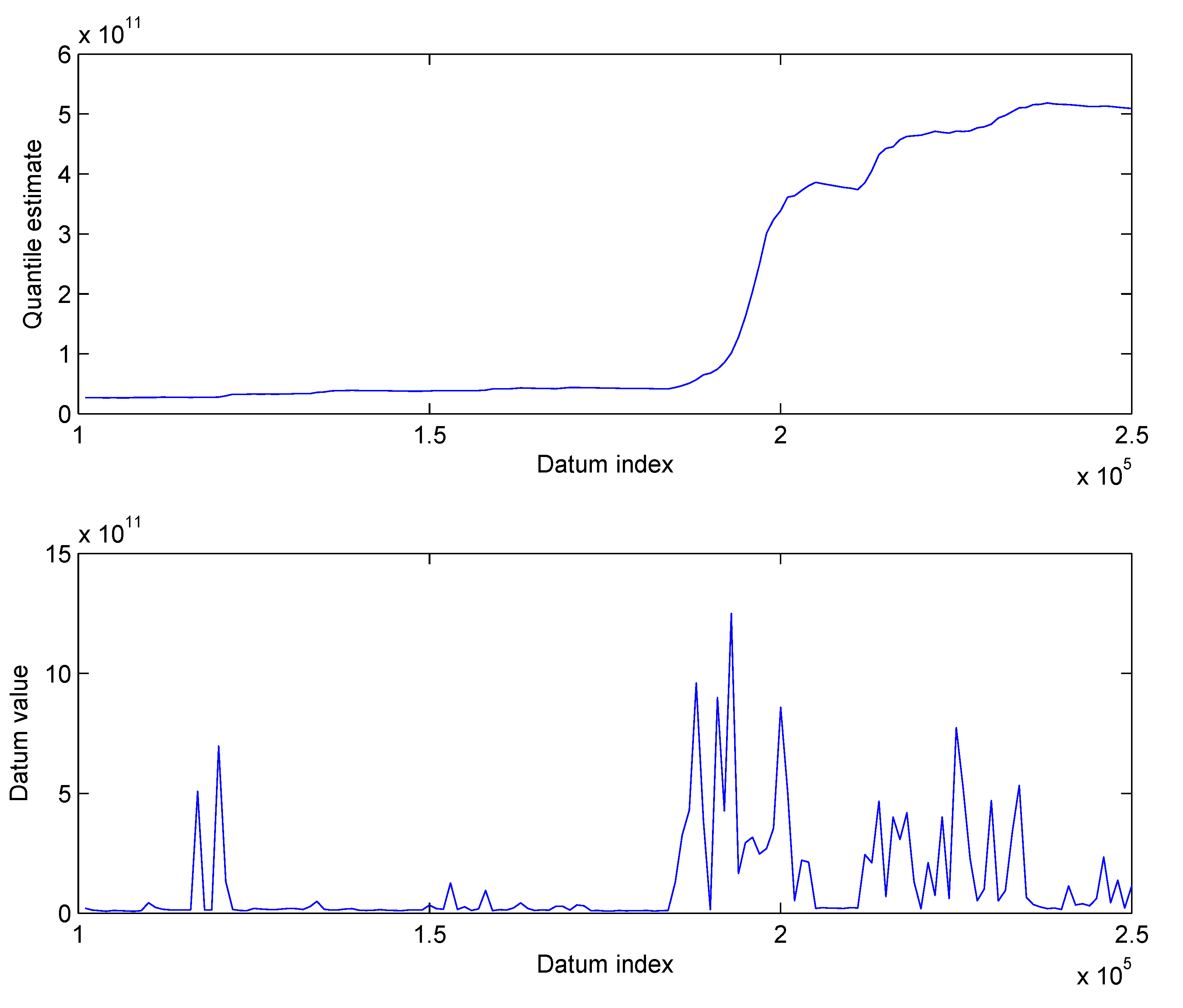
3.1.2. Real-World Surveillance Data
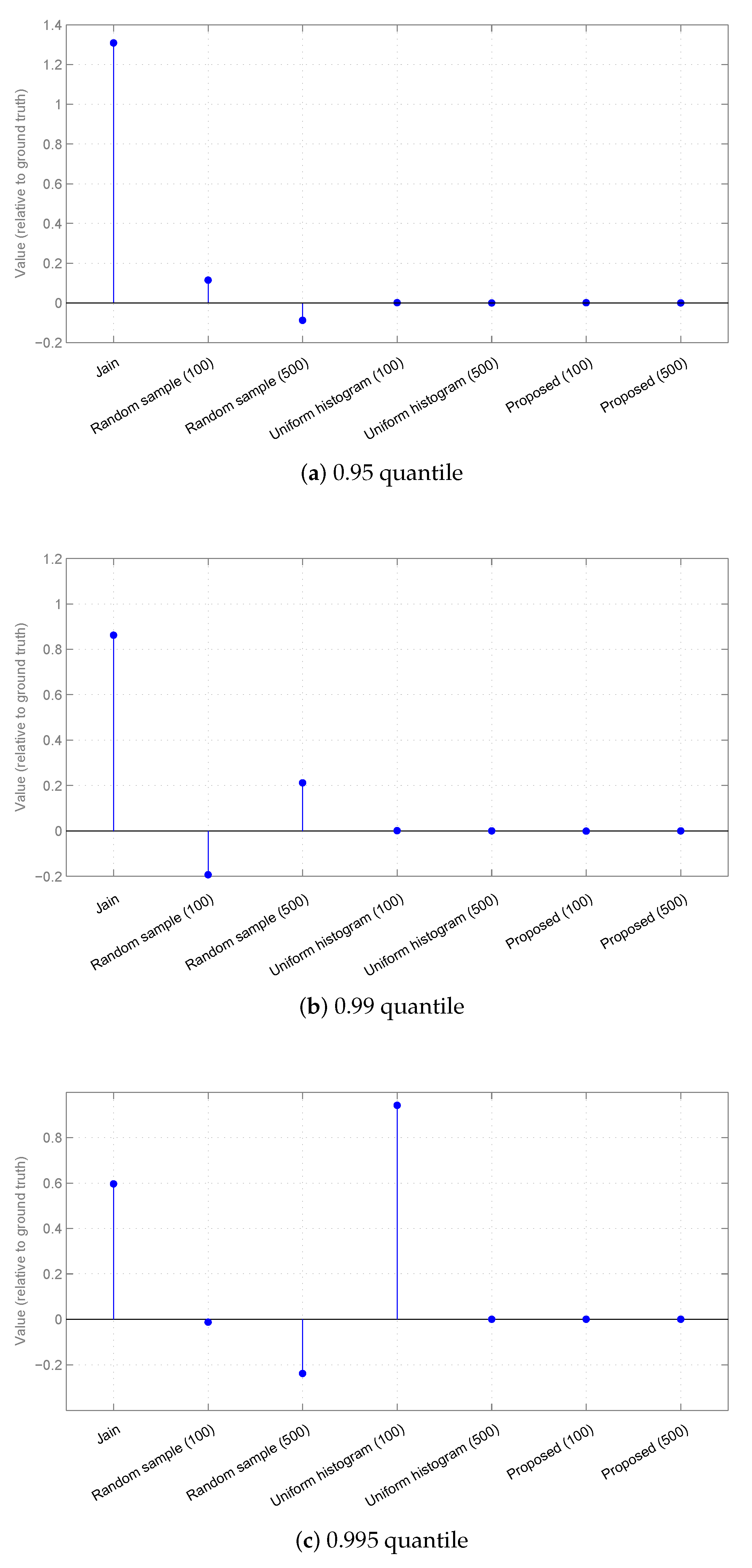
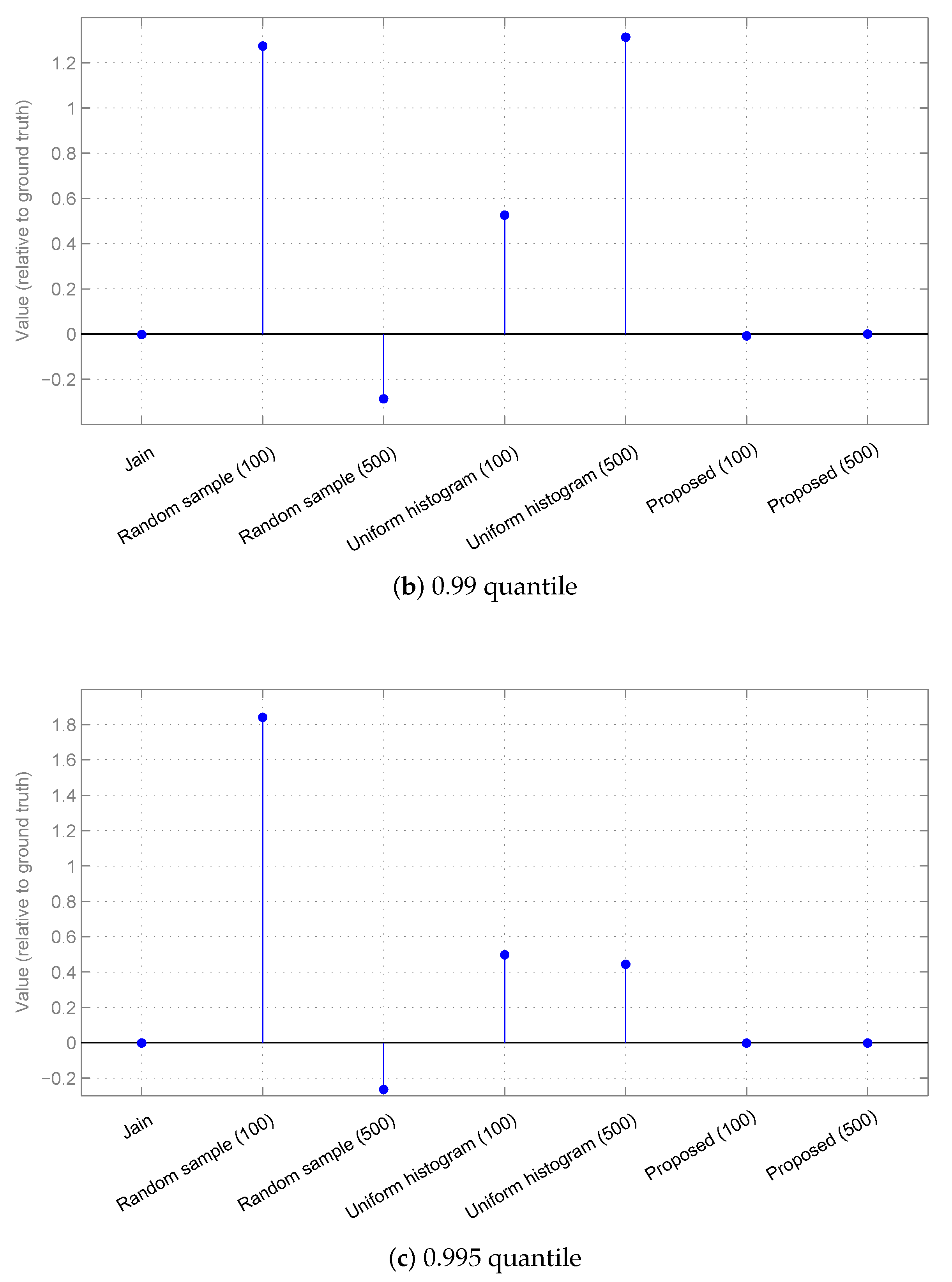
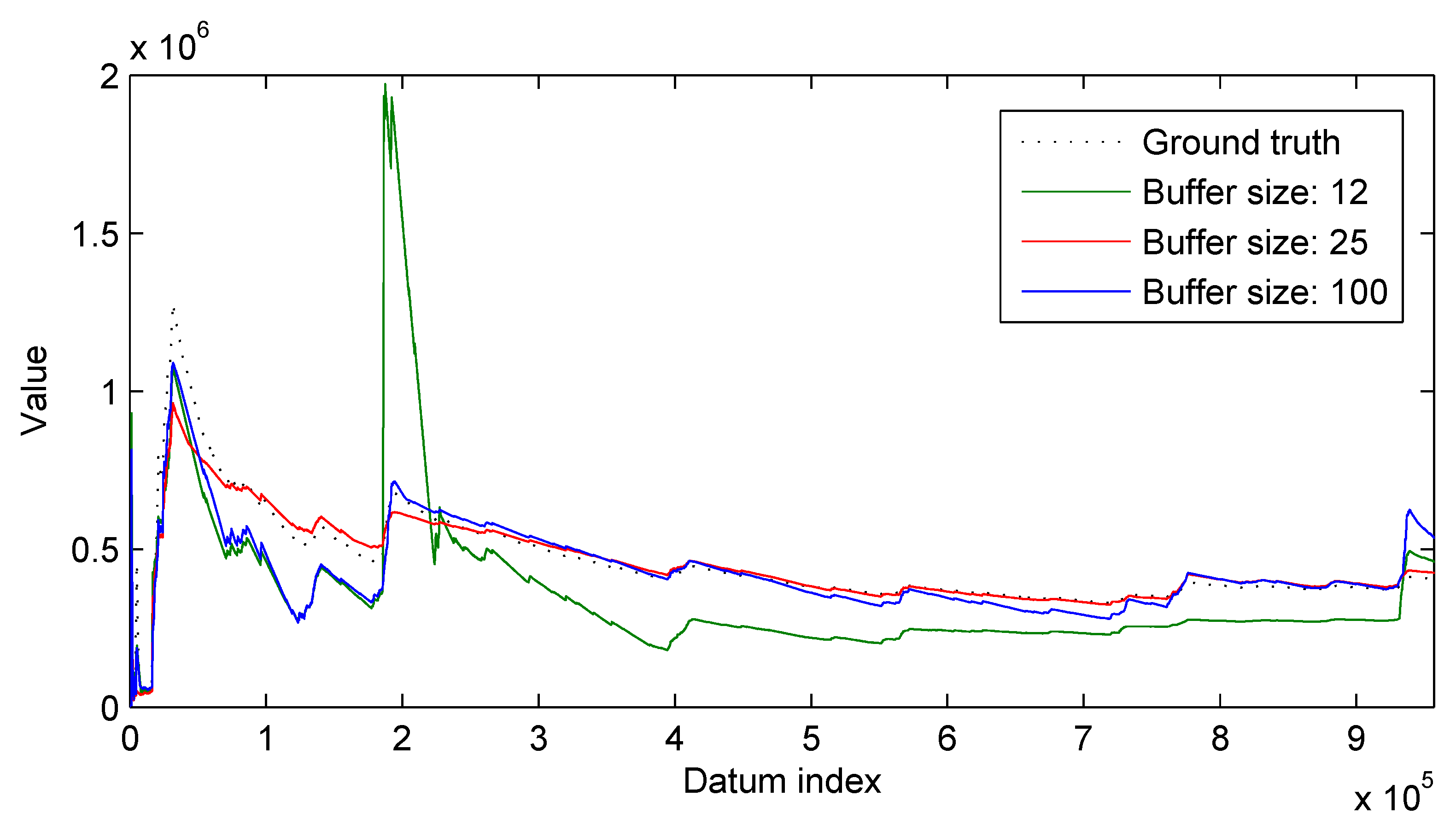
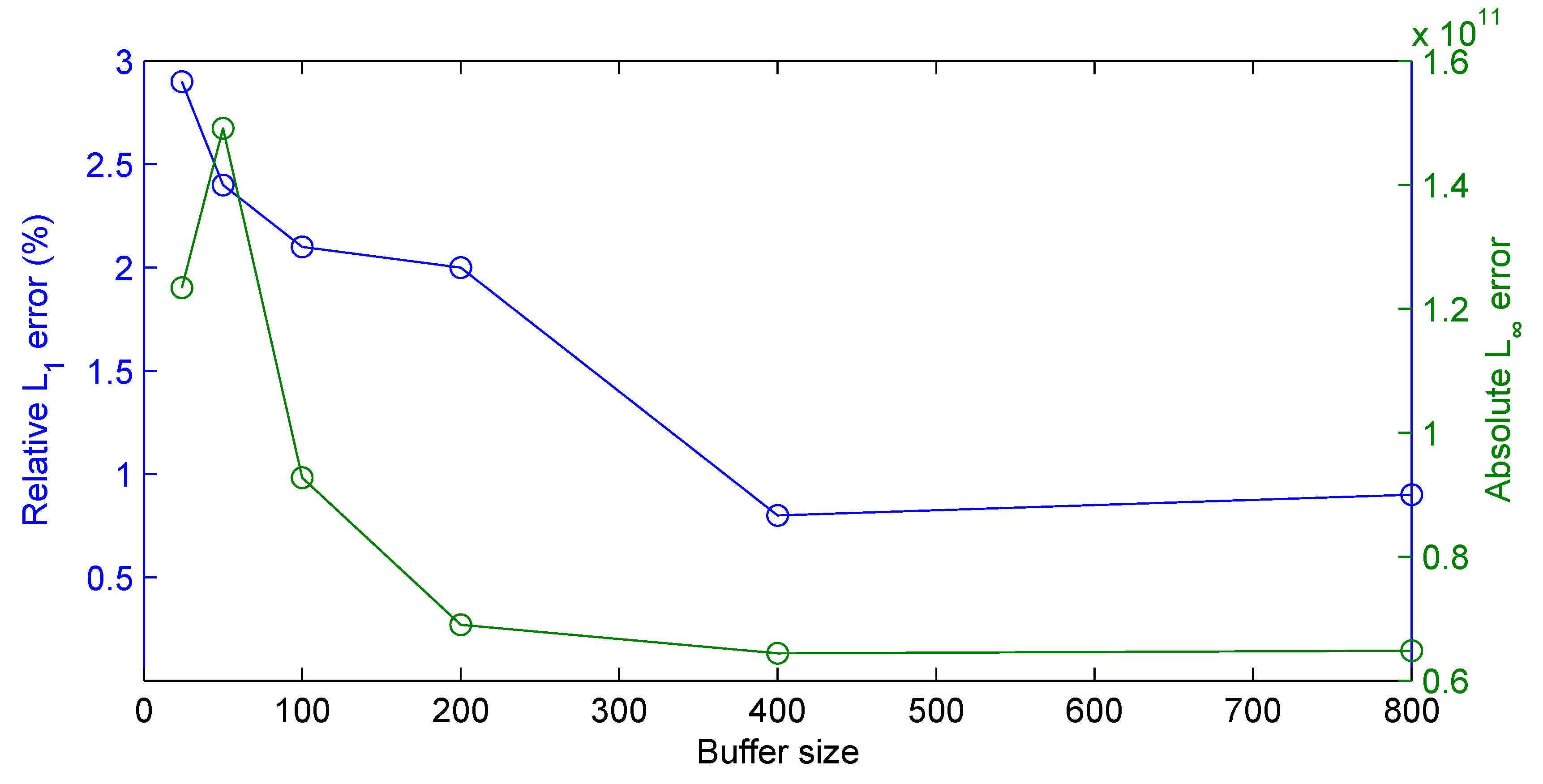
3.2. Results
3.2.1. Synthetic Data
3.2.2. Real-World Surveillance Data
4. Summary and Conclusions
Funding
Conflicts of Interest
References
- Beykikhoshk, A.; Arandjelović, O.; Phung, D.; Venkatesh, S.; Caelli, T. Data-mining Twitter and the autism spectrum disorder: A pilot study. In Proceedings of the IEEE/ACM International Conference on Advances in Social Network Analysis and Mining, Beijing, China, 17–20 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 349–356. [Google Scholar]
- Jain, R.; Chlamtac, I. The P2 Algorithm for Dynamic Calculation of Quantiles and Histograms Without Storing Observations. Commun. ACM 1985, 28, 1076–1085. [Google Scholar] [CrossRef]
- Adler, R.; Feldman, R.; Taqqu, M. (Eds.) A Practical Guide to Heavy Tails; Statistical Techniques and Applications, Birkhäuser: Basel, Switzerland, 1998. [Google Scholar]
- Sgouropoulos, N.; Yao, Q.; Yastremiz, C. Matching Quantiles Estimation; Technical Report; London School of Economics: London, UK, 2013. [Google Scholar]
- Macindoe, A.; Arandjelović, O. A standardized, and extensible framework for comparative analysis of quantitative finance algorithms—An open-source solution, and examples of baseline experiments with discussion. In Proceedings of the IEEE International Conference on Big Knowledge, Singapore, 17–18 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 409–414. [Google Scholar]
- Buragohain, C.; Suri, S. Encyclopedia of Database Systems; Chapter Quantiles on Streams; Springer: New York, NY, USA, 2009; pp. 2235–2240. [Google Scholar]
- Cormode, G.; Johnson, T.; Korn, F.; Muthukrishnany, S.; Spatscheck, O.; Srivastava, D. Holistic UDAFs at Streaming Speeds. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Paris, France, 13–18 June 2004; ACM: New York, NY, USA, 2004; pp. 35–46. [Google Scholar]
- Pham, D.; Arandjelović, O.; Venkatesh, S. Detection of dynamic background due to swaying movements from motion features. IEEE Trans. Image Process. 2015, 24, 332–344. [Google Scholar] [CrossRef] [PubMed]
- Arandjelović, O.; Pham, D.; Venkatesh, S. The adaptable buffer algorithm for high quantile estimation in non-stationary data streams. In Proceedings of the IEEE International Joint Conference on Neural Networks, Washington, DC, USA, 10–16 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–7. [Google Scholar]
- Guha, S.; McGregor, A. Stream Order and Order Statistics: Quantile Estimation in Random-Order Streams. SIAM J. Comput. 2009, 38, 2044–2059. [Google Scholar] [CrossRef]
- Munro, J.I.; Paterson, M. Selection and sorting with limited storage. Theor. Comput. Sci. 1980, 12, 315–323. [Google Scholar] [CrossRef]
- Gurajada, A.P.; Srivastava, J. Equidepth Partitioning of a Data Set Based on Finding its Medians; Technical Report TR 90-24; Computer Science Department, University of Minnesota: Minneapolis, MN, USA, 1990. [Google Scholar]
- Schmeiser, B.W.; Deutsch, S.J. Quantile Estimation from Grouped Data: The Cell Midpoint. Commun. Stat. Simul. Comput. 1977, B6, 221–234. [Google Scholar] [CrossRef]
- McDermott, J.P.; Babu, G.J.; Liechty, J.C.; Lin, D.K.J. Data skeletons: Simultaneous estimation of multiple quantiles for massive streaming datasets with applications to density estimation. Bayesian Anal. 2007, 17, 311–321. [Google Scholar] [CrossRef]
- Vitter, J.S. Random sampling with a reservoir. ACM Trans. Math. Softw. 1985, 11, 37–57. [Google Scholar] [CrossRef]
- Cormode, G.; Muthukrishnany, S. An improved data stream summary: The count-min sketch and its applications. J. Algorithms 2005, 55, 58–75. [Google Scholar] [CrossRef]
- Arandjelović, O.; Pham, D.; Venkatesh, S. Stream quantiles via maximal entropy histograms. In Proceedings of the International Conference on Neural Information Processing, Kuching, Malaysia, 3–6 November 2014; Springer: Cham, Switzerland, 2014; Volume II, pp. 327–334. [Google Scholar]
- Philips Electronics, N.V. A Surveillance System with Suspicious Behaviour Detection. U.S. Patent Application No. 10/014,228, 11 December 2001. [Google Scholar]
- Lavee, G.; Khan, L.; Thuraisingham, B. A framework for a video analysis tool for suspicious event detection. Multimed. Tools Appl. 2007, 35, 109–123. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, J.; Wang, L.; Zhang, Z.; Brown, L.M. Sparse representation for event recognition in video surveillance. Pattern Recognit. 2013, 46, 1748–1749. [Google Scholar] [CrossRef][Green Version]
- Bregonzio, M.; Xiang, T.; Gong, S. Fusing appearance and distribution information of interest points for action recognition. Pattern Recognit. 2012, 45, 1220–1234. [Google Scholar] [CrossRef]
- Tran, K.N.; Kakadiaris, I.A.; Shah, S.K. Part-based motion descriptor image for human action recognition. Pattern Recognit. 2012, 45, 2562–2572. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, C.; Hu, W.; Sun, C. Supervised class-specific dictionary learning for sparse modeling in action recognition. Pattern Recognit. 2012, 45, 3902–3911. [Google Scholar] [CrossRef]
- Intellvisions. iQ-Prisons. Available online: http://www.intellvisions.com/ (accessed on 23 July 2019).
- iCetana. Available online: https://icetana.com (accessed on 23 July 2019).





| Data Set | Number of Data Points | Mean Value | Standard Deviation |
|---|---|---|---|
| Stream 1 | 555,022 | ||
| Stream 2 | 10,424,756 | ||
| Stream 3 | 1,489,618 |
| Stream 1 | Stream 2 | Stream 3 | |||||
|---|---|---|---|---|---|---|---|
| Method | Bins | Relative | Absolute | Relative | Absolute | Relative | Absolute |
| Error | Error | Error | Error | Error | Error | ||
| Targeted adaptable | 500 | 2.1% | 1.00 | 4.7% | 24.20 | 5.2% | 4.8 |
| sample (proposed) | 100 | 1.6% | 1.07 | 9.2% | 54.73 | 3.6% | 2.89 |
| Data-aligned max. | 500 | 1.2% | 3.11 | 0.0% | 2.04 | 0.1% | 8.11 |
| entropy histogram [17] | 100 | 9.6% | 2.06 | 0.0% | 1.91 | 2.6% | 3.33 |
| algorithm [2] | n/a | 15.7% | 2.77 | 3.1% | 93.04 | 84.2% | 1.55 |
| Random sample [15] | 500 | 4.6% | 1.98 | 0.7% | 38.00 | 10.4% | 5.95 |
| Equispaced histogram [13] | 500 | 87.1% | 1.07 | 0.1% | 80.29 | 675.1% | 4.39 |
| Proposed Method | Data-Aligned Histogram | |||||
|---|---|---|---|---|---|---|
| Data Set | Quantile | Relative | Absolute | Relative | Absolute | Max Value to Quantile Ratio |
| Error | Error | Error | Error | |||
| 0.9500 | 1.6% | 1.07 | 9.6% | 2.06 | 15.8 | |
| 0.9900 | 1.2% | 9.59 | 27.9% | 5.69 | 5.9 | |
| Stream 1 | 0.9950 | 2.1% | 9.27 | 58.8% | 8.48 | 4.2 |
| 0.9990 | 0.7% | 9.80 | 48.0% | 9.47 | 2.1 | |
| 0.9995 | 0.3% | 2.69 | 36.8% | 8.72 | 1.5 | |
| 0.9500 | 9.2% | 54.73 | 0.0% | 1.91 | 30.1 | |
| 0.9900 | 2.4% | 26.31 | 0.3% | 2.45 | 2.5 | |
| Stream 2 | 0.9950 | 0.3% | 6.21 | 0.2% | 4.59 | 1.8 |
| 0.9990 | 0.2% | 16.05 | 0.4% | 30.29 | 1.4 | |
| 0.9995 | 0.2% | 20.17 | 2.0% | 34.44 | 1.3 | |
| 0.9500 | 3.6% | 2.89 | 2.6% | 3.33 | 520.3 | |
| 0.9900 | 1.2% | 3.32 | 2.4% | 3.25 | 122.7 | |
| Stream 3 | 0.9950 | 1.8% | 1.40 | 480.5% | 1.63 | 60.9 |
| 0.9990 | 1.6% | 3.35 | 368.6% | 2.35 | 11.7 | |
| 0.9995 | 4.2% | 1.30 | 364.2% | 2.34 | 7.2 | |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arandjelović, O. Targeted Adaptable Sample for Accurate and Efficient Quantile Estimation in Non-Stationary Data Streams. Mach. Learn. Knowl. Extr. 2019, 1, 848-870. https://doi.org/10.3390/make1030049
Arandjelović O. Targeted Adaptable Sample for Accurate and Efficient Quantile Estimation in Non-Stationary Data Streams. Machine Learning and Knowledge Extraction. 2019; 1(3):848-870. https://doi.org/10.3390/make1030049
Chicago/Turabian StyleArandjelović, Ognjen. 2019. "Targeted Adaptable Sample for Accurate and Efficient Quantile Estimation in Non-Stationary Data Streams" Machine Learning and Knowledge Extraction 1, no. 3: 848-870. https://doi.org/10.3390/make1030049
APA StyleArandjelović, O. (2019). Targeted Adaptable Sample for Accurate and Efficient Quantile Estimation in Non-Stationary Data Streams. Machine Learning and Knowledge Extraction, 1(3), 848-870. https://doi.org/10.3390/make1030049





