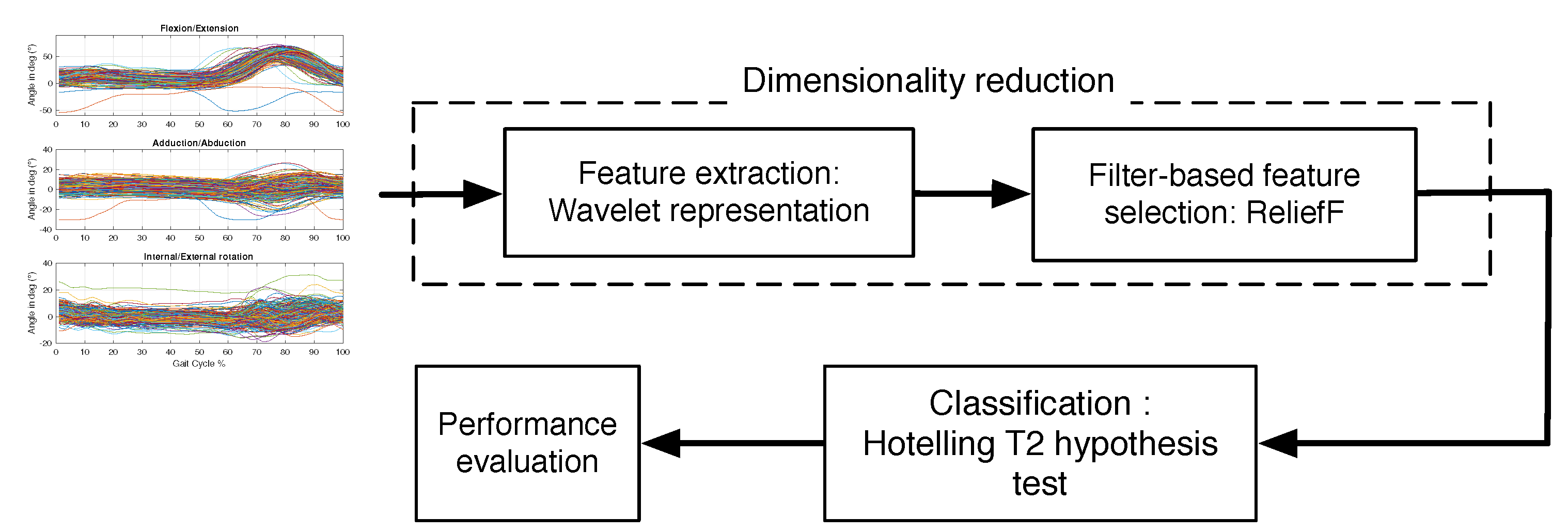
Comparisons relate to different ways of representation of the knee kinematic data by dimensionality reduction and to different ways of classifying this data.
4.5.2. Classification
Duch [
21] cites a large scale investigation that reviewed and compared the performance of several classifiers on several databases [
37]. Although some classifiers, such as the nearest neighbors, appeared frequently among the best performers, the investigation found no systematic trend in the behavior of one classifier compared to the others: for each classifier, the results can be very good on some datasets but not on others. This is not too surprising because classification performance depends on the classifier, which itself relies on a model and its assumptions, as well as on the data representation, and the amount and layout of the learning data in the representation space. Investigations such as [
37] legitimize the general practice in real world applications: seek the best classifier for the expected data inputs of a particular application rather than for data inputs at large. The choice of a particular classifier for an application is generally justified by the classifier better performance against the background of existing competing classifiers. Here, we will contrast the proposed Hotelling
statistic method to commonly used classifiers of biomedical data [
38], namely the K-nearest neighbor classifier (KNN), Linear discriminant analysis (LDA), and Support vector machine (SVM), a review and evaluation of which can be found in [
39]. These methods, which can be potent, and their classification behavior, are also reviewed in pattern recognition textbooks, notably in classic Duda, Hart, and Stork [
1]. Classification of OA data by these methods uses an average curve, or a single representative curve, rather than a sample, as a whole, of several measurement curves for each individual, to which it assigns a class membership according to a sample statistic such as Hotelling as in this study and [
22]. This comparison will justify sample representation of data, used by the Hotelling classification scheme, against single vector representation used by others. We used Matlab routines to implement the KNN, LDA, and SVM classifiers. The routines are: KNN: ClassificationKNN.fit; LDA: fitcdiscr; SVM: templateSVM and fitcecoc.
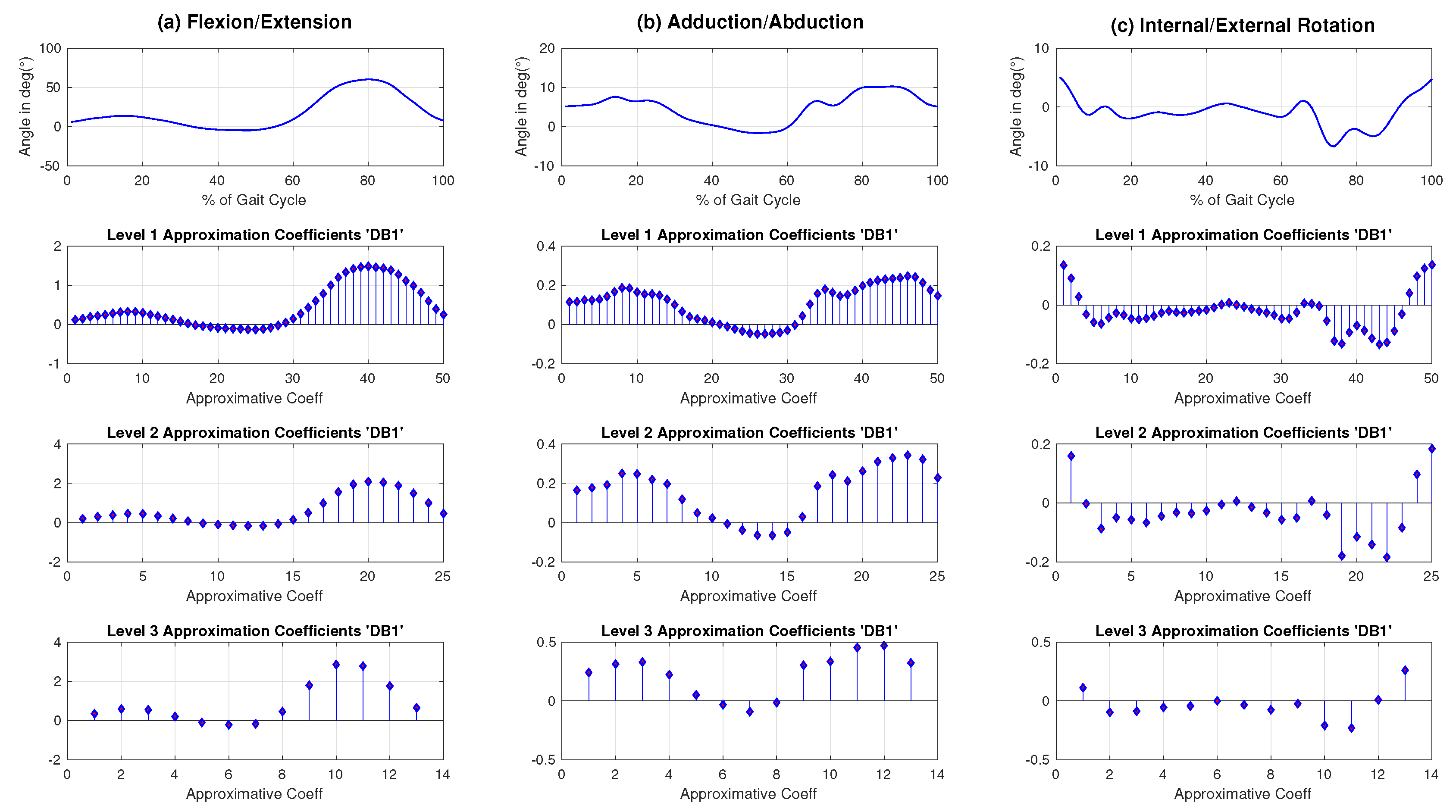
When the feature vector of data representation is the same for all the competing classifiers, then it is just a matter of running these classifiers and recording the various classification rates. However, when the feature vectors can vary with classifiers, as with the application in this study, the comparisons can be exceedingly laborious: for every classifier, the best possible score depends not just on the classification model but also on feature selection. Our study uses a wavelet representation of the original knee kinematic data curves. The wavelet coefficients of this representation are first ranked by the classifier-independent feature selection scheme ReliefF [
40]. This type of scheme uses neighborhood feature differences to evaluate the relevance of features in describing each pattern class and, therefore, provide a way of ranking the features for subsequent selection to be included in the data representation. Selection looks for the combination of features that give the best classification performance: this is theoretically a combinatorial problem. Selection from a small set of ranked features is manageable: this is the case for the Hotelling statistic method proposed in this study, thanks to the fact that we needed to drop the dimension of the representation vector below a dozen, as explained earlier, for the Hotelling hypothesis testing to be applicable. For larger sets, it can be significantly more involved and exceedingly costly: this is the case for the three benchmark methods we used in the comparisons, namely LDA, KNN, SVM (we will refer to these as the benchmarks). We can nevertheless select good sets of features for these methods, as explained here in the following. First, we note that we are not constrained by any maximum number of features for the benchmarks. Therefore, it is legitimate to use the original kinematic data to determine which of the reference planes, or combination of planes thereof, is the most informative in that it gives the best recognition rate. Doing so gives the combination of the transverse and frontal planes as the best for SVM, KNN, and LDA (
Table 5). This is the same best plane pair as for the Hotelling method. Assuming that the classifiers are all valid functions, this a reassuring result since it is then a property of the data that we are looking at. We can now proceed as with the Hotelling method: for each benchmark, use a multilevel wavelet decomposition of the data, rank the resulting coefficients using ReliefF, and select the combination of coefficients that yield the best recognition rate. However, the combinatorial dimension is excessive. Instead, we can have good features by selecting coefficients from the ranked coefficients at the best level of decomposition, which is level 3 (50 coefficients) for SVM, and 4 (25 coefficients) for KNN, and 1 (100 coefficients) for LDA (see
Table 6). Doing so yields
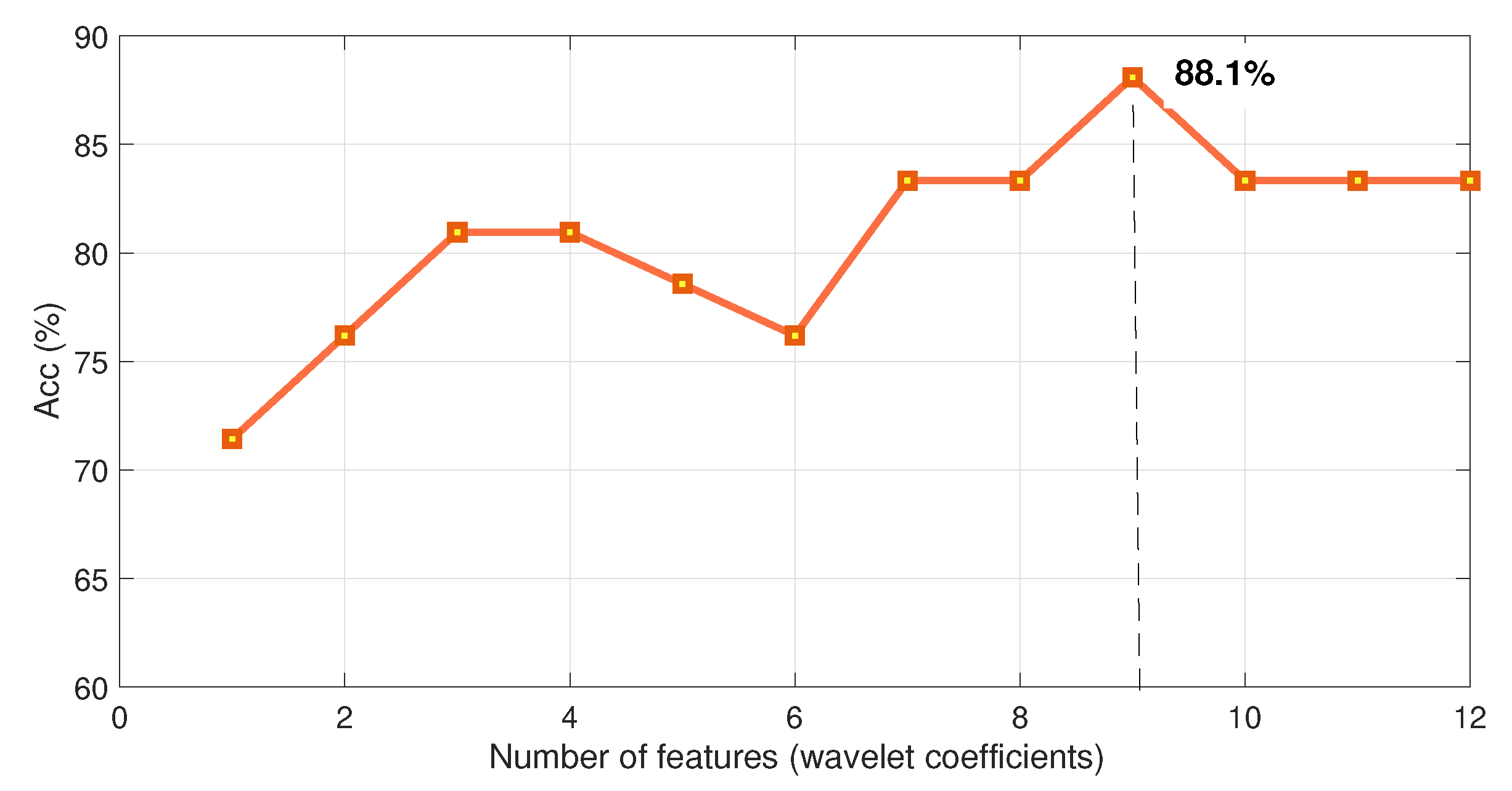
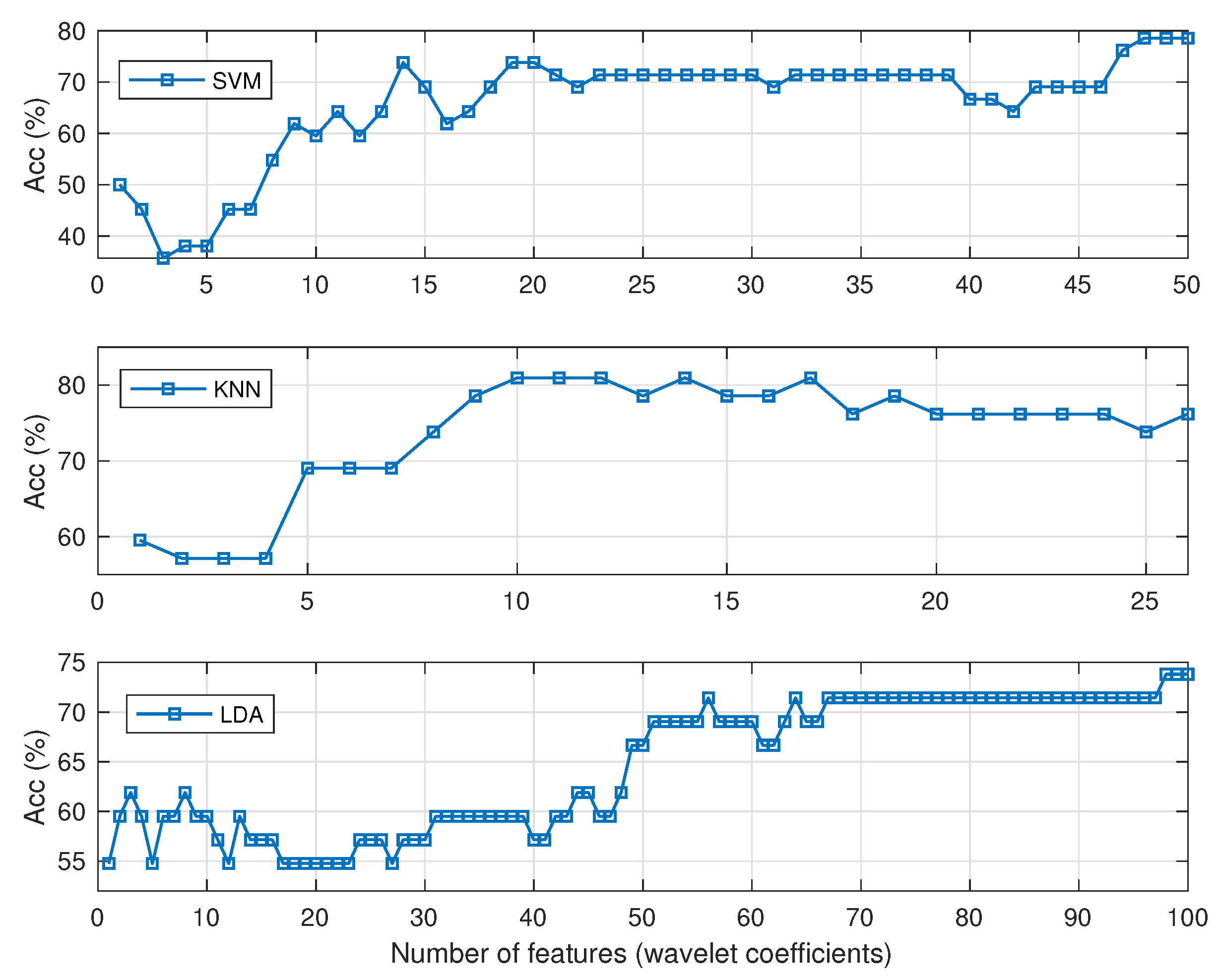
Figure 5, which shows the variation of the accuracy rate of each benchmark as a function of the number of selected coefficients expanded about the benchmark best decomposition level. The best performances are: SVM:
with 48 coefficients, KNN:
with 10 coefficients, and LDA:
with 98 coefficients, placing the Hotelling method as a better performer at
with nine coefficients.
Another way to gain some insight into the comparative performance of the classifiers is to look at the behavior of the benchmarks running on a dozen coefficients as with the Hotelling statistic method. To do so, and to remain consistent with the treatment of the Hotelling method, we applied the same feature extraction and selection processing as described in Section Feature extraction and selection, i.e., the sample average curves have been reduced using a DB1 wavelet decomposition (seven approximation coefficients in a 3-level decomposition in the frontal plane and two coefficients in the transverse plane). The extracted features have been ranked with the ReliefF ranking algorithm.
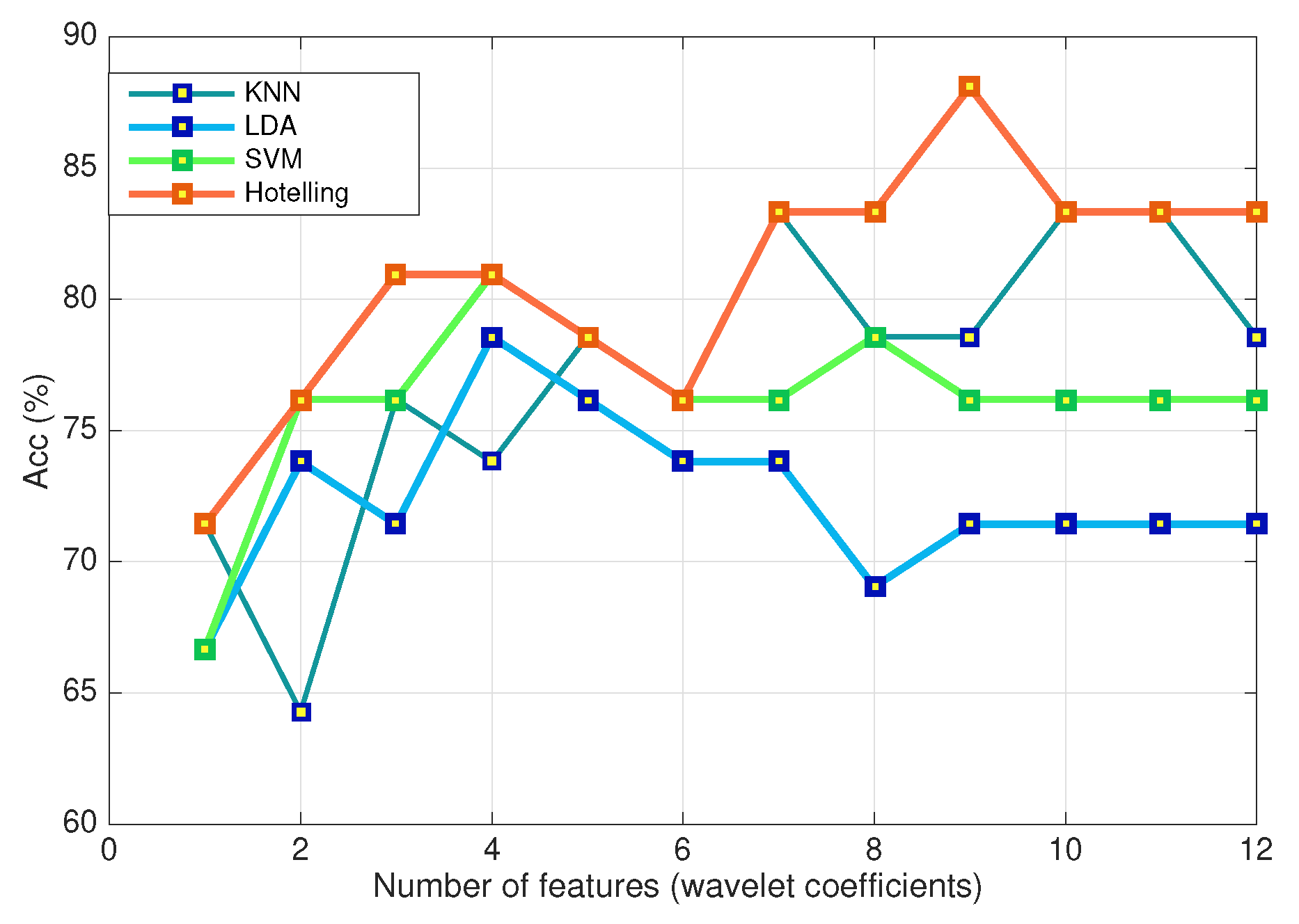
The comparative recognition rates (Acc %) as a function of the number of features are shown in
Figure 6. In almost all cases, the proposed Hotelling scheme gives a better recognition rate when tested on the dataset DS1. The results fit the expectation that using the average curve as input rather than the whole sample causes loss of information relevant to classification. In other words, averaging may suppress relevant information in the data which can be overcome when all the curves are retained for a more informative support to classification.
Ideally, one would be able to confirm the comparative experimentation conclusions by a run of all the methods on a validation database that has novel data, i.e., data yet unseen by any of the classifiers. In our case, unfortunately, we do not have such data, i.e., data that fits the application of OA pathology classification. Moreover, there are only 21 measurements for each pathology class (the small sample problem that the Hotelling method proposes to address), which is just too few to be able to cut out a portion to use as validation data.