Chaotic Vibration Prediction of a Laminated Composite Cantilever Beam Subject to Random Parametric Error

Abstract

Random parametric errors (RPEs) are introduced into the model establishment of a laminated composite cantilever beam (LCCB) to demonstrate the accuracy and robustness of a recurrent neural network (RNN) in predicting the chaotic vibration of a LCCB, and a comparative analysis of training performance and generalization capability is conducted with a convolutional neural network (CNN). In the process of dynamic modeling, the nonlinear dynamic system of a LCCB is established by considering RPEs. The displacement and velocity time series obtained from numerical simulation are used to train and test the RNN model. The RNN model converts the original data into a multi-step supervised learning format and normalizes it using the MinMaxScaler method. The prediction performance is comprehensively evaluated through three performance indicators: coefficient of determination (R²), mean absolute error (MAE), and root mean square error (RMSE). The results show that, under the condition of introducing RPEs, the RNN model still exhibits high prediction accuracy, with the maximum R² reaching 0.999984548634328, the maximum MAE being 0.075, and the maximum RMSE being 0.121. Furthermore, performing predictions at the free end of the LCCB verifies the applicability and robustness of the RNN model with respect to spatial position variations. These results fully demonstrate the accuracy and robustness of the RNN model in predicting the chaotic vibration of a LCCB.

1. Introduction

Due to the exceptional properties of composite materials, such as a high strength-to-weight ratio, they have been widely applied in aerospace [1], civil [2], and railway engineering [3]. However, owing to the influence of uncertain factors and structural complexity, composite structures often exhibit significant nonlinear dynamic characteristics in practical applications. Under complex external loads and the effects of RPEs, these structures may undergo chaotic vibrations and other intricate nonlinear dynamic phenomena. In recent years, the rapid development of deep learning has provided new methodologies for addressing complex nonlinear dynamic problems. Models such as the convolutional neural network (CNN), RNN, and Long Short-Term Memory (LSTM) have demonstrated outstanding performance in nonlinear vibration prediction and have been extensively applied in fields such as traffic flow forecasting [4] and chaotic wind speed prediction [5]. As a data-driven approach, the RNN has shown great potential in time series forecasting and modeling of complex nonlinear systems. However, research on predicting chaotic vibrations of LCCBs under the influence of RPEs remains unexplored.

In recent decades, extensive research has been conducted on the dynamic behavior of composite structures. Zhang et al. [6] modeled a cantilever beam using Euler–Bernoulli beam theory and formulated its dynamic equations with parametric and external excitations. Their results revealed that the nonlinear nonplanar vibrations of the cantilever beam may lead to chaotic motion under the combined influence of harmonic axial and transverse excitations. Bouadjadja et al. [7] proposed a model based on Euler–Bernoulli beam theory that is applicable to both symmetric and antisymmetric laminated beams. The validity of the proposed model was verified through a combination of theoretical analysis and experimental studies. Preethi et al. [8] used Timoshenko beam theory to derive the nonlocal nonlinear governing equations of laminated nano-cantilever beams subjected to surface stress, and investigated the effects of nonlocal parameters and surface stress on the vibration behavior of the cantilever beam. Viet et al. [9] derived the dynamic equations for LCCBs based on Timoshenko beam theory. They proposed a new model to study the dynamic behavior of shape memory alloy (SMA) LCCB under point loads at the free end and validated the model through numerical analysis. Guo et al. [10] established a multi-dimensional system considering first-order shear deformation effects and used numerical simulations to examine the influence of nonlinear terms on the nonlinear dynamic behavior of graphene-reinforced laminated composite plates. Their analysis revealed the presence of chaotic behavior in these composite structures. Li et al. [11] derived the dynamic equations of laminated beams based on third-order shear deformation theory, considering the Poisson effect. They proposed a new dynamic stiffness method to determine the natural frequencies of composite laminated beams and investigated their free vibration behavior. Zhang et al. [12] conducted a numerical analysis of the nonlinear dynamic response of laminated composite cantilever rectangular plates using higher-order shear deformation theory. The simulation results indicated the presence of chaotic motion during vibration. The authors further discussed the effects of various excitation types on the nonlinear vibration behavior of these structures. Zhang et al. [13] developed a dynamic model for laminated composite piezoelectric cantilever plates based on Reddy’s third-order shear deformation theory, considering both transverse and in-plane excitations. They studied the nonlinear dynamic response of the system and found that it exhibits chaotic motion. Guo et al. [14] established the nonlinear dynamic equations for cantilever macrofiber composite (MFC) laminated shells using Reddy’s third-order shear deformation theory. They simulated the complex nonlinear vibration response of the MFC shell and demonstrated that it undergoes chaotic motion. The findings indicate that both the electric field and external excitation have a significant impact on the dynamic response of the structure. Amabili et al. [15] developed a third-order shear deformation theory for the nonlinear vibration of cantilever beams, incorporating rotational inertia and in-plane rotational nonlinearity. They conducted both experimental and numerical studies on the nonlinear vibration of self-healing cantilever beams under five different excitation levels. The results showed good agreement between experimental data and numerical simulations. Liu et al. [16] established a geometric nonlinear model for laminated composite beams and proposed a higher-order shear deformation theory to analyze their nonlinear dynamic behavior. They investigated the effects of fiber orientation, flow velocity, and geometric nonlinearity on the beams’ vibration characteristics. Liu [17] established the dynamic equations for a LCCB based on Reddy’s third-order shear deformation theory and analyzed its nonlinear dynamics. Liu also investigated various parameters that influence the amplitude and frequency at the beam’s free end. Liu and Sun [18] established a multi-dimensional nonlinear dynamic system for a LCCB considering the third-order shear deformation effect. They conducted numerical simulations to study its chaotic vibration. In the above literature, although researchers have conducted extensive research on the nonlinear vibrations of cantilever structures, the influence of RPEs on the nonlinear vibrations of cantilever structures has been hardly mentioned.

In practical scenarios, uncertainties in structural parameters can profoundly affect the onset and development of dynamic behaviors. Consequently, incorporating RPEs into the analysis of nonlinear vibrations has become increasingly important. In recent years, extensive research has been conducted to explore the influence of RPEs on dynamic systems. In 2007, Kuo [19] proposed an adaptive fuzzy sliding-mode control (SMC) strategy to address the synchronization problem of the Sprott chaotic system affected by parametric errors. In 2012, Shirazi et al. [20] proposed a chaos synchronization controller based on the particle swarm optimization algorithm to address the synchronization problems under parametric uncertainty. Subsequently, Nozaki et al. [21] identified chaotic behavior in Atomic Force Microscopes (AFM) and proposed Optimal Linear Feedback Control (OLFC) and State-Dependent Riccati Equation (SDRE) methods to suppress the system’s chaotic behavior. They compared the effectiveness of these two methods in the presence of RPEs. A year later, Balthazar et al. [22] investigated the micro-cantilever beam in Tapping-Mode-AFM and observed chaotic motion. They proposed two control strategies, SDRE and OLFC, and evaluated their robustness in the presence of RPEs. In 2016, Peruzzi et al. [23] used OLFC to control the nonlinear dynamic behavior of a Micro-Electro-Mechanical (MEMS) oscillatory system affected by RPEs. In 2018, Amin et al. [24] modeled nanobeams using the Euler–Bernoulli beam theory and studied their nonlinear dynamic behavior. They proposed a robust SMC to eliminate the chattering effects in the presence of RPEs. In 2021, Youssef and Ayman [25] applied a nonlinear structural dynamics model to simulate the buffeting phenomenon in twin-tail fighter jets, revealing that parameter uncertainty could lead to different nonlinear dynamic responses of the aircraft wings. In the next year, Hao et al. [26] derived the dynamic equations of SMA laminated beams under transverse uniformly distributed loads. They investigated the parametric stochastic vibration of these beams and found that random parameters could induce large-amplitude vibrations. Recently, Sun et al. [27] conducted dynamic modeling of a composite cantilever beam based on third-order shear deformation theory and implemented control strategies to suppress large-amplitude vibrations. Their findings revealed that the presence of RPEs increases the cost of vibration control for a composite cantilever beam. The literature indicates that the influence of RPEs on nonlinear dynamic systems has been widely studied. However, for many complex structures exhibiting nonlinear and chaotic vibrations, constructing accurate physical models not only requires researchers to possess profound expertise but also demands the ability to formulate and solve complex differential equations. In this context, data-driven approaches have been increasingly recognized as a promising alternative for modeling and predicting nonlinear dynamic responses.

In recent years, RNNs have gradually become an important tool for predicting complex dynamic responses. In 2014, Qi et al. [28] derived the dynamic Euler–Bernoulli beam model for micro-cantilever beams by incorporating nonlinear terms and demonstrated that the RNN can effectively model such structures. In 2019, Teng and Zhang [29] proposed a new prediction model for nonlinear dynamic systems by combining a CNN, LSTM, deep neural network (DNN), and multi-step methods. They validated the model’s accuracy through different chaos examples. In the same year, Cestnik and Abel [30] used RNNs to predict various dynamic behaviors, including chaos, under external disturbances. They also compared the amount of training data required for effective inference between LSTM and Gated Recurrent Unit (GRU) architectures. In 2021, Huang et al. [31] designed the DA-SKIP model based on a RNN, which decomposes the prediction of periodic time series into three parts: linear, nonlinear, and periodic prediction. They evaluated the performance of the DA-SKIP model using different datasets. During the same year, Sangiorgio et al. [32] explored the predictive capabilities of RNN-based methods for different chaotic systems under various noise environments. They demonstrated that LSTM-no-teacher forcing exhibits robustness to system complexity and noise. In the following year, Dudukcu et al. [33] proposed a hybrid RNN structure and used chaotic time series data generated from the Lorenz system, Rössler system, and a Lorenz-like chaotic system. In the same year, Uribarri and Mindlin [34] trained a RNN to predict chaotic time series data generated from the Rössler system and demonstrated the effectiveness and applicability of RNNs in chaotic system modeling. In 2023, Sun et al. [35] used a five-degrees-of-freedom Duffing oscillator system as the subject of study, selecting different parameters to induce chaotic behavior. They employed various neural network models to predict the resulting dynamics and demonstrated that the LSTM encoder–decoder architecture achieves high accuracy in predicting chaotic behavior. In the same year, Moorthy and Marappan [36] applied the artificial neural network (ANN) model to predict shifts in the natural frequencies of laminated composite plates. The results showed that the ANN model accurately predicted these frequency changes. Recently, Wang et al. [37] proposed a CNN-convolutional LSTM model based on RNNs to predict the chaotic vibration of microbeams. They evaluated the accuracy and generalization capability of the proposed hybrid data-driven model. Although researchers have extensively studied chaos prediction, no work to date has employed a RNN to predict the chaotic behavior of LCCBs affected by RPEs.

Although existing studies have made progress in the nonlinear dynamic analysis of cantilever structures and neural network-based prediction, systematic research on the chaotic vibration prediction of LCCBs with RPEs is still lacking. The main contributions of this study are as follows:

(1)

By combining nonlinear dynamic modeling with the RNN data-driven approach, accurate prediction of the chaotic vibration of a LCCB under different levels of RPEs is achieved using the RNN model.

(2)

Through numerical validation under different external excitation amplitudes, circular frequencies, and spatial positions, the spatial applicability and generalization capability of the RNN model under RPEs are systematically evaluated.

Therefore, the nonlinear vibration prediction of a LCCB subjected to RPEs is the focus of the present study. The current structure of this work is organized as follows: In the second section, a multi-dimensional nonlinear dynamic system of a LCCB is established. In the third section, RPEs are introduced into the established nonlinear dynamic system. In the fourth section, the concept of a RNN, the model construction process, and the evaluation metrics are presented. In the fifth section, numerical simulations are conducted to evaluate the accuracy of the RNN data-driven model in predicting the chaotic vibrations of the LCCB subjected to RPEs. In the sixth section, the conclusions of the current work are summarized.

2. Beam Model Establish

As shown in Figure 1, a three-layered LCCB with a uniform rectangular cross-section is considered. The parameters $l$, $b$, and $h$ are the length, width, and thickness of the beam, respectively. A Cartesian coordinate system is defined at the fixed end of the cantilever beam, and $q$ denotes an evenly distributed sinusoidal load applied along the beam.

Based on previous research [27], the nondimensional vibration at a specified point $\mathrm{P}$ (where $x=x_{\mathrm{P}}$) is derived as follows:

$$w_{\mathrm{P}}={\sum }_{n=1}^2{\phi }_n\left(x_{\mathrm{P}}\right)w_{n,1}\left(t\right)=1.315382461w_{1,1}\left(t\right)+0.27008056w_{2,1}\left(t\right),$$

(1)

where $w_{\mathrm{P}}$ is the nondimensional displacement at $x_{\mathrm{P}}=0.75$, $t$ is the nondimensional time, and $w_{1,1}\left(t\right)$ and $w_{2,1}\left(t\right)$ are the first two order nondimensional vibrations of the beam with their specific expression given as

$$\left\{\begin{array}{c}{\dot{w}}_{1,1}=w_{1,2}\\ {\dot{w}}_{1,2}=\left(\begin{array}{c}{T}_{11}{w}_{1,2}+T_{12}{w}_{1,1}+T_{13}{w}_{2,2}+T_{14}{w}_{2,1}+T_{15}{w}_{1,1}^3\\ +T_{16}{w}_{1,1}^2{w}_{2,1}+T_{17}{w}_{2,1}^2{w}_{1,1}+T_{18}{w}_{2,1}^3+T_{19}q\end{array}\right)\end{array}\right.$$

(2)

$$\left\{\begin{array}{c}{\dot{w}}_{2,1}=w_{2,2}\\ {\dot{w}}_{2,2}=\left(\begin{array}{c}{T}_{21}{w}_{1,2}+T_{22}{w}_{1,1}+T_{23}{w}_{2,2}+T_{24}{w}_{2,1}+T_{25}{w}_{1,1}^3\\ +T_{26}{w}_{1,1}^2{w}_{2,1}+T_{27}{w}_{2,1}^2{w}_{1,1}+T_{28}{w}_{2,1}^3+T_{29}q\end{array}\right)\end{array}\right.$$

(3)

where the parameters $T_{1i}$ and $T_{2i}$ $\left(i=1,2,\cdots ,9\right)$ are defined in Appendix A. In the nonlinear dynamic equations, the coefficients $T_{1i}$ and $T_{2i}$ $\left(i=1,2,\cdots ,9\right)$ represent the influence of the material and geometric properties of the LCCB on its dynamic behavior. They are derived based on the third-order shear deformation theory [38] by projecting the governing equations onto the modal space and depend on the material’s Young’s modulus, shear modulus, Poisson’s ratio, layer thickness, beam length, beam width, as well as the mass and stiffness distribution of the beam. The detailed relationships between the coefficients $T_{1i}$ and $T_{2i}$ $\left(i=1,2,\cdots ,9\right)$ and the structural parameters are provided in

Table 1. Physical meanings and main parameters of coefficients $T_{1i}$ and $T_{2i}$ $\left(i=1,2,\cdots ,9\right)$.

${\mathit{T}}_{1\mathit{i}}$$, {\mathit{T}}_{2\mathit{i}}$	Physical Meaning	Main Parameters
$T_{11}$$, T_{21}$$, T_{13}$$, T_{23}$	Linear damping	$E$$, \rho$$, h$$, l$$, b$
$T_{12}$$, T_{22}$$, T_{14}$$, T_{24}$	Linear stiffness	$E$$, h$$, l$$, b$
$T_{15}$$, T_{18}$$, T_{25}$$, T_{28}$$, T_{16}$$, T_{17}$$, T_{26}$$, T_{27}$	Cubic nonlinear stiffness	$E$$, h$$, b$
$T_{19}$$, T_{29}$	External excitation	$\rho$$, h$$, q$

.

3. Introduction of RPEs

Corresponding to the multi-dimensional nonlinear dynamic system of the studied LCCB structure in Equations (2) and (3), the parameters $T_{1i}$ and $T_{2i}$ $\left(i=1,2,\cdots ,9\right),$ modified by RPEs, are defined as follows:

$$\begin{gathered} T_{11}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{11}, T_{21}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{21}, \\ {T}_{12}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{12}, T_{22}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{22}, \\ {T}_{13}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{13}, T_{23}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{23}, \\ {T}_{14}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{14}, T_{24}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{24}, \\ {T}_{15}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{15}, T_{25}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{25}, \\ {T}_{16}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{16}, T_{26}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{26}, \\ {T}_{17}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{17}, T_{27}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{27}, \\ {T}_{18}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{18}, T_{28}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{28}, \\ {T}_{19}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{19}, T_{29}^{\ast }=\left(1+\Gamma ·r\left(t\right)\right){·T}_{29}, \end{gathered}$$

(4)

where $r\left(t\right)$ is a normally distributed random function [20,21], and $\Gamma$ is the variation range of $r\left(t\right)$. In this study, RPEs are introduced at the coefficient level, where a random function $r\left(t\right)$ is used to uniformly perturb the parameters $T_{1i}$ and $T_{2i}$ $\left(i=1,2,\cdots ,9\right)$. This approach represents globally correlated parametric uncertainties while maintaining computational efficiency, and it captures the influence of RPEs on the dynamic behavior of the LCCB. In the established dynamic model of the LCCB, the system’s response to these perturbations is primarily reflected through the variations of the parameters $T_{1i}$ and $T_{2i}$ $\left(i=1,2,\cdots ,9\right)$. Therefore, introducing RPEs at the coefficient level not only simplifies the nonlinear dynamic modeling process but also preserves the intrinsic dynamic characteristics of the system. Such coefficient-based perturbation methods have been widely applied in the analysis of chaotic vibrations [20,22,24].

By substituting $T_{1i}^{\ast }$ and $T_{2i}^{\ast }$ $\left(i=1,2,\cdots ,9\right)$ from Equation (4) into Equations (2) and (3), the multi-dimensional nonlinear dynamic system of the studied LCCB structure incorporating RPEs is derived as follows:

$$\left\{\begin{array}{c}{\dot{w}}_{1,1}=w_{1,2}\\ {\dot{w}}_{1,2}=\left(\begin{array}{c}{T}_{11}^{\ast }{w}_{1,2}+T_{12}^{\ast }{w}_{1,1}+T_{13}^{\ast }{w}_{2,2}+T_{14}^{\ast }{w}_{2,1}+T_{15}^{\ast }{w}_{1,1}^3\\ +T_{16}^{\ast }{w}_{1,1}^2{w}_{2,1}+T_{17}^{\ast }{w}_{2,1}^2{w}_{1,1}+T_{18}^{\ast }{w}_{2,1}^3+T_{19}^{\ast }q\end{array}\right)\end{array}\right.$$

(5)

$$\left\{\begin{array}{c}{\dot{w}}_{2,1}=w_{2,2}\\ {\dot{w}}_{2,2}=\left(\begin{array}{c}{T}_{21}^{\ast }{w}_{1,2}+T_{22}^{\ast }{w}_{1,1}+T_{23}^{\ast }{w}_{2,2}+T_{24}^{\ast }{w}_{2,1}+T_{25}^{\ast }{w}_{1,1}^3\\ +T_{26}^{\ast }{w}_{1,1}^2{w}_{2,1}+T_{27}^{\ast }{w}_{2,1}^2{w}_{1,1}+T_{28}^{\ast }{w}_{2,1}^3+T_{29}^{\ast }q\end{array}\right)\end{array}\right.$$

(6)

4. RNN Data-Driven Model Establishment

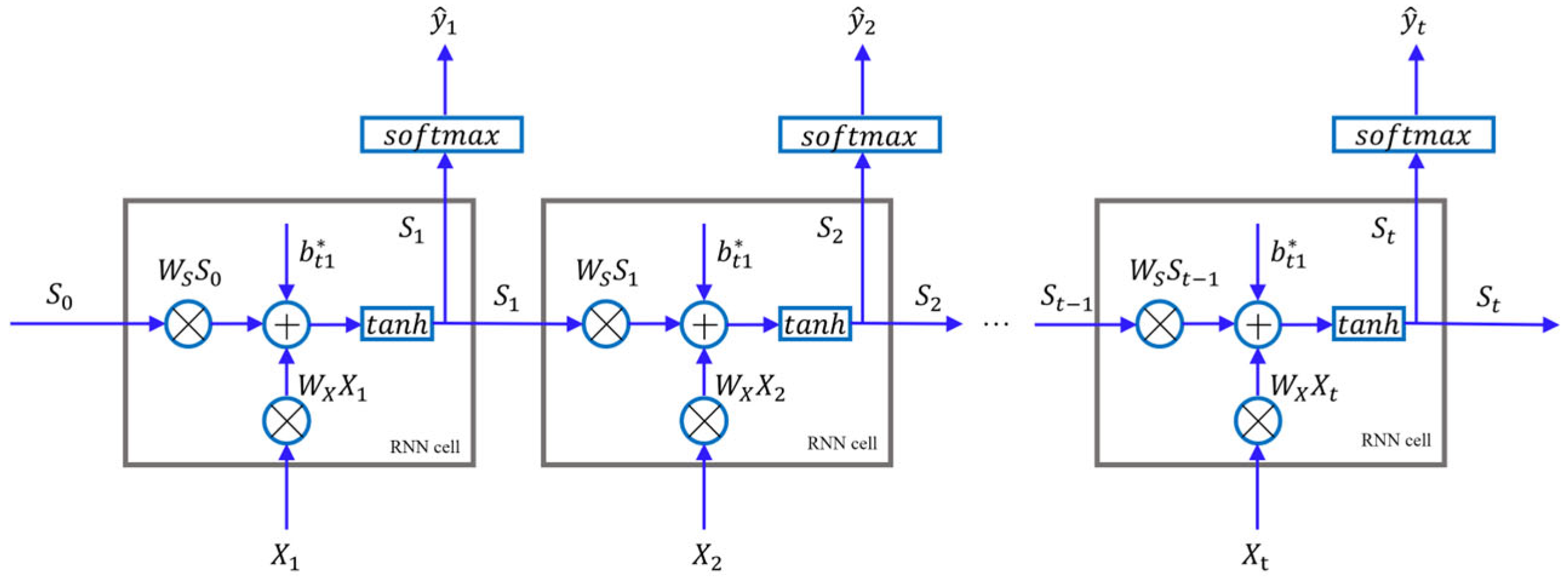
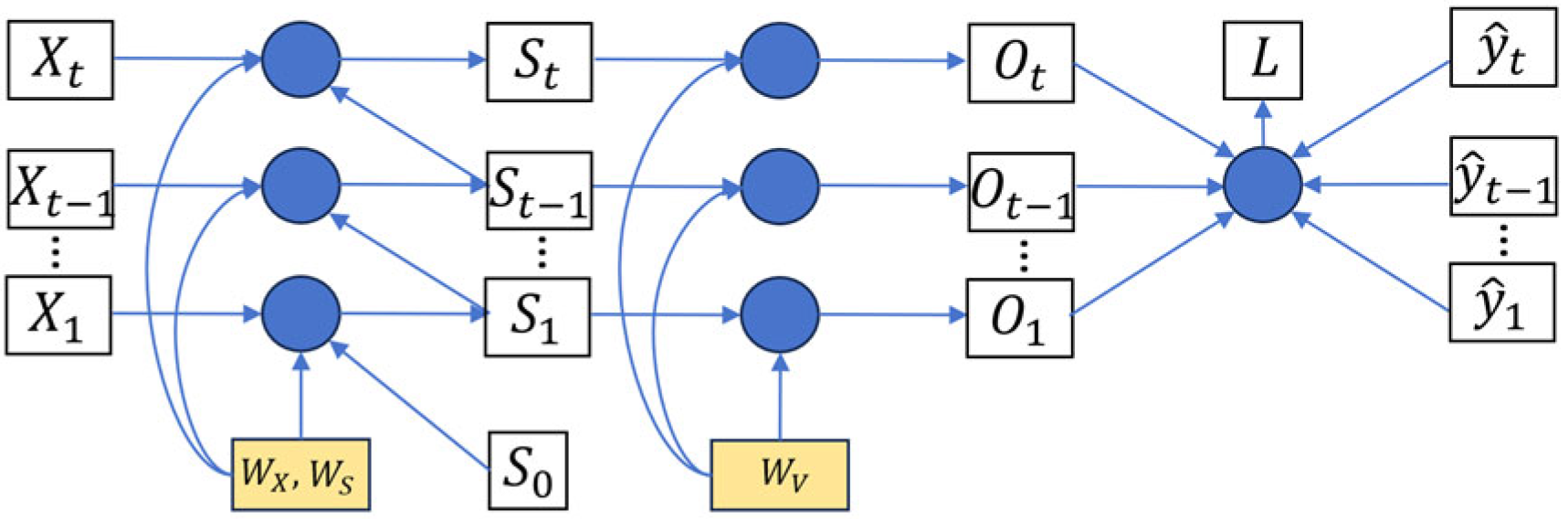
4.1. RNN Model Introduction

To demonstrate that the RNN data-driven model can be used to predict chaotic vibrations in the dynamic model of a LCCB under the influence of RPEs, the RNN is applied to analyze time-series data. As a deep learning method specifically designed for handling sequence data, the RNN has excellent predictive capabilities in time-series data [32]. It effectively captures the dynamic characteristics of the system state over time. Figure 2 shows a schematic diagram of the RNN’s recurrent structure, including the input $X_t$, hidden state $S_t$, output $O_t$, and the state update function $S$. The left part illustrates the basic unit structure of the RNN at a single time step $t$, while the right part displays the time-unfolded form across the time series. The hidden state $S_t$ is calculated based on the previous hidden state $S_{t-1}$ and the current input $X_t$, indicating how temporal correlations are formed across multiple time steps. In Figure 2, $W_X$ represents the weight matrix from input to hidden state, $W_S$ represents the weight matrix from hidden state to hidden state, and $W_V$ represents the weight matrix from hidden state to output layer.

Compared to the DNN, the RNN has significant advantages in handling time-series data. While a DNN is well suited for processing static data, it struggles to effectively capture temporal dependencies in dynamic features that evolve over time. In contrast, RNN utilizes its unique recurrent connection structure to transfer information from previous time steps to the current state, enabling more effective modeling of dependencies within time-series data. Similarly, CNNs focus on local feature extraction, making them effective for analyzing spatial data with localized correlations. RNNs demonstrate higher accuracy and stability in nonlinear predictions of complex systems, making them a powerful tool for processing dynamic temporal data.

The forward propagation of a RNN is a recursive computation process across time steps, making it well suited for handling time-series data. At each time step, the RNN receives the current input and the hidden state from the previous time step and then updates the hidden state through an activation function. Finally, the output is computed through the output layer. As shown in Figure 3, the RNN unfolds over time, computing hidden states sequentially and passing information step by step. Furthermore, as illustrated in Figure 4, during forward propagation, the output $O_t$ is computed and evaluated using a loss function, which serves as the basis for subsequent gradient updates. The forward propagation equations of the RNN are given as follows:

$$S_t=\mathit{tanh}\left(W_X{X}_t+W_S{S}_{t-1}+b_{t1}^{\ast }\right),$$

(7)

$${\widehat{y}}_t=softmax\left(W_V{S}_t+b_{t2}^{\ast }\right),$$

(8)

where ${\widehat{y}}_t$ is the predicted output at the time step $t$. Here, $b_{t1}^{\ast }$ is the bias of the hidden state, $b_{t2}^{\ast }$ is the bias of the output layer, and $softmax$ is the normalized exponential function.

To optimize the parameters of the RNN, the Back-Propagation Through Time (BPTT) algorithm is applied based on the loss function, using gradient descent to update model parameters. Unlike the traditional back-propagation algorithm, BPTT introduces the time dimension and considers the temporal dependencies in sequential data. In BPTT, the update rule for the hidden state $S_t$ includes the current input $X_t$ and the previous hidden state $S_{t-1}$, thereby capturing the temporal correlations in sequential data more effectively. The gradient descent of the loss function $L_t$ with respect to $W_s$, $W_X$, and $W_V$ is as follows:

$${\displaystyle \frac{\partial L_t}{\partial W_S}}={\displaystyle \frac{\partial L_t}{\partial W_S^{\left(t\right)}}}+\cdots +{\displaystyle \frac{\partial L_t}{\partial W_S^{\left(3\right)}}}+{\displaystyle \frac{\partial L_t}{\partial W_S^{\left(2\right)}}}+{\displaystyle \frac{\partial L_t}{\partial W_S^{\left(1\right)}}}={\displaystyle \frac{\partial L_t}{\partial O_t}}{\displaystyle \frac{\partial O_t}{\partial S_t}}{\displaystyle \frac{\partial S_t}{\partial W_S^{\left(t\right)}}}+{\sum }_{k=1}^{t-1}{\displaystyle \frac{\partial L_t}{\partial O_t}}{\displaystyle \frac{\partial O_t}{\partial S_t}}\left({\prod }_{j=k+1}^t{\displaystyle \frac{\partial S_j}{\partial S_{j-1}}}\right){\displaystyle \frac{\partial S_k}{\partial W_S^{\left(k\right)}}},$$

(9)

$$\begin{array}{ll}{\displaystyle \frac{\partial L_t}{\partial W_X}}& ={\displaystyle \frac{\partial L_t}{\partial W_X^{\left(t\right)}}}+\cdots +{\displaystyle \frac{\partial L_t}{\partial W_X^{\left(3\right)}}}+{\displaystyle \frac{\partial L_t}{\partial W_X^{\left(2\right)}}}+{\displaystyle \frac{\partial L_t}{\partial W_X^{\left(1\right)}}}\\ & ={\displaystyle \frac{\partial L_t}{\partial O_t}}{\displaystyle \frac{\partial O_t}{\partial S_t}}{\displaystyle \frac{\partial S_t}{\partial W_X^{\left(t\right)}}}+{\sum }_{k=1}^{t-1}{\displaystyle \frac{\partial L_t}{\partial O_t}}{\displaystyle \frac{\partial O_t}{\partial S_t}}\left({\prod }_{j=k+1}^t{\displaystyle \frac{\partial S_j}{\partial S_{j-1}}}\right){\displaystyle \frac{\partial S_k}{\partial W_X^{\left(k\right)}}},\end{array}$$

(10)

$${\displaystyle \frac{\partial L_t}{\partial W_V}}={\sum }_{t=1}^n\left({\displaystyle \frac{\partial L_t}{\partial O_t}}{\displaystyle \frac{\partial O_t}{\partial S_t}}{\displaystyle \frac{\partial S_t}{\partial W_V^{\left(t\right)}}}\right),$$

(11)

where ${\displaystyle \frac{\partial S_j}{\partial S_{j-1}}}=tanh\prime \left(W_X{X}_t+W_s{S}_{t-1}+b_{t1}^{\ast }\right)W_s$. $W_S^{\left(t\right)}$ represents the weight matrix from hidden state to hidden state at the $t^{th}$ time step, $W_X^{\left(t\right)}$ represents the weight matrix from input to hidden state at the $t^{th}$ time step, and $W_V^{\left(t\right)}$ represents the weight matrix from hidden state to output layer at the $t^{th}$ time step.

4.2. The Main Steps to Establish the Data-Driven Model of RNN

In this study, a data-driven RNN model is established for multivariate time series prediction. The input to the model is a chaotic vibration time series comprising two features—displacement and velocity—obtained from numerical simulations of the LCCB. The goal is to predict the future states of the system. The flowchart shown in Figure 5 illustrates the overall process of the RNN predicting the chaotic vibration of the LCCB.

The dataset used for time-series prediction consists of displacement and velocity data. To address the issue of feature scale variation in the raw data, a Min–Max normalization function is applied to scale the raw data to the range $[0,1]$. The expression for the Min–Max normalization function is defined in Equation (12):

$$X_{scaled}={\displaystyle \frac{X-X_{min}}{X_{max}-X_{min}}},$$

(12)

where $X_{scaled}$ is the normalized value, $X$ is the original input, and $X_{min}$ and $X_{max}$ denote the minimum and maximum values of the original input data, respectively.

After normalized, the data proceeds to the sliding window construction phase. The sliding window method converts time series data into a supervised learning format by generating a structured dataset containing two components: an input sequence and a corresponding target output sequence. Subsequently, the dataset is partitioned into training and testing sets. The training set is used for RNN model training, and the test set is used to evaluate the prediction performance and generalization ability of the RNN. During the training process, the test set is also used as validation data to monitor the loss changes but does not participate in parameter updates. Through strict time series partitioning, the RNN model learns only from historical data, thereby effectively avoiding overfitting and information leakage risks caused by ignoring the temporal order. To satisfy the input requirements of the RNN model, the data are reshaped into a three-dimensional tensor with the shape $(B,T,F)$, where $B$ represents the batch size, $T$ represents the number of time steps, and $F$ represents the number of features. In this three-dimensional structure, each sample consists of data spanning multiple time steps, and each time step contains multiple feature values. This format enables the RNN to capture the temporal dynamics of the time-series data and to perform sequence prediction tasks effectively.

Following data preprocessing, the data are fed into the RNN data-driven model. The RNN comprises multiple hidden units and employs the ReLU activation function. The final layer of the network is a fully connected layer, whose output dimension matches that of the target variable. During training, the Adam optimizer is used, and the MAE is selected as the loss function for optimization. Time-series features are extracted using a fixed-length time window, enabling the RNN to learn the temporal dependencies present in data.

Upon completion of training, the model makes predictions on the test dataset. The predicted values are then rescaled to the original data range using an inverse normalization operation. The inverse normalization is defined in Equation (13):

$$X=X_{scaled}\times \left(X_{max}-X_{min}\right)+X_{min .}$$

(13)

4.3. Loss Evaluation

This study evaluates the predictive performance of the RNN data-driven model using three commonly used metrics: $RMSE$, $MAE$, and $R^2$. The corresponding formulas are defined as follows:

$$RMSE=\sqrt{{\displaystyle \frac{1}{m}}{\sum }_{i=1}^m{\left(y_i^{pred}-y_i^{real}\right)}^2}$$

(14)

$$MAE={\displaystyle \frac{1}{m}}{\sum }_{i=1}^m\left|y_i^{pred}-y_i^{real}\right|$$

(15)

$$R^2=1-{\displaystyle \frac{{\sum }_i^m{\left(y_i^{pred}-y_i^{real}\right)}^2}{{\sum }_i^m{\left(\overline{y_i^{real}}-y_i^{real}\right)}^2}}$$

(16)

where $y_i^{real}$ is the real value, $\overline{y_i^{real}}$ is the average of the real values, $y_i^{pred}$ is the predicted value at the $i^{th}$ time step, and $m$ is the total number of the prediction points.

$RMSE$ is used to evaluate the generalization ability of the RNN model, whereas $MAE$ reflects the model’s stability. In general, lower $RMSE$ values indicate higher predictive accuracy, and lower $MAE$ values correspond to greater model stability. $MAE$ is also employed as the loss function to handle parameter updates during BPTT. $R^2$ ranges from 0 to 1, with values closer to 1 indicating a better goodness of fit between the predicted and real data.

5. Numerical Simulations

In this section, the chaotic vibrations at different specified points on the studied LCCB are identified and subsequently predicted using the RNN model defined in Equations (7)–(16). Subsequently, the chaotic vibrations of the LCCB are predicted using the CNN model, and the corresponding analyses are presented to show the difference between the prediction with the RNN model and the prediction with the CNN model.

The numerical simulations are carried out under the following initial conditions:

$$w_{1,1}\left(0\right)=0, w_{1,2}\left(0\right)=0, w_{2,1}\left(0\right)=0, w_{2,2}\left(0\right)=0.$$

(17)

The geometric parameters of the beam are defined as

$$l=0.5 \mathrm{m}, b=0.02 \mathrm{m}, h=0.01 \mathrm{m}.$$

(18)

The external load is defined as

$$q=q_0\sin \left(\omega t\right)\mathrm{P}\mathrm{a},$$

(19)

where $q_0$ is the amplitude of the uniformly distributed load, and $\omega$ is the angular frequency.

The values of $q_0$ and $\omega$ in Equation (19) and the values of $\Gamma$ in Equation (4) are summarized in

Table 2. Parameters of $q_0$, $\omega$ and $\Gamma$.

Cases	${\mathit{q}}_0$	$\mathit{\omega }$	$\mathit{\Gamma }$	Dynamic Phenomena
Case 1	4500	$22\pi$	0%	Chaotic
Case 2	4500	$22\pi$	4%	Chaotic
Case 3	4500	$22\pi$	8%	Chaotic
Case 4	4500	$22\pi$	10%	Chaotic

.

5.1. Case 1

As shown in Figure 6, the LCCB exhibits chaotic vibrations under the parameter setting $q_0=4500$, $\omega =22\pi$, and $\Gamma =0\%$, within the dimensionless time interval $t\in \left[0,500\right]$. The maximum amplitude of $w_{\mathrm{P}}$ reaches $2.35528$. Figure 7 presents the first and second vibration modes of the chaotic response, where the maximum amplitude of the first-order vibration $w_{1,1}$ is $1.72536$, and that of the second-order vibration $w_{2,1}$ is $0.325271$. Figure 8 shows the 2D phase portrait of the chaotic vibration of the LCCB, highlighting the characteristics of chaotic motion from a two-dimensional perspective. The Poincaré map is shown in Figure 9.

Figure 10 illustrates the comparison of real and predicted values for the chaotic vibration response of the LCCB. As illustrated in Figure 10, the predicted values closely overlap with the real values, indicating that the RNN can effectively track the dynamic behavior of the real response and accurately capture the nonlinear characteristics of chaotic vibrations.

The 2D and 3D phase portraits of the chaotic vibration are shown in Figure 11 and Figure 12, respectively, demonstrating the agreement between the RNN predictions and the real data in phase space. As observed from Figure 11 and Figure 12, the predicted trajectories exhibit a high degree of agreement with the real trajectories, which verifies the strong predictive capability of the RNN for the chaotic vibration of the LCCB.

Figure 13 presents the overall prediction results of the RNN and CNN models for the chaotic vibrations of the LCCB. It can be observed that both models capture the overall trend of the real vibrations well, demonstrating satisfactory predictive capability.

To provide an intuitive comparison of the detailed prediction accuracy of the two models, Figure 14 further illustrates an enlarged view over a local time interval. As shown in Figure 14, the RNN prediction curve aligns more closely with the real vibrations in terms of vibration phase and vibration amplitude, whereas the CNN prediction exhibits noticeable phase lag and amplitude deviation at certain time instants. These results indicate that the RNN model achieves higher accuracy in predicting the chaotic vibrations.

5.2. Case 2

Under the parameters of $q_0=4500$, $\omega =22\pi$, and $\Gamma =4\%$, the LCCB exhibits chaotic vibration within the dimensionless time interval $t\in \left[0,500\right]$, as shown in Figure 15. The maximum vibration amplitude is approximately $w_{\mathrm{P}}=3.66701$, which increases by about $55.6932\%$ compared to the maximum amplitude in Case 1.

Figure 16 illustrates the first and second vibration modes of the chaotic response. In Figure 16a, the maximum amplitude of $w_{1,1}$ is approximately $2.65470$, representing an increase of about $53.8635\%$ compared to $w_{1,1}$ in Case 1. In Figure 16b, the maximum amplitude of $w_{2,1}$ is approximately $0.70961$, showing an increase of about $118.1596\%$ compared to $w_{2,1}$ in Case 1. When $\Gamma =4\%$, the effective stiffness of the LCCB slightly decreases, and modal interactions become more pronounced. This enhances the nonlinear coupling and energy concentration in the dominant vibration modes, resulting in a significant increase in the amplitude of chaotic vibrations. Such an RPE amplifies the sensitivity of the LCCB to nonlinear effects, triggering more intense chaotic vibrations.

Figure 17 presents the 2D phase portrait of the LCCB’s chaotic vibration, illustrating the phase relationship between displacement and velocity and highlighting the system’s chaotic behavior from a two-dimensional perspective. The Poincaré map is provided in Figure 18.

Figure 19 illustrates the comparison between the predicted values obtained from the RNN and the corresponding real values under a RPE of $4\%$. Specifically, Figure 19a presents the displacement responses of the LCCB. It can be observed that the predicted curve closely overlaps with the real curve, indicating high prediction accuracy. Figure 19b shows the velocity responses, where the predicted values exhibit strong agreement with the real values at each time step, demonstrating a high level of prediction accuracy.

Furthermore, Figure 20 and Figure 21 depict the 2D and 3D phase portraits of the chaotic vibration under a RPE of $4\%$, highlighting the comparison between the predicted and real responses in the phase space. The trajectories of the predicted and real values exhibit an almost complete overlap, confirming that the RNN can accurately capture the overall dynamic evolution and nonlinear characteristics of the chaotic vibration, even in the presence of RPEs.

Under $\Gamma =4\%$, the prediction performance of the RNN and CNN models is further compared. Figure 22 presents the predicted displacement and velocity of the LCCB within $t\in \left[400,450\right]$, while Figure 23 shows an enlarged view of a local time interval to provide a clearer comparison of the models’ capability in capturing detailed features.

As observed in Figure 22, the prediction curves of both RNN and CNN models are generally close to the real vibrations. However, Figure 23 reveals pronounced differences in the detailed responses. The RNN model demonstrates higher fitting accuracy, particularly around vibration amplitudes, where its predictions align closely with the real vibrations and better capture the nonlinear characteristics and response details of the chaotic vibrations. In contrast, the CNN model exhibits noticeable deviations in the enlarged regions, in terms of phase lag and over-smoothed predictions. These differences indicate that, under RPEs, the RNN model exhibits higher robustness and generalization capability than the CNN model.

5.3. Case 3

Under the parameter setting $q_0=4500$, $\omega =22\pi$, and $\Gamma =8\%$, Figure 24 shows the chaotic vibration of the LCCB. The maximum amplitude $w_{\mathrm{P}}$ reaches $2.47882$, representing an increase of approximately $5.2452\%$ compared to Case 1, indicating that the amplitude does not change significantly. Figure 25 shows the first and second vibration mode responses of the LCCB. In Figure 25a, the maximum amplitude of $w_{1,1}$ is $1.78933$, showing an increase of approximately $3.7076\%$ compared to Case 1. In Figure 25b, the maximum amplitude of $w_{2,1}$ is about $0.46700$, representing an increase of approximately $43.5726\%$ relative to in Case 1. At an $8\%$ RPE level, the vibration amplitude is nearly saturated. The system has already entered a highly nonlinear state, where additional RPEs primarily enhance the irregularity of the vibrations rather than further increasing the amplitude. This indicates that the LCCB reaches a chaotic state in the presence of RPE.

Figure 26 shows the 2D phase portrait of the chaotic vibration, illustrating the displacement–velocity relationship, and highlighting the chaotic behavior from a phase–space perspective. The Poincaré map is presented in Figure 27.

Figure 28 shows the comparison between the RNN predictions and the corresponding real values. Figure 28a shows the displacement comparison. As shown in Figure 28a, the predicted and real curves exhibit a high degree of agreement, with the two curves almost completely overlapping throughout most of the time interval. Figure 28b shows the velocity comparison. Figure 28b indicates the RNN can accurately capture the velocity variation, with a high level of agreement between the predicted and real curves. Figure 29 and Figure 30 show the 2D and 3D phase–space comparisons between the predicted and real values, respectively, further indicating that the RNN model can accurately capture the overall variation trend of the chaotic vibration of the LCCB in the presence of RPEs.

Figure 31 presents the prediction results of the chaotic vibrations obtained by the RNN and CNN models under an 8% RPE, along with a comparison with the real vibration. From the overall trend, both models effectively capture the chaotic vibrations of the LCCB; however, a noticeable phase lag is observed in the CNN model in the regions around vibration amplitudes.

To further highlight the difference between the two models in capturing detailed features, Figure 32 provides an enlarged view of the vibrations within a local time interval. The results indicate that the RNN model achieves higher accuracy in predicting both the vibration amplitudes and phase variations, whereas the CNN predictions display local phase lags and amplitude deviations. These observations demonstrate that the RNN model offers higher accuracy in predicting the chaotic vibrations of the LCCB.

5.4. Case 4

With the parameters of $q_0=4500$, $\omega =22\pi$, and $\Gamma =10\%$, Figure 33 shows the chaotic vibration of the LCCB within the dimensionless time interval $t\in \left[0,500\right]$. The maximum amplitude of $w_{\mathrm{P}}$ is $2.08143$, representing a reduction of about $11.6271\%$ compared to Case 1. Figure 34 presents the first and second vibration mode responses of the LCCB. In Figure 34a, the maximum amplitude of $w_{1,1}$ is $1.52406$, representing a reduction of about $11.6671\%$ compared to Case 1. In Figure 34b, the maximum amplitude of $w_{2,1}$ is $0.289587$, showing a decrease of about $10.9701\%$ compared to Case 1. At a 10% RPE, the vibration amplitude decreases. Excessive RPE induces modal detuning and energy redistribution among multiple modes, which disperses the vibration energy and reduces the peak response. Figure 35 shows the displacement–velocity relationship, providing a two-dimensional phase–space perspective on the chaotic vibration of the LCCB. The Poincaré map is provided in Figure 36.

Figure 37 shows the comparison between the RNN predictions and the real values. Figure 37a presents the displacement comparison between the predicted and real values. Figure 37a presents the predicted and real curves exhibit a high degree of agreement, with the two curves almost completely overlapping. Figure 37b shows the velocity comparison. In Figure 37b, the two curves show strong agreement, and the RNN predictions accurately match the real values, showing high prediction accuracy. Figure 38 and Figure 39 show 2D and 3D phase–space comparisons between the predicted and real responses, respectively, demonstrating that the RNN can accurately capture the chaotic vibration characteristics of the LCCB even in the presence of RPEs.

Figure 40 presents the overall prediction results of the chaotic vibrations of the LCCB obtained by the RNN and CNN models under a 10% RPE. In terms of the overall trend, both models fit the real vibration curves well.

To further assess the capability of the RNN and CNN models in capturing the detailed features of the chaotic vibrations of the studied LCCB, Figure 41 provides an enlarged view over a selected time interval. The results show that the RNN model exhibits higher accuracy in predicting complex nonlinear fluctuations and peak–valley variations, with its prediction curve closely following the real vibration, particularly around real vibration amplitudes. The CNN model, by contrast, exhibits noticeable errors in the regions where the real vibration reaches its amplitudes. This comparative analysis further confirms the prediction accuracy and robustness of the RNN model for chaotic vibrations of the LCCB under RPEs.

5.5. Spatial Applicability and Generalization

To further evaluate the applicability and generalization capability of the RNN model under spatial position variations, different external excitations and circular frequencies, the nondimensional vibration at ${\mathrm{P}}^{*}$, which corresponds to the free end of the studied LCCB ($x=l$), is derived as follows based on Equation (1) and the previous research [27]:

$$w_{{\mathrm{P}}^{\ast }}={\sum }_{n=1}^2{\phi }_n\left(x_{{\mathrm{P}}^{\ast }}\right)w_{n,1}\left(t\right)=1.999847202w_{1,1}\left(t\right)-1.99981439w_{2,1}\left(t\right)$$

(20)

In this section, the chaotic vibrations of the LCCB under various external excitation amplitudes and circular frequencies are predicted and analyzed with a 10% RPE, and the results are compared with those obtained using the CNN model. These specific parameter settings are given as follows:

$$q_0=3000, \omega =20\pi , \Gamma =10\%$$

(21)

Based on the parameters in Equation (21), the chaotic vibrations of the LCCB are shown in Figure 42. Within the nondimensional time interval $t\in \left[0,500\right]$, chaotic vibration phenomena can be clearly observed, and the maximum amplitude of the LCCB reaches 2.8609. Figure 43 and Figure 44 illustrate the responses of the first two vibration modes and the corresponding two-dimensional phase portraits, further revealing the nonlinear dynamic characteristics of the chaotic vibrations. Figure 45 presents the Poincaré map, which more intuitively demonstrates the irregularity of the chaotic vibrations.

Figure 46 illustrates the overall prediction performance of the RNN and CNN models for the chaotic vibrations of the LCCB under the conditions $q_0=3000$, $\omega =20\pi$, $\Gamma =10\%$. Both models can predict the real vibration responses well, while the RNN model shows higher accuracy, featuring $R^2=0.999972$, $MAE=0.060$, and $RMSE=0.099$. In comparison, the CNN model attains slightly lower accuracy, with $R^2=0.999741$, $MAE=0.163$, and $RMSE=0.276$.

To further assess the models’ capability to capture the details of chaotic vibrations, Figure 47 provides a locally enlarged view of the response within a selected time interval. The results show that the RNN model exhibits higher accuracy in predicting complex nonlinear fluctuations, with its advantage particularly evident in the time intervals where the real response reaches vibration amplitudes. In contrast, the CNN model shows noticeable deviations in the regions where the real response reaches vibration amplitudes. These observations demonstrate that the RNN model would better achieve accurate and robust predictions of the LCCB vibrations at the free end.

Table 3. Comparison of RNN testing results under four different cases.

	Case 1	Case 2	Case 3	Case 4
$R^2$	0.999938334582534	0.999984548634328	0.999900810476744	0.999494832355506
$MAE$	0.032	0.046	0.051	0.075
$w_{\mathrm{P}}$	0.06	0.089	0.096	0.140
$\mathrm{d}{w}_{\mathrm{P}}/\mathrm{d}t$	0.003	0.003	0.006	0.011
$RMSE$	0.044	0.093	0.099	0.121
$w_{\mathrm{P}}$	0.062	0.132	0.140	0.171
$\mathrm{d}{w}_{\mathrm{P}}/\mathrm{d}t$	0.004	0.004	0.007	0.014

provides a detailed comparison of the RNN’s prediction performance for the nonlinear dynamic response of the LCCB under four different RPE conditions (Cases 1–4). The evaluation is conducted using multiple key performance metrics, including $R^2$, $MAE$, and $RMSE$. The results exhibit clear trends and good comparability across different cases.

Firstly, in terms of the goodness-of-fit indicator $R^2$, all four cases achieve high values, each exceeding 0.999, indicating that the RNN has a strong capability to capture the vibration of the LCCB. Specifically, Case 1 yields the highest $R^2$ value of $0.999938334582534$, showing the best fitting performance, while Case 4 yields the lowest value of $0.999494832355506$, which still falls within an excellent fitting range. These results reflect the overall stability of the RNN model across varying RPE conditions.

Table 4. Comparison of CNN testing results under four different cases.

	Case 1	Case 2	Case 3	Case 4
$R^2$	0.999646	0.999965	0.999461	0.993126
$MAE$	0.055	0.064	0.09	0.268
$w_{\mathrm{P}}$	0.098	0.12	0.163	0.47
$\mathrm{d}{w}_{\mathrm{P}}/\mathrm{d}t$	0.013	0.007	0.016	0.066
$RMSE$	0.09	0.112	0.162	0.39
$w_{\mathrm{P}}$	0.126	0.159	0.228	0.546
$\mathrm{d}{w}_{\mathrm{P}}/\mathrm{d}t$	0.016	0.009	0.028	0.072

summarizes the test results of the CNN model under different RPEs. A comparison presented in Table 4 shows that the CNN model achieves consistently high $R^2$ values, all exceeding $0.993$, across the different RPE levels. However, as the RPE increases, both $MAE$ and $RMSE$ exhibit a clear upward trend, with the prediction errors becoming particularly pronounced in Case 4. These results indicate that, compared with the CNN model, the RNN model exhibits relatively higher robustness in predicting the chaotic vibrations of the LCCB.

Figure 48 and Figure 49 illustrate the variations in the prediction errors of the RNN and CNN models under different RPEs. As the RPE increases, both the values of $MAE$ and $RMSE$ for the two models increase; however, the error growth of the CNN model is more pronounced and reaches its maximum in Case 4, indicating that it is more sensitive to RPEs. In contrast, the RNN model consistently maintains lower error levels, demonstrating higher accuracy and robustness in predicting the chaotic vibrations of the LCCB. For the RNN predictions, compared with Case 1, $MAE$ increases by $0.014$, $0.019$, and $0.043$ in Case 2, Case 3, and Case 4, respectively, while $RMSE$ increases by $0.049$, $0.055$, and $0.077$, respectively.

6. Conclusions

Based on the RNN data-driven model, this study investigates the prediction of the chaotic vibration of the LCCB subjected to RPEs. The main conclusions are as follows:

(a)

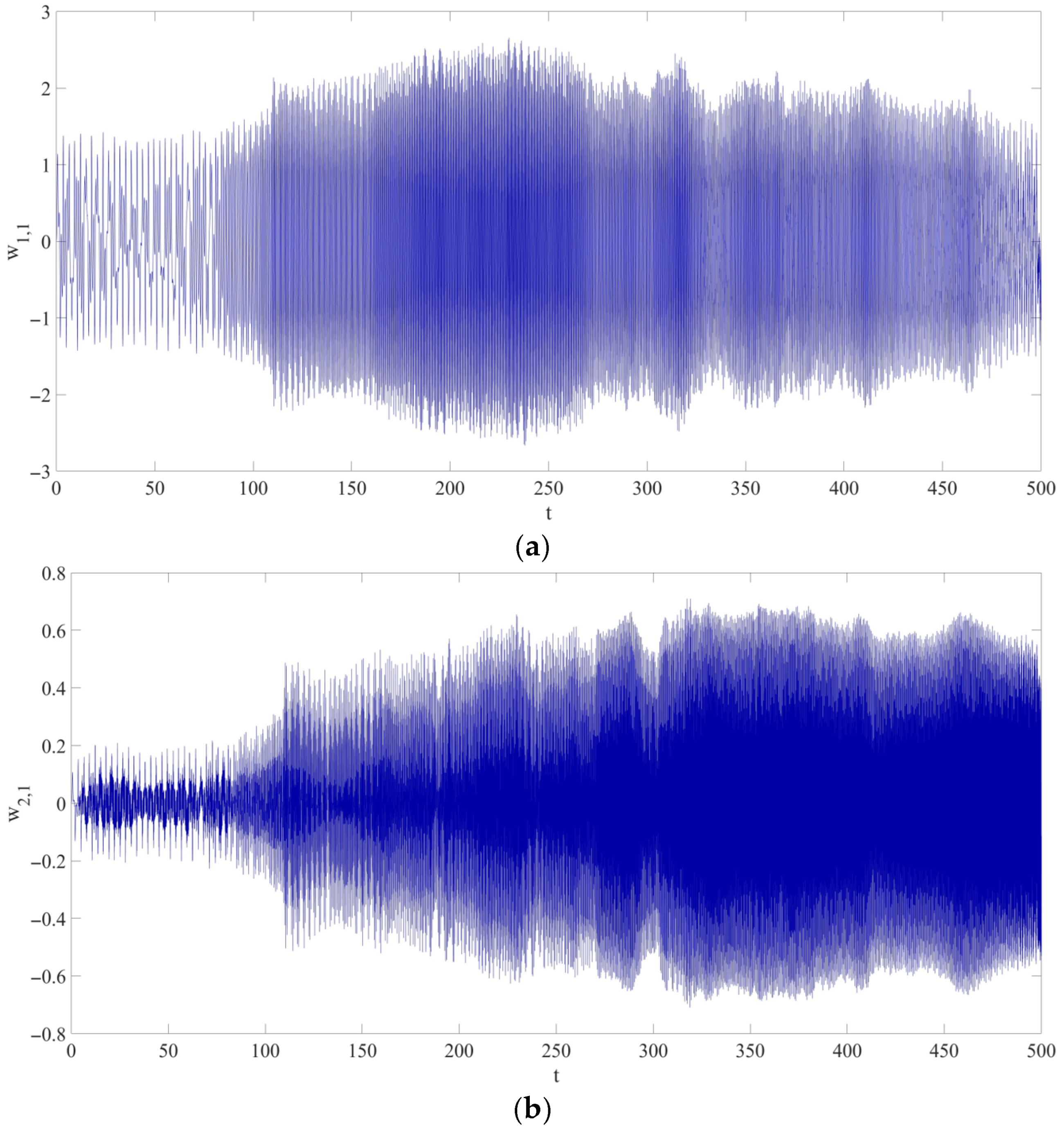
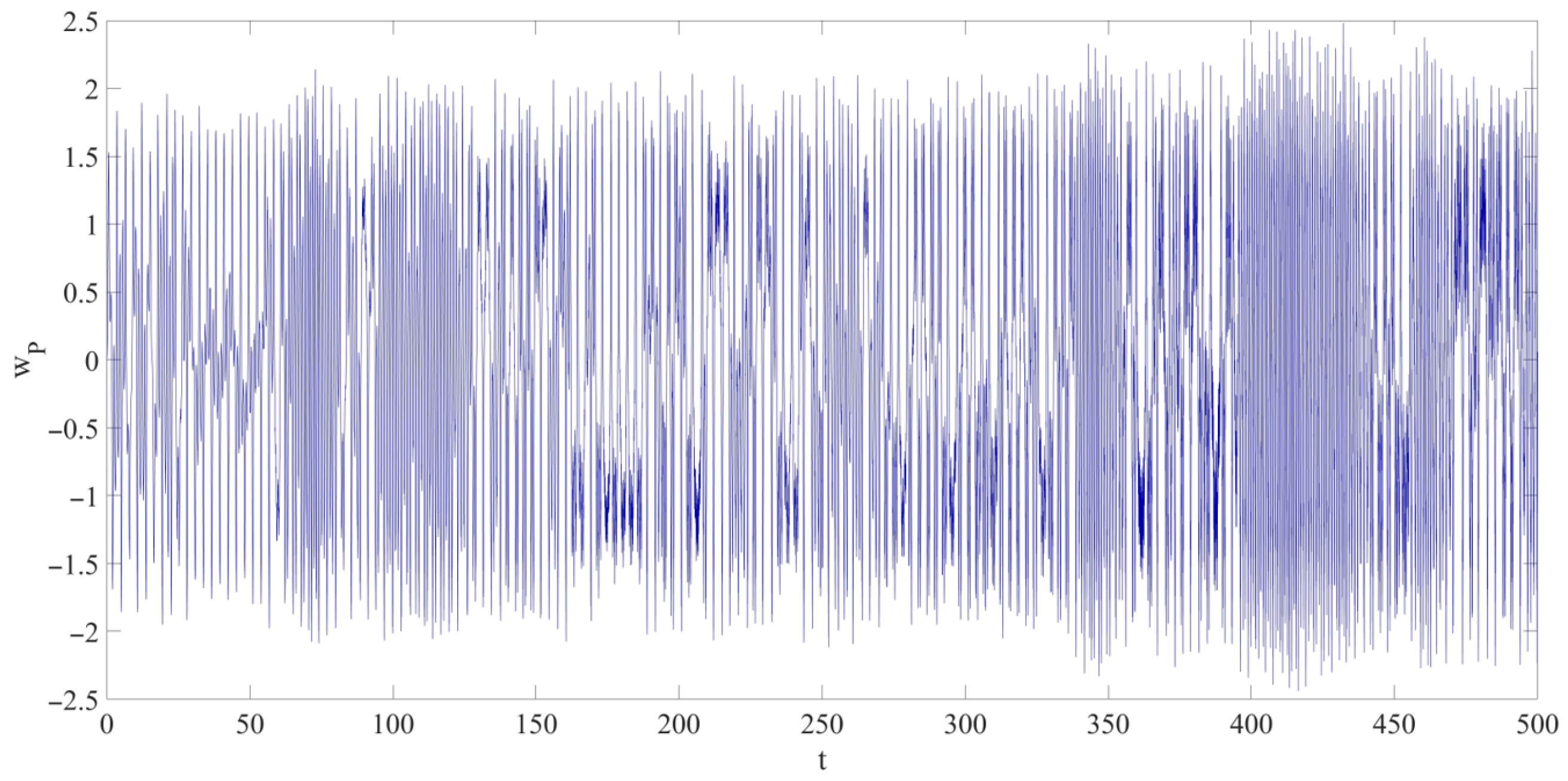
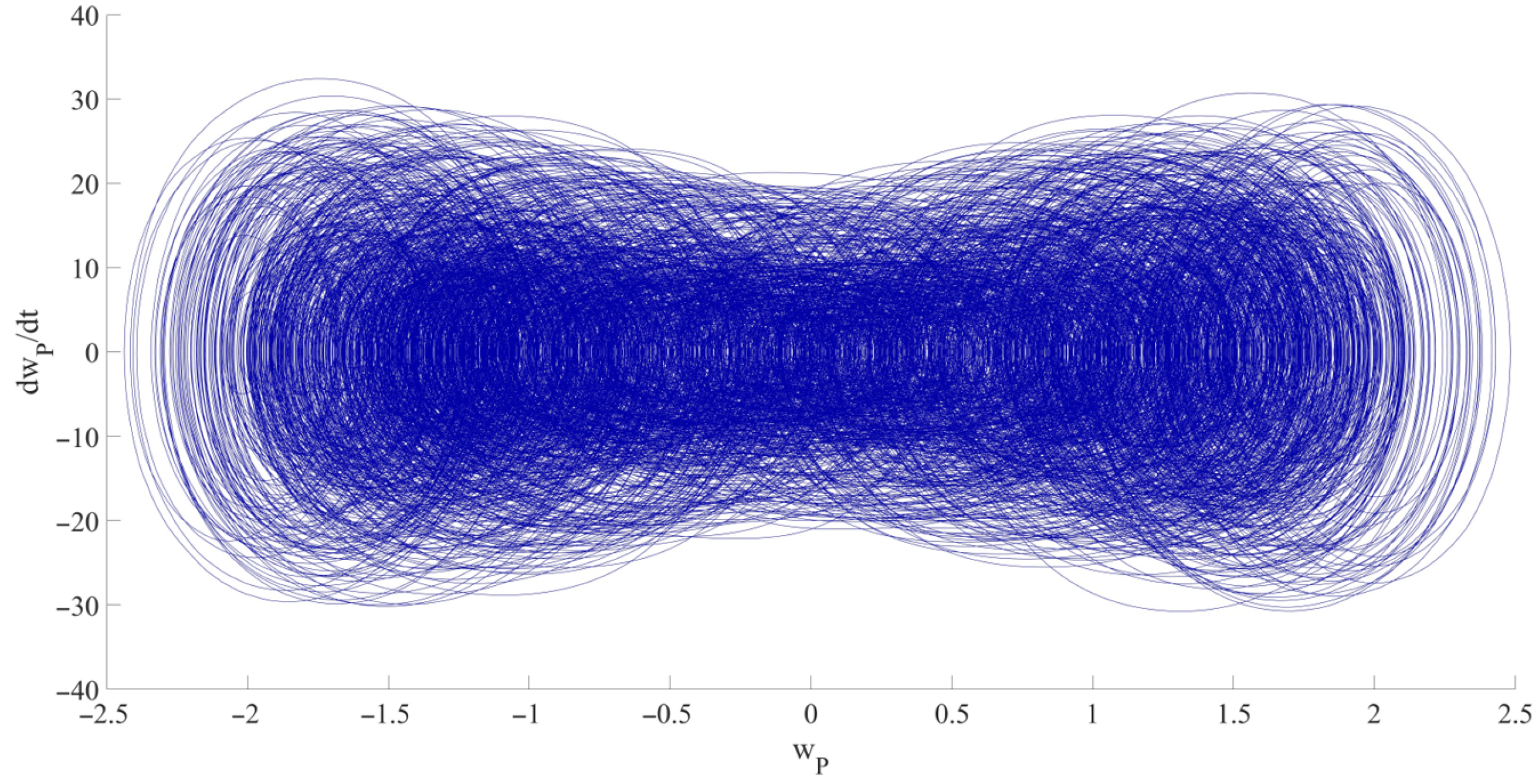
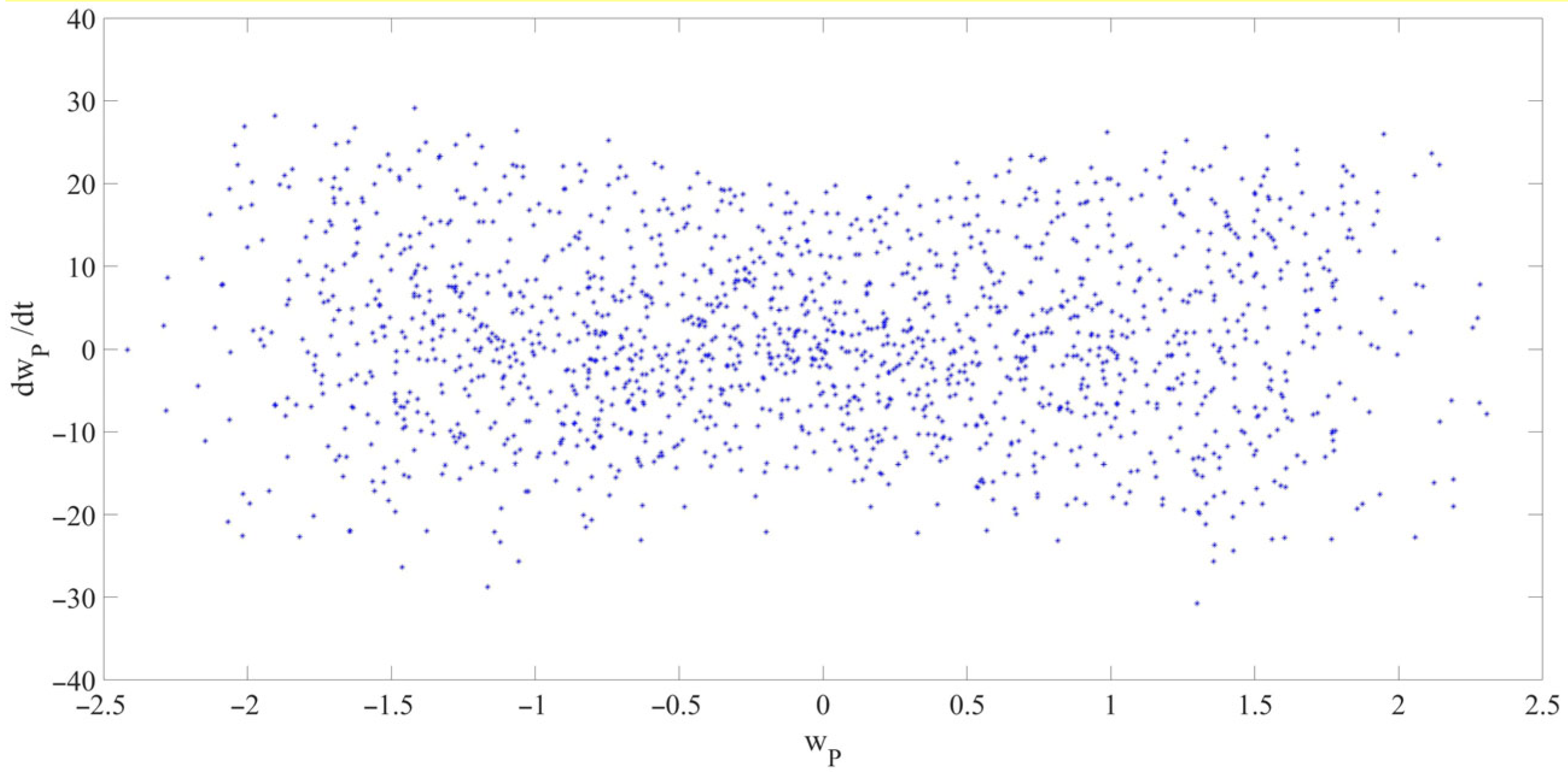
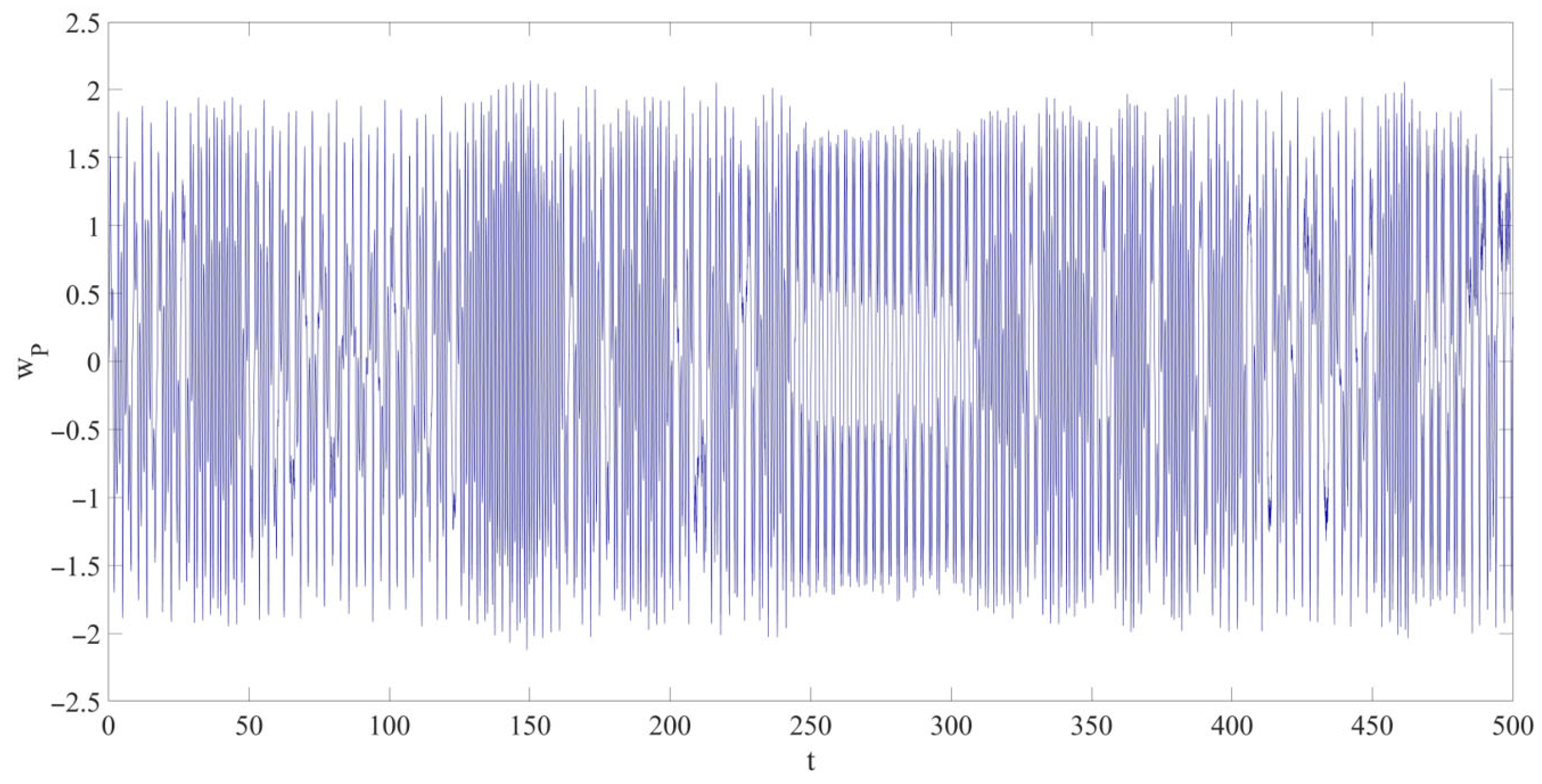
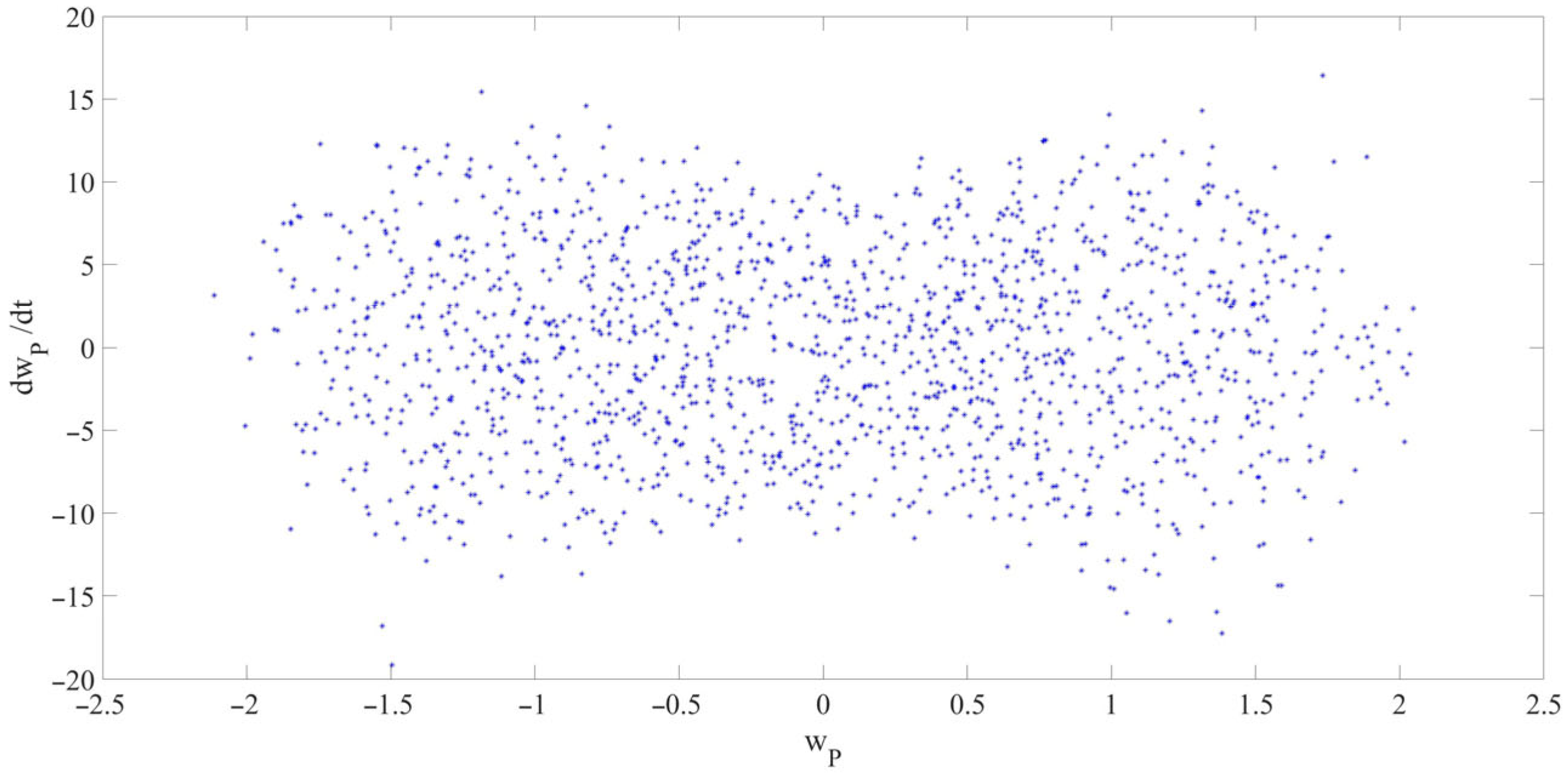
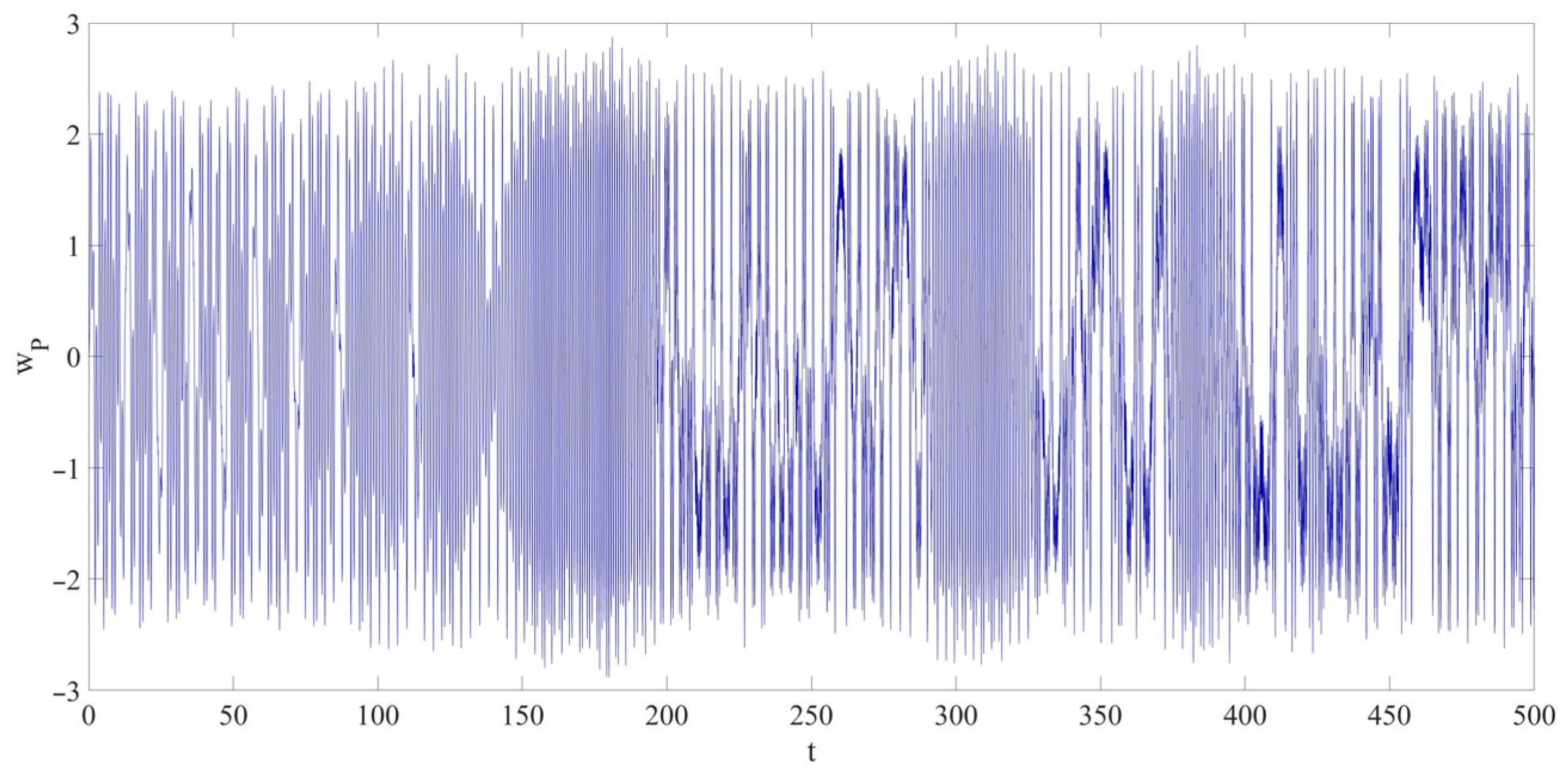
A nonlinear dynamic model of the LCCB considering RPEs was successfully developed. The results indicate that RPEs significantly affect the amplitude of chaotic vibrations in the LCCB system. Comparative analysis under four RPE conditions (Cases 1–4) shows that RPEs may lead to increasing, stable, or decreasing trends in vibration amplitude. Specifically, compared to Case 1, Case 2 exhibits an increase in the chaotic vibration amplitude; Case 3 shows that the amplitude remains almost unchanged; and Case 4 demonstrates a decrease in the chaotic vibration amplitude.

(b)

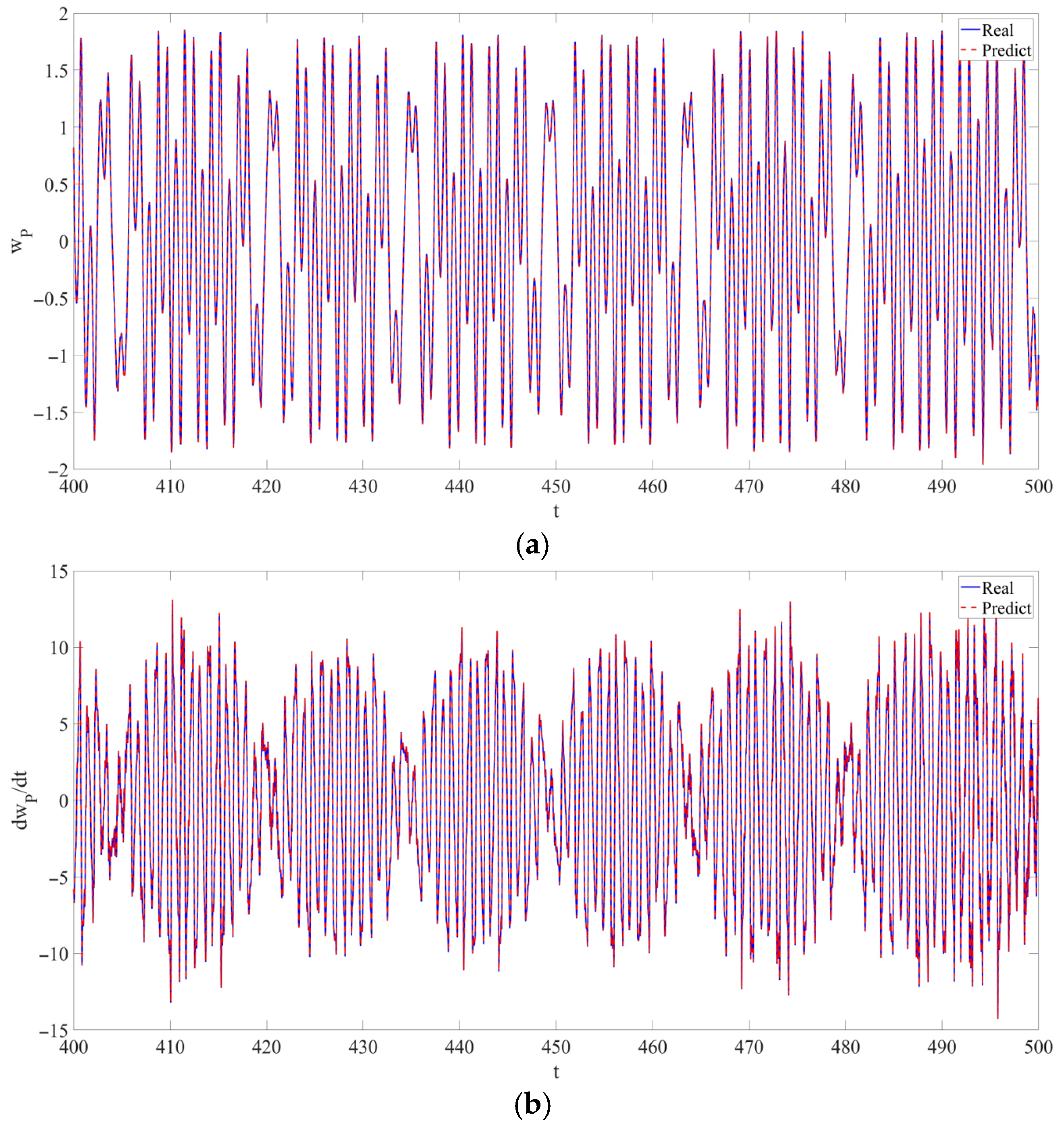
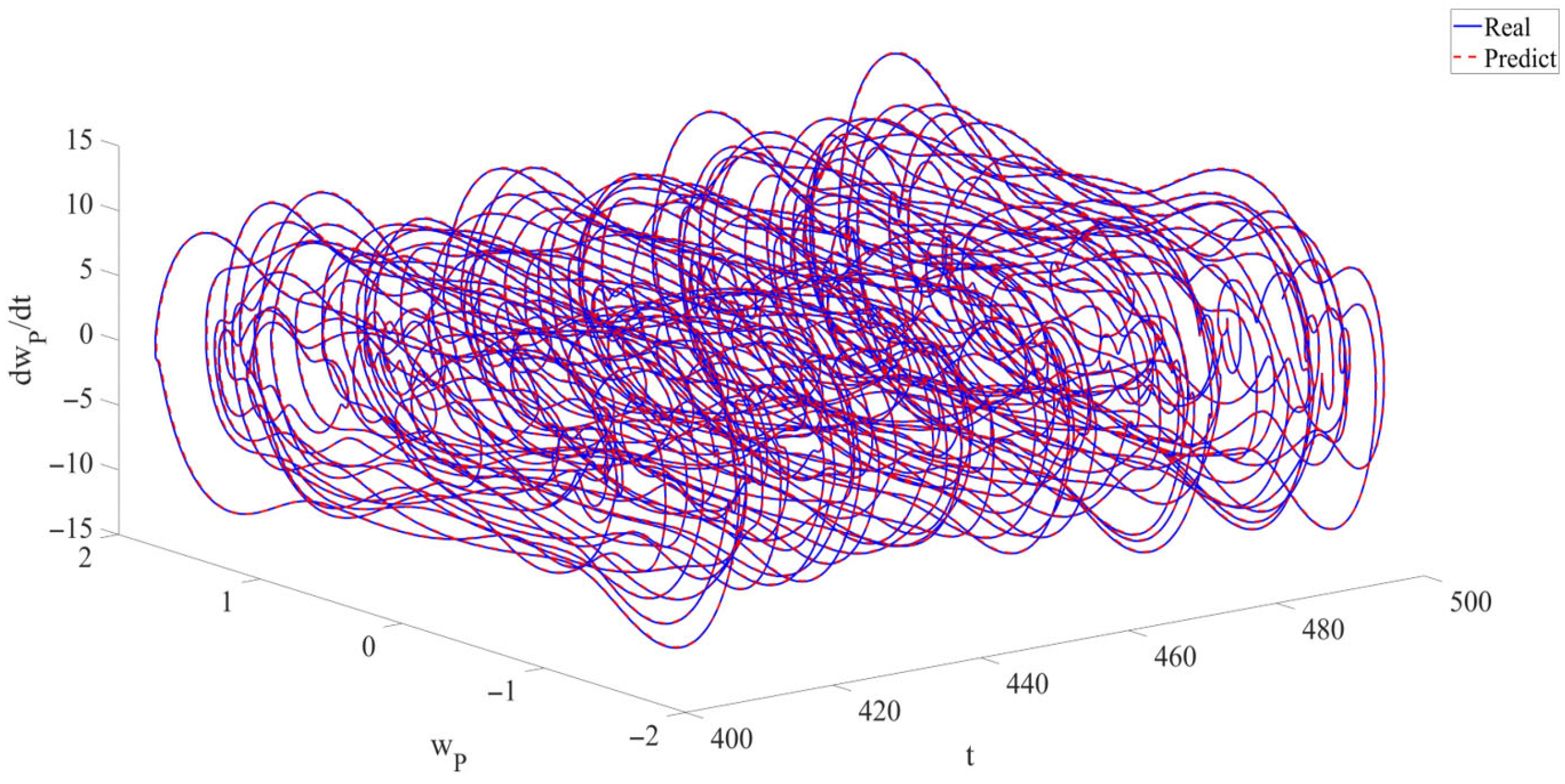
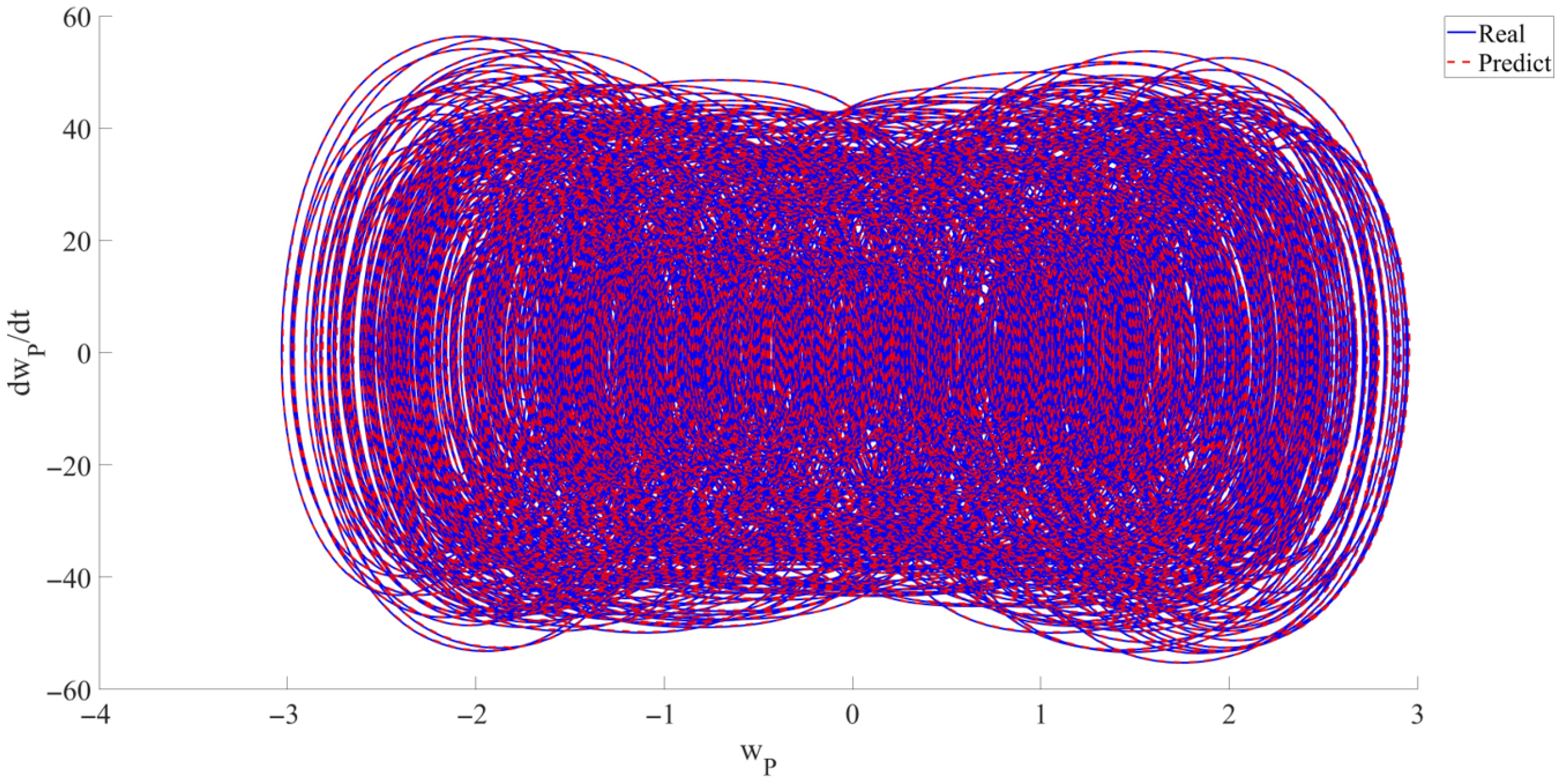
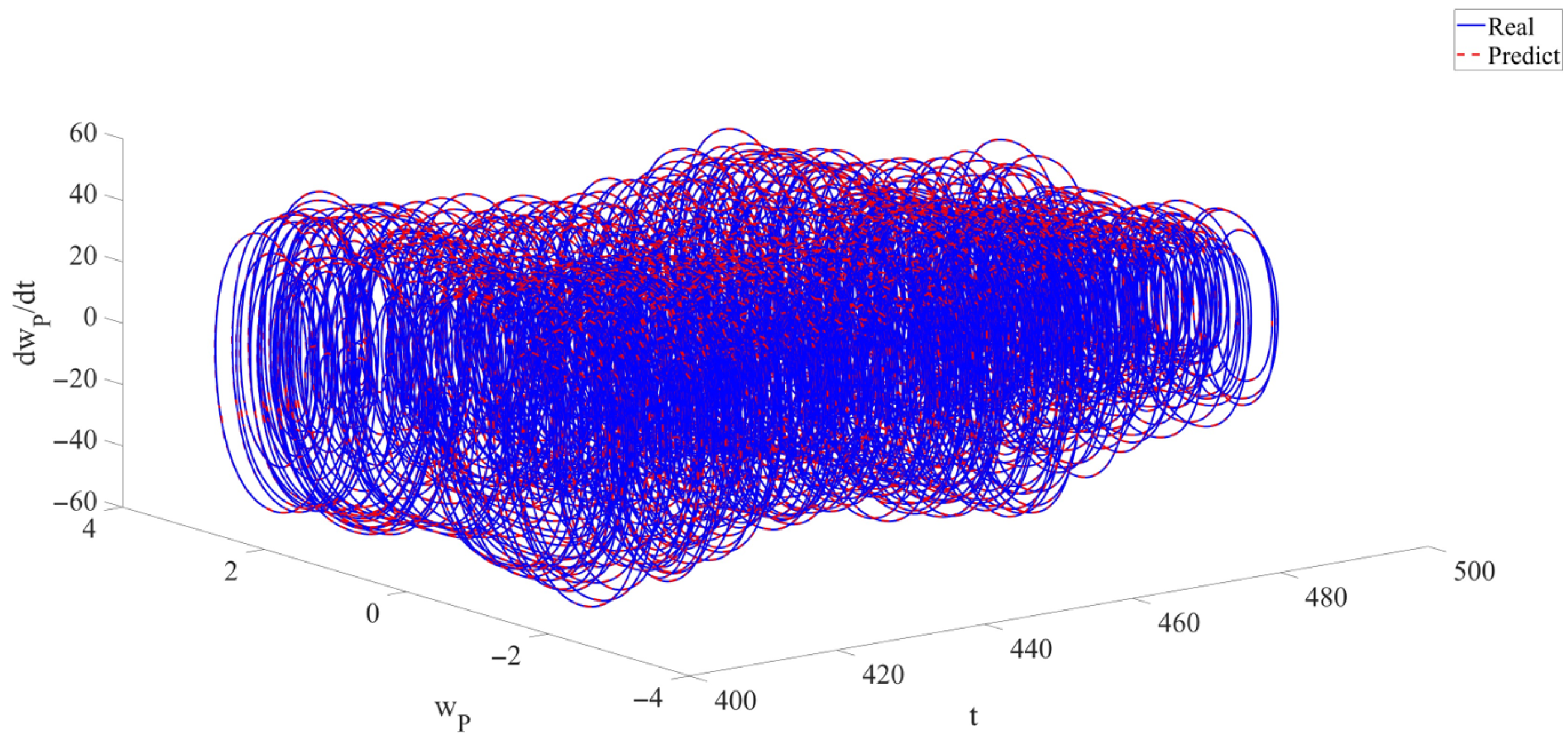
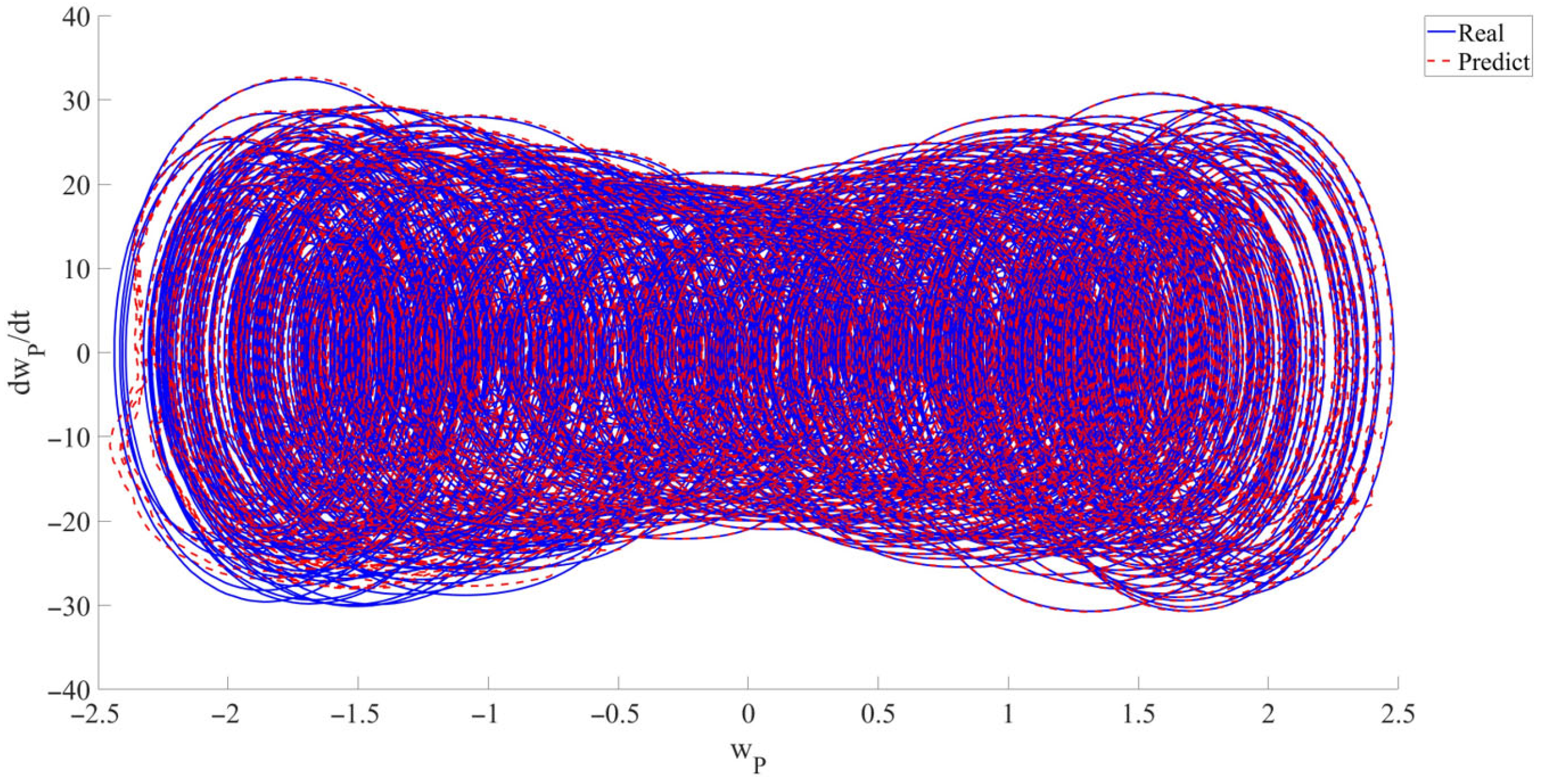
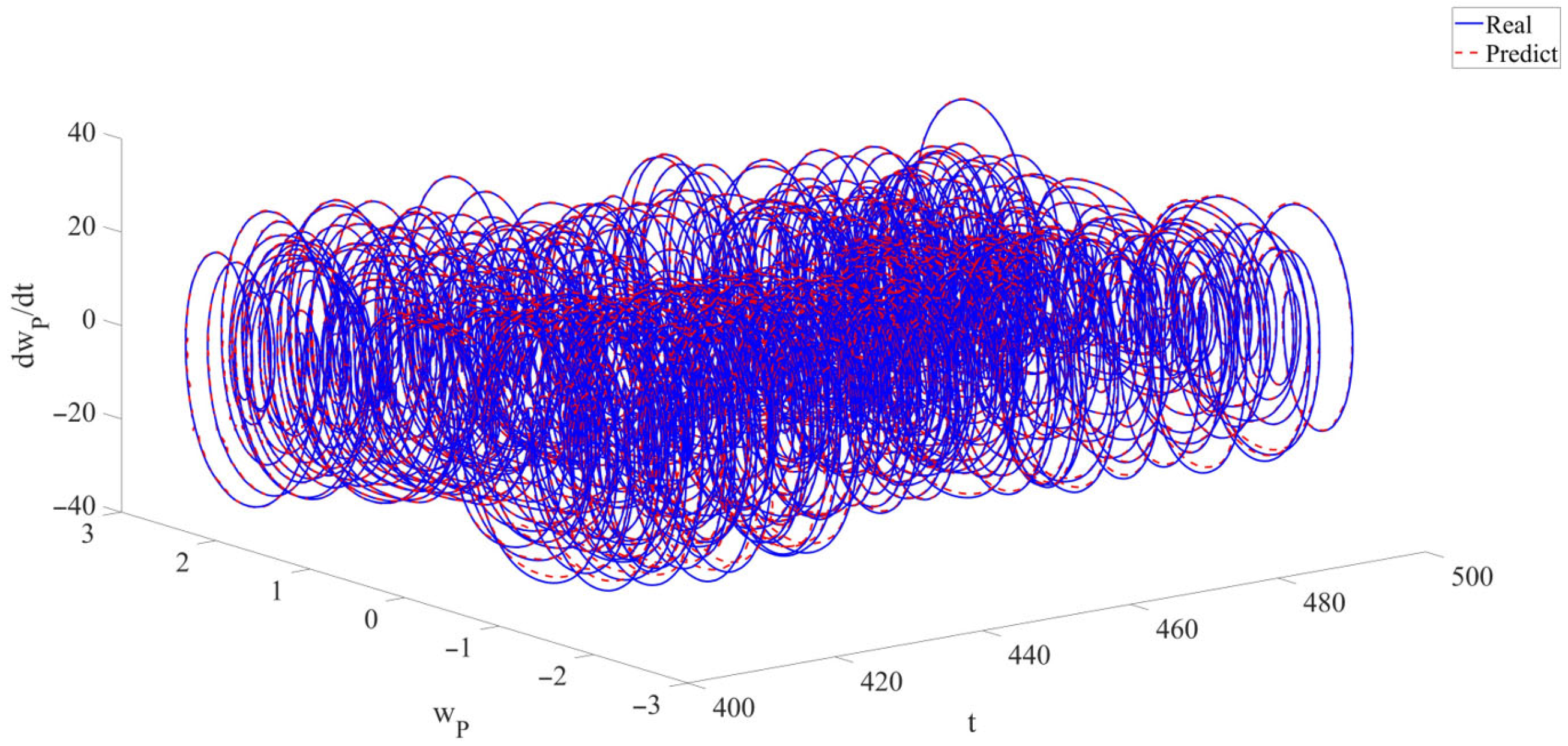
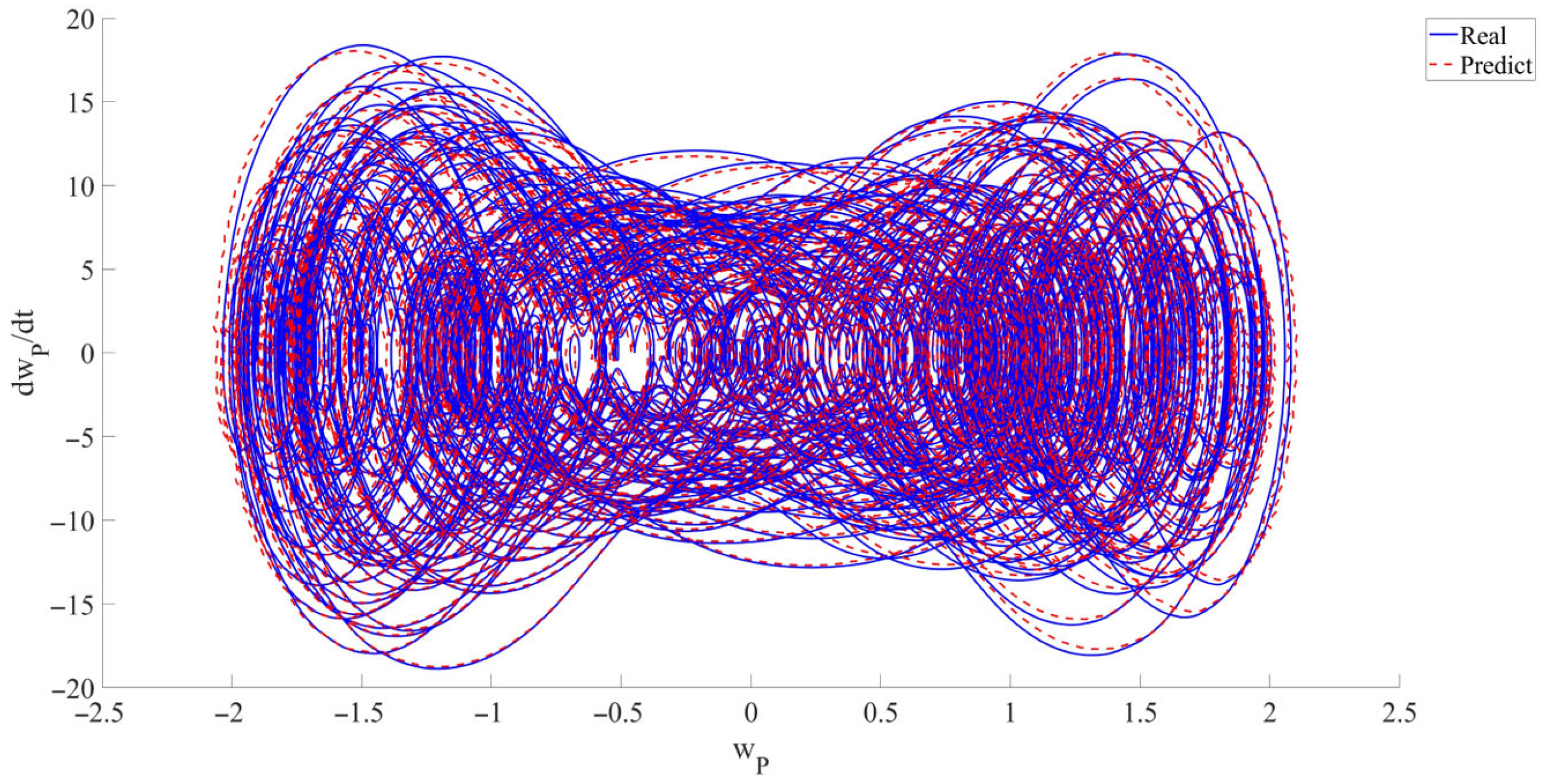
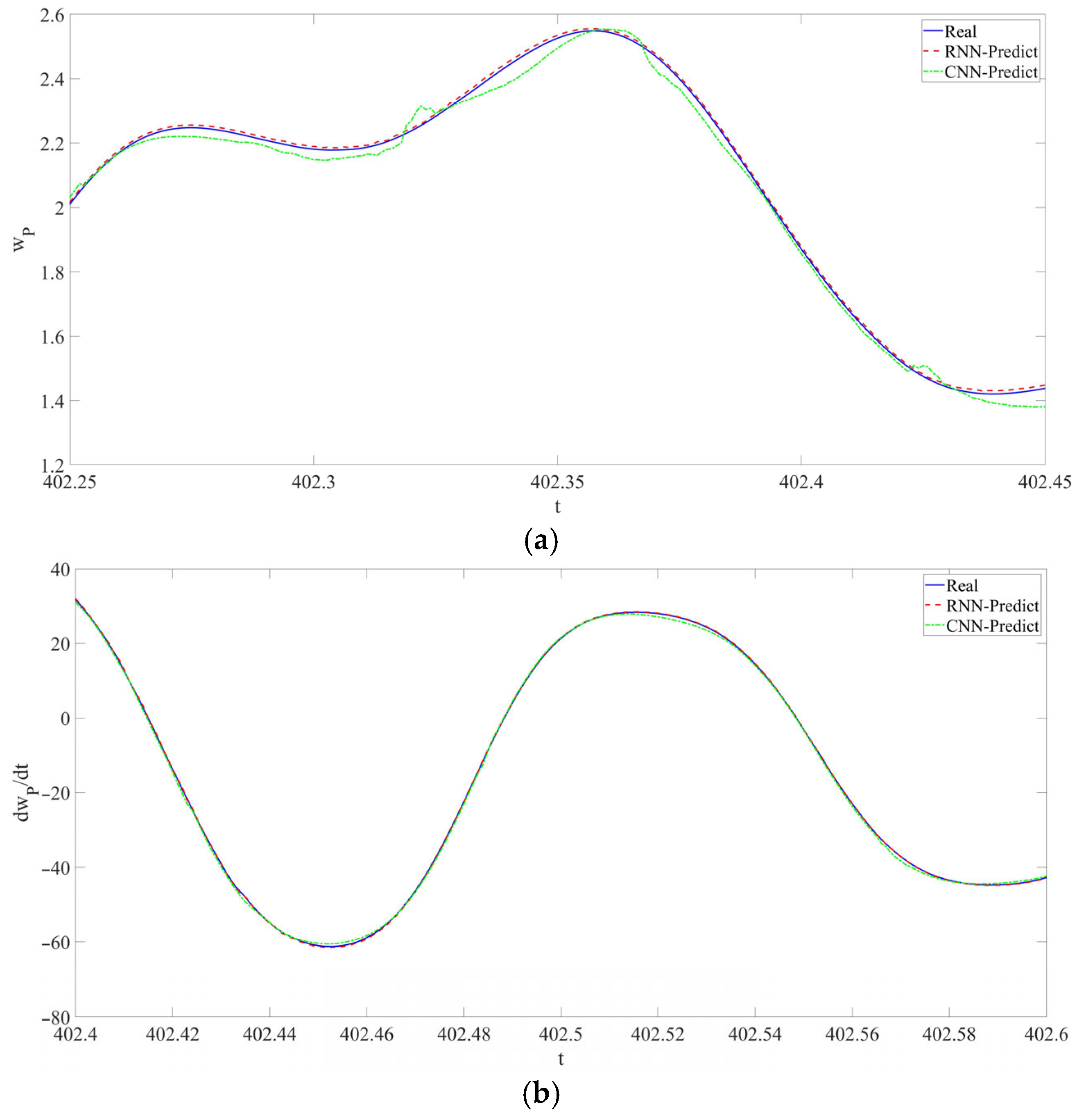
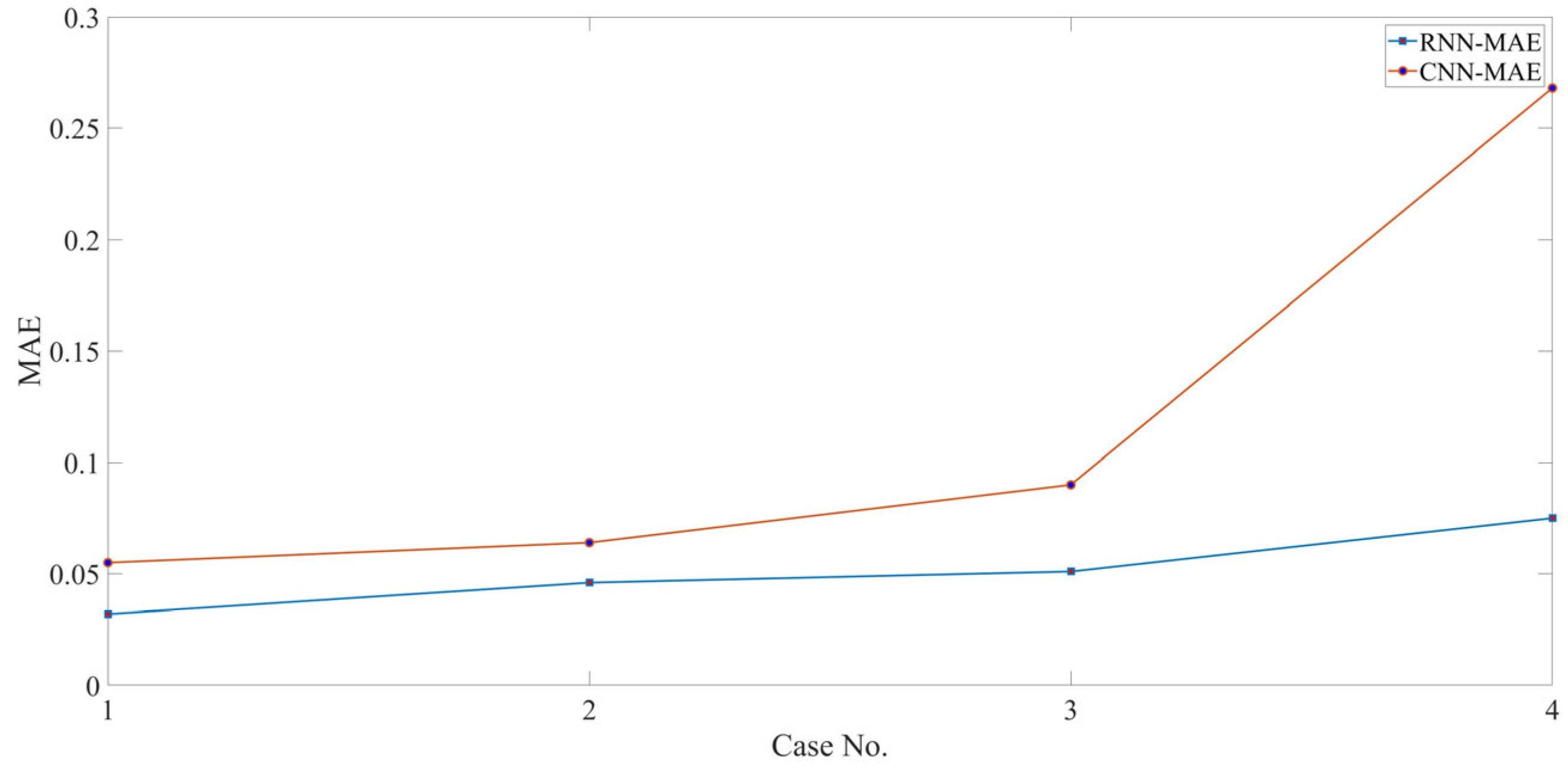
In this research, for the first time, RPEs are introduced into the modeling of the LCCB to demonstrate the accuracy and robustness of RNN in predicting the chaotic vibrations of the LCCB. Across varying levels of RPEs, the predicted results remain highly consistent with the real data. The prediction curves almost completely overlap the real curves. The model’s predictive capability is quantitatively evaluated using metrics such as $R^2$, $MAE$, and $RMSE$. Using the CNN model as a baseline, the performance of the RNN data-driven model is evaluated. The results reveal that the CNN model exhibits a certain phase lag in capturing the response details of chaotic vibrations, whereas the RNN model maintains high accuracy in predicting response variations. In addition, the RNN model outperforms the CNN model in terms of both $MAE$ and $RMSE$. The predictive analysis demonstrates that the RNN data-driven model maintains high prediction accuracy and strong stability in predicting the chaotic vibrations of the LCCB subjected to RPEs.

(c)

The prediction results at the free end of the LCCB indicate that the RNN model maintains high prediction accuracy under spatial position variations, demonstrating its spatial applicability. Furthermore, when the external excitation amplitude and circular frequency change, the RNN model can still accurately capture the chaotic vibrations of the LCCB, confirming both its robustness and generalization performance. This study provides a data-driven approach for predicting the chaotic vibrations of complex laminated composite structures and shows engineering applications in structural health monitoring, vibration control, and nonlinear dynamic analysis under complex environmental conditions.

7. Future Development

This study verifies that the RNN model achieves high accuracy and robustness in predicting the chaotic vibrations of the LCCB under the influence of RPEs. However, several aspects remain worthy of further investigation. The main directions for future research include the following.

Firstly, future research should incorporate experimental validation to evaluate the predictive performance of the RNN model under practical conditions and further conduct a comprehensive assessment of its applicability, accuracy, and generalization capability.

Secondly, future studies may consider developing spatially varying or parameter-wise independent noise models to more accurately represent the potential local inhomogeneity and parameter randomness of multi-layer composites under practical conditions. This approach can enhance the physical fidelity of uncertainty modeling and verify the robustness of the RNN model in vibration prediction.

Thirdly, future research will further extend the dynamic model so that RPEs can directly perturb material parameters (such as Young’s modulus, density, and layer thickness), thereby more accurately and realistically reflecting the physical sources of material and manufacturing uncertainties.

Fourthly, future research could extend the prediction approach to multiple measurement points, which would not only facilitate a more comprehensive representation of the spatial dynamic characteristics of laminated composite cantilever structures but also enable a more systematic evaluation of the applicability, accuracy, and robustness of the RNN model.