Time-Dependent Rheological Behavior and MPS Simulation of Cement–Bentonite Slurries with Hydration Accelerators for Borehole Backfilling Applications
Abstract
1. Introduction
- (1)
- Assessing the flowability and phase segregation resistance of different formulations through standardized flow and bleeding tests.
- (2)
- Developing an MPS-based numerical model capable of reproducing the observed experimental behavior, with particular attention to time-dependent rheological changes.
- (3)
- Quantitatively investigating the effects of viscosity changes on flow behavior and phase segregation through sequential updating of rheological parameters in the numerical model.
- (4)
- Establishing relationships between material composition, rheological properties, and practical performance to guide the development of improved backfilling materials.
2. Background and Literature Review
2.1. Classification and Properties of Backfill Materials
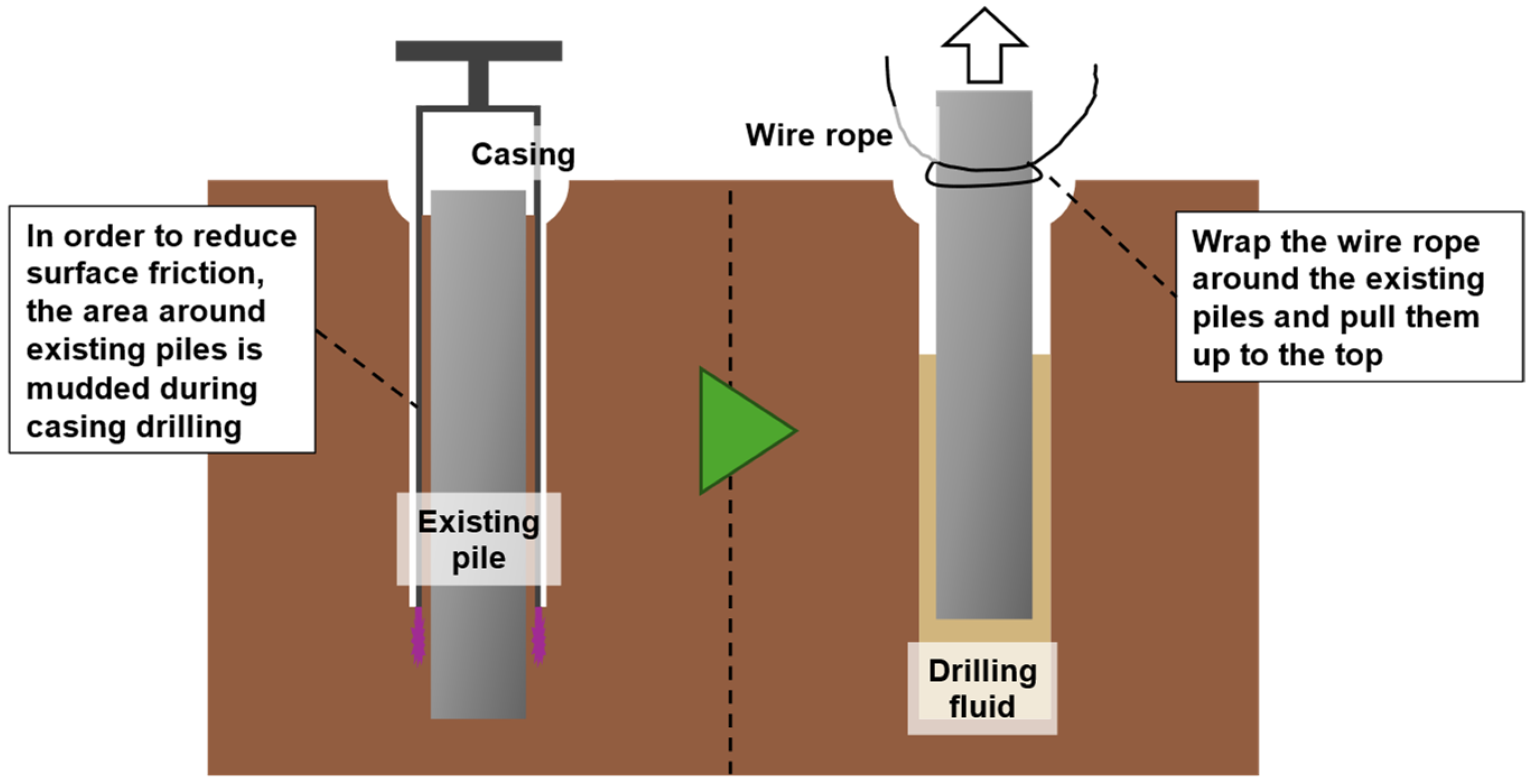
2.2. Extraction Methods and Backfilling Processes
2.3. Previous Studies on Rheological Properties of Backfill Materials
2.4. Application of Numerical Methods in Backfill Analysis
3. Materials and Methods
3.1. Materials and Mix Design
3.2. Experimental Procedures
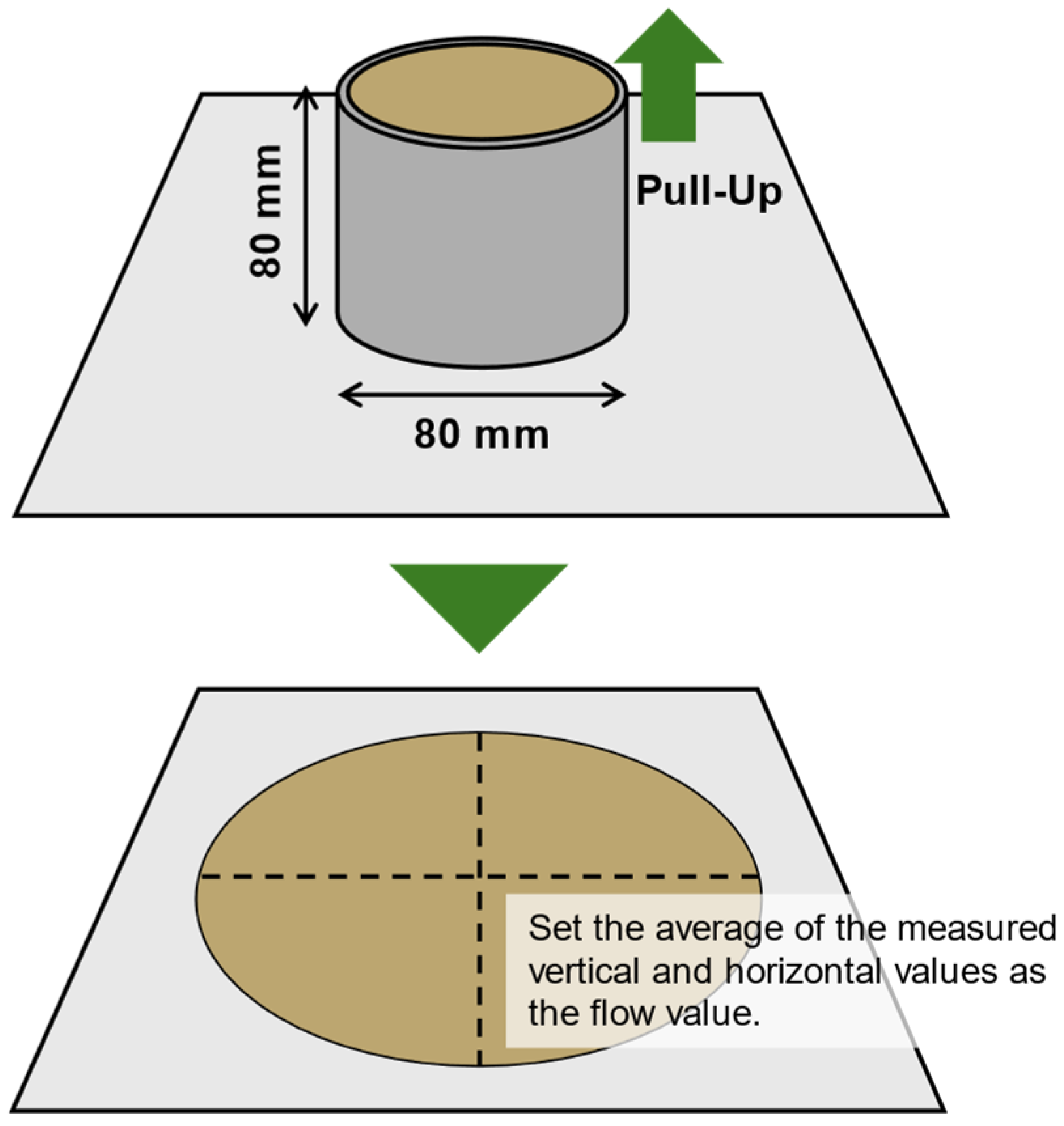
3.2.1. Flow Test Protocol
3.2.2. Bleeding Test Protocol
3.3. Numerical Simulation Framework
3.3.1. MPS Method Implementation
3.3.2. Rheological Modeling
3.3.3. Model Validation
4. Results
4.1. Flow Test Results
4.2. Bleeding Test Results
4.3. MPS Simulation Results
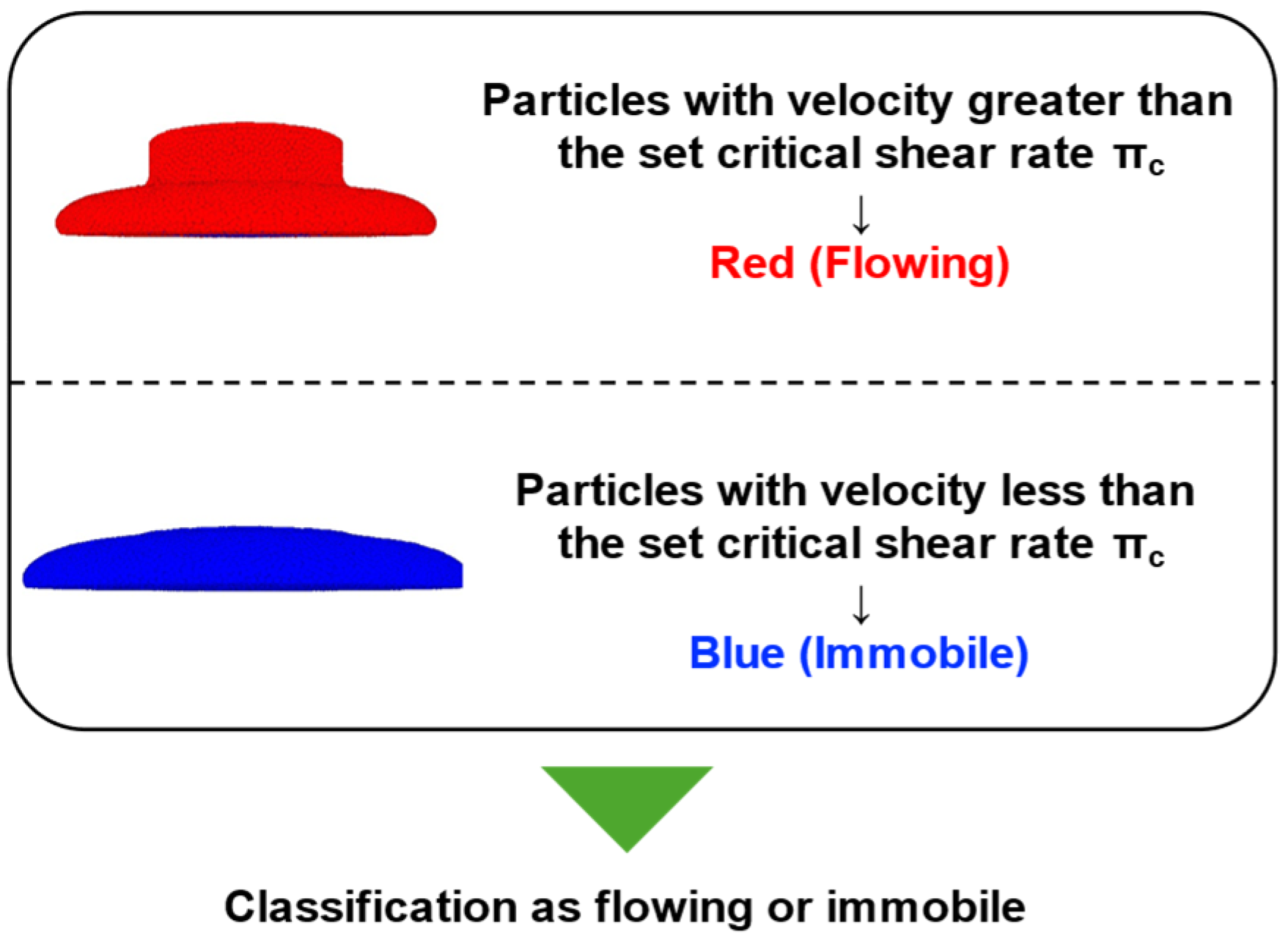
4.3.1. Flow Behavior Simulation
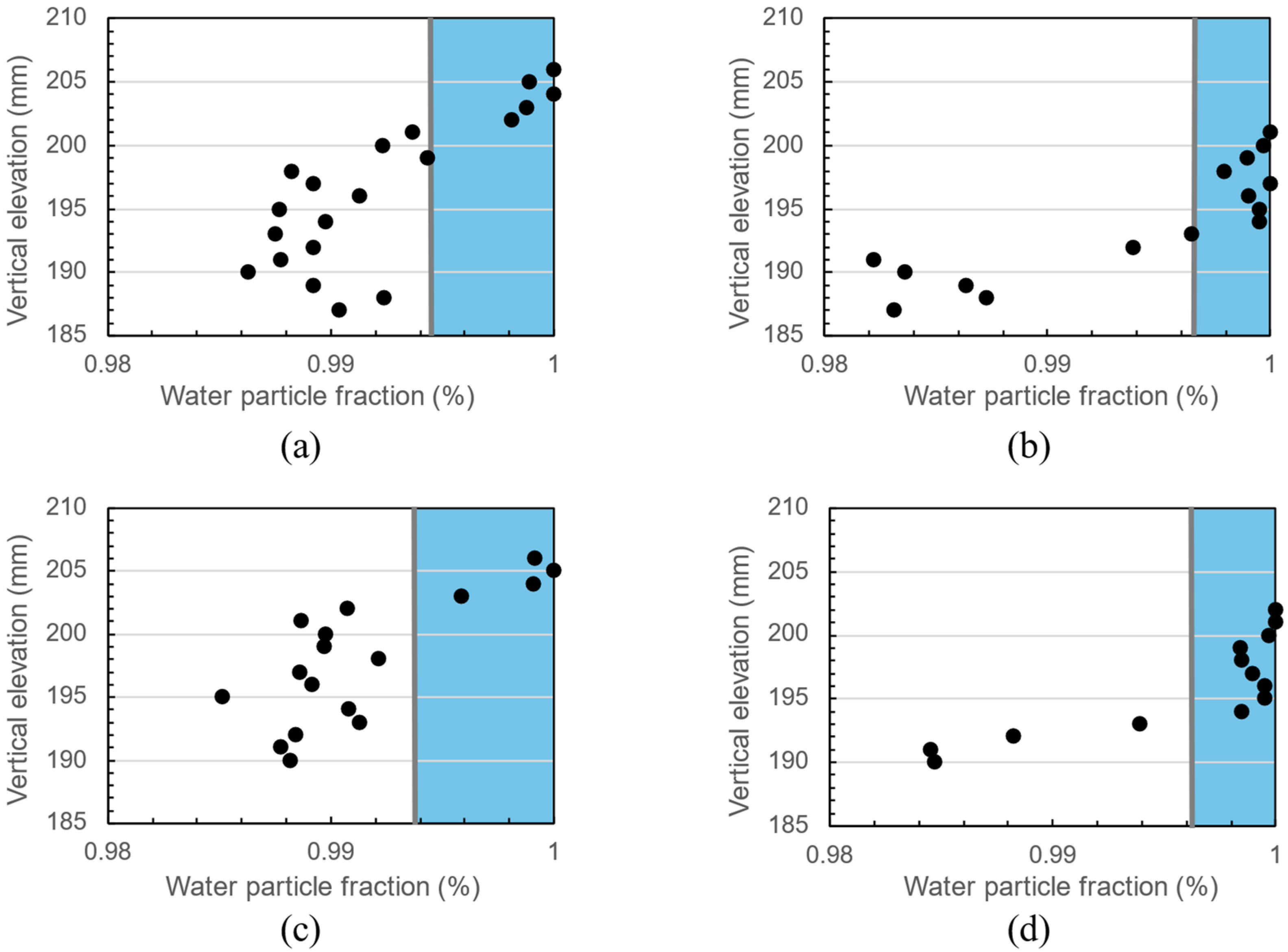
4.3.2. Bleeding Behavior Simulation
4.4. Rheological Parameter Evolution
5. Discussion
5.1. Experimental–Numerical Correlation
5.2. Effect of Hydration Accelerator on Rheological Development
- Providing additional calcium ions that accelerate silicate phase dissolution;
- Creating nucleation sites for C-S-H precipitation;
- Modifying the calcium/silicate ratio in the pore solution;
- Interacting with sulfate phases to regulate aluminate reactions.
5.3. Time-Dependent Viscosity and Phase Stability
5.4. Practical Applications and Engineering Implications
- Sequential mixing of multiple batches with staggered preparation times;
- Use of compatible retarding admixtures to counterbalance acceleration effects;
- Two-component systems with separate storage and mixing at point of placement;
- Chilled water usage to slow reaction kinetics under warm ambient conditions.
5.5. Model Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ministry of Land, Infrastructure, Transport and Tourism. Infrastructure Maintenance in Japan: Current Status and Future Challenges; MLIT: Tokyo, Japan, 2022. Available online: https://www.mlit.go.jp/en/statistics/content/001586035.pdf (accessed on 16 June 2025).
- Ministry of Land, Infrastructure, Transport and Tourism. Roads in Japan 2023; MLIT: Tokyo, Japan, 2023. Available online: https://www.mlit.go.jp/road/road_e/pdf/Road2023web.pdf (accessed on 16 June 2025).
- Ministry of the Environment, Japan. Construction Material Recycling Law; Ministry of the Environment: Tokyo, Japan, 2001. Available online: https://www.env.go.jp/content/900452889.pdf (accessed on 16 June 2025).
- Nakajima, S.; Arikawa, S.; Koga, J.; Futaki, M. The state of deconstruction in Japan. In CIB Publication 300: Deconstruction and Materials Reuse; International Council for Research and Innovation in Building and Construction: Rotterdam, The Netherlands, 2005; pp. 113–126. Available online: https://www.irbnet.de/daten/iconda/CIB1297.pdf (accessed on 16 June 2025).
- Inazumi, S. Technical challenges and innovations in existing pile extraction and associated borehole backfilling in Japan. Case Stud. Constr. Mater. 2024, 20, e03111. [Google Scholar] [CrossRef]
- Olutoge, F.A. Study of Causes of Foundation Failures. Project List 2009. Available online: https://projectlist.com.ng/project-material-on-study-causes-foundation-failures (accessed on 16 June 2025).
- Mathern, A.; Magnusson, J. Lessons learned from the construction, inspection, and defect assessment of reinforced concrete foundations for wind turbines. Appl. Sci. 2022, 12, 1443. [Google Scholar] [CrossRef]
- Wu, Y.; Fu, J.; Ni, P.; Shen, S. Engineering properties of novel vertical cutoff wall backfills composed of MgO-activated GGBS, bentonite, and polyacrylamide cellulose. Materials 2023, 16, 4971. [Google Scholar] [CrossRef]
- Ryan, C.R.; Day, S.R.; McLeod, D.W. Long-distance grouting, materials and methods. In Proceedings of the Grouting Conference 2003, New Orleans, LA, USA, 10–12 February 2003; Geo-Solutions: Pittsburgh, PA, USA, 2003; pp. 1–22. [Google Scholar]
- U.S. Environmental Protection Agency. Slurry Trench Construction for Pollution Migration Control (EPA/540/S-97/504); U.S. EPA: Washington, DC, USA, 2000.
- Yin, S.H.; Yan, Z.P. The effect of coarse aggregate on the bleeding and mechanical properties of cemented paste backfill. J. Cent. South Univ. 2023, 30, 555–567. [Google Scholar] [CrossRef]
- Inazumi, S.; Kuwahara, S. Numerical simulation of backfilling behavior of boreholes. Results Eng. 2024, 21, 101907. [Google Scholar] [CrossRef]
- Inazumi, S.; Shiina, M.; Nakao, K. Aeration curing for recycling construction-generated sludge and its effect of immobilizing carbon dioxide. Case Stud. Constr. Mater. 2024, 20, e02704. [Google Scholar] [CrossRef]
- Wang, Y.; Qi, T.; Xu, C.; Gong, J. Rheological properties and permeation grouting reinforcement effect of cement-bentonite slurry. Buildings 2025, 15, 744. [Google Scholar] [CrossRef]
- Sun, H.; Jiang, Y.; Zhang, Y.; Jiang, L. A review of constitutive models for non-Newtonian fluids. Fract. Calc. Appl. Anal. 2024, 27, 1483–1526. [Google Scholar] [CrossRef]
- Liang, W.; Fang, H.; Yin, Z.Y.; Zhao, J. A mortar segment-to-segment frictional contact approach in material point method. Comput. Methods Appl. Mech. Eng. 2024, 431, 117294. [Google Scholar] [CrossRef]
- Kondo, M.; Koshizuka, S. Improvement of stability in moving particle semi-implicit method. Int. J. Numer. Methods Fluids 2011, 65, 638–654. [Google Scholar] [CrossRef]
- Shakya, S.; Inazumi, S. Applicability of numerical simulation by particle method to unconfined compression tests on geomaterials. Civ. Eng. J. 2024, 10, 1–19. [Google Scholar] [CrossRef]
- Dev, K.L.; Kumar, D.R.; Wipulanusat, W. Performance evaluation of pond ash-enhanced flowable fill for plastic concrete cutoff walls in earthen dams using advanced machine learning models. Arab. J. Sci. Eng. 2025; in press. [Google Scholar] [CrossRef]
- Sharma, A.; Gupta, S.; Husain, M.N.; Chaudhary, S. Factors affecting the rheology of cement-based composites: A review. J. Am. Ceram. Soc. 2025, 108, e20429. [Google Scholar] [CrossRef]
- Nagaraju, T.V.; Ravindran, G. Ground Improvement Techniques for Sustainable Engineering; Bentham Science Publishers: Sharjah, United Arab Emirates, 2025. [Google Scholar]
- Shigematsu, Y.; Inazumi, S.; Hashimoto, R.; Yamauchi, H. Experimental study on properties of liquefied stabilized soil produced with different types of solidifiers and thickeners. Case Stud. Constr. Mater. 2023, 19, e02407. [Google Scholar] [CrossRef]
- Chen, M.; Liu, B.; Li, L.; Cao, L.; Huang, Y.; Wang, S.; Zhao, P.; Li, Y. Rheological parameters, thixotropy and creep of 3D-printed calcium sulfoaluminate cement composites modified by bentonite. Compos. B Eng. 2020, 186, 107821. [Google Scholar] [CrossRef]
- Strnadel, B.; Ma, M.; He, X.; Tan, H.; Wang, Y.; Su, Y.; Zhang, H. A comparative study on concrete slurry waste: Performance optimization from the wet-milling process. Mater. Struct. 2021, 54, 184. [Google Scholar] [CrossRef]
- Nontananandh, S.; Kuwahara, S.; Shishido, K.; Inazumi, S. Influence of perforated soils on installation of new piles. Appl. Sci. 2022, 12, 7712. [Google Scholar] [CrossRef]
- Inazumi, S.; Tanaka, S.; Komaki, T.; Kuwahara, S. Evaluation of effect of insertion of casing by rotation on existing piles. Geotech. Res. 2021, 8, 25–37. [Google Scholar] [CrossRef]
- Weijie, Z.; Yuanlin, Y.; Chenghao, C.; Pengfei, P.; Yue, G.; Yixiang, W. Experimental study on stability and hydration process of ultra-fine cement-based slurry. Powder Technol. 2025, 459, 121012. [Google Scholar] [CrossRef]
- Gaurina-Međimurec, N.; Pašić, B.; Mijić, P.; Medved, I. Drilling fluid and cement slurry design for naturally fractured reservoirs. Appl. Sci. 2021, 11, 767. [Google Scholar] [CrossRef]
- Altay, B.N.; Lewis, C.L. Rheological characterization. In Standardized Procedures and Protocols for Starch. Methods and Protocols in Food Science; Bangar, S.P., Ed.; Humana: New York, NY, USA, 2024. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Zhou, A.; Liu, R.; Duan, S.; Wang, M. Influence of the bleeding characteristic on density and rheology in cement slurry. Constr. Build. Mater. 2021, 269, 121316. [Google Scholar] [CrossRef]
- Ji, Y.; Pott, U.; Mezhov, A.; Rößler, C.; Stephan, D. Modelling and experimental study on static yield stress evolution and structural build-up of cement paste in early stage of cement hydration. Cem. Concr. Res. 2025, 187, 107710. [Google Scholar] [CrossRef]
- Elgeti, S.; Sauerland, H. Deforming fluid domains within the finite element method: Five mesh-based tracking methods in comparison. Arch. Comput. Methods Eng. 2016, 23, 323–361. [Google Scholar] [CrossRef]
- Koshizuka, S.; Shibata, K.; Kondo, M.; Matsunaga, T. Moving Particle Semi-Implicit Method: A Meshfree Particle Method for Fluid Dynamics; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Xu, Z.; Li, Z.; Jiang, F. The applicability of SPH and MPS methods to numerical flow simulation of fresh cementitious materials. Constr. Build. Mater. 2021, 274, 121736. [Google Scholar] [CrossRef]
- Weng, Y.; Lu, B.; Li, M.; Liu, Z.; Tan, M.J.; Qian, S. Empirical models to predict rheological properties of fiber reinforced cementitious composites for 3D printing. Constr. Build. Mater. 2018, 189, 676–685. [Google Scholar] [CrossRef]
- Liu, C.; Qian, R.; Liu, Z.; Liu, G.; Zhang, Y. Multi-scale modelling of thermal conductivity of phase change material/recycled cement paste incorporated cement-based composite material. Mater. Des. 2020, 191, 108646. [Google Scholar] [CrossRef]
- Mangal, D.; Jha, A.; Dabiri, D.; Jamali, S. Data-driven techniques in rheology: Developments, challenges and perspective. Curr. Opin. Colloid Interface Sci. 2024, 67, 101873. [Google Scholar] [CrossRef]
- Fareh, F.; Demers, V.; Demarquette, N.R.; Turenne, S.; Scalzo, O. Influence of segregation on rheological properties of wax-based feedstocks. Powder Technol. 2017, 320, 273–284. [Google Scholar] [CrossRef]
- ASTM C305-20; Standard Practice for Mechanical Mixing of Hydraulic Cement Pastes and Mortars of Plastic Consistency. ASTM International: West Conshohocken, PA, USA, 2020.
- Japan Society of Civil Engineers. JSCE-F 522: Test Method for Bleeding Rate and Expansion Rate of Injected Mortar of Prepacked Concrete (Polyethylene Bag Method); JSCE: Tokyo, Japan, 2017. [Google Scholar]
- Sharma, A.K.; Sivapullaiah, P.V. Ground granulated blast furnace slag amended fly ash as an expansive soil stabilizer. Soils Found. 2016, 56, 205–212. [Google Scholar] [CrossRef]
- Inazumi, S.; Hashimoto, R.; Aizawa, E.; Kuwahara, S.; Shishido, K. Applicability of waste silica-based additive with surfactant-type liquid thickener as borehole filler. J. Mater. Cycles Waste Manage. 2023, 25, 3776–3790. [Google Scholar] [CrossRef]
- Sonebi, M.; Abdalqader, A.; Fayyad, T.; Perrot, A.; Bai, Y. Optimisation of rheological parameters, induced bleeding, permeability and mechanical properties of supersulfated cement grouts. Constr. Build. Mater. 2020, 262, 120078. [Google Scholar] [CrossRef]
- Duan, G.; Koshizuka, S.; Yamaji, A.; Chen, B.; Li, X.; Tamai, T. An accurate and stable multiphase moving particle semi-implicit method based on a corrective matrix for all particle interaction models. Int. J. Numer. Methods Eng. 2018, 115, 1287–1314. [Google Scholar] [CrossRef]
- Kuwano, J.; Katagiri, M.; Kita, K.; Nakano, M.; Kuwano, R. A review of Japanese standards for laboratory shear tests. In Advanced Laboratory Stress-Strain Testing of Geomaterials; Routledge: London, UK, 2018; pp. 53–64. [Google Scholar]
- Ai, D.; Lin, C.; Zhu, H. Embedded piezoelectric transducers based early-age hydration monitoring of cement concrete added with accelerator/retarder admixtures. J. Intell. Mater. Syst. Struct. 2021, 32, 847–866. [Google Scholar] [CrossRef]
- Long, K.; Li, B.; Ma, J.; Liu, H.; Li, J. Ecological risk analysis of leakage caused by coal-based solid waste backfill slurry bleeding: An experimental study. J. Clean Prod. 2025, 486, 144993. [Google Scholar] [CrossRef]
- de Miranda, L.R.; Marchesini, F.H.; Lesage, K.; De Schutter, G. The evolution of the rheological behavior of hydrating cement systems: Combining constitutive modeling with rheometry, calorimetry and mechanical analyses. Cem. Concr. Res. 2023, 164, 107046. [Google Scholar] [CrossRef]
- Huang, F.; Chen, L.; Sheng, W.; Shang, X.; Zhang, Z. Thixotropy and gelation characteristics of thermosensitive polymer nanofluids at high temperature. Colloids Surf. A Physicochem. Eng. Asp. 2025, 709, 136340. [Google Scholar] [CrossRef]
- Gurt, A.; Khonsari, M. A review of the rheological consistency of materials. Lubricants 2024, 12, 236. [Google Scholar] [CrossRef]
- Roussel, N.; Coussot, P. “Fifty-cent rheometer” for yield stress measurements: From slump to spreading flow. J. Rheol. 2005, 49, 705–718. [Google Scholar] [CrossRef]
- Bentz, D.P.; Ferraris, C.F.; Galler, M.A.; Hansen, A.S.; Guynn, J.M. Influence of particle size distributions on yield stress and viscosity of cement-fly ash pastes. Cem. Concr. Res. 2012, 42, 404–409. [Google Scholar] [CrossRef]
- Wallevik, O.H.; Wallevik, J.E. Rheology as a tool in concrete science: The use of rheographs and workability boxes. Cem. Concr. Res. 2011, 41, 1279–1288. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, Z.; Ke, G.; Dong, X. Strengthening mechanism of red mud with calcium oxide. Constr. Build. Mater. 2024, 424, 135932. [Google Scholar] [CrossRef]
- Li, J.Q.; Fan, T.H. Phase-field modeling of macroscopic freezing dynamics in a cylindrical vessel. Int. J. Heat Mass Transf. 2020, 156, 119915. [Google Scholar] [CrossRef]
- Loewinger, G.; Cui, E.; Lovinger, D.; Pereira, F. A statistical framework for analysis of trial-level temporal dynamics in fiber photometry experiments. Elife 2025, 13, RP95802. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.C.; Larrahondo, J.M.; Yeboah, N.N.N. Fate of bentonite in slag–cement–bentonite slurry trench cut-off walls for polluted sites. Environ. Geotech. 2021, 10, 319–331. [Google Scholar] [CrossRef]









| Case | Unit Content (kg/m3) | |||
|---|---|---|---|---|
| C (s.g. 3.14) | B (s.g. 2.60) | EH (s.g. 2.30) | W (s.g. 1.00) | |
| 1 | 250 | 25 | 5 | 908.85 |
| 2 | 10 | 906.65 | ||
| Case | Mixture Density (kg/m3) |
|---|---|
| 1 | 1191 |
| 2 | 1191 |
| Component | Volume Fraction (%) | Particle Color |
|---|---|---|
| Water | 91.04 | Light blue |
| Cement | 7.99 | Red |
| Bentonite | 0.97 | Yellow |
| Component | Density (kg/m3) |
|---|---|
| Water | 1000 |
| Cement | 2849 |
| Bentonite | 1093 |
| Case | Testing Intervals (min) | Flow Stoppage Time (Seconds) |
|---|---|---|
| 1 | 0, 10, 20, 30, 40, 50, 60 | 0.3–0.4 |
| 2 |
| Case | Bleeding Rate (%) | Standard Deviation (%) | Number of Replicates |
|---|---|---|---|
| 1 | 2.5 ± 0.3 | 0.3 | 3 |
| 2 | 1.5 ± 0.2 | 0.2 | 3 |
| Case | Viscosity Change with Time | Bleeding Rate (%) |
|---|---|---|
| 1 | Time-dependent | 2.43 |
| Constant | 3.98 | |
| 2 | Time-dependent | 1.94 |
| Constant | 4.46 |
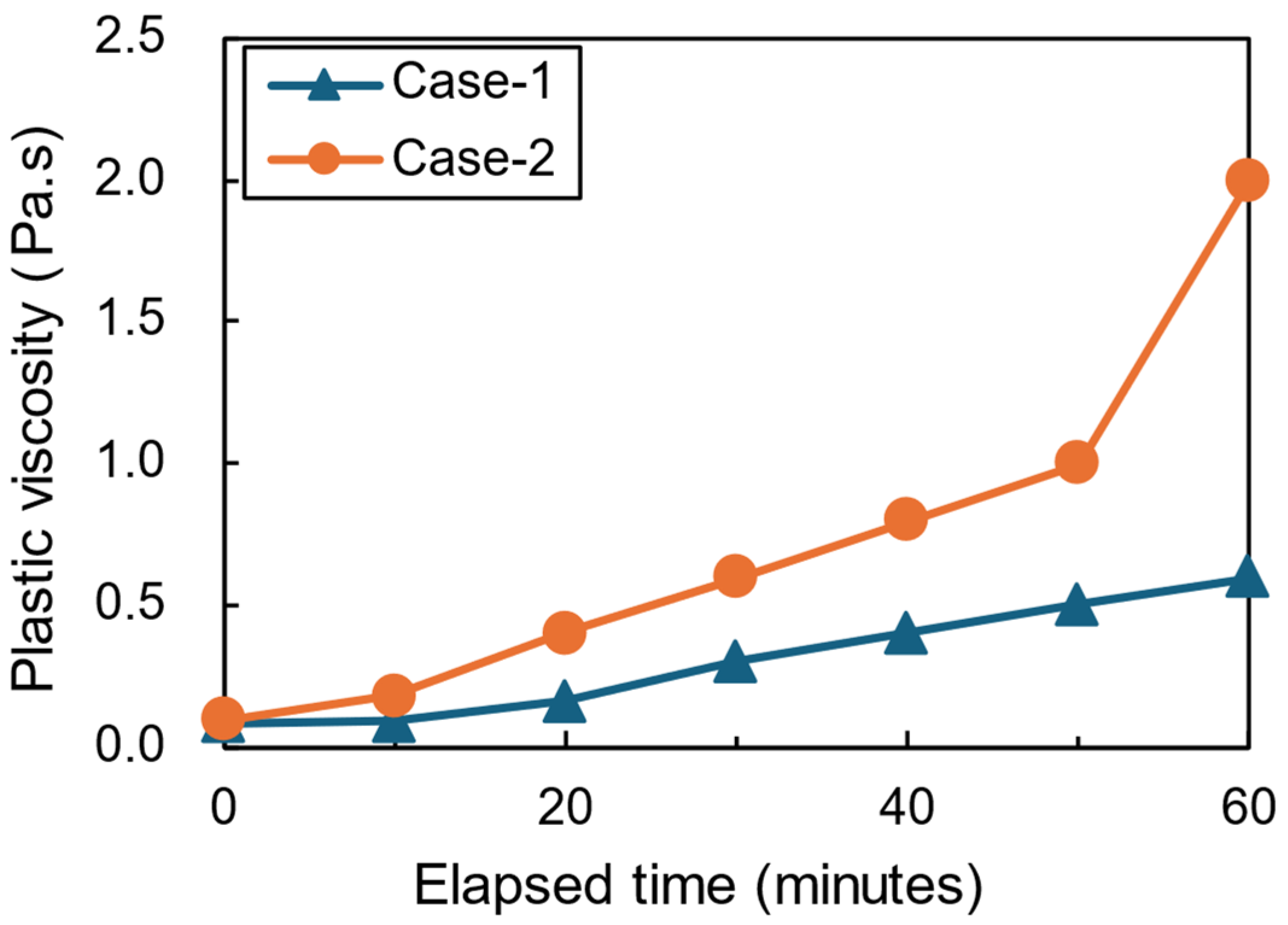
| Case | Time (min) | Yield Stress (Pa) | Plastic Viscosity (Pa·s) | Critical Shear Rate (s−1) |
|---|---|---|---|---|
| 1 | 0 | 1.8 | 0.09 | 0.05 |
| 30 | 6 | 0.3 | ||
| 60 | 29 | 0.6 | ||
| 2 | 0 | 2 | 0.18 | 0.05 |
| 30 | 30 | 0.6 | ||
| 60 | 170 | 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inazumi, S.; Tazuke, K.; Kashima, S. Time-Dependent Rheological Behavior and MPS Simulation of Cement–Bentonite Slurries with Hydration Accelerators for Borehole Backfilling Applications. J. Compos. Sci. 2025, 9, 361. https://doi.org/10.3390/jcs9070361
Inazumi S, Tazuke K, Kashima S. Time-Dependent Rheological Behavior and MPS Simulation of Cement–Bentonite Slurries with Hydration Accelerators for Borehole Backfilling Applications. Journal of Composites Science. 2025; 9(7):361. https://doi.org/10.3390/jcs9070361
Chicago/Turabian StyleInazumi, Shinya, Kazuhiko Tazuke, and Seiya Kashima. 2025. "Time-Dependent Rheological Behavior and MPS Simulation of Cement–Bentonite Slurries with Hydration Accelerators for Borehole Backfilling Applications" Journal of Composites Science 9, no. 7: 361. https://doi.org/10.3390/jcs9070361
APA StyleInazumi, S., Tazuke, K., & Kashima, S. (2025). Time-Dependent Rheological Behavior and MPS Simulation of Cement–Bentonite Slurries with Hydration Accelerators for Borehole Backfilling Applications. Journal of Composites Science, 9(7), 361. https://doi.org/10.3390/jcs9070361






