Study on Dynamic Response of Damping Type Composite Floor Slabs Considering Interlayer Interaction Influences
Abstract
1. Introduction
2. Theoretical Derivation of Vibration
2.1. Analysis Model
2.2. Free Vibration Theory
2.3. Dynamic Response Solution
2.4. Case Verification
2.4.1. Free Vibration
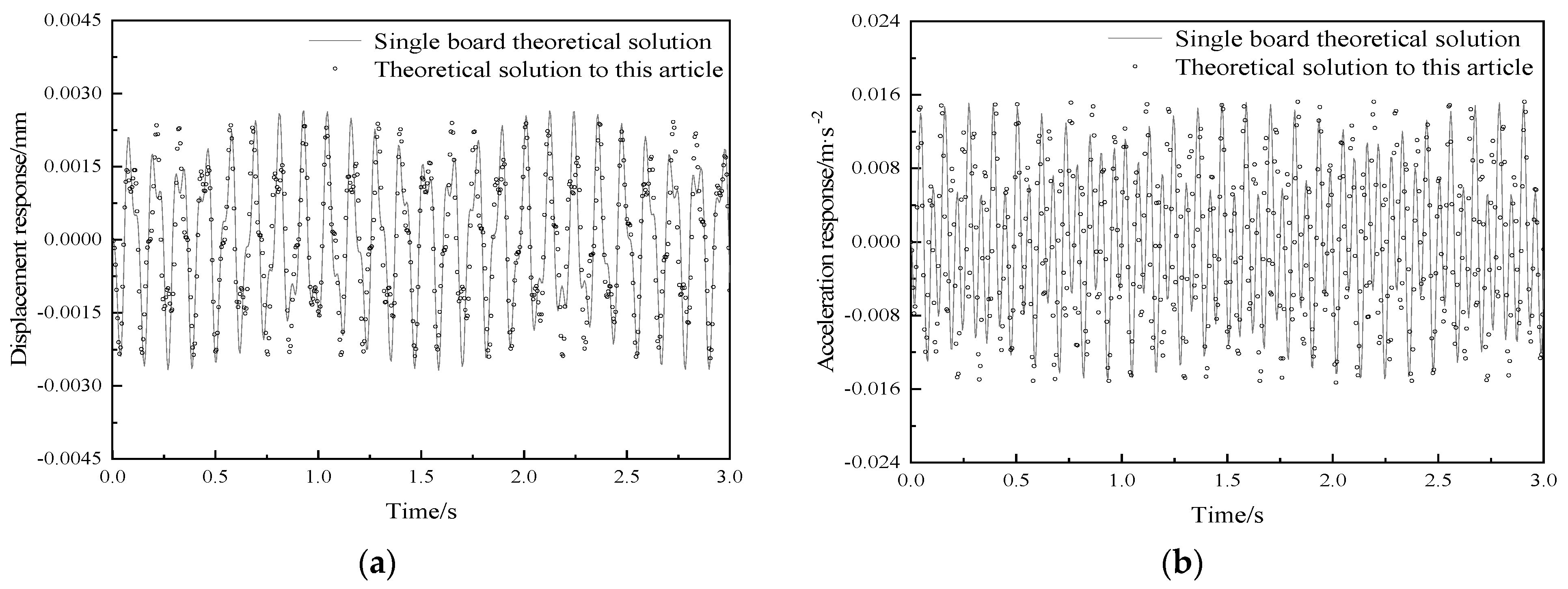
2.4.2. The Action of Fixed Loads
| M × N × R | Dimensionless Frequency | ||||
|---|---|---|---|---|---|
| f1 | f2 | f3 | f4 | f5 | |
| 5-5-3 | 12.083 | 19.706 | 35.056 | 40.451 | 45.017 |
| 6-6-4 | 12.019 | 19.604 | 34.783 | 39.692 | 44.227 |
| 6-6-5 | 12.019 | 19.604 | 34.782 | 39.691 | 44.226 |
| 6-6-6 | 12.018 | 19.599 | 34.750 | 39.688 | 44.221 |
| 7-7-6 | 12.018 | 19.599 | 34.750 | 39.688 | 44.221 |
| 8-8-6 | 12.018 | 19.599 | 34.750 | 39.688 | 44.221 |
| 9-9-6 | 12.018 | 19.599 | 34.750 | 39.688 | 44.221 |
| 10-10-6 | 12.018 | 19.599 | 34.750 | 39.688 | 44.221 |
| 12-12-6 | 12.018 | 19.599 | 34.750 | 39.688 | 44.221 |
| ANSYS | 12.018 | 19.598 | 34.725 | 39.700 | 44.244 |
| Ref. [29] | 12.017 | 19.592 | 34.714 | 39.680 | 44.211 |
| Elastic Modulus/GPa | Density/kg·m−3 | Poisson’s Ratio | Thickness/m |
|---|---|---|---|
| 30 | 2500 | 0.3 | 0.13 |
| Mass /kg | Rotational Speed of the Machine/r·min−1 | Equivalent Eccentricity/m | Load Amplitude/N | Load Amplitude/rad·s−1 |
|---|---|---|---|---|
| 180 | 500 | 0.00008 | 39.69 | 52.5 |
| Working Condition | Peak Displacement Response (10−3·mm) | Peak Acceleration Response (mm·s−2) | Peak Displacement Error | Peak Acceleration Error |
|---|---|---|---|---|
| Theoretical solution proposed in this research | 2.43 | 15.30 | −9.33% | 0.72% |
| Single board theoretical solution | 2.68 | 15.19 |
2.4.3. The Action of Moving Loads
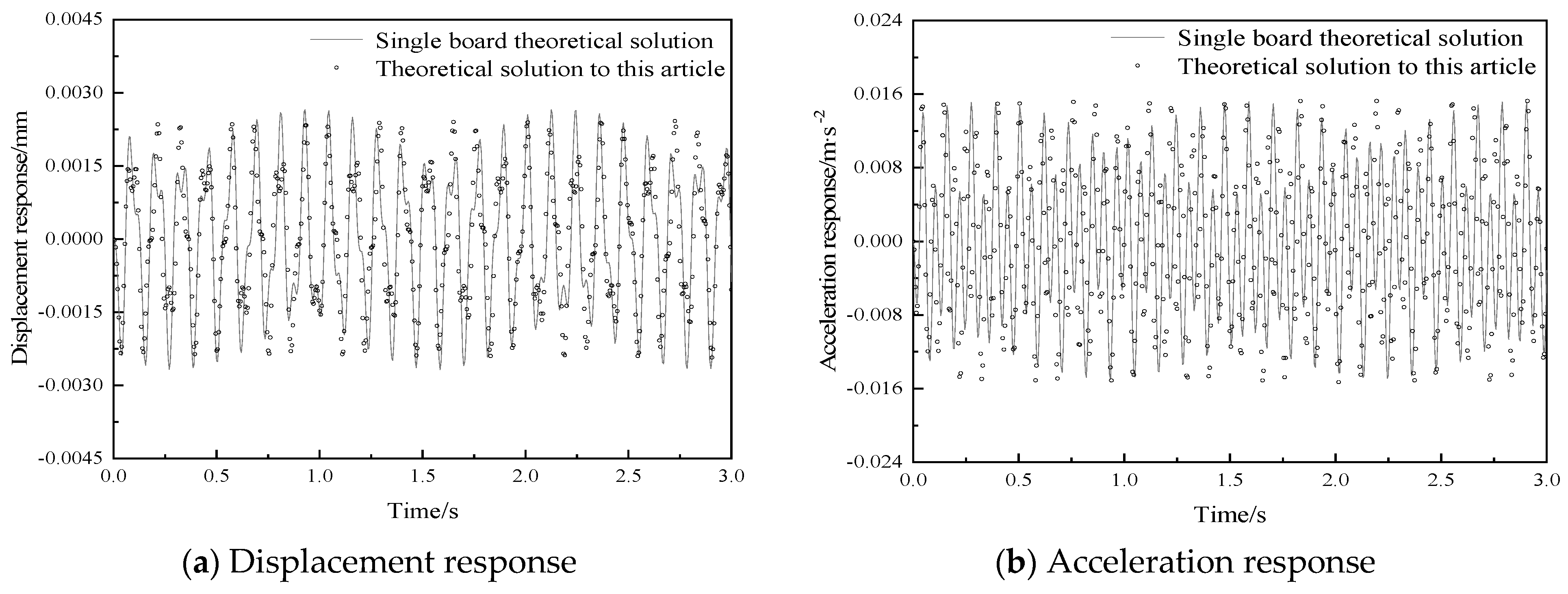
2.4.4. The Action of Multi-Source Excitation
3. Dynamic Response Parametric Analysis
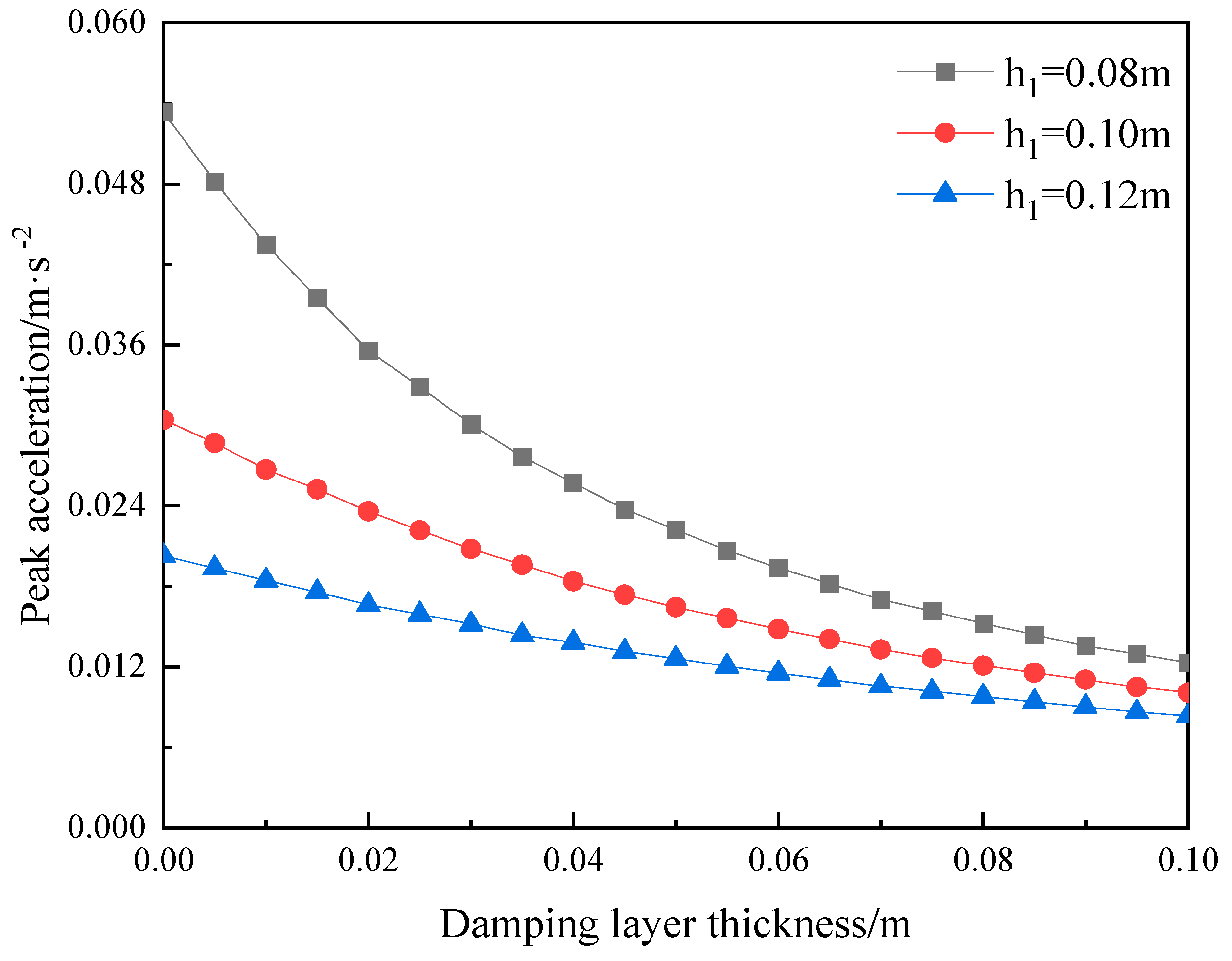
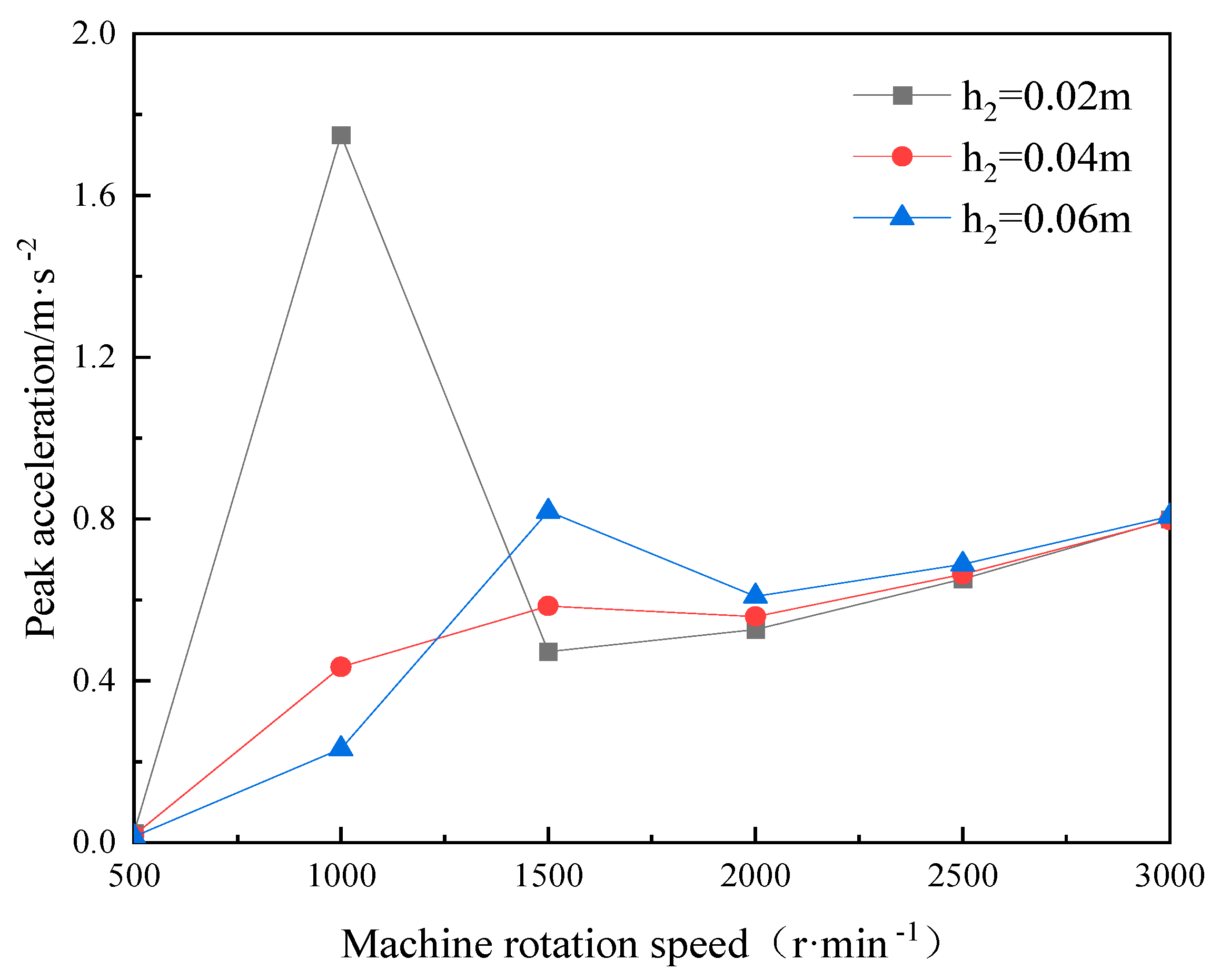
3.1. The Influence of Damping Layer Thickness
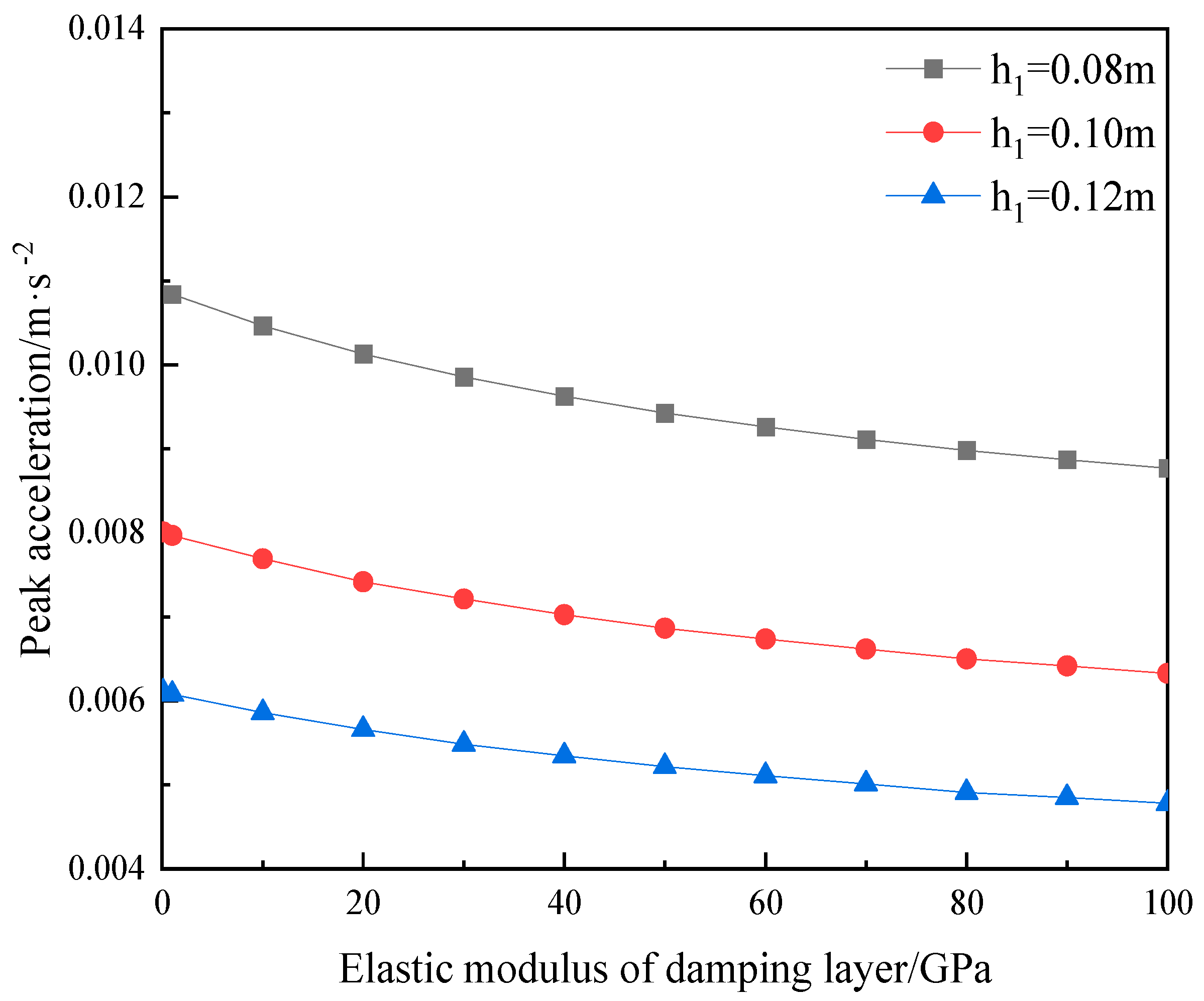
3.2. The Influence of Elastic Modulus of Damping Layer
3.3. The Influence of the Load
3.3.1. The Influence of Fixed Harmonic Loads
3.3.2. The Influence of Moving Loads
Amplitude of Moving Load
Speed of Moving Load
3.3.3. The Influence of Load Position
4. Conclusions
- Based on the theory proposed in this paper, the free vibration characteristics of the vibration damped composite floor slabs with simply supported edges on all four sides are calculated. When compared with the results in [26], the error of the dimensionless frequency is no more than 0.104%. When compared with the finite element results, the maximum error of the dimensionless frequency is no more than 0.720%. Evidently, the accuracy of the method presented in this paper is verified. Meanwhile, the matrix dimension required for the spectral method in this paper to reach the convergent value is only one-fourth of that in [26], which demonstrates the high efficiency of the calculation method proposed in this paper.
- Based on the theory presented in this paper, the dynamic response of the vibration damped composite floor slabs with four-side simply supported boundaries is calculated. Under the action of fixed loads, the results of displacement responses and acceleration responses at the center point of the composite floor slab calculated by the method proposed in this paper are basically in line with those obtained from the single-plate theoretical solution. Under the action of moving loads or multi-source excitations, the displacement and acceleration responses calculated by the method in this paper are consistently greater than those calculated by the single-plate theoretical solution.
- Based on the theory in this paper, a parametric analysis is carried out for the vibration damping composite floor slabs with four-side simply supported conditions. The impact of the thickness of the vibration reduction layer on the vertical vibration of the vibration reduction type composite floor slab is quite evident. However, after the thickness of the vibration reduction layer reaches 0.06 m, the curve of the peak acceleration of the composite floor slab declines rather gently. The peak value of the acceleration response of the floor slab exhibits exponential growth as the elastic modulus of the vibration reduction layer decreases. However, when the elastic modulus of the vibration reduction layer is greater than that of the structural layer (30 GPa), the increase in the elastic modulus has no significant impact on the peak acceleration of the building composite floor slab. The peak accelerations of the composite floor slabs with different thicknesses of the vibration reduction layer all increase linearly with the growth of the load amplitude. When the moving load moves along the short side of the floor slab, the displacement response of the floor slab is greater than that when the floor slab moves along its long side. Moreover, when the fixed load and the moving load act together, the closer the moving path of the moving load is to the fixed load, the greater the dynamic response of the floor slab near the position of the fixed load.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Xu, Z.; Lou, Y.; Chen, L. Vibration Measurement and Prediction for Foundation Slab Design of a High-tech Lab Based on in Situ Testing. Shock Vib. 2020, 2020, 8892597. [Google Scholar] [CrossRef]
- Kawrza, M.; Furtmüller, T.; Adam, C. Experimental and Numerical Modal Analysis of a Cross Laminated Timber Floor System in Different Construction States. Constr. Build. Mater. 2022, 344, 128032. [Google Scholar] [CrossRef]
- He, H.L.; Zhou, N.L.; Yuan, W.D. Evolutionary Topology Optimization of Damped Plates Based on Multiple Modes’ Damping Ratio. Chin. J. Eng. Des. 2015, 4, 351–358+364. [Google Scholar]
- Stochino, F.; Alibeigibeni, A.; Zucca, M.; Valdes, M.; Concu, G.; Simoncelli, M.; Pisani, M.A.; Bernuzzi, C. Mechanical behavior of composite slabs with recycled concrete aggregates: A preliminary study. Structures 2024, 70, 107838. [Google Scholar] [CrossRef]
- Zhai, Y.C.; Ma, J.; Sun, J.M.; Liang, S. Influence of Damping Thickness Layer Thickness on Free Vibration of Composites Sandwich Plate. Mach. Des. Manuf. 2017, 7, 78–81. [Google Scholar]
- Hu, S.W.; Zhong, R.; Qin, B.; Wang, Q.S. Vibration Characteristics of Arbitrary Straight Quadrilateral Composite Laminates. J. Harbin Eng. Univ. 2022, 43, 385–391. [Google Scholar]
- Yuan, W.H.; Li, F.L.; Lv, M. Free Vibration Characteristics of Corrugated Sandwich Plates Under Different Boundary Conditions. Acta Mater. Compos. Sin. 2020, 37, 3149–3159. [Google Scholar]
- Devin, A.; Fanning, P.; Pavic, A. Modelling Effect of Non-structural Partitions on Floor Modal Properties. Eng. Struct. 2015, 91, 58–69. [Google Scholar] [CrossRef]
- Cao, D.; Pan, Z.; Fang, Y. Dynamic Response Analysis of the Floor Structure Under Random Crowd Excitation. Shock Vib. 2024, 2024, 1451839. [Google Scholar] [CrossRef]
- Chen, S.M.; Zhang, R.; Zhang, J. Human-induced Vibration of Steel-concrete Composite Floors. Proc. Inst. Civ. Eng.-Struct. Build. 2018, 171, 50–63. [Google Scholar] [CrossRef]
- Lee, C.; Wang, Y.; Su, R.K.L.; Chen, Y.T. Fragility Analysis of Floor Micro Vibrations Induced by Internal Vehicles in High Technology Factories. Structures 2022, 40, 679–692. [Google Scholar] [CrossRef]
- Lu, H.; Zhou, L.; Fang, C.; Wu, B.T.; Gao, Z.C. An Effective Equivalent Vibration Analysis Method of the Profiled Steel Sheet-concrete Composite Floor Caused by High-speed Train. J. Vib. Eng. Technol. 2023, 11, 2361–2372. [Google Scholar] [CrossRef]
- Lu, H.X.; Zhou, L.; Liu, M.H.; Wu, B.T. Analysis of Vibration Characteristics of Different Forms of Floor Slab of Steel Frame Structures Under Train Excitation. Noise Vib. Control 2023, 43, 221–227. [Google Scholar]
- Ju, S.H.; Kuo, H.H.; Yu, S.W.; Ni, S.H. Investigation of Vibration Induced By Moving Cranes in High-tech Factories. J. Low Freq. Noise Vib. Act. Control 2019, 39, 84–97. [Google Scholar] [CrossRef]
- Li, S.J.; Zhang, T.; Wang, J.F. Analysis of Vibration Serviceability of Composite Floor with Steel Truss under Walking Load. J. Hefei Univ. Technol. (Nat. Sci.) 2021, 44, 801–805. [Google Scholar]
- Sun, L.M.; Liu, S.G.; Zhao, H.B.; Muhammad, U.; Chen, D.; Li, W.G. Dynamic Performance of Fiber-reinforced Ultra-high Toughness Cementitious Composites: A Comprehensive Review from Materials to Structural Applications. Eng. Struct. 2024, 317, 118647. [Google Scholar] [CrossRef]
- Sun, L.M.; Liu, S.G.; Kong, F.; Zhao, H.B. Analytical Solution for Dynamic Response of a Reinforced Concrete Beam with Viscoelastic Bearings Subjected to Moving Loads. Materials 2024, 17, 4491. [Google Scholar] [CrossRef]
- Kim, J.H.; Jeon, J.Y. Effects of Upper Surface Layers on the Vibration Characteristics of Floating Floor Systems in Concrete Slab Structures. J. Acoust. Soc. Am. 2012, 131, 3320. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.M.; Wang, Y.S.; Li, Q. Experimental and Analytical Study on the Vibration Performance of U-Shaped Steel-Concrete Composite Hollow Waffle Slab. Shock. Vib. 2020, 2020, 1928075. [Google Scholar] [CrossRef]
- Afzali, S.A.; Özer, C.; Bayrak, B.; Bayrak, B.; Sadid, A.J.; Celebi, O. the Bending Behavior and Free Vibration of the Concrete-Steel Composite Floors. Adv. Steel Constr. 2023, 19, 209–222. [Google Scholar]
- Guo, J.Y.; Lin, Q.L.; Di, G.Q. The Transmission Characteristics and Influence Prediction of Impulsive Vibration Caused by a Solid Metal Ball Impact in Buildings. J. Low Freq. Noise Vib. Act. Control 2023, 42, 839–850. [Google Scholar] [CrossRef]
- Tahmasebinia, F.; Yip, C.S.; Lok, C.F.; Lok, C.F.; Sun, Y.F.; Wu, J.Y. Dynamic Behavior of the Composite Steel-Concrete Beam Floor Systems under Free and Forced Vibration. Buildings 2022, 12, 320. [Google Scholar] [CrossRef]
- Lu, H.X.; Liu, M.H.; Fang, C.; Wu, B.T.; Liang, P.Y. Study on Equivalent Calculation Model of Profiled Steel Sheet and Concrete Composite Floors Based on Vibration Analysis. Noise Vib. Control 2022, 42, 212–218. [Google Scholar]
- Zhou, D.; Cheung, Y.K.; Au, F.T.K.; Lo, S.H. Three-dimensional Vibration Analysis of Thick Rectangular Plates Using Chebyshev Polynomial and Ritz Method. Int. J. Solids Struct. 2002, 39, 6339–6353. [Google Scholar] [CrossRef]
- Qu, Y.; Wu, S.; Li, H.; Meng, G. Three-dimensional Free and Transient Vibration Analysis of Composite Laminated and Sandwich Rectangular Parallelepipeds: Beams, Plates and Solids. Compos. Part B Eng. 2015, 73, 96–110. [Google Scholar] [CrossRef]
- Ye, T.G.; Jin, G.Y.; Liu, Z.G. Effects of transverse shear and normal deformations on the vibration characteristics of laminated plates. J. Vib. Shock 2019, 38, 118–125. [Google Scholar]
- JGJ/T 441-2019; Technical Standard for Vibration Comfort of Building Floor Structures. Architecture & Building Press: Beijing, China, 2020.
- He, S.G.; Tang, H.; Shi, K.R.; Jiang, Z.R.; Chen, R.Y. Evaluation of Human Comfort for Floor Vibration Induced by Equipment in High-rise Industrial Building. Spec. Struct. 2023, 40, 6–13. [Google Scholar]
- Cao, Z.Y. Vibration Theory of Plates and Shells; Railway Publishing House: Beijing, China, 1989. [Google Scholar]
- Lee, C.; Wang, Y. Assessment of Floor Micro-vibrations Induced by Moving Vehicles in High Technology Factories Using a Fragility-based Method. IOP Conf. Ser. Earth Environ. Sci. 2019, 283, 012067. [Google Scholar] [CrossRef]



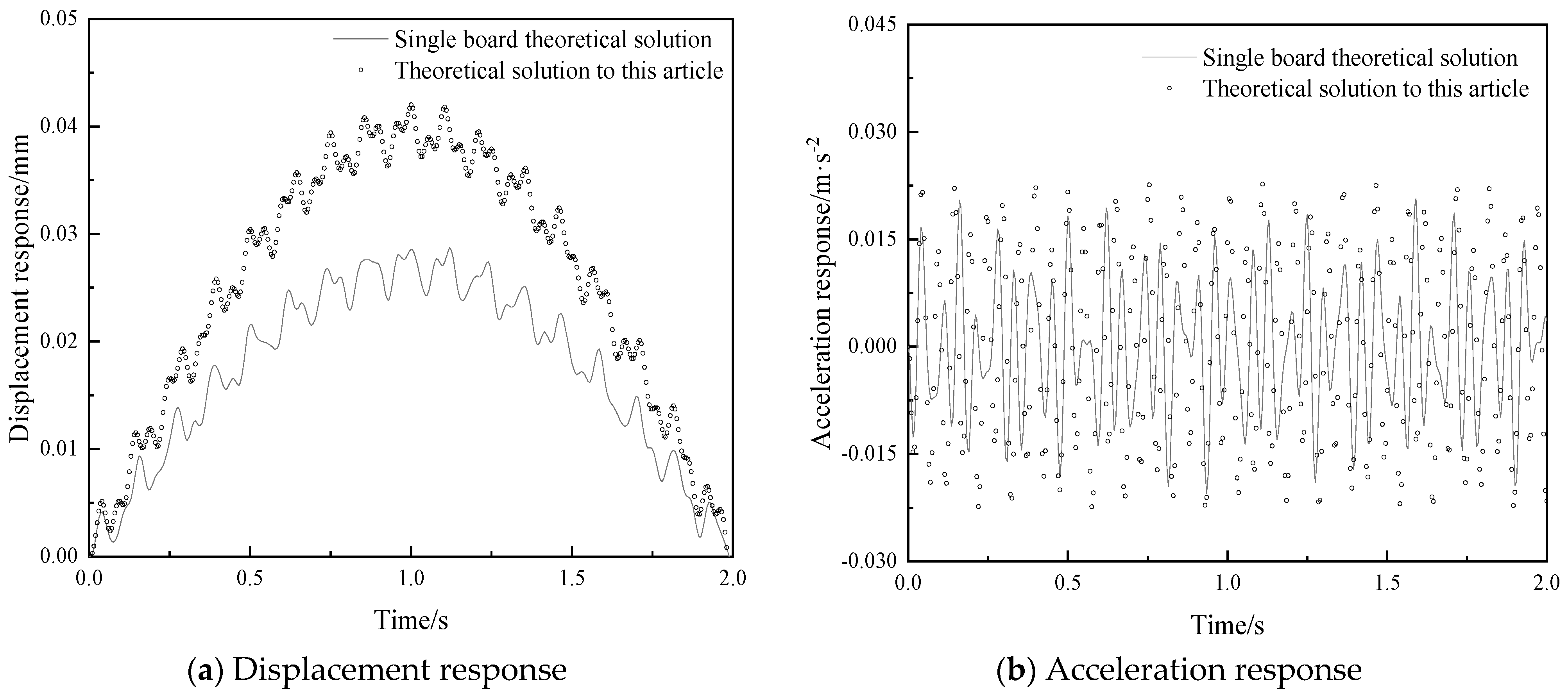




| Working Condition | Peak Displacement Response (10 −3·mm) | Peak Acceleration Response (mm·s−2) | Peak Displacement Error | Peak Acceleration Error |
|---|---|---|---|---|
| Theoretical solution proposed in this research | 40.00 | 7.52 | 47.06% | 23.29% |
| Single board theoretical solution | 27.20 | 6.10 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Moving load amplitude/N | 2000 | Fixed harmonic load amplitude/N | 39.69 |
| Moving load speed/m·s−1 | 2 | Fixed harmonic load frequency/rad·s−1 | 52.5 |
| Working Condition | Peak Displacement Response (10−3·mm) | Peak Acceleration Response (mm·s−2) | Peak Displacement Error | Peak Acceleration Error |
|---|---|---|---|---|
| Theoretical solution proposed in this research | 42.00 | 22.71 | 46.34% | 9.55% |
| Single board theoretical solution | 28.70 | 20.73 |
| Structural Layer Parameters | Value | Damping Layer Parameters | Value | Decorative Layer Parameters | Value |
|---|---|---|---|---|---|
| Elastic modulus | 30 GPa | Elastic modulus | 0.3 GPa | Elastic modulus | 27 GPa |
| Density | 2500 kg·m−3 | Density | 1000 kg·m−3 | Density | 2500 kg·m−3 |
| Poisson’s ratio | 0.3 | Poisson’s ratio | 0.2 | Poisson’s ratio | 0.2 |
| Thickness | 0.10 m | Thickness | 0.02 m | Thickness | 0.02 m |
| Machine Rotational Speed (r/min) | 500 | 1000 | 1500 | 2000 | 2500 | 3000 |
|---|---|---|---|---|---|---|
| Load frequency (rad/s) | 52.5 | 105 | 157.5 | 210 | 262.5 | 315 |
| Load amplitude (N) | 39.69 | 158.76 | 357.21 | 635.04 | 992.25 | 1428.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Xu, T.; Tian, F.; Zhang, Y.; Zhao, H.; Mahmood, A.H. Study on Dynamic Response of Damping Type Composite Floor Slabs Considering Interlayer Interaction Influences. J. Compos. Sci. 2025, 9, 57. https://doi.org/10.3390/jcs9020057
Sun L, Xu T, Tian F, Zhang Y, Zhao H, Mahmood AH. Study on Dynamic Response of Damping Type Composite Floor Slabs Considering Interlayer Interaction Influences. Journal of Composites Science. 2025; 9(2):57. https://doi.org/10.3390/jcs9020057
Chicago/Turabian StyleSun, Liangming, Ting Xu, Feng Tian, Yijie Zhang, Hanbing Zhao, and Aziz Hasan Mahmood. 2025. "Study on Dynamic Response of Damping Type Composite Floor Slabs Considering Interlayer Interaction Influences" Journal of Composites Science 9, no. 2: 57. https://doi.org/10.3390/jcs9020057
APA StyleSun, L., Xu, T., Tian, F., Zhang, Y., Zhao, H., & Mahmood, A. H. (2025). Study on Dynamic Response of Damping Type Composite Floor Slabs Considering Interlayer Interaction Influences. Journal of Composites Science, 9(2), 57. https://doi.org/10.3390/jcs9020057






