Enhanced FDM Printing Accuracy in Low-Carbon Production Mode Using RSM-NSGA-II and Entropy Weight TOPSIS Method

Abstract

Compared to traditional processes, fused deposition modeling 3D printing can manufacture parts of various shapes without the need for additional equipment, moulds, fixtures, or other tools. Its excellent characteristics have been widely applied in many industries. However, balancing product quality with low-carbon production has always been a pressing issue for 3D printing companies to address. To improve the stability of 3D printing in terms of part size accuracy and sustainable development, an orthogonal experimental design method, RSM-NSGA-II, and an entropy weight TOPSIS method were employed to optimise the factors affecting size accuracy and carbon emissions. The layer height, nozzle temperature, filling density, first layer height, and printing pattern were selected as factor variables, and the circular runout tolerance value and carbon emissions of printed parts were set as optimisation objectives. An L18 orthogonal experimental design was established. The influence of process parameters on quality indicators and the optimal combination of process parameters were analysed through range calculation. In addition, the NSGA-II-based optimisation model was constructed using the experimental design method in response surface methodology, and combined with the entropy weight TOPSIS method, to determine the optimal FDM 3D printing process parameter scheme with the best comprehensive performance. The results indicate that the response surface model established in this paper has good adaptability. When the layer height is 0.2 mm, the nozzle temperature is 243 °C, the filling density is 70%, and the first layer height is 0.15 mm, the circular runout tolerance value and carbon emissions are reduced by 64.29% and 53.45% respectively, compared to the original values. This study provides a theoretical basis and technical support for optimising the FDM manufacturing process in low-carbon and environmentally friendly production.

1. Introduction

Climate change has become one of the most critical and urgent environmental challenges of this century, posing a significant threat to human survival and socio-economic activities. Given the increasing tension between the need to address climate change and the necessity of economic development, adopting a balanced approach to these issues remains a crucial consideration in global climate governance [1,2,3]. We must address this challenge in depth and rigorously to promote sustainable solutions. It is urgent to reduce carbon emissions during the manufacturing process to implement sustainable development strategies [4,5,6].

Additive manufacturing is undergoing a noteworthy transformation from prototype development to mass production. This technology has several advantages, including design flexibility, efficient material utilization, and the ability to customize solutions [7,8]. The global additive manufacturing market shows strong growth potential, with a compound annual growth rate exceeding 20%. The forecast suggests that by 2030, this number may exceed $100 billion, indicating a promising future for this innovative field [9]. In addition, the share of industrial-grade applications is expected to expand, especially in high-end manufacturing and rapid maintenance scenarios, which is crucial for improving operational efficiency. FDM has attracted attention due to its cost-effectiveness, user friendliness, and material diversity [10,11]. Looking ahead, the integration of sustainable materials and hybrid manufacturing systems is expected to enhance the importance of FDM in promoting sustainable manufacturing practices and distributed production, thereby supporting economic and environmental goals [12]. AM is a new manufacturing technology that utilizes computer-aided design data to deposit materials layer by layer, thereby manufacturing solid objects. This method is in sharp contrast to traditional subtractive manufacturing techniques, which involve removing material from the blank [13,14,15]. The “bottom-up” approach of additive manufacturing offers significant advantages, including shortened manufacturing cycles and reduced production costs, making it an ideal solution for rapidly producing small batches, customized components, and complex geometries. Currently, additive manufacturing has been effectively applied in various fields. Additive manufacturing is positioned as a key force for the sustainable development of the manufacturing industry. Among numerous additive manufacturing technologies, fused deposition modeling is one of the most widely used methods [16,17,18].

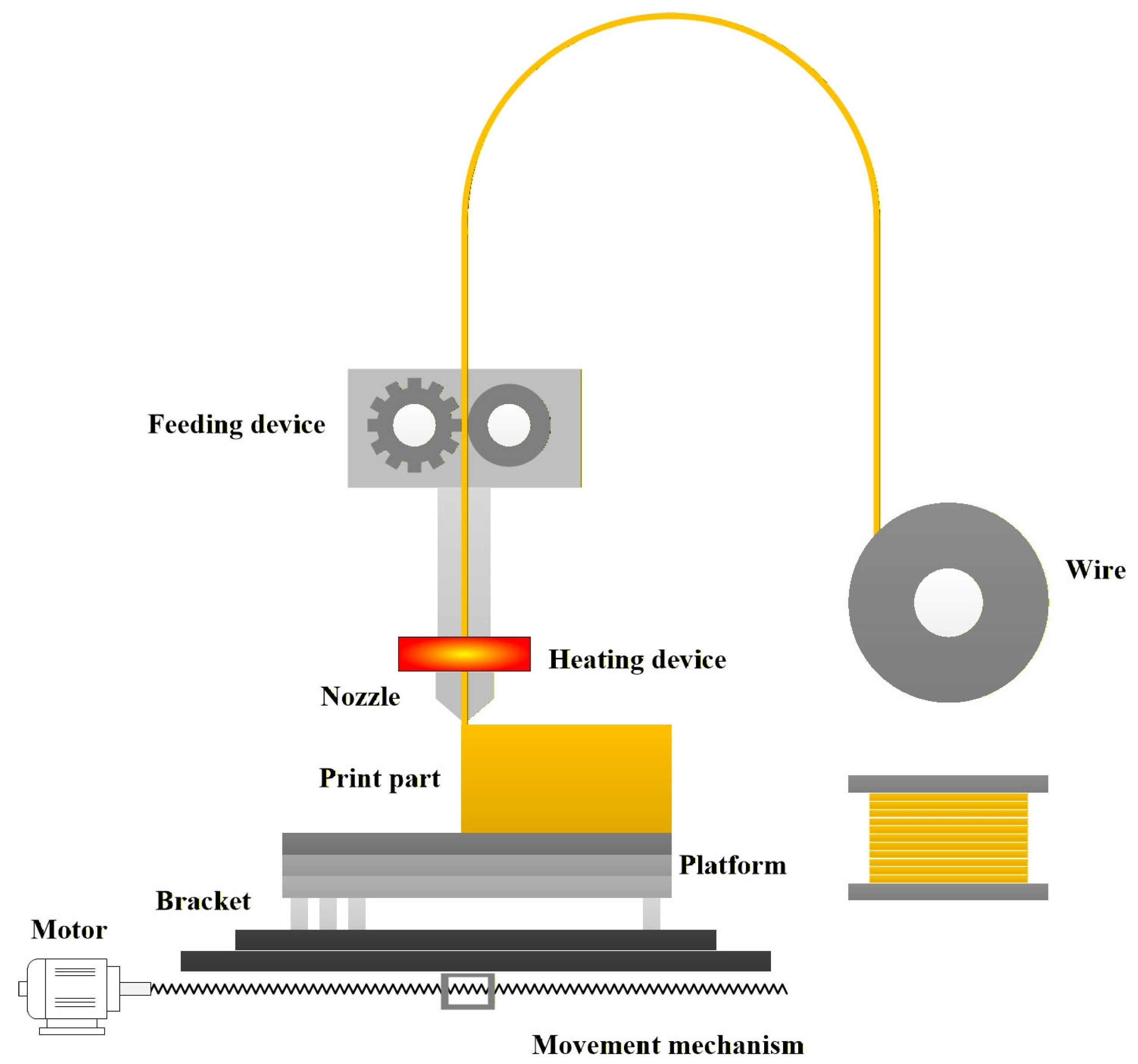
FDM 3D printing technology is a digital manufacturing technique that produces three-dimensional entities by stacking materials layer by layer, enabling the rapid transformation of designs into physical objects and accelerating production cycles [19,20,21,22]. The schematic diagram of FDM 3D printing is shown in Figure 1. Compared with traditional manufacturing techniques, it can achieve precise material usage and reduce waste. Due to its high degree of production freedom and resource utilization, 3D printing has become a widely used manufacturing technology, with its applications in aerospace, medical, automotive, and precision manufacturing fields becoming increasingly widespread [23,24,25]. The FDM printing process can be primarily divided into three stages: feeding, melt extrusion, and deposition moulding [26,27]. Each stage is not only closely related to printing materials, but also inseparable from printing equipment and pre-printing preparation work [28].

The characteristics of FDM include its economic efficiency, simplicity of operation, compatibility with various materials, and high production efficiency. Although FDM technology has significant advantages, it also faces some challenges that may hinder its long-term effectiveness [29]. The limited dimensional accuracy, insufficient surface quality, and poor mechanical performance pose significant obstacles. Therefore, improving the quality of FDM-manufactured parts is an urgent issue that requires attention. Addressing these challenges is crucial for fully unleashing the potential of this innovative technology and advancing its application in the manufacturing industry [30]. The process parameters related to fused deposition modeling play a crucial role in determining the quality of plastic parts during layer-by-layer printing [31,32]. These parameters are interrelated and jointly affect fundamental performance indicators, including dimensional accuracy, mechanical strength, surface smoothness, and overall component durability. By setting reasonable process parameters, it is possible to improve the quality of parts significantly, meet the requirements of various specific applications, and expand the application scope of FDM technology across multiple industries [33,34].

In studies conducted by numerous scholars, Marsavina et al. [35] investigated the performance characteristics of various FDM printers in generating tensile and fracture specimens from PLA. Their analysis carefully considered several manufacturing parameters, including forming direction, structural direction, and printer type. It evaluated the influence of process parameters on the tensile and fracture properties of the specimens. The results emphasise the importance of each parameter in influencing performance outcomes, highlighting the complexity of the FDM process. The work of Daly et al. [36] demonstrated a significant contribution to the effect of different FDM printing speeds on the tensile strength of ABS specimens. Similarly, Ouazzani et al. [37] identified printing speed, layer thickness, and extrusion temperature as key variables. They attempted to analyse the influence of FDM (Fused Deposition Modeling) process parameters on the surface quality of ABS parts using Taguchi experiments. The research results indicate that layer thickness has the most significant impact on surface quality. To improve surface quality, it is recommended to implement higher scanning speeds, reduce layer thickness, and select appropriate extrusion temperatures. In addition, Yankin et al. [38] employed orthogonal experiments and finite element analysis methods to investigate the effects of internal geometry, printing speed, and nozzle diameter on the fatigue life of FDM-printed ABS and nylon. Their analysis emphasises that nylon typically has better fatigue performance than ABS.

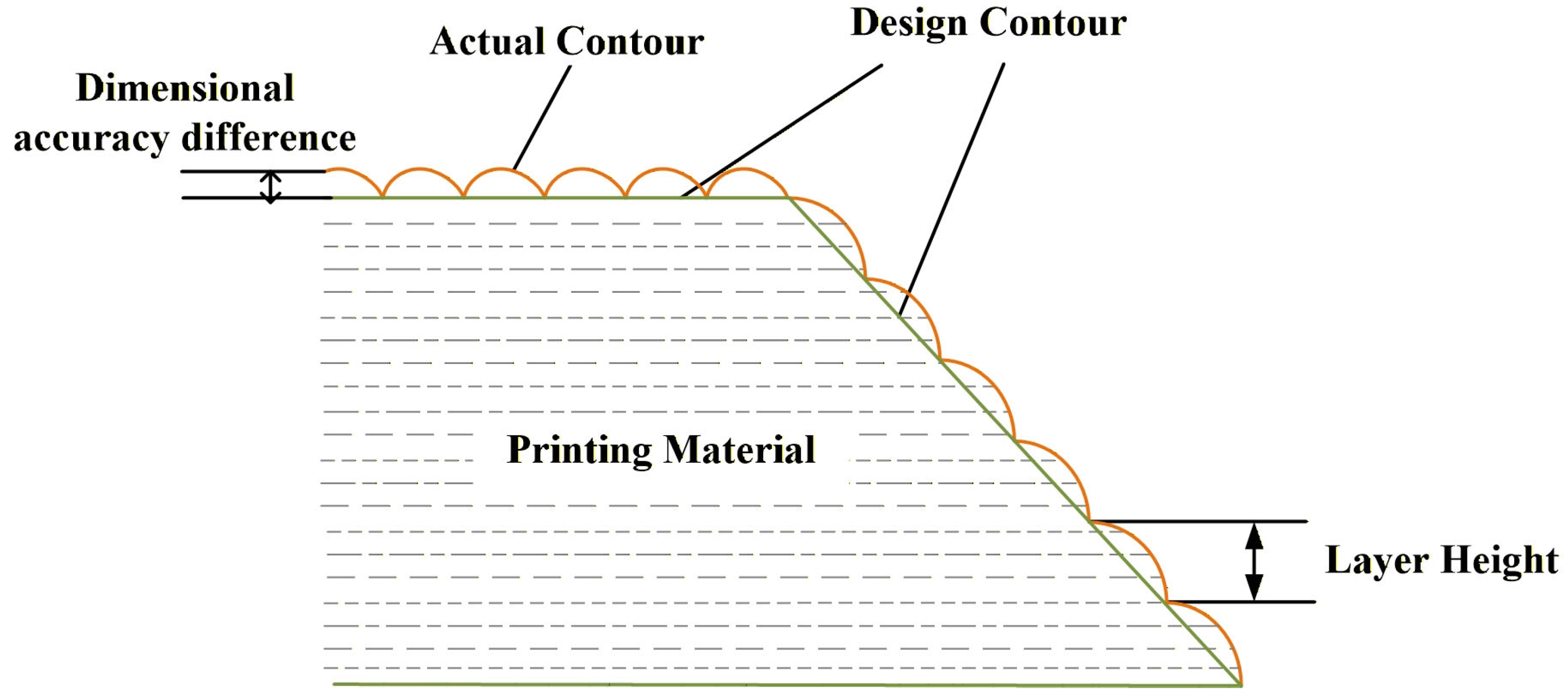
Figure 2 shows the surface microstructure of FDM melt deposition [39]. Additionally, printing platforms are typically designed with preset temperatures to enhance interlayer fusion and minimise the risk of warping. To improve the printing process, a fan cooling system is usually combined to cool the printing layer and protect the equipment [40,41].

The quality of fused deposition modeling products is closely related to the specific printing conditions used in the manufacturing process. The traditional printing configuration encompasses several key factors, including nozzle temperature, platform temperature, printing speed, grating angle, filling density, and layer thickness [42]. These factors are interrelated and collectively affect the mechanical strength and lifespan of the final product. Raising the temperature of the nozzle and platform can increase the available energy of the printing process, thereby enhancing the flowability and formability of the material [43]. This enhancement can improve the infiltration and diffusion of sedimentary filaments between layers, promote adequate interlayer adhesion, and significantly reduce the risk of warping [44]. In contrast, excessively high printing speeds may lead to incomplete and intermittent filament deposition, which can have adverse effects on the adhesion properties of the material [45]. In addition, the grating angle and filling density are key factors determining the mechanical strength of the final product. Higher filling density is usually associated with a smoother surface finish. In addition, specific porosity and filling structures help improve the damping and energy absorption capacity of printed components [46]. A significant advancement by Benié et al. [47]. The use of innovative dynamic simulations to correlate printing parameters with the diffusion, entanglement, and crystallisation phenomena of polymer chains. This method can predict the microstructure of printed products, enabling the accurate evaluation of their mechanical properties.

The dimensional accuracy of 3D-printed products is an essential indicator of whether they can be put into production use [26,29,48]. The moulding process parameters of plastic parts often affect their strength and stiffness, determining their service life [49,50]. Many researchers have conducted extensive research on improving the performance of 3D printed products [51,52,53]. Wang et al. [54] found through experiments that FDM process parameters can affect the quality of printed materials, including interlayer adhesion strength, air gap, and other factors, which are the main reasons for the different mechanical properties of printed materials. Hsueh et al. [55] found that printing angle and grating angle significantly affect the tensile properties of PLA materials. At the same time, UV curing reduces their ductility and increases brittleness. This rule was verified through experiments with different parameters. Rodríguez Panes et al. [56] conducted a comparative analysis of the tensile properties of PLA and ABS, two commonly used thermoplastic materials in FDM additive manufacturing. The study focused on investigating the influence of layer height, filling density, and layer direction on the mechanical properties of the materials. Yadav et al. [57] investigated the effects of filling density, material density, and extrusion temperature on the mechanical properties of multi-material parts printed using ME technology. In recent years, many researchers have studied the process parameters of FDM. To study the influence of process parameters on dimensional accuracy, a large number of experiments are required [58,59,60,61,62,63]. Reasonable experimental design is conducive to reducing experimental errors [64].

Fused Deposition Modeling (FDM) printing utilizes various materials, primarily derived from thermoplastic polymers. In industrial applications, commonly used materials include PEEK, PLA, acrylonitrile butadiene styrene (ABS), and polyvinyl alcohol (PVA) [65,66,67,68]. ABS has several beneficial properties, with a printing temperature range of 215 to 250 °C [68]. It has significant strength, high modulus, high temperature resistance, and UV radiation resistance, making it an ideal choice for shell applications. PVA is considered a water-soluble material, characterized by a printing temperature range of 160 to 230 °C, which allows for effective utilization at relatively low nozzle temperatures [67]. This material is mainly used as a support structure for hanging components during the printing process. On the contrary, PEEK requires a higher nozzle temperature of 340 to 440 °C [66]. It is known for its excellent mechanical properties, lubrication ability, and chemical resistance, making it an excellent choice for high-temperature environments, such as those encountered in aerospace applications and competitive racing. Polylactic acid (PLA) is a wholly organic and environmentally sustainable material recognized for its excellent biocompatibility and biodegradability [69]. It operates within a printing temperature range of 160 to 230 °C, making it highly suitable for processing. PLA is suitable for a wide range of applications, including basic applications and advanced fields such as biosensors and tissue engineering. The biological and chemical production technology of PLA has been established and demonstrated to be a low-cost, biodegradable, and recyclable material. Its utilization rate is showing a continuous upward trend, indicating that PLA has excellent potential for widespread use as a 3D printing material in the industrial field [70].

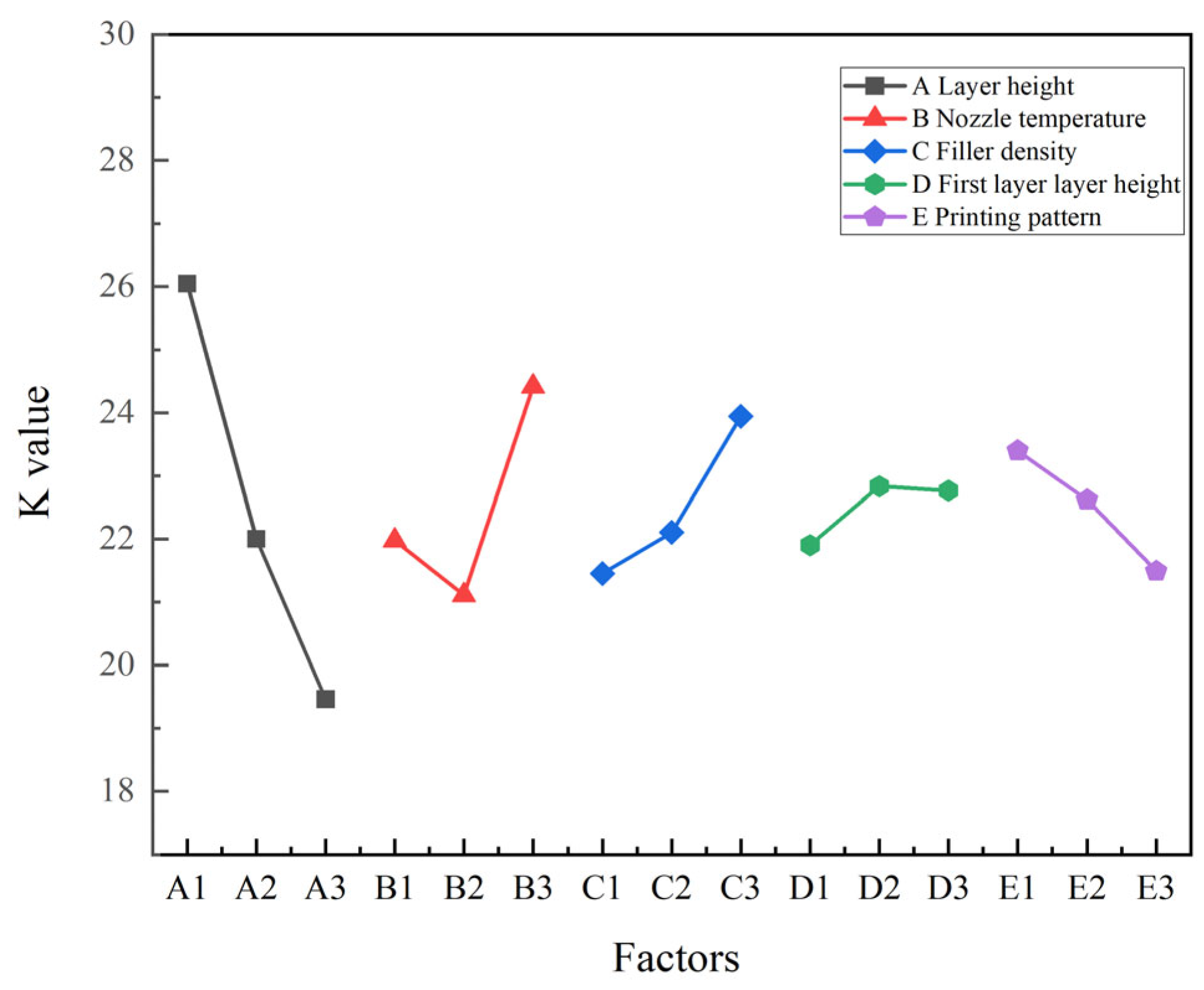
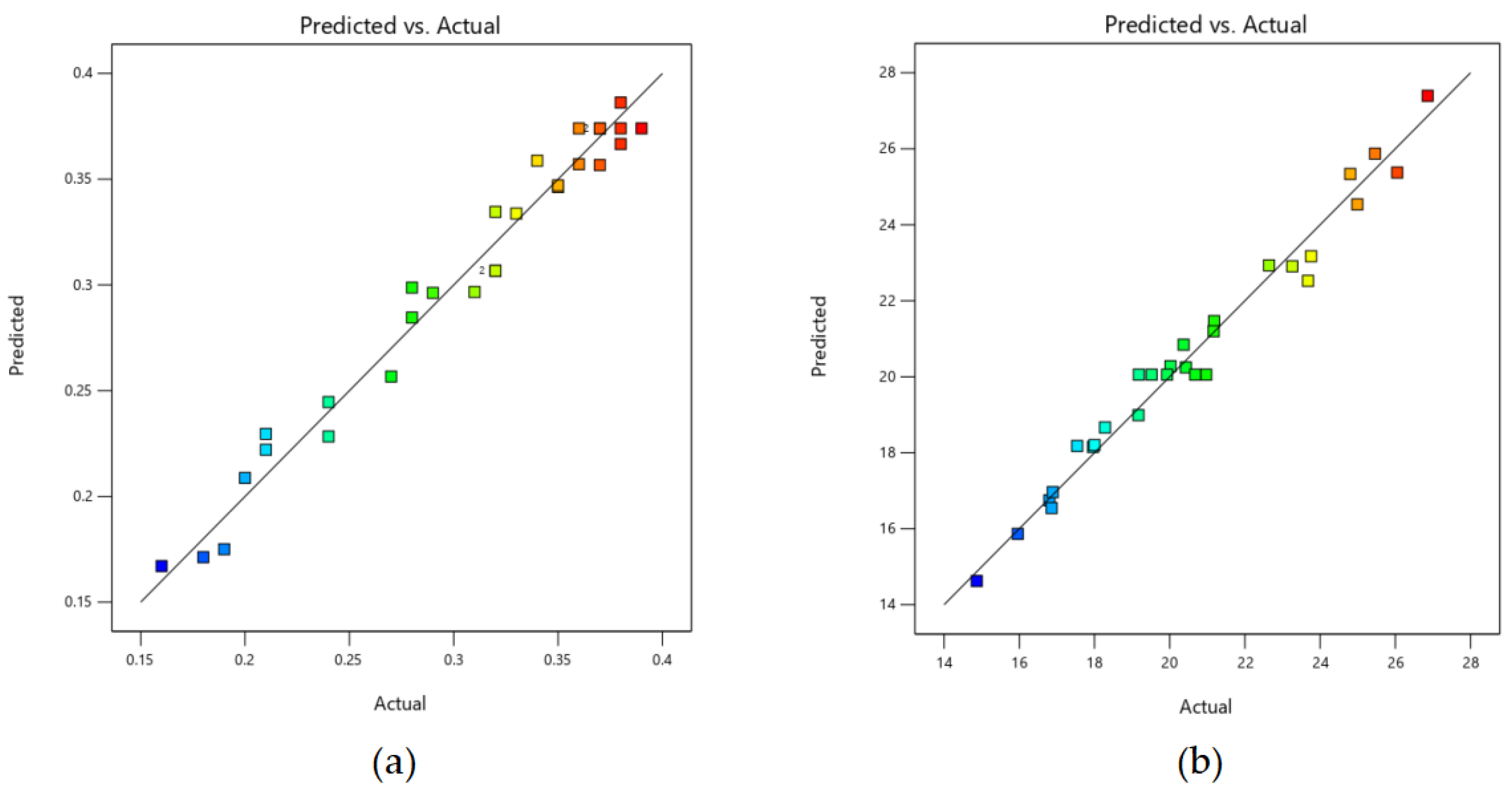
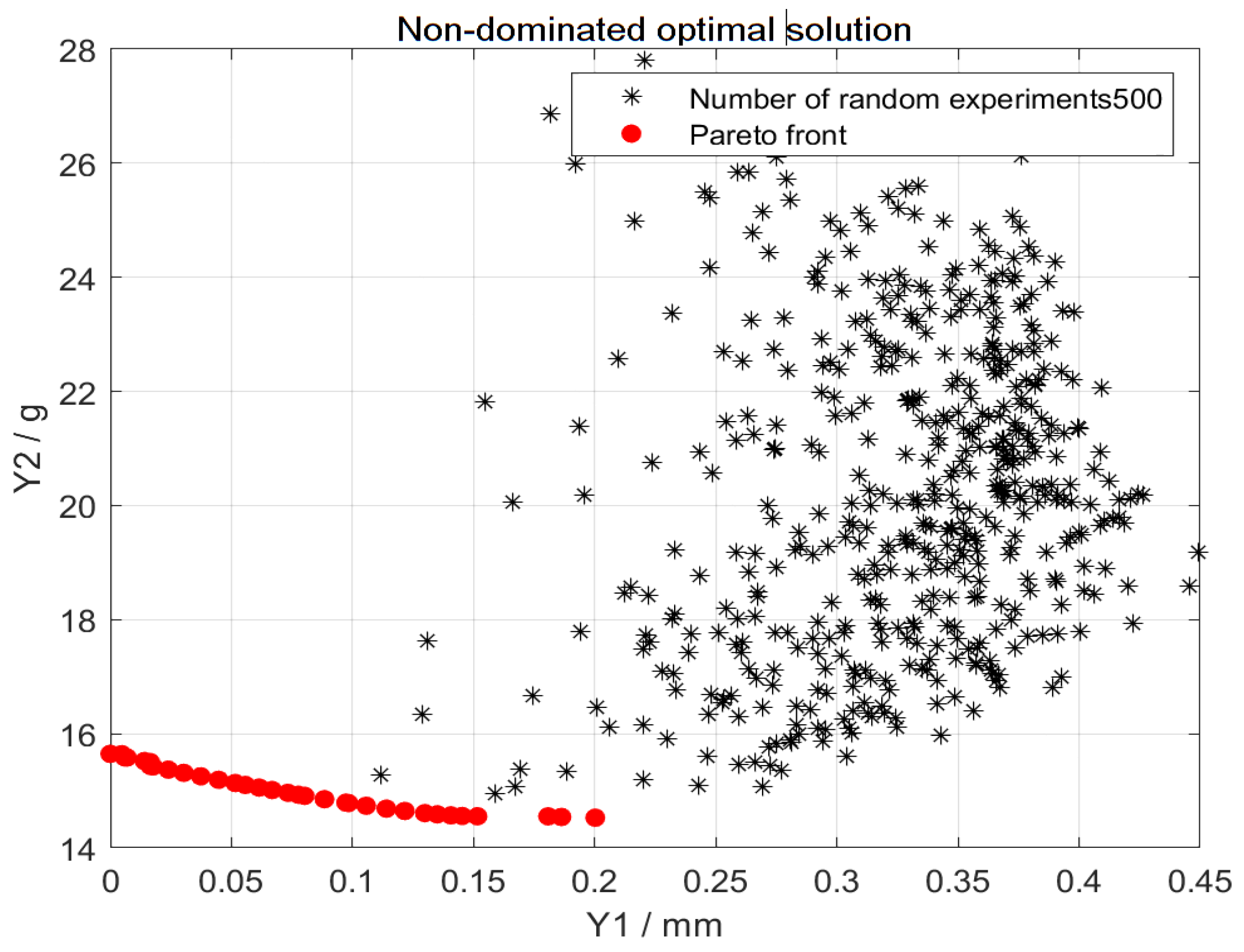
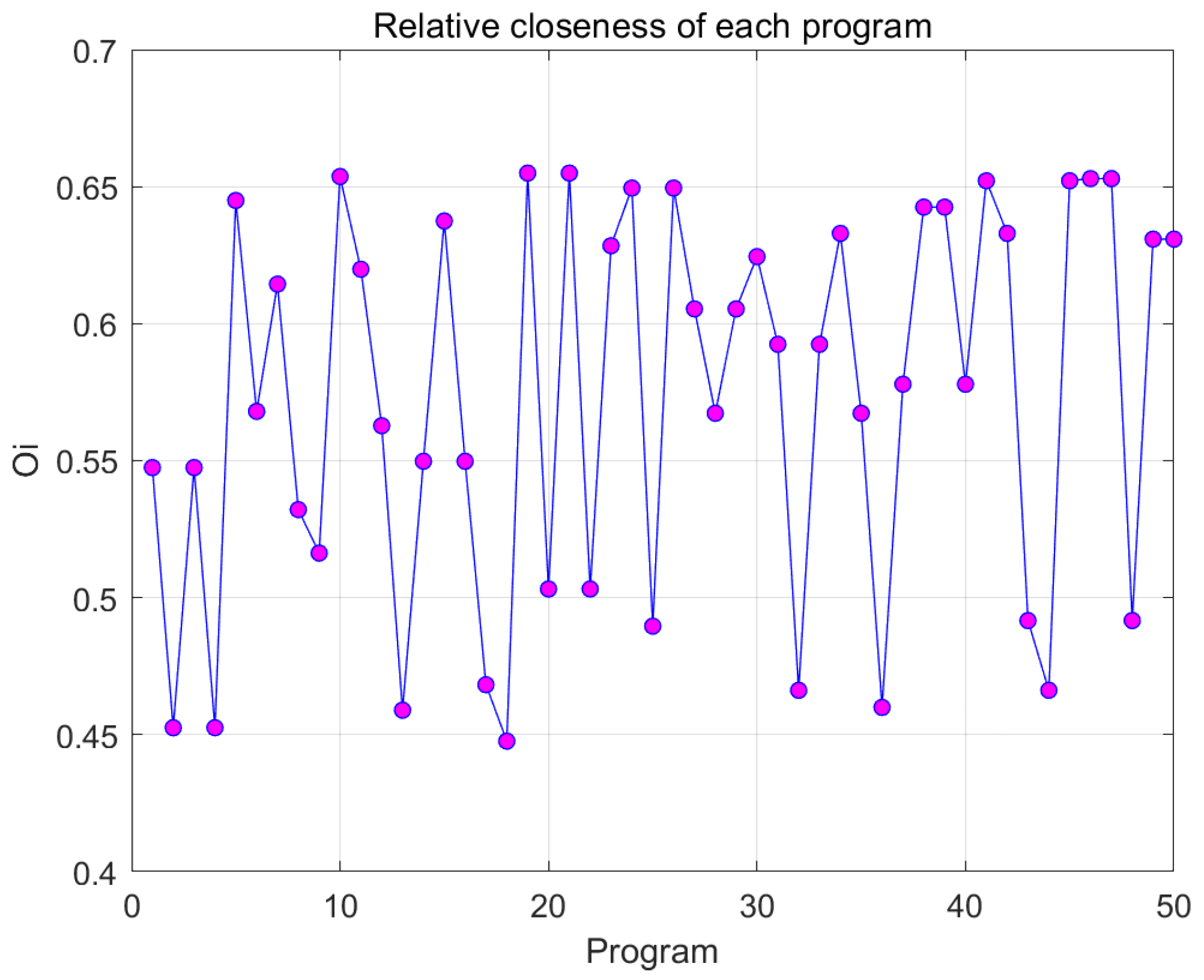
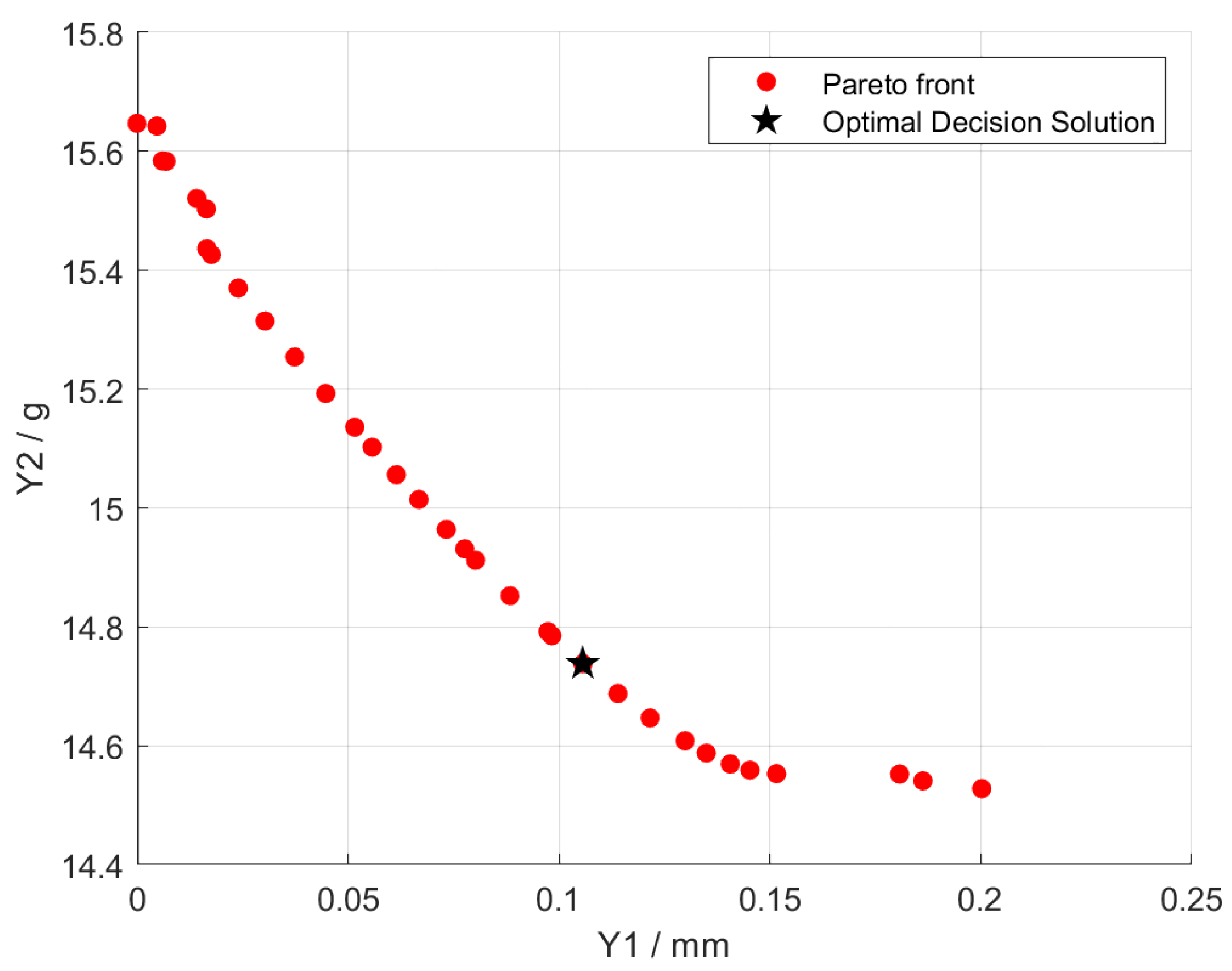
With the continuous development of modern processing technology, it is necessary to achieve sustainable development strategies, reduce carbon emissions during the manufacturing process, and enhance FDM printing accuracy. FDM printing equipment and printing moulding process parameters have become key factors in the manufacturing process. To enhance the stability of 3D printing in terms of dimensional accuracy and carbon emissions, this study optimised and analysed the influencing factors of dimensional accuracy and carbon emissions using the orthogonal experimental method, NSGA-II, and the entropy weight method. Taking layer height, nozzle temperature, filling density, first layer height, and filling pattern as factor variables, and plastic part circular runout tolerance and carbon emissions as optimization objectives, an L18 orthogonal experimental design was established to explore the effects of various parameters on tolerance and carbon emissions at different factor levels. Using the Box-Behnken experimental design method in RSM, a prediction model for jump tolerance and carbon emissions is established. The NSGA-II coupled entropy weight TOPSIS method is then employed to determine the optimal combination scheme for comprehensive performance. This article aims to develop a production system that reduces greenhouse gas emissions and improves FDM printing accuracy.

2. Materials and Methods

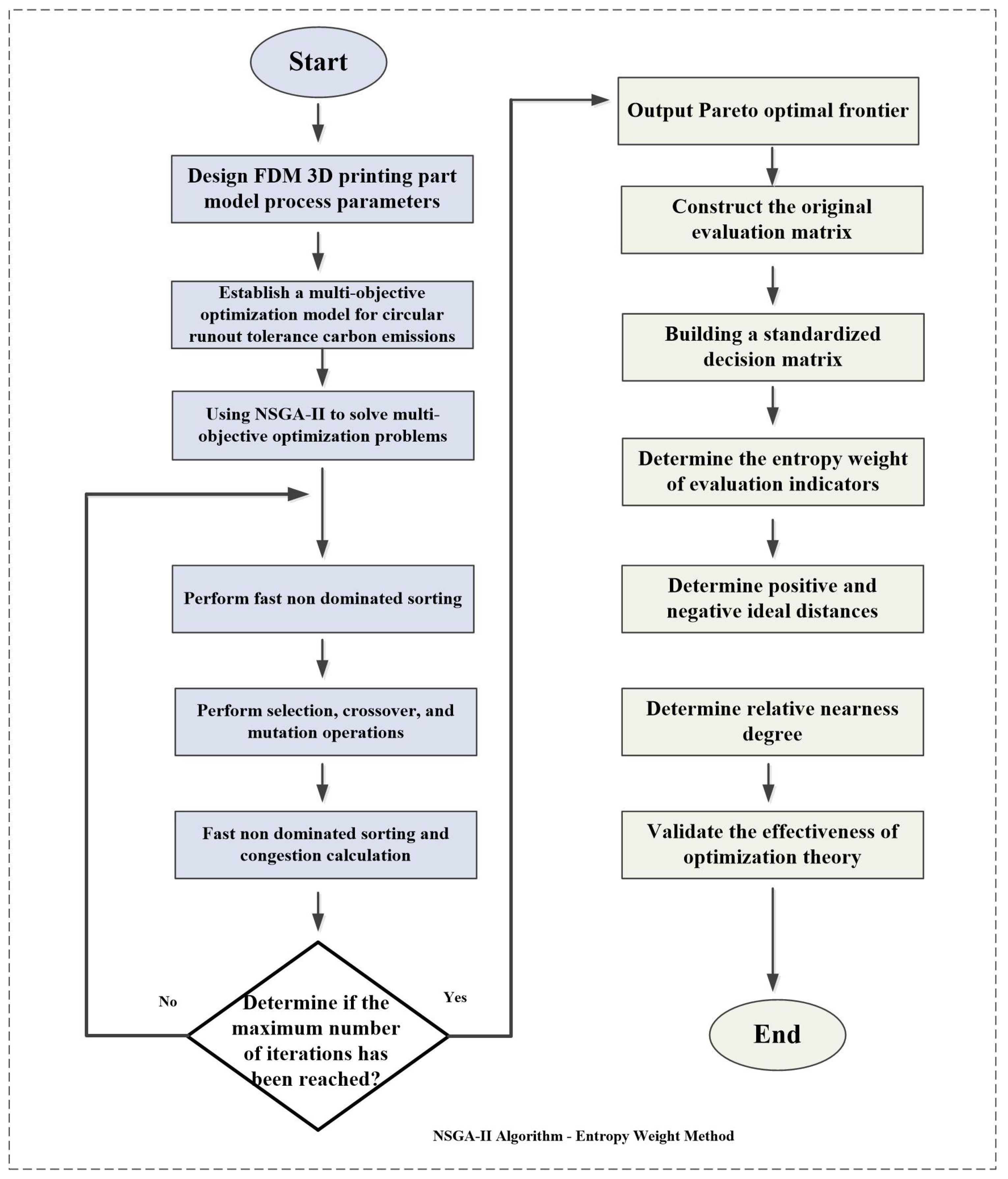
The flowchart of the specific experimental procedure is shown in Figure 3.

The experiment used Bambu Lab X1 FDM 3D printing equipment, as shown in Figure 4a. The main components of the FDM 3D printer include the bed, nozzle, and stepper motor, as shown in Figure 4b. The 3D printing consumables used are PLA with a diameter of 1.75 mm. Three-dimensional printing requires designing and printing parts in modeling software, with dimensions of 30 mm in diameter and 30 mm in height, as shown in Figure 4c, and importing files from modeling software into Bambu Studio slicing software (Linux version) in STL format. After completing the parameter settings, the automatically generated G-code file should be saved to the 3D printer for printing.

The printer has four main stages throughout the entire printing process: standby, preheating, printing, and cooling. After printing, all samples were left at room temperature for 5 h and allowed to cool naturally to a stable state. As shown in Figure 5, the FDM printed part is fixed onto the chuck fixture with a wrench, and a dial gauge is used to measure the circular runout tolerance value of the workpiece. Magnetic suction cups are used to fix the dial gauge on the spindle lifting platform and adjust the spindle lifting platform to select the appropriate measurement angle (perpendicular to the C-axis direction). As shown in Figure 6, the power consumption of each FDM 3D printed part was measured using a WiFi intelligent socket monitoring device (Shenzhen Juwei Technology Co., Ltd., Shenzhen, China), which is made of PCB/ABS, and the device model is S1BW.

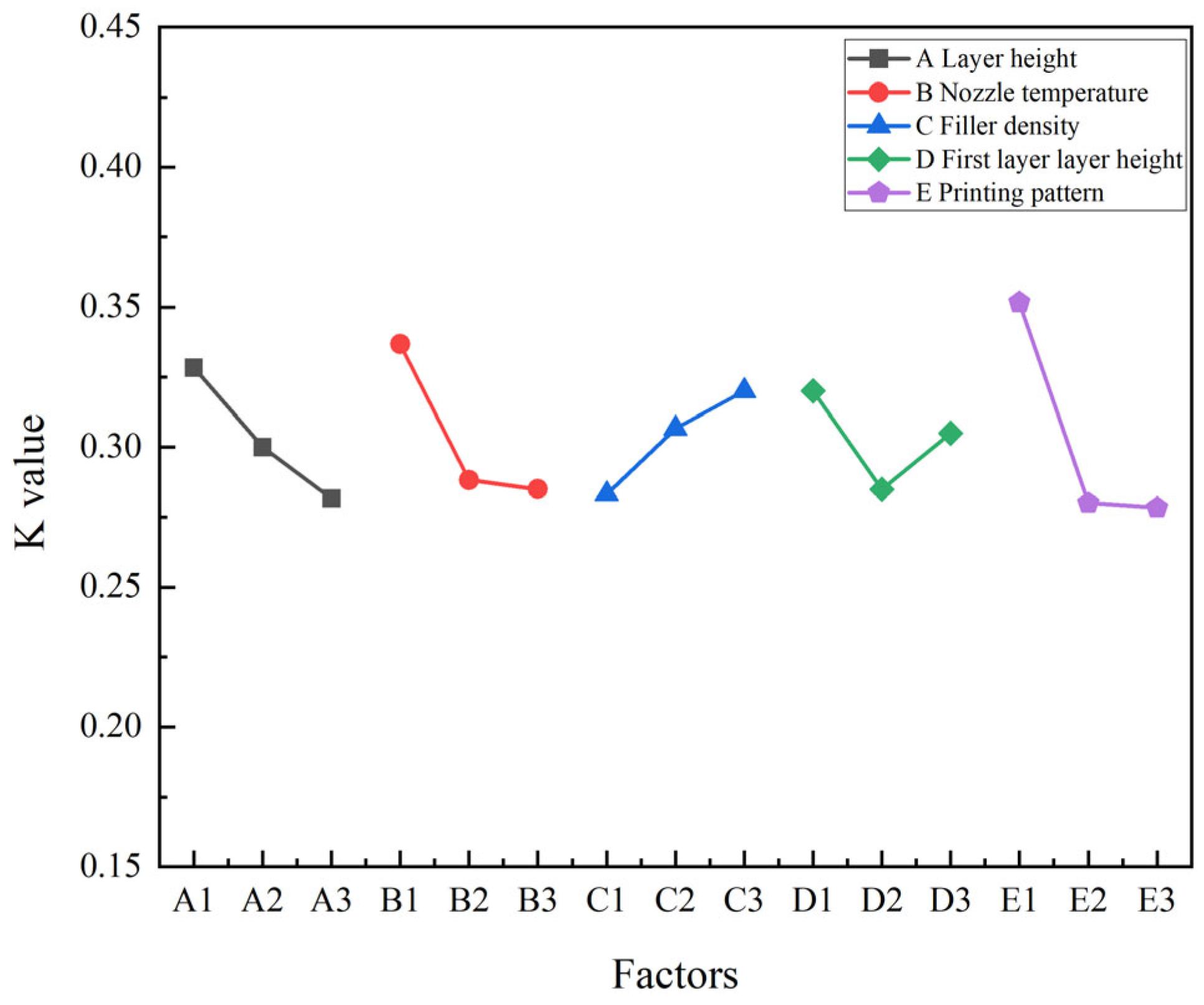
During FDM printing, uneven cooling of the printing material can lead to severe dimensional warping of the printed components. Therefore, it is necessary to choose appropriate process parameter values to maximize the dimensional accuracy and quality stability of the parts. The following factors were selected for the experiment: layer height (A), nozzle temperature (B), filling density (C), first layer layer height (D), and printing pattern (E), with circular runout tolerance value and carbon emissions as the main objectives, and an orthogonal experimental design was adopted. The orthogonal experimental factor level table is shown in

Table 1. Control factors and levels.

Factor Level	A: Layer Height	B: Nozzle Temperature	C: Filler Density	D: First Layer Height	E: Printing Pattern
1	0.10	230	70	0.05	Grid type (1)
2	0.15	240	80	0.10	Linear type (2)
3	0.20	250	90	0.15	Concentric type (3)

. The L18 orthogonal experimental platform was selected, orthogonal experiments were designed according to Table 1, and 18 experimental schemes were obtained as shown in

Table 2. The results of the orthogonal experiment.

No.	A/mm	B/°C	C/%	D/mm	E
1	0.1	230	70	0.05	1
2	0.1	240	80	0.1	2
3	0.1	250	90	0.15	3
4	0.15	230	70	0.1	2
5	0.15	240	80	0.15	3
6	0.15	250	90	0.05	1
7	0.2	230	80	0.05	3
8	0.2	240	90	0.1	1
9	0.2	250	70	0.15	2
10	0.1	230	90	0.15	2
11	0.1	240	70	0.05	3
12	0.1	250	80	0.1	1
13	0.15	230	80	0.15	1
14	0.15	240	90	0.05	2
15	0.15	250	70	0.1	3
16	0.2	230	90	0.1	3
17	0.2	240	70	0.15	1
18	0.2	250	80	0.05	2

. The actual printed sample is shown in Figure 7.

3. Results and Discussion

3.1. Analysis of Orthogonal Experiment Results

Figure 8 and Figure 9 illustrate the impact of various parameters on shrinkage depth and price at different factor levels. From the figure, it can be seen that under the principle of prioritizing circular runout tolerance, the combination of forming parameters A3-B3-C1-D2-E3 obtained using the orthogonal experimental method exhibits the smallest tolerance. The order of influence of each factor from high to low is E > B > A > C > D. Under the principle of prioritising carbon emissions, the combination of moulding parameters A3-B2-C1-D1-E3 is optimal. The order of factor influence from high to low is: A > B > C > E > D.

3.2. Analysis of Response Surface Test Results

The layer height (A), nozzle temperature (B), filling density (C), and first layer height (D) are selected as factors with print circular runout tolerance and carbon emissions as optimization objectives. The response surface experimental design method optimized the model, with three levels assigned to each factor, as shown in

Table 3. Design of the experimental factor level.

Control Factors	Level
	−1	0	1
A. Layer height/mm	0.10	0.15	0.20
B. Nozzle temperature/°C	230	240	250
C. Filler density/%	70	80	90
D. First layer layer height/mm	0.05	0.10	0.15

, using the Design Expert software (13 version) for Box–Behnken design optimization. A quadratic polynomial response surface model was established using an L29 orthogonal array, and the experimental data are shown in

Table 4. Response surface optimization, experimental design, and results.

No.	Control Factors				Quality Index
	A	B	C	D	Circular Runout Tolerance/mm	Carbon Emissions/g
1	0.15	240	90	0.05	0.18	21.18
2	0.15	240	80	0.1	0.38	19.52
3	0.15	250	80	0.15	0.35	20.37
4	0.1	230	80	0.1	0.29	25.46
5	0.15	240	90	0.15	0.38	22.64
6	0.15	230	90	0.1	0.24	23.76
7	0.15	240	80	0.1	0.39	19.93
8	0.1	240	90	0.1	0.20	26.86
9	0.15	240	80	0.1	0.37	19.18
10	0.2	240	70	0.1	0.16	14.87
11	0.2	240	90	0.1	0.34	17.54
12	0.1	250	80	0.1	0.32	24.8
13	0.15	250	70	0.1	0.19	19.17
14	0.2	250	80	0.1	0.24	16.89
15	0.1	240	80	0.15	0.37	26.05
16	0.15	230	70	0.1	0.32	18.28
17	0.15	240	70	0.05	0.28	17.96
18	0.1	240	70	0.1	0.36	23.26
19	0.15	240	70	0.15	0.21	18.00
20	0.15	240	80	0.1	0.36	20.68
21	0.1	240	80	0.05	0.32	24.99
22	0.2	240	80	0.15	0.38	16.86
23	0.15	240	80	0.1	0.37	20.97
24	0.15	250	90	0.1	0.31	23.68
25	0.15	230	80	0.05	0.28	20.43
26	0.15	230	80	0.15	0.33	21.17
27	0.2	230	80	0.1	0.35	16.80
28	0.2	240	80	0.05	0.27	15.96
29	0.15	250	80	0.05	0.21	20.02

.

Design Export software (13 version) was used to process experimental data from response surface methodology (Table 4) to investigate the effects of layer height, nozzle temperature, filling density, and first layer height on circular runout tolerance and carbon emissions. The data was fit to a polynomial model using analysis of variance (ANOVA). The variance analysis results for the response surface model, regarding circular runout tolerance and carbon emissions, are presented in

Table 5. Regression analysis of variance for circular runout tolerance.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value	Significant
Model	0.1355	14	0.0097	36.01	<0.0001	**
A	0.0012	1	0.0012	4.47	0.0530
B	0.0030	1	0.0030	11.20	0.0048
C	0.0014	1	0.0014	5.24	0.0381
D	0.0192	1	0.0192	71.46	<0.0001	**
AB	0.0049	1	0.0049	18.24	0.0008
AC	0.0289	1	0.0289	107.56	<0.0001	**
AD	0.0009	1	0.0009	3.35	0.0886
BC	0.0100	1	0.0100	37.22	<0.0001	**
BD	0.0020	1	0.0020	7.54	0.0158
CD	0.0182	1	0.0182	67.83	<0.0001
A2	0.0036	1	0.0036	13.52	0.0025
B2	0.0131	1	0.0131	48.70	<0.0001	**
C2	0.0389	1	0.0389	144.69	<0.0001	**
D2	0.0053	1	0.0053	19.84	0.0005
Residual	0.0038	14	0.0003
Lack of Fit	0.0032	10	0.0003	2.49	0.1962	ns
Pure Error	0.0005	4	0.0001
Cor Total	0.1392	28

Note: p < 0.01 is highly significant and is denoted by **, p > 0.05 is not significant and is denoted by ns. R² = 0.9730, Adj R² = 0.9460.

and

Table 6. Regression analysis of variance for carbon emissions.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value	Significant
Model	285.22	14	20.37	41.68	<0.0001	**
A	229.69	1	229.69	469.90	<0.0001	**
B	0.0784	1	0.0784	0.1604	0.6948
C	48.48	1	48.48	99.18	<0.0001	**
D	1.73	1	1.73	3.53	0.0813
AB	0.1406	1	0.1406	0.2877	0.6001
AC	0.2162	1	0.2162	0.4424	0.5168
AD	0.0064	1	0.0064	0.0131	0.9105
BC	0.2352	1	0.2352	0.4812	0.4992
BD	0.0380	1	0.0380	0.0778	0.7844
CD	0.5041	1	0.5041	1.03	0.3271
A2	2.01	1	2.01	4.10	0.0623
B2	2.47	1	2.47	5.06	0.0411
C2	0.1738	1	0.1738	0.3555	0.5606
D2	0.0069	1	0.0069	0.0141	0.9072
Residual	6.84	14	0.4888
Lack of Fit	4.55	10	0.4548	0.7926	0.6529	ns
Pure Error	2.30	4	0.5738
Cor Total	292.06	28

Note: p < 0.01 is highly significant and is denoted by **, p > 0.05 is not significant and is denoted by ns. R² = 0.9766, Adj R² = 0.9531.

. According to the results, the quadratic model has been proven to be the most significant. Equations (1) and (2) were used to calculate the regression equation model for circular runout tolerance and carbon emissions.

$$\begin{gathered} Y_{\alpha }=-19.167+5.24A+0.180017B-0.03405C-19.40667D-0.07AB+0.17AC+6AD \\ +0.0005BC+0.045BD+0.135CD-9.46667A^2-0.000449B^2-0.000774C^2-11.46667D^2 \end{gathered}$$

(1)

$$\begin{gathered} Y_{\beta }=+351.38450-205.44A-2.81443B+0.519883C+2.59D+0.375AB-0.465AC-16AD \\ -0.002425BC-0.195BD+0.71CD+222.46667A^2+0.006174B^2+0.001637C^2-13.03333D^2 \end{gathered}$$

(2)

The layer height, nozzle temperature, filling density, and first layer height are represented as A, B, C, and D, respectively. The responses of circular runout tolerance (α) and carbon emissions (β) are used for multiple regression fitting.

The significance of establishing a second-order polynomial model was demonstrated by analysing the variance of the constructed model. The smaller the p-value in the analysis of variance, the more significant the impact of the corresponding factors. When the p-values are all less than 0.05, it indicates significance, and p-values less than 0.0001 indicate extreme importance, as shown in Table 5 and Table 6. The p-values of the regression model are all less than 0.0001, indicating that the regression model has statistical significance and is highly significant. The p-values of missing fitting terms (p = 0.1962 in Table 5 and p = 0.6529 in Table 6) are all greater than 0.05, indicating that the lack of fitting terms is not significant and the model fits well.

Figure 10a,b show that the predicted values and experimental values of the response surface model are almost on a straight line. The model number is used to check and evaluate the correlation, goodness of fit, and prediction accuracy of all models. The multiple correlation coefficients R² are 0.9730 and 0.9766, respectively, which are close to 1, indicating that the response surface model established in this paper has good adaptability.

3.3. Analysis of NSGA-II Global Optimization Results

NSGA-II is a multi-objective optimisation algorithm based on the Pareto optimal solution concept, which performs multi-objective optimisation on the circular runout tolerance value and carbon emissions of printed parts. The optimisation problem function and constraint interval are shown in Formula (3).

$$\begin{gathered} \left\{\begin{array}{c}{\mathrm{Min}Y}_1 \left(X_1, X_2, X_3, X_4\right)\\ \\ {\mathrm{Min}Y}_2 \left(X_1, X_2, X_3, X_4\right)\end{array}\right. \\ \left\{\begin{array}{c}0.1 \mathrm{m}\mathrm{m}⩽X_1⩽0.2 \mathrm{m}\mathrm{m}\\ 230 °\mathrm{C}⩽X_2⩽250 °\mathrm{C}\\ 70\%⩽X_3⩽90\%\\ 0.05 \mathrm{m}\mathrm{m}⩽X_4⩽0.15 \mathrm{m}\mathrm{m}\end{array}\right. \end{gathered}$$

(3)

where Y₁/Y₂ represent the function objective value (circular runout tolerance value and carbon emissions), X₁, X₂, X₃ and X₄ are layer height, nozzle temperature, filling density, and first layer height, respectively.

Using MATLAB (2024a) software, Equation (3) is solved based on NSGA-II. The operating parameters of the algorithm are set as follows: the population size is 50, the maximum number of generations is 400, the crossover probability is 0.9, and the mutation probability is 0.1. The Pareto optimal frontier obtained by solving is shown in Figure 11. To verify the convergence of the Pareto optimal solution, 500 random experiments were conducted to validate the results of the Pareto front, as shown in Figure 12.

3.4. Analysis of the Results Obtained from the Entropy Weight TOPSIS Method

Based on the entropy weight TOPSIS method, comprehensive evaluation and decision analysis are conducted for 50 population individuals and 50 mix proportion optimisation schemes on the Pareto optimal frontier, aiming to identify the ideal solution within this frontier. The entropy weight TOPSIS method is a multi-objective comprehensive optimisation analysis method based on a dimensionless decision matrix. It introduces the concept of information entropy to determine the objective weights of indicators, calculates the Euclidean distance between the evaluated object and the idealised target, sorts based on relative closeness, and extracts the optimal solution. The steps of this method are summarised as follows:

Construct an evaluation matrix as shown in Equation (4).

$$X={\left(x_{ij}\right)}_{m\times n}=\left(\begin{array}{ccccc}{x}_{11}& x_{12}& x_{13}& \cdots & x_{1n}\\ x_{21}& x_{22}& x_{23}& \cdots & x_{2n}\\ x_{31}& x_{32}& x_{33}& \cdots & x_{3n}\\ ⋮& ⋮& ⋮& & ⋮\\ x_{m1}& x_{m2}& x_{m3}& \cdots & x_{mn}\end{array}\right)$$

(4)

where $X$ is the evaluation Matrix.

Dimensionless processing was performed on matrix X, and each indicator was normalized. The positive indicator formula is shown in Equation (5).

$$b_{ij}={\displaystyle \frac{x_{ij}-x_{j\mathrm{m}\mathrm{i}\mathrm{n}}}{x_{j\mathrm{m}\mathrm{a}\mathrm{x}}-x_{j\mathrm{m}\mathrm{i}\mathrm{n}}}}$$

(5)

The reverse indicator formula is shown in Equation (6).

$$b_{ij}={\displaystyle \frac{x_{jmax}-x_{ij}}{x_{j\mathrm{m}\mathrm{a}\mathrm{x}}-x_{j\mathrm{m}\mathrm{i}\mathrm{n}}}}$$

(6)

where $b_{ij}$ is the elements in the standardized decision matrix.

The formula for calculating entropy weight is shown in Equation (7).

$$w_j={\displaystyle \frac{1-e_j}{\sum _{j=1}^n(1-e_j)}}$$

(7)

where $w_j$ is the entropy weight for the jth evaluation metric.

The formula for calculating information entropy is shown in (8)–(10).

$$e_j=-k[\sum _{i=1}^m{f}_{ij}\ln f_{ij}]$$

(8)

$$\begin{array}{ccc}k& =& 1/\ln m\end{array}$$

(9)

$$f_{ij}=(1+b_{ij})/\sum _{i=1}^m(1+b_{ij})$$

(10)

where $e_j$ represents the information entropy of the jth evaluation metric.

The calculation formula for constructing a weighted decision matrix is shown in (11).

$$c_{ij}=w_j\times b_{ij}$$

(11)

where $c_{ij}$ is an element in the weighted decision matrix.

The formulas for determining the optimal vector and the worst vector are shown in (12).

$$\left\{\begin{array}{ll}{\mathbf{C}}^{+}= \{c_1^{+}, c_2^{+}, \cdots , c_n^{+}\}& \\ {\mathbf{C}}^{-}= \{c_1^{-}, c_2^{-}, \cdots , c_n^{-}\}& \end{array}\right.$$

(12)

where ${\mathbf{C}}^{+}$ and ${\mathbf{C}}^{-}$, respectively, represent the positive ideal solution set and the negative ideal solution set.

Using the Euclidean distance calculation formula, the formula for calculating the positive and negative ideal solution sets for each sample is shown in (13).

$$\left\{\begin{array}{ll}{D}_i^{+}=\sqrt{{{\displaystyle \sum _{j=1}^n}\left(c_{ij}^{+}-c_{ij}\right)}^2}& \\ & \\ D_i^{-}=\sqrt{{{\displaystyle \sum _{j=1}^n}\left(c_{ij}^{-}-c_{ij}\right)}^2}& \end{array}\right.$$

(13)

where $D_i^{+}$ and $D_i^{-}$ represent the distances between the i-th optimization solution and the positive and negative ideal solutions, respectively.

The relative closeness of each optimization scheme to the ideal solution is determined as shown in Formula (14).

$$O_i={\displaystyle \frac{D_i^{-}}{D_i^{-}+D_i^{+}}}$$

(14)

where $O_i$ is the relative closeness of the i-th mix proportion optimization scheme, and the closer the value is to 1, the better the evaluation effect of the scheme.

The objective weights of each evaluation index in the Pareto optimal frontier were calculated, and the results are shown in

Table 7. Information entropy and entropy weight of each evaluation index.

Evaluation Index	Information Entropy	Entropy Weight
Circular runout tolerance	0.9961	0.4059
Carbon emissions	0.9943	0.5941

.

From Figure 13, it can be seen that the 19th scheme has the highest relative closeness and is closest to the ideal solution, indicating that its comprehensive performance is the best. The optimal decision solution is shown in Figure 14. Using this scheme as the operating condition for testing, the circular runout tolerance values and carbon emissions obtained are shown in

Table 8. Verification test results.

Evaluation Index	Circular Runout Tolerance/mm	Carbon Emissions/g
Original value	0.42	32.07
Test value (Optimization)	0.15	14.93

.

According to Table 8, the experimental values decreased by 64.29% and 53.45% respectively, compared to the original values. The effectiveness and reliability of the RSM-NSGA-II coupled entropy weight TOPSIS method for multi-objective optimisation design of FDM 3D printing process parameters have been verified. This study provides a theoretical basis and technical support for optimising the FDM manufacturing process in low-carbon and environmentally friendly generation.

4. Conclusions

This article aims to develop a production system that reduces greenhouse gas emissions and improves FDM printing accuracy. The following progress conclusions were obtained through the RSM-NSGA-II coupled entropy weight TOPSIS method:

(1)

Under the principle of prioritising circular runout tolerance, the combination of forming parameters A3-B3-C1-D2-E3 obtained using the orthogonal experimental method exhibits the smallest tolerance. The order of influence of each factor from high to low is E > B > A > C > D. Under the principle of prioritising carbon emissions, the combination of moulding parameters A3-B2-C1-D1-E3 is optimal. The order of factor influence from high to low is: A > B > C > E > D.

(2)

The multiple correlation coefficients R² are 0.9730 and 0.9766, respectively, which are close to 1, indicating that the response surface model established in this paper has good adaptability.

(3)

When the layer height is 0.2 mm, the nozzle temperature is 243 °C, the filling density is 70%, and the first layer height is 0.15 mm, the circular runout tolerance value and carbon emissions are reduced by 64.29% and 53.45% respectively, compared to the original values.