The Influence of Microstructural Heterogeneities on the Thermal Response of CFRTP Composite Tapes at the Ply-Scale
Abstract
1. Introduction
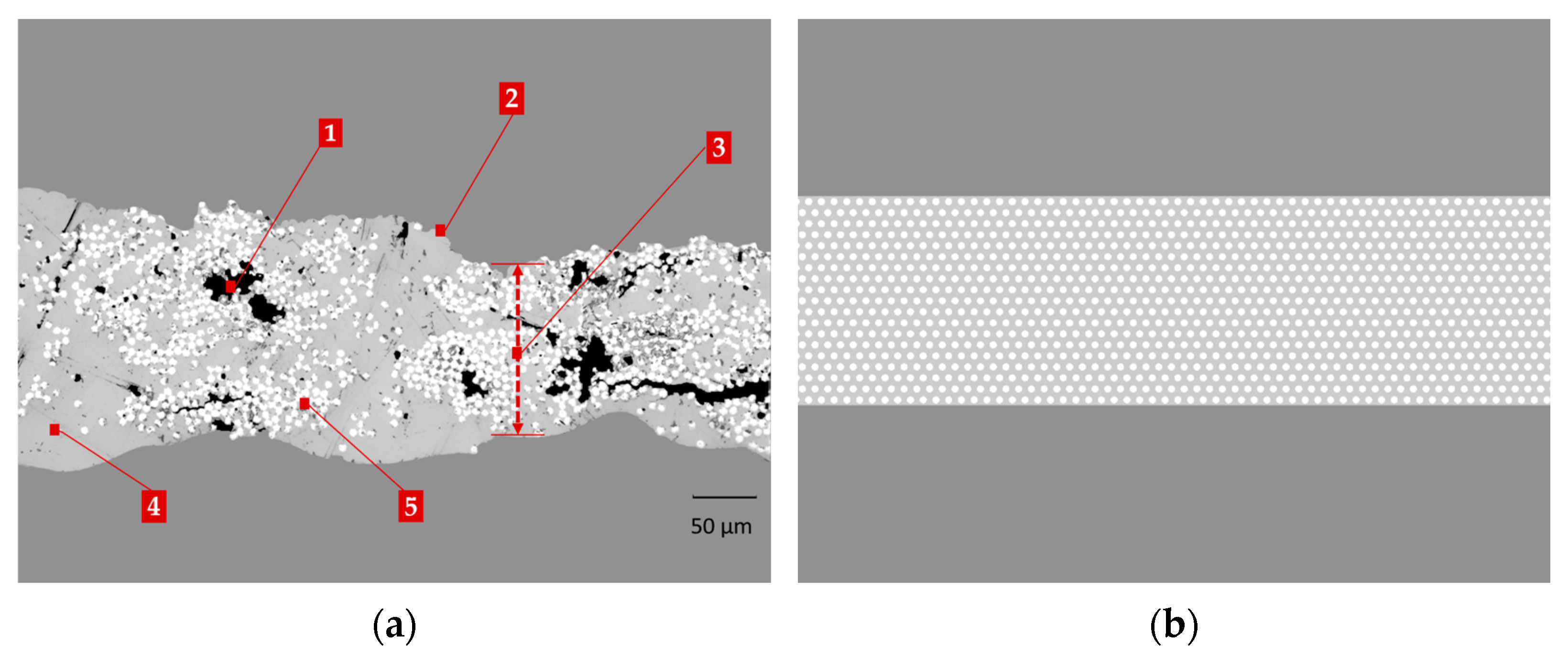
2. Materials and Methods
2.1. Materials
2.2. Experimental Setup for Infrared Thermography
2.3. Numerical Model
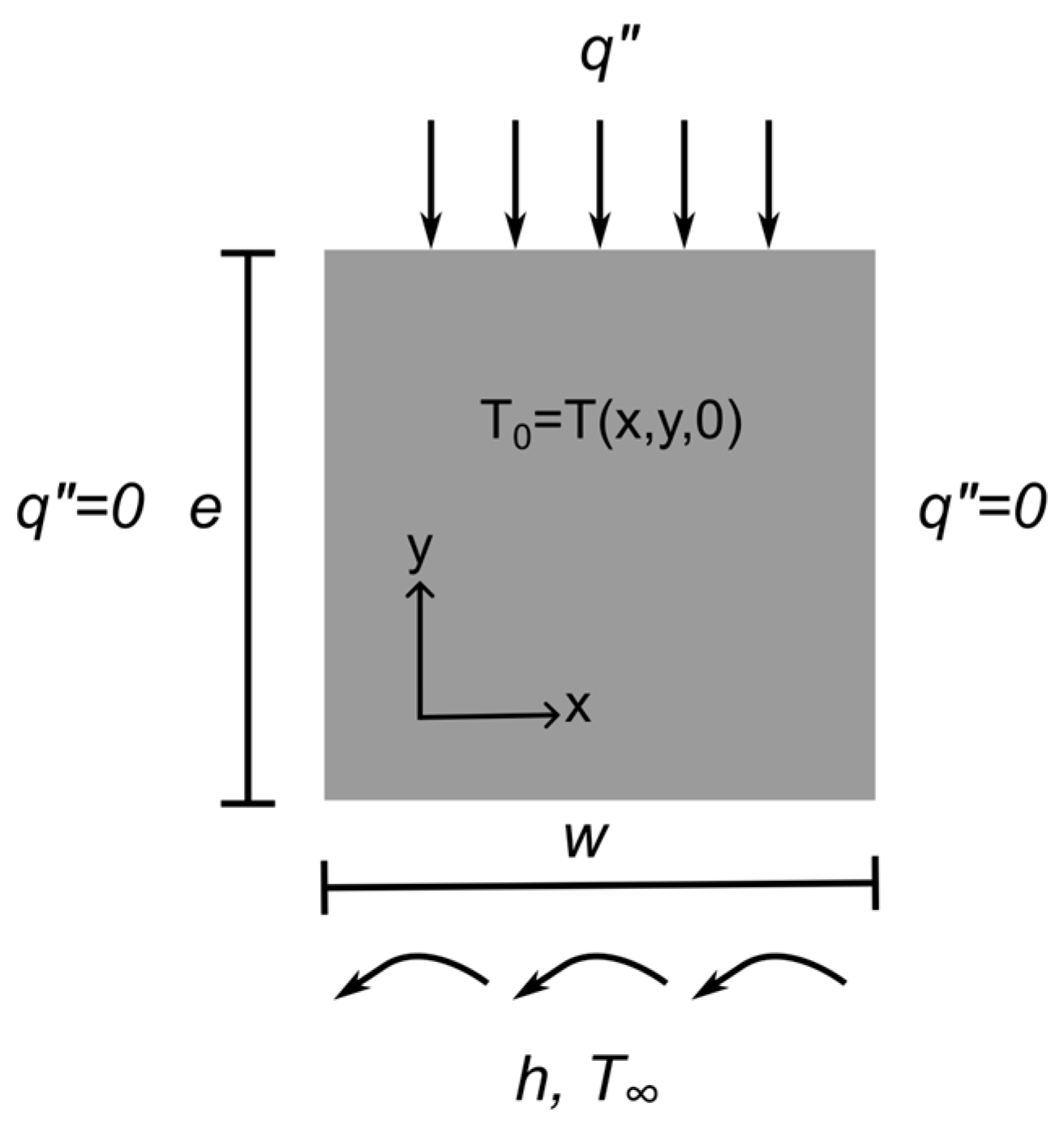
2.3.1. Governing Equation and Boundary Conditions
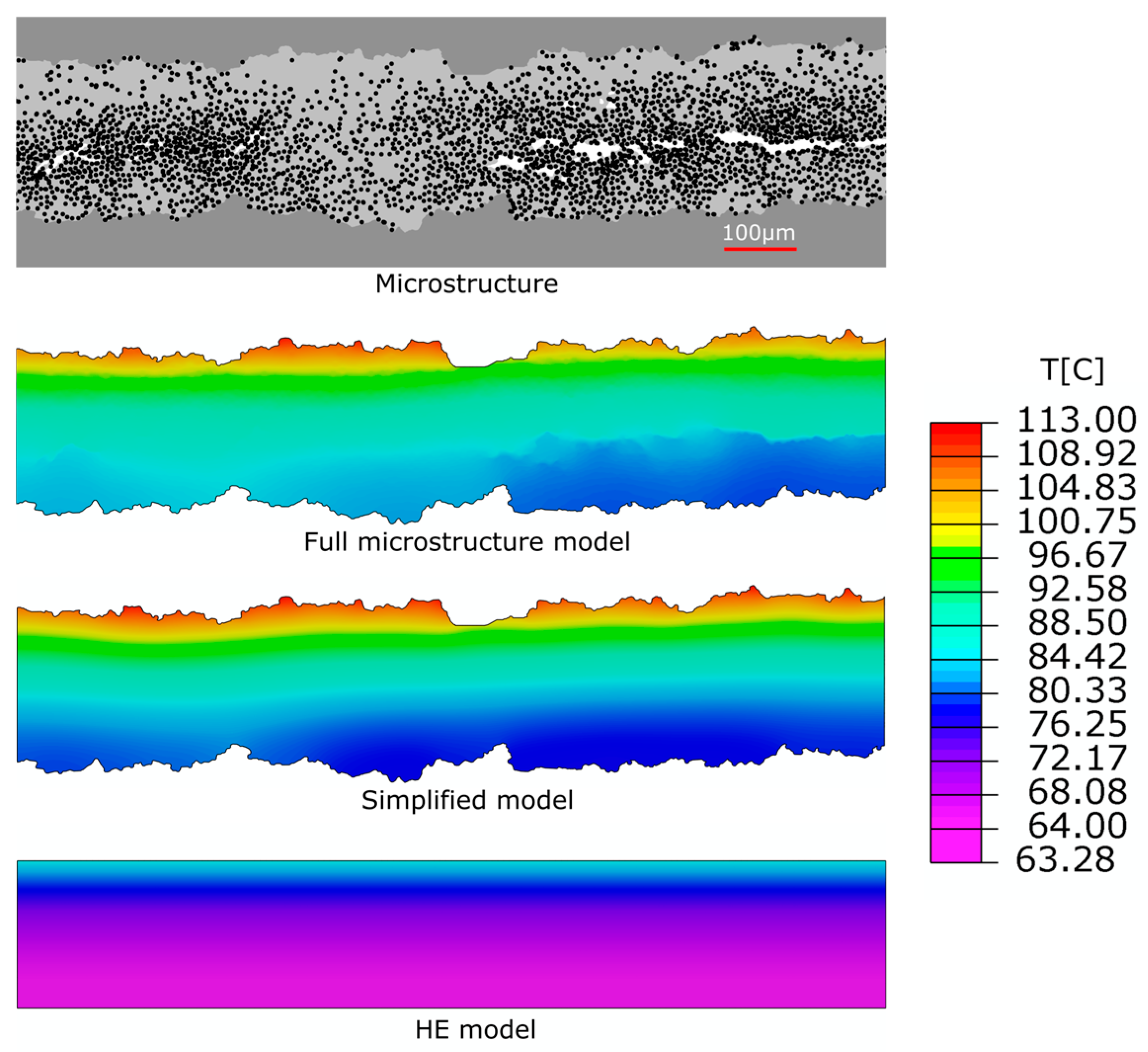
2.3.2. Model Configurations: Full Microstructure, Isolated Heterogeneities, and Homogeneous Equivalent
2.3.3. Meshing
3. Results
3.1. Experimental Evaluation of Surface Temperature Response
3.2. Numerical Modeling Results
3.2.1. Sensitivity Analysis of Isolated Microstructural Heterogeneities
3.2.2. Pores Geometry and Location Effects
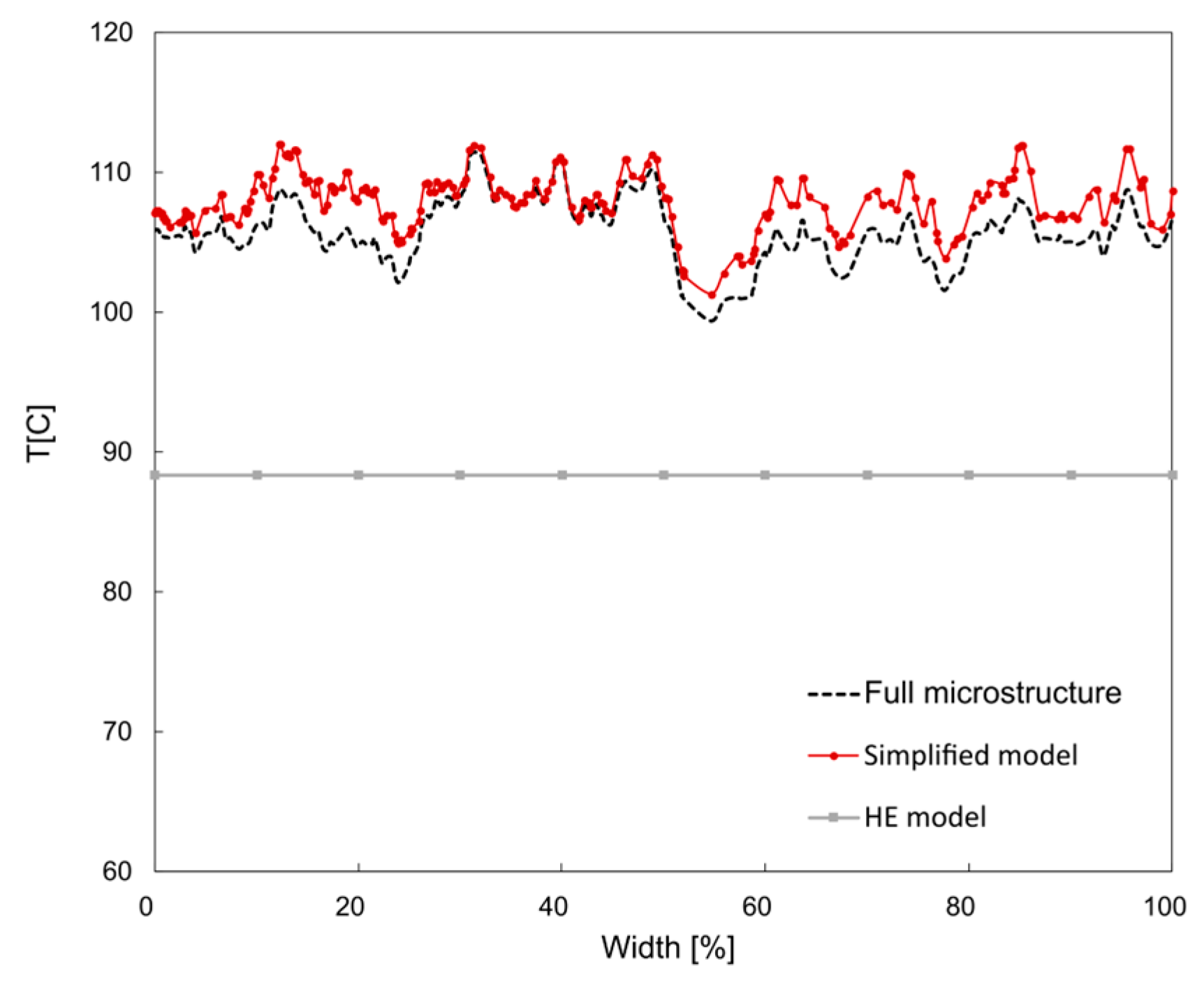
3.2.3. Microstructure-Aware vs. HE Model
4. Discussion
4.1. On the Impact of Microstructural Heterogeneities
4.2. Numerical Model-Experiment Consistency and Limitations
4.3. Future Work and Industrial Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFRTP | Carbon Fiber Reinforced Thermoplastics |
| UD | Unidirectional |
| FW | Filament Winding |
| ATP | Automated Tape Placement |
| IR | Infrared |
| HE | Homogeneous-Equivalent |
| FEM | Finite Element Method |
References
- Teltschik, J.; Matter, J.; Woebbeking, S.; Jahn, K.; Borja Adasme, Y.; Van Paepegem, W.; Drechsler, K.; Tallawi, M. Review on Recycling of Carbon Fibre Reinforced Thermoplastics with a Focus on Polyetheretherketone. Compos. Part A Appl. Sci. Manuf. 2024, 184, 108236. [Google Scholar] [CrossRef]
- Yao, S.-S.; Jin, F.-L.; Rhee, K.Y.; Hui, D.; Park, S.-J. Recent Advances in Carbon-Fiber-Reinforced Thermoplastic Composites: A Review. Compos. Part B Eng. 2018, 142, 241–250. [Google Scholar] [CrossRef]
- Condé-Wolter, J.; Ruf, M.G.; Liebsch, A.; Lebelt, T.; Koch, I.; Drechsler, K.; Gude, M. Hydrogen Permeability of Thermoplastic Composites and Liner Systems for Future Mobility Applications. Compos. Part A Appl. Sci. Manuf. 2023, 167, 107446. [Google Scholar] [CrossRef]
- Wazeer, A.; Das, A.; Abeykoon, C.; Sinha, A.; Karmakar, A. Composites for Electric Vehicles and Automotive Sector: A Review. Green Energy Intell. Transp. 2023, 2, 100043. [Google Scholar] [CrossRef]
- Ismail, K.B.M.; Kumar, M.A.; Mahalingam, S.; Raj, B.; Kim, J. Carbon Fiber-Reinforced Polymers for Energy Storage Applications. J. Energy Storage 2024, 84, 110931. [Google Scholar] [CrossRef]
- Murray, R.E.; Beach, R.; Barnes, D.; Snowberg, D.; Berry, D.; Rooney, S.; Jenks, M.; Gage, B.; Boro, T.; Wallen, S.; et al. Structural Validation of a Thermoplastic Composite Wind Turbine Blade with Comparison to a Thermoset Composite Blade. Renew. Energy 2021, 164, 1100–1107. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, G.; Vaidya, U.; Wang, H. Past, Present and Future Prospective of Global Carbon Fibre Composite Developments and Applications. Compos. Part B Eng. 2023, 250, 110463. [Google Scholar] [CrossRef]
- Torquato, S. Random Heterogeneous Materials; Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2002; Volume 16, ISBN 978-1-4757-6357-7. [Google Scholar]
- Hyer, M.; Waas, A. Micromechanics of Linear Elastic Continuous Fiber Composites. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 978-0-12-803581-8. [Google Scholar]
- Jiang, J.; Wu, J.; Chen, Q.; Chatzigeorgiou, G.; Meraghni, F. Physically Informed Deep Homogenization Neural Network for Unidirectional Multiphase/Multi-Inclusion Thermoconductive Composites. Comput. Methods Appl. Mech. Eng. 2023, 409, 115972. [Google Scholar] [CrossRef]
- Kamiński, M.; Ostrowski, P. Homogenization of Heat Transfer in Fibrous Composite with Stochastic Interface Defects. Compos. Struct. 2021, 261, 113555. [Google Scholar] [CrossRef]
- Peng, X.-L.; Fathidoost, M.; Lin, B.; Yang, Y.; Xu, B.-X. What Can Machine Learning Help with Microstructure-Informed Materials Modeling and Design? MRS Bull. 2024, 50, 61–79. [Google Scholar] [CrossRef]
- Baskaran, A.; Kautz, E.J.; Chowdhary, A.; Ma, W.; Yener, B.; Lewis, D.J. The Adoption of Image-Driven Machine Learning for Microstructure Characterization and Materials Design: A Perspective. JOM 2021, 73, 3639–3657. [Google Scholar] [CrossRef]
- Chung, D.D.L. Processing-Structure-Property Relationships of Continuous Carbon Fiber Polymer-Matrix Composites. Mater. Sci. Eng. R Rep. 2017, 113, 1–29. [Google Scholar] [CrossRef]
- Grouve, W.J.B.; Warnet, L.L.; Rietman, B.; Visser, H.A.; Akkerman, R. Optimization of the Tape Placement Process Parameters for Carbon–PPS Composites. Compos. Part A Appl. Sci. Manuf. 2013, 50, 44–53. [Google Scholar] [CrossRef]
- Henninger, F.; Hoffmann, J.; Friedrich, K. Thermoplastic Filament Winding with Online-Impregnation. Part B. Experimental Study of Processing Parameters. Compos. Part A Appl. Sci. Manuf. 2002, 33, 1684–1695. [Google Scholar] [CrossRef]
- Martin, I.; Saenz del Castillo, D.; Fernandez, A.; Güemes, A. Advanced Thermoplastic Composite Manufacturing by In-Situ Consolidation: A Review. J. Compos. Sci. 2020, 4, 149. [Google Scholar] [CrossRef]
- Ziaee, S.; Kerr-Anderson, E.; Johnson, A.; Eastep, D.; Abdel-Magid, B. Effect of High Fiber Content on Properties and Performance of CFRTP Composites. J. Compos. Sci. 2024, 8, 364. [Google Scholar] [CrossRef]
- Mehdikhani, M.; Petrov, N.A.; Straumit, I.; Melro, A.R.; Lomov, S.V.; Gorbatikh, L. The Effect of Voids on Matrix Cracking in Composite Laminates as Revealed by Combined Computations at the Micro- and Meso-Scales. Compos. Part A Appl. Sci. Manuf. 2019, 117, 180–192. [Google Scholar] [CrossRef]
- Nasri, W.; Driss, Z.; Djebali, R.; Lee, K.-Y.; Park, H.-H.; Bezazi, A.; Reis, P.N.B. Thermal Study of Carbon-Fiber-Reinforced Polymer Composites Using Multiscale Modeling. Materials 2023, 16, 7233. [Google Scholar] [CrossRef]
- Bard, S.; Schönl, F.; Demleitner, M.; Altstädt, V. Influence of Fiber Volume Content on Thermal Conductivity in Transverse and Fiber Direction of Carbon Fiber-Reinforced Epoxy Laminates. Materials 2019, 12, 1084. [Google Scholar] [CrossRef]
- Kang, R.; Wang, S.; Liu, Y.; Ye, H.; Li, M.; Gu, Y. Analysis of Transverse Thermal Conductivity for Mesophase Pitch-Based Carbon Fibers and the through-Thickness Heat Conduction of Their Composites. Heliyon 2024, 10, e24349. [Google Scholar] [CrossRef]
- de Almeida, S.F.M.; Neto, Z.d.S.N. Effect of Void Content on the Strength of Composite Laminates. Compos. Struct. 1994, 28, 139–148. [Google Scholar] [CrossRef]
- Sisodia, S.; Gamstedt, E.K.; Edgren, F.; Varna, J. Effects of Voids on Quasi-Static and Tension Fatigue Behaviour of Carbon-Fibre Composite Laminates. J. Compos. Mater. 2015, 49, 2137–2148. [Google Scholar] [CrossRef]
- Saenz-Castillo, D.; Martín, M.I.; Calvo, S.; Rodriguez-Lence, F.; Güemes, A. Effect of Processing Parameters and Void Content on Mechanical Properties and NDI of Thermoplastic Composites. Compos. Part A Appl. Sci. Manuf. 2019, 121, 308–320. [Google Scholar] [CrossRef]
- Yang, L.; Wu, Z.; Cao, Y.; Ye, Y. Micromechanical Modelling and Simulation of Unidirectional Fibre-Reinforced Composite under Shear Loading. J. Reinf. Plast. Compos. 2015, 34, 72–83. [Google Scholar] [CrossRef]
- Wongsto, A.; Li, S. Micromechanical FE Analysis of UD Fibre-Reinforced Composites with Fibres Distributed at Random over the Transverse Cross-Section. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1246–1266. [Google Scholar] [CrossRef]
- Melro, A.R.; Camanho, P.P.; Pinho, S.T. Generation of Random Distribution of Fibres in Long-Fibre Reinforced Composites. Compos. Sci. Technol. 2008, 68, 2092–2102. [Google Scholar] [CrossRef]
- Pulungan, D.; Lubineau, G.; Yudhanto, A.; Yaldiz, R.; Schijve, W. Identifying Design Parameters Controlling Damage Behaviors of Continuous Fiber-Reinforced Thermoplastic Composites Using Micromechanics as a Virtual Testing Tool. Int. J. Solids Struct. 2017, 117, 177–190. [Google Scholar] [CrossRef]
- Kumar, S.; Anderson, D.P.; Crasto, A.S. Carbon Fibre Compressive Strength and Its Dependence on Structure and Morphology. J. Mater. Sci. 1993, 28, 423–439. [Google Scholar] [CrossRef]
- Thermtest Inc. Materials Database—Thermal Properties. Available online: https://thermtest.com/thermal-resources/materials-database (accessed on 25 September 2025).
- Zhang, H.; Robitaille, F.; Grosse, C.U.; Ibarra-Castanedo, C.; Martins, J.O.; Sfarra, S.; Maldague, X.P.V. Optical Excitation Thermography for Twill/Plain Weaves and Stitched Fabric Dry Carbon Fibre Preform Inspection. Compos. Part A Appl. Sci. Manuf. 2018, 107, 282–293. [Google Scholar] [CrossRef]
- Rodrigo, O.; Bertrand, G. Radial Thermal Conductivity of a PAN Type Carbon Fiber Using the 3 Omega Method. Int. J. Therm. Sci. 2022, 172, 107321. [Google Scholar] [CrossRef]
- ISO 4287; Geometrical Product Specifications (GPS) — Surface Texture: Profile Method — Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 1997.
- Zaami, A.; Baran, I.; Bor, T.C.; Akkerman, R. 3D Numerical Modeling of Laser Assisted Tape Winding Process of Composite Pressure Vessels and Pipes—Effect of Winding Angle, Mandrel Curvature and Tape Width. Materials 2020, 13, 2449. [Google Scholar] [CrossRef]
- Grouve, W.J.B. Weld Strength of Laser-Assisted Tape-Placed Thermoplastic Composites; University of Twente: Enschede, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Lewis, T.B.; Nielsen, L.E. Dynamic Mechanical Properties of Particulate-Filled Composites. J. Appl. Polym. Sci. 1970, 14, 1449–1471. [Google Scholar] [CrossRef]
- Schutzeichel, M.O.H.; Kletschkowski, T.; Monner, H.P. Microscale Thermal Modelling of Multifunctional Composite Materials Made from Polymer Electrolyte Coated Carbon Fibres Including Homogenization and Model Reduction Strategies. Appl. Mech. 2021, 2, 739–765. [Google Scholar] [CrossRef]
- Zaami, A.; Baran, I.; Bor, T.C.; Akkerman, R. Optical Characterization of Fiber-Reinforced Thermoplastic Tapes for Laser-Based Composite Manufacturing. Compos. Part A Appl. Sci. Manuf. 2021, 146, 106402. [Google Scholar] [CrossRef]
- Ferrándiz, B.; Palacios, M.; Mailhé, C.; Barasinski, A.; Chinesta, F. Thermal Field Estimation in CFRTP Composites Using an Attention-Enhanced U-Net. Int. J. Mater. Form. 2025, 18, 76. [Google Scholar] [CrossRef]






| Matrix 1 | Fiber | Air | |
|---|---|---|---|
| Density [kg m−3] | 1030 | 1960 [30] | 1.29 [31] |
| Specific Heat [J kg−1 K−1] | 1260 | 1296 [32] | 1004 [31] |
| Thermal conductivity [W m−1 K−1] | 0.27 | 1.05 (Transverse) [33] | 0.025 [31] |
| Minimum | Maximum | |
|---|---|---|
| Fiber volume fraction Vf | 0.32 | 0.36 |
| Pore volume fraction Va | 0.01 | 0.08 |
| Surface roughness Ra [µm] ISO 4287 [34] | 0.97 | 7.92 |
| Surface roughness Rt [µm] ISO 4287 | 7.67 | 57.41 |
| Thickness variation Δe [µm] | 10 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palacios, M.; Barasinski, A. The Influence of Microstructural Heterogeneities on the Thermal Response of CFRTP Composite Tapes at the Ply-Scale. J. Compos. Sci. 2025, 9, 617. https://doi.org/10.3390/jcs9110617
Palacios M, Barasinski A. The Influence of Microstructural Heterogeneities on the Thermal Response of CFRTP Composite Tapes at the Ply-Scale. Journal of Composites Science. 2025; 9(11):617. https://doi.org/10.3390/jcs9110617
Chicago/Turabian StylePalacios, Mabel, and Anaïs Barasinski. 2025. "The Influence of Microstructural Heterogeneities on the Thermal Response of CFRTP Composite Tapes at the Ply-Scale" Journal of Composites Science 9, no. 11: 617. https://doi.org/10.3390/jcs9110617
APA StylePalacios, M., & Barasinski, A. (2025). The Influence of Microstructural Heterogeneities on the Thermal Response of CFRTP Composite Tapes at the Ply-Scale. Journal of Composites Science, 9(11), 617. https://doi.org/10.3390/jcs9110617








