Influence of Long-Term Moisture Exposure and Temperature on the Mechanical Properties of Hybrid FRP Composite Specimens
Abstract
1. Introduction
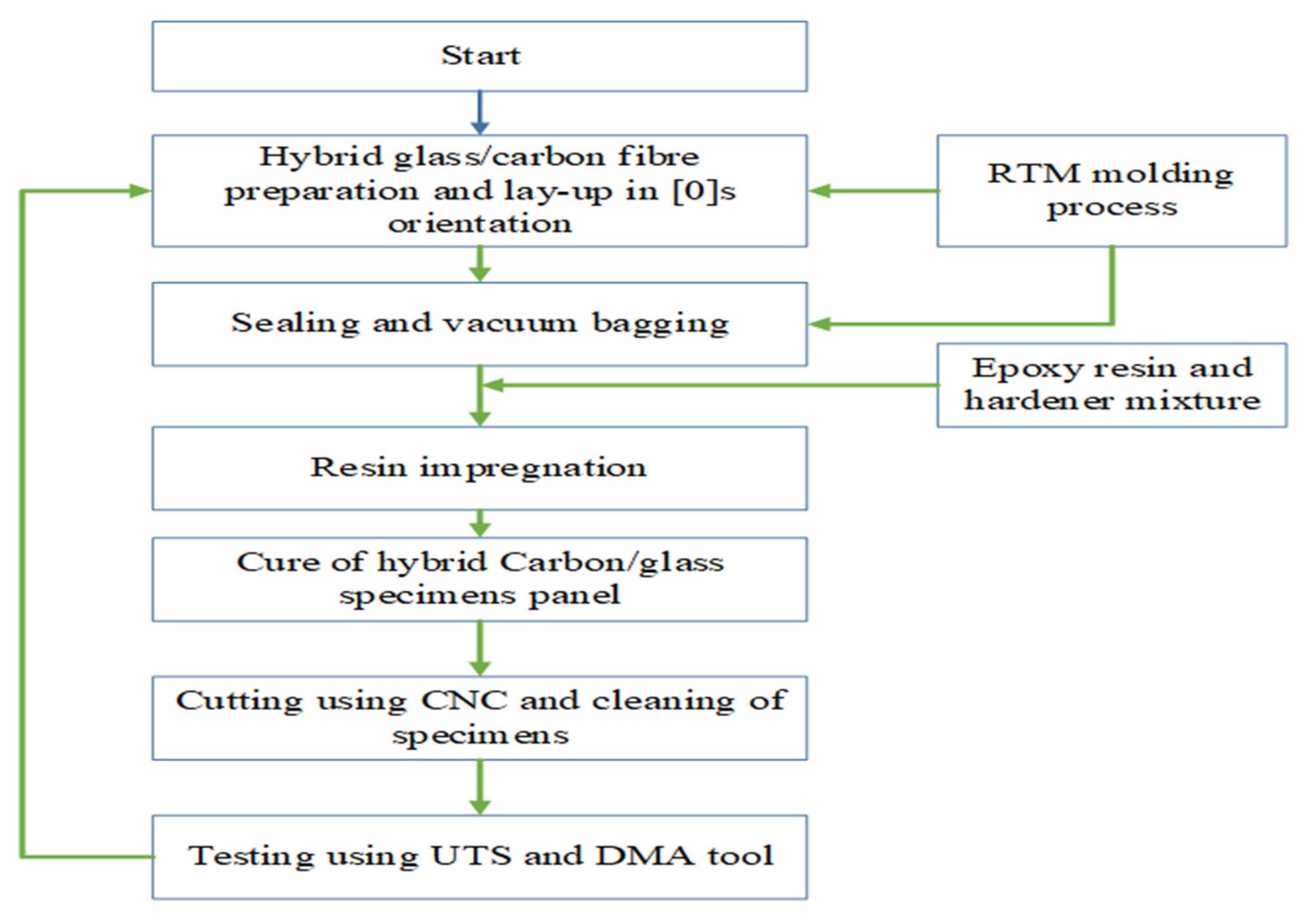
2. Experimental Programme
2.1. Materials
Composite Laminate Preparation Procedures
2.2. Test Methods
3. Results and Discussion
3.1. Mechanical Properties of the Hybrid Laminates at Different Temperatures
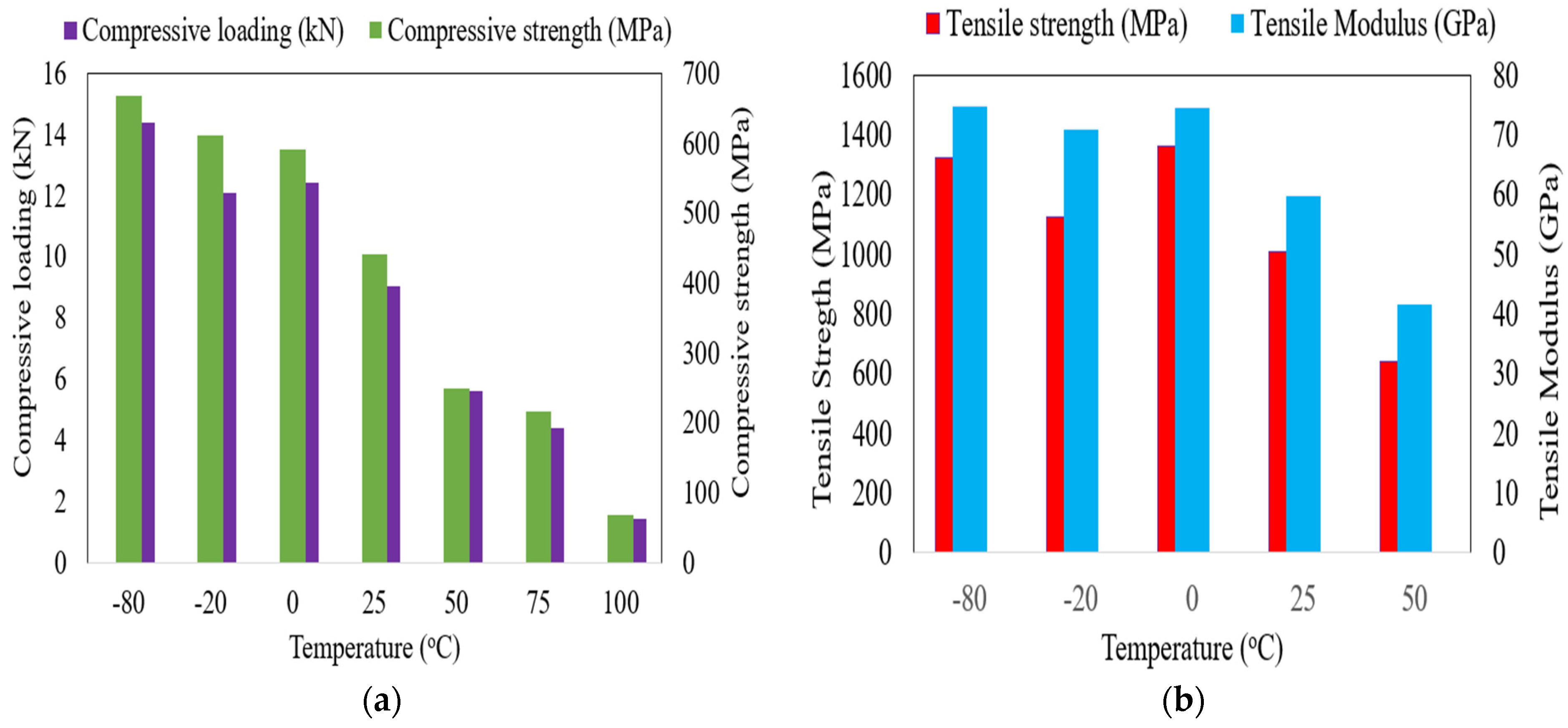
3.1.1. Compressive Properties
3.1.2. Tensile and Stiffness Properties
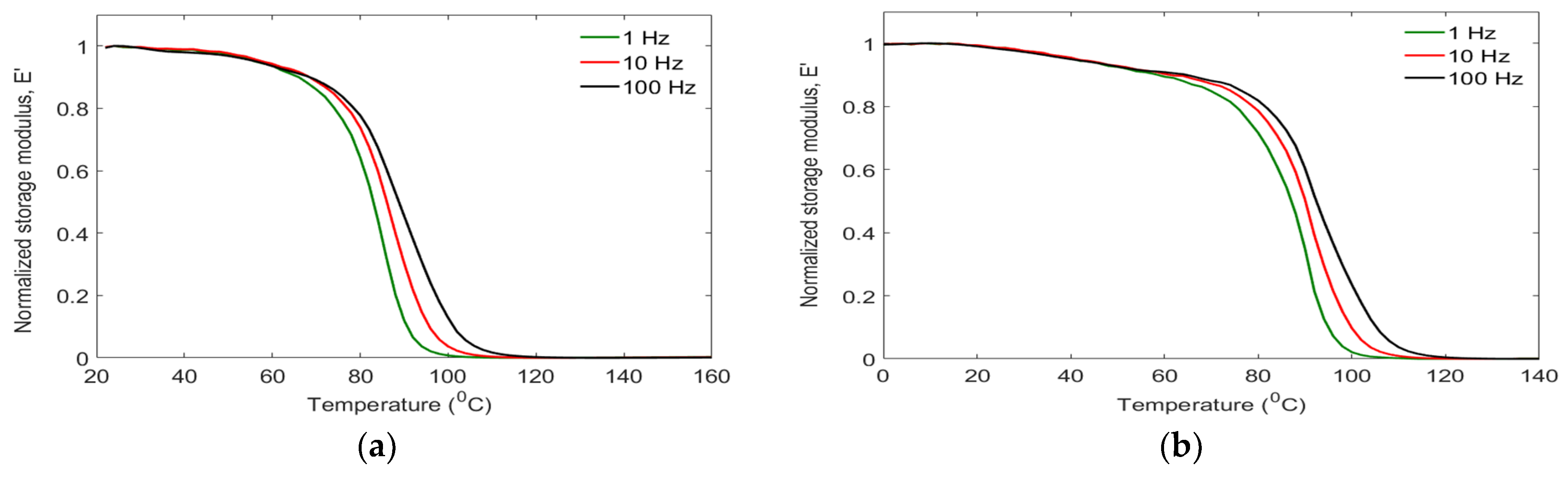
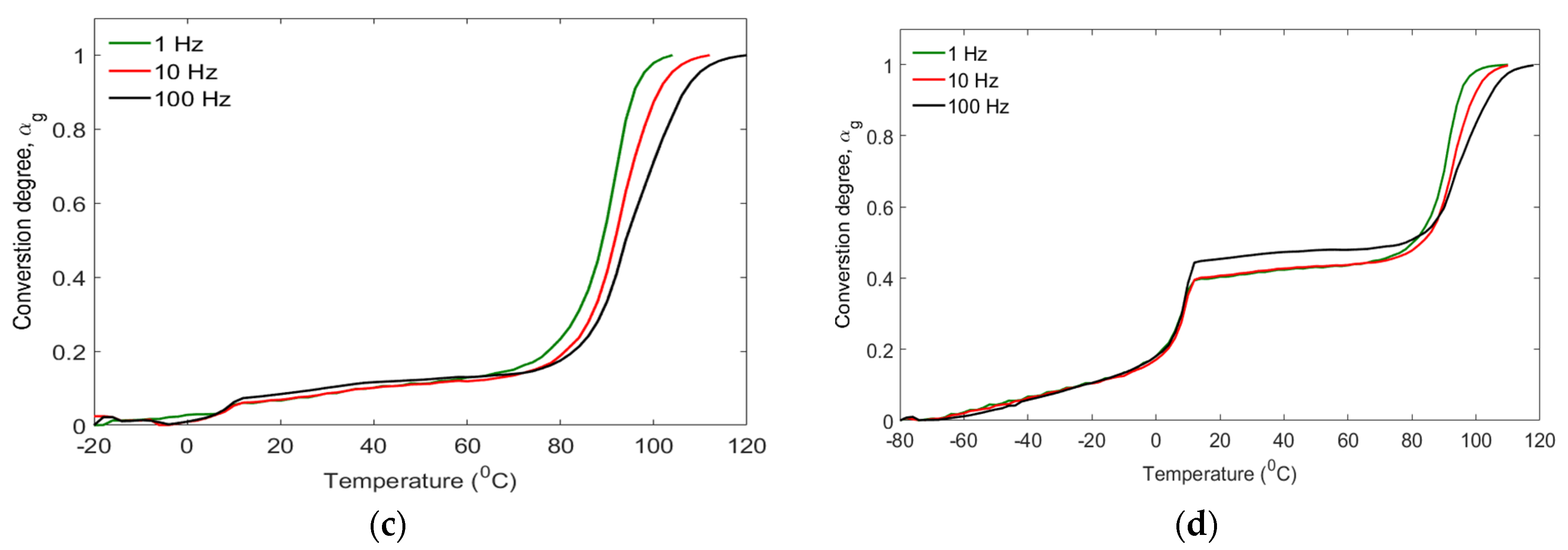
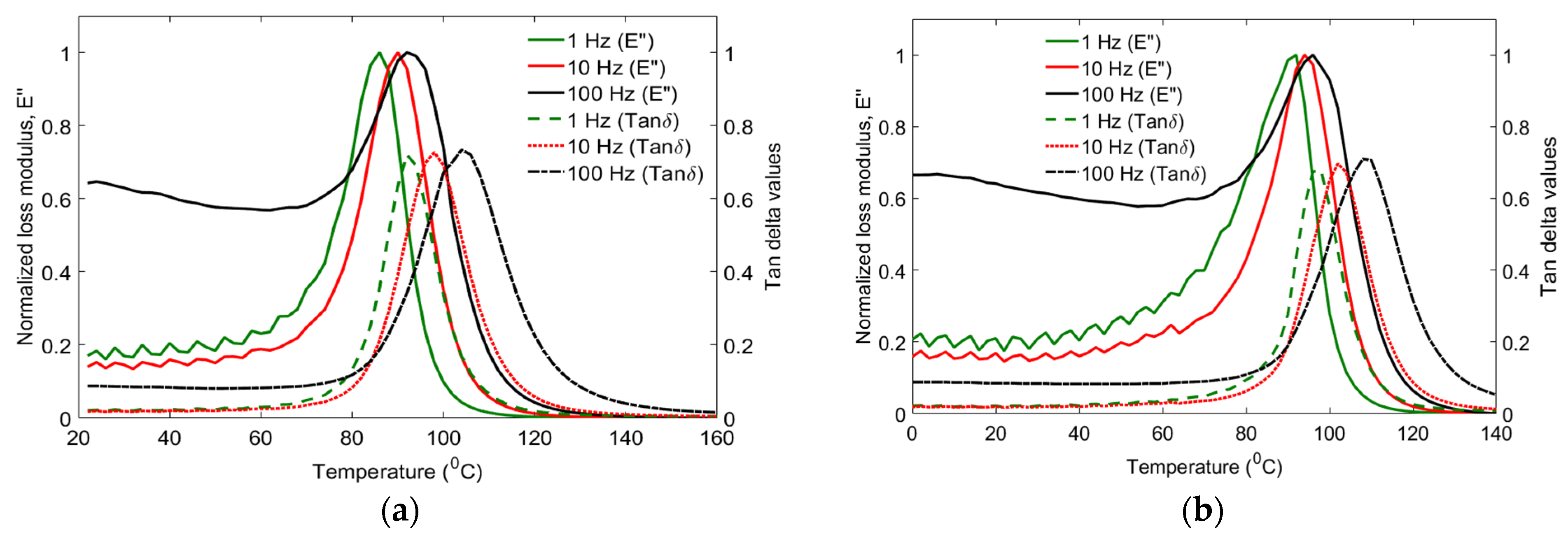
3.2. Dynamic Mechanical Properties of Hybrid Laminates
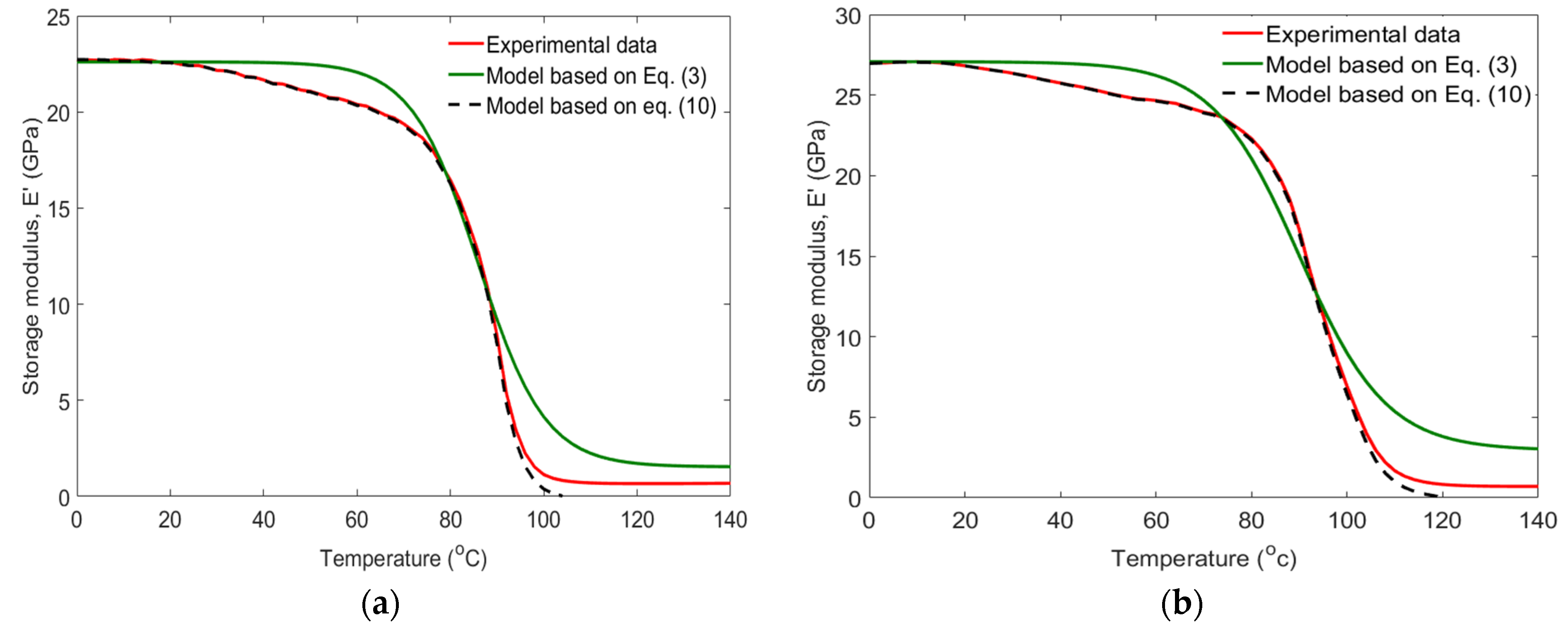
4. Models of Temperature-Dependent Storage Modulus
Comparison of the Storage Modulus Results with Analytical Models
5. Conclusions
- The highest and lowest compressive strength properties were obtained when the GCG laminates were tested at temperatures of −80 °C and 100 °C, respectively. This variation is likely due to an increased crosslinking of the polymer network at lower temperatures and an increased mobility of the polymer material at higher environmental conditions.
- The tensile strength and tensile modulus results of all groups of GCG composite laminates exhibited minor differences between them for the laminates preserved in a deep freezer for extended periods. Both properties were reduced as the test temperature approached 50 °C. This indicates the initial onset of the mobility of polymeric matrix material, which reduces the transfer capacity of the loads to the fibres before reaching their glass transition temperature.
- The storage modulus, loss modulus, and damping properties of the GCG laminates decreased as the testing temperature approached the glass transition. The highest stiffness parameter was observed at −80 °C/GCG laminates, likely due to the presence of beta transitions in the glassy regions of the laminates.
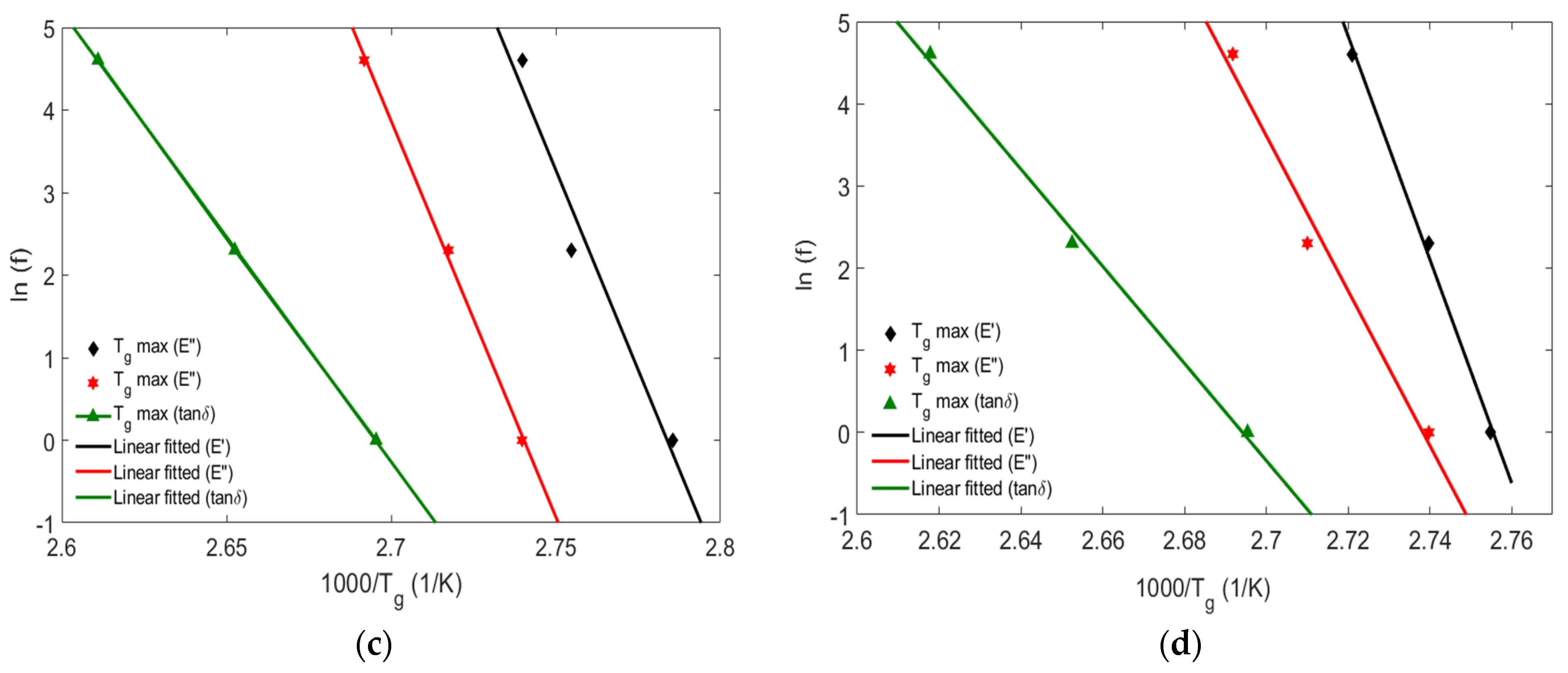
- The relationships between the glass transition temperatures of the polymer matrix and vibration frequency were assessed. A delay in glass transition temperature was observed as the testing frequency increased.
- The storage modulus results of GCG composite laminates are compared with empirical models. The model developed using the Arrhenius law accurately predicted the storage model results. However, the model developed by Gibson et al. [51] requires further research to accurately predict the storage modulus results of laminates that were preserved at the lowest temperatures for extended periods.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chowdhury, I.R.; Summerscales, J. Woven Fabrics for Composite Reinforcement: A Review. J. Compos. Sci. 2024, 8, 280. [Google Scholar] [CrossRef]
- Vieira, P.S.C.; Desouza, F.S.; Cardoso, D.C.T.; Vieira, J.D.; Silva, F.D. Influence of moderate/high temperatures on the residual flexural behavior of pultruded GFRP. Compos. Part. B Eng. 2020, 200, 108335. [Google Scholar] [CrossRef]
- Guermazi, N.; Tarjem, A.B.; Ksouri, I.; Ayedi, H.F. On the durability of FRP composites for aircraft structures in hygrothermal conditioning. Compos. Part. B Eng. 2013, 85, 294–304. [Google Scholar] [CrossRef]
- Bazli, M.; Jafari, A.; Ashrafi, H.; Zhao, X.L.; Bai, Y.; Raman, R.K.S. Effects of UV radiation, moisture and elevated temperature on mechanical properties of GFRP pultruded profiles. Constr. Build. Mater. 2020, 231, 117137. [Google Scholar] [CrossRef]
- Rajak, D.K.; Wagh, P.H.; Linul, E. Manufacturing technologies of carbon/glass fiber-reinforced polymer composites and their properties: A review. Polymers 2021, 13, 3721. [Google Scholar] [CrossRef] [PubMed]
- Jacquet, L.; Duigou, A.; Kerbrat, O. A Proposal for a Carbon Fibre-Manufacturing Life-Cycle Inventory: A Case Study from the Competitive Sailing Boat Industry. J. Compos. Sci. 2024, 8, 276. [Google Scholar] [CrossRef]
- Pacheco, E.P.; Cupul, J.I.C.; González, A.V.; Franco, P.J.H. Effect of moisture absorption on the mechanical behavior of carbon fiber/epoxy matrix composites. J. Mater. Sci. 2013, 48, 1873–1882. [Google Scholar] [CrossRef]
- Martinez, P.; Nutt, S. Flax–Reinforced Vitrimer Epoxy Composites Produced via RTM. J. Compos. Sci. 2024, 8, 275. [Google Scholar] [CrossRef]
- Wang, T.; Song, B.; Qiao, K.; Ding, C.; Wang, L. Influence of the hybrid ratio and stacking sequence on mechanical and damping properties of hybrid composites. Polym. Compos. 2019, 40, 2368–2380. [Google Scholar] [CrossRef]
- da Silva Monte Vidal, D.C.; Ornaghi, H.L., Jr.; Ornaghi, F.G.; Monticeli, F.M.; Hila, M.O. Effect of different stacking sequences on hybrid carbon/glass / epoxy composites laminate: Thermal, dynamic mechanical and long-term behavior. J. Compos. Mater. 2020, 54, 731–743. [Google Scholar] [CrossRef]
- Correia, J.R.; Gomes, M.M.; Pires, J.M.; Branco, F.A. Mechanical behvaior of Pultruded glass fibre reinforced polymer composites at elevated temperature: Experiments and model assessment. Compos. Struct. 2013, 98, 303–313. [Google Scholar] [CrossRef]
- Sujon, M.A.; Habib, M.A.; Abedin, M.Z. Experimental investigation of the mechanical and water absorption properties on fiber stacking sequence and orientation of jute/carbon epoxy hybrid composites. J. Mater. Res. Technol. 2020, 9, 10970–10981. [Google Scholar] [CrossRef]
- Alessi, S.; Pitarresi, G.; Spadaro, G. Effect of hydrothermal ageing on the thermal and delamination fracture behaviour of CFRP composites. Compos. Part. B Eng. 2014, 67, 145–153. [Google Scholar] [CrossRef]
- Liu, T.Q.; Liu, X.; Feng, P. A comprehensive review on mechanical properties of pultruded FRP composites subjected to long-term environmental effects. Compos. Part. B Eng. 2020, 191, 107958. [Google Scholar] [CrossRef]
- Frigione, M.; Lettieri, M. Durability issues and challenges for material advancements in FRP employed in the construction industry. Polymers 2018, 10, 247. [Google Scholar] [CrossRef] [PubMed]
- Batista, M.; Teixeira, L.; da Luz, S. Hygrothermal exposure and residual strength after cyclic loading on epoxy composites reinforced with sisal fibers. Polym. Test. 2023, 127, 108192. [Google Scholar] [CrossRef]
- Bazli, M.; Abolfazli, M. Mechanical properties of fibre reinforced polymers under elevated temperatures: An overview. Polymers 2020, 12, 2600. [Google Scholar] [CrossRef] [PubMed]
- Mlyniec, A.; Korta, J.; Kudelski, R.; Uhl, T. The influence of the laminate thickness, stacking sequence and thermal aging on the static and dynamic behavior of carbon/epoxy composites. Compos. Struct. 2014, 118, 208–216. [Google Scholar] [CrossRef]
- Aklilu, G.; Adali, S.; Bright, G. Tensile behaviour of hybrid and non-hybrid polymer composite specimens at elevated temperatures. Eng. Sci. Technol. Int. J. 2020, 23, 732–743. [Google Scholar] [CrossRef]
- Cao, S.; Wu, Z.; Wang, X. Tensile properties of CFRP and hybrid FRP composites at elevated temperatures. J. Compos. Mater. 2009, 43, 315–330. [Google Scholar]
- Jia, Z.; Li, T.; Chiang, F.P.; Wang, L. An experimental investigation of the temperature effect on the mechanics of carbon fiber reinforced polymer composites. Compos. Sci. Technol. 2018, 154, 53–63. [Google Scholar] [CrossRef]
- Tefera, G.; Adali, S.; Bright, G. Mechanical behaviour of carbon fibre reinforced polymer composite material at different temperatures: Experimental and model assessment. Polym. Polym. Compos. 2022, 30, 1–12. [Google Scholar] [CrossRef]
- Zhou, F.; Zhang, J.; Song, S.; Yang, D.; Wang, C. Effect of temperature on material properties of carbon fiber reinforced polymer (CFRP) Tendons: Experiments and model assessment. Materials 2019, 12, 1025. [Google Scholar] [CrossRef]
- Bazli, M.; Ashrafi, H.; Oskouei, A.V. Effect of harsh environments on mechanical properties of GFRP pultruded profiles. Compos. Part. B Eng. 2016, 99, 203–215. [Google Scholar] [CrossRef]
- Wang, K.; Young, B.; Smith, S.T. Mechanical properties of pultruded carbon fibre-reinforced polymer (CFRP) plates at elevated temperatures. Eng. Struct. 2011, 33, 2154–2161. [Google Scholar] [CrossRef]
- Jarrah, M.; Najafabadi, E.P.; Khaneghahi, M.H.; Oskouei, A.V. The effect of elevated temperatures on the tensile performance of GFRP and CFRP sheets. Constr. Build. Mater. 2018, 190, 38–52. [Google Scholar] [CrossRef]
- Jafari, A.; Bazli, M.; Ashrafi, H.; Oskouei, A.V.; Azhari, S.; Zhao, X.-L.; Gholipour, H. Effect of fibers configuration and thickness on tensile behavior of GFRP laminates subjected to elevated temperatures. Constr. Build. Mater. 2019, 202, 189–207. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Obeidah, A.A.; Abdalla, J.A.; Tamimi, A.A. Temperature effect on the mechanical properties of carbon, glass and carbon-glass FRP laminates. Constr. Build. Mater. 2015, 75, 342–348. [Google Scholar] [CrossRef]
- Zafar, A.; Bertocco, F.; Thomsen, J.S.; Rauhe, J.C. Investigation of the long term effects of moisture on carbon fibre and epoxy matrix composites. Compos. Sci. Technol. 2012, 72, 656–666. [Google Scholar] [CrossRef]
- Aniskevich, K.; Aniskevich, A.; Arnautov, A.; Jansons, J. Mechanical properties of pultruded glass fiber-reinforced plastic after moistening. Compos. Struct. 2012, 94, 2914–2919. [Google Scholar] [CrossRef]
- Bazli, M.; Ashrafi, H.; Jafari, A.; Zhao, X.L.; Raman, R.K.S.; Bai, Y. Effect of fibers configuration and thickness on tensile behavior of GFRP laminates exposed to harsh environment. Polymers 2019, 11, 1401. [Google Scholar] [CrossRef]
- Reyes, L.Q.; Swan, S.R.; Gan, H.; Seraji, S.M.; Zhang, J.; Varley, R.J. The role of β relaxations in determining the compressive properties of an epoxy amine network modified with POSS and mono-functional epoxy resins. Polym. Test. 2021, 93, 106873. [Google Scholar] [CrossRef]
- Tefera, G.; Adali, S.; Bright, G. Mechanical Behavior of GFRP Laminates Exposed to Thermal and Moist Environmental Conditions: Experimental and Model Assessment. Polymers 2022, 14, 1523. [Google Scholar] [CrossRef]
- Thomason, J.; Xypolias, G. A Study of the Moisture Absorption Characteristics of Vinyl Ester Polymer and Unidirectional Glass Fibre Vinyl Ester Laminates. J. Compos. Sci. 2024, 8, 214. [Google Scholar] [CrossRef]
- Spagnuolo, S.; Meda, A.; Rinaldi, Z.; Nanni, A. Residual behaviour of glass FRP bars subjected to high temperatures. Compos. Struct. 2018, 203, 886–893. [Google Scholar] [CrossRef]
- Robert, M.; Benmokrane, B. Behavior of GFRP Reinforcing Bars Subjected to Extreme Temperatures. J. Compos. Constr. 2010, 14, 353–360. [Google Scholar] [CrossRef]
- Lundgren, J.E.; Gudmundson, P. Moisture absorption in glass-fibre/epoxy laminates with transverse matrix cracks. Compos. Sci. Technol. 1999, 59, 1983–1991. [Google Scholar] [CrossRef]
- Ellyin, F.; Rohrbacher, C. Effect of aqueous environment and temperature on glass-fibre expoxy resin composites. J. Reinf. Plast. Compos. 2000, 17, 1405–1423. [Google Scholar] [CrossRef]
- Behera, A.; Ishwakarma, A.V.; Thawre, M.M.; Ballal, A. Effect of hygrothermal aging on static behavior of quasi-isotropic CFRP composite laminate. Compos. Commun. 2020, 17, 51–55. [Google Scholar] [CrossRef]
- Jhao, Y.S.; Ouyang, H.; Huang, C.C.; Yang, F.; Lee, S. A Mechanical Model for Stress Relaxation of Polylactic Acid/Thermoplastic Polyurethane Blends. J. Compos. Sci. J. Compos. Sci. 2024, 8, 169. [Google Scholar] [CrossRef]
- Karvanis, K.; Rusnáková, S.; Žaludek, M.; Čapka, A. Preparation and Dynamic Mechanical Analysis of Glass or carbon Fiber/Polymer Composites. IOP Conf. Ser. Mater. Sci. Eng. 2018, 362, 012005. [Google Scholar] [CrossRef]
- Trauth, A.; Kirchenbauer, K.; Weidenmann, K.A. Dynamic-mechanical-thermal analysis of hybrid continuous–discontinuous sheet molding compounds. Compos. Part C 2021, 5, 100148. [Google Scholar] [CrossRef]
- Alvarez, V.A.; Valdez, M.E.; Vázquez, A. Dynamic mechanical properties and interphase fiber/matrix evaluation of unidirectional glass fiber/epoxy composites. Polym. Test. 2003, 22, 611–615. [Google Scholar] [CrossRef]
- Tsai, Y.I.; Bosze, E.J.; Barjasteh, E.; Nutt, S.R. Influence of hygrothermal environment on thermal and mechanical properties of carbon fiber/fiberglass hybrid composites. Compos. Sci. Technol. 2009, 69, 432–437. [Google Scholar] [CrossRef]
- Bai, Y.; Keller, T. Time dependence of material properties of frp composites in fire. J. Compos. Mater. 2009, 43, 2469–2484. [Google Scholar] [CrossRef]
- Mouritz, A.P.; Feih, S.; Kandare, E.; Mathys, Z.; Gibson, A.G.; Jardin, P.E.D.; Case, S.W.; Lattimer, B.Y. Review of fire structural modelling of polymer composites. Compos. Part. A Appl. Sci. Manuf. 2009, 40, 1800–1814. [Google Scholar] [CrossRef]
- Mahieux, C.A.; Reifsnider, K.L. Property modeling across transition temperatures in polymers: Application to thermoplastic systems. J. Mater. Sci. 2002, 37, 911–920. [Google Scholar] [CrossRef]
- Bai, Y.; Keller, T. Modeling of post-fire stiffness of E -glass fiber-reinforced polyester composites. Compos. Part. A Appl. Sci. Manuf. 2007, 38, 2142–2153. [Google Scholar] [CrossRef]
- Aklilu, G.; Adali, S.; Bright, G. Long-term effects of low and high temperatures on the mechanical performance of hybrid FRP composite laminates: Experimental and model assessment. Compos. Part. C. 2023, 11, 100352. [Google Scholar] [CrossRef]
- Bai, Y.; Keller, T. Modeling of strength degradation for Fiber-reinforced polymer composites in fire. J. Compos. Mater. 2009, 43, 2371–2385. [Google Scholar] [CrossRef]
- Gibson, A.G.; Wu, Y.S.; Evans, J.T.; Mouritz, A.P. Laminate theory analysis of composites under load in fire. J. Compos. Mater. 2006, 40, 639–658. [Google Scholar] [CrossRef]
- Bai, Y.; Keller, T.; Vallée, T. Modeling of stiffness of FRP composites under elevated and high temperatures. Compos. Sci. Technol. 2008, 68, 3099–3106. [Google Scholar] [CrossRef]
- Feng, J.; Guo, Z. Temperature-frequency-dependent mechanical properties model of epoxy resin and its composites. Compos. Part B Eng. 2016, 85, 161–169. [Google Scholar] [CrossRef]
- Ghabezi, P.; Harrison, N.M. Multi-scale modelling and life prediction of aged composite materials in salt water. J. Reinf. Plast. Compos. 2024, 43, 205–219. [Google Scholar] [CrossRef]
- Aklilu, G.; Adali, S.; Bright, G. Experimental characterization of hybrid and non-hybrid polymer composites at elevated temperatures. Int. J. Eng. Res. Africa 2018, 36, 37–52. [Google Scholar] [CrossRef]
- ASTM D 695 Standard; Test Method for Compressive Properties of Plastic Materials SRM 1R-94. ASTM International: West Conshohocken, PA, USA, 2002.
- ASTM 3039/D 3039M Standard; Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2002.
- Menard, K. Dynamic Mechanical Analysis: A Practical Introduction; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- ASTM D 3171 Standard; Test Methods for Constituent Content of Composite Materials. ASTM International: West Conshohocken, PA, USA, 2000.








| Materials | Young’s Modulus [GPa] | Tensile Strength [MPa] | Density [Kg/m3] | Poisson’s Ratio |
|---|---|---|---|---|
| T-300 carbon | 230 | 3530 | 1760 | 0.30 |
| E-glass | 72.5 | 2350 | 2570 | 0.25 |
| Epoxy resin | 3.3 | 69.9 | 1020 | 0.36 |
| Temperature (°C) | Designation of GCG Composite Laminates | Maximum Force during Failure (N) | Compressive Strength (MPa) | Standard Deviation (SD) and Coefficient of Variation (CV) |
|---|---|---|---|---|
| −80 | −80/GCG | 14,382.19 | 668.19 | (63.78, 9.54%) |
| −20 | −20/GCG | 12,072.99 | 589.46 | (60.11, 9.83%) |
| 0 | 0/GCG | 12,414.76 | 591.41 | (23.25, 3.93%) |
| 25 | 25/GCG | 9004.27 | 441.42 | (34.34, 7.78%) |
| 50 | 50/GCG | 5572.57 | 249.47 | (21.78, 8.73%) |
| 75 | 75/GCG | 4370.02 | 216.88 | (17.08, 7.87%) |
| 100 | 100/GCG | 1412.86 | 68.06 | (6.39, 9.40%) |
| Temperature (°C) | Designation of GCG Composite Laminates | Force during Failure (N) | Tensile Strength (MPa), SD, and CV | Tensile Modulus (GPa), SD, and (CV) |
|---|---|---|---|---|
| −80 | −80 °C/GCG | 27,234.64 | 1321.20 (37.53, 2.84%) | 74.63 (1.71, 2.29%) |
| −20 | −20 °C/GCG | 23,365.99 | 1125.01 (35.63, 3.17%) | 70.89 (0.53, 0.74%) |
| 0 | 0 °C/GCG | 27,437.70 | 1358.16 (29.54, 2.18%) | 74.35 (5.64, 7.58%) |
| 25 | 25 °C/GCG | 20,715.62 | 1005.39 (92.28, 9.18%) | 59.78 (5.14, 8.60%) |
| 50 | 50 °C/GCG | 12,958.90 | 637.66 (1.09, 0.17%) | 41.55 (3.31, 7.96%) |
| Activation Energy (kJ/mol) Group of Hybrid Laminates | Tgmax (Storage Modulus) | Tgmax (Loss Modulus) | |
|---|---|---|---|
| Control GCG | 781.03 | 672.05 | 439.00 |
| 0 °C/GCG | 981.15 | 933.28 | 534.95 |
| −20 °C/GCG | 805.02 | 797.49 | 453.33 |
| −80 °C/GCG | 1130.87 | 783.79 | 491.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tefera, G.; Bright, G.; Adali, S. Influence of Long-Term Moisture Exposure and Temperature on the Mechanical Properties of Hybrid FRP Composite Specimens. J. Compos. Sci. 2024, 8, 312. https://doi.org/10.3390/jcs8080312
Tefera G, Bright G, Adali S. Influence of Long-Term Moisture Exposure and Temperature on the Mechanical Properties of Hybrid FRP Composite Specimens. Journal of Composites Science. 2024; 8(8):312. https://doi.org/10.3390/jcs8080312
Chicago/Turabian StyleTefera, Getahun, Glen Bright, and Sarp Adali. 2024. "Influence of Long-Term Moisture Exposure and Temperature on the Mechanical Properties of Hybrid FRP Composite Specimens" Journal of Composites Science 8, no. 8: 312. https://doi.org/10.3390/jcs8080312
APA StyleTefera, G., Bright, G., & Adali, S. (2024). Influence of Long-Term Moisture Exposure and Temperature on the Mechanical Properties of Hybrid FRP Composite Specimens. Journal of Composites Science, 8(8), 312. https://doi.org/10.3390/jcs8080312





