1. Introduction
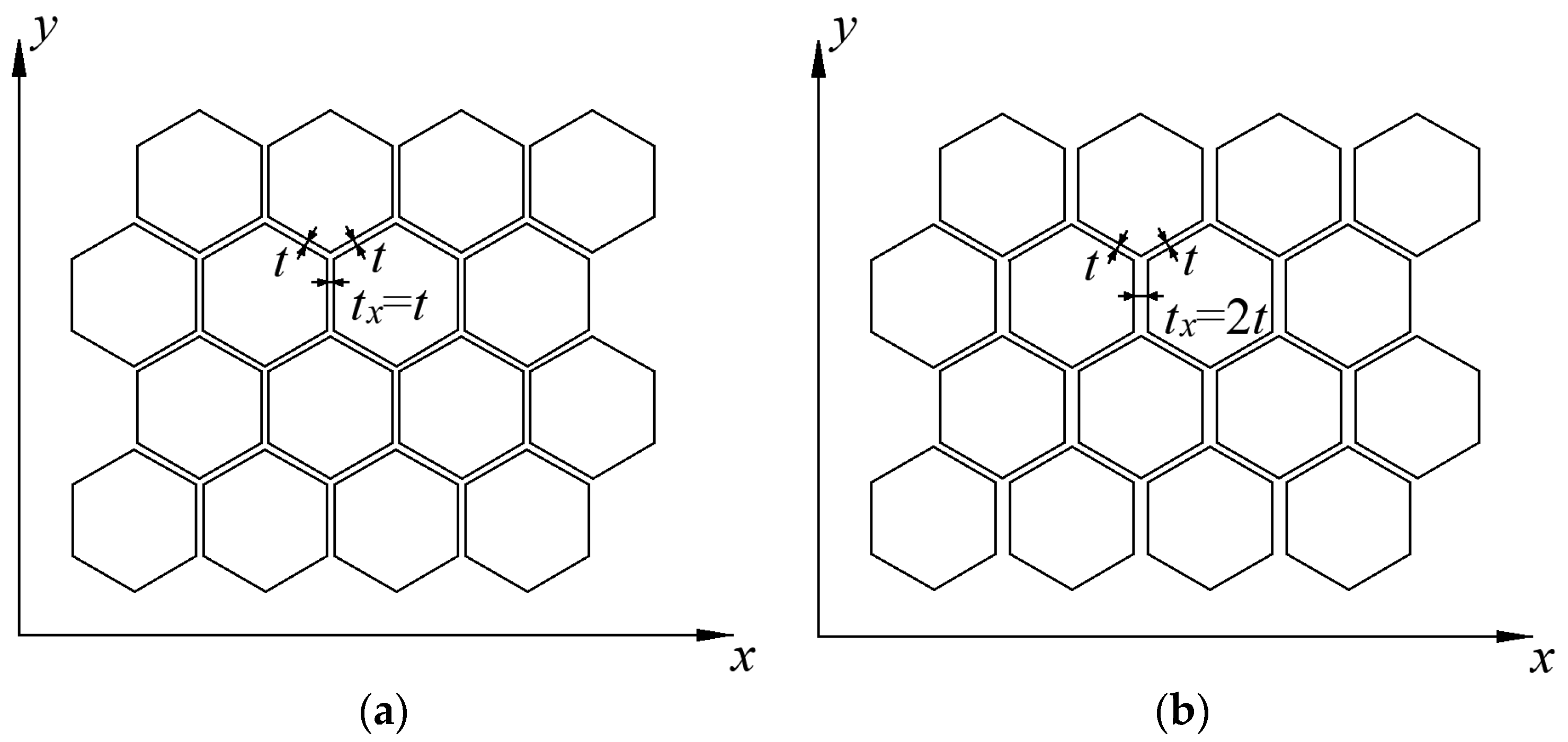
Nomex honeycomb material, a typical composite with soft and brittle characteristics, is prepared from lightweight phenolic resins impregnated with aramid paper and is a honeycomb core composite with favorable properties [
1,
2]. The aramid paper matrix provides the material with flame retardancy, corrosion resistance, electrical insulation, as well as good electromagnetic permeability and high temperature stability [
3,
4]. Additionally, due to the topology of the honeycomb structure, Nomex honeycomb composites possess several mechanical properties, such as high specific strength, high specific stiffness, negative Poisson’s ratio, resilience, and vibration damping properties [
5,
6]. These physical and chemical properties have made Nomex honeycomb materials a popular choice among aerospace vehicle designers. They are widely used in various modern aerospace applications [
7,
8,
9,
10,
11].
The conventional fixation of Nomex honeycomb composites primarily relies on double-sided adhesive tapes, which necessitate special fixtures tailored to the contour characteristics of the honeycomb parts [
12,
13]. During the fixing process, one side of the blank is aligned with the contour side of the special tooling, and the bottom of the part is secured by the adhesive effect of the double-sided tape. After machining, alcohol must be sprayed on the part-holding surface to release it. This traditional fixation process incurs high material and labor costs, involves lengthy preparation times, and the alcohol used can damage the outer contour morphology of the target part, affecting its performance in use [
10].
There are various clamping methods for metal parts, which can be broadly categorized into dedicated and flexible fixtures [
14,
15]. Specialized fixtures can efficiently clamp machine-shaped parts [
16]. Naeem et al. [
17] designed a new milling fixture pallet system using Fusion 360 CAD/CAM, capable of clamping 10 alligator jaws on an inter-changeable pallet with good repeatability and no deformation. Aoyama et al. [
18] designed a multipin support frame to clamp slender metal workpieces, effectively suppressing workpiece deformation caused by machining forces. However, specialized fixtures have high manufacturing costs, poor robustness, and limited generalizability, which flexible fixtures can mitigate [
19,
20]. Under the influence of a magnetic field, magnetic fluid can be transformed from liquid to solid in a few milliseconds, making it an ideal material for flexible clamping [
21,
22]. Ma et al. [
23] developed a flexible fixture based on magnetorheological fluid (MRF), utilizing its rapid state transformation to inhibit regeneration and vibration during metal workpiece machining. Liu et al. [
24,
25] innovatively proposed a green ice-based fixture (IBF), which securely holds parts throughout the machining process to inhibit deformation, offering a low-cost, stress-free clamping method that reduces clamping-induced damage. Recently, vacuum adsorption fixtures have been adopted for fabricating thin-walled workpieces. Hu et al. [
26] employed reconfigurable vacuum fixtures to hold aircraft skins during trimming. These methods have advanced the clamping process for metal parts, though little research has been conducted on the clamping process for Nomex honeycomb composites.
To improve the processing efficiency and reduce the manufacturing cost of Nomex honeycomb composites, new holding methods tailored to their material characteristics have been proposed. Liu et al. [
27] proposed a honeycomb paper workpiece holding method based on a magnetic field control platform and spring precompression, coupled with an iron-powder-filled actuator mechanism to achieve a tight fit of the workpiece to the mold surface through wall tension generated by the interaction of the magnetic powders and the prepressure of a cylindrical compression spring mechanism. Tavares et al. [
28] proposed a vacuum adsorption-based diaphragm holding method for honeycomb paper workpieces, utilizing the cell closure property of the honeycomb structure to overlay a film on the upper surface of the nonmachined area and adsorb on the lower surface through a vacuum bench to complete the holding of the part. Additionally, a honeycomb core clamping method based on diaphragm bonding supports the bottom of the part using a plastic film or glass fiber-reinforced plastic diaphragm, which is removed after machining [
29]. Some scholars utilize the curing properties of polyethylene glycol to fix the lower surface of the part, insert the part while the polyethylene glycol is heated and melted, and clean it with an organic solvent when decoupling [
30,
31].
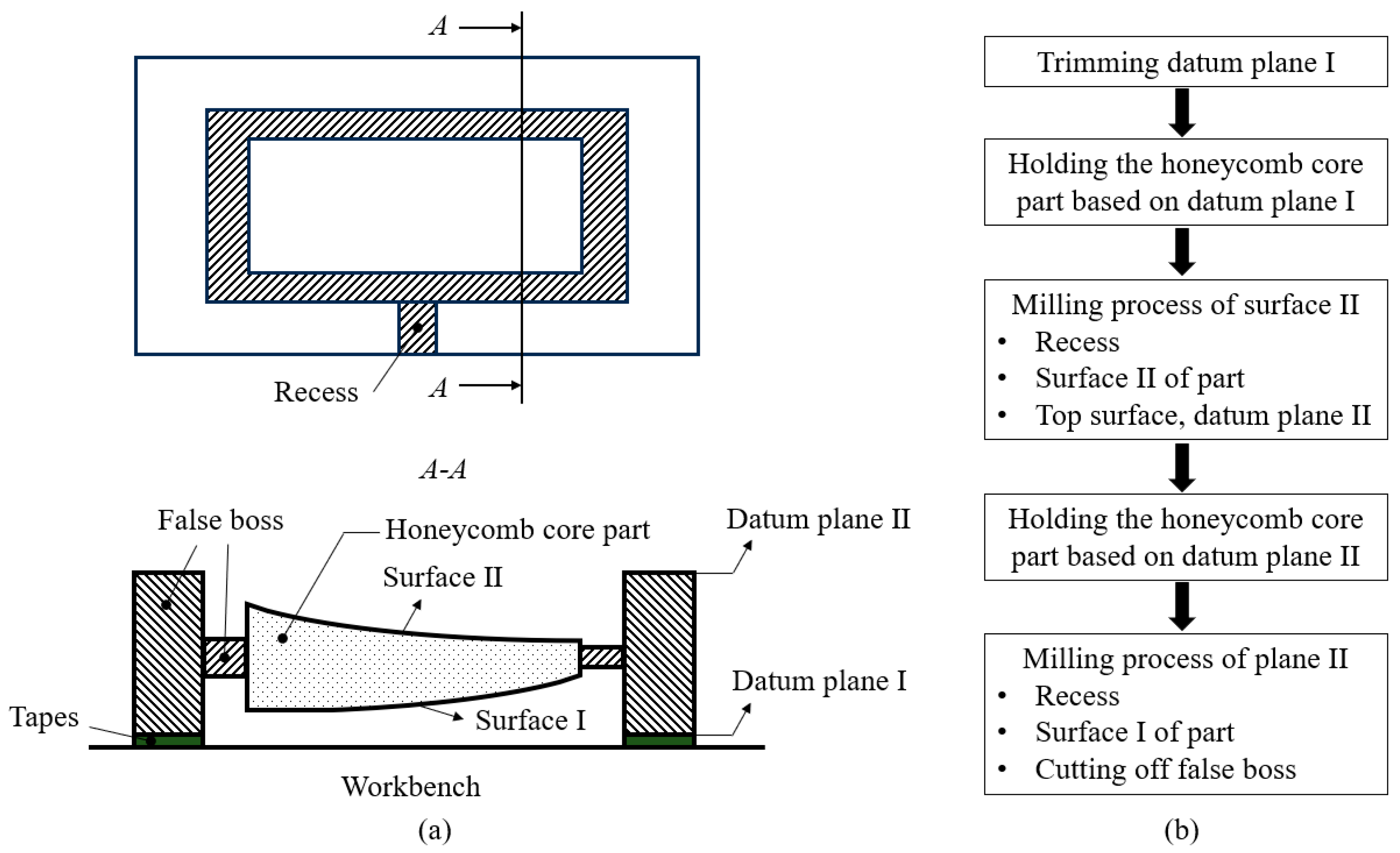
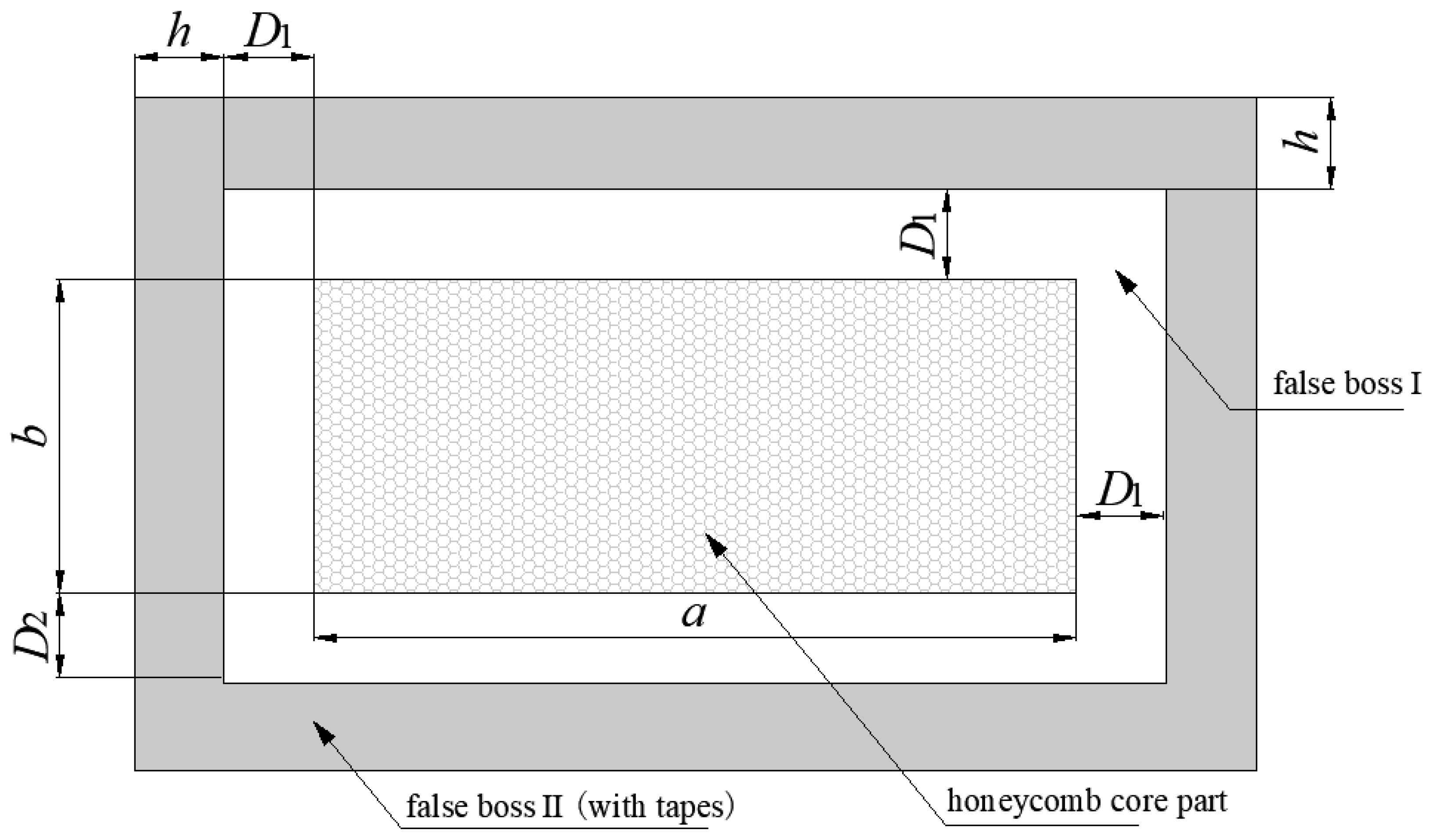
These clamping methods have significantly improved the machining quality of honeycomb core parts. However, they all have the disadvantages of being cumbersome and costly and have long lead times, and they cannot avoid the use of dedicated molds for double-sided honeycomb core parts. To eliminate the reliance on dedicated molds, our team proposed a method for holding honeycomb core parts based on the false boss for Nomex honeycomb composites. A sufficient margin of the false boss is left around the parts, and the false boss is fixed on the general workbench with double-sided adhesive tape. After machining the upper side, the false boss is flipped over, and the lower side is machined. This method avoids the use of specialized tooling, dramatically reduces the overall process preparation time, and avoids direct contact with organic solvents on the part. However, the critical parameters for the false boss, such as the width of the false boss, still rely heavily on engineers’ experience, leading to a high safety margin in actual production, which often results in a large amount of material waste [
32].
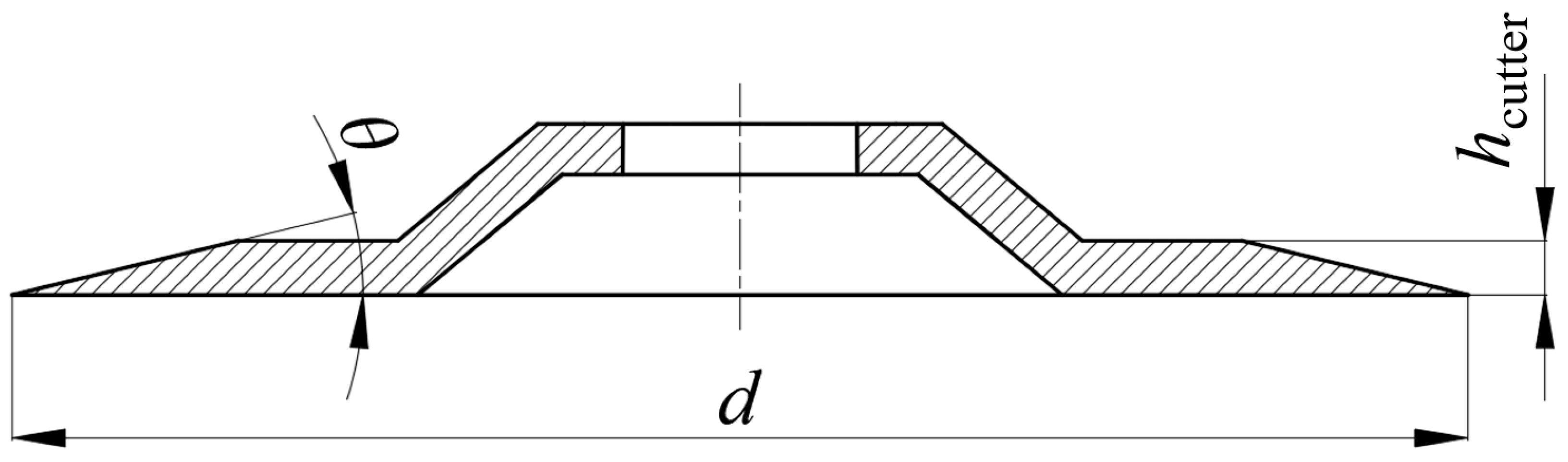
To improve the stability of the honeycomb composite false boss design, a false boss machining model for Nomex honeycomb core parts is proposed in this paper. The false boss model for honeycomb composites was established by simulation, and false boss experiments verified the reliability of the simulation model. Additionally, the stability of the false boss process was analyzed based on the simulation model, and the weak points of the false boss process were studied in different processing areas. The difference in different part shapes was taken into account to obtain reasonable critical parameters of the false boss process, which effectively solved the problem of designing the critical parameters for honeycomb parts, improved the safety and stability of the honeycomb false boss process, and effectively reduced the cost of the manufacturing process.
4. Analysis of Irregular-Shaped Workpieces
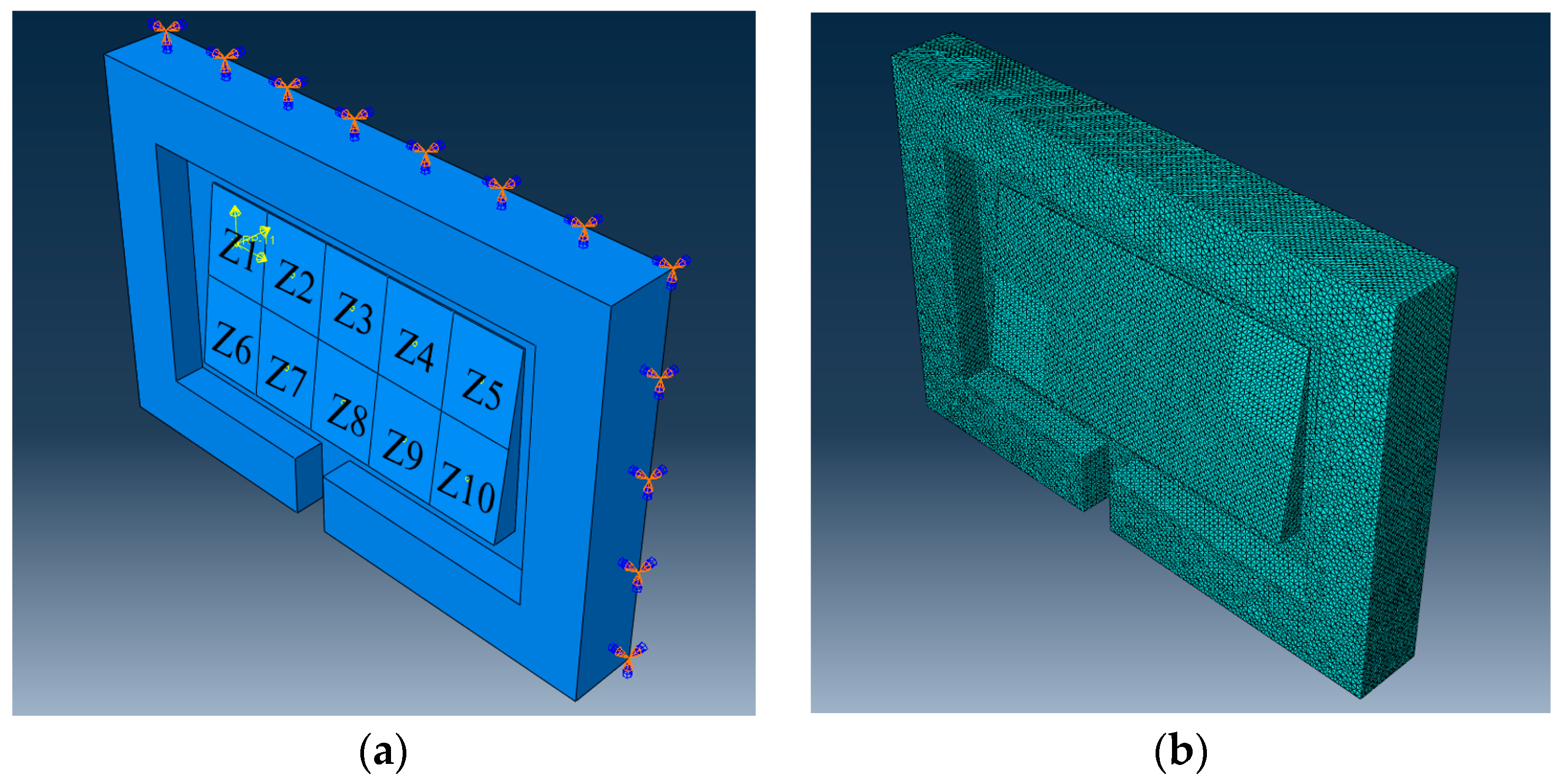
Further, the false boss design for the drum-shaped part and saddle-shaped part was analyzed. Keeping the part in the shape of a wing, surface I and surface II were modified, as shown in
Figure 10. Based on the finite element simulation model in
Section 2, the false boss design of irregular-shaped parts was analyzed. The steps, such as material intrinsic structure and load constraints, were maintained, and only the shape of the part was changed. The simulation results of the drum-shaped part are shown in
Table 6, and the simulation results of the saddle-shaped part are shown in
Table 7.
According to the data in
Table 6 and
Table 7, it can be found that the maximum shear stress of both drum-shaped and saddle-shaped parts decreased and then increased as the width of the false boss was increased from
h = 20 mm to
h = 40 mm, with a minimal value at
h = 30 mm. Therefore, it can be assumed that
h = 30 is the generalized optimal critical parameter for the false boss with different morphological parts. When
h = 30 mm, the maximum shear stresses of the drum-shaped part, standard part, and saddle-shaped part were 0.02580 MPa, 0.03142 MPa, and 0.04022 MPa, respectively. In addition, the above maximum shear stresses at the bottom of the false boss II all occurred as the parts were machined to zone 3. The trend was the same as that of the standard parts.
The local machining stability of the three different shaped parts at
h = 30 mm was further compared, and the results are shown in
Figure 11. The same pattern was found: the maximum shear stress at the bottom was more significant when machining zones 1–4, the maximum shear stress at the bottom was moderate when machining zones 5–6, and the maximum shear stress at the bottom was smaller when machining zones 7–10. In addition, the maximum shear stress of the drum-shaped parts when machining all zones (except zone 9) was the smallest among the three forms of parts, while the maximum shear stress of the saddle-shaped parts when machining all zones (except zone 9) was the largest. It implied that the drum-shaped parts were the most difficult to hold, while the saddle-shaped parts were the easiest to maintain.
Whether it is a standard, drum or saddle-shaped part, zones 6–10 of the part are thicker. Therefore, the cutting force is spread over more area, and the shear stress at the bottom is significantly less than zones 1–5. In addition, we applied cutting force Fx in the x-direction. When machining up to zone 5, the short edge of the false boss (next to Z5) acted as a larger dispersion of the cutting force. When machining the Z1–Z4 area, the short side of the false boss (next to Z5) was farther away, and Fx was mainly supported by the long side (much thinner). It was easy to cause stress concentration. This explains the fact that the maximum stress at the bottom of the tab decreases significantly when machining areas beyond 4.
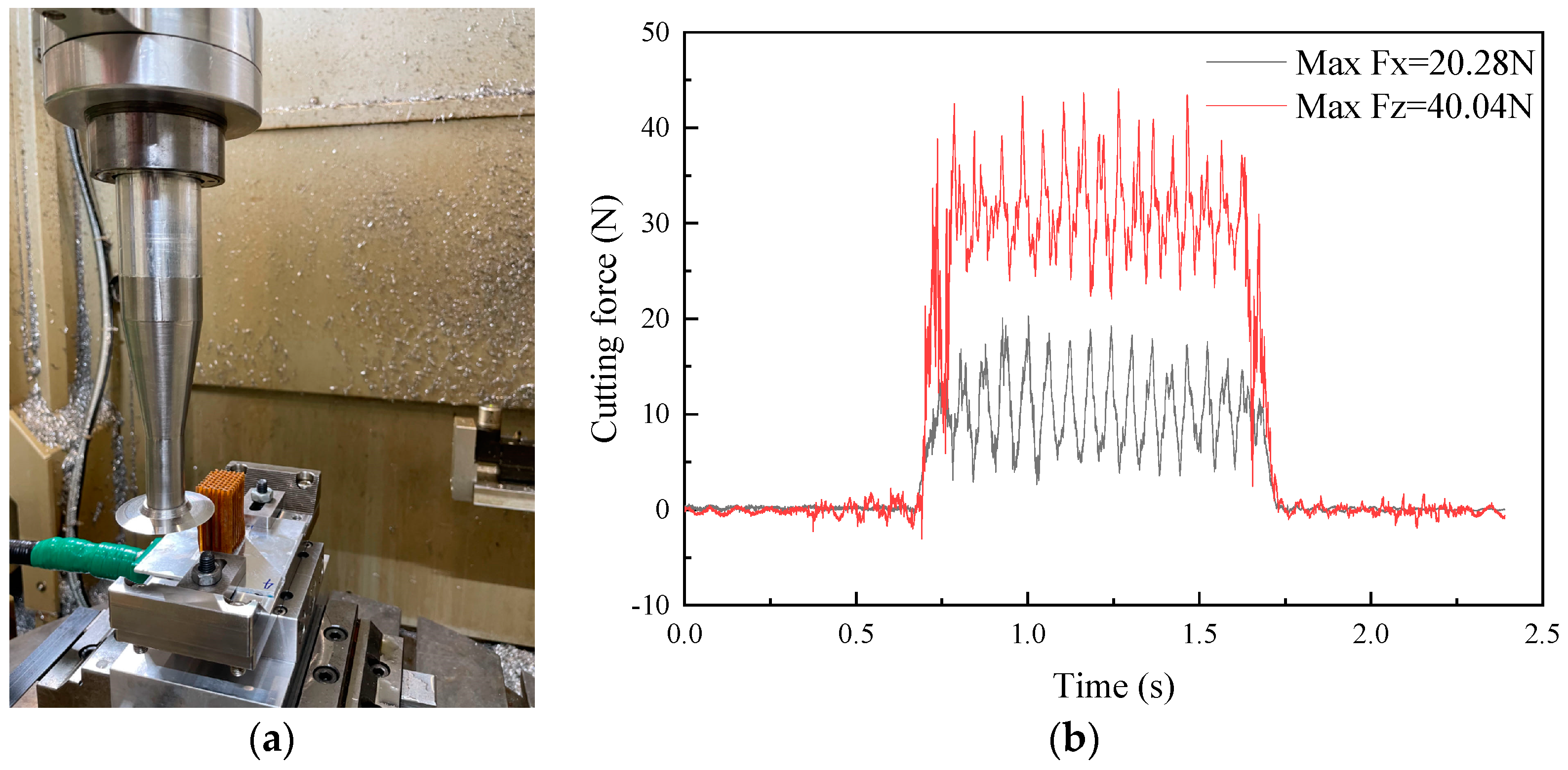





 indicated that the area was not debonded, ▲ indicated that the area appeared to be debonded).
indicated that the area was not debonded, ▲ indicated that the area appeared to be debonded).
 indicated that the area was not debonded, ▲ indicated that the area appeared to be debonded).
indicated that the area was not debonded, ▲ indicated that the area appeared to be debonded).











































































