Finite Element Analysis of Cutting Temperature in Precision Cutting of Composite Energetic Material
Abstract
1. Introduction
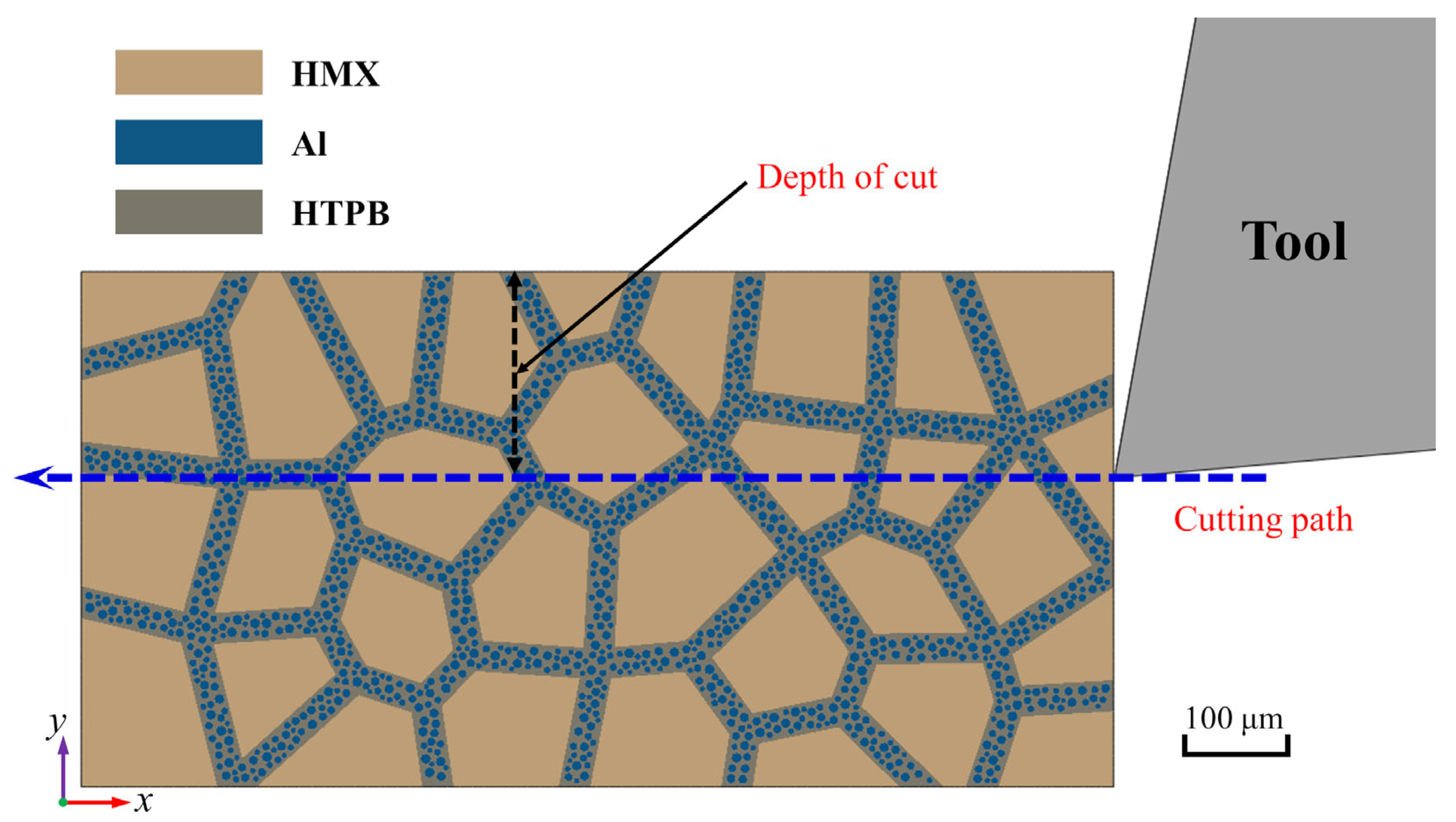
2. FE Modeling of Cutting of Composite Energetic Material
3. Results and Discussion
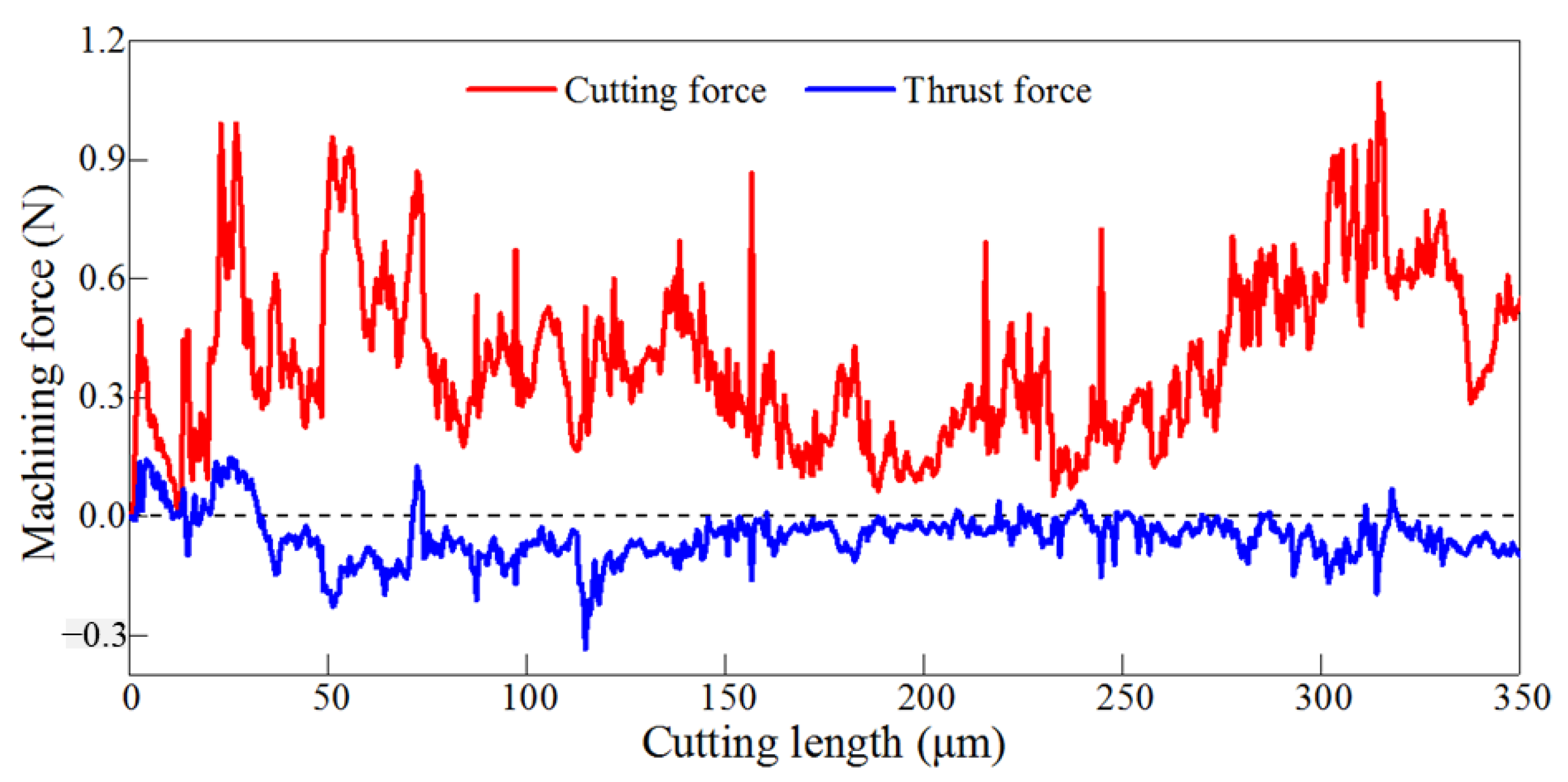
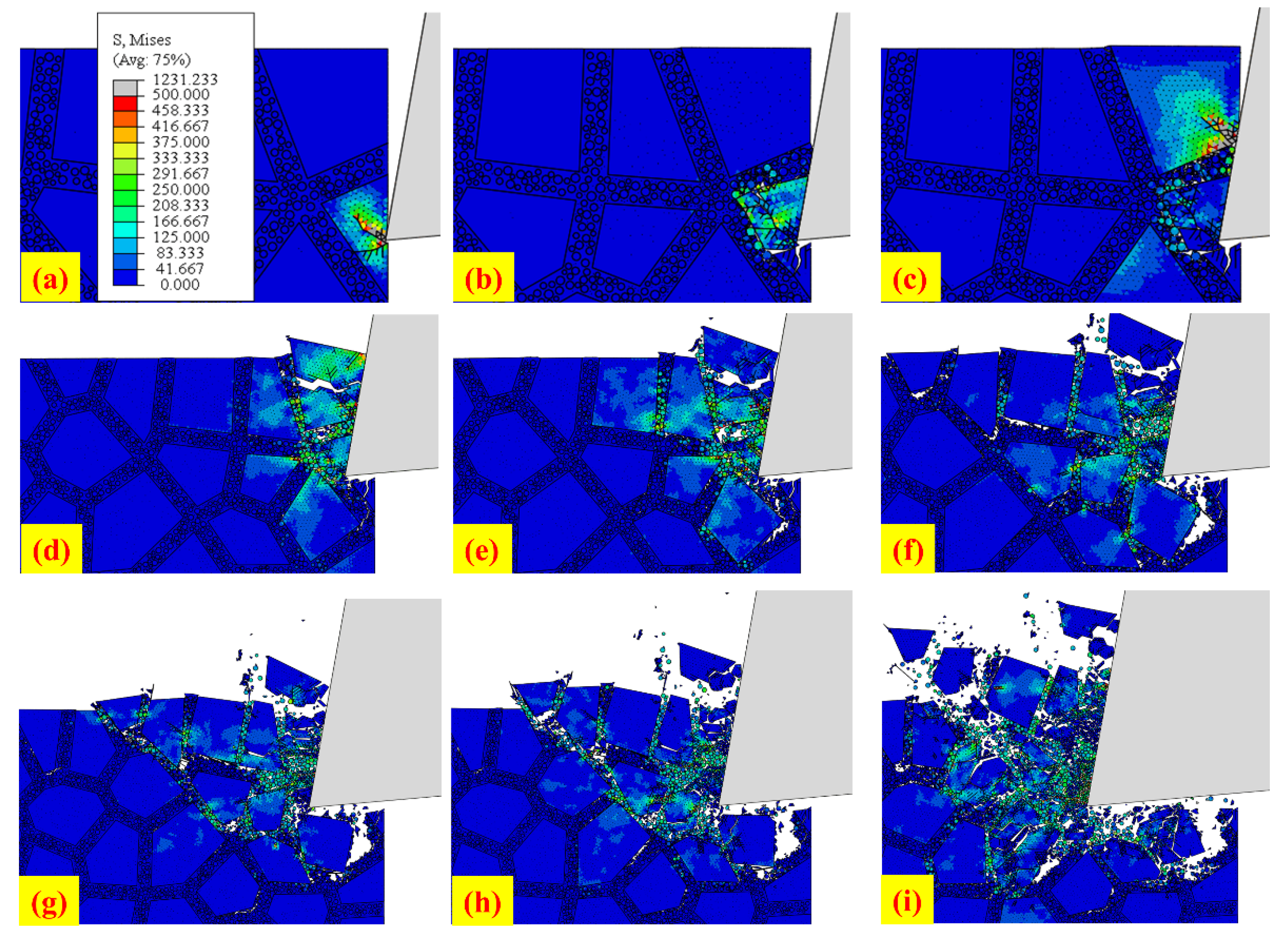
3.1. Cutting Mechanisms of Composite Energetic Material
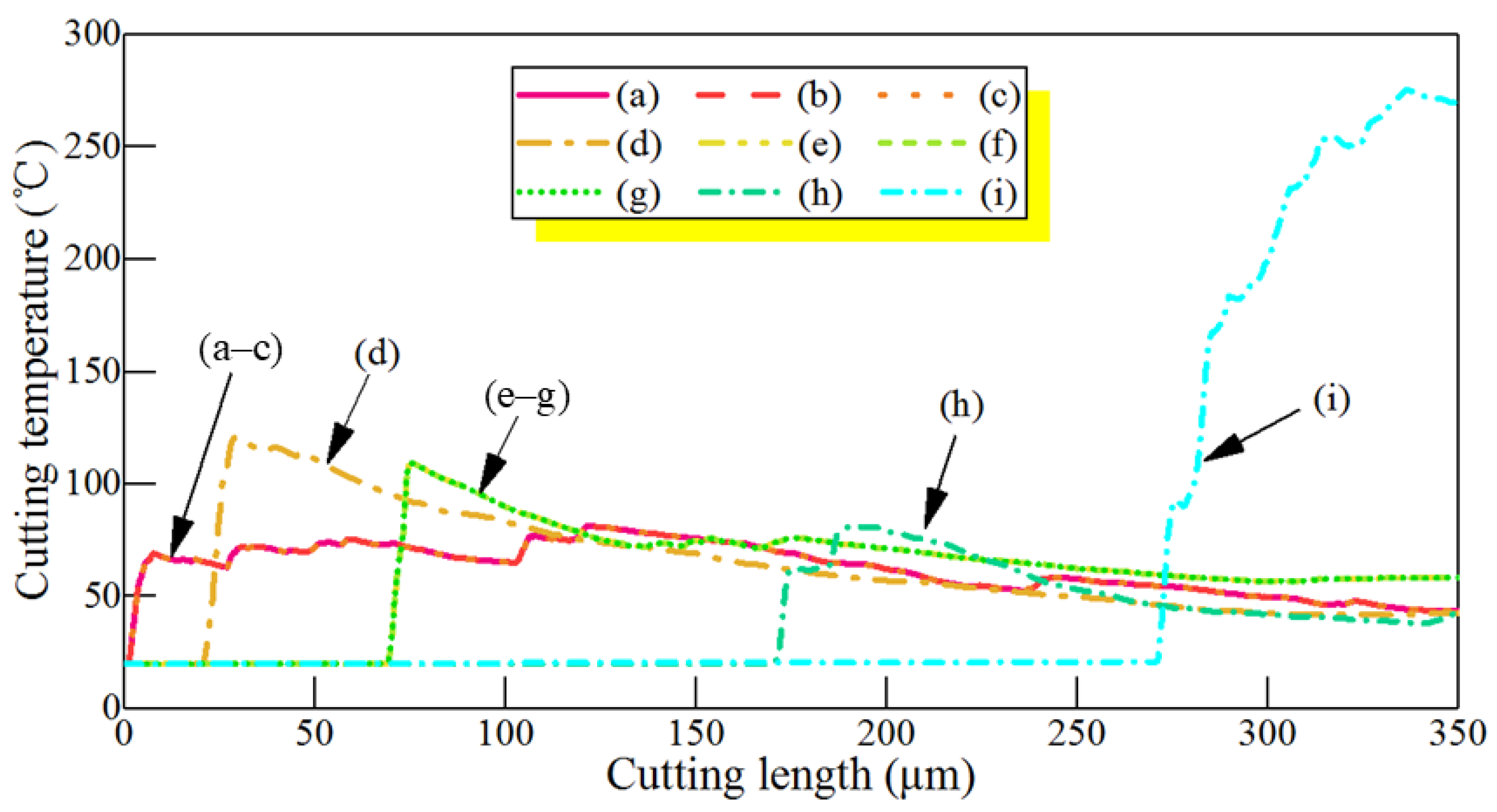
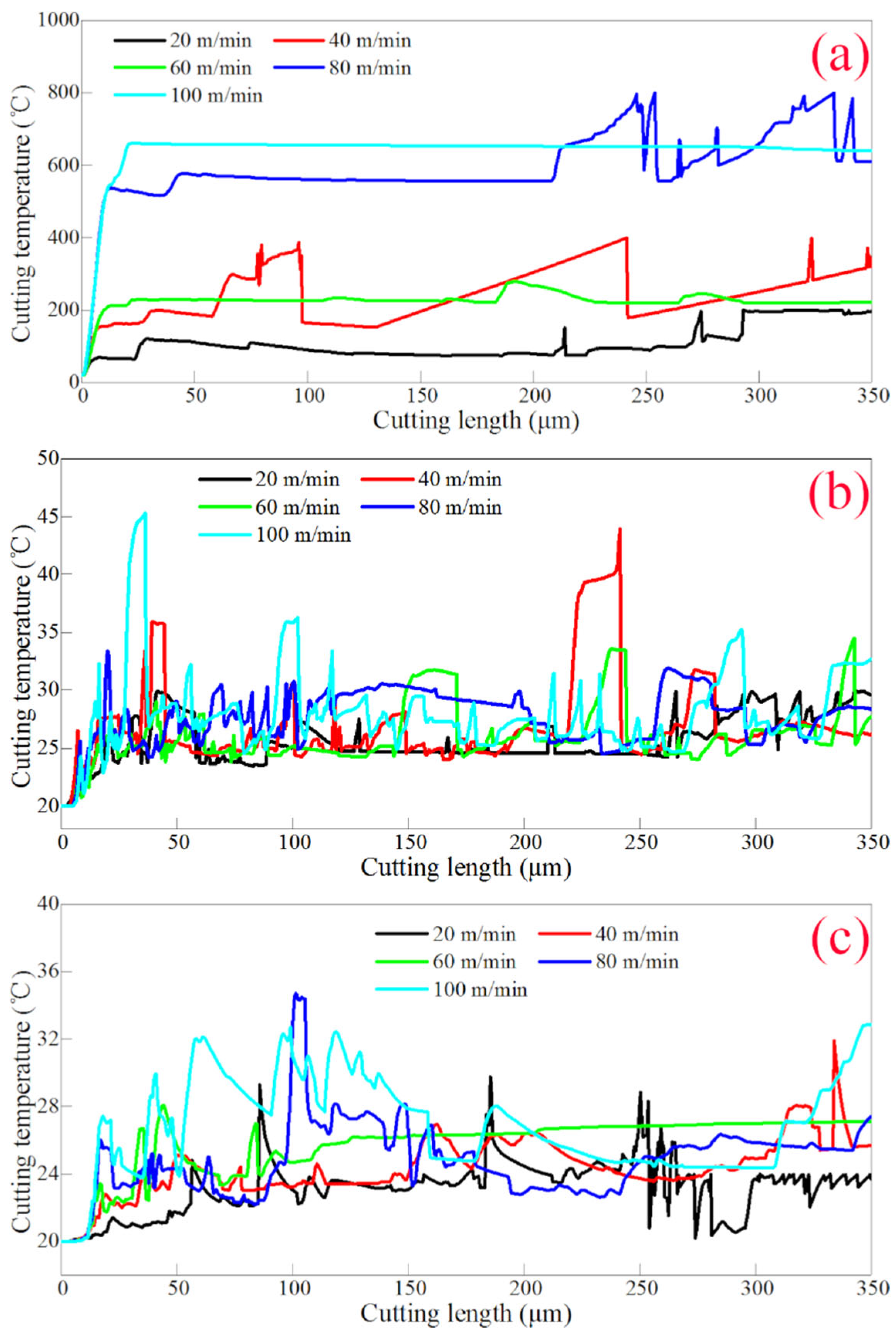
3.2. Influence of Cutting Speed on Cutting Temperature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Altman, I. Burn time of metal nanoparticles. Materials 2019, 12, 1368. [Google Scholar] [CrossRef] [PubMed]
- Zapata, J.; Nicollet, A.; Julien, B.; Lahiner, G.; Esteve, A.; Rossi, C. Self-propagating combustion of sputter-deposited Al/CuO nanolaminates. Combust. Flame 2019, 205, 389–396. [Google Scholar] [CrossRef]
- Griego, C.; Yilmaz, N.; Atmanli, A. Analysis of aluminum particle combustion in a downward burning solid rocket propellant. Fuel 2019, 237, 405–412. [Google Scholar] [CrossRef]
- Yang, Z.; Kang, G.; Liu, R.; Chen, P. Predicting the mechanical behavior of highly particle-filled polymer composites using the nonlinear finite element method. Compos. Struct. 2022, 286, 115275. [Google Scholar] [CrossRef]
- Huang, J.; Lu, S.; Xie, F.; Liu, W.; Xiao, C.; Zhang, J.; Sun, T. Finite element analysis of synergetic deformation in precision cutting of polymer bonded explosive. Mater. Des. 2020, 188, 108471. [Google Scholar] [CrossRef]
- Xie, F.Y.; Zhang, Z.W.; Huang, J.H.; Liu, W.; Xiao, C.W. Cutting Force Response of Orthogonal Cutting of Polymer Bonded Explosive Simulants. Chin. J. Energetic Mater. 2019, 28, 151–156. [Google Scholar]
- Soori, M.; Asmael, M. Cutting temperatures in milling operations of difficult-to-cut materials. J. New Technol. Mater. 2021, 11, 47–56. [Google Scholar] [CrossRef]
- Özbek, O.; Saruhan, H. The effect of vibration and cutting zone temperature on surface roughness and tool wear in eco-friendly MQL turning of AISI D2. J. Mater. Res. Technol. 2020, 9, 2762–2772. [Google Scholar] [CrossRef]
- Sakkaki, M.; Moghanlou, F.S.; Vajdi, M.; Pishgar, F.; Shokouhimehr, M.; Asl, M.S. The effect of thermal contact resistance on the temperature distribution in a WC made cutting tool. Ceram. Int. 2019, 45, 22196–22202. [Google Scholar] [CrossRef]
- He, G.S.; Dai, Y.; Wang, P.; Zhang, C.Y.; Lin, C.M.; Yang, K.; Zhang, J.; Zhong, R.; Liu, S.; Yang, Z.J. Achieving superior thermal conductivity in polymerbonded explosives using a preconstructed 3D graphene framework. Energ. Mater. Front. 2023, 4, 202–212. [Google Scholar] [CrossRef]
- Akiki, M.; Gallagher, T.P.; Menon, S. Mechanistic approach for simulating hot-spot formations and detonation in polymer-bonded explosives. AIAA J. 2017, 55, 585–598. [Google Scholar] [CrossRef]
- Tang, W.; Zong, H.-H.; Wei, Z.-Y.; Huang, J.-H. Influence of ultrasonic vibration cutting on cutting temperature of explosive simulation material. Chin. J. Energ. Mater. 2014, 22, 71–74. [Google Scholar]
- Roeske, F.; Benterou, J.; Lee, R.; Roos, E. Cutting and machining energetic materials with a femtosecond laser. Propellants Explos. Pyrotech. Int. J. Deal. Sci. Technol. Asp. Energ. Mater. 2003, 28, 53–57. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, J.; Zhang, J.; Dai, H.; Hartmaier, A.; Sun, T. Numerical simulation of materials-oriented ultra-precision diamond cutting: Review and outlook. Int. J. Extrem. Manuf. 2023, 5, 022001. [Google Scholar] [CrossRef]
- Liu, R.P.; Jia, X.Z.; Wang, Y.S. Theoretical analysis and numerical simulation on influence factors of cutting temperature of explosive charge. Chin. J. Explos. Propellants 2018, 41, 484–488. [Google Scholar]
- Yang, Y.; Zhu, W. Study on cutting temperature during milling of titanium alloy based on FEM and experiment. Int. J. Adv. Manuf. Technol. 2014, 73, 1511–1521. [Google Scholar] [CrossRef]
- Dandekar, C.R.; Shin, Y.C. Multi-step 3-D finite element modeling of subsurface damage in machining particulate reinforced metal matrix composites. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1231–1239. [Google Scholar] [CrossRef]
- Bhagavat, S.; Kao, I. A finite element analysis of temperature variation in silicon wafers during wiresaw slicing. Int. J. Mach. Tools Manuf. 2008, 48, 95–106. [Google Scholar] [CrossRef]
- Moradi, M.; Moghadam, M.K.; Shamsborhan, M.; Beiranvand, Z.M.; Rasouli, A.; Vahdati, M.; Bakhtiari, A.; Bodaghi, M. Simulation, statistical modeling, and optimization of CO2 laser cutting process of polycarbonate sheets. Optik 2021, 225, 164932. [Google Scholar] [CrossRef]
- Barua, A.; Zhou, M. A Lagrangian framework for analyzing microstructural level response of polymer-bonded explosives. Model. Simul. Mater. Sci. Eng. 2011, 19, 055001. [Google Scholar] [CrossRef]
- Miller, C.; Olsen, D.; Wei, Y.; Zhou, M. Three-dimensional microstructure-explicit and void-explicit mesoscale simulations of detonation of HMX at millimeter sample size scale. J. Appl. Phys. 2020, 127, 125105. [Google Scholar] [CrossRef]
- Duarte, C.A.; Koslowski, M. Hot-spots in polycrystalline β-tetramethylene tetranitramine (β-HMX): The role of plasticity and friction. J. Mech. Phys. Solids 2023, 171, 105157. [Google Scholar] [CrossRef]
- Coffelt, C.; Olsen, D.; Miller, C.; Zhou, M. Effect of void positioning on the detonation sensitivity of a heterogeneous energetic material. J. Appl. Phys. 2022, 131, 065101. [Google Scholar] [CrossRef]
- Walters, D.J.; Luscher, D.J.; Yeager, J.D.; Patterson, B.M. Cohesive finite element modeling of the delamination of HTPB binder and HMX crystals under tensile loading. Int. J. Mech. Sci. 2018, 140, 151–162. [Google Scholar] [CrossRef]
- Schwer, L.E.; Windsor, C.A. Aluminum plate perforation: A comparative case study using Lagrange with erosion, multi-material ALE, and smooth particle hydrodynamics. In Proceedings of the 7th European LS-DYNA Conference, Salzburg, Austria, 14–15 May 2009; p. 28. [Google Scholar]
- Roy, U.; Kim, S.; Miller, C.; Horie, Y.; Zhou, M. Computational study of ignition behavior and hotspot dynamics of a potential class of aluminized explosives. Model. Simul. Mater. Sci. Eng. 2018, 26, 085004. [Google Scholar] [CrossRef]
- Keyhani, A.; Kim, S.; Horie, Y.; Zhou, M. Energy dissipation in polymer-bonded explosives with various levels of constituent plasticity and internal friction. Comput. Mater. Sci. 2019, 159, 136–149. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, J.H.; Yin, R.; Tang, W. Micro-appearance and formation mechanisms of PBX cutting surface. Acta Armamentarii 2010, 31, 1337–1340. [Google Scholar]
- Tang, Z.; Yang, L.; Qiao, X.J.; Zhang, T.L.; Yu, W.F. On thermal decomposition kinetics and thermal safety of HMX. Chin. J. Energetic Mater. 2011, 19, 396–400. [Google Scholar]
- Ni, F.D.; Cong, W.L. Ultrasonic vibration-assisted (UV-A) manufacturing processes: State of the art and future perspectives. J. Manuf. Process. 2020, 51, 174–190. [Google Scholar]
- Kawade, P.; Bokade, S. Review of cooling techniques used in metal cutting processes. Adv. Mater. Process. Technol. 2022, 9, 1137–1182. [Google Scholar] [CrossRef]





| Material | Unit | HMX | HTPB | Al | Tool |
|---|---|---|---|---|---|
| Density | g/cm3 | 1.58 | 0.9 | 2.8 | 3.52 |
| Young’s modulus | MPa | 25,352 | 0.77 | 69,000 | 1,147,000 |
| Poisson’s ratio | — | 0.25 | 0.499 | 0.33 | 0.07 |
| Thermal conductivity | W/(m·K) | 193 | 123 | 193 | 2100 |
| Specific heat capacity | J/(Kg·K) | 1254 | 1500 | 2000 | 525 |
| Parameters | Unit | Value |
|---|---|---|
| Cutting speed | m/min | 20.0, 40.0, 60.0, 80.0, 100.0 |
| Depth of cut | μm | 200 |
| Edge radius | μm | 0 |
| Rake angle | ° | 10 |
| Relief angle | ° | 5 |
| Element Position | Unit | Interior of HMX | Interior of HTPB | HMX-HTPB Interface |
|---|---|---|---|---|
| Initial separation distance | μm | 0.05 | 0.01 | 0.0462 |
| Critical tensile stress | MPa | 100 | 38.4 | 35 |
| Destruction separation | μm | 5 | 10 | 4.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, C.; Lu, S.; Zhang, W.; Zhang, J.; Liu, J. Finite Element Analysis of Cutting Temperature in Precision Cutting of Composite Energetic Material. J. Compos. Sci. 2024, 8, 525. https://doi.org/10.3390/jcs8120525
Xiao C, Lu S, Zhang W, Zhang J, Liu J. Finite Element Analysis of Cutting Temperature in Precision Cutting of Composite Energetic Material. Journal of Composites Science. 2024; 8(12):525. https://doi.org/10.3390/jcs8120525
Chicago/Turabian StyleXiao, Caiwei, Shijin Lu, Wenxin Zhang, Junjie Zhang, and Junwei Liu. 2024. "Finite Element Analysis of Cutting Temperature in Precision Cutting of Composite Energetic Material" Journal of Composites Science 8, no. 12: 525. https://doi.org/10.3390/jcs8120525
APA StyleXiao, C., Lu, S., Zhang, W., Zhang, J., & Liu, J. (2024). Finite Element Analysis of Cutting Temperature in Precision Cutting of Composite Energetic Material. Journal of Composites Science, 8(12), 525. https://doi.org/10.3390/jcs8120525









