Development of a Shape Replicating Draping Unit for Continuous Layup of Unidirectional Non-Crimp Fabrics on Complex Surface Geometries
Abstract
1. Introduction
2. Materials and Methods
2.1. Fiber Fabric Model
2.2. Experimantal Setup and Metrology
3. Results
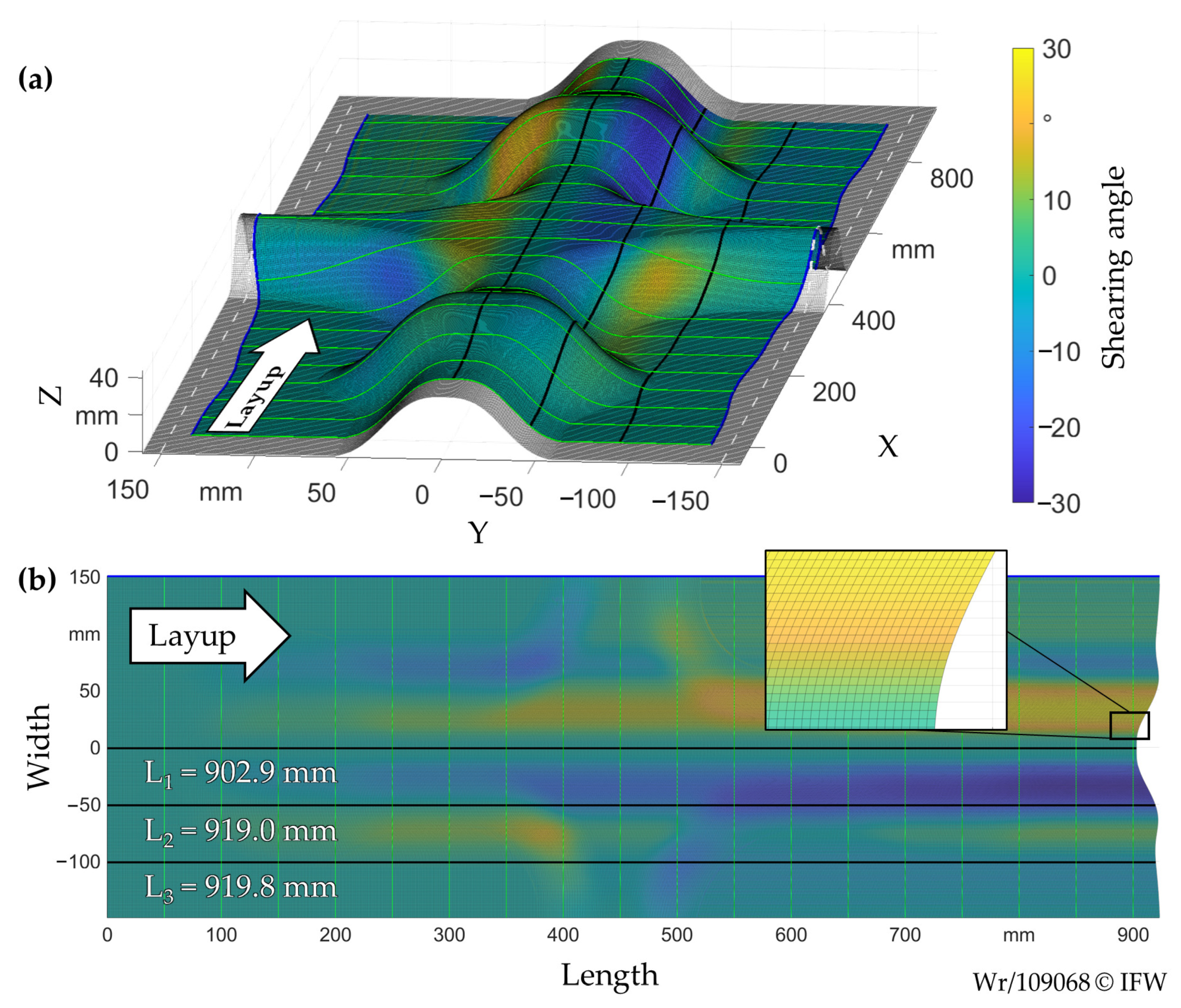
3.1. Kinematic Draping Simulation
3.2. Process Modeling
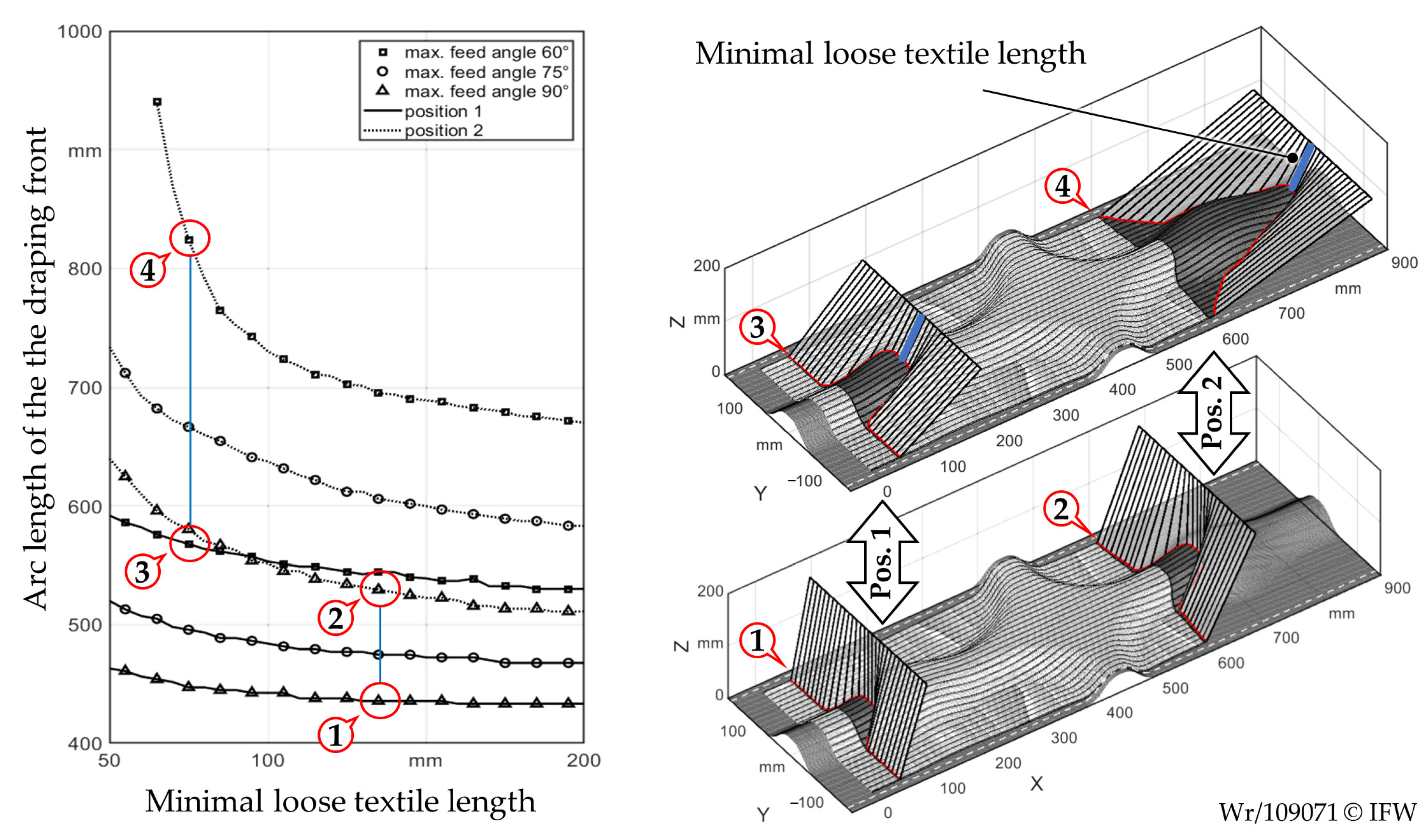
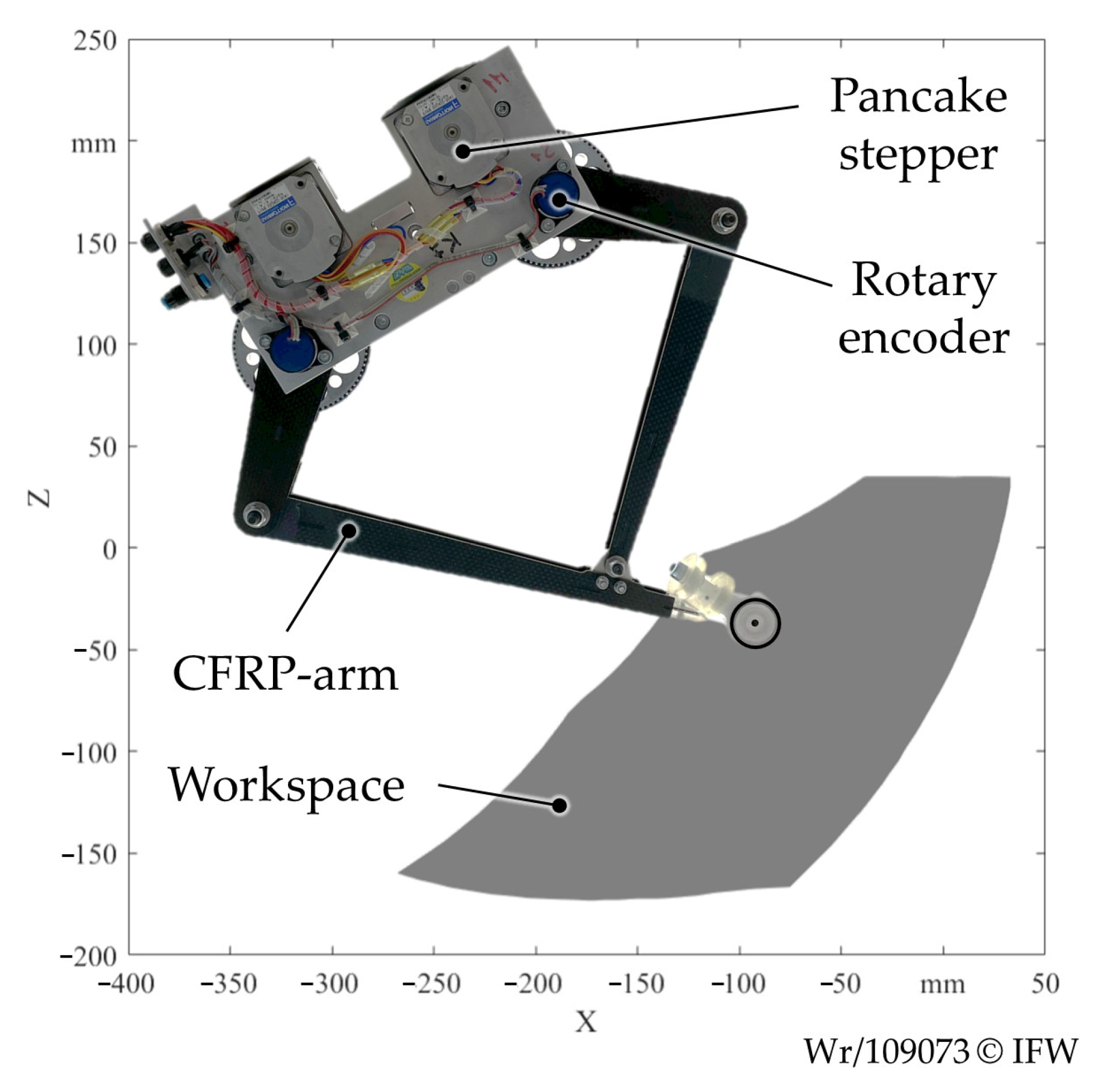
3.3. Development of the Draping Unit
3.3.1. Kinematics for Support Point Positioning
3.3.2. Fluid-Driven Consolidation Element
3.3.3. Pivoting Connection for Tangential Continuity
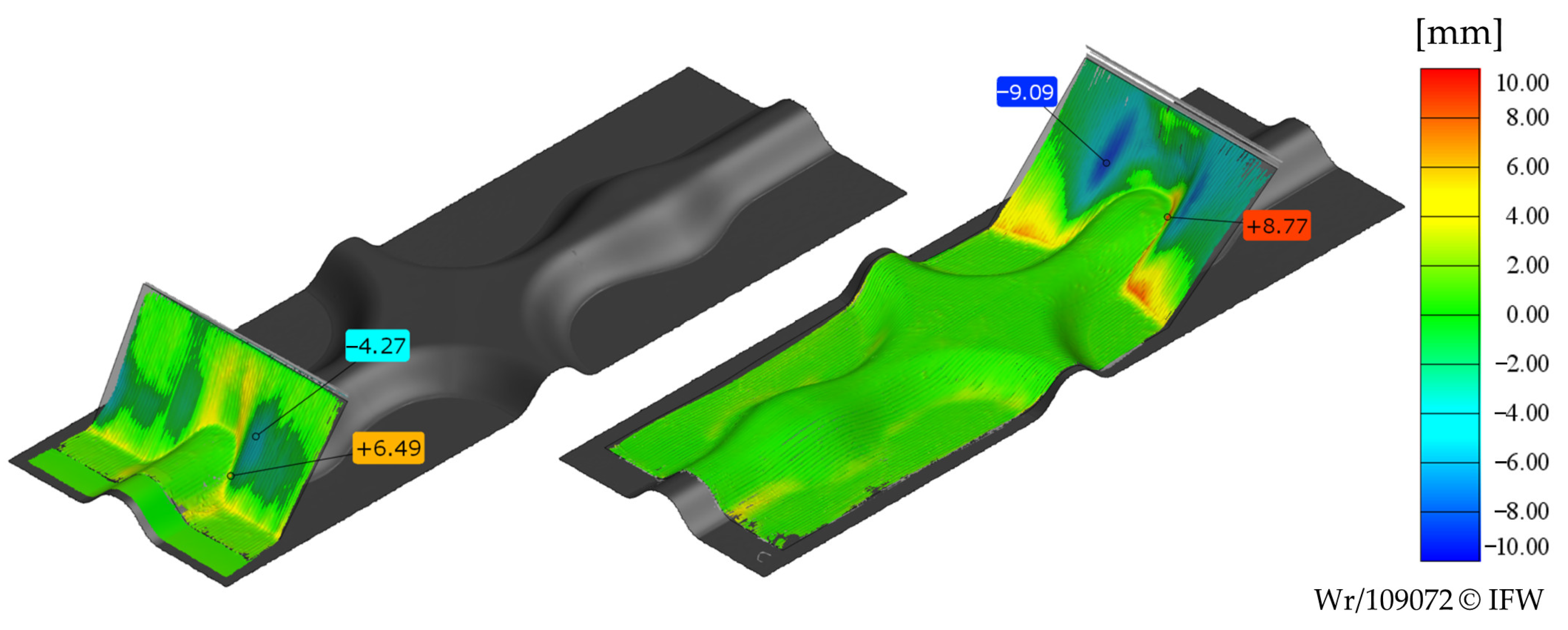
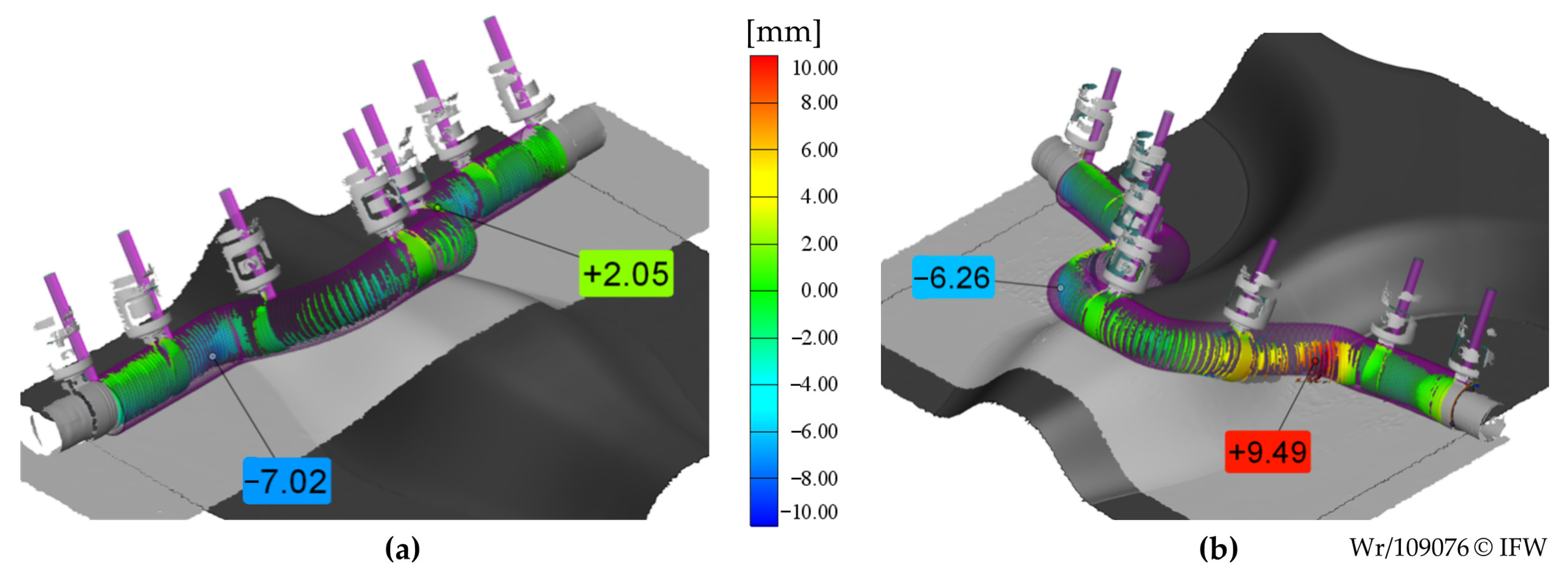
3.3.4. Investigation of Shape Replication Ability
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deniz, O.; Horst, P.; Schmidt, C. Production-based Multi-criteria Design Optimisation of an Unconventional Composite Fuselage Side Panel by Evolutionary Strategies and a Surrogate Model of Manufacturability Analysis. In Proceedings of the 11th World Congress on Structural and Multidisciplinary Optimisation, Sydney, Australia, 7–12 June 2015. [Google Scholar]
- Szcesny, M.; Heieck, F.; Carosella, S.; Middendorf, P.; Sehrschön, H.; Schneiderbauer, M. The advanced ply placement process-an innovative direct 3D placement technology for plies and tapes. Adv. Manuf. Polym. Compos. Sci. 2017, 3, 2–9. [Google Scholar] [CrossRef]
- Helber, F.; Amann, A.; Carosella, S.; Middendorf, P. Intrinsic fibre heating: A novel approach for automated dry fibre placement. IOP Conf. Ser. Mater. Sci. Eng. 2018, 406, 012064. [Google Scholar] [CrossRef]
- Niefnecker, D. AZIMUT-Automatisierung Zukunftsweisender Industrieller Methoden und Technologien für CFK-Rümpfe, Abschlussbericht; Laufzeit des Vorhabens: 01.01.2010–30-06.2014; Premium AEROTEC GmbH: Augsburg, Germany, 2014. [Google Scholar] [CrossRef]
- Kaumfann, P.; Braun, G.; Buchheim, A.; Malecha, M. Automated Draping of Wide Textiles on Double Curved Surfaces; SCITEPRESS-Science and Technology Publications: Augsburg, Germany, 2019. [Google Scholar]
- Richrath, M.; Franke, J.; Ohlendorf, J.-H.; Thoben, K.-D. Effector for automated direct textile placement in rotor blade production. Light. Des. Worldw. 2017, 10, 42–47. [Google Scholar] [CrossRef]
- Zhu, S.; Magnussen, C.J.; Judd, E.L.; Frank, M.C.; Peters, F.E. Automated Composite Fabric Layup for Wind Turbine Blades. J. Manuf. Sci. Eng. 2017, 139, 061001. [Google Scholar] [CrossRef]
- Gardiner, G. Automated Preforming, Part 2: Glide Forming. Available online: https://www.compositesworld.com/blog/post/automated-preforming-glide-forming (accessed on 5 February 2020).
- Redondo, C.B. A+ Glide Forming System/Automatic Stringer Manufacturing Technology. In Proceedings of the SAMPE Conference, Long Beach, CA., USA, 23–26 May 2016. [Google Scholar]
- Bruns, C.; Micke-Camuz, M.; Bohne, F.; Raatz, A. Process design and modelling methods for automated handling and draping strategies for composite components. CIRP Ann. 2018, 67, 1–4. [Google Scholar] [CrossRef]
- Cherouat, A.; Bourouchaki, H. Numerical Tools for Composite Woven Fabric Preforming. Adv. Mater. Sci. Eng. 2013, 2013, 1–18. [Google Scholar] [CrossRef]
- Shuai, C. Fabric Forming Simulation and Process Optimisation for Composites. Ph.D. Thesis, University of Nottingham, Nottingham, UK, September 2016. [Google Scholar]
- Mack, C.; Taylor, H.M. 39—The Fitting of Woven Cloth to Surfaces. J. Text. Inst. Trans. 1956, 47, T477–T488. [Google Scholar] [CrossRef]
- Denkena, B.; Schmidt, C.; Werner, S. Continuous Draping of Double Curved Geometries. In Proceedings of the SAMPE Europe Conference, Southampton, UK, 11–13 September 2018. [Google Scholar]
- Krishnan, G.; Bishop-Moser, J.; Kim, C.; Kota, S. Kinematics of a Generalized Class of Pneumatic Artificial Muscles. J. Mech. Robot. 2015, 7, 041014. [Google Scholar] [CrossRef]





| Manufacturer | Area Density | Reinforcement Yarn | Weft |
|---|---|---|---|
| Gerster TechTex | 395 g/m2 | 0° CF 24k 1600 tex | Polyester: 5, 4 weft/cm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Denkena, B.; Schmidt, C.; Werner, S.; Schwittay, D. Development of a Shape Replicating Draping Unit for Continuous Layup of Unidirectional Non-Crimp Fabrics on Complex Surface Geometries. J. Compos. Sci. 2021, 5, 93. https://doi.org/10.3390/jcs5040093
Denkena B, Schmidt C, Werner S, Schwittay D. Development of a Shape Replicating Draping Unit for Continuous Layup of Unidirectional Non-Crimp Fabrics on Complex Surface Geometries. Journal of Composites Science. 2021; 5(4):93. https://doi.org/10.3390/jcs5040093
Chicago/Turabian StyleDenkena, Berend, Carsten Schmidt, Simon Werner, and Dietmar Schwittay. 2021. "Development of a Shape Replicating Draping Unit for Continuous Layup of Unidirectional Non-Crimp Fabrics on Complex Surface Geometries" Journal of Composites Science 5, no. 4: 93. https://doi.org/10.3390/jcs5040093
APA StyleDenkena, B., Schmidt, C., Werner, S., & Schwittay, D. (2021). Development of a Shape Replicating Draping Unit for Continuous Layup of Unidirectional Non-Crimp Fabrics on Complex Surface Geometries. Journal of Composites Science, 5(4), 93. https://doi.org/10.3390/jcs5040093






