Assessment of Analytical Orientation Prediction Models for Suspensions Containing Fibers and Spheres
Abstract
1. Introduction
1.1. Motivation
1.2. Measuring Fiber Orientation States by Orientation Tensors
1.3. Orientation Prediction by Jeffery and Folgar Tucker
1.4. Further Analytical Orientation Prediction Models
2. Method
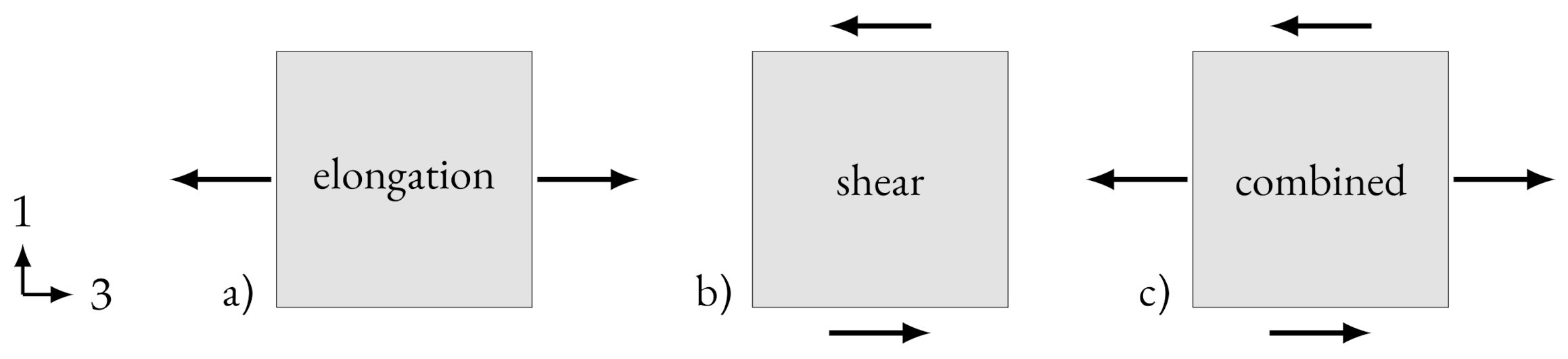
2.1. Suspension Simulations
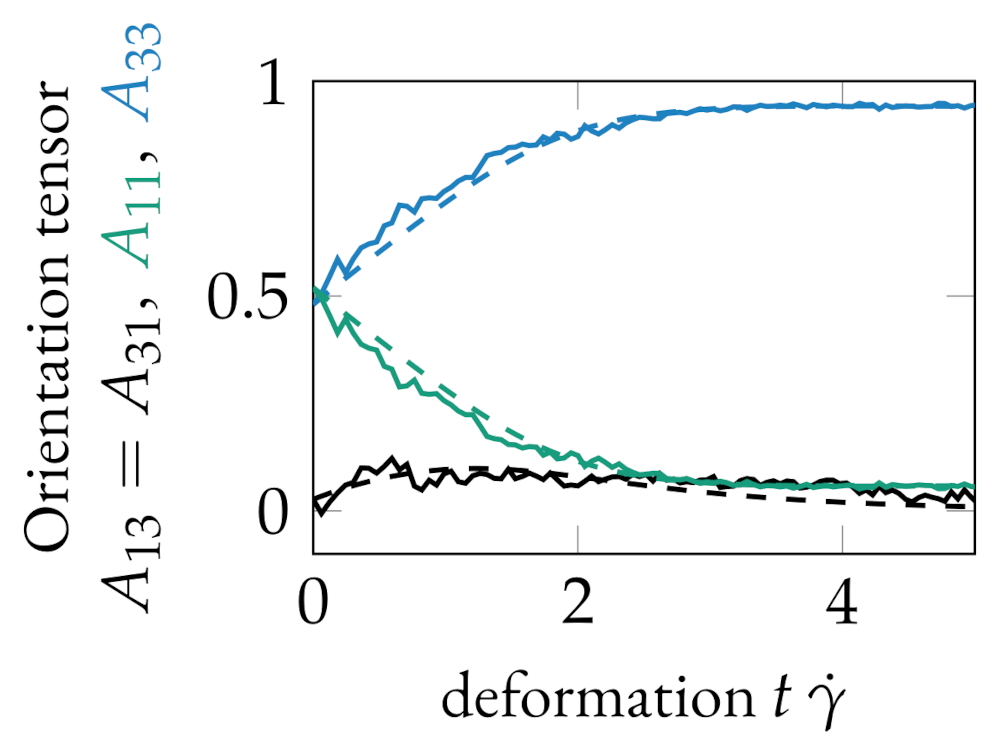
2.2. Computation of FT Parameters
3. Results
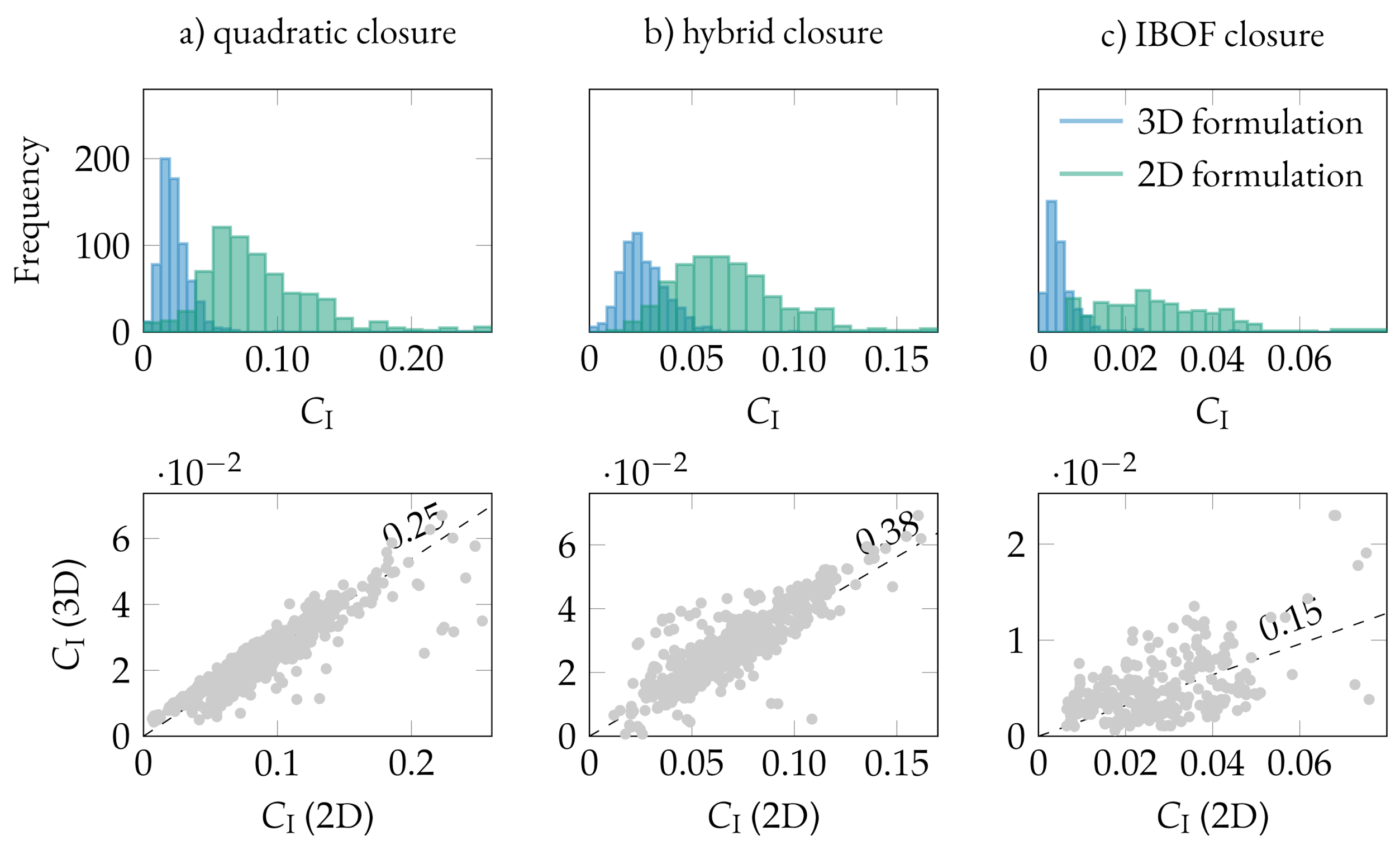
3.1. Influence of the FT Model Formulation
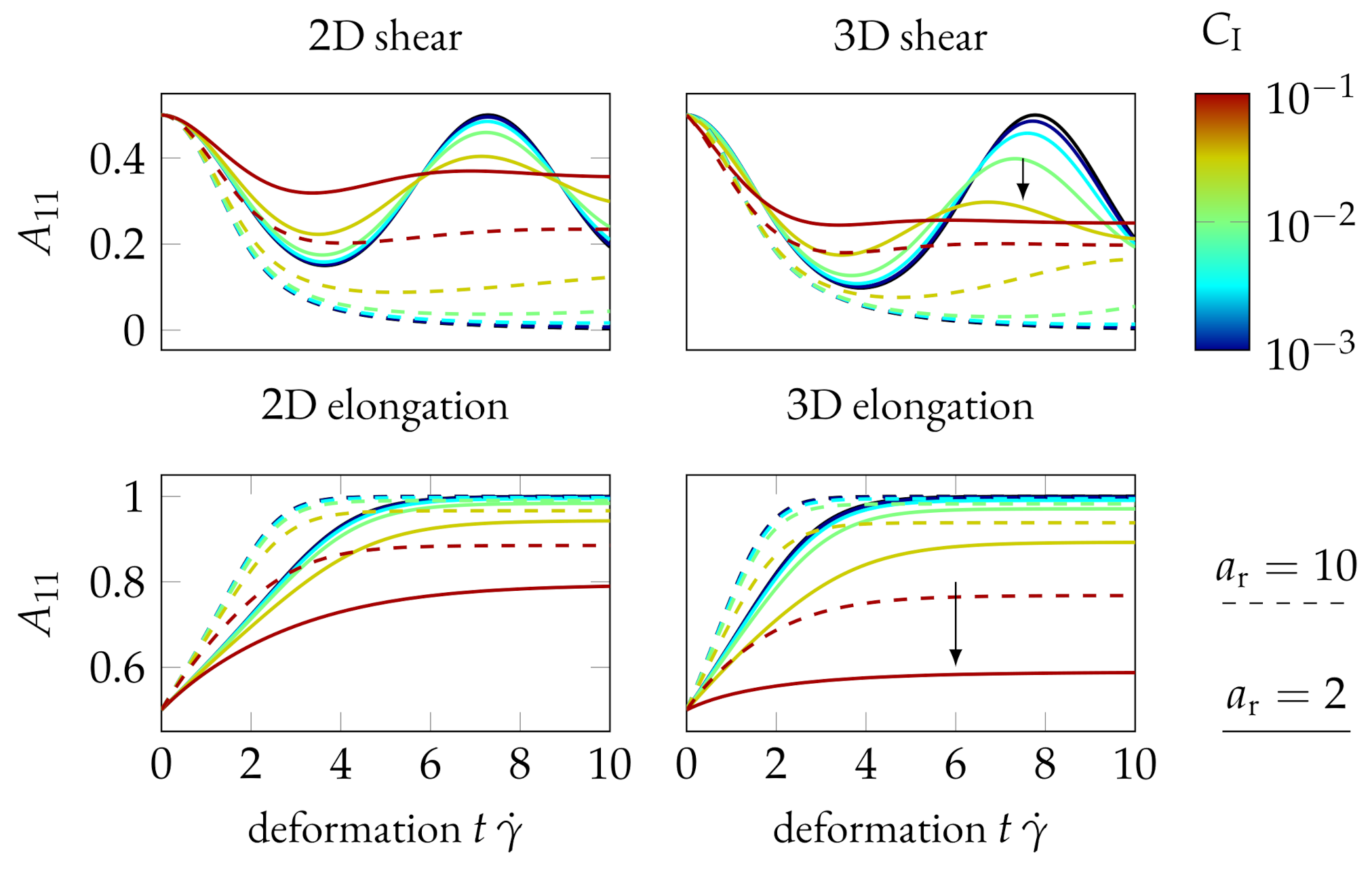
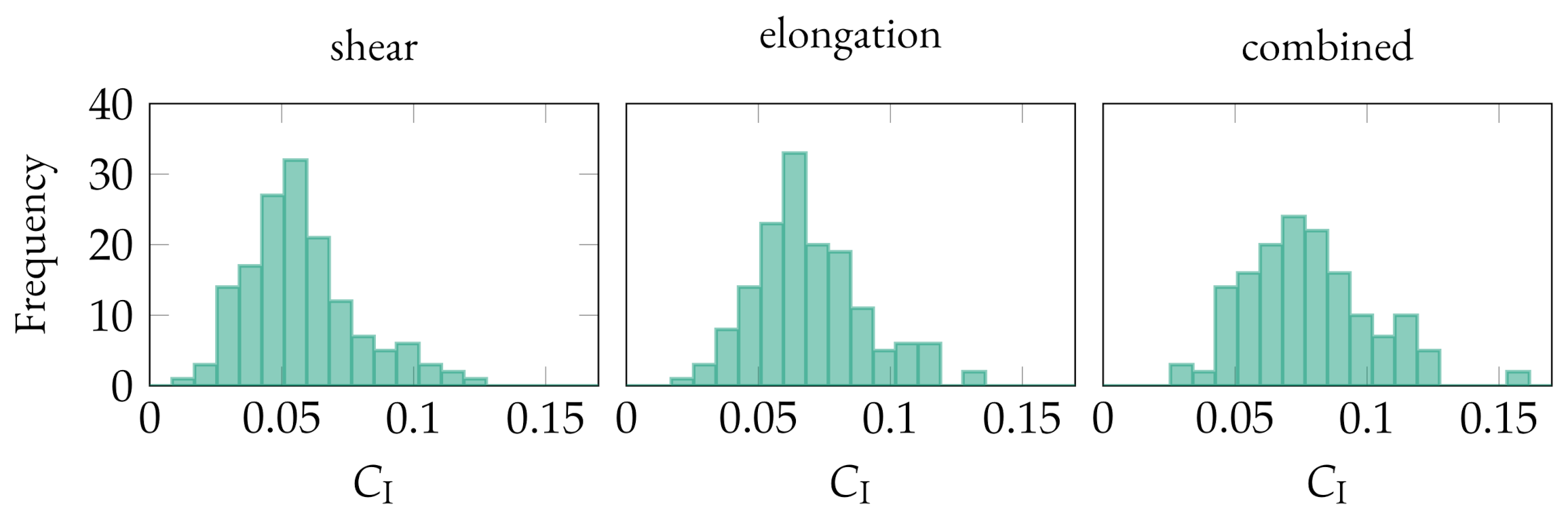
3.2. Influence of the Flow Type
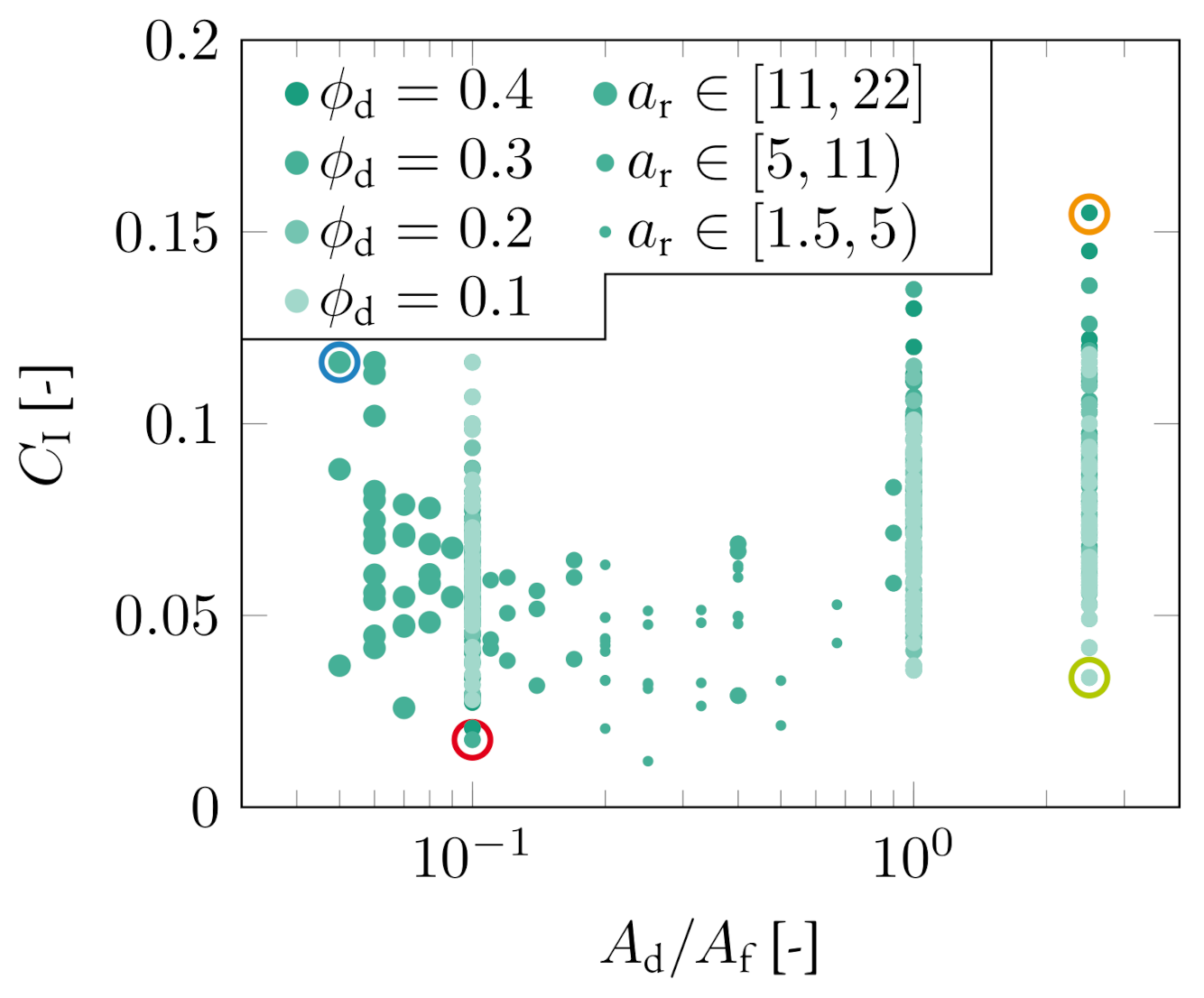
3.3. Influence of Disk Size
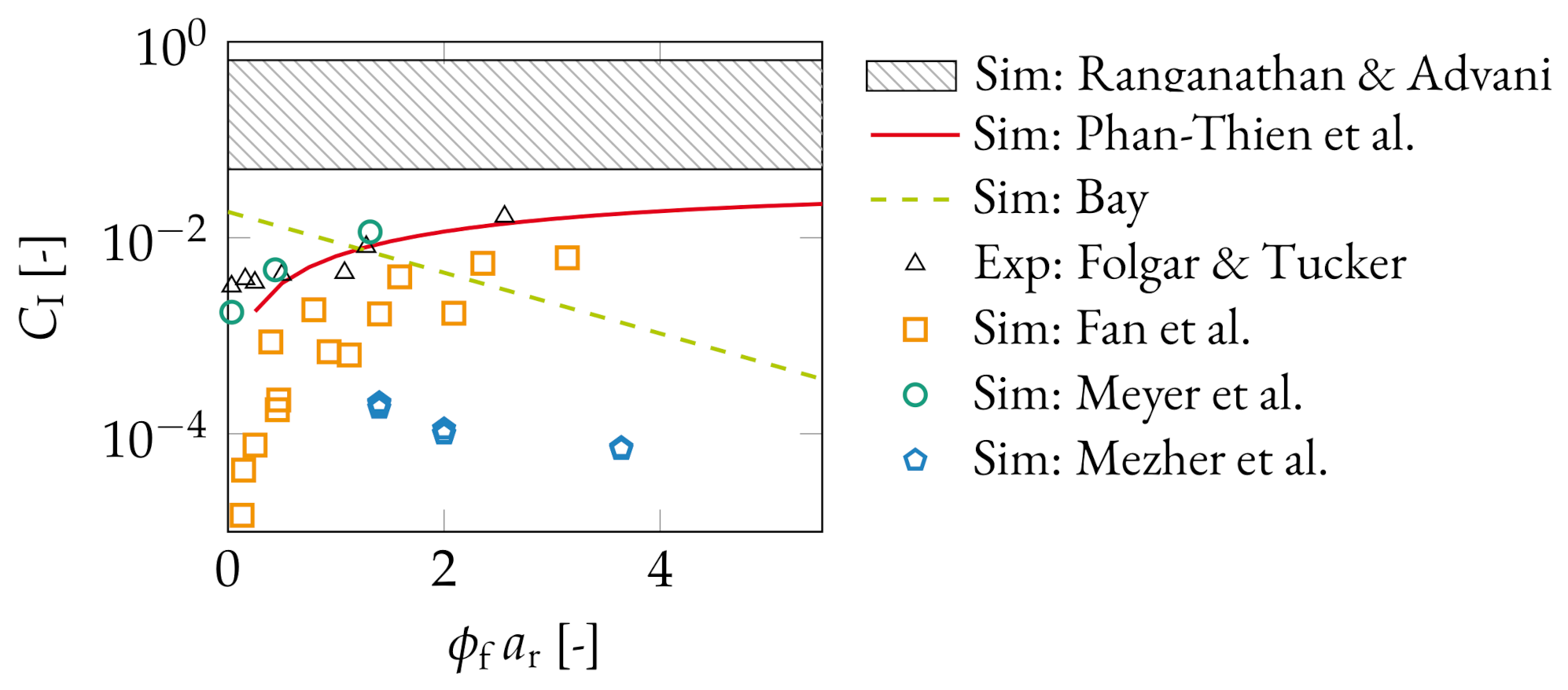
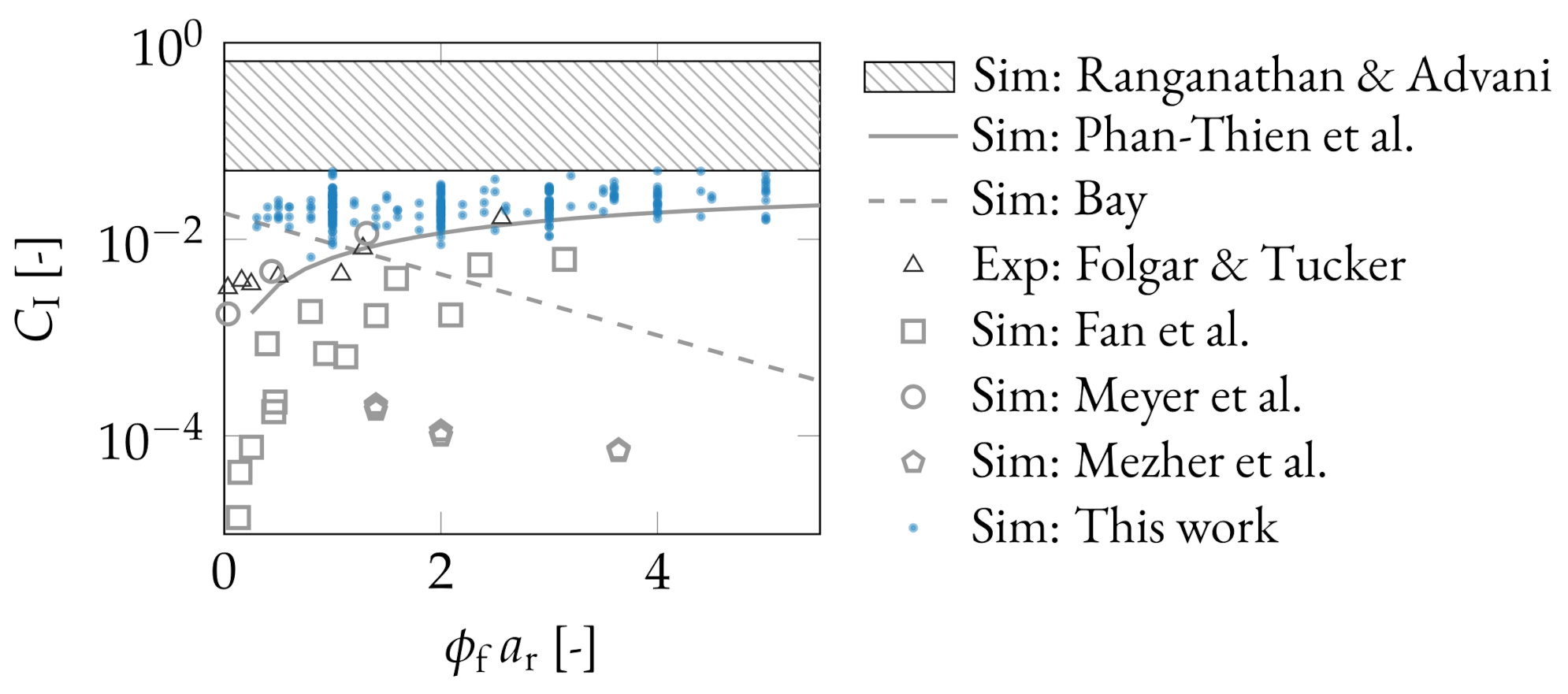
3.4. Comparison of Existing Data
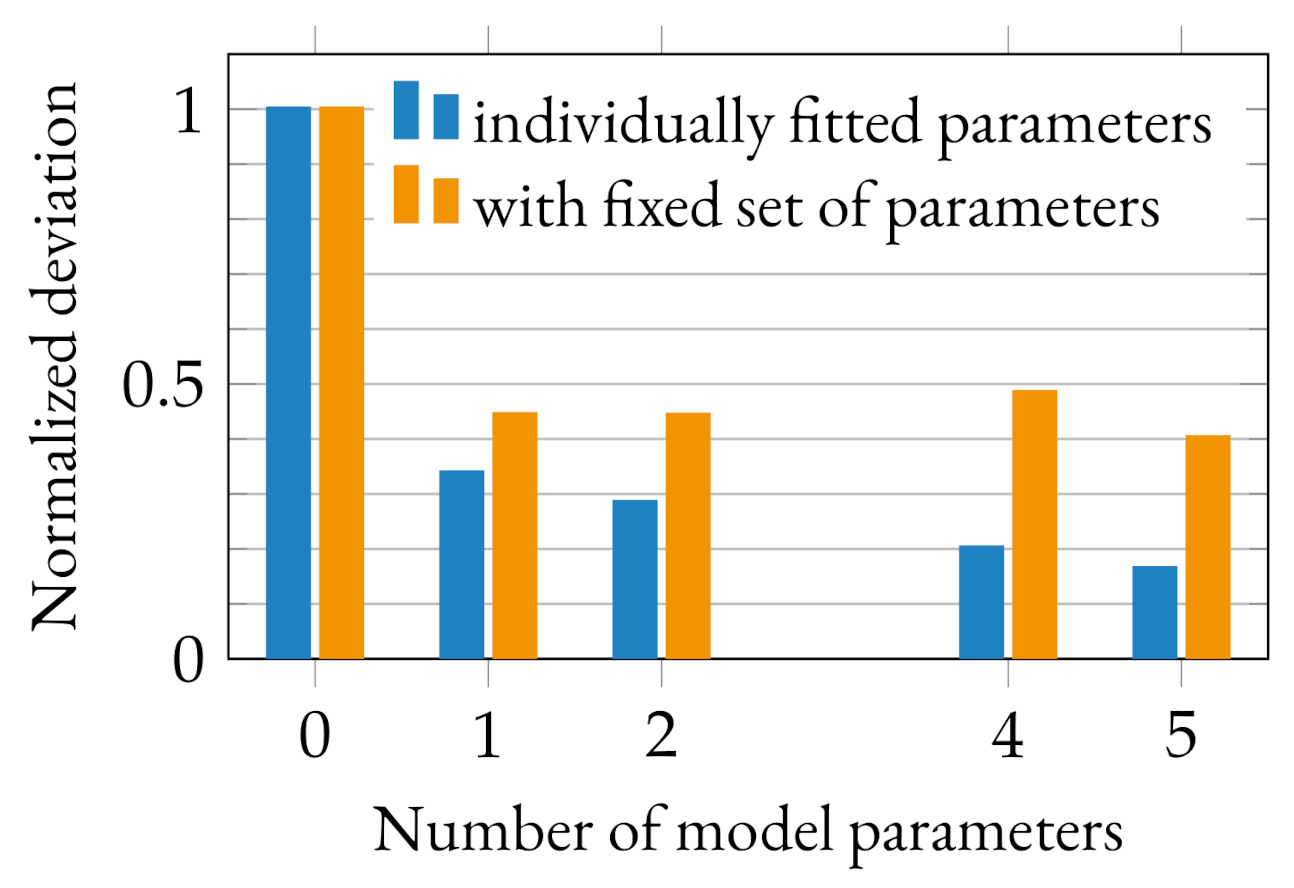
3.5. Accuracy of FT Model in Contrast to Other Analytical Orientation Prediction Models
4. Discussion
4.1. Formulation
4.2. Underlying Flow Profile
4.3. Suspension Composition
4.4. Comparison with Literature
4.5. Accuracy of the FT Model in Comparison to Other Prediction Models
4.6. Limitation of This Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| 3D | three-dimensional |
| ARD | Anisotropic Rotary Diffusion |
| ARD-RSC | Anisotropic Rotary Diffusion Method with Reduced Strain Closure |
| DNS | Direct Numerical Simulations |
| FT | Folgar Tucker |
| iARD | improved Anisotropic Rotary Diffusion |
| IBOF | Invariant-based optimal fitting |
| IRD | Isotropic Rotary Diffusion |
| MRD | Moldflow Rotational Diffusion |
| NAT | Natural Closure Approximiation |
| OWR | Orthotropic Closure Approximation |
| OWC | one-way coupling |
| pARD | principle Anisotropic Rotary Diffusion |
| RPR | Retarding Principal Rate |
| RSC | Reduced Strain Closure |
| RVE | Representative Volume Element |
| SPH | Smoothed Particle Hydrodynamics |
| TWC | two-way coupling |
References
- Wang, Z.; Smith, D.E. Rheology Effects on Predicted Fiber Orientation and Elastic Properties in Large Scale Polymer Composite Additive Manufacturing. J. Compos. Sci. 2018, 2, 10. [Google Scholar] [CrossRef]
- Simon, S.A.; Bechara Senior, A.; Osswald, T. Experimental Validation of a Direct Fiber Model for Orientation Prediction. J. Compos. Sci. 2020, 4, 59. [Google Scholar] [CrossRef]
- Fu, S.Y.; Hu, X.; Yue, C.Y. Effects of Fiber Length and Orientation Distribution On The Mechanical Properties of Short-Fiber-Reinforced Polymers. J. Soc. Mater. Sci. Jpn. 1999, 48, 74–83. [Google Scholar] [CrossRef]
- Terao, T.; Zhi, C.; Bando, Y.; Mitome, M.; Tang, C.; Golberg, D. Alignment of Boron Nitride Nanotubes in Polymeric Composite Films for Thermal Conductivity Improvement. J. Phys. Chem. C 2010, 114, 4340–4344. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, H.; Wu, J.; McCarthy, E.D. Fibre flow and void formation in 3D printing of short-fibre reinforced thermoplastic composites: An experimental benchmark exercise. Addit. Manuf. 2020, 101686. [Google Scholar] [CrossRef]
- Hashemi, M.R.; Fatehi, R.; Manzari, M.T. SPH simulation of interacting solid bodies suspended in a shear flow of an Oldroyd-B fluid. J. Non–Newton. Fluid Mech. 2011, 166, 1239–1252. [Google Scholar] [CrossRef]
- Meyer, N.; Saburow, O.; Hohberg, M.; Hrymak, A.N.; Henning, F.; Kärger, L. Parameter Identification of Fiber Orientation Models Based on Direct Fiber Simulation with Smoothed Particle Hydrodynamics. J. Compos. Sci. 2020, 4, 77. [Google Scholar] [CrossRef]
- Do-Quang, M.; Amberg, G.; Brethouwer, G.; Johansson, A.V. Simulation of finite-size fibers in turbulent channel flows. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 89. [Google Scholar] [CrossRef]
- Lu, J.; Das, S.; Peters, E.; Kuipers, J. Direct numerical simulation of fluid flow and mass transfer in dense fluid-particle systems with surface reactions. Chem. Eng. Sci. 2018, 176, 1–18. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C. Numerical Study of Lateral Migration of Elliptical Magnetic Microparticles in Microchannels in Uniform Magnetic Fields. Magnetochemistry 2018, 4, 16. [Google Scholar] [CrossRef]
- Hwang, H.; Son, G. Direct numerical simulation of 3D particle motion in an evaporating liquid film. J. Mech. Sci. Technol. 2016, 30, 3929–3934. [Google Scholar] [CrossRef]
- Polfer, P.; Kraft, T.; Bierwisch, C. Suspension modeling using smoothed particle hydrodynamics: Accuracy of the viscosity formulation and the suspended body dynamics. Appl. Math. Model. 2016, 40, 2606–2618. [Google Scholar] [CrossRef]
- Gudžulić, V.; Dang, T.S.; Meschke, G. Computational modeling of fiber flow during casting of fresh concrete. Comput. Mech. 2018, 31, 751. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Y.; Zhang, S.; Hou, B.; Zhou, H. Experimental investigation and modeling study of the fiber orientation behavior. Eng. Comput. 2020, 367. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L. The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Jeffery, G.B. The Motion of Ellipsoidal Particles Immersed in a Viscous Fluid. Proc. R. Soc. A: Math. Phys. Eng. Sci. 1922, 102, 161–179. [Google Scholar] [CrossRef]
- Folgar, F.; Tucker, C.L. Orientation Behavior of Fibers in Concentrated Suspensions. J. Reinf. Plast. Compos. 1984, 3, 98–119. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L. A numerical simulation of short fiber orientation in compression molding. Polym. Compos. 1990, 11, 164–173. [Google Scholar] [CrossRef]
- Hand, G.L. A theory of anisotropic fluids. J. Fluid Mech. 1962, 13, 33–46. [Google Scholar] [CrossRef]
- Doi, M. Molecular dynamics and rheological properties of concentrated solutions of rodlike polymers in isotropic and liquid crystalline phases. J. Polym. Sci. Polym. Phys. Ed. 1981, 19, 229–243. [Google Scholar] [CrossRef]
- Lipscomb, G.G.; Denn, M.M.; Hur, D.U.; Boger, D.V. The flow of fiber suspensions in complex geometries. J. Non–Newton. Fluid Mech. 1988, 26, 297–325. [Google Scholar] [CrossRef]
- Du Chung, H.; Kwon, T.H. Invariant-based optimal fitting closure approximation for the numerical prediction of flow-induced fiber orientation. J. Rheol. 2002, 46, 169–194. [Google Scholar] [CrossRef]
- Verleye, V.; Couniot, A.; Dupret, F. Numerical prediction of fibre orientation in complex injection-moulded parts. Eng. Sci. 1994, 4. [Google Scholar] [CrossRef]
- Bay, R.S. Fiber Orientation in Injection-Molded Composites: A Comparison of Theory and Experiment. Ph.D. Thesis, University of Illinois, Champaign, IL, USA, 1991. [Google Scholar]
- Mezher, R.; Perez, M.; Scheuer, A.; Abisset-Chavanne, E.; Chinesta, F.; Keunings, R. Analysis of the Folgar & Tucker model for concentrated fibre suspensions in unconfined and confined shear flows via direct numerical simulation. Compos. Part A Appl. Sci. Manuf. 2016, 91, 388–397. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Fan, X.J.; Tanner, R.I.; Zheng, R. Folgar–Tucker constant for a fibre suspension in a Newtonian fluid. J. Non–Newton. Fluid Mech. 2002, 103, 251–260. [Google Scholar] [CrossRef]
- Fan, X.; Phan-Thien, N.; Zheng, R. A direct simulation of fibre suspensions. J. Non–Newton. Fluid Mech. 1998, 74, 113–135. [Google Scholar] [CrossRef]
- Ranganathan, S.; Advani, S.G. Fiber–fiber interactions in homogeneous flows of nondilute suspensions. J. Rheol. 1991, 35, 1499–1522. [Google Scholar] [CrossRef]
- Advani, S.G. Flow and Rheology in Polymer Composites Manufacturing: Processing Short-Fiber Systems, 1st ed.; Composite Materials Series; Elsevier Science: Amsterdam, The Netherlands, 1994; Volume 10. [Google Scholar]
- Wang, J.; O’Gara, J.F.; Tucker, C.L. An objective model for slow orientation kinetics in concentrated fiber suspensions: Theory and rheological evidence. J. Rheol. 2008, 52, 1179–1200. [Google Scholar] [CrossRef]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. Phenomenological improvements to predictive models of fiber orientation in concentrated suspensions. J. Rheol. 2013, 57, 1597–1631. [Google Scholar] [CrossRef]
- Phelps, J.H.; Tucker, C.L. An anisotropic rotary diffusion model for fiber orientation in short- and long-fiber thermoplastics. J. Non–Newton. Fluid Mech. 2009, 156, 165–176. [Google Scholar] [CrossRef]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. Comparison of recent fiber orientation models in injection molding simulation of fiber-reinforced composites. J. Thermoplast. Compos. Mater. 2020, 33, 35–52. [Google Scholar] [CrossRef]
- Favaloro, A.J.; Tucker, C.L. Analysis of anisotropic rotary diffusion models for fiber orientation. Compos. Part A Appl. Sci. Manuf. 2019, 126, 105605. [Google Scholar] [CrossRef]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. The use of principal spatial tensor to predict anisotropic fiber orientation in concentrated fiber suspensions. J. Rheol. 2018, 62, 313–320. [Google Scholar] [CrossRef]
- Bakharev, A. (Ed.) Using New Anisotropic Rotational Diffusion Model to Improve Prediction of Short Fibers in Thermoplastic Injection Molding; Society of Plastics Engineers: Lubbock, TX, USA, 2018. [Google Scholar]
- Dietemann, B.; Bosna, F.; Kraft, T.; Kruggel-Emden, H.; Bierwisch, C. Folgar Tucker constants fitted against simulations of various suspensions under shear and/or elongation. Fraunhofer Fordatis 2021. [Google Scholar] [CrossRef]
- Dietemann, B.; Bosna, F.; Lorenz, M.; Travitzky, N.; Kruggel-Emden, H.; Kraft, T.; Bierwisch, C. Modeling Robocasting with Smoothed Particle Hydrodynamics: Printing gap-spanning filaments. Addit. Manuf. 2020, 36, 101488. [Google Scholar] [CrossRef]
- Dietemann, B.; Bosna, F.; Lorenz, M.; Travitzky, N.; Kruggel-Emden, H.; Kraft, T.; Bierwisch, C. Numerical study of texture in material extrusion: Orientation in a multicomponent system of spheres and ellipsoids. J. Non–Newton. Fluid Mech. 2021, 291, 104532. [Google Scholar] [CrossRef]
- Cintra, J.S.; Tucker, C.L. Orthotropic closure approximations for flow–induced fiber orientation. J. Rheol. 1995, 39, 1095–1122. [Google Scholar] [CrossRef]
- Du Chung, H.; Kwon, T.H. Improved model of orthotropic closure approximation for flow induced fiber orientation. Polym. Compos. 2001, 22, 636–649. [Google Scholar] [CrossRef]
- Takano, M. Viscosity Effect on Flow Orientation of Short Fibers; Monsanto Research Corporation: Springfield, MO, USA, 1973. [Google Scholar]
- Yamane, Y.; Kaneda, Y.; Dio, M. Numerical simulation of semi-dilute suspensions of rodlike particles in shear flow. J. Non–Newton. Fluid Mech. 1994, 54, 405–421. [Google Scholar] [CrossRef]
- Férec, J.; Ausias, G.; Heuzey, M.C.; Carreau, P.J. Modeling fiber interactions in semiconcentrated fiber suspensions. J. Rheol. 2009, 53, 49–72. [Google Scholar] [CrossRef]
- Bertevas, E.; Férec, J.; Khoo, B.C.; Ausias, G.; Phan-Thien, N. Smoothed particle hydrodynamics (SPH) modeling of fiber orientation in a 3D printing process. Phys. Fluids 2018, 30, 103103. [Google Scholar] [CrossRef]
- Jezek, J.; Schulmann, K.; Paterson, S. Modified Jeffery model: Influence of particle concentration on mineral fabric in moderately concentrated suspensions. J. Geophys. Res. Solid Earth 2013, 118, 852–861. [Google Scholar] [CrossRef]
- Cieslinski, M.J.; Wapperom, P.; Baird, D.G. Fiber orientation evolution in simple shear flow from a repeatable initial fiber orientation. J. Non–Newton. Fluid Mech. 2016, 237, 65–75. [Google Scholar] [CrossRef]
- Willems, F.; Reitinger, P.; Bonten, C. Calibration of Fiber Orientation Simulations for LFT—A New Approach. J. Compos. Sci. 2020, 4, 163. [Google Scholar] [CrossRef]
- Favaloro, A.J.; Tseng, H.C.; Pipes, R.B. A new anisotropic viscous constitutive model for composites molding simulation. Compos. Part A Appl. Sci. Manuf. 2018, 115, 112–122. [Google Scholar] [CrossRef]
- Tseng, H.C.; Favaloro, A.J. The use of informed isotropic constitutive equation to simulate anisotropic rheological behaviors in fiber suspensions. J. Rheol. 2019, 63, 263–274. [Google Scholar] [CrossRef]
- Li, T.; Luyé, J.F. Flow-Fiber Coupled Viscosity in Injection Molding Simulations of Short Fiber Reinforced Thermoplastics. Int. Polym. Process. 2019, 34, 158–171. [Google Scholar] [CrossRef]




| Model Name | Abbreviation | Parameters |
|---|---|---|
| Jeffery [16] | - | 0 |
| Folgar Tucker [17] | FT | 1 |
| Reduced Strain Closure [30] | RSC | 2 |
| improved Anisotropic Rotary Diffusion Retarding Principal Rate [31] | iARD-RPR | 3 |
| principle Anisotropic Rotary Diffusion [35] | pARD | 3 |
| Principal Anisotropic Rotary Diffusion Retarding Principal Rate [35] | pARD-RPR | 3 |
| Moldflow Rotational Diffusion [36] | MRD | 4 |
| Anisotropic Rotary Diffusion [32] | ARD | 5 |
| Anisotropic Rotary Diffusion Reduced Strain Closure [32] | ARD-RSC | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dietemann, B.; Bosna, F.; Kruggel-Emden, H.; Kraft, T.; Bierwisch, C. Assessment of Analytical Orientation Prediction Models for Suspensions Containing Fibers and Spheres. J. Compos. Sci. 2021, 5, 107. https://doi.org/10.3390/jcs5040107
Dietemann B, Bosna F, Kruggel-Emden H, Kraft T, Bierwisch C. Assessment of Analytical Orientation Prediction Models for Suspensions Containing Fibers and Spheres. Journal of Composites Science. 2021; 5(4):107. https://doi.org/10.3390/jcs5040107
Chicago/Turabian StyleDietemann, Bastien, Fatih Bosna, Harald Kruggel-Emden, Torsten Kraft, and Claas Bierwisch. 2021. "Assessment of Analytical Orientation Prediction Models for Suspensions Containing Fibers and Spheres" Journal of Composites Science 5, no. 4: 107. https://doi.org/10.3390/jcs5040107
APA StyleDietemann, B., Bosna, F., Kruggel-Emden, H., Kraft, T., & Bierwisch, C. (2021). Assessment of Analytical Orientation Prediction Models for Suspensions Containing Fibers and Spheres. Journal of Composites Science, 5(4), 107. https://doi.org/10.3390/jcs5040107






