Integrated Seismic and Energy Retrofitting System for Masonry Walls Using Textile-Reinforced Mortars Combined with Thermal Insulation: Experimental, Analytical, and Numerical Study
Abstract
:1. Introduction
2. Experimental Work
2.1. Οut-of-Plane Loading
2.1.1. Test Setup, Instrumentation, and Procedure for Out-of-Plane Loading
2.1.2. Experimental Results for Out of-Plane Loading
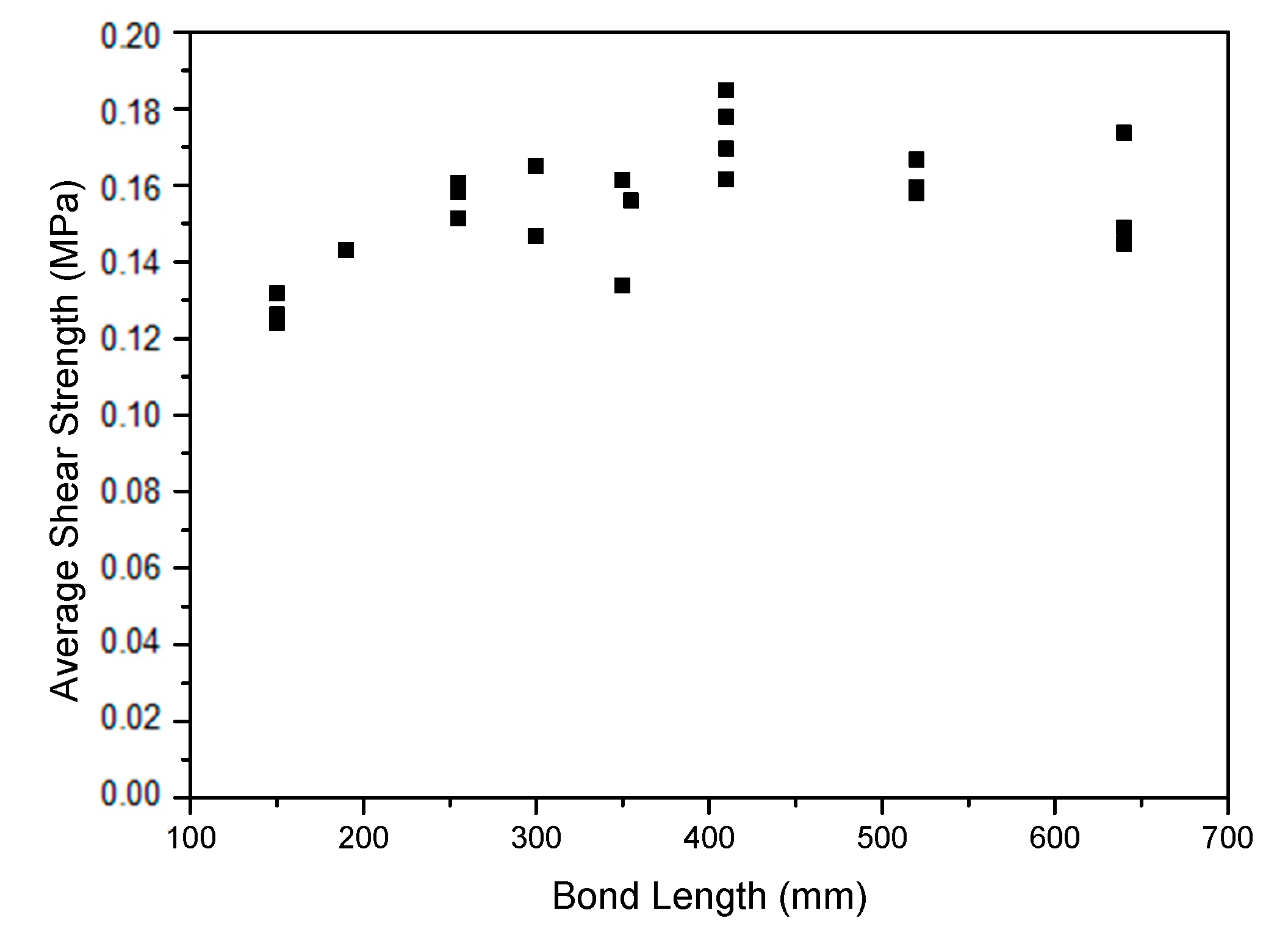
2.2. Bond Tests
3. Simplified Failure Analysis for Specimens Subject to Out-of-Plane Bending
3.1. Tension Failure of TRM or Compression Failure of Masonry
3.2. Debonding
3.3. Comparison of Analytical and Experimental Results
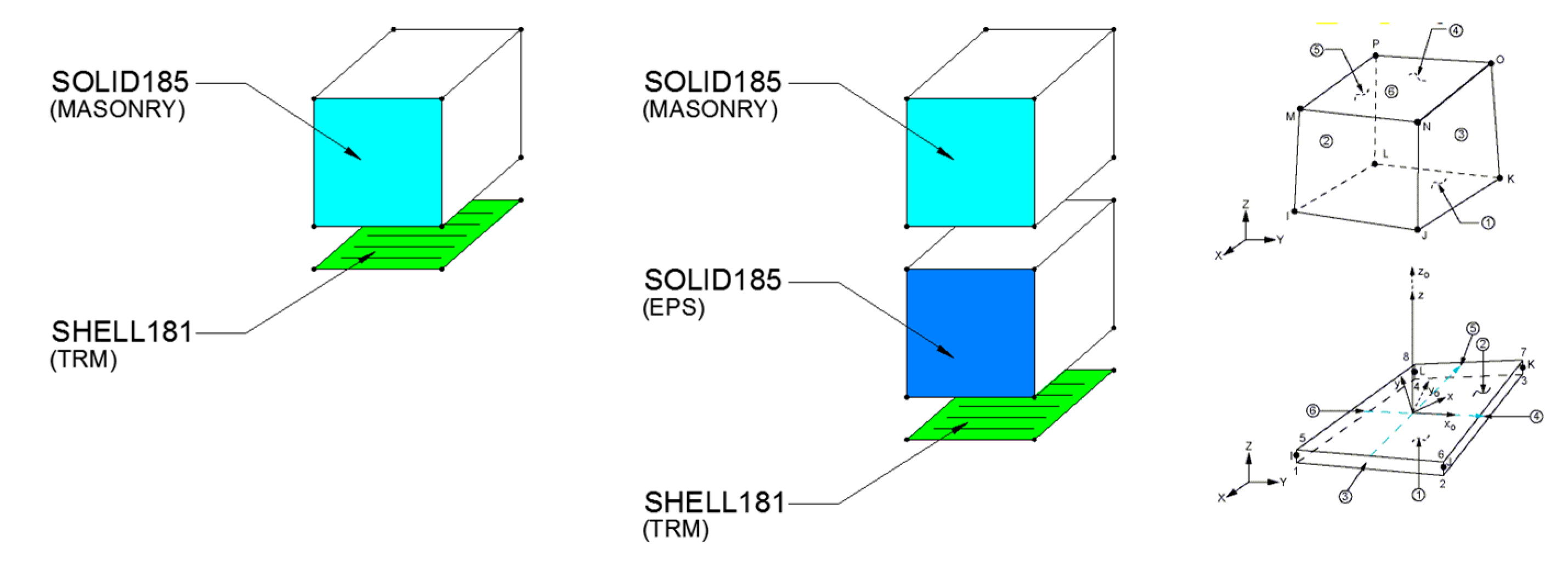
4. Numerical Simulation
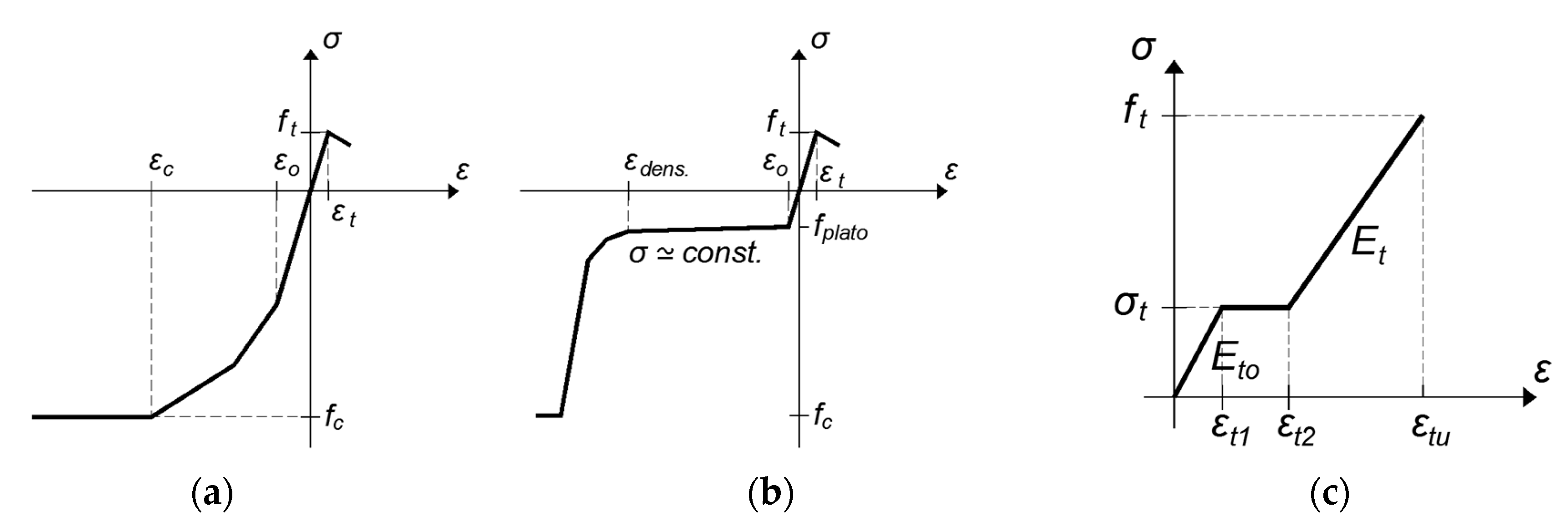
4.1. Mechanical Parameters
4.2. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Papanicolaou, C.G.; Triantafillou, T.C.; Papathanasiou, M.; Karlos, K. Textile reinforced mortar (TRM) versus FRP as strengthening material of URM Walls: Out-of-plane cyclic loading. Mater. Struct. 2008, 41, 143–157. [Google Scholar] [CrossRef]
- Harajli, M.H.; ElKhatib, H.; San-Jose, J.T. Static and cyclic out-of-plane response of masonry walls strengthened using textile-mortar system. J. Mater. Civ. Eng. 2010, 22. [Google Scholar] [CrossRef]
- Babaeidarabad, S.; De Caso y Basalo, F.; Nanni, A. Out-of-plane behavior of URM walls strengthened with fabric-reinforced cementitious matrix composite. J. Compos. Constr. 2013, 18. [Google Scholar] [CrossRef]
- De Santis, S.; De Canio, G.; de Felice, G.; Meriggi, P.; Roselli, I. Out-of-plane seismic retrofitting of masonry walls with Textile Reinforced Mortar composites. Bull. Earthq. Eng. 2019, 17, 6265–6300. [Google Scholar] [CrossRef]
- Meriggi, P.; de Felice, G.; De Santis, S. Design of the out-of-plane strengthening of masonry walls with fabric reinforced cementitious matrix composites. Constr. Build. Mater. 2020, 240. [Google Scholar] [CrossRef]
- De Risi, M.T.; Furtado, A.; Rodrigues, H.; Melo, J.; Verderame, G.M.; Antonio, A.; Varum, H.; Manfredi, G. Experimental analysis of strengthening solutions for the out-of-plane collapse of masonry infills in RC structures through textile reinforced mortars. Eng. Struct. 2020, 207. [Google Scholar] [CrossRef]
- Kolaitis, D.; Malliotakis, E.; Kontogeorgos, D.; Mandilaras, I.; Katsourinis, D.; Founti, M. Comparative assessment of internal and external thermal insulation systems for energy efficient retrofitting of residential buildings. Energy Build. 2013, 64, 123–131. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Karlos, K.; Kefalou, K.; Argyropoulou, E. An innovative structural and energy retrofitting system for URM walls using textile reinforced mortars combined with thermal insulation: Mechanical and fire behavior. Constr. Build. Mater. 2017, 133, 1–13. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Karlos, K.; Kapsalis, P.; Georgiou, L. Innovative structural and energy retrofitting system for masonry walls using textile reinforced mortars combined with thermal insulation: In-plane mechanical behaviour. J. Compos. Constr. 2018, 22, 04018029. [Google Scholar] [CrossRef]
- Gkournelos, P.D.; Bournas, D.A.; Triantafillou, T.C. Combined seismic and energy upgrading of existing reinforced concrete buildings using TRM jacketing and thermal insulation. Earthq. Struct. 2019, 16, 625–639. [Google Scholar] [CrossRef]
- Gkournelos, P.D.; Triantafillou, T.C.; Bournas, D.A. Integrated structural and energy retrofitting of masonry walls: The effect of in-plane damage on the out-of-plane response. J. Compos. Constr. 2020, 24, 04020049. [Google Scholar] [CrossRef]
- Askouni, P.D.; Papanicolaou, C.G. Experimental investigation of bond between TRM overlays and masonry. In Proceedings of the 10th International Conference on Structural Analysis of Historical Constructions, SAHC, Leuven, Belgium, 13–15 September 2016; pp. 315–321. [Google Scholar]
- Allen, H.G. (Ed.) CHAPTER 2-SANDWICH BEAMS. In Analysis and Design of Structural Sandwich Panels; Pergamon Press: Oxford, UK, 1969; pp. 8–47. ISBN 978-0-08-012870-2. [Google Scholar]














| Specimen Notation | Peak Load (kN) | Mid-Span Displacement at Failure (mm) | Cumulative Dissipated Energy (kNmm) at Cycle | Failure Mode b (Failure Direction) | |||
|---|---|---|---|---|---|---|---|
| Push | Pull | Push | Pull | 4 (8 a) | 7 (14 a) | ||
| M | 3.42 | -- | 0.72 | -- | -- | -- | Flexural crack |
| 2M2 | 9.28 | 9.28 | 13.78 | 15.69 | 154.29 | 421.19 | FR (both) |
| 2iMi2 | 11.47 | 12.45 | 33.68 | 22.44 | 95.77 | 283.47 | D (push), FR (pull) |
| 2iMi2_na | 10.50 | 10.25 | >28.23 | 27.48 | 80.23 | 221.12 | D (pull) |
| 1i1M1i1 | 12.70 | 12.21 | 19.66 | 20.17 | 104.80 | 326.91 | FR (both) |
| 2ii2M | 20.26 | 3.66 | 25.97 | 24.20 | 75.06 | 250.09 | FR (push), MC (pull) |
| 2iiM2 | 13.92 | 15.14 | 17.14 | 24.70 | 146.71 | 470.77 | FR (push), D (pull) |
| 2M2s | 8.06 | 9.28 | 12.31 | 14.15 | 208.39 | 626.35 | FR (both) |
| 2iMi2s | 12.97 | 12.17 | 23.49 | 23.49 | 144.79 | 461.72 | FR (both) |
| 1i1M1i1s | 10.01 | 10.01 | 16.30 | 15.12 | 114.48 | 419.46 | FR (both) |
| 2ii2Ms | 20.26 | 3.66 | 29.64 | 1.00 | 121.86 | 402.59 | FR (push) |
| 2iiM2s | 11.96 | 13.18 | 17.26 | 18.91 | 194.51 | 657.37 | FR (push), D (pull) |
| Specimen Length (mm) | Specimen Width (mm) | Failure Load (kN) | Average Shear Strength (MPa) |
|---|---|---|---|
| 150 | 85 | 1.68 | 0.131 |
| 150 | 85 | 1.58 | 0.123 |
| 150 | 85 | 1.61 | 0.126 |
| 190 | 85 | 2.31 | 0.143 |
| 255 | 85 | 3.28 | 0.151 |
| 255 | 85 | 3.48 | 0.160 |
| 255 | 85 | 3.43 | 0.158 |
| 300 | 85 | 4.21 | 0.165 |
| 300 | 85 | 3.74 | 0.146 |
| 300 | 85 | 4.21 | 0.165 |
| 350 | 85 | 4.80 | 0.161 |
| 350 | 85 | 4.80 | 0.161 |
| 350 | 85 | 3.98 | 0.133 |
| 355 | 85 | 4.71 | 0.156 |
| 410 | 85 | 6.44 | 0.184 |
| 410 | 85 | 6.20 | 0.177 |
| 410 | 85 | 5.63 | 0.161 |
| 410 | 85 | 5.91 | 0.169 |
| 520 | 85 | 6.98 | 0.157 |
| 520 | 85 | 7.05 | 0.159 |
| 520 | 85 | 7.37 | 0.166 |
| 640 | 85 | 9.45 | 0.173 |
| 640 | 85 | 8.10 | 0.148 |
| 640 | 85 | 7.87 | 0.144 |
| Mean Value | 0.154 | ||
Specimen | Experimental Failure Load and Failure Mode | Theoretical Failure Load and Failure Mode | ||
|---|---|---|---|---|
| Pmax,exp (kN) | Failure Mode a | Pmax,th (kN) | Failure Mode | |
| M | 3.42 | Flexural crack | 1.60 | Flexural crack |
| 2M2 | 9.28 | FR (both) b | 8.15 | FR |
| 2M2s | 8.06 | FR (both) | ||
| 2iMi2 | 11.47 | D (push) b | 9.60 | FR |
| 2iMi2s | 12.17 | FR (both) | ||
| 2iMi2_na | 10.25 | D (pull) b | 9.60 | FR |
| 1i1M1i1 | 12.21 | FR (both) | 10.25 | FR |
| 1i1M1i1s | 10.01 | FR (both) | ||
| 2ii2M | 20.26 | FR (push) | 16.43 | FR |
| 2ii2Ms | 20.26 | FR (push) | ||
| 2iiM2 | 13.92 | FR (push) | 12.22 | FR |
| 2iiM2s | 11.96 | FR (push) | ||
| Notation | Cross Section | Finite Element Mesh |
|---|---|---|
| M |  |  |
| 1i1M1i1 |  | 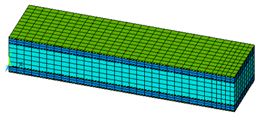 |
| 2M2 |  | 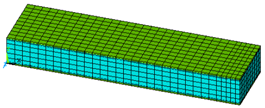 |
| 2iMi2 |  |  |
| 2ii2M |  | 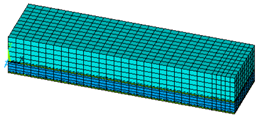 |
| Specimen | Compressive Strength fc (MPa) | Strain at Failure εc (%) |
|---|---|---|
| All specimens | 11.58 | 0.434 |
| Type | Density D (kg/m3) | Normal Stress at ε = 10% σ10 (MPa) | Ultimate Tension Strength σt (MPa) | Ultimate Shear Strength τy (MPa) |
|---|---|---|---|---|
| EPS 200 | 29 | 0.2 | 0.3 | 0.125 |
| TRM | Thickness t (mm) | Initial Stiffness Et0 (MPa) | Cracking Stress 1 σt (MPa) | Stress at Failure 1 ft (MPa) | Cracking Strain εt1 (%) | Intermediate Strain εt2 (%) | Strain at Failure εtu (%) |
|---|---|---|---|---|---|---|---|
| 1 layer | 5 | 7897 | 3.38 | 9.0 2 | 0.0428 | 0.75 | 3.0 |
| 2 layers | 8 | 6353 | 3.85 | 9.0 2 | 0.0606 | 1.18 | 3.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karlos, K.; Tsantilis, A.; Triantafillou, T. Integrated Seismic and Energy Retrofitting System for Masonry Walls Using Textile-Reinforced Mortars Combined with Thermal Insulation: Experimental, Analytical, and Numerical Study. J. Compos. Sci. 2020, 4, 189. https://doi.org/10.3390/jcs4040189
Karlos K, Tsantilis A, Triantafillou T. Integrated Seismic and Energy Retrofitting System for Masonry Walls Using Textile-Reinforced Mortars Combined with Thermal Insulation: Experimental, Analytical, and Numerical Study. Journal of Composites Science. 2020; 4(4):189. https://doi.org/10.3390/jcs4040189
Chicago/Turabian StyleKarlos, Kyriakos, Aristomenis Tsantilis, and Thanasis Triantafillou. 2020. "Integrated Seismic and Energy Retrofitting System for Masonry Walls Using Textile-Reinforced Mortars Combined with Thermal Insulation: Experimental, Analytical, and Numerical Study" Journal of Composites Science 4, no. 4: 189. https://doi.org/10.3390/jcs4040189
APA StyleKarlos, K., Tsantilis, A., & Triantafillou, T. (2020). Integrated Seismic and Energy Retrofitting System for Masonry Walls Using Textile-Reinforced Mortars Combined with Thermal Insulation: Experimental, Analytical, and Numerical Study. Journal of Composites Science, 4(4), 189. https://doi.org/10.3390/jcs4040189




