Characterization and Numerical Modelling of Through-Thickness Metallic-Pin-Reinforced Fibre/Thermoplastic Composites under Bending Loading
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Specification
2.2. Specimen Configuration
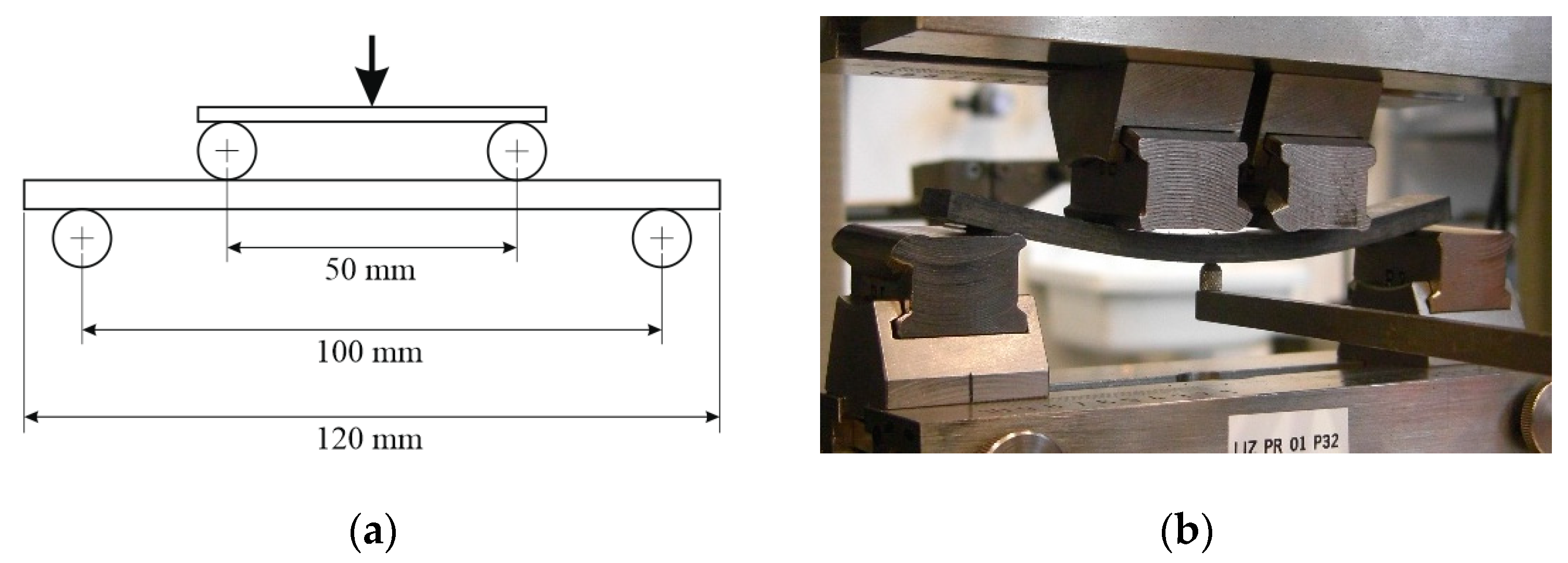
2.3. Experimental Setup and Measurement Techniques
3. Experimental Results
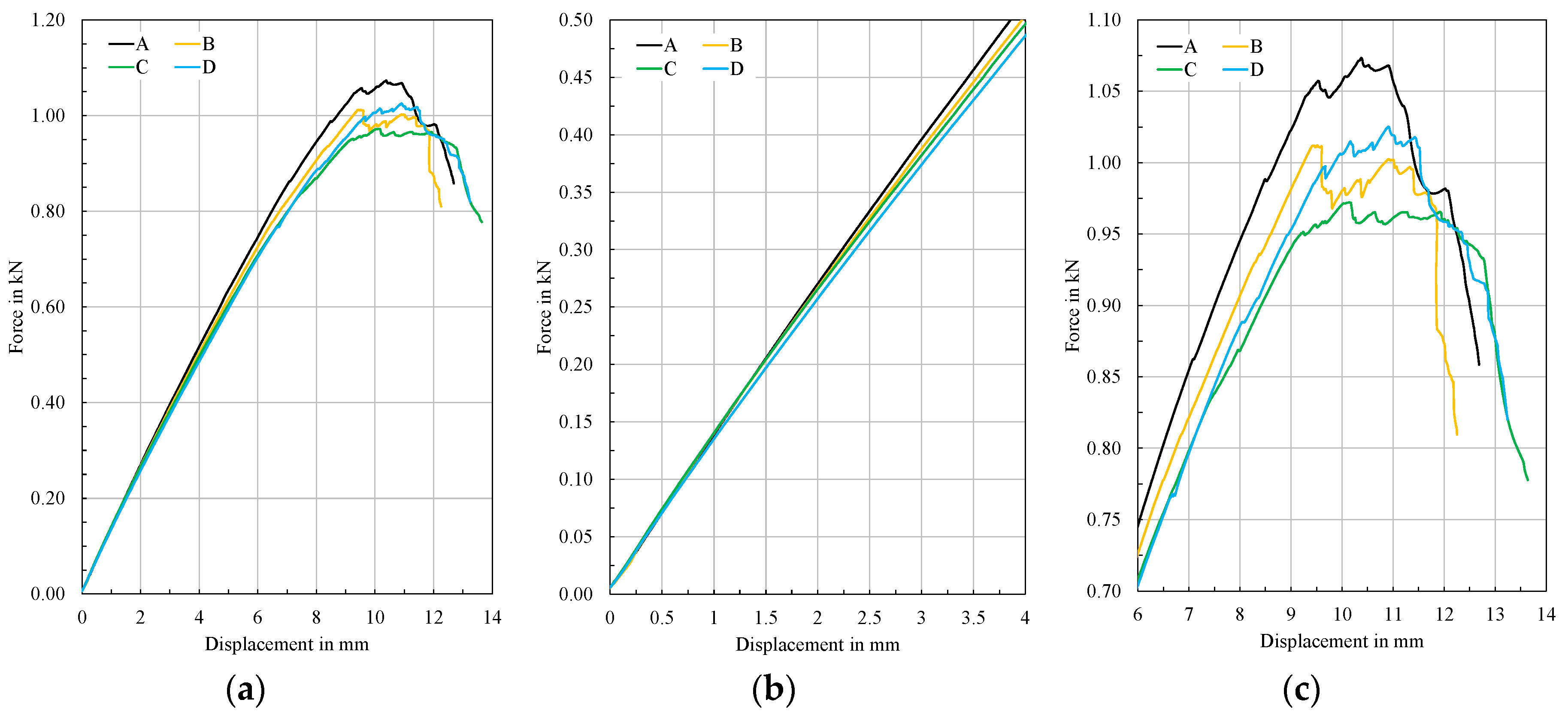
3.1. Force-Displacement Curves
3.2. Failure Pattern
4. Numerical Analysis
4.1. Finite Element Model
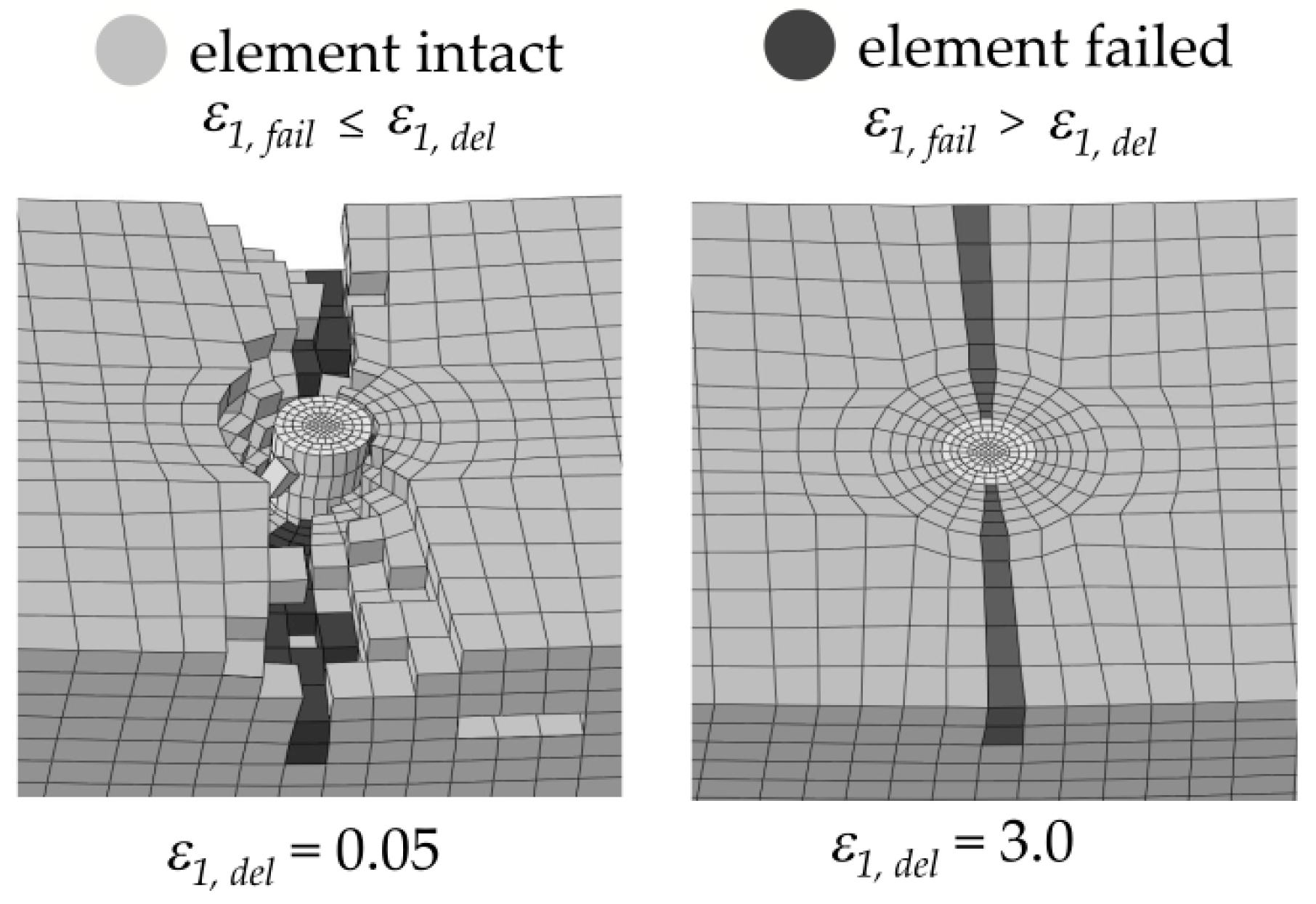
4.2. Material Modelling
4.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bourban, P.E.; Bögli, A.; Bonjour, F.; Månson, J.A. Integrated processing of thermoplastic composites. Compos. Sci. Technol. 1998, 58, 633–637. [Google Scholar] [CrossRef]
- Vaidya, U.K.; Chawla, K.K. Processing of fibre reinforced thermoplastic composites. Int. Mater. Rev. 2008, 53, 185–218. [Google Scholar] [CrossRef]
- Hufenbach, W.; Böhm, R.; Thieme, M.; Winkler, A.; Mäder, E.; Rausch, J.; Schade, M. Polypropylene/glass fibre 3D-textile reinforced composites for automotive applications. Mater. Des. 2011, 32, 1468–1476. [Google Scholar] [CrossRef]
- Budhe, S.; Banea, M.D.; De Barros, S.; Da Silva, L.F.M. An updated review of adhesively bonded joints in composite materials. Int. J. Adhes. Adhes. 2017, 72, 30–42. [Google Scholar] [CrossRef]
- Yousefpour, A.; Hojjati, M.; Immarigeon, J.P. Immarigeon: Fusion Bonding/Welding of Thermoplastic Composites. J. Thermoplast. Compos. Mater. 2004, 17, 303–341. [Google Scholar] [CrossRef]
- Galińska, A.; Galiński, C. Mechanical Joining of Fibre Reinforced Polymer Composites to Metals—A Review. Part II: Riveting, Clinching, Non-Adhesive Form Locked Joints, Pin and Loop Joining. Polymers 2020, 12, 1681. [Google Scholar] [CrossRef]
- Seidlitz, H.; Kuke, F.; Tsombanis, N. Advanced joining technology for the production of highly stressable lightweight structures, with fiber-reinforced plastics and metals. Technol. Lightweight Struct. 2017, 1, 54–67. [Google Scholar] [CrossRef]
- Hufenbach, W.; Kupfer, R.; Hornig, A. Thermoactivated Pinning—A novel joining technique for thermoplastic composites. In Solid State Phenomena; Trans Tech Publications Ltd.: Bäch, Switzerland, 2012; Volume 188, pp. 176–181. [Google Scholar] [CrossRef]
- Parkes, P.N.; Butler, R.; Meyer, J.; De Oliveira, A. Static strength of metal-composite joints with penetrative reinforcement. Compos. Struct. 2014, 118, 250–256. [Google Scholar] [CrossRef] [Green Version]
- Wisnom, M.R. The role of delamination in failure of fibre-reinforced composites. Philos. Trans. R. Soc. 2012, 370, 1850–1870. [Google Scholar] [CrossRef]
- Gnaba, I.; Legrand, X.; Wang, P.; Soulat, D. Through-the-thickness reinforcement for composite structures: A review. J. Ind. Text. 2019, 49, 71–96. [Google Scholar] [CrossRef]
- Mouritz, A.P. Mechanics of 3D fibre reinforced polymer composites. In Encyclopedia of Continuum Mechanics; Altenbach, H., Öchsner, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Kostopoulos, V.; Sarantinos, N.; Tsantzalis, S. Review of Through-the-Thickness Reinforced z-Pinned Composites. J. Compos. Sci. 2020, 4, 31. [Google Scholar] [CrossRef] [Green Version]
- Pingkarawat, K.; Mouritz, A.P. Comparative study of metal and composite z-pins for delamination fracture and fatigue strengthening of composites. Eng. Fract. Mech. 2016, 154, 180–190. [Google Scholar] [CrossRef]
- Cartié, D.D.; Cox, B.N.; Fleck, N.A. Mechanics of crack bridging by composite and metallic rods. Compos. Part A Appl. Sci. Manuf. 2004, 35, 1325–1336. [Google Scholar] [CrossRef] [Green Version]
- Son, J.H.; Chun, H.J.; Kang, K.T.; Lee, H.Y.; Byun, J.H.; Um, M.K.; Kim, B.S. Effect of Z-Pin on the through-the-Thickness Strength of Woven Composite Laminates. In Advanced Materials Research; Trans Tech Publications Ltd.: Bäch, Switzerland, 2010; Volume 123, pp. 47–50. [Google Scholar] [CrossRef]
- M’membe, B.; Gannon, S.; Yasaee, M.; Hallett, S.R.; Partridge, I.K. Mode II delamination resistance of composites reinforced with inclined z-pins. Mater. Des. 2016, 94, 565–572. [Google Scholar] [CrossRef] [Green Version]
- M’membe, B.; Yasaee, M.; Hallett, S.R.; Partridge, I.K. Effective use of metallic z-pins for composites’ through-thickness reinforcement. Compos. Sci. Technol. 2019, 175, 77–84. [Google Scholar] [CrossRef] [Green Version]
- Pegorin, F.; Pingkarawat, K.; Daynes, S.; Mouritz, A.P. Mode II interlaminar fatigue properties of z-pinned carbon fibre reinforced epoxy composites. Compos. Part A Appl. Sci. Manuf. 2014, 67, 8–15. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Sun, P.; Cui, Y.; Wu, G. Microstructure and Flexural Properties of Z-pinned Carbon Fiber-Reinforced Aluminum Matrix composites. Materials 2019, 12, 174. [Google Scholar] [CrossRef] [Green Version]
- Bisagni, C.; Furfari, D.; Pacchione, M. Experimental investigation of reinforced bonded joints for composite laminates. J. Compos. Mater. 2018, 52, 431–447. [Google Scholar] [CrossRef] [Green Version]
- Chun, H.J.; Son, J.; Kang, K.T.; Byun, J.H.; Um, M.K.; Lee, S.K. Prediction of elastic properties for woven z-pinned composites. Compos. Part B Eng. 2014, 64, 59–71. [Google Scholar] [CrossRef]
- Grassi, M.; Zhang, X.; Meo, M. Prediction of stiffness and stresses in z-fibre reinforced composite laminates. Compos. Part A Appl. Sci. Manuf. 2002, 33, 1653–1664. [Google Scholar] [CrossRef] [Green Version]
- Chang, P.; Mouritz, A.P.; Cox, B.N. Flexural properties of z-pinned laminates. Compos. Part A Appl. Sci. Manuf. 2007, 38, 244–251. [Google Scholar] [CrossRef]
- Chang, P.; Mouritz, A.P.; Cox, B.N. Properties and failure mechanisms of z-pinned laminates in monotonic and cyclic tension. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1501–1513. [Google Scholar] [CrossRef]
- Pinho, S.T.; Iannucci, L.; Robinson, P. Physically-based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking: Part I: Development. Compos. Part A Appl. Sci. Manuf. 2006, 37, 63–73. [Google Scholar] [CrossRef] [Green Version]
- Matzenmiller, A.L.J.T.R.; Lubliner, J.; Taylor, R.L. A constitutive model for anisotropic damage in fiber-composites. Mech. Mater. 1995, 20, 125–152. [Google Scholar] [CrossRef]
- Böhm, R.; Gude, M.; Hufenbach, W. A phenomenologically based damage model for textile composites with crimped reinforcement. Compos. Sci. Technol. 2010, 70, 81–87. [Google Scholar] [CrossRef]
- Cuntze, R.G. Strength failure conditions of various structural materials: Is there some common basis existing. Sdhm Struct. Durab. Health Monit. 2007, 3, 87–105. [Google Scholar]
- Böhm, H.; Weck, D.; Hornig, A.; Langkamp, A.; Adam, F.; Gude, M. Experimental and numerical study on the axial crushing behavior of textile-reinforced thermoplastic composite tubes. Adv. Eng. Mater. 2016, 18, 437–443. [Google Scholar] [CrossRef]
- Zhang, B.; Allegri, G.; Yasaee, M.; Hallett, S.R. Micro-mechanical finite element analysis of z-pins under mixed-mode loading. Compos. Part A Appl. Sci. Manuf. 2015, 78, 424–435. [Google Scholar] [CrossRef]
- Bianchi, F.; Koh, T.M.; Zhang, X.; Partridge, I.K.; Mouritz, A.P. Finite element modelling of z-pinned composite T-joints. Compos. Sci. Technol. 2012, 73, 48–56. [Google Scholar] [CrossRef]
- Taotao, Z.; Wenbo, L.; Wei, X.; Ying, Y. Numerical simulation of single-lap adhesive joint of composite laminates. J. Reinf. Plast. Compos. 2018, 37, 520–532. [Google Scholar] [CrossRef]
- ABAQUS, Version 6.7; Analysis User’s Manual; Dassault Systemes Simulia, Inc.: Waltham, MA, USA, 2017.
- Kuhtz, M.; Hornig, A.; Gude, M.; Jäger, H. A method to control delaminations in composites for adjusted energy dissipation characteristics. Mater. Des. 2017, 123, 103–111. [Google Scholar] [CrossRef]
- DIN EN 1993-1-8:2010-12: Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings; German Version EN 1993-1-1:2005 + AC: 2009, Standard. 2010. Available online: https://www.beuth.de/de/norm/din-en-1993-1-8/134178148 (accessed on 16 November 2020). [CrossRef]
- Polymerdatabase.com Polypropylene. In Polymer Properties Database. 2020. Available online: https://polymerdatabase.com/Commercial%20Polymers/PP.html (accessed on 5 May 2020).
- Böhm, R.; Hufenbach, W. Experimentally based strategy for damage analysis of textile-reinforced composites under static loading. Compos. Sci. Technol. 2010, 70, 1330–1337. [Google Scholar] [CrossRef] [Green Version]
- Hufenbach, W.; Langkamp, A.; Hornig, A.; Ebert, C. Experimental determination of the strain rate dependent out-of-plane properties of textile reinforced composites. In Proceedings of the 17th International Conference on Composite Materials (ICCM 17), Edinburgh, UK, 27–31 July 2009. [Google Scholar]
- Brown, K.A.; Brooks, R.; Warrior, N.A. The static and high strain rate behavior of a commingled E-glass/polypropylene woven fabric composite. Compos. Sci. Technol. 2010, 70, 272–283. [Google Scholar] [CrossRef]






| (N/mm) | (MPa) | (N/mm) |
|---|---|---|
| 74,670 | 12.6 | 2.5 |
| 26,670 | 92.0 | 3.5 |
| 26,670 | 92.0 | 3.5 |
| Material Parameter | Unit | Value |
|---|---|---|
| E1 | (GPa) | 14.9 |
| E2 | (GPa) | 14.9 |
| E3 | (GPa) | 1.50 |
| ν12 | (-) | 0.08 |
| ν13 | (-) | 0.17 |
| ν23 | (-) | 0.17 |
| G12 | (MPa) | 7500 |
| G13 | (MPa) | 1050 |
| G23 | (MPa) | 1050 |
| Rd1t | (MPa) | 60 |
| Rd1c | (MPa) | 35 |
| Rd2t | (MPa) | 60 |
| Rd2c | (MPa) | 35 |
| Rd3t | (MPa) | 12.4 |
| Rd3c | (MPa) | 477 |
| Rd12 | (MPa) | 25 |
| Rd13 | (MPa) | 9 |
| Rd23 | (MPa) | 9 |
| ε1t, fail | (-) | 0.1 |
| ε1c, fail | (-) | 0.03 |
| ε2t, fail | (-) | 0.1 |
| ε2c, fail | (-) | 0.03 |
| ε3t, fail | (-) | 0.2 |
| ε3c, fail | (-) | 0.08 |
| γ12, fail | (-) | 0.016 |
| γ13, fail | (-) | 0.014 |
| γ23, fail | (-) | 0.014 |
| Material Parameter | Unit | Value |
|---|---|---|
| ε1, del | (-) | 3.0 |
| ε2, del | (-) | 3.0 |
| γ12, del | (-) | 0.15 |
| Rc | (MPa) | 0.5 |
| Rs | (MPa) | 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Böhm, H.; Zhang, H.; Gröger, B.; Hornig, A.; Gude, M. Characterization and Numerical Modelling of Through-Thickness Metallic-Pin-Reinforced Fibre/Thermoplastic Composites under Bending Loading. J. Compos. Sci. 2020, 4, 188. https://doi.org/10.3390/jcs4040188
Böhm H, Zhang H, Gröger B, Hornig A, Gude M. Characterization and Numerical Modelling of Through-Thickness Metallic-Pin-Reinforced Fibre/Thermoplastic Composites under Bending Loading. Journal of Composites Science. 2020; 4(4):188. https://doi.org/10.3390/jcs4040188
Chicago/Turabian StyleBöhm, Holger, Hailun Zhang, Benjamin Gröger, Andreas Hornig, and Maik Gude. 2020. "Characterization and Numerical Modelling of Through-Thickness Metallic-Pin-Reinforced Fibre/Thermoplastic Composites under Bending Loading" Journal of Composites Science 4, no. 4: 188. https://doi.org/10.3390/jcs4040188
APA StyleBöhm, H., Zhang, H., Gröger, B., Hornig, A., & Gude, M. (2020). Characterization and Numerical Modelling of Through-Thickness Metallic-Pin-Reinforced Fibre/Thermoplastic Composites under Bending Loading. Journal of Composites Science, 4(4), 188. https://doi.org/10.3390/jcs4040188







