Damping Characterization of Hybrid Carbon Fiber Elastomer Metal Laminates using Experimental and Numerical Dynamic Mechanical Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Aluminum
2.1.2. CFRP Prepreg
2.1.3. Elastomer
2.1.4. Hybrid Laminates
2.2. Methods
2.2.1. Tension DMA
2.2.2. Three Point Bending DMA
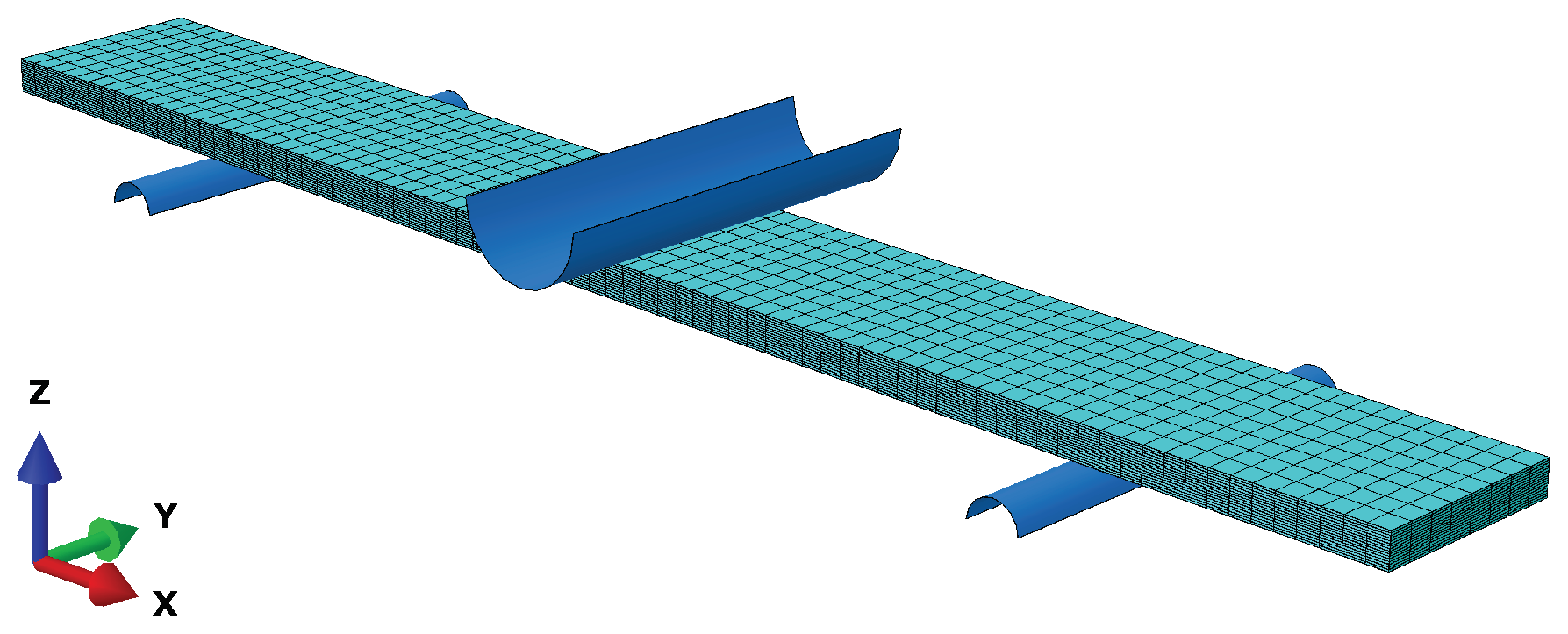
2.2.3. Finite Element Modeling
3. Results
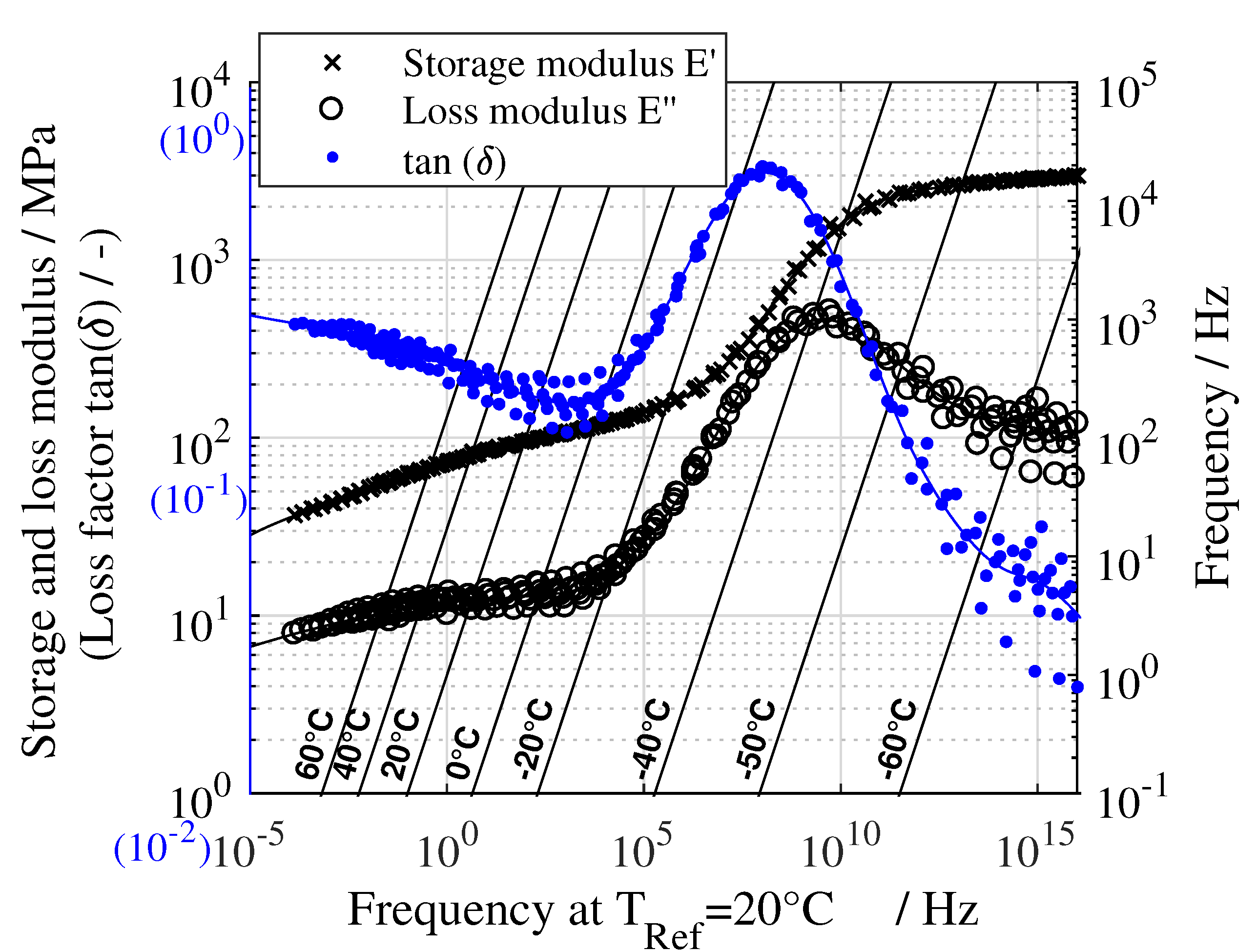
3.1. Elastomer
3.2. Hybrid Laminates
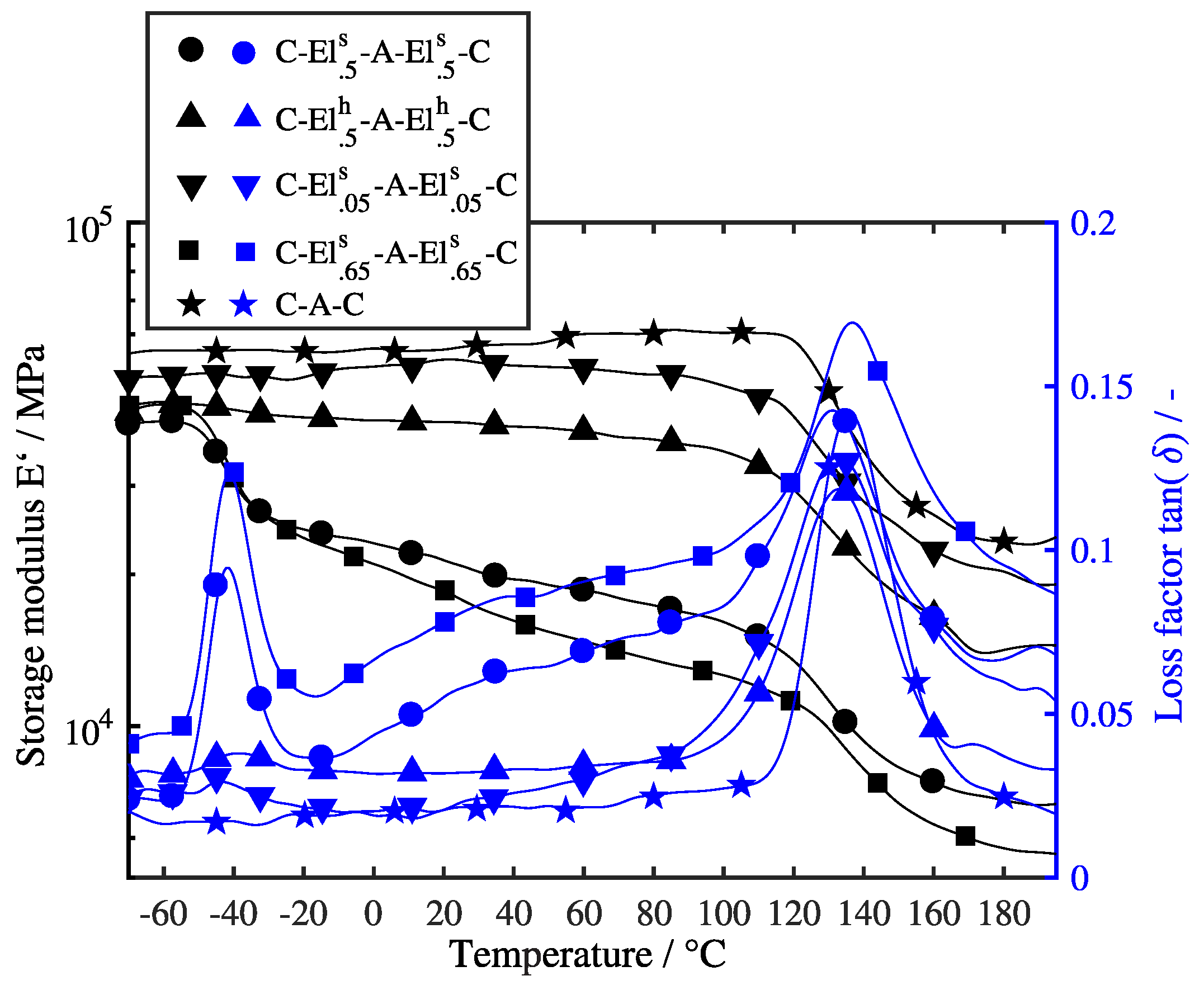
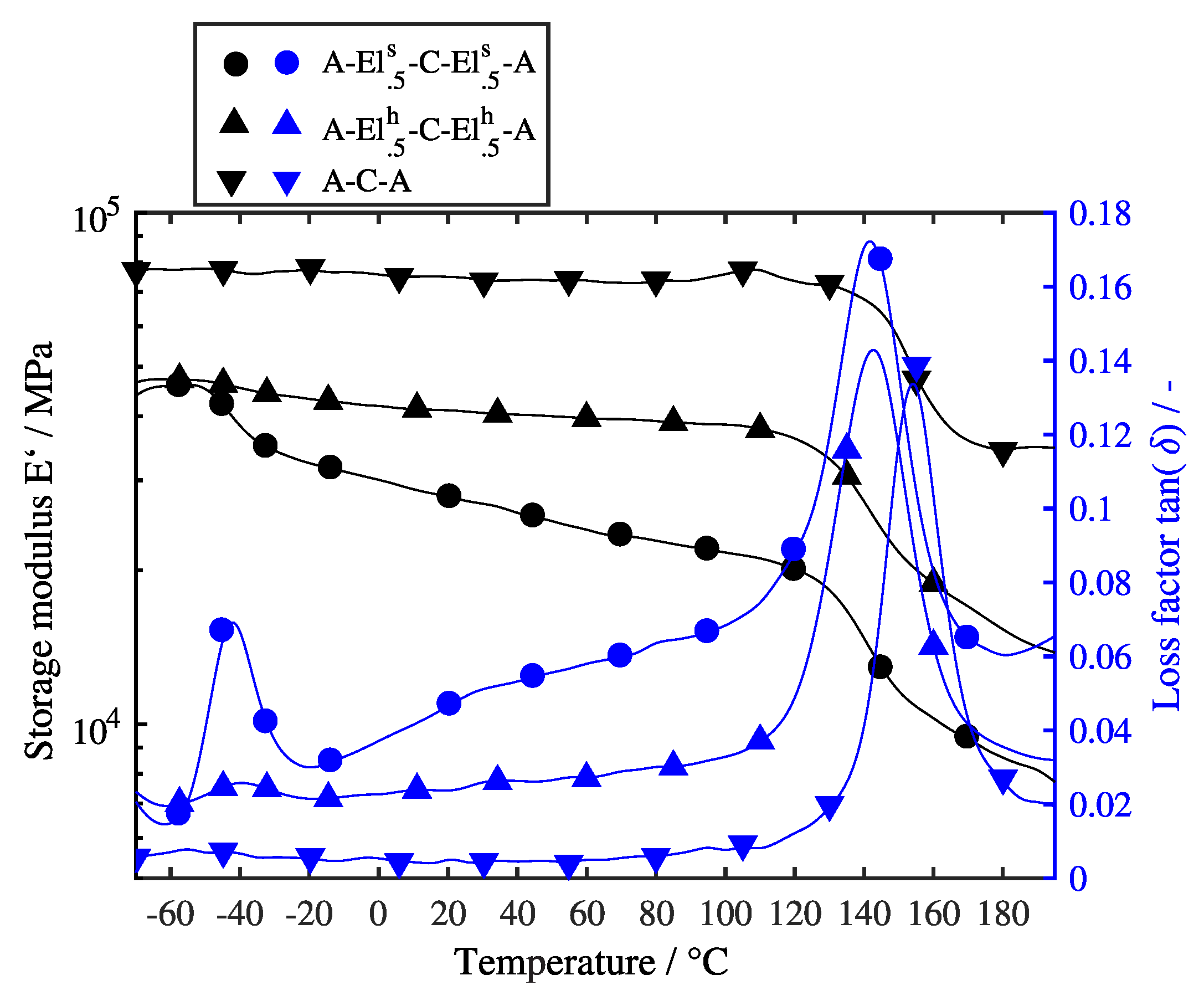
3.2.1. Temperature Sweep
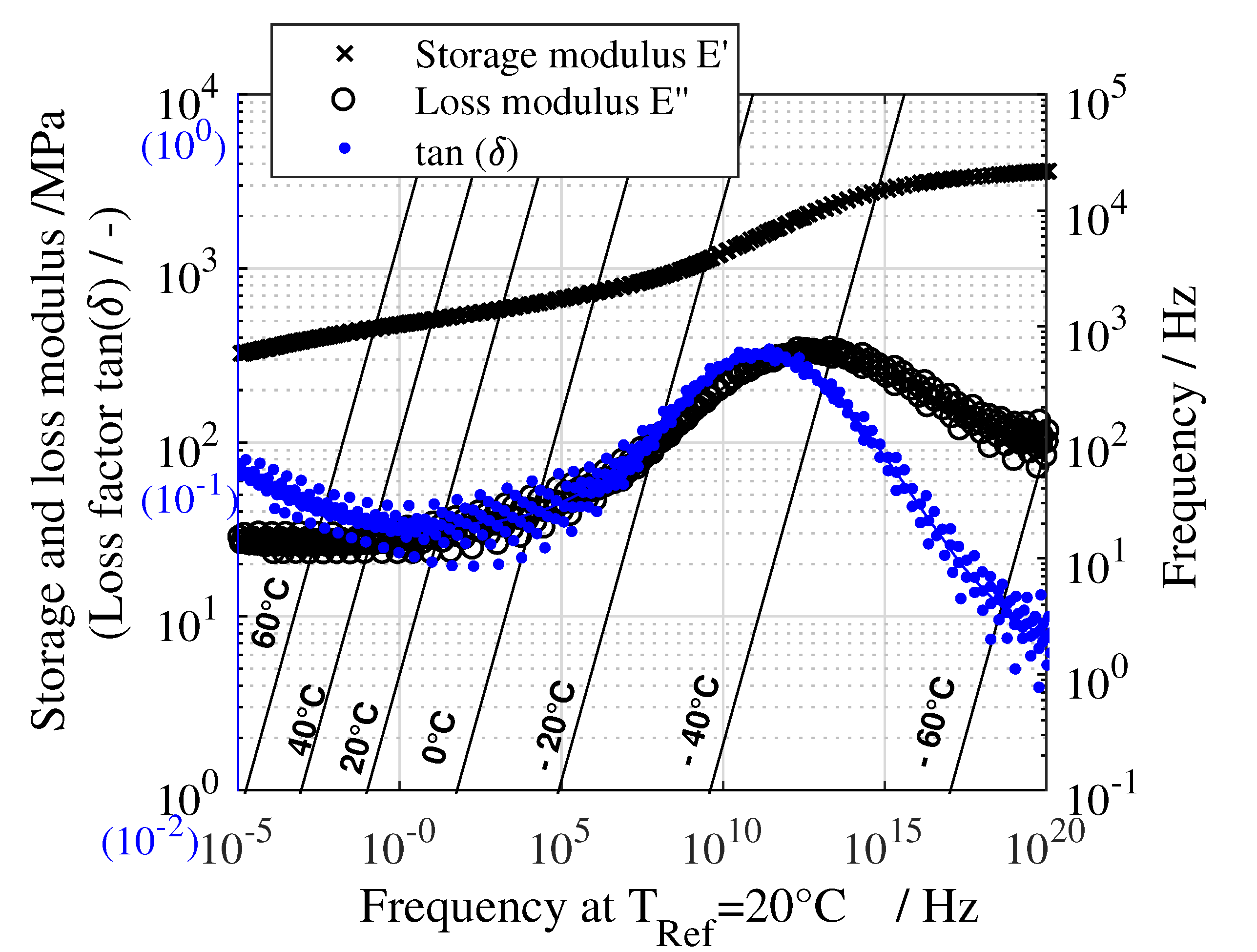
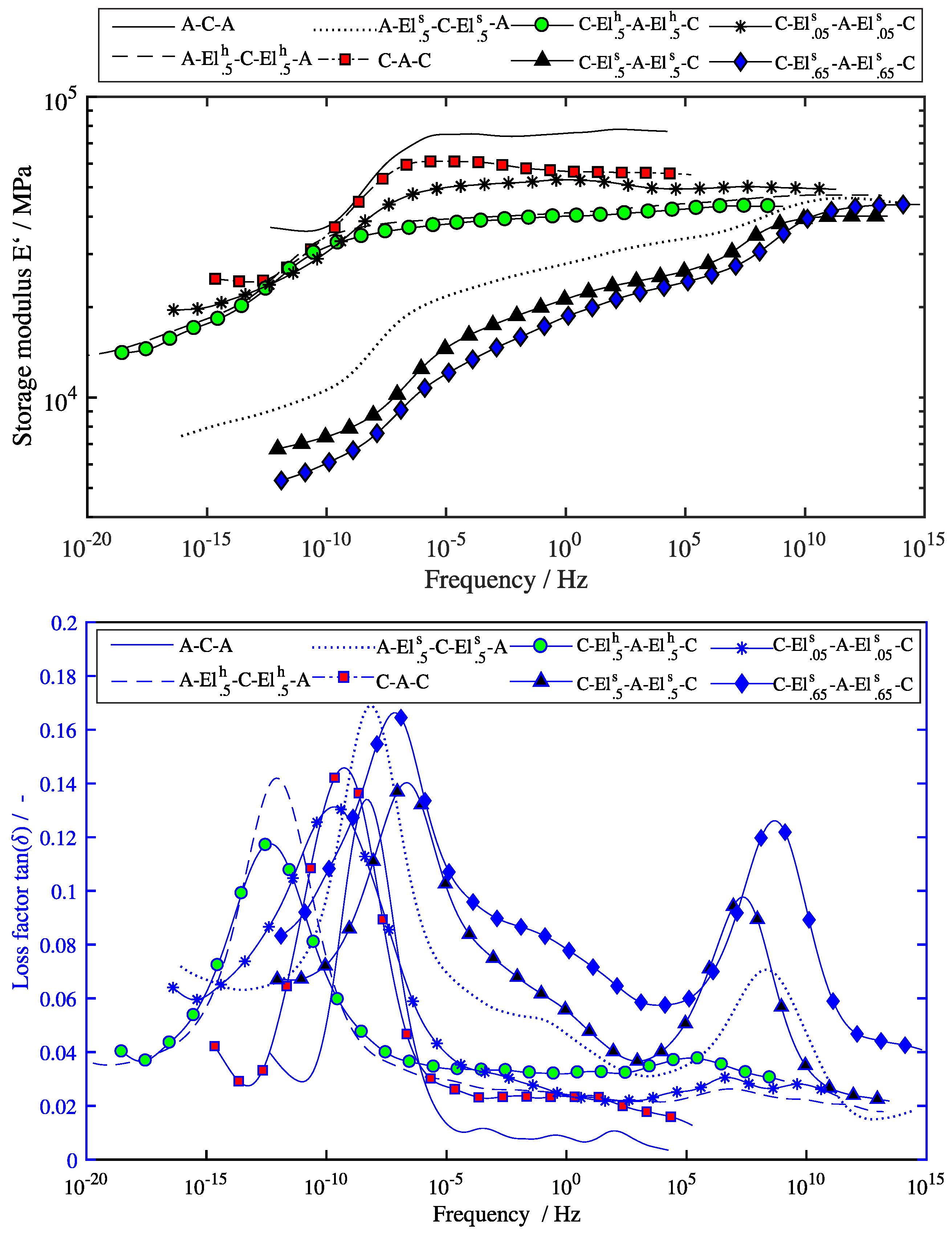
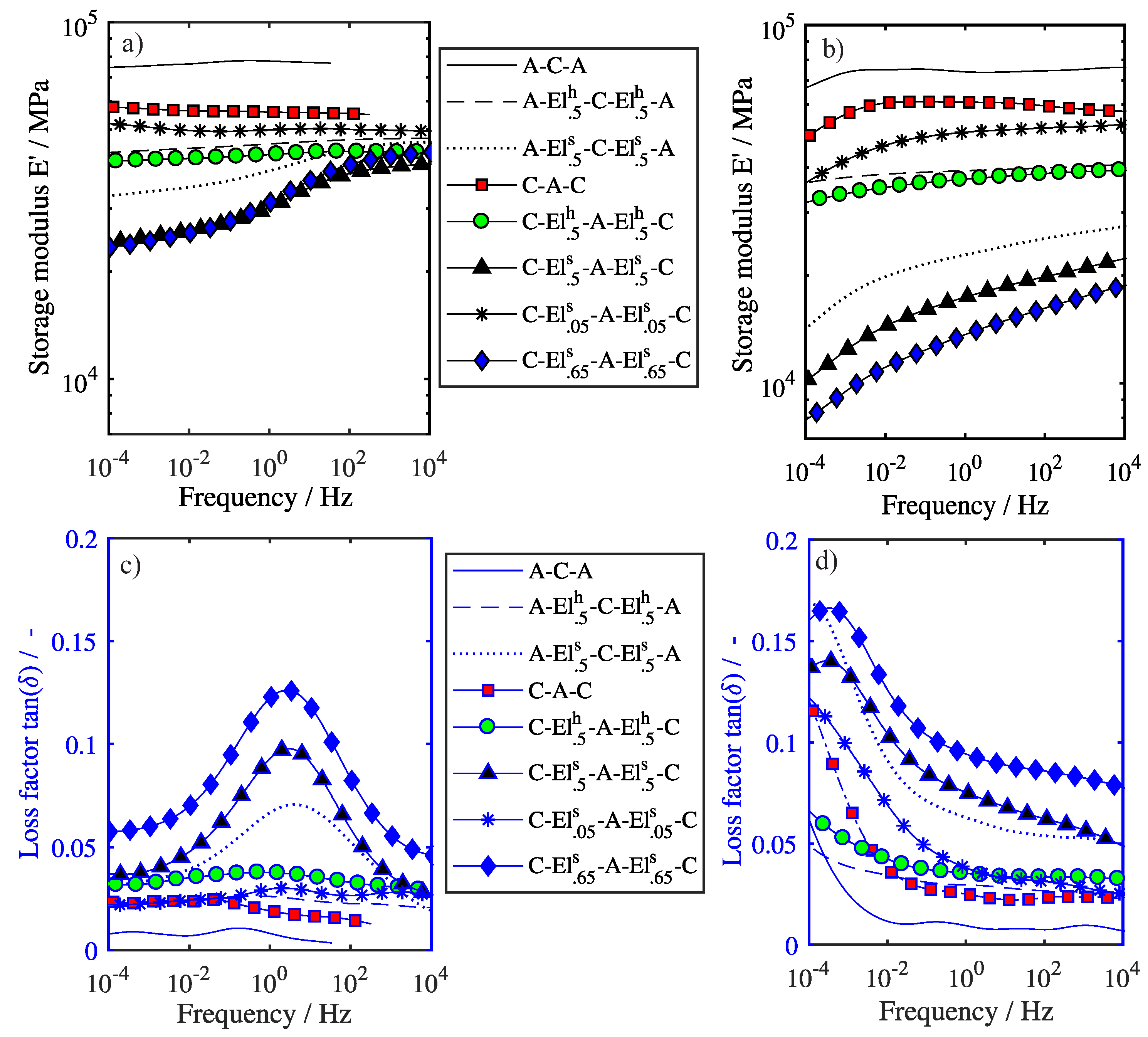
3.2.2. Master Curves
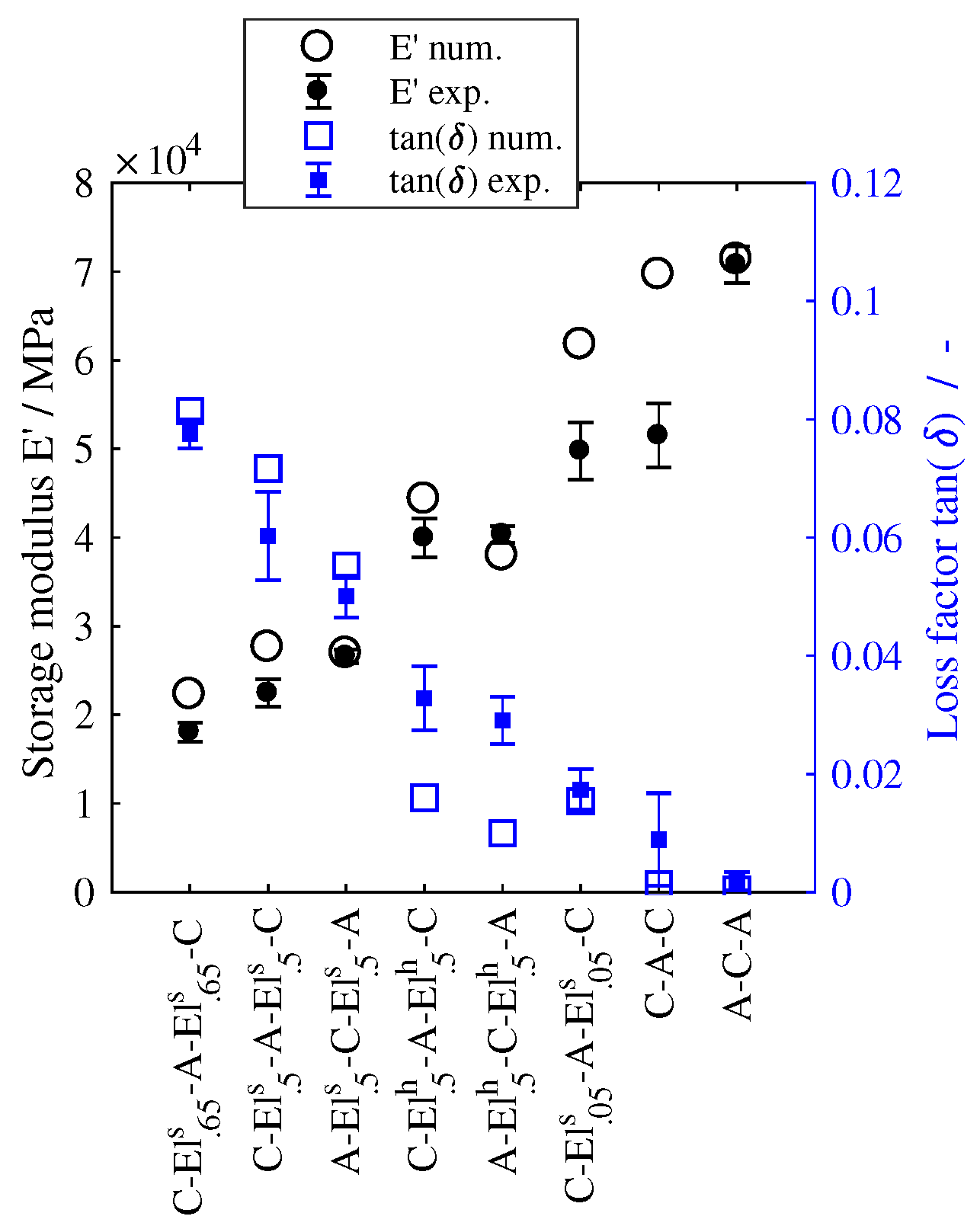
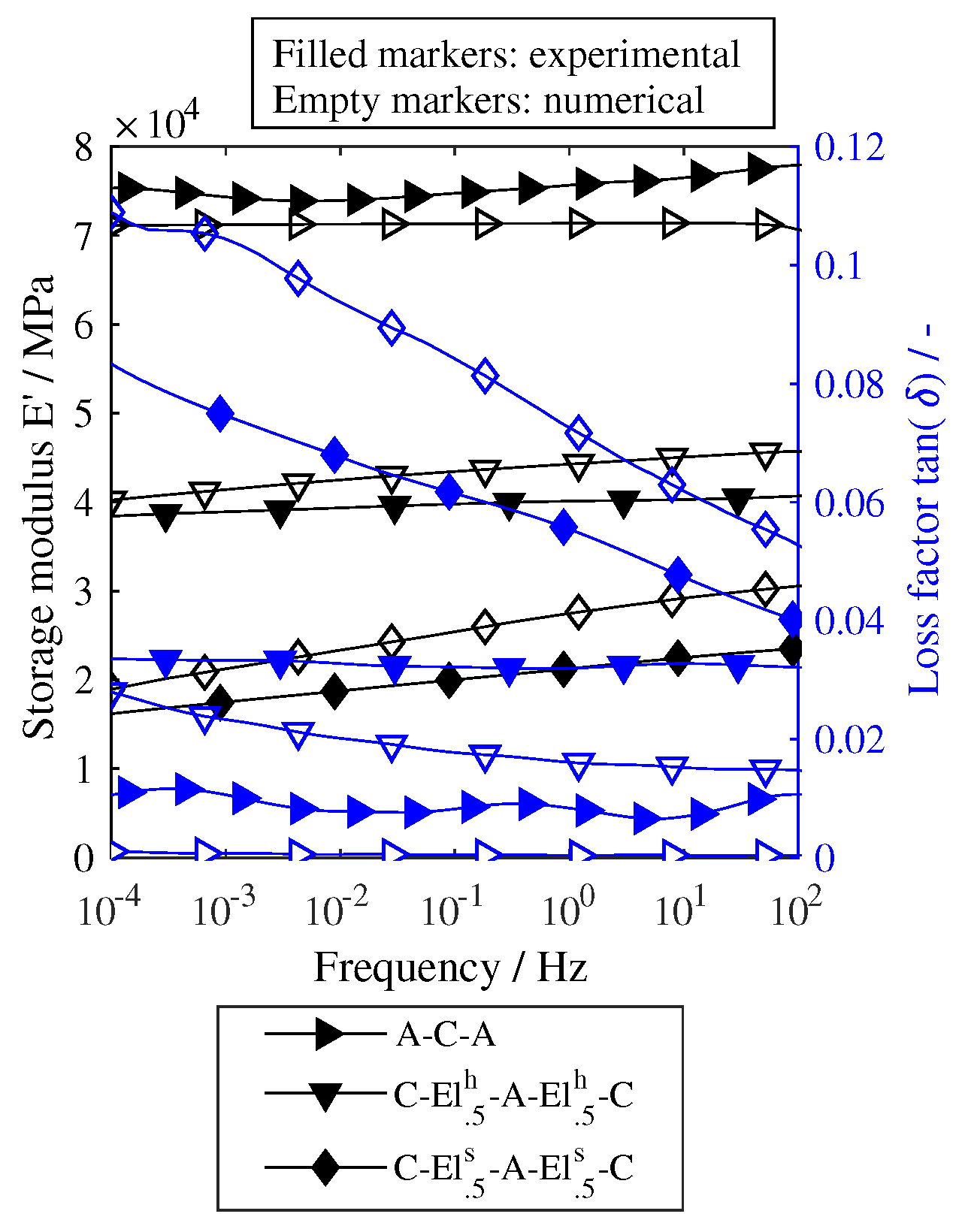
3.2.3. Finite Element Modeling
4. Discussion
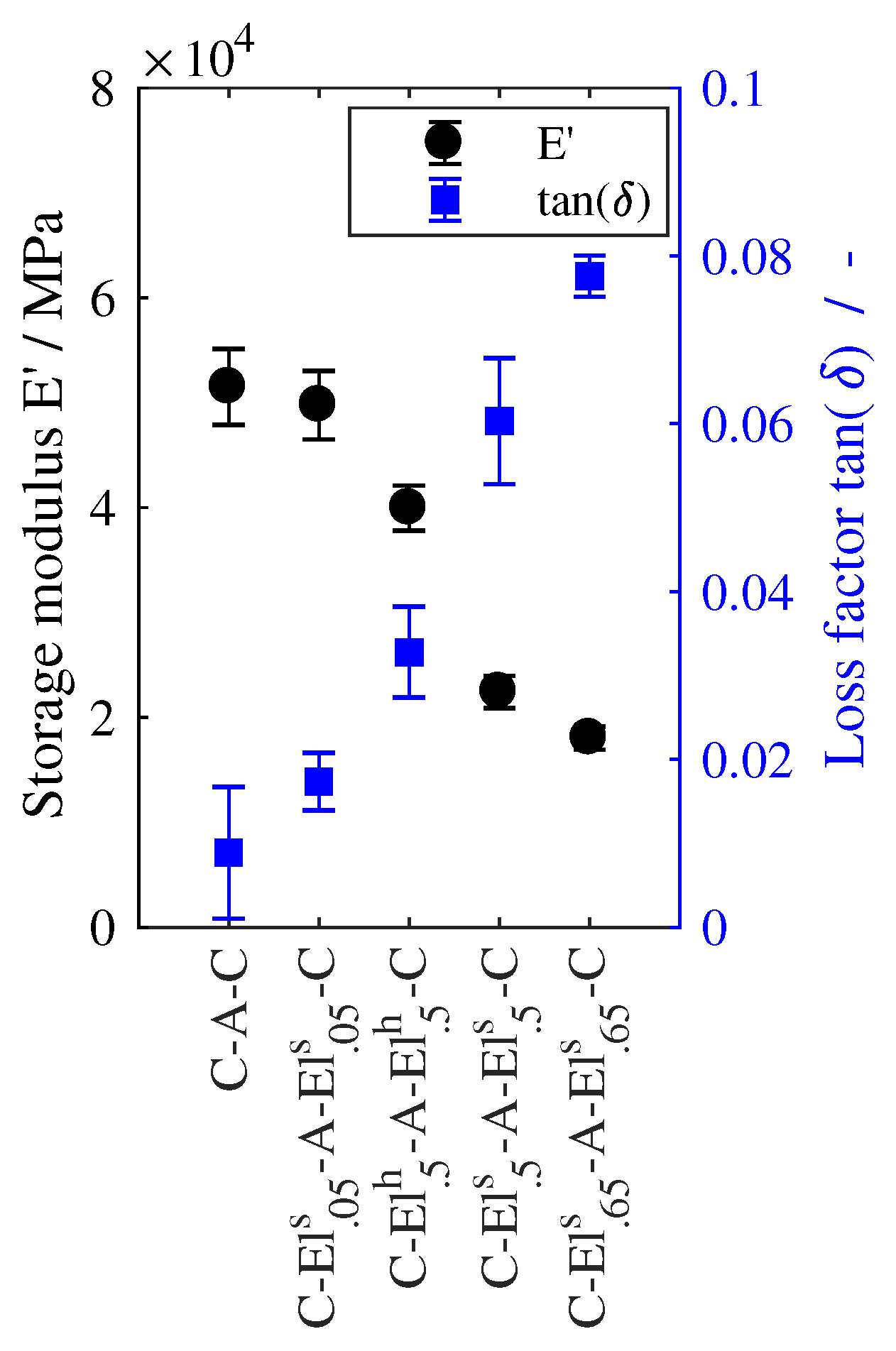
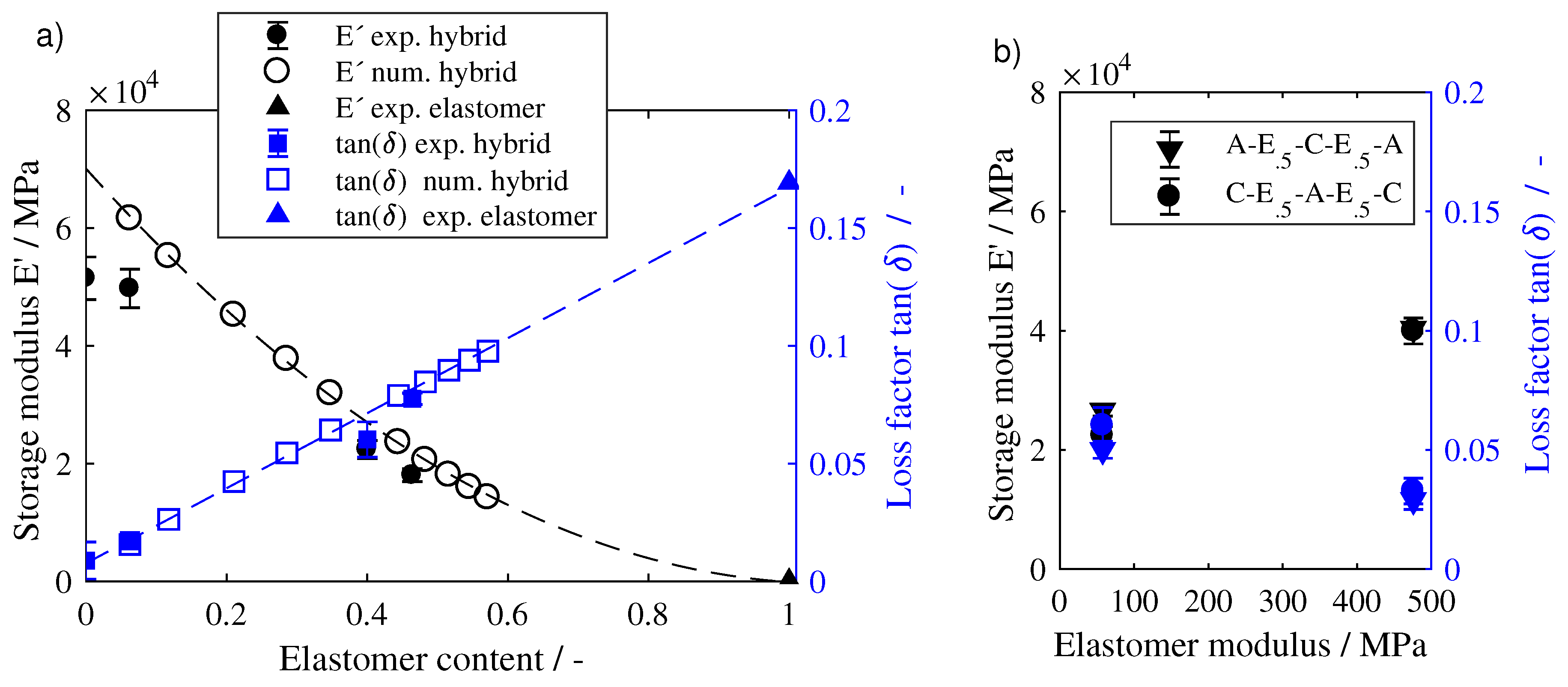
4.1. Influence of Elastomer Content
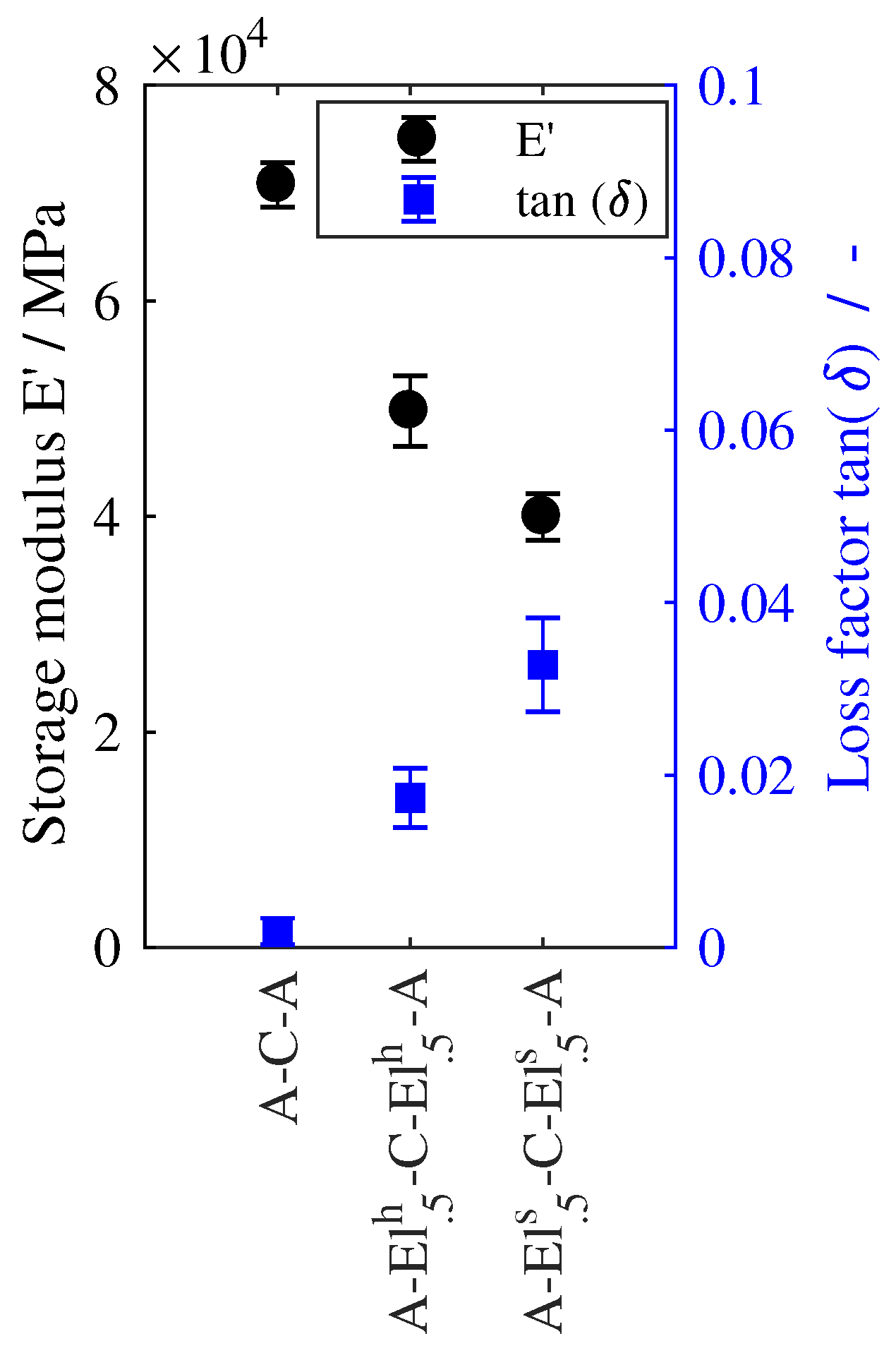
4.2. Influence of Elastomer Modulus
4.3. Influence of Lay-up
4.4. Influence of Temperature
4.5. Influence of Frequency
5. Summary and Conclusions
- The additional elastomer layer increases the damping behavior depending on its modulus, thickness and position in the laminate. This results in a decrease in stiffness if the temperature is far from the glass transition range of the used polymers.
- With increasing thickness of the elastomer layers and decreasing modulus the damping increases and the bending stiffness decreases as well.
- Laminates with aluminum layers on the outside showed lower damping values at higher bending stiffnesses for the investigated lay-ups due to different positions of the elastomer layer in the laminate and different thickness ratios of the constraining and base layers.
- With the same bending stiffness, the mass of a lay-up with a soft elastomer increases by around 35% due to a thicker elastomer layer, compared to the same laminate lay-up with a hard elastomer. At the same time, the damping is increased by around 300%.
- A rule of mixture that takes the elastomer content in the laminate into account can be applied to estimate the loss factor of the hybrid fiber metal elastomer laminate.
- The glass transition range can be used to increase the damping and the stiffness of the specimens. However, it is limited to a small temperature range of about 30 C for the investigated materials.
- The numerical model based on the DMA data of the individual materials can reproduce the quasi-static and dynamic material behavior of most lay-ups in good accordance to the experimental results. The frequency dependence of the laminate is also well represented by master curves of the individual materials.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Generalized Maxwell Model for CFRP
| GPa | GPa | GPa | GPa | GPa |
References
- Sinmazçelik, T.; Avcu, E.; Bora, M.Ö.; Çoban, O. A review: Fibre metal laminates, background, bonding types and applied test methods. Mater. Des. 2011, 32, 3671–3685. [Google Scholar] [CrossRef]
- Sadighi, M.; Alderliesten, R.C.; Benedictus, R. Impact resistance of fiber-metal laminates: A review. Int. J. Impact Eng. 2012, 49, 77–90. [Google Scholar] [CrossRef]
- Alderliesten, R. Solid mechanics and its applications. In Fatigue and Fracture of Fibre Metal Laminates; Springer: Cham, Switzerland, 2017; Volume 236. [Google Scholar]
- Botelho, E.C.; Silva, R.A.; Pardini, L.C.; Rezende, M.C. A Review on the Development and Properties of Continuous Fiber/epoxy/aluminum Hybrid Composites for Aircraft Structures. Mater. Res. 2006, 9, 247–256. [Google Scholar] [CrossRef]
- Lin, C.T.; Kao, P.W. Effect of fiber bridging on the fatigue crack propagation in carbon fiber-reinforced aluminum laminates. Mater. Sci. Eng. A 1995, 190, 65–73. [Google Scholar] [CrossRef]
- Lin, C.T.; Kao, P.W. Fatigue delamination growth in carbon fibre-reinforced aluminum laminates. Compos. Part A 1996, 27, 9–15. [Google Scholar] [CrossRef]
- Sarlin, E.; Hoikkanen, M.; Frisk, L.; Vuorinen, J.; Vippola, M.; Lepistö, T. Ageing of corrosion resistant steel/rubber/composite hybrid structures. Int. J. Adhes. Adhes. 2014, 49, 26–32. [Google Scholar] [CrossRef]
- Stoll, M.; Stemmer, F.; Ilinzeer, S.; Weidenmann, K.A. Optimization of corrosive properties of carbon fiber reinforced aluminum laminates due to integration of an elastomer interlayer. In 21st Symposium on Composites; Key Engineering Materials Vol. 742, Series; Herrmann, A.S., Ed.; Trans Tech Publications Ltd.: Zurich, Switzerland, 2017; pp. 187–293. [Google Scholar]
- Stoll, M.; Weidenmann, K.A. Characterization of interface properties of Fiber-Metal-Laminates (FML) with optimized surfaces. In Internationale Konferenz Euro Hybrid Materials and Structures; Hausmann, J.M., Siebert, M., Eds.; Deutsche Gesellschaft für Materialkunde e.V.: Frankfurt, Germany, 2016; pp. 38–43. [Google Scholar]
- Nashif, A.D.; Jones, D.I.G.; Henderson, J.P. Vibration Damping; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Ross, D.; Ungar, E.E.; Kerwin, E.M. Damping of plate flexural vibrations by means of viscoelastic laminae. Struct. Damp. 1959, 1959, 49–87. [Google Scholar]
- Zhou, X.Q.; Yu, D.Y.; Shao, X.Y.; Zhang, S.Q.; Wang, S. Research and applications of viscoelastic vibration damping materials: A review. Compos. Struct. 2016, 136, 460–480. [Google Scholar] [CrossRef]
- Rao, M.D. Recent applications of viscoelastic damping for noise control in automobiles and commercial airplanes. J. Sound Vib. 2003, 262, 457–474. [Google Scholar] [CrossRef]
- Ghiringhelli, G.L.; Terraneo, M.; Vigoni, E. Improvement of structures vibroacoustics by widespread embodiment of viscoelastic materials. Aerosp. Sci. Technol. 2013, 28, 227–241. [Google Scholar] [CrossRef]
- Sarlin, E.; Liu, Y.; Vippola, M.; Zogg, M.; Ermanni, P.; Vuorinen, J.; Lepistö, T. Vibration damping properties of steel/rubber/composite hybrid structures. Compos. Struct. 2012, 94, 3327–3335. [Google Scholar] [CrossRef]
- Botelho, E.C.; Campos, A.N.; de Barros, E.; Pardini, L.C.; Rezende, M.C. Damping behavior of continuous fiber/metal composite materials by the free vibration method. Compos. Part B Eng. 2005, 37, 255–263. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA; Chichester, UK; Brisbane, Australia; Toronto, ON, Canada; Singapore, 1980. [Google Scholar]
- Takayanagi, M.; Uemura, S.; Minami, S. Application of equivalent model method to dynamic rheo-optical properties of crystalline polymer. J. Polym. Sci. Part C Polym. Symp. 1964, 5, 113–122. [Google Scholar] [CrossRef]
- Caruthers, J.M.; Cohen, R.E. Consequences of thermorheological complexity in viscoelastic materials. Rheol. Acta 1980, 19, 606–613. [Google Scholar] [CrossRef]
- Kaplan, D.; Tschoegl, N.W. Time-Temperature Superposition in Two-Phase Polyblends. In Recent Advances in Polymer Blends, Grafts, and Blocks; Vol. 4, Polymer Science and Technology; Sperling, L.H., Ed.; Springer: Boston, MA, USA, 1974; pp. 43–49. [Google Scholar] [CrossRef]
- Fesko, D.G.; Tschoegl, N.W. Time-temperature superposition in thermorheologically complex materials. J. Polym. Sci. Part C Polym. Symp. 1971, 1971, 51–69. [Google Scholar] [CrossRef]
- Nakano, T. Applicability condition of time–temperature superposition principle (TTSP) to a multi-phase system. Mech. Time-Depend. Mater. 2013, 17, 439–447. [Google Scholar] [CrossRef]
- DIN. ISO 527-5: Bestimmung der Zugeigenschaften Teil 5: Prüfbedinungen für Unidirektional Faserverstärkte Kunstoffverbundwerkstoffe; Deutsches Institut für Normung e.V.: Berlin, Germany, 1997. [Google Scholar]
- DIN EN 6031. Luft-und Raumfahrt–Faserverstärkte Kunststoffe–Prüfverfahren – Bestimmung der Schubeigenschaften (± 45-Zugversuch); Deutsches Institut für Normung e.V.: Berlin, Germany, 2016. [Google Scholar]
- Liebig, W.V.; Jackstadt, A.; Sessner, V.; Weidenmann, K.A.; Kärger, L. Multi-Scale Approach Describing the Transversely Isotropic Viscoelastic Material Behaviour of Carbon-Fibre-Reinforced Plastics in the Frequency Domain; Preprint Series of the PP 1897; University of Stuttgart, Institute of Engineering and Computational Mechanics: Stuttgart, Germany, 2018. [Google Scholar]
- ISO 37:2017 Rubber, Vulcanized or Thermoplastic—Determination of Tensile Stress-Strain Properties; International Organization for Standardization: Geneva, Switzerland, 2017.
- ASM Aerospace Specification Metals, Inc. Data Sheet Aluminum 2024-T3; ASM Aerospace Specification Metals, Inc.: Pompano Beach, FL, USA, 2018. [Google Scholar]
- Hexcel Corporation. HexPly® M77/38%/UD150/CHS-12K T700 Datasheet; Hexcel Corporation: Stamford, CT, USA, 2014. [Google Scholar]
- Gummiwerk Kraiburg GmbH & Co. KG. Technical Data Sheet SAA9579/52; Gummiwerk Kraiburg GmbH & Co. KG: Waldkraiburg, Germany, 2014. [Google Scholar]
- Gummiwerk Kraiburg GmbH & Co. KG. Technical Data Sheet HAA9275-45; Gummiwerk Kraiburg GmbH & Co. KG: Waldkraiburg, Germany, 2014. [Google Scholar]
- VDI. 2014-Development of FRP Components (Fibre-Reinforced Plastics) Analysis; Verein Deutscher Ingeniuere: Dusseldorf, Germany, 2006. [Google Scholar]
- Jones, D.I.G. An Attractive Method lfor Displaying Material Damping Data. J. Aircr. 1981, 18, 644–649. [Google Scholar] [CrossRef]
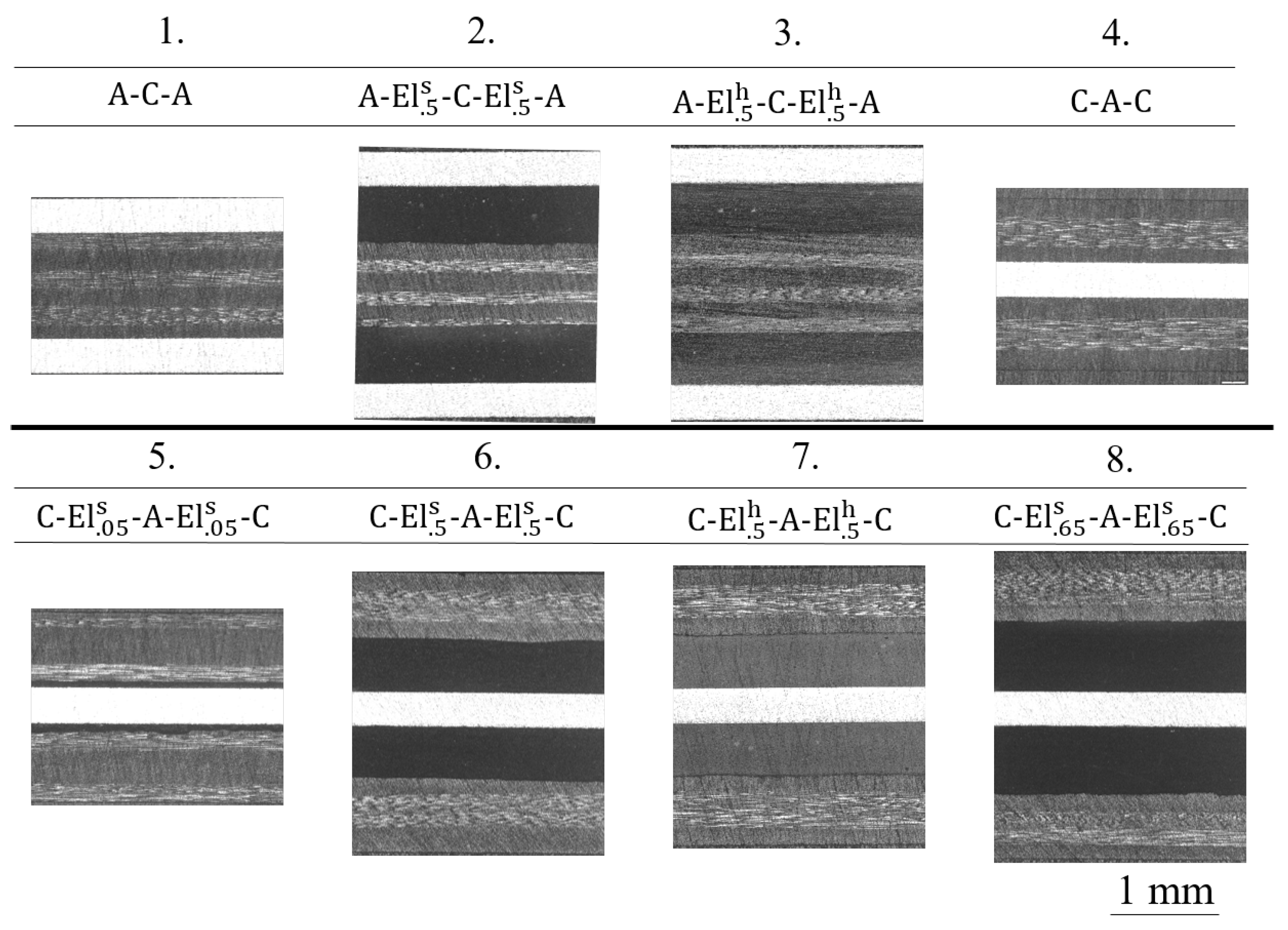
| Aluminum | CFRP | Elastomer | |||
|---|---|---|---|---|---|
| Soft | Hard | ||||
| Elastic modulus/GPa | E1 | 73.1 * | 113.7 () | 0.045 () | 0.483 () |
| E2 | 7.75 () | ||||
| E3 | 7.75 () | ||||
| Shear modulus/GPa | G21 | 28.0 * | 3.76 () | 0.015 () | 0.15 () |
| G31 | 3.76 () | ||||
| G32 | 2.75 () | ||||
| Poisson’s ratio/- | v21 | 0.31 * | 0.34 | 0.48 | 0.45 |
| v31 | 0.34 | ||||
| v32 | 0.40 | ||||
| Density/kg/m3 | 2780 * | 1496 * | 1180 * | 1250 * | |
| Nbr. | Detailed Lay-Up | Thickness/mm | Abbr. Lay-Up |
|---|---|---|---|
| 1. | 1.5 | A-C-A | |
| 2. | 2.5 | A--C--A | |
| 3. | 2.5 | A--C--A | |
| 4. | 1.5 | C-A-C | |
| 5. | 1.6 | C--A--C | |
| 6. | 2.5 | C--A--C | |
| 7. | 2.5 | C--A--C | |
| 8. | 2.8 | C--A--C |
| Material | Symmetry | Material Model |
|---|---|---|
| Aluminum | isotropic | linear elastic |
| Elastomer | isotropic | linear viscoelastic (tabular data) |
| CFRP | transversely isotropic | linear viscoelastic (GMM) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sessner, V.; Jackstadt, A.; Liebig, W.V.; Kärger, L.; Weidenmann, K.A. Damping Characterization of Hybrid Carbon Fiber Elastomer Metal Laminates using Experimental and Numerical Dynamic Mechanical Analysis. J. Compos. Sci. 2019, 3, 3. https://doi.org/10.3390/jcs3010003
Sessner V, Jackstadt A, Liebig WV, Kärger L, Weidenmann KA. Damping Characterization of Hybrid Carbon Fiber Elastomer Metal Laminates using Experimental and Numerical Dynamic Mechanical Analysis. Journal of Composites Science. 2019; 3(1):3. https://doi.org/10.3390/jcs3010003
Chicago/Turabian StyleSessner, Vincent, Alexander Jackstadt, Wilfried V. Liebig, Luise Kärger, and Kay A. Weidenmann. 2019. "Damping Characterization of Hybrid Carbon Fiber Elastomer Metal Laminates using Experimental and Numerical Dynamic Mechanical Analysis" Journal of Composites Science 3, no. 1: 3. https://doi.org/10.3390/jcs3010003
APA StyleSessner, V., Jackstadt, A., Liebig, W. V., Kärger, L., & Weidenmann, K. A. (2019). Damping Characterization of Hybrid Carbon Fiber Elastomer Metal Laminates using Experimental and Numerical Dynamic Mechanical Analysis. Journal of Composites Science, 3(1), 3. https://doi.org/10.3390/jcs3010003





