1. Introduction
Optical microscopy is a common method for measuring fiber orientation in fiber-filled composite material systems such as short fiber-filled injection molding compounds, bulk molding compounds, or prepreg tape systems such as platelet molding compounds or composite laminates. The method for measuring fiber orientation of fibers with circular cross-section, the so-called method of ellipses, is relatively straightforward and has been well-studied [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10]. While most applications of carbon fiber to date have been with fibers having circular cross-sections, one of the innovations in carbon fiber processing technology that hopes to expand the marketability of carbon fiber through lower cost is the utilization of textile grade polyacrylonitrile (PAN) as a carbon fiber precursor [
11,
12]. This is a very promising development for markets that are more cost constricted than the traditional carbon fiber markets such as the automotive industry. One ramification of this reduced cost manufacturing process, however, is that the fibers often have a kidney-bean shaped cross-section instead of a circular cross-section [
13,
14]. An example of the cross-sections of kidney-bean shaped carbon fibers under a scanning electron microscope is shown in
Figure 1. For such high volume applications, Dow has introduced the VORAFUSE™M6400 [
15,
16] system, which utilizes PAN-based carbon fibers to create a molding system similar to sheet molding compounds. To predict mechanical properties [
17], validate computed tomography based orientation measurement [
18], and validate orientation state predictions through flow simulation methods [
19,
20], the orientation state of molded geometries must be sufficiently measured.
The projected shape of a kidney bean fiber can be fit easily with an ellipse. Unfortunately, the orientations of these fibers cannot be determined accurately using the standard method of ellipses due to the assumption of a circular cross-section in the method development. In the standard method, the projection of a circular fiber onto a viewing plane is fit with an ellipse. With the fiber orientation described by the vector
expressed in terms of the spherical coordinates
and
, the orientation of the major-axis of the fit ellipse is directly interpreted as
. The ratio of the minor-axis,
m, to the major-axis,
M, of the fit ellipse is then
. The standard method then has an ambiguity in determining the sign of the angle
which requires more sophisticated techniques to resolve [
7]. As an example of the deficiency of the standard method when considering non-circular cross-section fibers, consider a fiber with an elliptical cross-section with a major-axis that is two times the minor-axis.
Figure 2a shows the same fiber with
and out-of-plane angles,
, varying between 0 and 90 degrees from the
-axis towards the
-axis. For a circular fiber, this exercise would yield a cross-section varying from an initial circle to ellipses with monotonically increasing ratio of observed major axis to minor axis. However, with an elliptical fiber, the 0 degree fiber will have a non-circular cross-section and an off angle fiber can have a circular cross-section, as shown in
Figure 2b. The actual angles versus those apparent to the standard method for
Figure 2 are shown in
Table 1. From this example, it is clear that a modification to the standard method is necessary to determine the fiber orientation if the fiber cross-section is not circular.
In this work, a method is presented by which the orientation state of elliptical fibers can be determined from their projected ellipses on a viewing plane. While the standard method of ellipses for circular fibers produces a single ambiguity on the resulting fiber orientation that must be handled by specialized methods [
7], the projected cross-section of an elliptical fiber could be associated with four fiber orientations from two ambiguities due to the additional degree-of-freedom of roll about the fiber axis. Herein, the additional ambiguity is treated in the special case that fibers are in bundles. Finally, measurement bias is considered and found to be equivalent to that considered by Bay and Tucker [
3] except in the case of fibers nearly parallel to the viewing plane. The developed measurement technique was verified through several in silico exercises, validated by the measurement of a laminate with prescribed orientation, and demonstrated on a micrograph of a prepreg platelet molding compound.
2. Theory
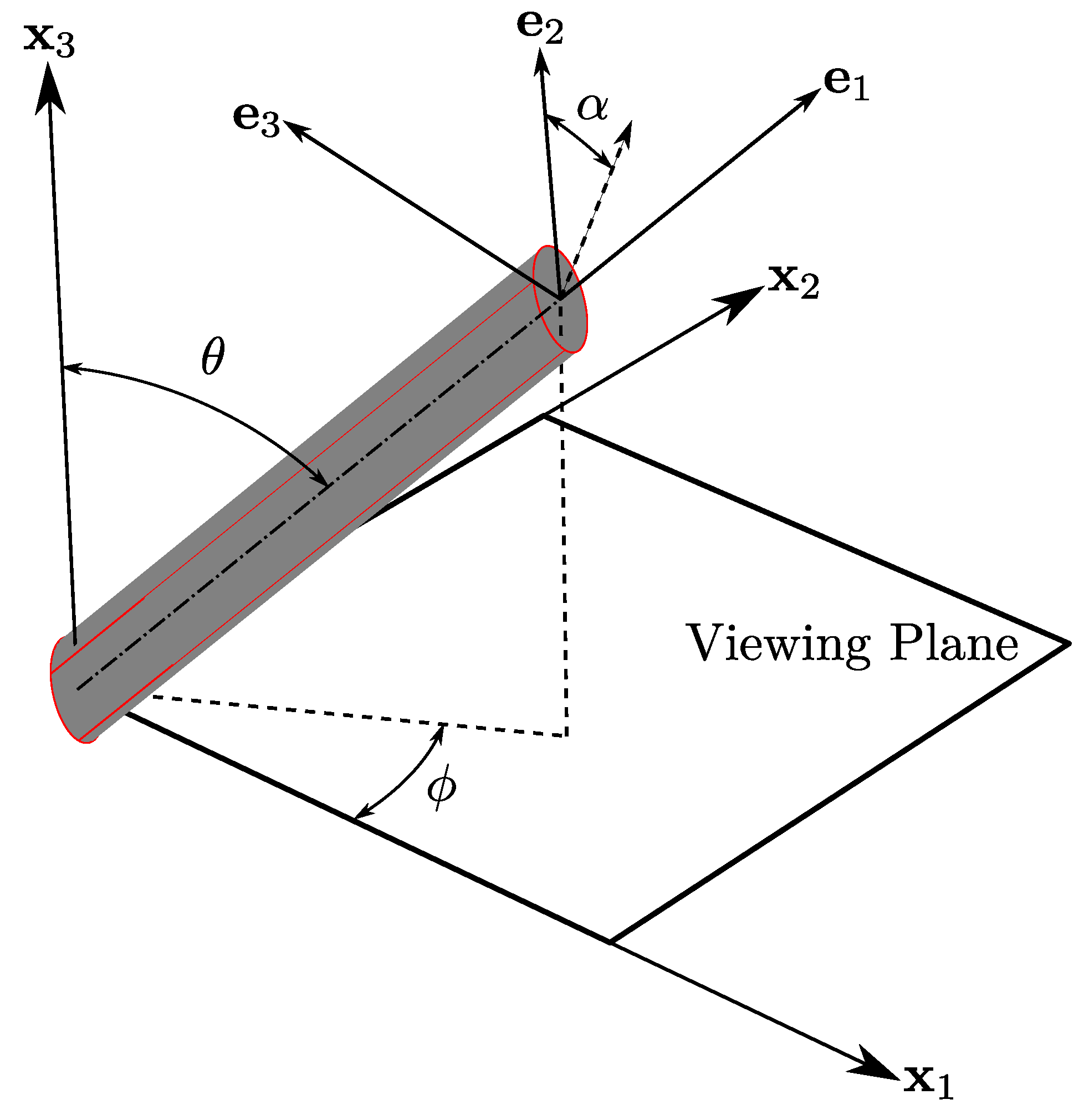
Orientation measurement by optical microscopy is performed by creating a viewing plane in a fiber-filled system and using the cross-sections of fibers in the viewing plane to estimate the orientation that must have created the observed cross-section. To begin, consider a fiber in three-dimensional space, as shown in
Figure 3. The fiber orientation is defined by three angles: the angle from the
-axis towards the
-axis,
; the angle from the
-axis towards the
-
plane,
; and, for elliptical fibers, a roll angle,
, about the fiber axis,
. The equation of the projection of an elliptical fiber onto the
-
plane in terms of
,
, and
is then determined.
2.1. Equation of Projection
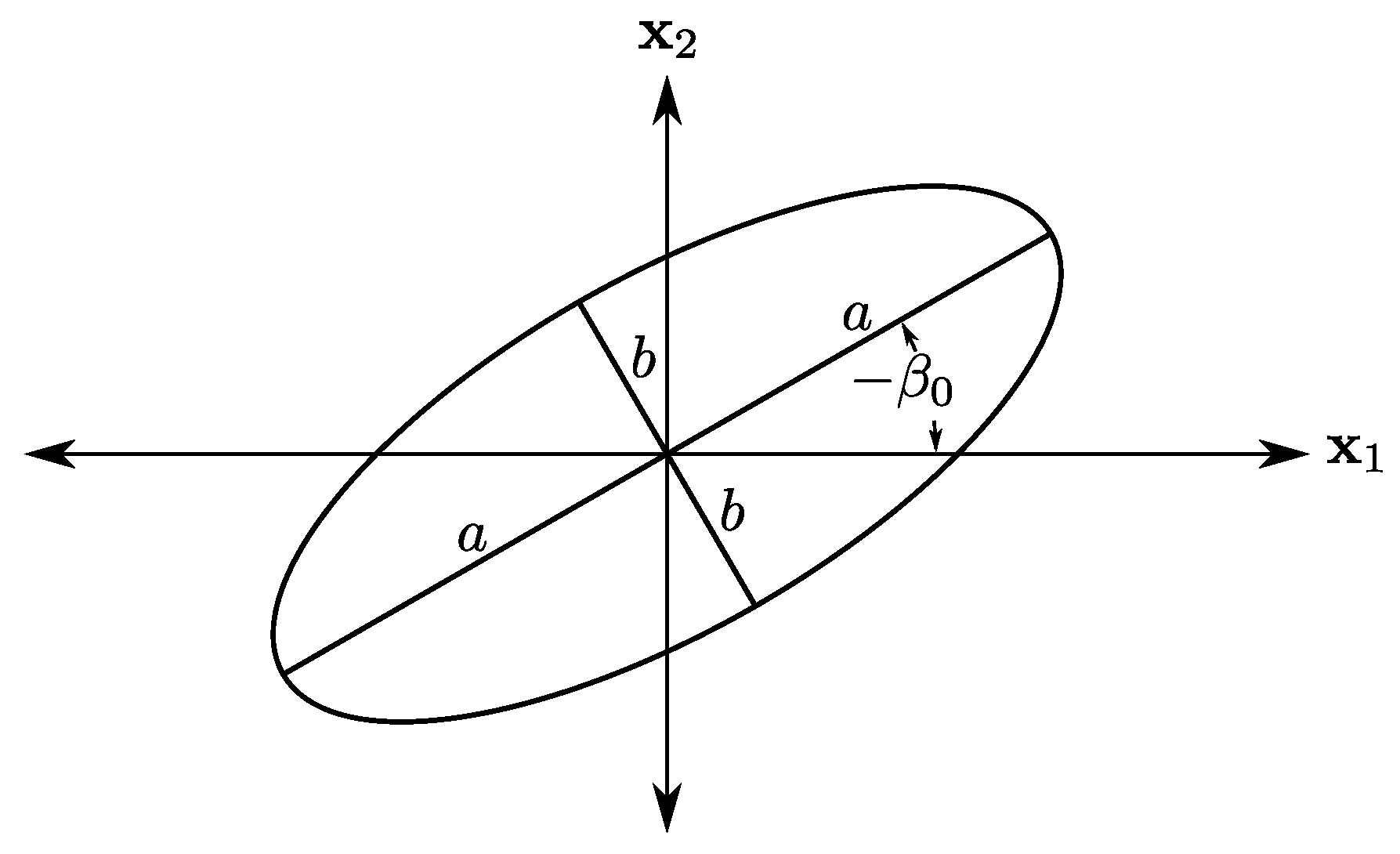
Assume an elliptic cylinder initially lies along the
-direction with semi-major axis,
, in the
-direction and semi-minor axis,
, in the
-direction and attach a coordinate system to the elliptic cylinder of
,
, and
initially parallel to
,
, and
. The initial projection of the ellipse is onto the
-
plane with:
where
is a parametric variable. Now, the following sequence of rotations are applied updating the attached coordinate system at each step:
From the -axis towards the -axis by the angle .
Out of the - plane towards the axis (i.e., in the - plane) by the angle ().
About the -axis (i.e., in the - plane) by the angle .
The total rotation matrix is expressed by the three sequential rotations as:
The compiled rotation matrix is then:
Note that
is the typical fiber orientation expression in spherical coordinates. Using the developed notation, it is clear that the fibers in
Figure 2 have a roll angle of
. From this setup, the projection of the elliptical fiber onto the
-
plane (i.e., the viewing plane) is determined as:
Next, assume an ellipse is measured from a micrograph (see
Figure 4), and the semi-major axis is determined as
, the semi-minor axis is determined as
, and the rotation angle is determined as
, then the equation of the projection is written as:
where
is a parametric variable. As there is no guarantee that the parameterizations of the projected ellipse, Equation (
4), and measured ellipse, Equation (
5), will match, a shift factor is introduced into the parameterization,
. The measured information,
, and
, can be used to determine the angles that define the fiber orientation,
, and
. One simple relationship that can be analytically determined provides that the angles
and
are related to
a and
b through:
However, as the semi-major axis, , and semi-minor axis, , can vary from fiber to fiber, analytic results are not pursued further; rather, numerical fitting techniques are used as discussed below. Finally, there is a clear degenerate case of this analysis when . In this case, and have the same effect upon the projected cross-section. Fortunately, near , the angle has very little impact on the resulting fiber orientation vector, .
2.2. Ambiguity
The parametric expression for the projection cross-section, Equation (
4), directly reveals the same ambiguity as encountered in circular fibers as
appears in the equations only as
. Thus, the projected ellipse is independent of the sign of
. Unfortunately, a second ambiguity is present and more complex. Provided one valid set of angles is determined as
, then a second valid set of angles is determined as
with
given as:
Clearly when
, this ambiguity collapses as Equation (
7) reduces to
. As an example of this second ambiguity, consider the projected cross-section determined from
,
, and
with
and
as shown in
Figure 5.
Upon fitting,
,
, and
are determined as the “measured” features of this ellipse. Then, by fitting Equation (
4) to the projected ellipse, four solutions are determined, as shown in
Figure 6,
and
.
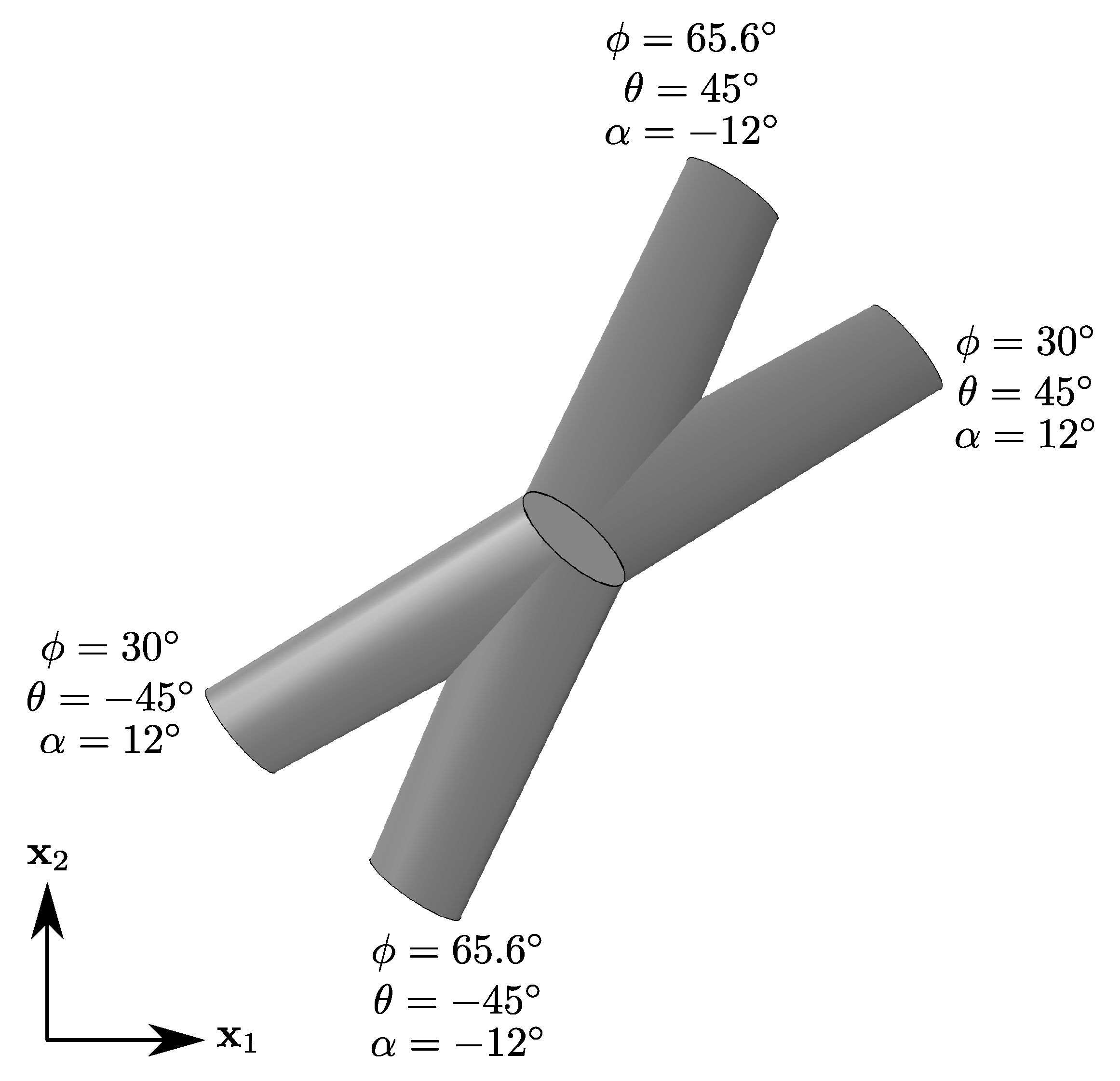
This additional ambiguity can be resolved in the case of identifiable fiber bundles. If two fibers are measured with known equivalence of and but a different roll angle, , then this additional ambiguity beyond circular fibers can be resolved. Consider the previous example again, but now with . In this case, four solutions are determined and . By comparison to the first fiber, two of the solutions can be eliminated giving . In dispersed fiber systems, this indeterminacy cannot be resolved using the method described here.
2.3. Sample Bias
As discussed by Fischer [
1] and later by Bay and Tucker [
3], when measuring fiber orientation, it is important to note biasing inherent in a polished cross-section so that the relative volume associated with each measurement is appropriately determined. Fortunately, the elliptical fiber does not present additional difficulty in this respect as the probability of the
nth fiber appearing on a polished cross-section is only a function of the angle
and the fiber length
. Thus, the weighting function of Bay and Tucker is used with:
Equation (
8) is valid for fibers that are not nearly parallel to the viewing plane such that they appear as rectangles. In this case, an effective diameter,
, between
and
must be chosen giving the weighting function of
. For a fiber lying in the viewing plane,
, the height of the fiber in the
direction is a function of the roll angle,
:
However, in the case of a fiber lying in the viewing plane,
cannot be determined. Thus, one approach to determine an effective diameter is to assume a uniform distribution of
such that:
This average can be easily computed for a given cross-section aspect ratio,
. Although some uncertainty remains in the bias correction for fibers lying nearly in the viewing plane, as noted by Bay and Tucker, this regime is so narrow that additional investigation is not necessary. With the weighting function available, an effective volume averaged quantity from a micrograph is then given as:
where
is the quantity associated with the
nth measurement and
is the bias-corrected quantity. Typically, these quantities are the second-order orientation tensor as introduced by Advani and Tucker [
21] as a primary description of orientation state. While fibers often experience damage in processing leading to a distribution of fiber lengths, it is not practical to be able to correlate a given fiber length measurement with a fiber orientation measurement except on a global/part scale. Thus, for local measurements, the length distribution is often assumed to be independent of the orientation distribution. Provided that no fibers are nearly parallel to the viewing plane, with this assumption, the fiber length no longer impacts the bias correction and is not required to be known. As a final note on bias correction, this method assumes that all fibers present in a micrograph are measured. When measuring fiber bundles, it may be convenient to only measure the ellipses of a subset of the apparent bundle. In this case, an alternate weighting scheme must be devised.
2.4. Numerical Methods
Using the developments in the previous section, the measurement method takes the following sequence given a viewing plane image:
Measure fiber cross-sections and fit an ellipse to each cross-section to determine values a, b, and .
Solve for one possible fiber orientation solution by minimizing the error between the test projected ellipse, Equation (
4), and the measured ellipse, Equation (
5), where the error expression is the sum of the square error for evenly spaced parameterized points,
, given as:
This procedure gives one solution for and the parameterization shift factor, .
Substitute the solution from Step 2 into Equation (
7) to determine
. The possible solutions are then given as
and
. Provided that fibers are bundled, the next steps are taken to resolve the
ambiguity.
Compare all possible solutions for in a fiber bundle. One of the solutions for each fiber in the bundle should be near a specific value of (i.e., an apparent peak in a histogram). Select this solution for each fiber.
Compare all selected solutions in a fiber bundle. Estimate the fiber orientation for each fiber in a bundle using the median values of selected solutions.
This method can be seen in better detail from the examples shown in
Section 3.
3. Results
In the following sections, several verification and validation exercises for the proposed method are presented. However, the ambiguity was not treated herein. Thus, all inputs and results were limited to the branch of solutions. First, a simple check was performed to demonstrate the claim that the ambiguity can be resolved given fiber bundles. The error associated with varying fiber dimensions, and , was investigated. As a final verification, a synthetic micrograph was generated using the software Digimat to generate a representative volume and taking a view-cut of the result. Validation was performed by manufacturing a plate with a prescribed orientation state and applying the method to a resulting micrograph. Finally, an example application of the method was performed.
3.1. Verification without Fiber Diameter Variation
The simplest way to verify that the method described above will accurately predict fiber orientation is to synthetically generate cross-section data and check the performance of the method. If there is no variation to the fiber size, then the method should only require two fibers in a bundle (i.e., two fibers with the same
and
but different
) to accurately predict their orientation. Therefore, this is the theoretical limit to the effectiveness of this method; in a system where groups of fibers cannot be identified or do not exist, there is no way to resolve the indeterminacy of
. As a demonstration, the method was run for generated fiber projections with
,
,
, and
. The
angle was assigned a random value between
and 90 degrees.
Table 2 shows the estimates of
,
, and
for the generated fiber projections. To reiterate,
is the angle initially fit by the numerical scheme in Step 2, and
is the angle calculated using the ambiguity equation in Step 3. For each individual fiber measurement, it is unknown which angle is correct. However, when viewed as a dataset arising from a fiber bundle, it can easily be seen that either
or
is correctly determined as
and is selected as the result for each fiber.
3.2. Verification with Fiber Diameter Variation
Since the measurement method described above requires a priori knowledge of the fiber dimensions, to use this method on real fibers, the fiber dimensions must be measured using a micrograph where the sample was carefully prepared so that all fibers are perpendicular to the viewing plane. The fibers, of course, have a distribution of sizes.
Figure 7 shows a micrograph of fibers perpendicular to the viewing plane. The image was converted to binary using a thresholding method and the ellipses were fit to several fibers, as shown in
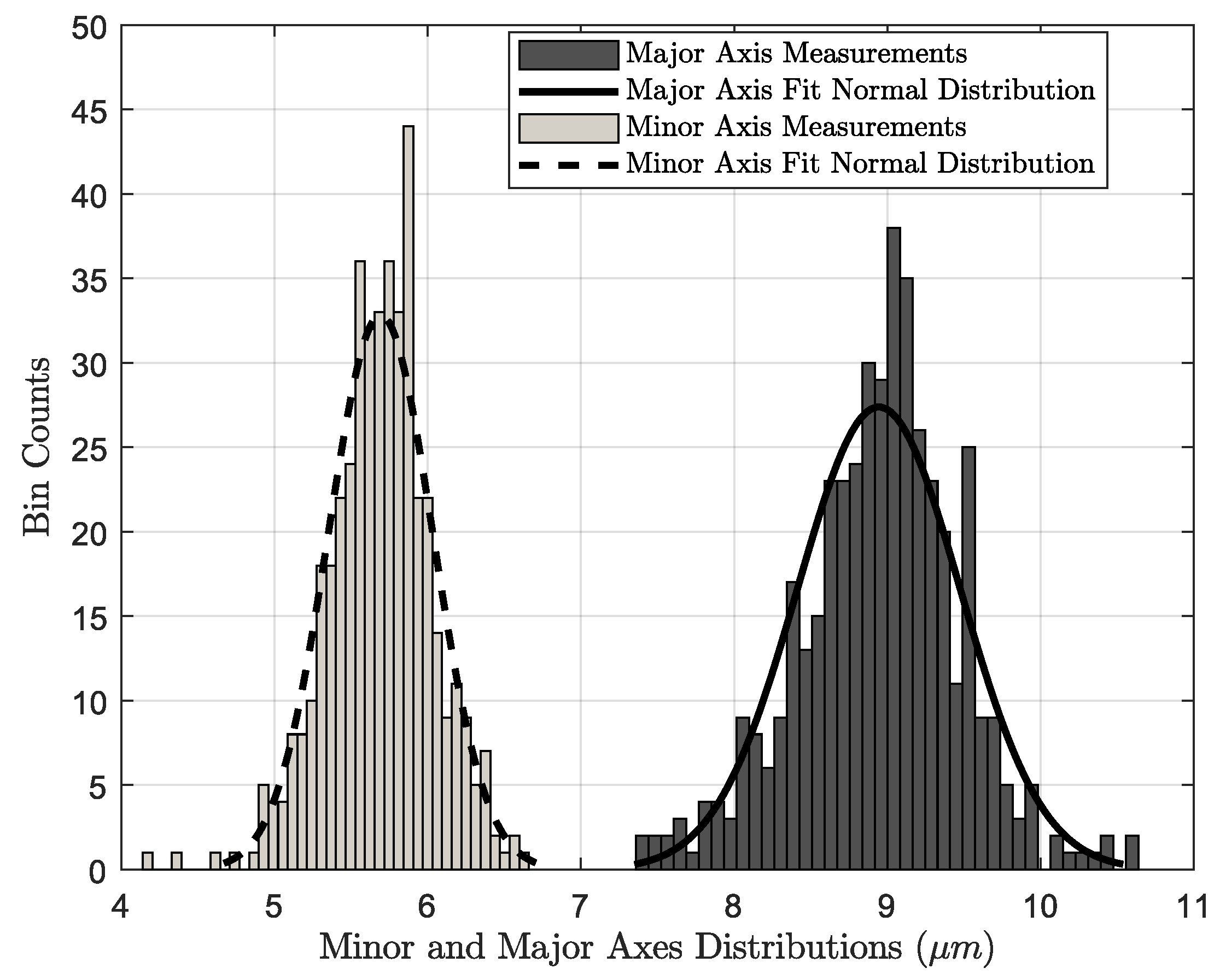
Figure 8. The distribution of major and minor axes of the fibers are shown in
Figure 9. Both fiber dimensions were found to be approximately normally distributed with coefficients of variation of around
. The statistics of the fiber dimensions are shown in
Table 3. Little correlation was found between the measured major and minor diameters. Thus, independent variation was assumed in the investigation.
With the fiber size measurements, an in silico verification could be performed using simulations of real fiber projections by inputting the measured fiber data into the projections. An error map was generated by comparing actual fiber orientations with the determined estimates from running bundles with
N fibers each. The simulation was performed through the possible ranges of
(excluding
),
was randomized for each fiber, and
was prescribed in the simulation but not varied as
does not impact the shape of the projection, only its rotation about the viewing plane normal. In each prescribed condition, an estimate was determined for the bundle fiber orientation and compared with the orientation used to generate the projections. The error was then calculated merely as the angular error between the two fiber orientations (i.e., the dot product between the prescribed vector and the estimated vector was used to determine the angular distance between the orientation vectors). For each prescribed
and fiber bundle group size, the simulation was run 10,000 times to generate a range of results.
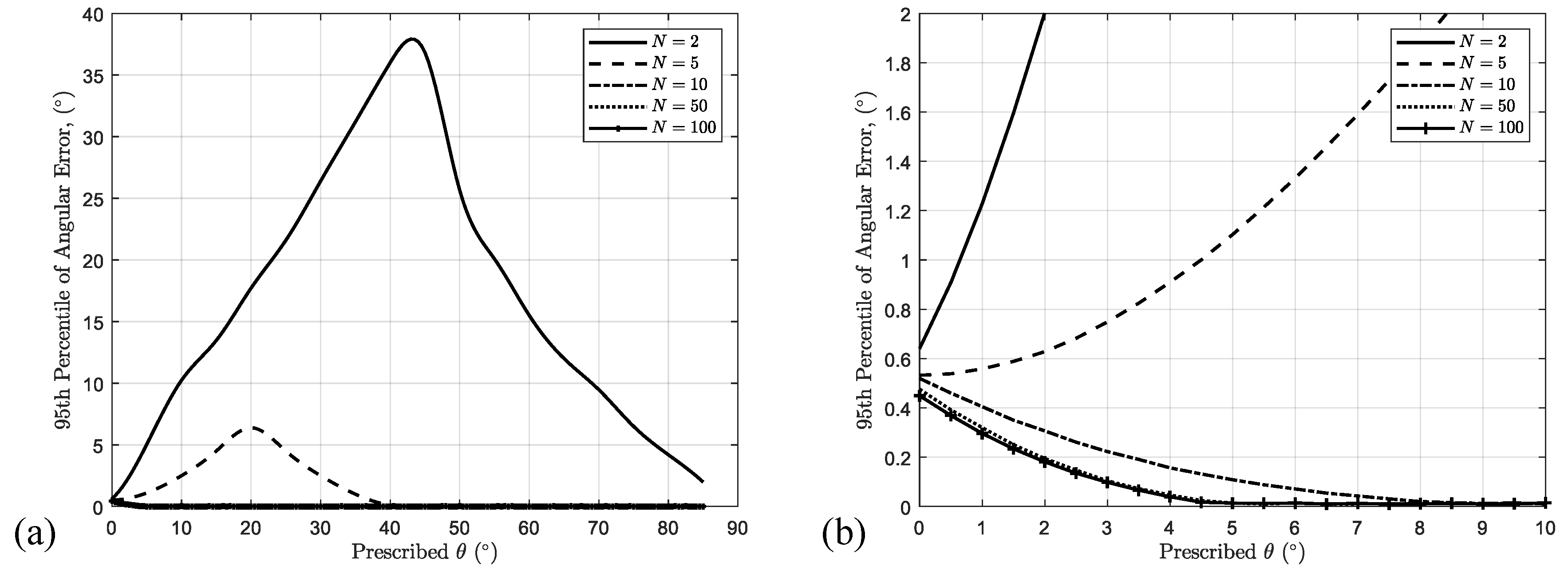
Figure 10 shows a map of the error results as a function of
and fiber bundle group size, where the lines indicate the 95th percentile of the error. The results show that, at very small angles (less than 5 degrees), there was a small estimation error regardless of the bundle size, but that as long as there were at least 10 fibers in a bundle, the error dropped very quickly to near zero.
An additional conclusion can be drawn from this analysis related to measurement error. Bay and Tucker [
3] noted that pixel scale measurement errors can have a drastic effect on the angular error in fiber orientation measurements. They noted that, for a circular fiber with
, for the angular error resulting from a single pixel measurement error to be less than
, the resolution of the micrograph must be such that the fiber diameter is represented by at least 65 pixels. In other words, a
error in measurement produces a
error in resulting
. A similar error is certainly possible in the present method. However, in this analysis, projections were generated using a distribution of fiber diameters with standard deviation of
of the nominal fiber diameters. While large errors are probable when only a small number of fibers are measured, in the case of bundles as shown, such errors reduce rapidly as the number of fibers measured per bundle is increased.
3.3. Synthetic Validation of the Fiber Orientation Tensor
The ability of the method to accurately estimate the fiber orientation tensor from a micrograph can be validated by generating a volume with a prescribed orientation state, taking a slice of that volume to generate a synthetic micrograph, estimating the fiber orientation tensor from the generated micrograph, and comparing the estimate/measurement to the prescribed value. A volume with three equally spaced regions was created in Digimat with the conditions outlined in
Table 4 and with fibers having a random
.
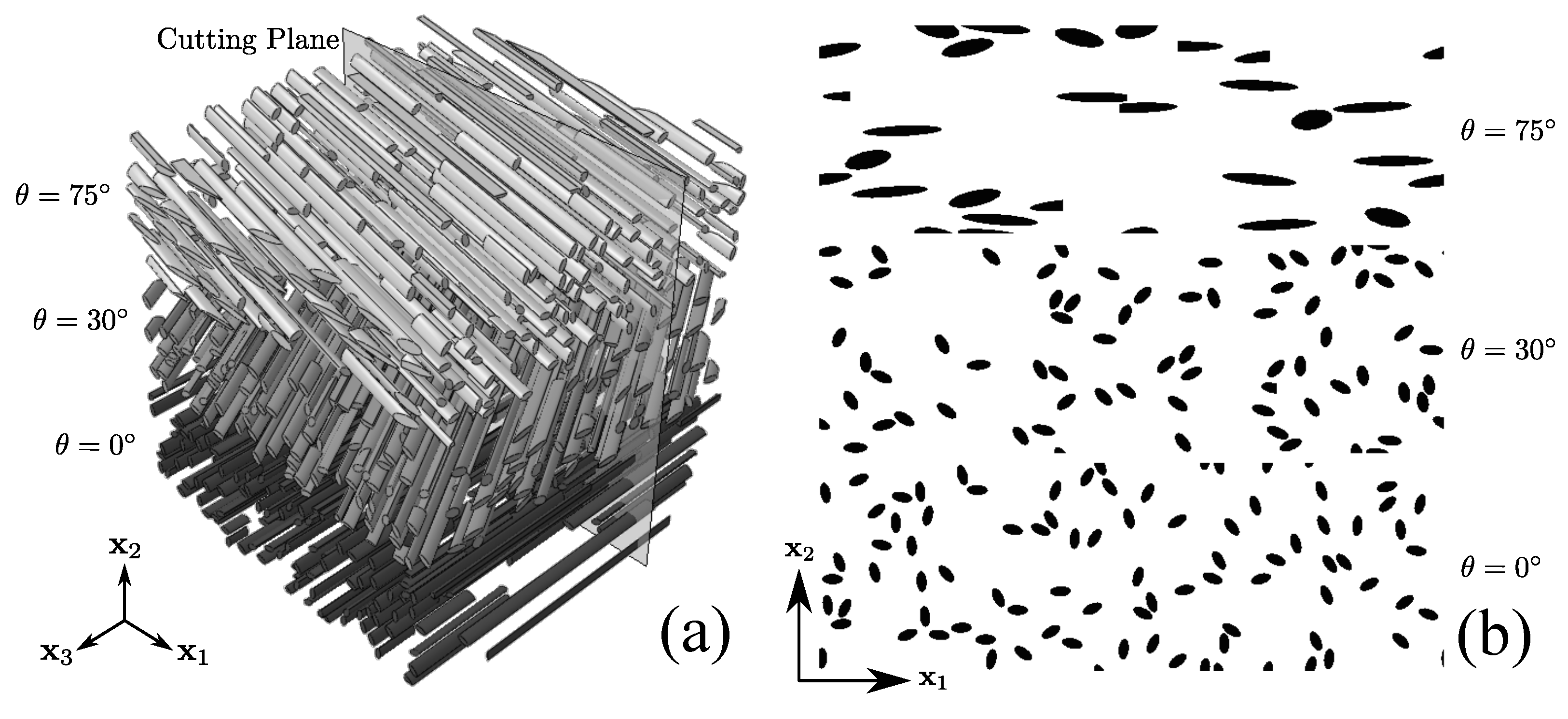
Figure 11a shows the volume of fibers generated by Digimat, which was sliced to generate a synthetic micrograph, as shown in
Figure 11b.
It can be easily shown that the diagonal components of the second order orientation,
, for this volume were
,
, and
. A synthetic micrograph image was created and the fiber orientation was estimated.
Figure 12 shows the fit colored ellipses drawn with the ellipse color corresponding to the estimated
for each particular fiber. The estimated fiber orientation results of each layer are shown in
Table 4. Without correcting for bias as outlined in
Section 2.3, the estimated
tensor diagonal components were
,
, and
. With the bias correction, the estimates were
,
, and
, matching the prescribed case. As a comparison with the traditional method for circular fibers, the
tensor components were also calculated using the standard method, and the diagonal components were estimated to be
,
, and
. This showcases the need for the proposed method if fibers do not have a circular cross-section.
3.4. Experimental Validation
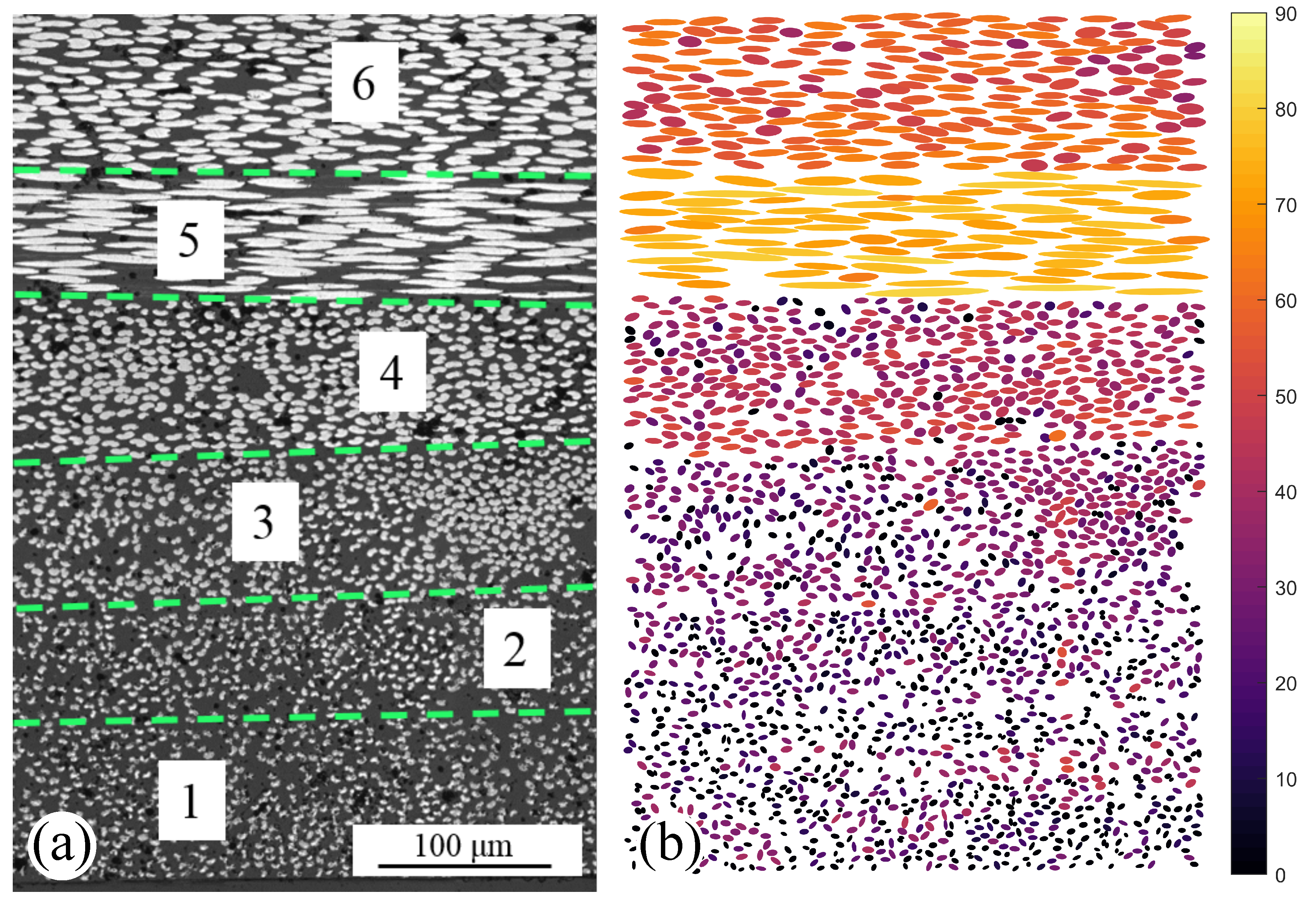
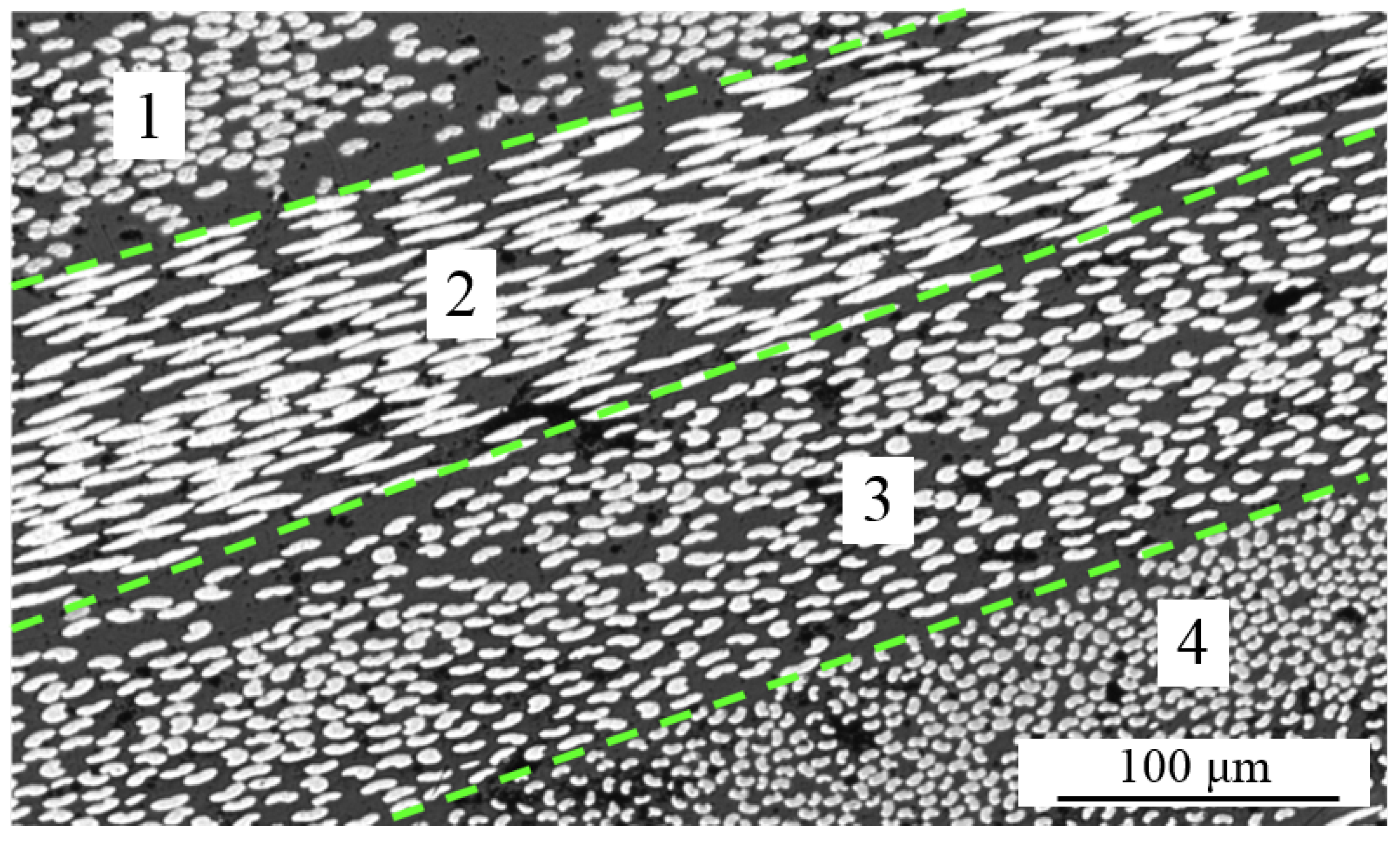
To validate the method experimentally, a
laminate was manufactured to provide a broad range of known fiber orientations with which to test the method. The laminate was cured and consolidated in a press at 34.5 bar. The laminate was then sectioned and polished and imaged at 200× magnification.
Figure 13a shows a microscope image of one half of the thickness of the laminate. The ply layers, which were used to group the results in the analysis, are also marked with the areas numbered (from bottom to top) one to six.
Figure 13b shows the microscope image with identified ellipses overlayed on top of the fibers with the ellipses color-coded depending on the calculated
angle.
Table 5 shows the estimated angle for each ply compared to the prescribed angle. All estimated angles match the actual angles within two degrees, which is likely within the manufacturing uncertainty.
3.5. Application
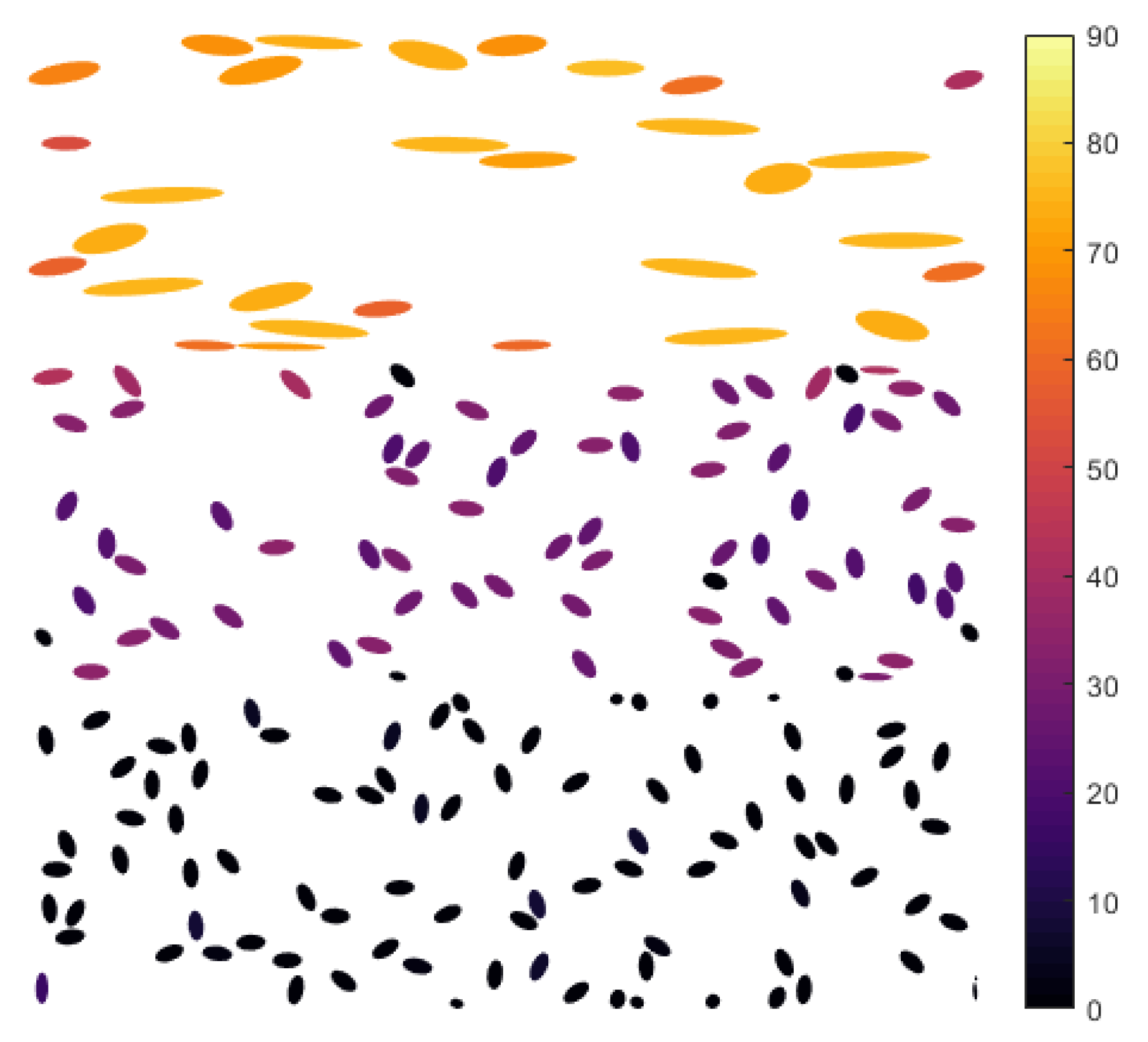
As an example of an application of the method described here, a prepreg platelet molding compound, VORAFUSE™M6400, was molded, and a sample was imaged, as shown in
Figure 14. Platelet regions were identified manually, and the fiber orientation of each fiber was estimated; the results of which are shown in
Figure 15. The estimates of each ply are shown in
Table 6. The diagonal components of the second order orientation tensor,
, in this region were determined to be
,
,
.
4. Conclusions
Optical microscopy is an important tool in evaluating fiber orientation for validating simulation or predicting mechanical properties. The standard method for measuring fiber orientation in fiber-filled systems breaks down when fibers do not have circular cross-sections. To account for fibers with approximately elliptical cross-sections such as kidney bean shaped fibers, a modification to the standard method was derived and validated using in silico fiber projections and experimental fiber projections. While the standard method of ellipses can be applied without knowledge of the fiber diameter, the proposed method requires, at minimum, the fiber major-axis, , and fiber minor-axis, , which can be determined by careful preparation of a sample. Validation exercises showed that the method works very well and eliminates the additional ambiguity introduced by the roll degree-of-freedom as long as the system has distinguishable groups of fibers that have roughly the same fiber orientation.