On the Representativeness of the Cohesive Zone Model in the Simulation of the Delamination Problem
Abstract
1. Introduction
2. The Models Employed in the Present Study
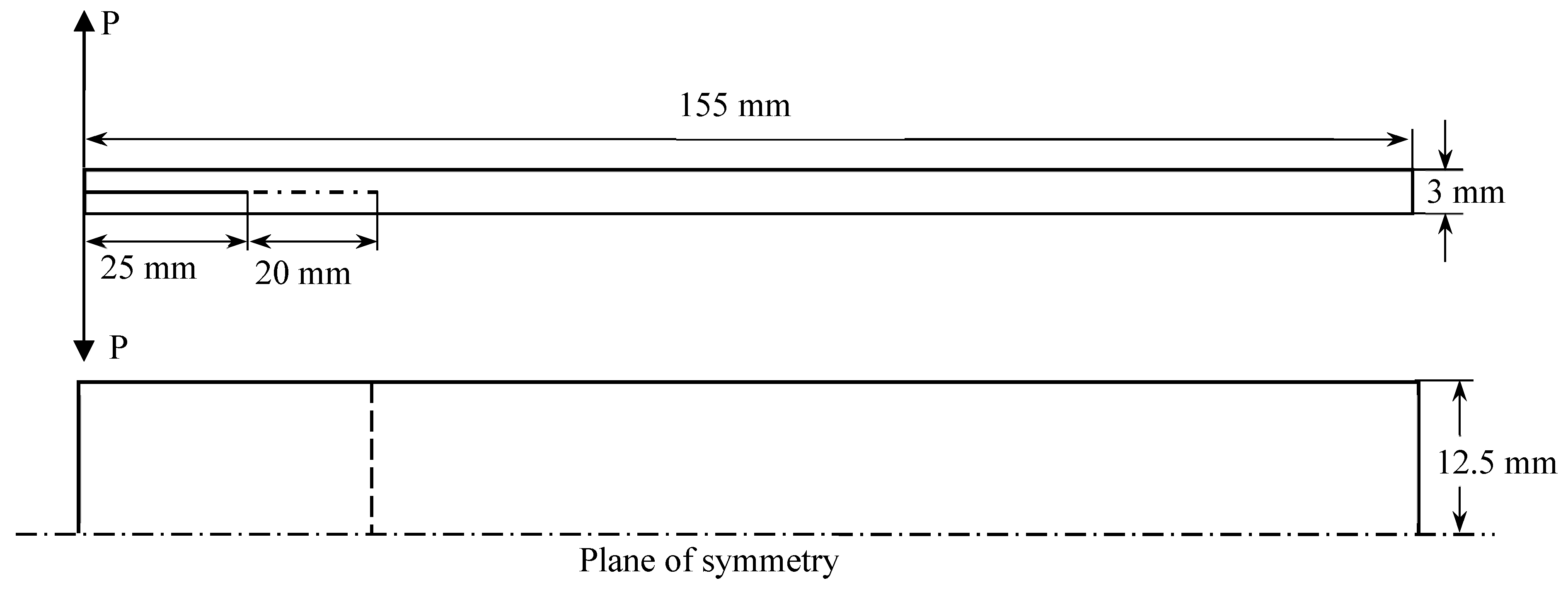
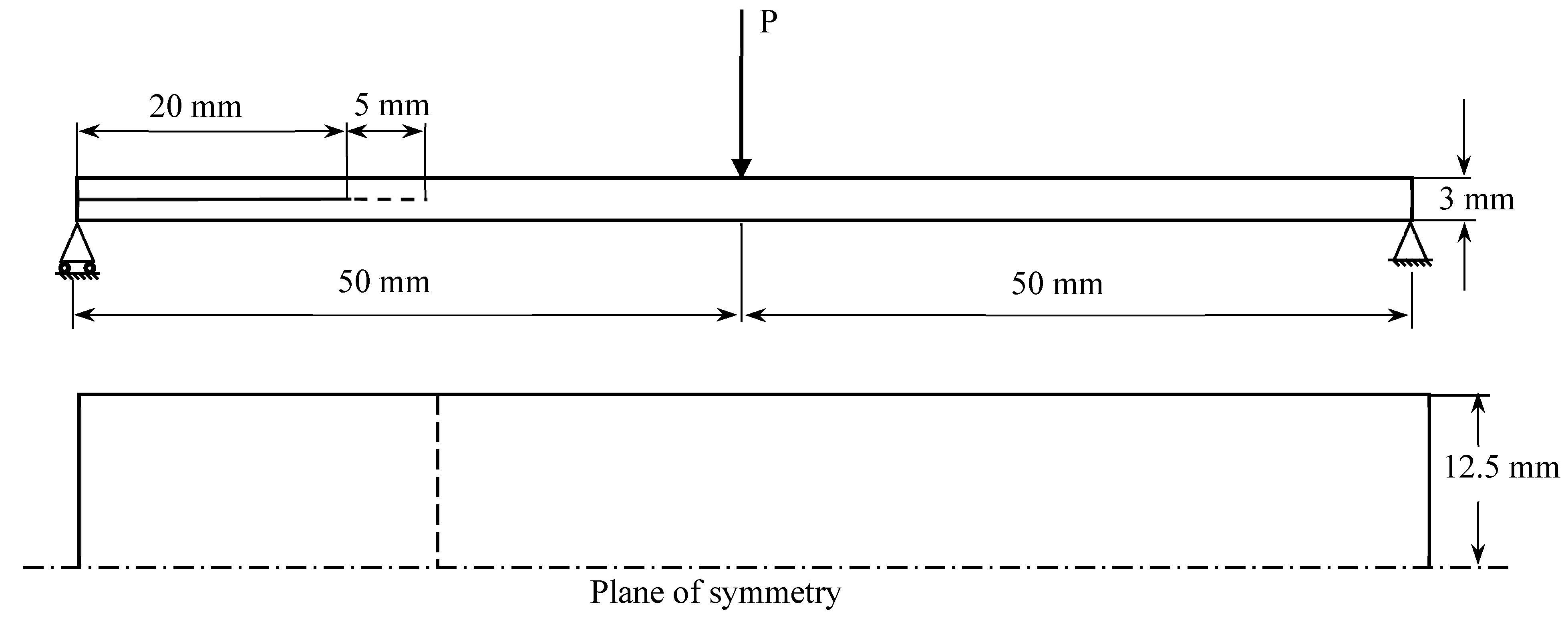
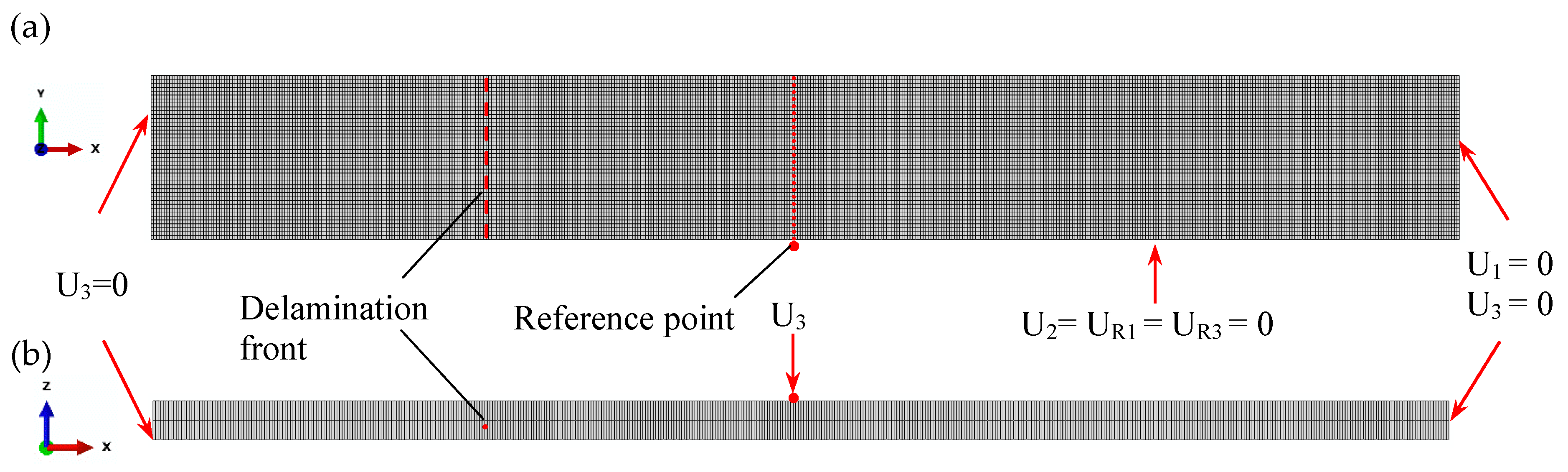
2.1. Geometry of the Models
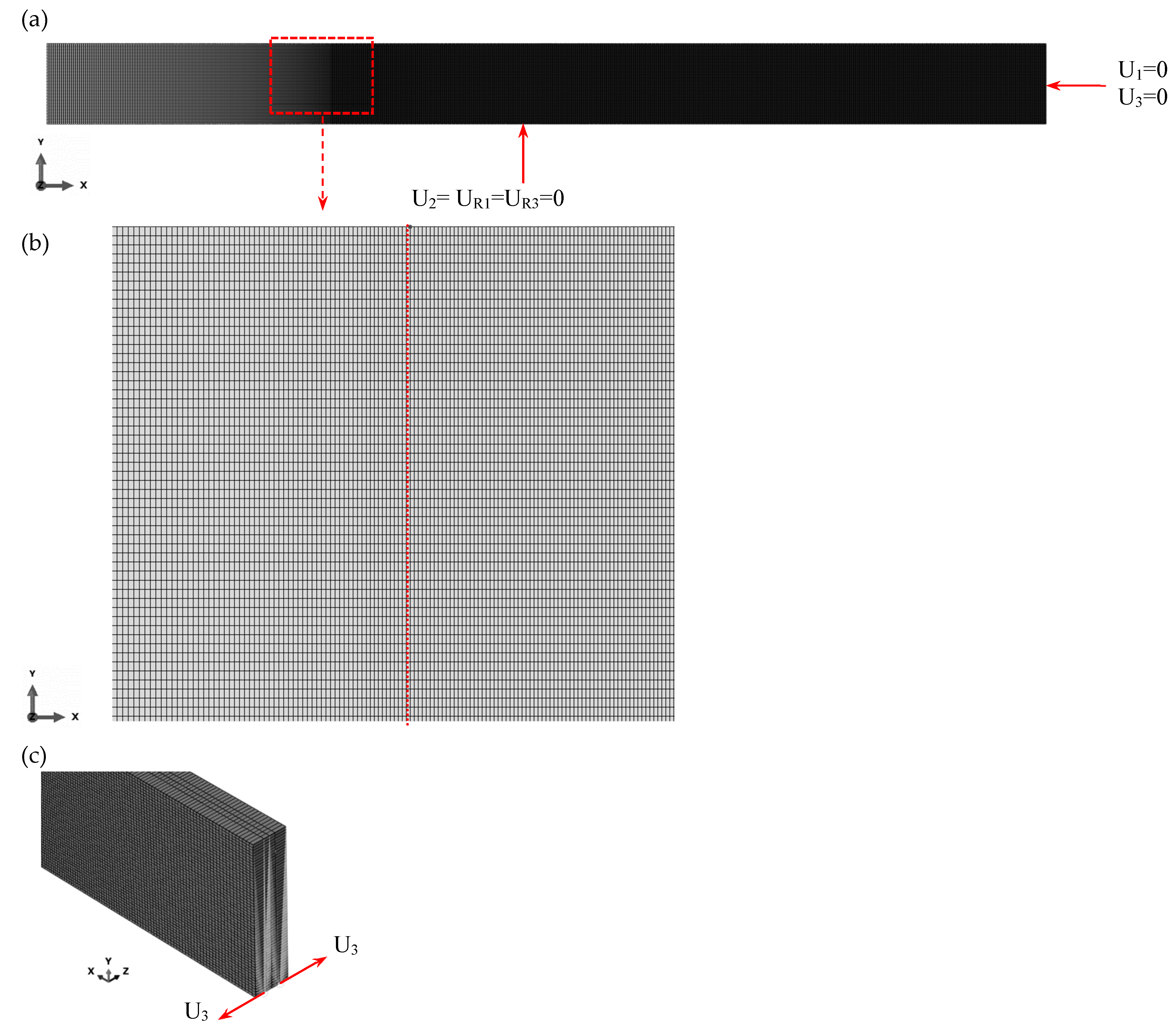
2.2. Finite Element Implementation
2.3. Definition of Material Behaviour
2.4. Definition of the Parameters of the Model
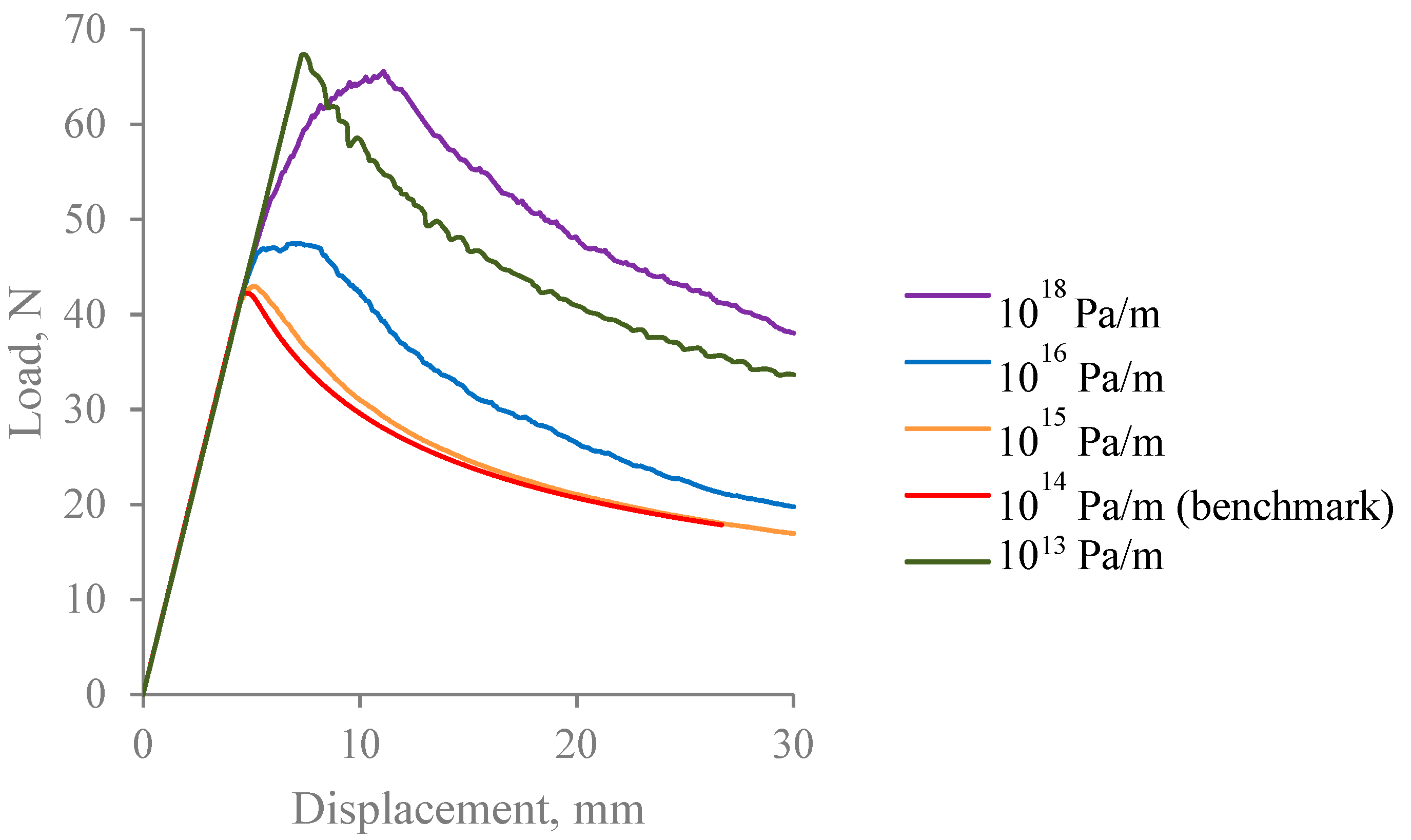
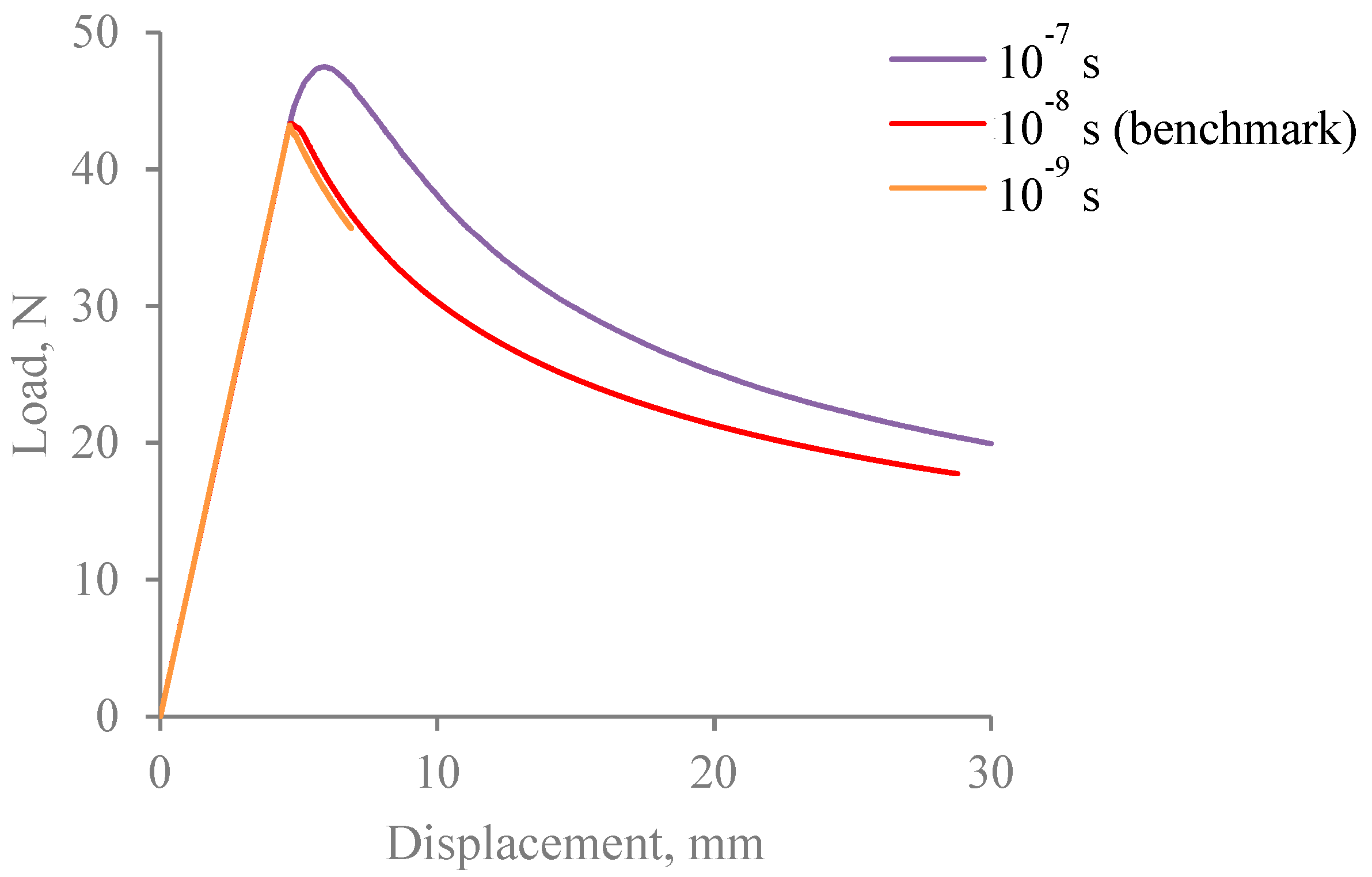
3. Studies on the Factors Affecting Convergence of the Cohesive Model
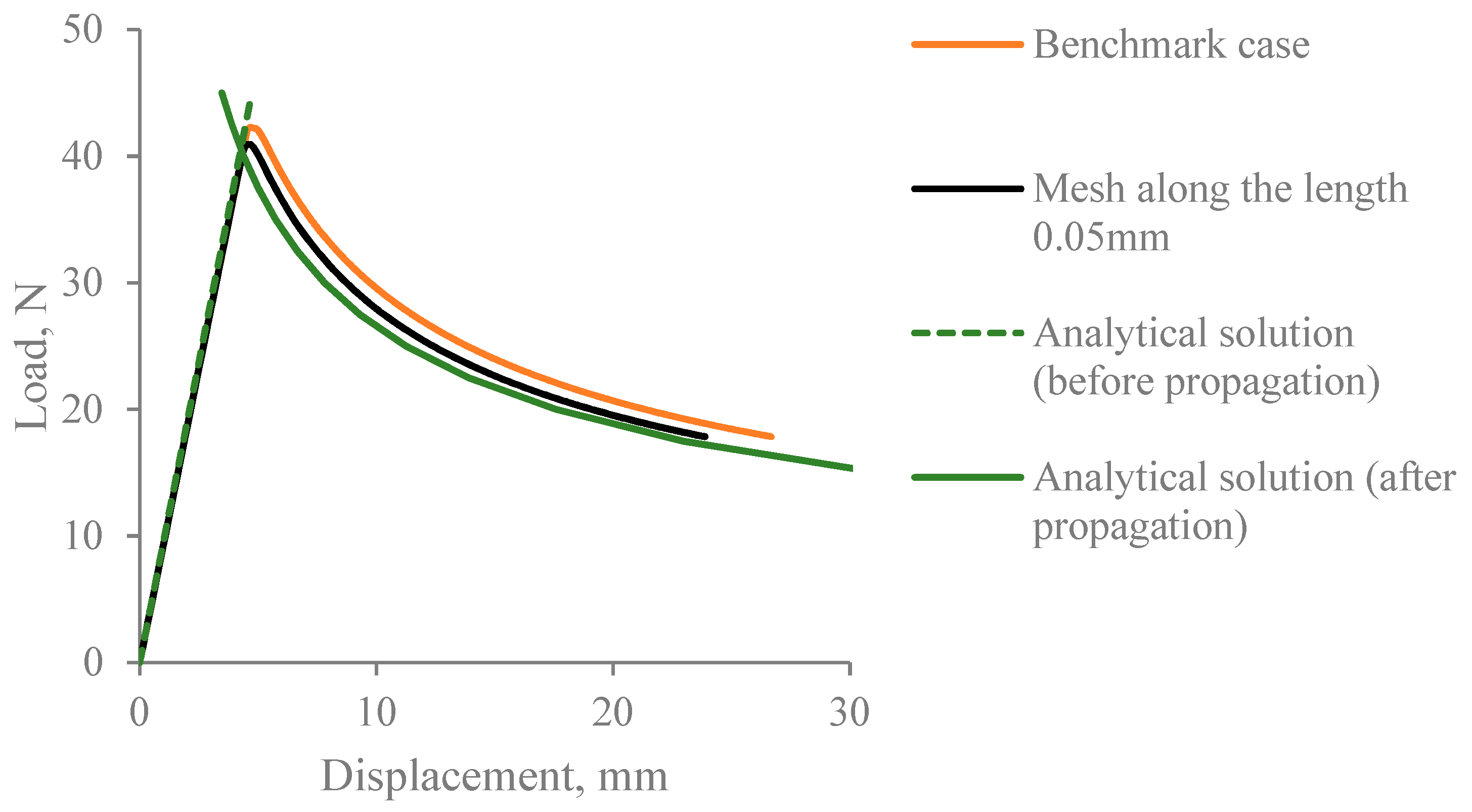
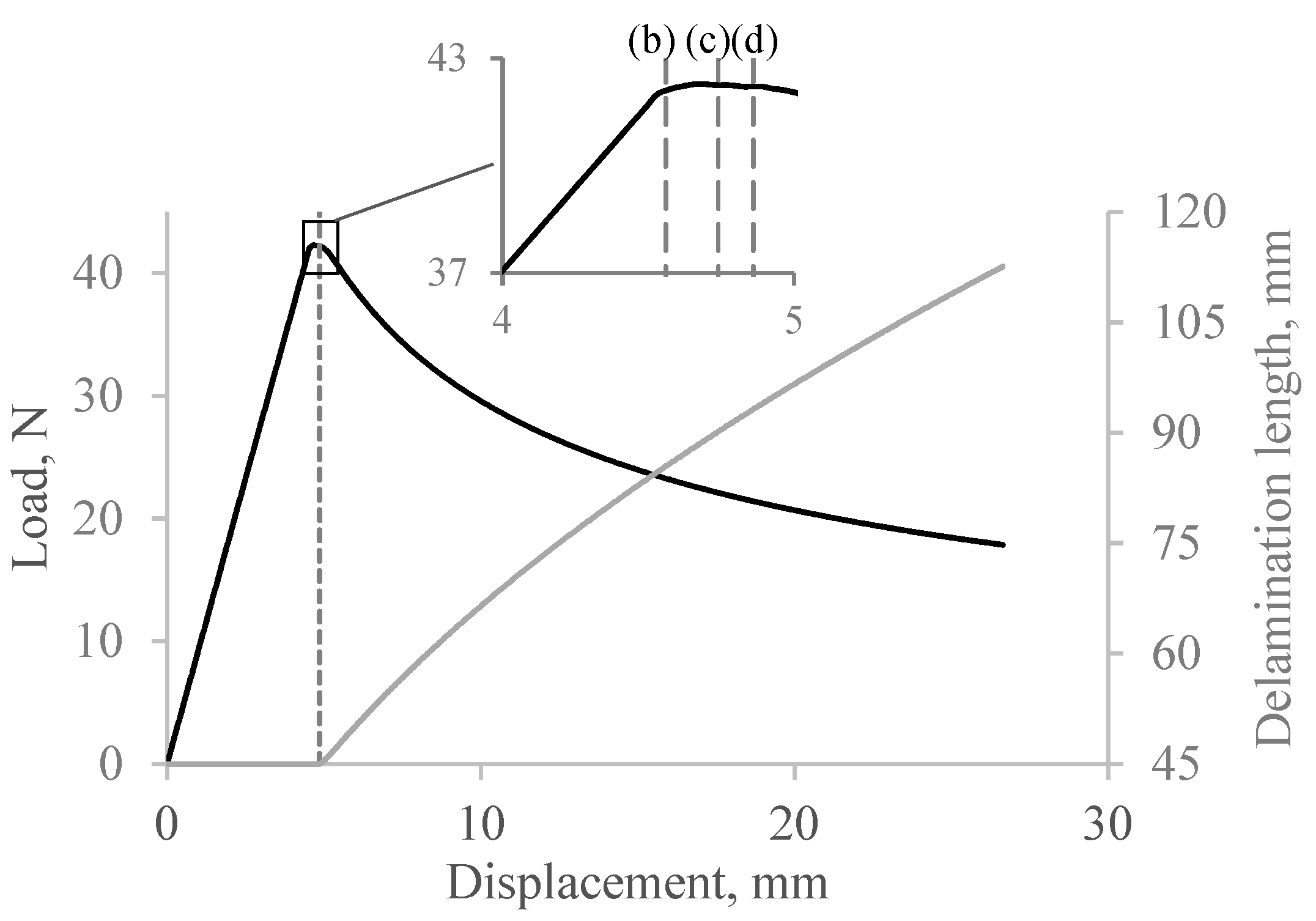
3.1. Mode I
- (i)
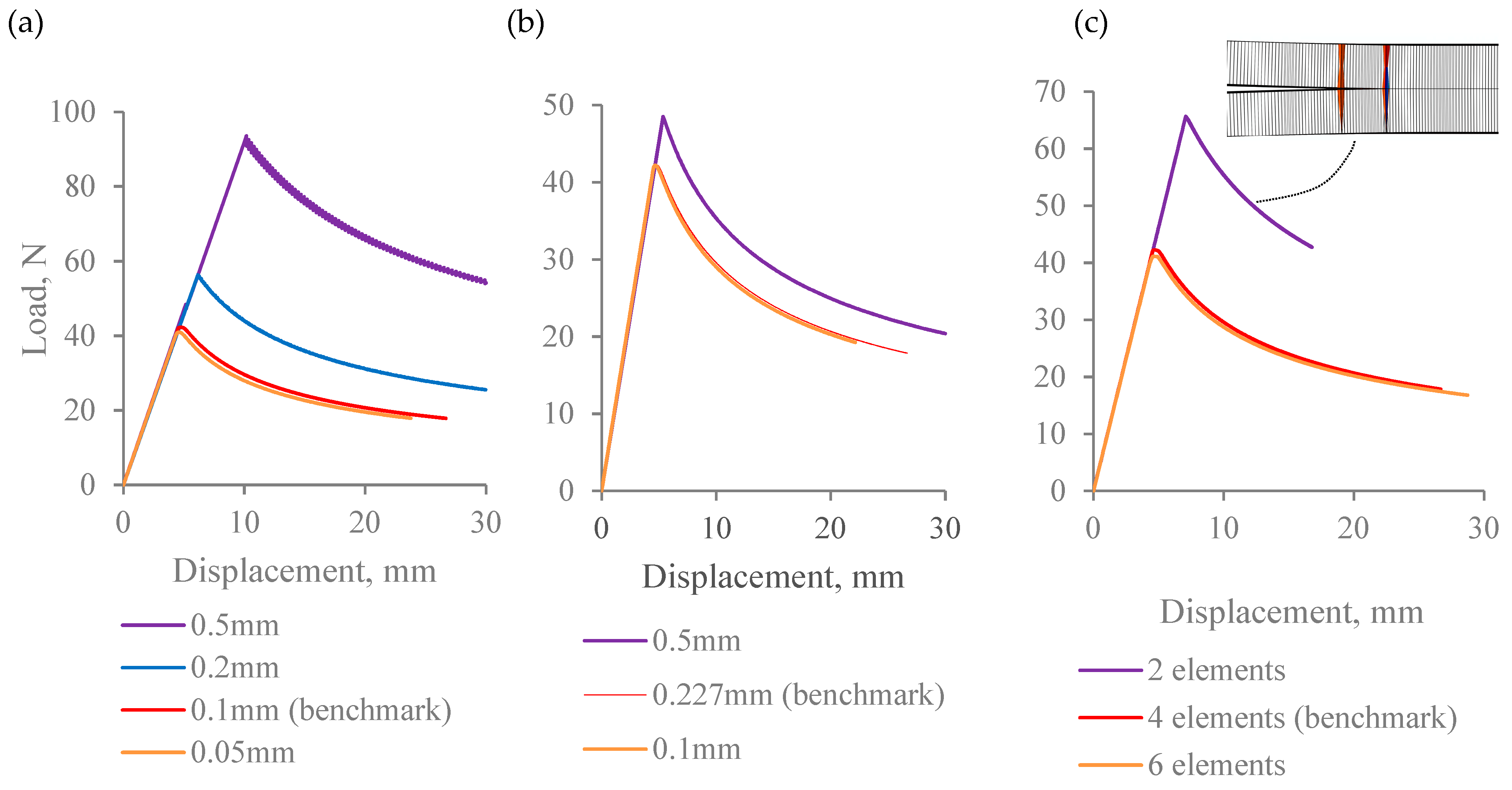
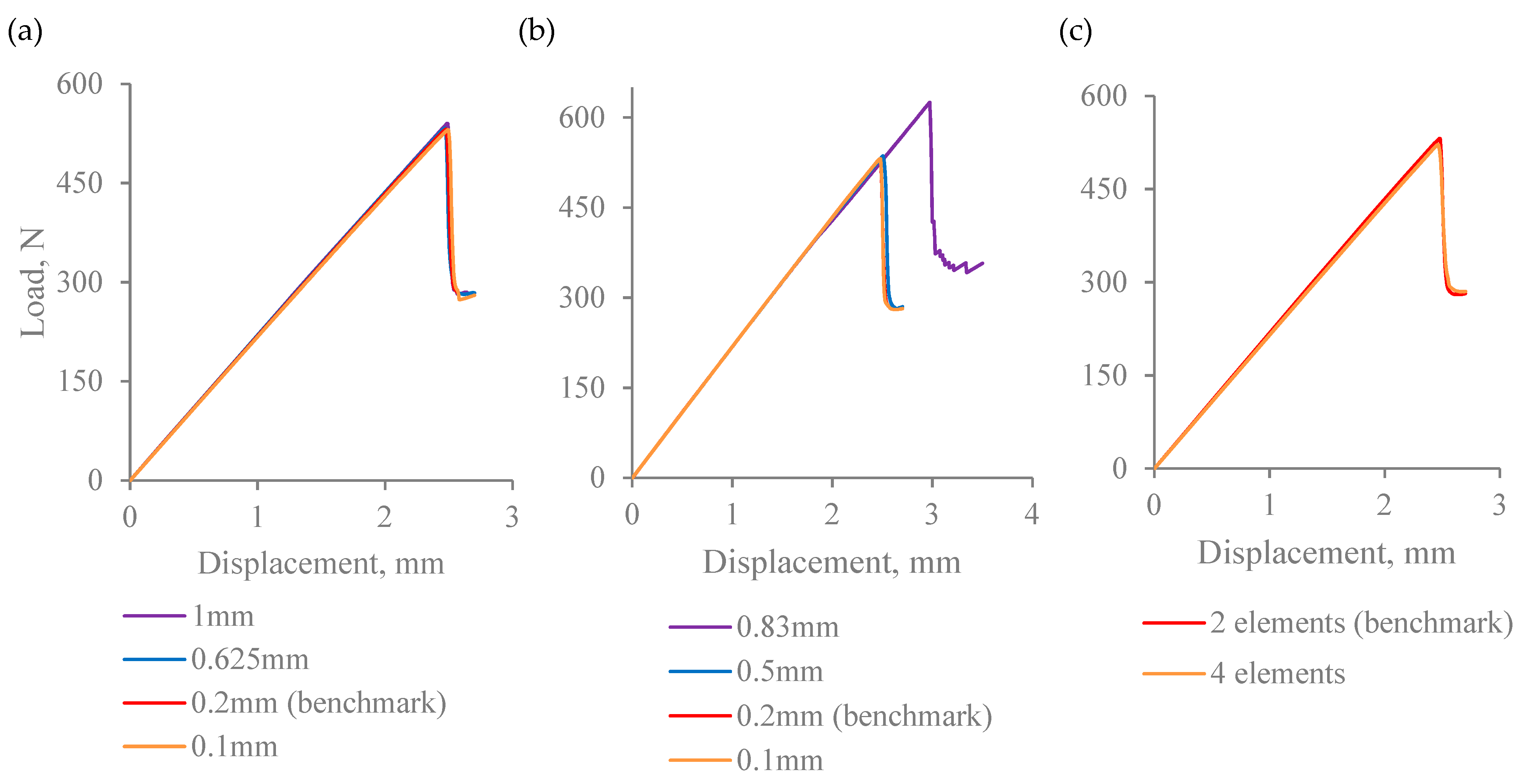
- Converged solution in Mode I simulation requires very fine meshing. This results in lengthy computational times, even with the use of high-performance computing. Specifically, the benchmark Mode I model contained over 350 K elements. Further mesh refinement substantially increased the computational demands, hence the load-displacement curves obtained at the smallest mesh size in Figure 7a,b were not computed for the full range.
- (ii)
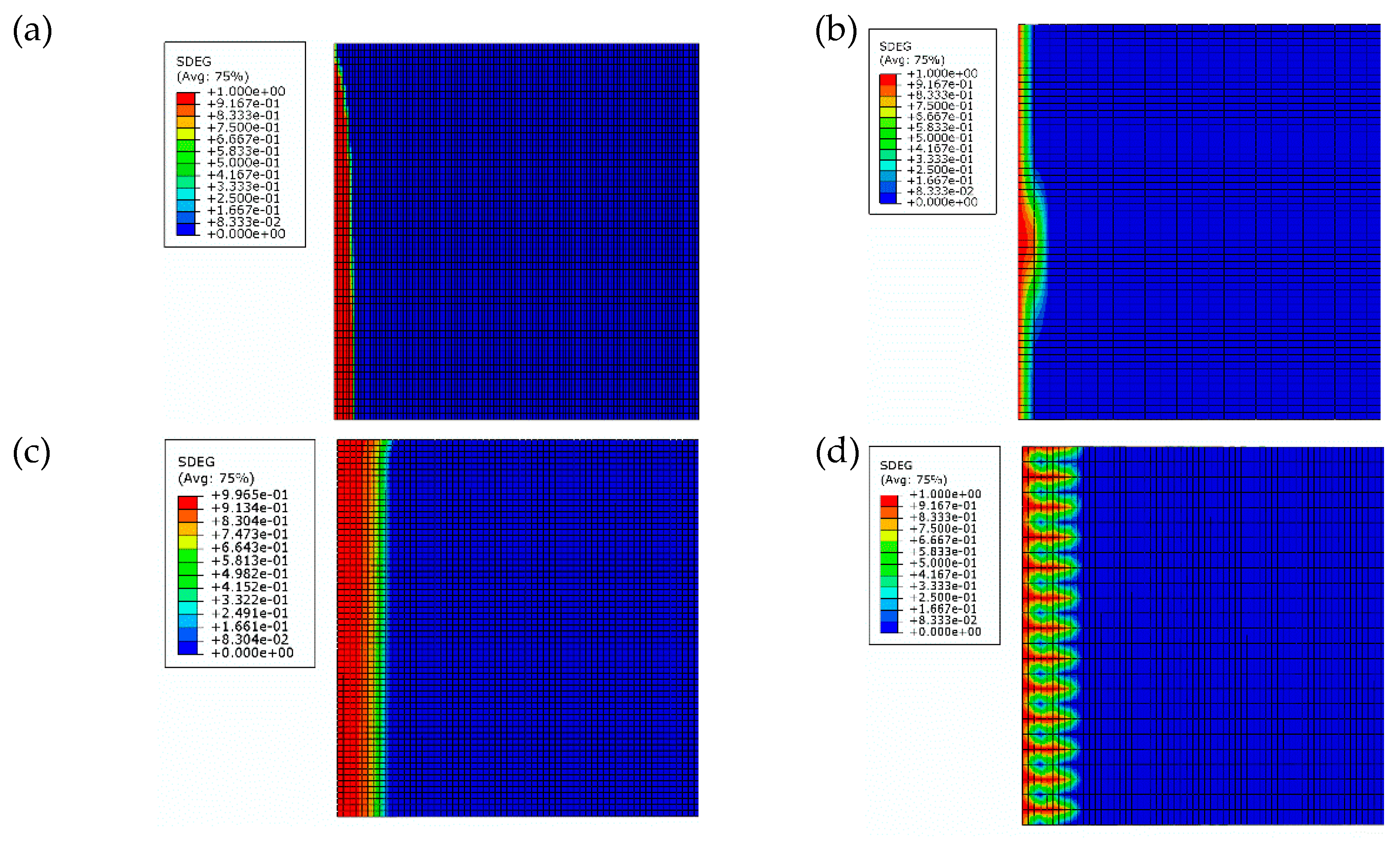
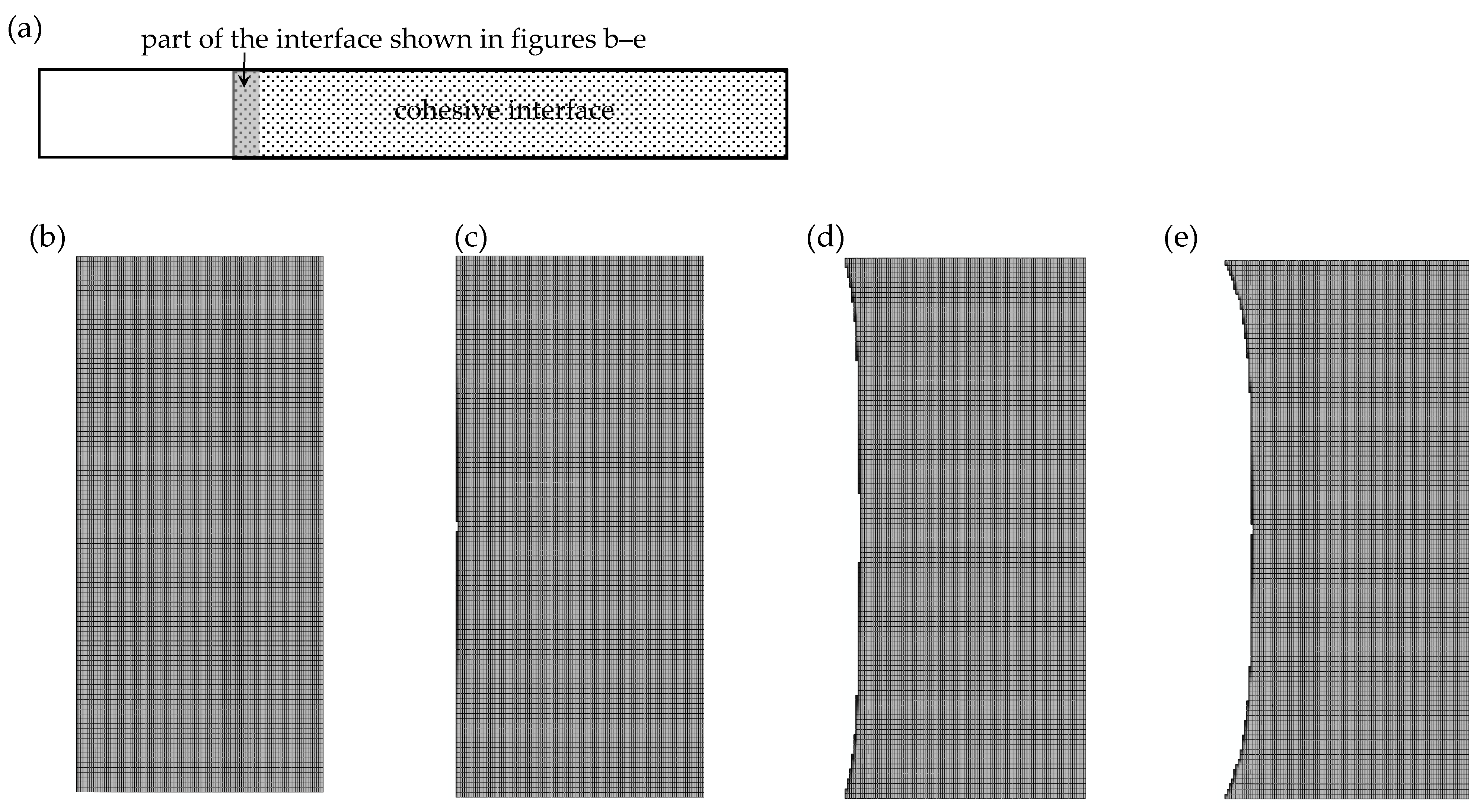
- Insufficient mesh refinement in thickness direction results in convergence difficulties. The model with two elements in the thickness direction in Figure 7c, has shown a lack of convergence because of the distortion of continuum shell elements, as shown in sub-figure on the same plot. It has confirmed that the mesh, in this case, was not fine enough, hence the analysis was manually interrupted.
- (iii)
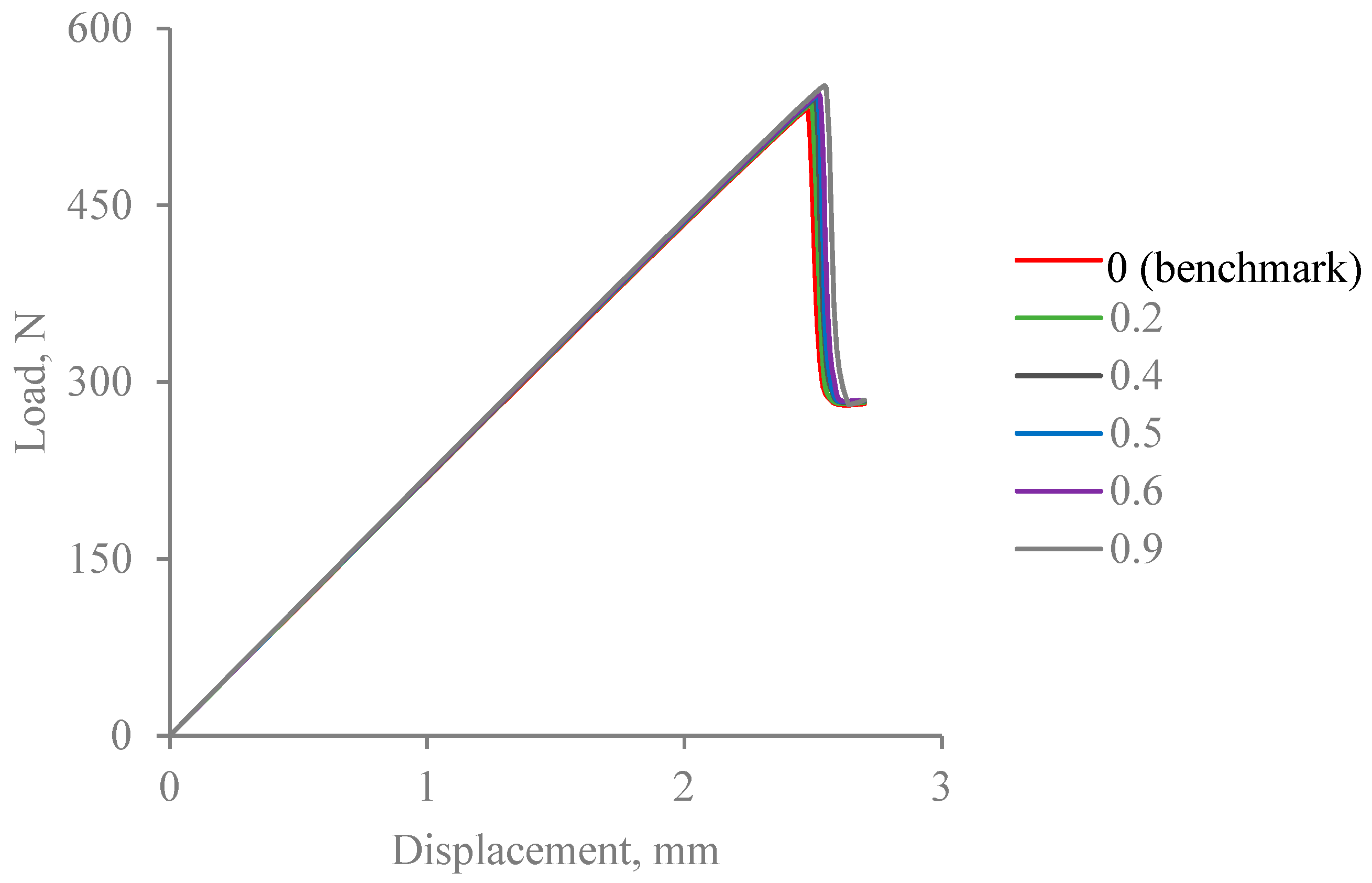
- It is apparent that whilst the results are sensitive to mesh density in all three directions, the most pronounced differences between the load-displacement curves were captured when the element size was varied along the length of the beam. In particular, with the largest element size considered, 0.5 mm along the length, the load values exceeded those in the converged solution by over 100%.
3.2. Mode II
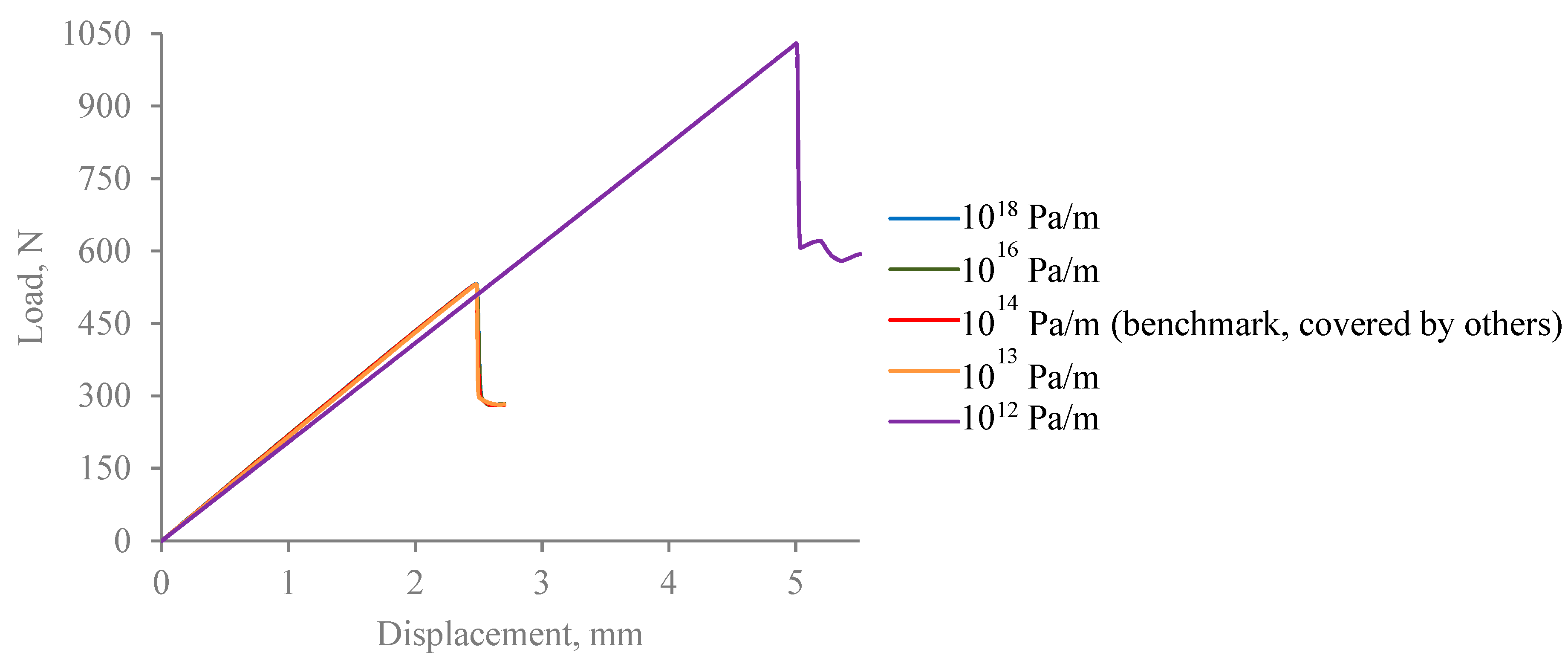
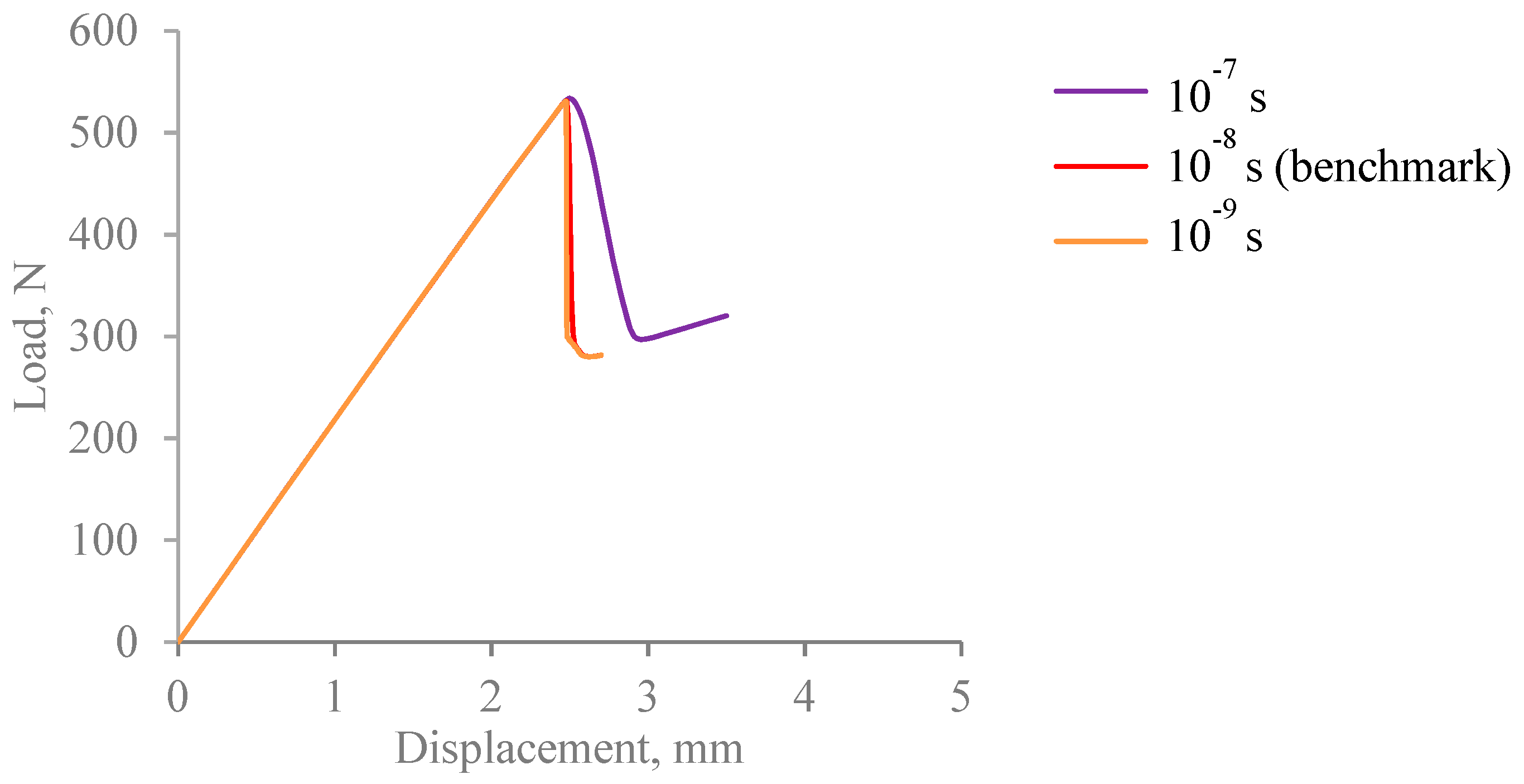
3.3. Implications of Insufficient Mesh Refinement
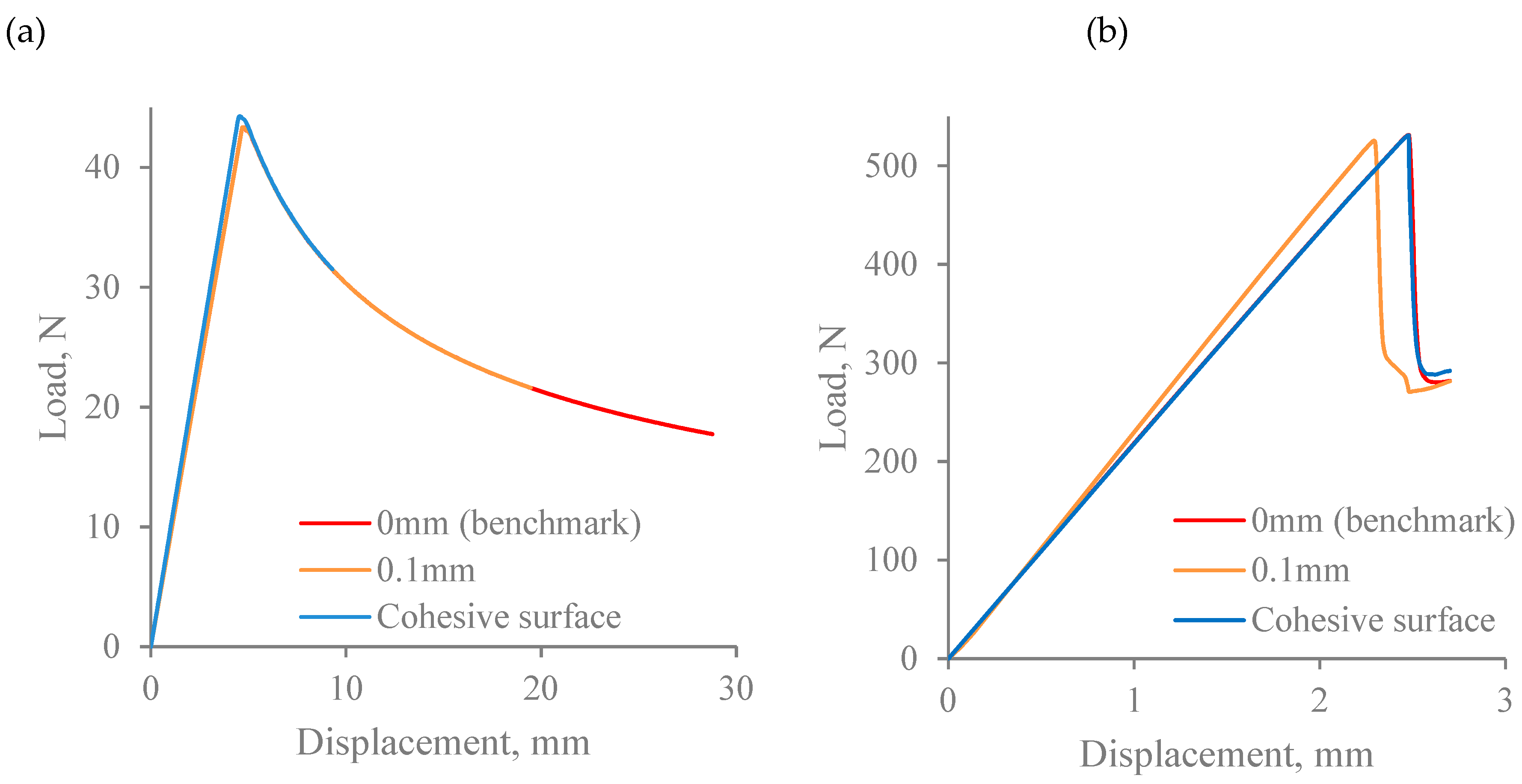
3.4. Cohesive Surface as an Alternative Presentation of the Cohesive Zone Model
3.5. Geometric Thickness of the Interface
4. Verification Based on the Critical Energy Release Rates
4.1. Mode I
4.2. Mode II
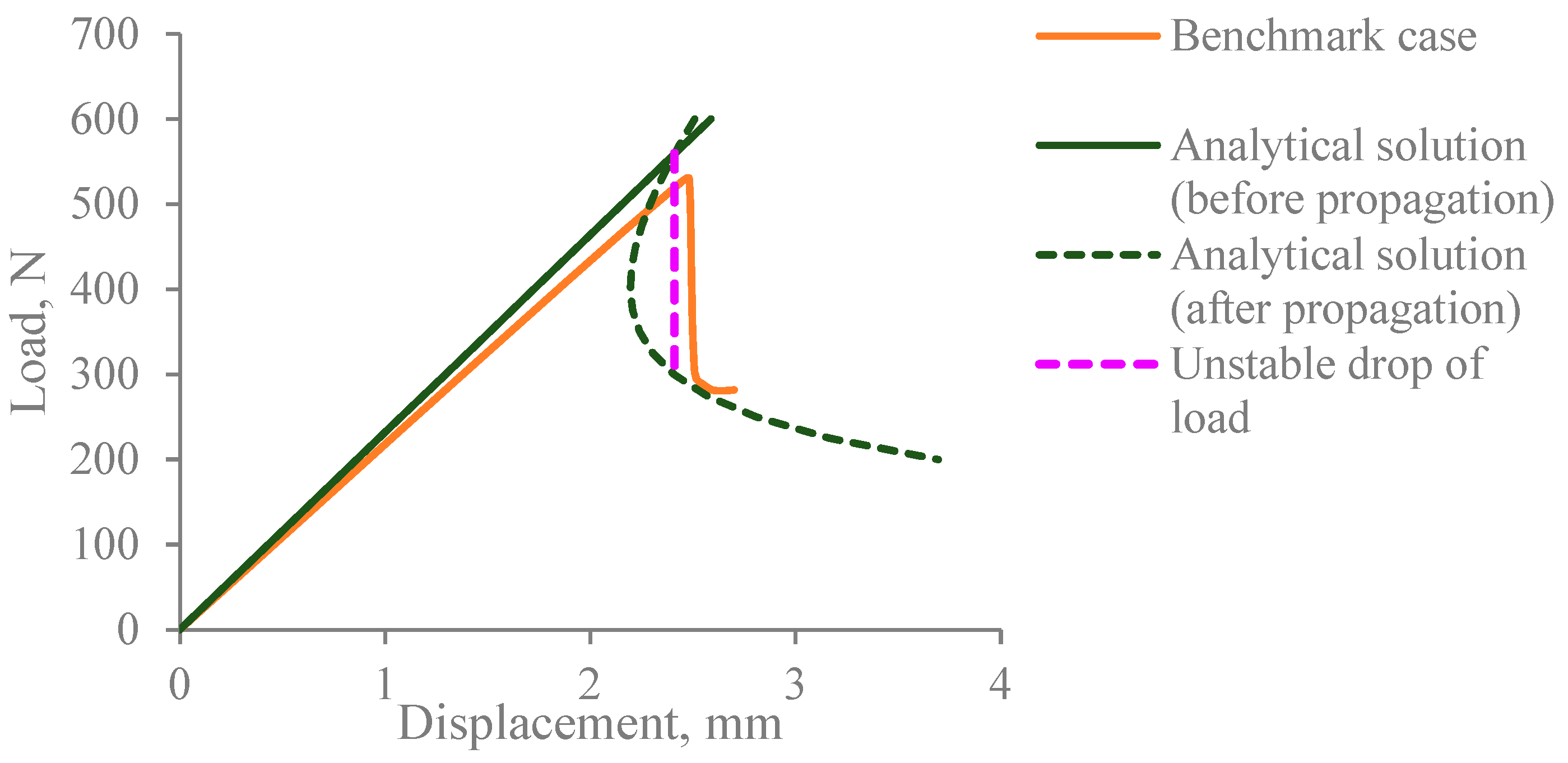
4.3. Critical Assessment of the Cohesive Model in General Applications to the Delamination Problem
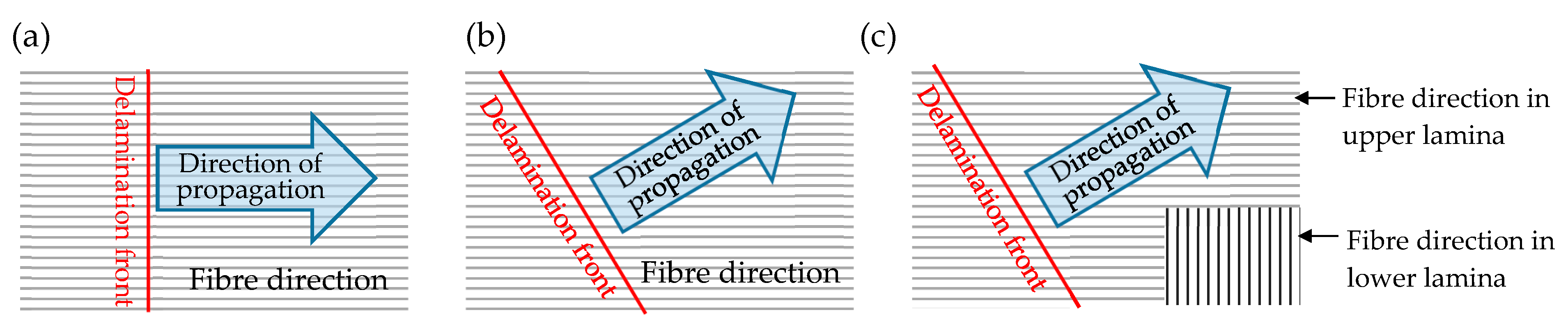
- Critical energy release rates are measured in the experiments under very restrictive conditions: (i) Delamination takes place between laminae of the same fibre orientation; (ii) delamination propagates in the fibre direction; (iii) effects of finite specimen width are not accounted for when conducting the measurements. Data obtained under such conditions are far from being sufficient to cover all practical scenarios. For instance, one can easily differentiate the efforts required to propagate a crack in a UD composite along the direction of the fibres, referring to Figure 1a, and a different direction, referring to Figure 1b, let alone interlaminar delamination propagating in a direction different from fibre directions in the laminae on either side of the delamination, as illustrated in Figure 1c. Apparently, the scope of applicability has been blindly extrapolated when the same set of critical energy release rates is assumed for all delamination propagating in any direction.
- The evolution criterion (3) has been rather arbitrarily equipped. It was adopted from the fracture mechanics, but even in fracture mechanics no conclusive agreement has been reached about what power value was to be employed, linear or quadratic, let alone any other possible combinations. One set of them defines one problem and another set is applicable for another problem.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- FAA. Composite Aircraft Structure, Federal Aviation Administration Advisory Circular; AC No:20-107B; FAA: Washington, DC, USA, 2010.
- Barenblatt, G.I. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. In Advances in Applied Mechanics; Dryden, H.L., Ed.; Elsevier: Amsterdam, The Netherlands, 1962; pp. 55–129. [Google Scholar]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Yu, R.C.; Pandolfi, A. 15—Modeling of delamination fracture in composites: A review A2—Sridharan, Srinivasan. In Delamination Behaviour of Composites; Woodhead Publishing: Cambridge, UK, 2008; pp. 429–457. [Google Scholar]
- Hongkarnjanakul, N.; Bouvet, C.; Rivallant, S. Validation of low velocity impact modelling on different stacking sequences of CFRP laminates and influence of fibre failure. Compos. Struct. 2013, 106, 549–559. [Google Scholar] [CrossRef]
- ASME. Guide for Verification and Validation in Computational Solid Mechanics; An overview of the PTC 60/V&V 10; ASME: New York, NY, USA, 2006. [Google Scholar]
- Li, S.; Sitnikova, E. An Excursion into Representative Volume Elements and Unit Cells. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Li, S. On the unit cell for micromechanical analysis of fibre-reinforced composites. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 455, 815. [Google Scholar] [CrossRef]
- ASTM International. ASTM Standard D5528-13: Standard Testing Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- ASTM International. ASTM Standard D7905/D7905M-14: Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- The British Standards Institution. BS EN 6033:2015: Aerospace Series—Carbon Fibre Reinforced Plastics—Test Method—Determination of Interlaminar Fracture Toughness Energy—Mode I—GIC; The British Standards Institution: London, UK, 2015. [Google Scholar]
- The British Standards Institution. BS EN 6034:2015: Aerospace Series—Carbon Fibre Reinforced Plastics—Test Method—Determination of Interlaminar Fracture Toughness Energy—Mode II—GIIC; The British Standards Institution: London, UK, 2015. [Google Scholar]
- ISO. International Standard ISO 15024:2001: Fibre-Reinforced Plastic Composites—Determination of Mode I Interlaminar Fracture Toughness, GIC, for Unidirectionally Reinforced Materials; ISO: Geneva, Switzerland, 2001. [Google Scholar]
- Standard of Chinese Aviation. HB 7402-96: Testing Method for Mode I Interlaminar Fracture Toughness of Carbon Fiber Reinforced Plastics. Available online: https://news.efucai.net/article/pro/details?articleId=5573 (accessed on 27 February 2019).
- Standard of Chinese Aviation. HB 7403-96: Testing Method for Mode II Interlaminar Fracture Toughness of Carbon Fiber Reinforced Plastic. Available online: https://news.efucai.net/article/pro/details?articleId=4993 (accessed on 27 February 2019).
- Sitnikova, E.; Li, S.; Li, D.; Yi, X. Subtle features of delamination in cross-ply laminates due to low speed impact. Compos. Sci. Technol. 2017, 149, 149–158. [Google Scholar] [CrossRef]
- Turon, A.; Dávila, C.G.; Camanho, P.P.; Costa, J. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng. Fract. Mech. 2007, 74, 1665–1682. [Google Scholar] [CrossRef]
- Harper, P.W.; Hallett, S.R. Cohesive zone length in numerical simulations of composite delamination. Eng. Fract. Mech. 2008, 75, 4774–4792. [Google Scholar] [CrossRef]
- Alfano, G.; Crisfield, M.A. Finite element interface models for the delamination analysis of laminated composites: Mechanical and computational issues. Int. J. Numer. Methods Eng. 2001, 50, 1701–1736. [Google Scholar] [CrossRef]
- Zou, Z.; Reid, S.R.; Li, S. A continuum damage model for delaminations in laminated composites. J. Mech. Phys. Solids 2003, 51, 333–356. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G.; De Moura, M.F. Numerical Simulation of Mixed-Mode Progressive Delamination in Composite Materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- ABAQUS Inc. Abaqus Analysis User’s Guide; Abaqus 2016 HTML Documentation; ABAQUS Inc.: Alto, CA, USA, 2016. [Google Scholar]
- Barbero, E.J. Finite Element Analysis of Composite Materials Using ABAQUS; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2013. [Google Scholar]
- Girão Coelho, A.M. Finite Element Guidelines for Simulation of Delamination Dominated Failures in Composite Materials Validated by Case Studies. Arch. Comput. Methods Eng. 2016, 23, 363–388. [Google Scholar] [CrossRef]
- Cheng, Q.; Fang, Z.; Yi, X.-S.; An, X.; Tang, B.; Xu, Y. “Ex situ” concept for toughening the RTMable BMI matrix composites, Part. I: Improving the interlaminar fracture toughness. J. Appl. Polym. Sci. 2008, 109, 1625–1634. [Google Scholar] [CrossRef]
- Zou, Z.; Reid, S.R.; Soden, P.D.; Li, S. Mode separation of energy release rate for delamination in composite laminates using sublaminates. Int. J. Solids Struct. 2001, 38, 2597–2613. [Google Scholar] [CrossRef]
- Charalambides, M.; Kinloch, A.J.; Wang, Y.; Williams, J.G. On the analysis of mixed-mode failure. Int. J. Fract. 1992, 54, 269–291. [Google Scholar]
- Cheng, Q.; Fang, Z.; Yi, X.-S.; An, X.; Tang, B.; Xu, Y. Ex-situ concept for toughening the RTMable BMI matrix composites. II. Improving the compression after impact. J. Appl. Polym. Sci. 2008, 108, 2211–2217. [Google Scholar] [CrossRef]
- Li, S.; Jeanmeure, L.F.C.; Pan, Q. A composite material characterisation tool: UnitCells. J. Eng. Math. 2015, 95, 279–293. [Google Scholar] [CrossRef]
- Li, D.; Sitnikova, E.; Li, S.; Yi, X. Modelling Damage due to Low Speed Impact in Laminated Composites of Toughened Interfaces through ‘Ex Situ’ Technique. In Proceedings of the 20th International Conference on Composite Materials, Copenhagen, Denmark, 19–24 July 2015. [Google Scholar]
- Zou, Z.; Reid, S.R.; Li, S.; Soden, P.D. General expressions for energy–release rates for delamination in composite laminates. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2002, 458, 645. [Google Scholar] [CrossRef]
- Carlsson, L.A.; Gillespie, J.W. Chapter 4—Mode-II Interlaminar Fracture of Composites. In Composite Materials Series; Friedrich, K., Ed.; Elsevier: Amsterdam, The Netherlands, 1989; pp. 113–157. [Google Scholar]
- Jiang, Z.; Wan, S.; Zhong, Z.; Li, M.; Shen, K. Determination of mode-I fracture toughness and non-uniformity for GFRP double cantilever beam specimens with an adhesive layer. Eng. Fract. Mech. 2014, 128, 139–156. [Google Scholar] [CrossRef]
- Schön, J. Coefficient of friction of composite delamination surfaces. Wear 2000, 237, 77–89. [Google Scholar] [CrossRef]

| Longitudinal tensile modulus, E1 (GPa) | 102 [28] |
| Transverse tensile modulus E2 = E3 (GPa) | 4.8 |
| Longitudinal shear modulus G12 = G13 (GPa) | 2.0 |
| Transverse shear modulus G23 (GPa) | 1.7 |
| Longitudinal Poisson’s ratio, ν12 | 0.32 [28] |
| Transverse Poisson’s ratio ν23 | 0.42 |
| Interlaminar tensile strength, σc (MPa) | 67.6 [25] |
| Interlaminar shear strength, τc (MPa) | 103 [28] |
| GIc (J/m2) | 215 [25] |
| GIIc = GIIIc (J/m2) | 510 [25] |
| Element direction | Mode I | Mode II |
|---|---|---|
| Element size/number along the length of the model | 0.1 mm/1100 elements | 0.2 mm/500 elements |
| Element size/number along the width of the model | ≈0.227 mm/55 elements | 0.2 mm/63 elements |
| Number of elements in through-thickness direction | 4 | 2 |
| Penalty stiffness | Knn = Kss = Ktt = 1014 Pa/m |
| Viscosity parameter | 10−8 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sitnikova, E.; Li, D.; Wei, J.; Yi, X.; Li, S. On the Representativeness of the Cohesive Zone Model in the Simulation of the Delamination Problem. J. Compos. Sci. 2019, 3, 22. https://doi.org/10.3390/jcs3010022
Sitnikova E, Li D, Wei J, Yi X, Li S. On the Representativeness of the Cohesive Zone Model in the Simulation of the Delamination Problem. Journal of Composites Science. 2019; 3(1):22. https://doi.org/10.3390/jcs3010022
Chicago/Turabian StyleSitnikova, Elena, Dafei Li, Jiahu Wei, Xiaosu Yi, and Shuguang Li. 2019. "On the Representativeness of the Cohesive Zone Model in the Simulation of the Delamination Problem" Journal of Composites Science 3, no. 1: 22. https://doi.org/10.3390/jcs3010022
APA StyleSitnikova, E., Li, D., Wei, J., Yi, X., & Li, S. (2019). On the Representativeness of the Cohesive Zone Model in the Simulation of the Delamination Problem. Journal of Composites Science, 3(1), 22. https://doi.org/10.3390/jcs3010022





