Enabling Composite Optimization through Soft Computing of Manufacturing Restrictions and Costs via a Narrow Artificial Intelligence
Abstract
1. Introduction
1.1. Motivation
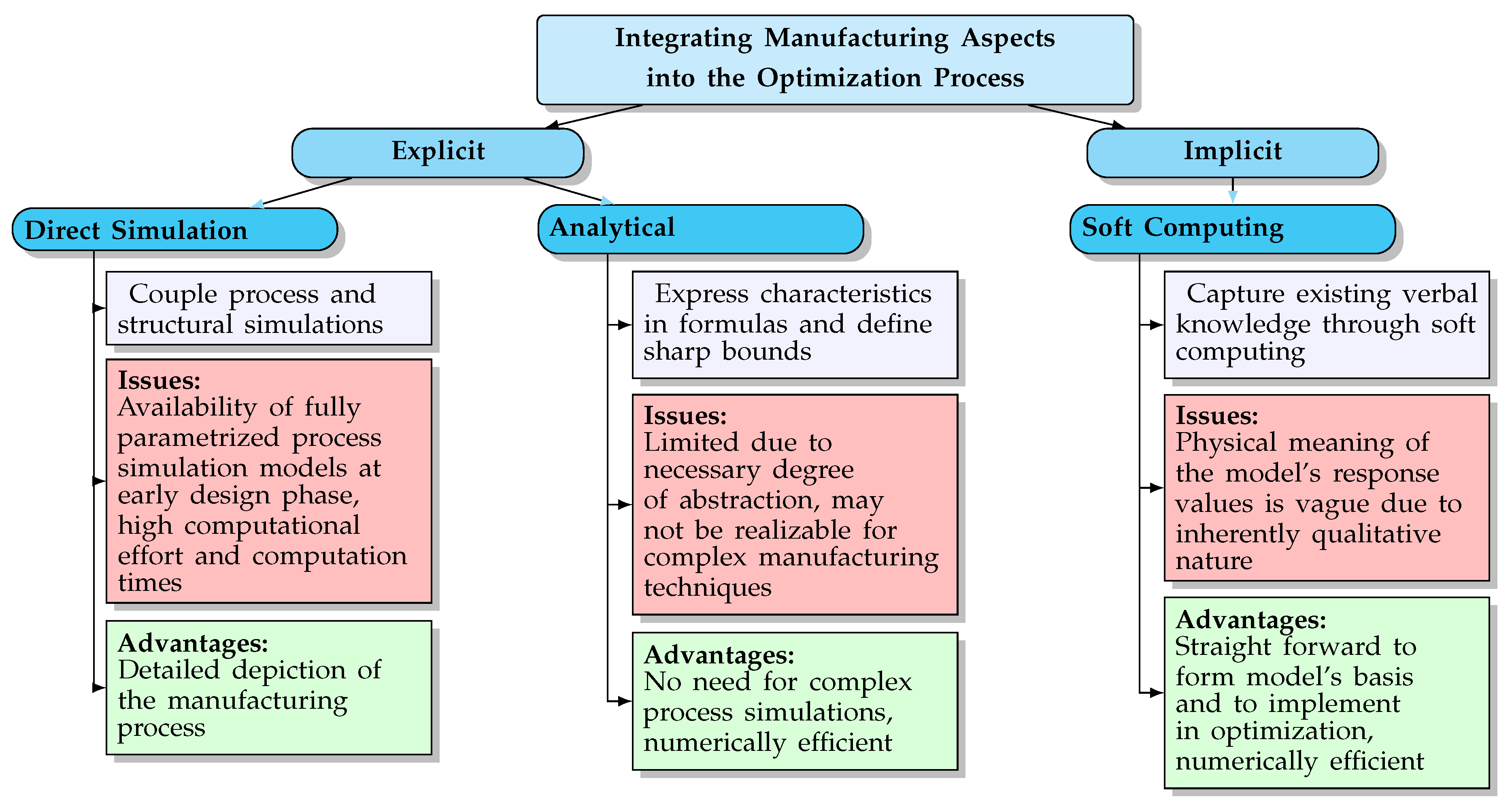
1.2. Brief Literature Review on Capturing Manufacturing Restriction and Costs
1.3. Application Cases
1.4. Used Material Properties
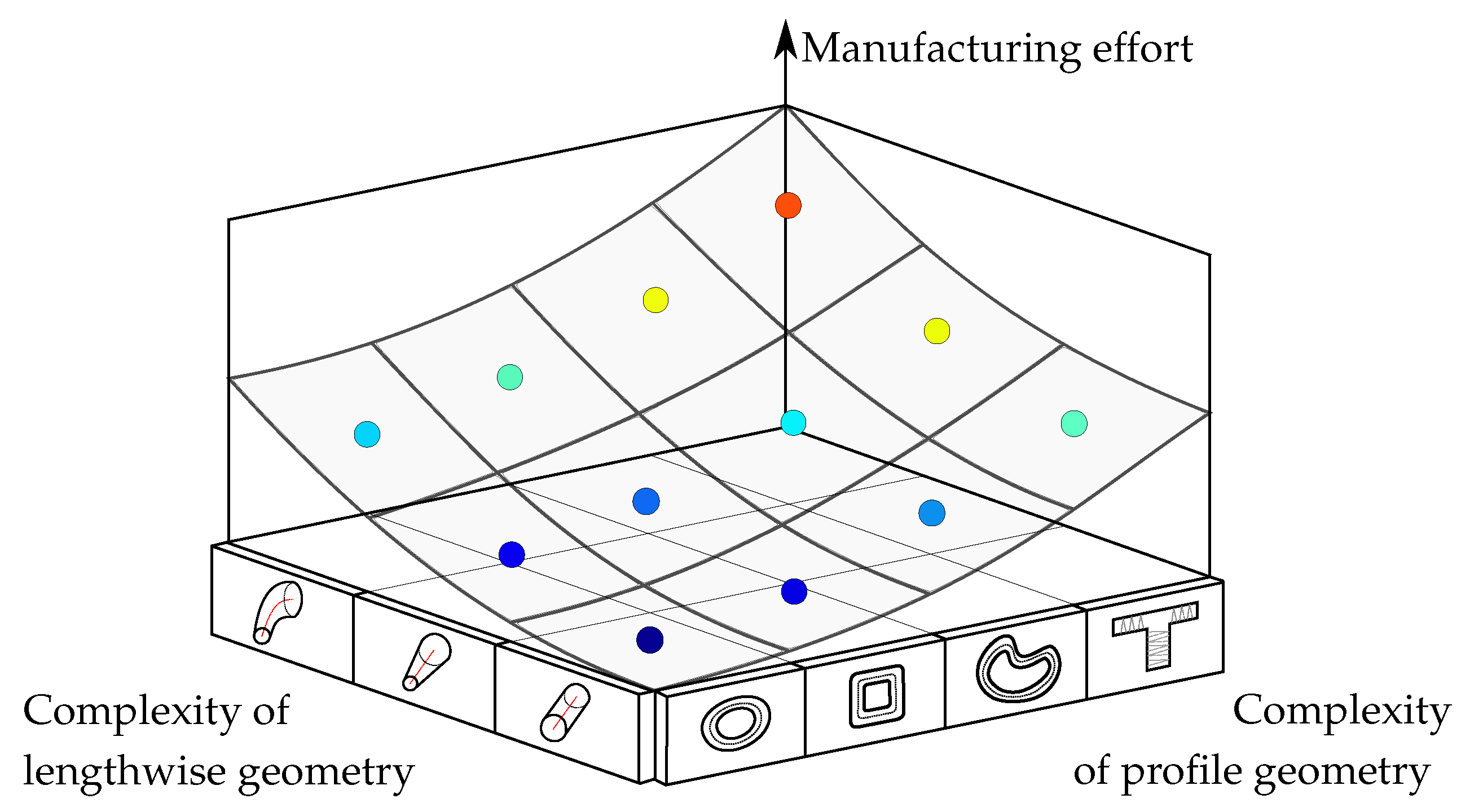
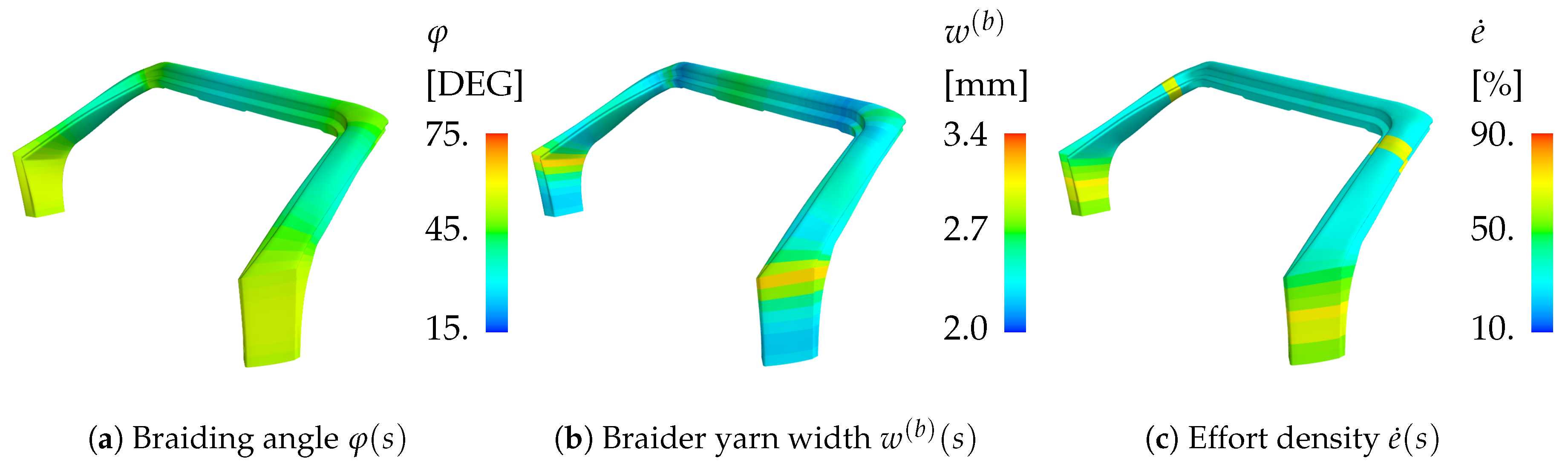
2. Modeling Manufacturing Effort
2.1. Quantification via Measure Effort
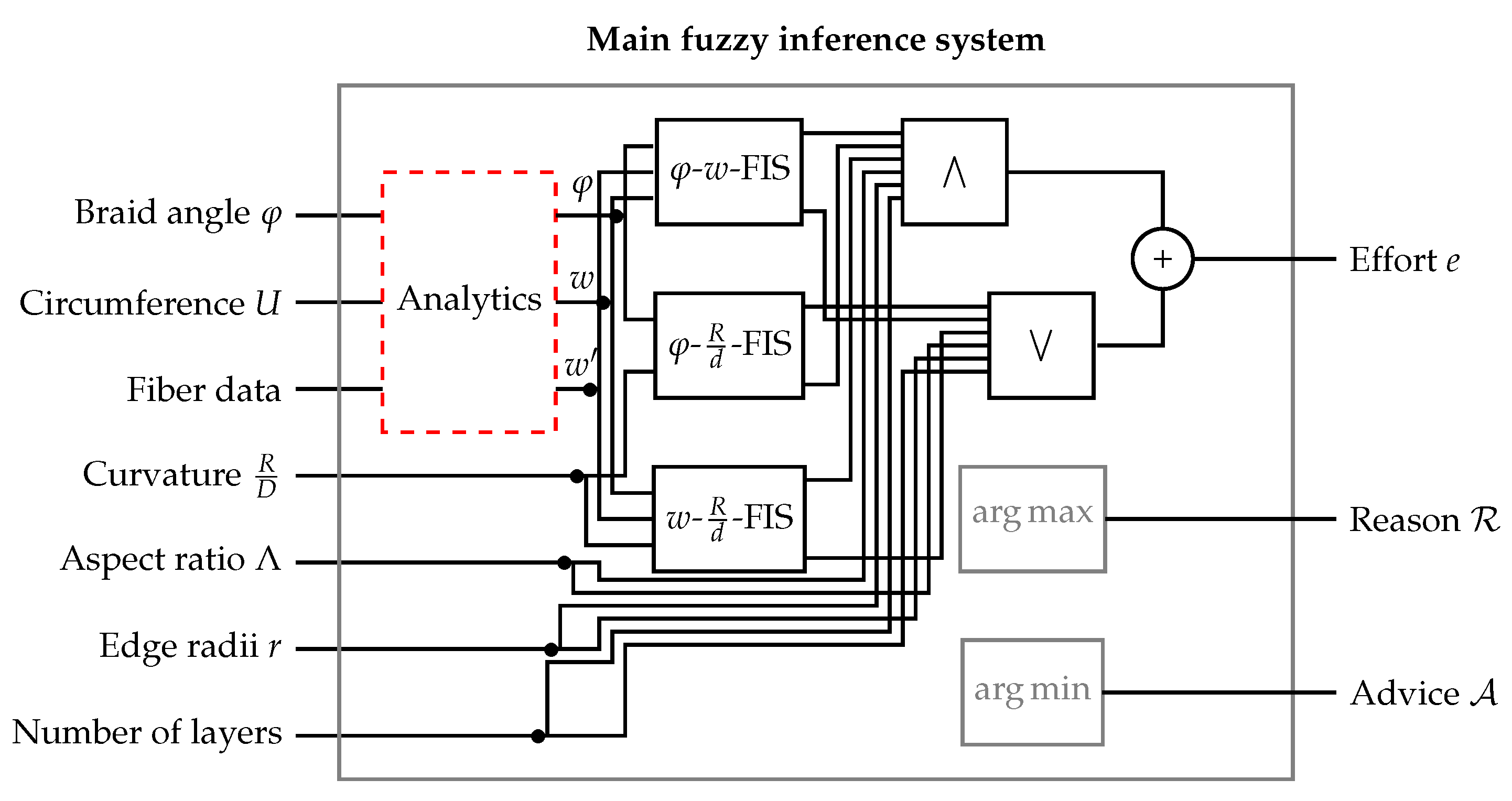
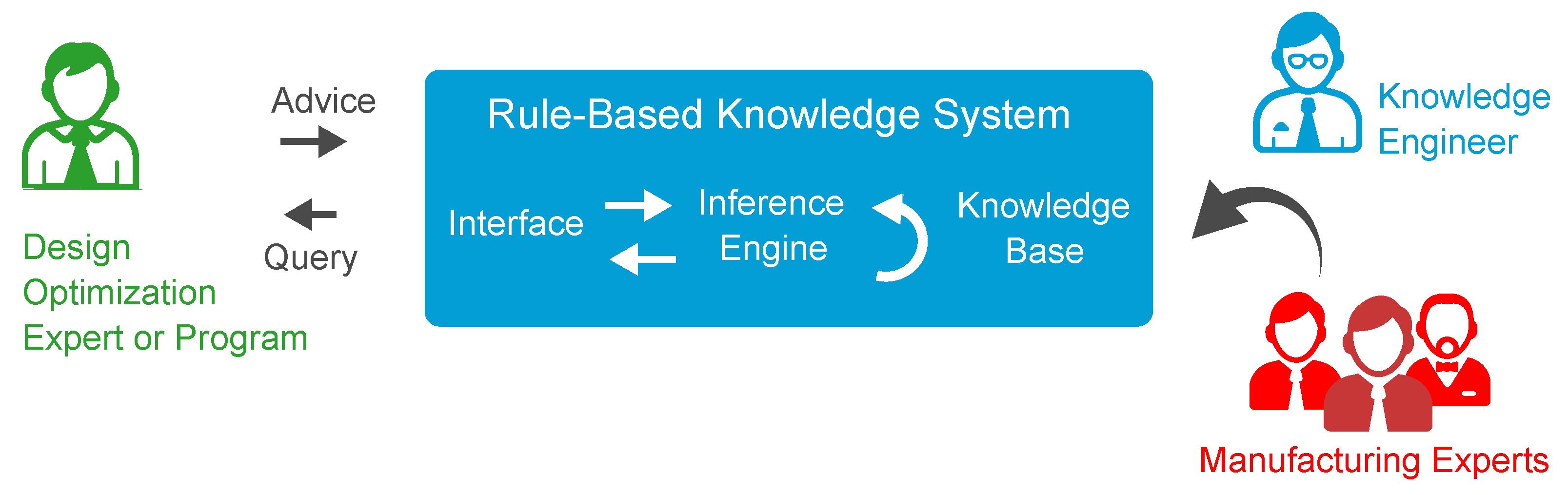
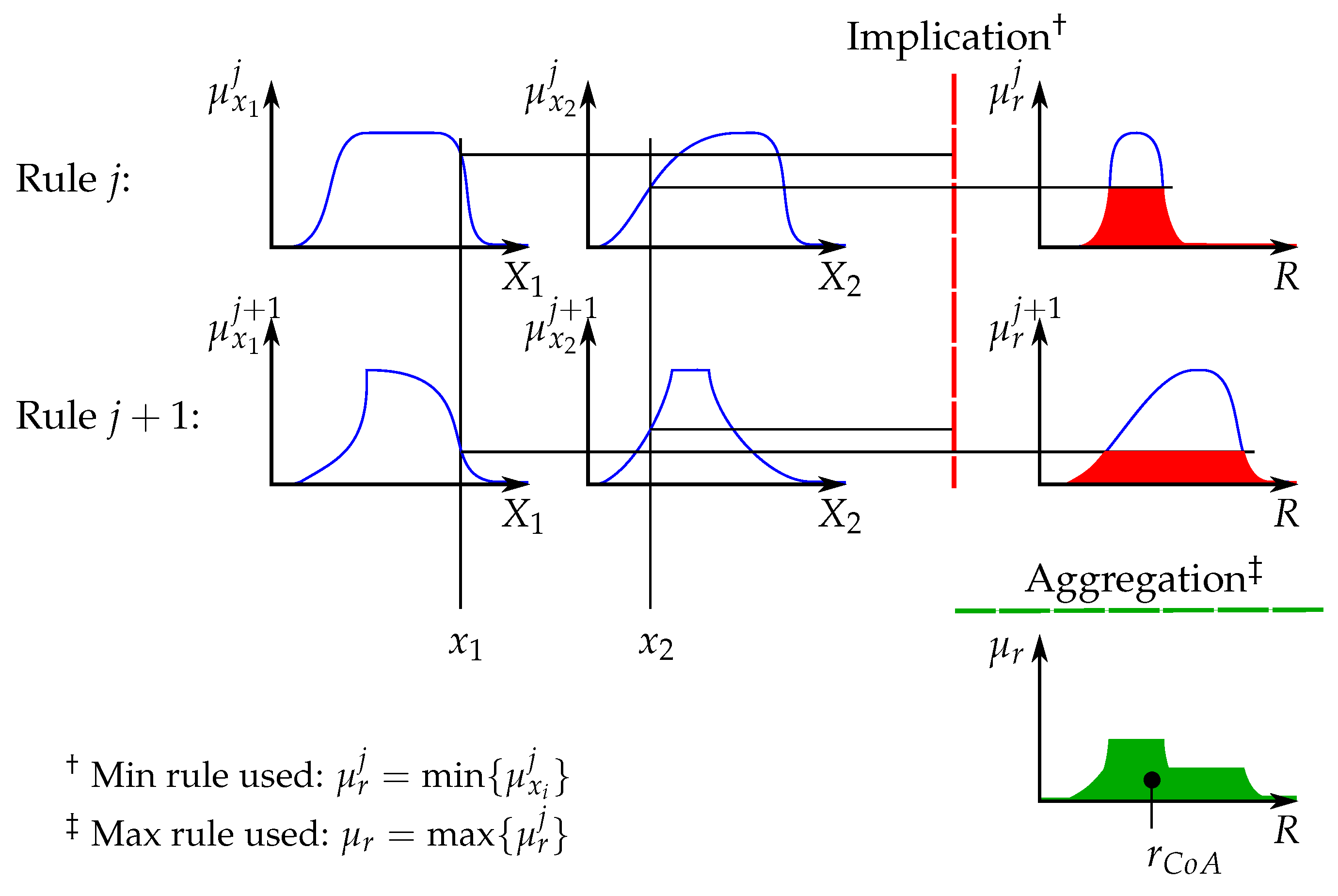
2.2. Extension via Reasoning and Advising
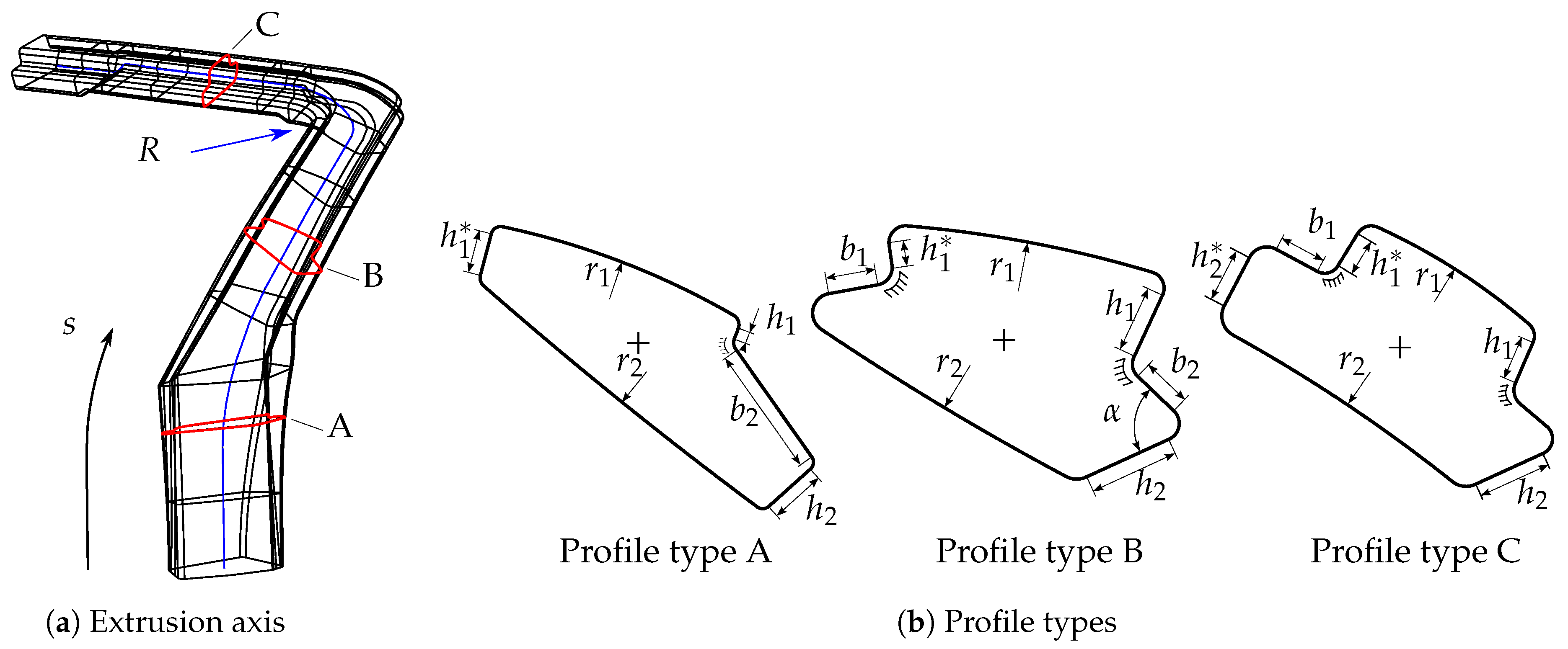
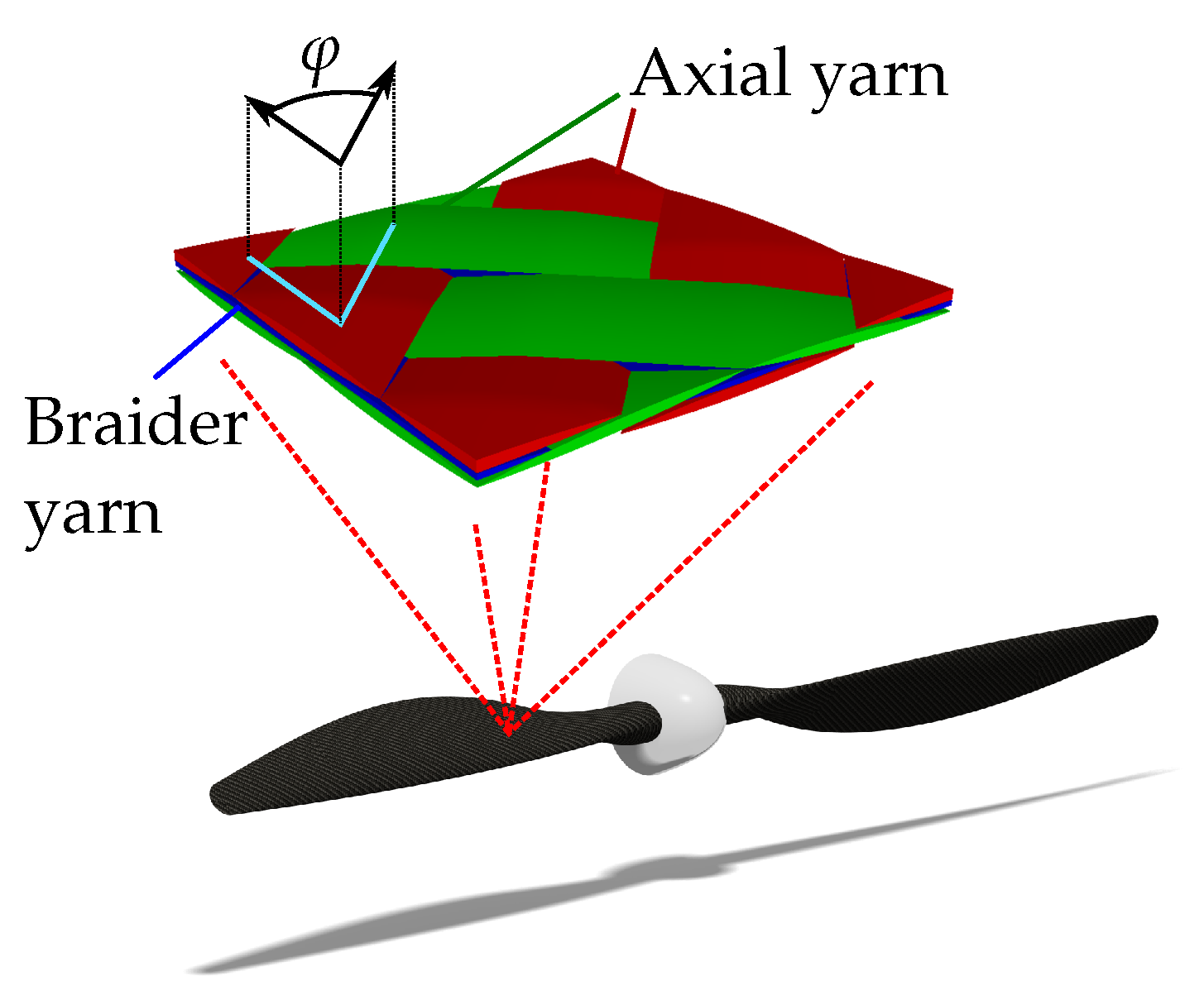
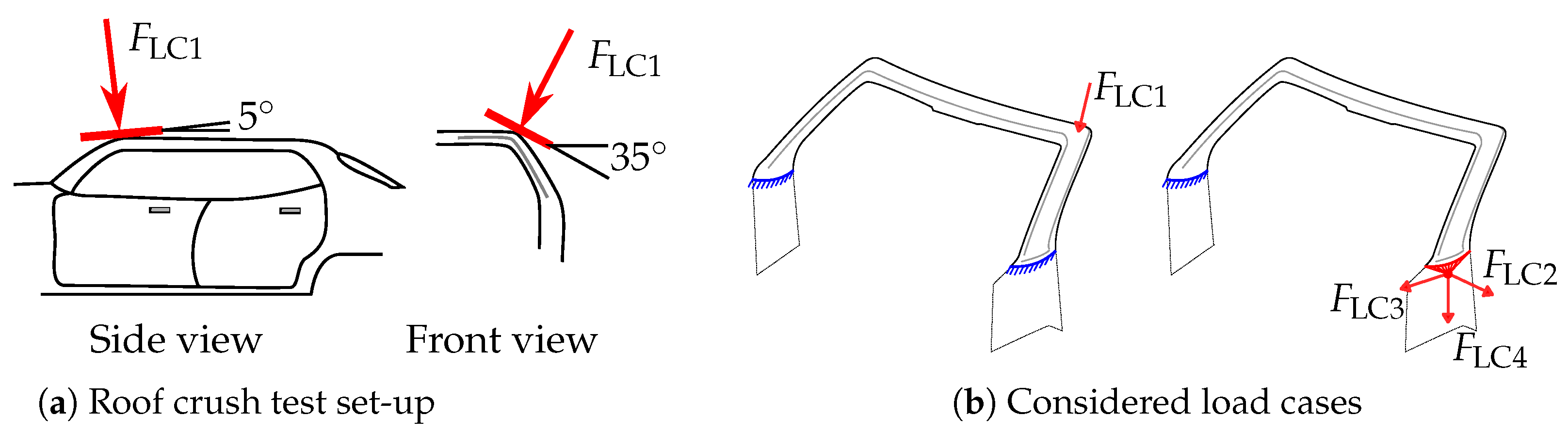
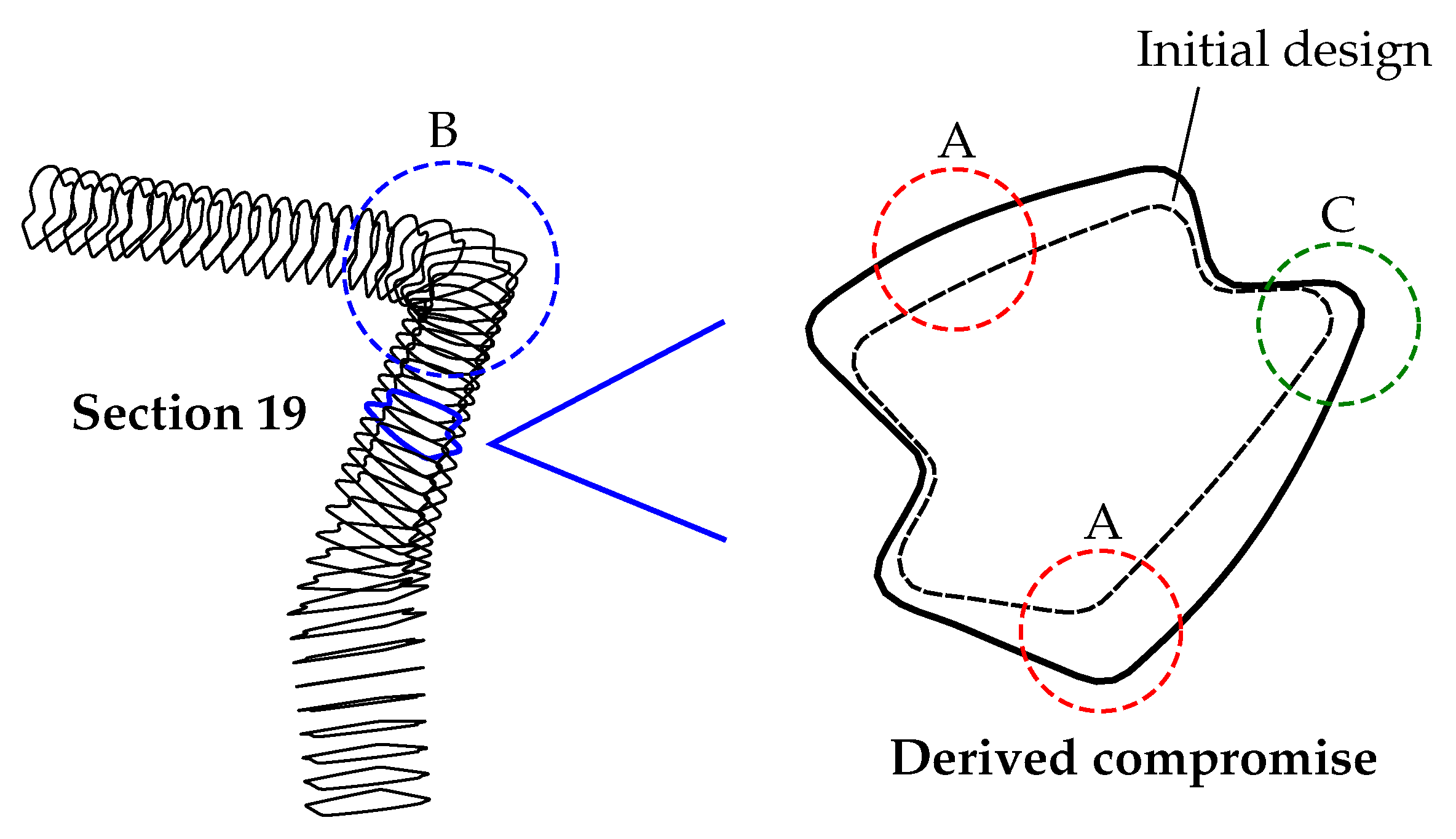
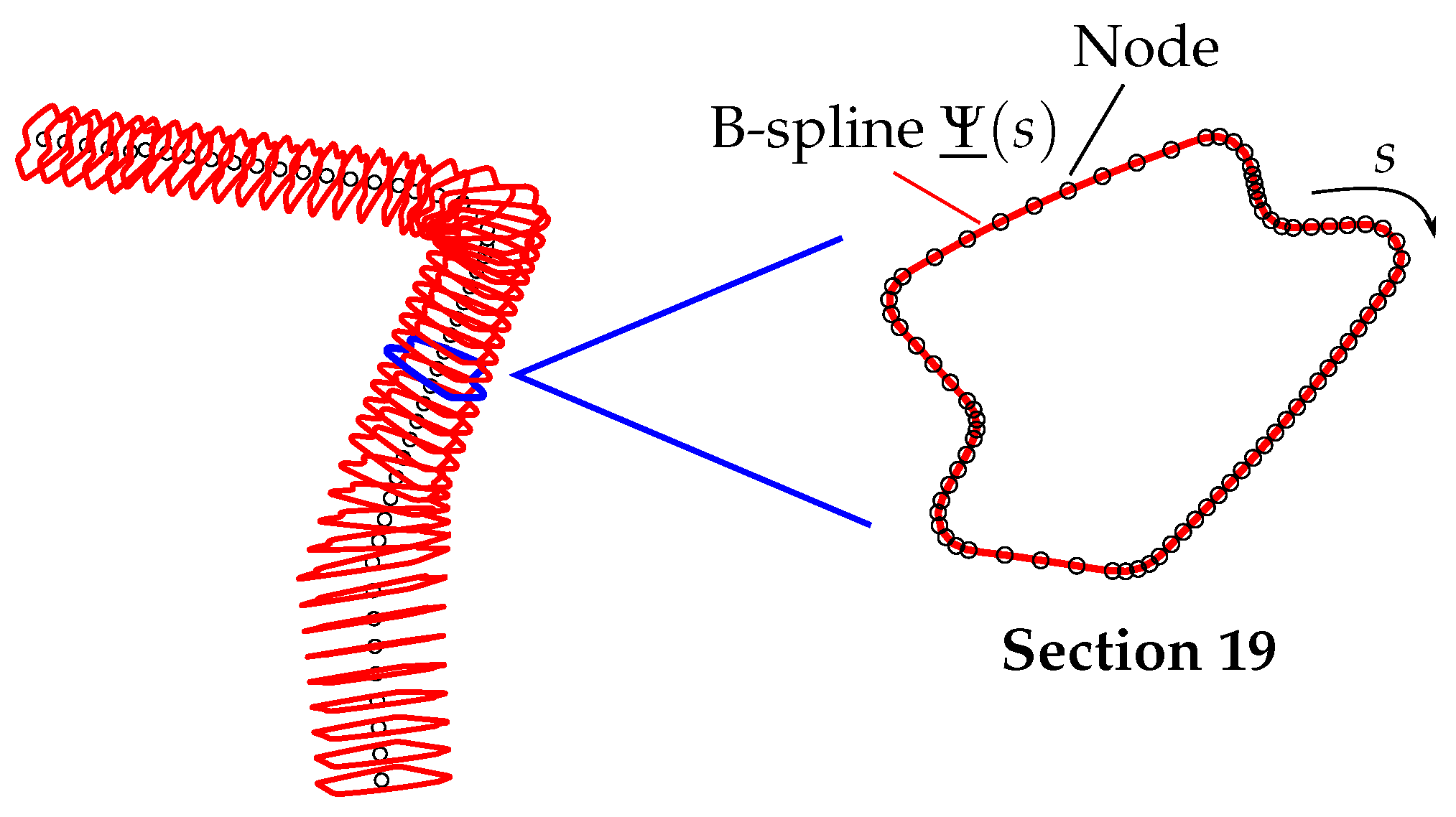
3. The Demonstration Structure: A-Pillar
4. Application of Approach and Usage of Its Novelties
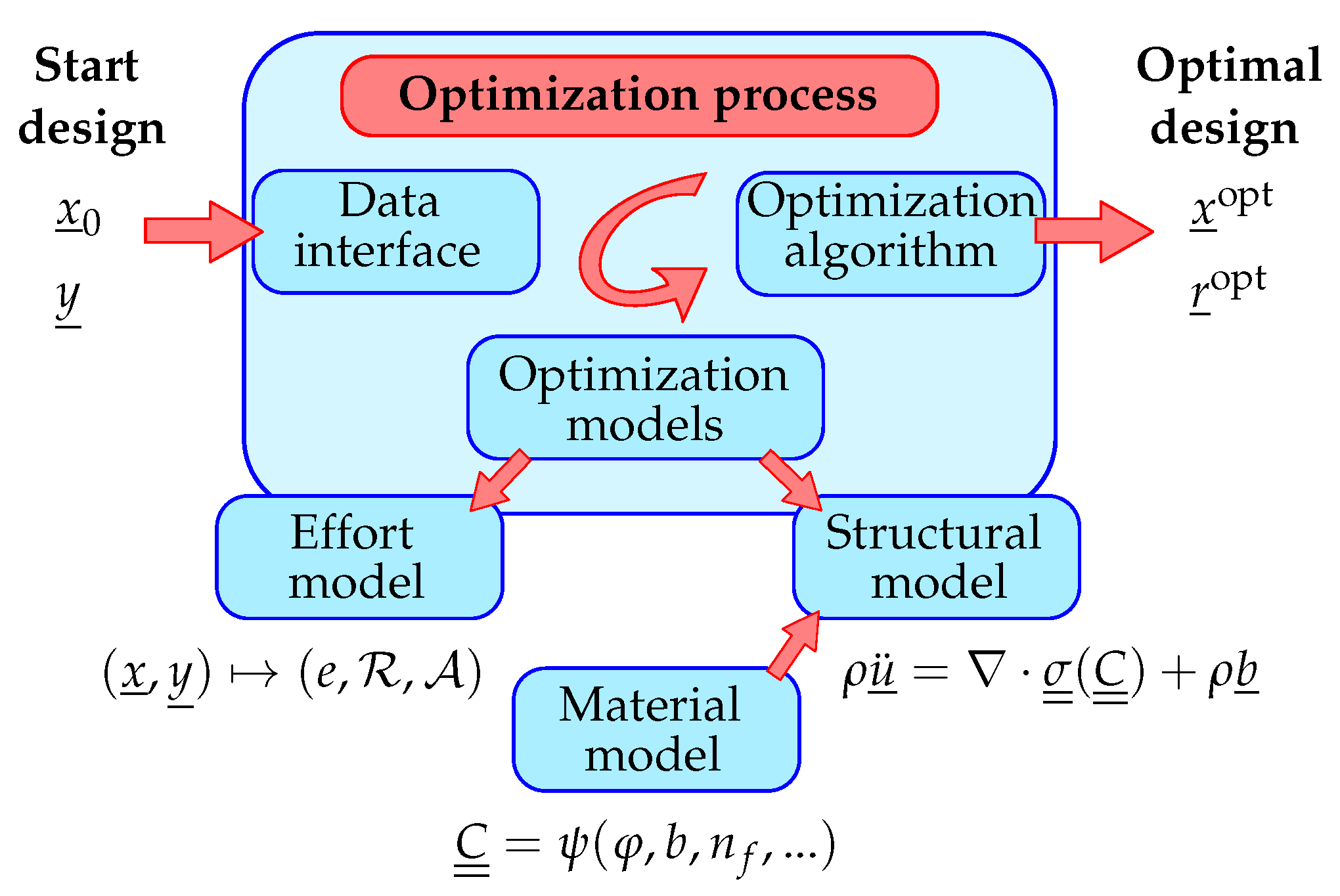
4.1. Embedding into Optimization Frame
4.2. Computer Added Evaluation Capabilities
5. Discussion
6. Materials and Methods
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CAE | Computer Added Engineering |
| FEM | Finite Element Method |
| FIS | Fuzzy Inference System |
| KBS | Knowledge-Based System |
| MDDO | Multi-Disciplinary Design Optimization |
| MEM | Manufacturing Effort Model |
| NASTRAN | NASA Structural Analysis System (FFE software) |
| NLQLP | Gradient-based Nonlinear Programming Aalgorithm |
Appendix A. Design Space and Parametrization
| Unit | ID | |||
|---|---|---|---|---|
| −10. | 20. | mm | 1 | |
| −5. | 15. | mm | 2 | |
| −5. | 30. | mm | 3 | |
| −5. | 10. | mm | 4 | |
| −3. | 20. | mm | 5 | |
| −2. | 20. | mm | 6 | |
| −3. | 20. | mm | 7 | |
| −10. | 15. | mm | 8 | |
| −10. | 15. | mm | 9 | |
| −10. | 20. | mm | 10 | |
| −10. | 20. | DEG | 11 | |
| −10. | 50. | DEG | 12 | |
| −10. | 20. | DEG | 13 | |
| −2000. | 2000. | mm | 14 | |
| −2000. | 2000. | mm | 15 | |
| −4000. | 4000. | mm | 16 | |
| −1000. | 1000. | mm | 17 | |
| −10. | 20. | mm | 18 | |
| −7. | 10. | mm | 19 | |
| −7. | 10. | mm | 20 | |
| −1000. | 1000. | mm | 21 | |
| −4000. | 2000. | mm | 22 | |
| −4000. | 3000. | mm | 23 | |
| R | −1. | 0.5 | - | 24 |
| 2. | 8. | mm | 25 | |
| 2. | 8. | mm | 26 | |
| 2. | 8. | mm | 27 | |
| 0.001 | 0.6 | mm | 28 | |
| 0.001 | 0.6 | mm | 29 | |
| 0.001 | 0.6 | mm | 30 | |
| 0.001 | 0.6 | mm | 31 | |
| 15. | 75. | DEG | 32 | |
| 15. | 75. | DEG | 33 | |
| 15. | 75. | DEG | 34 | |
| 15. | 75. | DEG | 35 | |
| 15. | 75. | DEG | 36 |
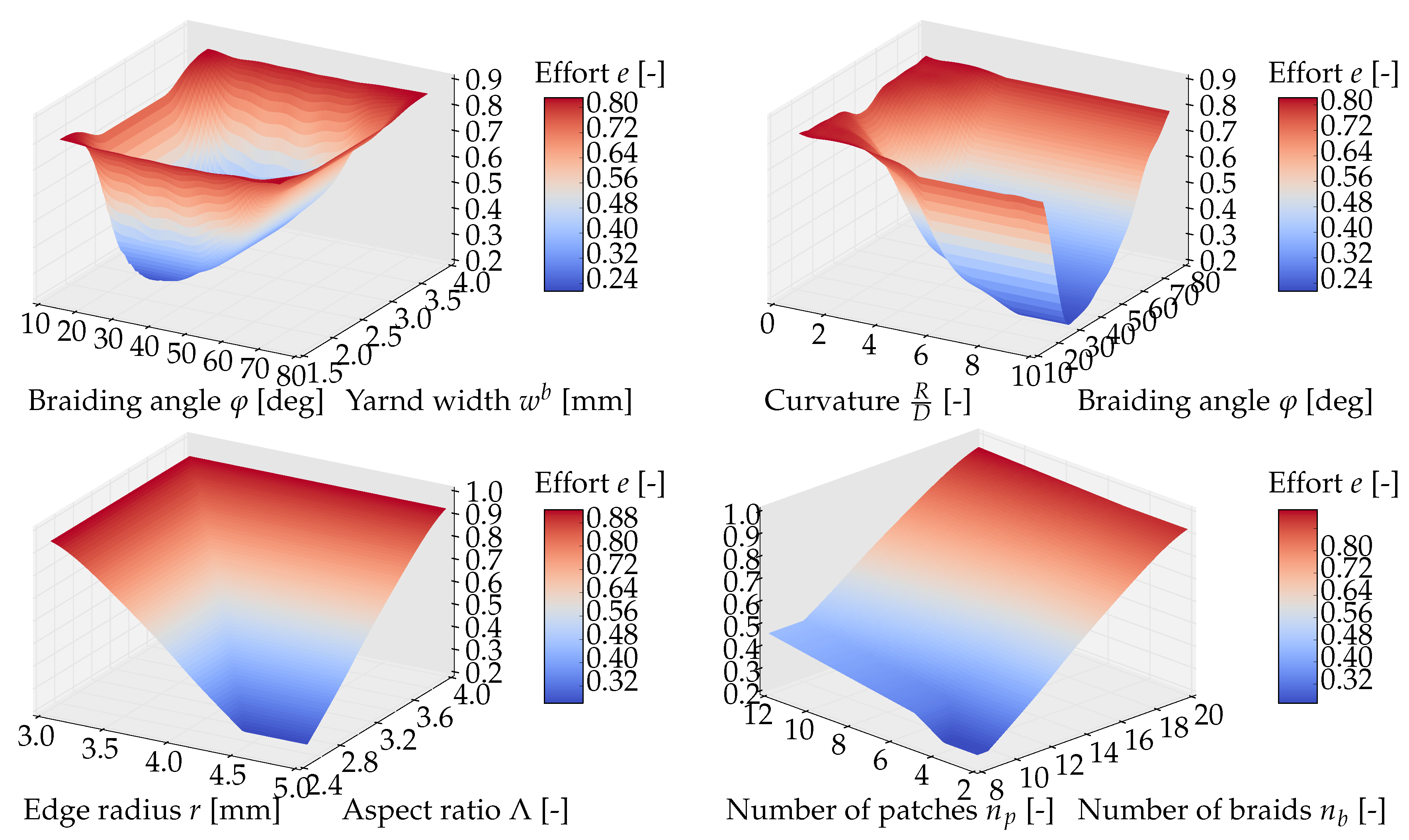
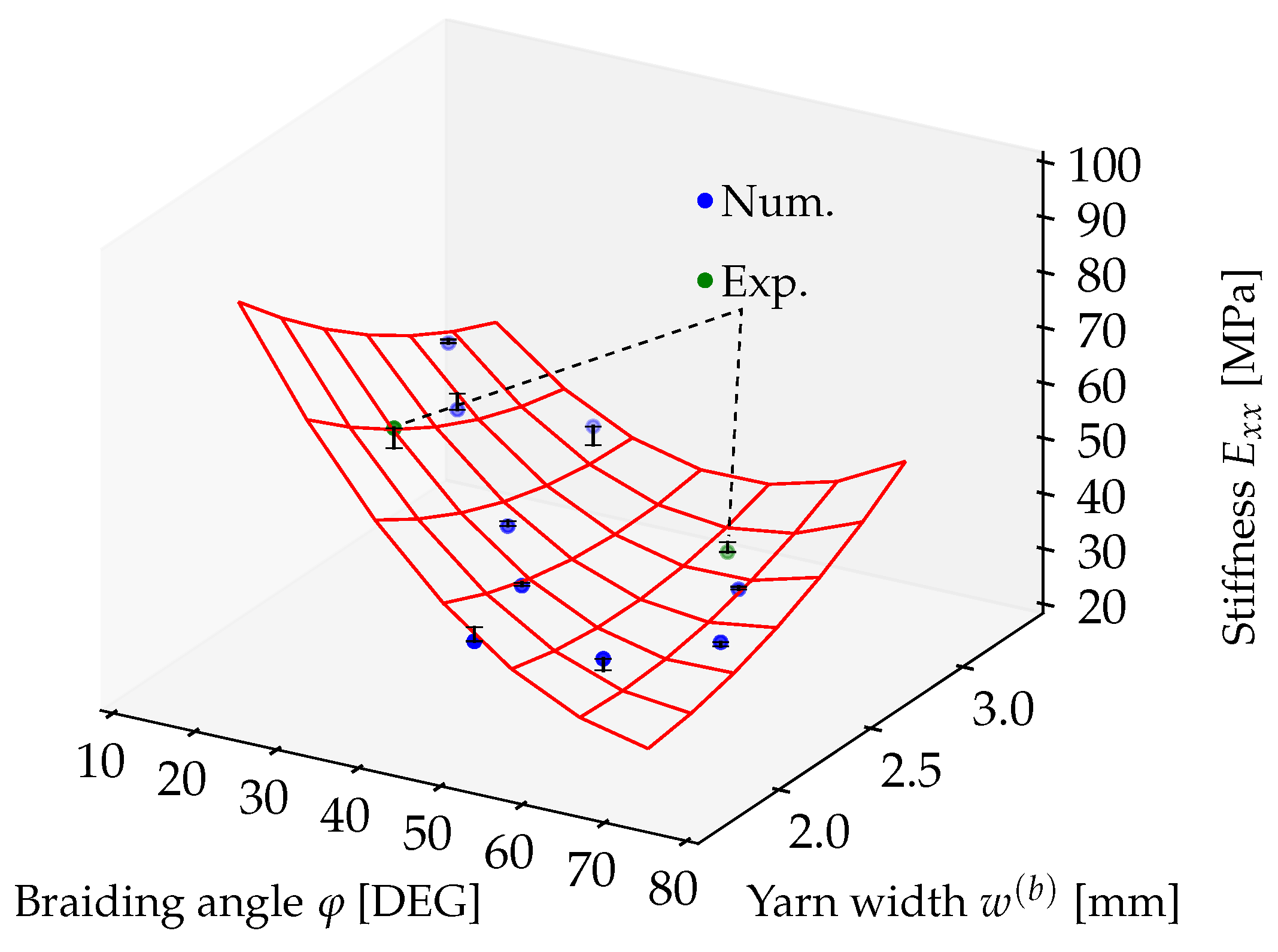
Appendix B. Overview on Response Surfaces of the Braiding Manufacturing Effort Model
Appendix C. Graph of Knowledge-Basis
References
- Schatz, M.E.; Hermanutz, A.; Baier, H.J. Multi-criteria optimization of an aircraft propeller considering manufacturing. J. Struct. Multidiscip. Optim. 2017, 55, 899–911. [Google Scholar] [CrossRef]
- Mazumdar, S.K. Composite Manufacturing—Materials, Product and Process Engineering; CRC Press LLC: Baco Raton, FL, USA, 2002; ISBN 162870926X, 9781628709261. [Google Scholar]
- Jones, R.M. Mechanics of Composite Materials; Taylor & Francis: New York, NY, USA, 1999; ISBN 978-1560327127. [Google Scholar]
- Pickett, A.K.; Sirtautas, J.; Erber, A. Braiding Simulation and Prediction of Mechanical Properties. Appl. Compos. Mater. 2009, 16. [Google Scholar] [CrossRef]
- Chen, C.S.; Chen, T.J.; Chen, S.C.; Chien, R.D. Optimization of the injection molding process for short-fiber-reinforced composites. Mech. Compos. Mater. 2011, 47. [Google Scholar] [CrossRef]
- Mackerle, J. Finite element analyses and simulations of manufacturing processes of composites and their mechanical properties: A bibliography. Comput. Mater. Sci. 2004, 31, 187–219. [Google Scholar] [CrossRef]
- Wang, B.P.; Costin, D.P. Optimum Design of a Composite Structure with Three Types of Manufacturing Constraints. AIAA J. 1992, 30, 1667–1669. [Google Scholar] [CrossRef]
- Henderson, J.L.; Gurdal, Z.; Loos, A.C. Combined Structural and Manufacturing Optimization of Stiffened Composite Panels. J. Aircr. 1999, 36, 246–254. [Google Scholar] [CrossRef]
- Ghiasi, H.; Pasini, D.; Lessard, L. Constraint Globalized Nelder-Mead Method for Simultaneous Structural and Manufacturing Optimization of a Composite Bracket. J. Compos. Mater. 2008, 42, 717–736. [Google Scholar] [CrossRef]
- Iqbal, A.; He, N.; Li, L.; Dar, N.U. A fuzzy expert system for optimizing parameters and predicting performance measures in hard-milling process. Expert Syst. Appl. 2007, 32, 1020–1027. [Google Scholar] [CrossRef]
- Zhou, Y.; Saitou, K. Multi-Objective Topology Optimization of Composite Structures Considering Resin Filling Time. In Proceedings of the 11th World Congress of Structural and Multidisciplinary Optimisation (WCSMO-11), Sydney, Australia, 7–12 June 2015. [Google Scholar]
- Huang, J.; Gao, L.; Li, X. An effective teaching-learning-based cuckoo search algorithm for parameter optimization problems in structure designing and machining processes. Appl. Soft Comput. 2015, 36, 349–356. [Google Scholar] [CrossRef]
- Wehrle, E.; Wedekind, M.; Baier, H. Fuzzy modeling of imprecise material parameters in the analysis of metal matrix composite structures. In Proceedings of the ASME 2011 International Mechanical Engineering Congress and Exposition, IMECE 2011, Denver, CO, USA, 11–17 November 2011. [Google Scholar]
- Shortliffe, E.H.; Buchanan, B.G. A model of inexact reasoning in medicine. Math. Biosci. 1975, 23, 351–379. [Google Scholar] [CrossRef]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2009; ISBN 9789332543515. [Google Scholar]
- Hajela, P. Soft Computing in Multidisciplinary Aerospace Design. Aerosp. Sci. 2002, 38, 1–21. [Google Scholar] [CrossRef]
- Schatz, M.E.; Baier, H.J. An Approach towards the Incorporation of Soft Aspects Such as Manufacturing Efforts into Structural Design Optimization. J. Mech. Eng. Autom. 2014, 4, 847–857. [Google Scholar] [CrossRef]
- Perez, R.E.; Jansen, P.W.; Martins, J.R.R.A. pyOpt: A Python-Based Object-Oriented Framework for Nonlinear Constrained Optimization. Struct. Multidiscip. Optim. 2012, 45, 101–118. [Google Scholar] [CrossRef]

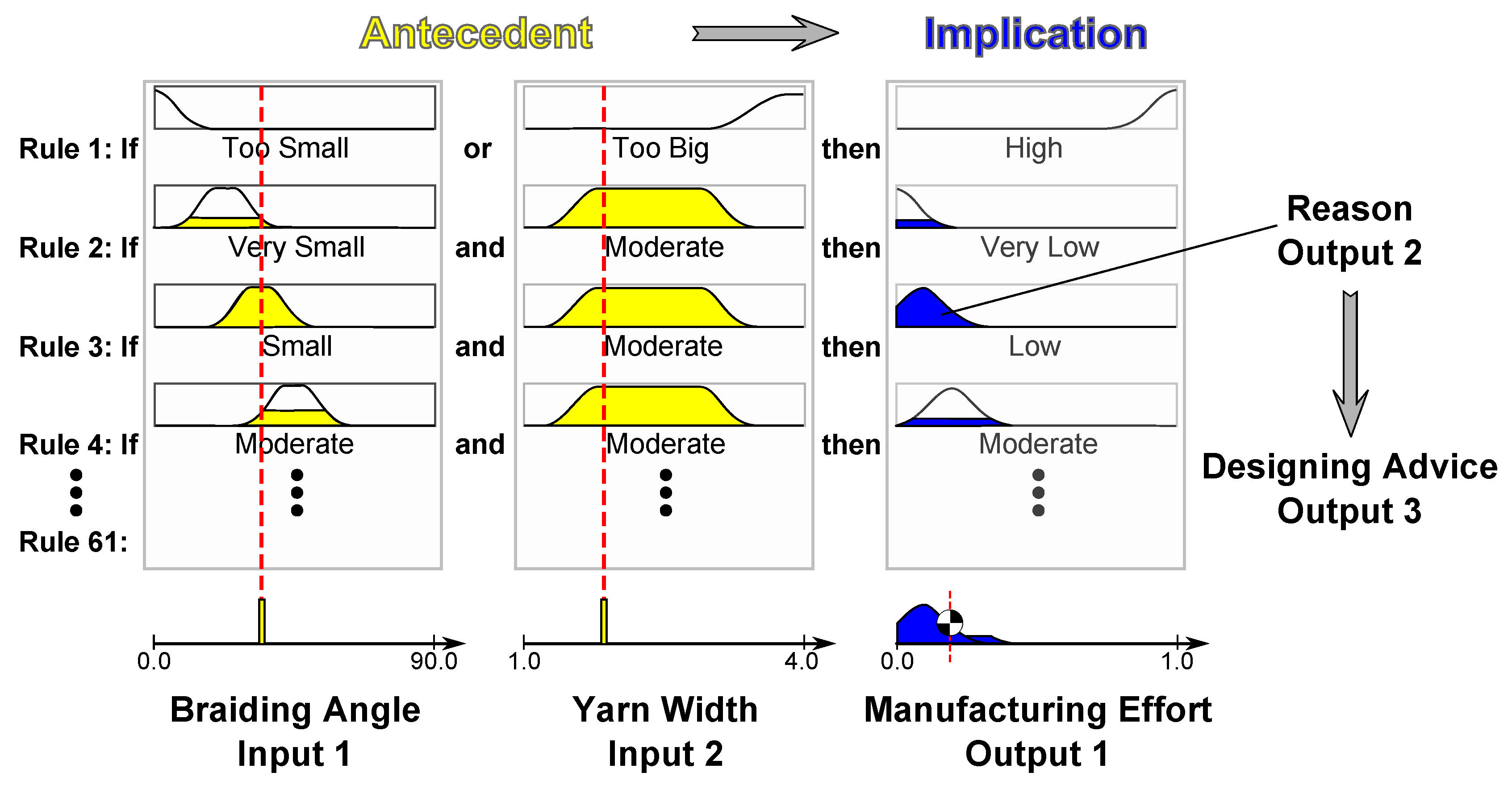



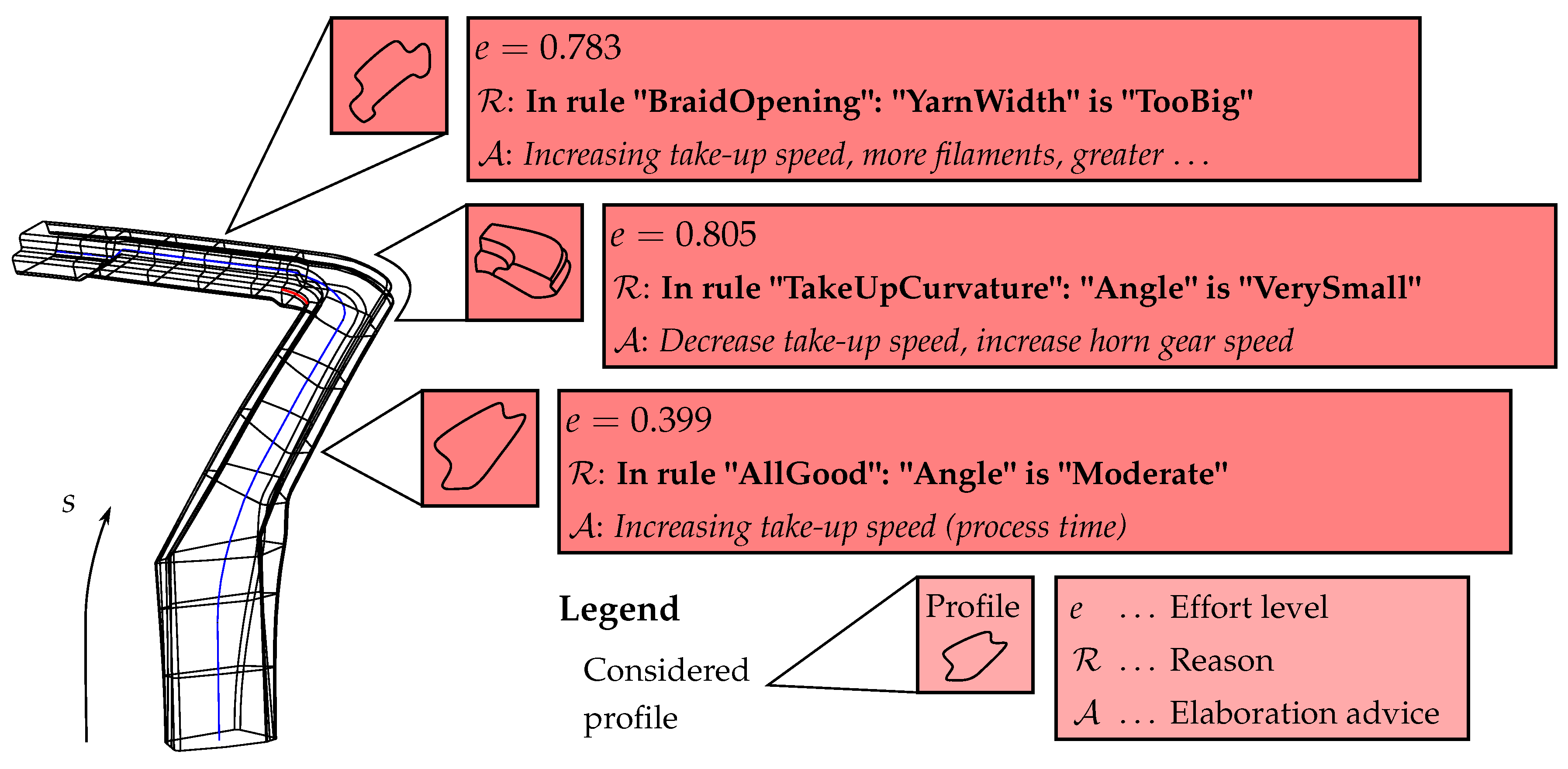
| Reason | Advice | ||
|---|---|---|---|
| 1 | 1 | In rule BraidOpening: | Reduce take-up speed |
| Angle is Too Small | |||
| 1 | 2 | In rule BraidOpening: | Increase take-up speed, more filaments, |
| Yarn Width is Too Small | greater yarn size et cetera | ||
| 3 | 1 | In rule AllGood: | Increase take-up speed |
| Angle is Moderate | (process time) | ||
| 3 | 2 | In rule AllGood: | Increase take-up speed |
| Yarn Width is Moderate | (process time) |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schatz, M.E. Enabling Composite Optimization through Soft Computing of Manufacturing Restrictions and Costs via a Narrow Artificial Intelligence. J. Compos. Sci. 2018, 2, 70. https://doi.org/10.3390/jcs2040070
Schatz ME. Enabling Composite Optimization through Soft Computing of Manufacturing Restrictions and Costs via a Narrow Artificial Intelligence. Journal of Composites Science. 2018; 2(4):70. https://doi.org/10.3390/jcs2040070
Chicago/Turabian StyleSchatz, Markus Edwin. 2018. "Enabling Composite Optimization through Soft Computing of Manufacturing Restrictions and Costs via a Narrow Artificial Intelligence" Journal of Composites Science 2, no. 4: 70. https://doi.org/10.3390/jcs2040070
APA StyleSchatz, M. E. (2018). Enabling Composite Optimization through Soft Computing of Manufacturing Restrictions and Costs via a Narrow Artificial Intelligence. Journal of Composites Science, 2(4), 70. https://doi.org/10.3390/jcs2040070





