Axial Compressive Stress-Strain Model Developed for FRP-Confined Concrete Columns with Elliptical Cross Sections
Abstract
:1. Introduction
2. Experimental Program
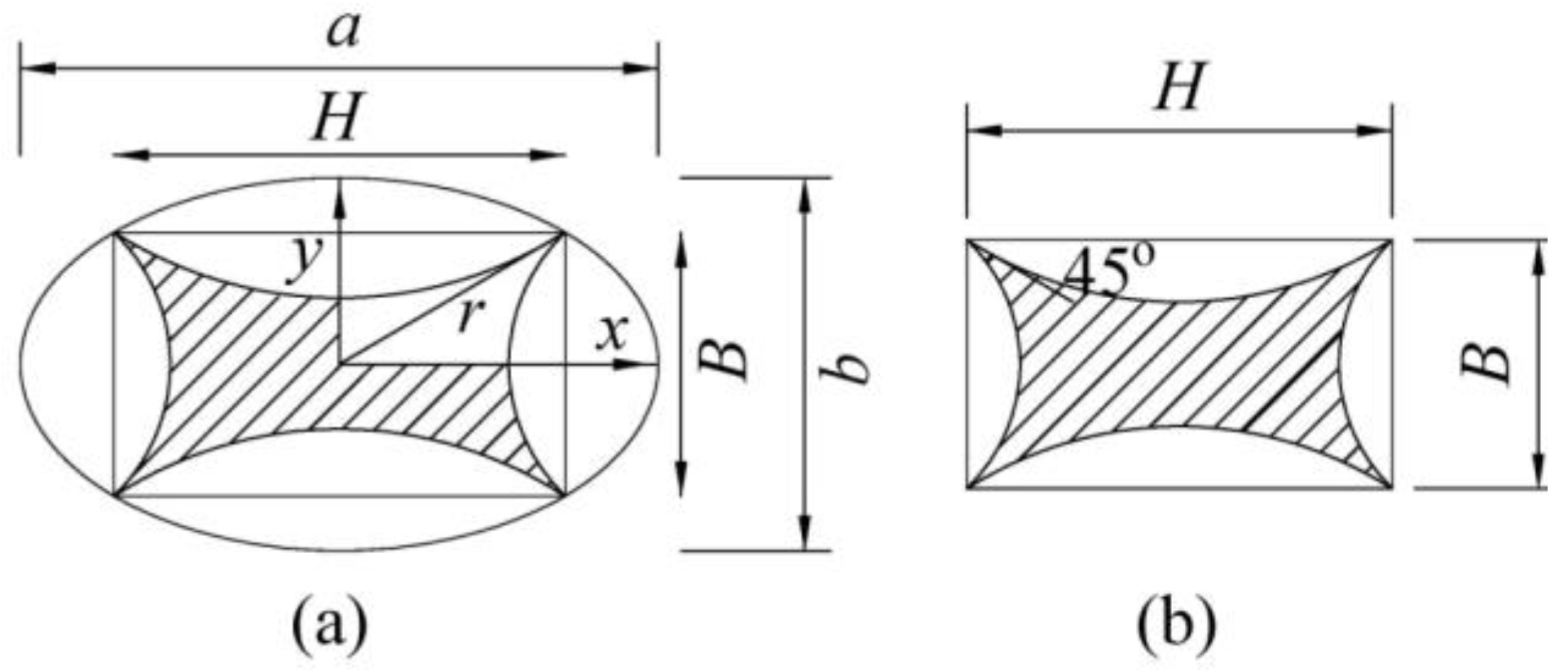
2.1. Overview of Specimen Details
2.2. Overview of Experimental Test Results
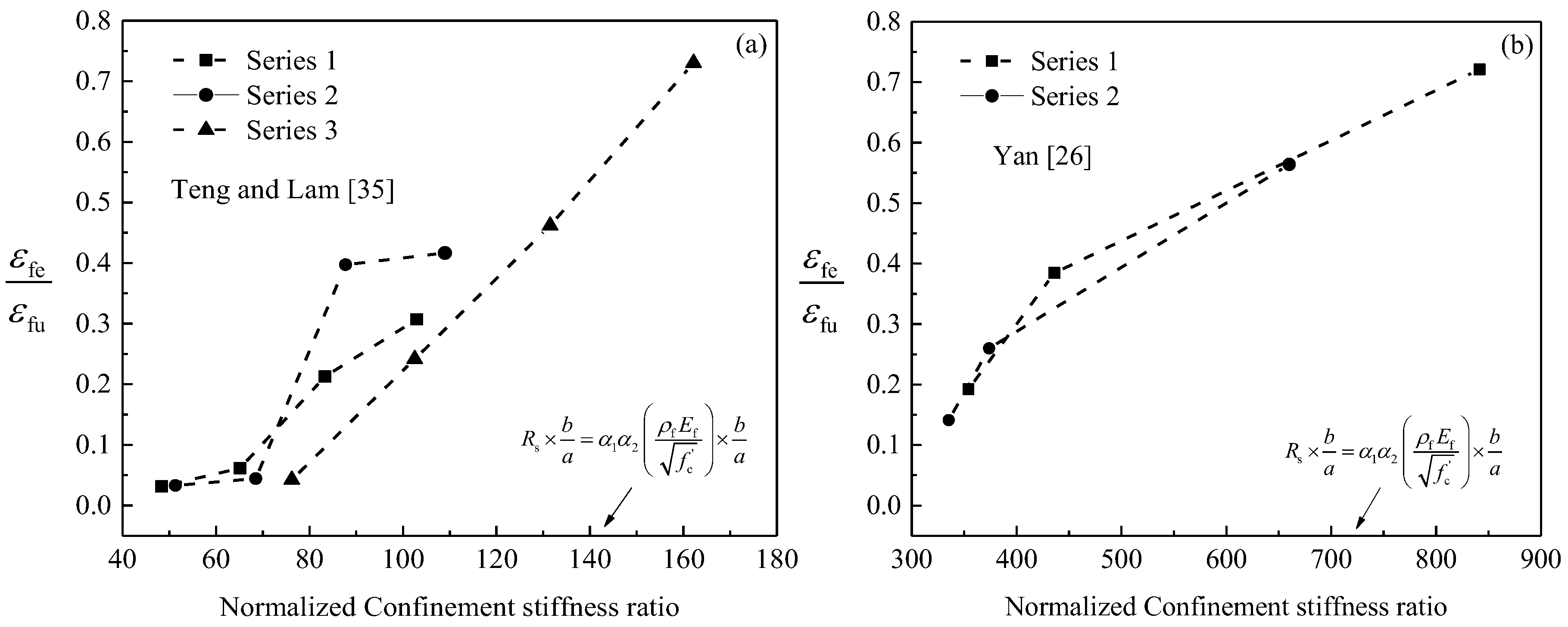
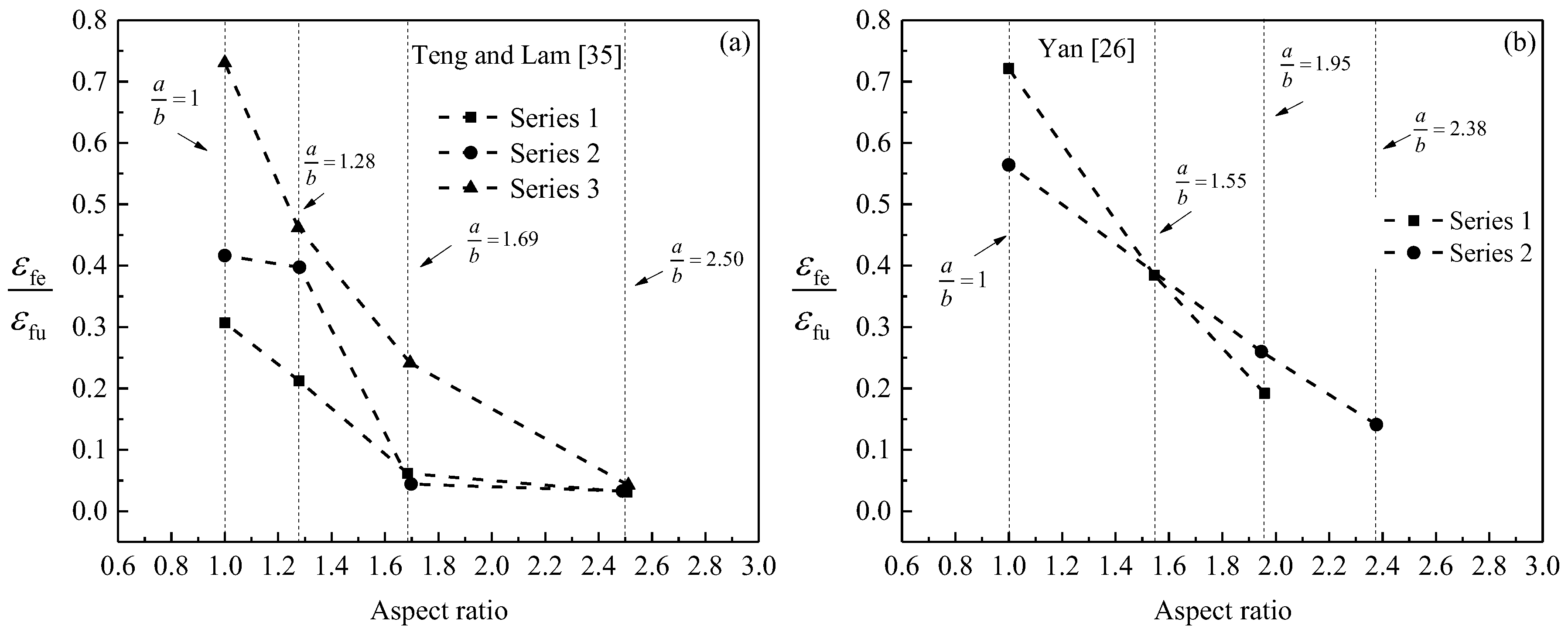
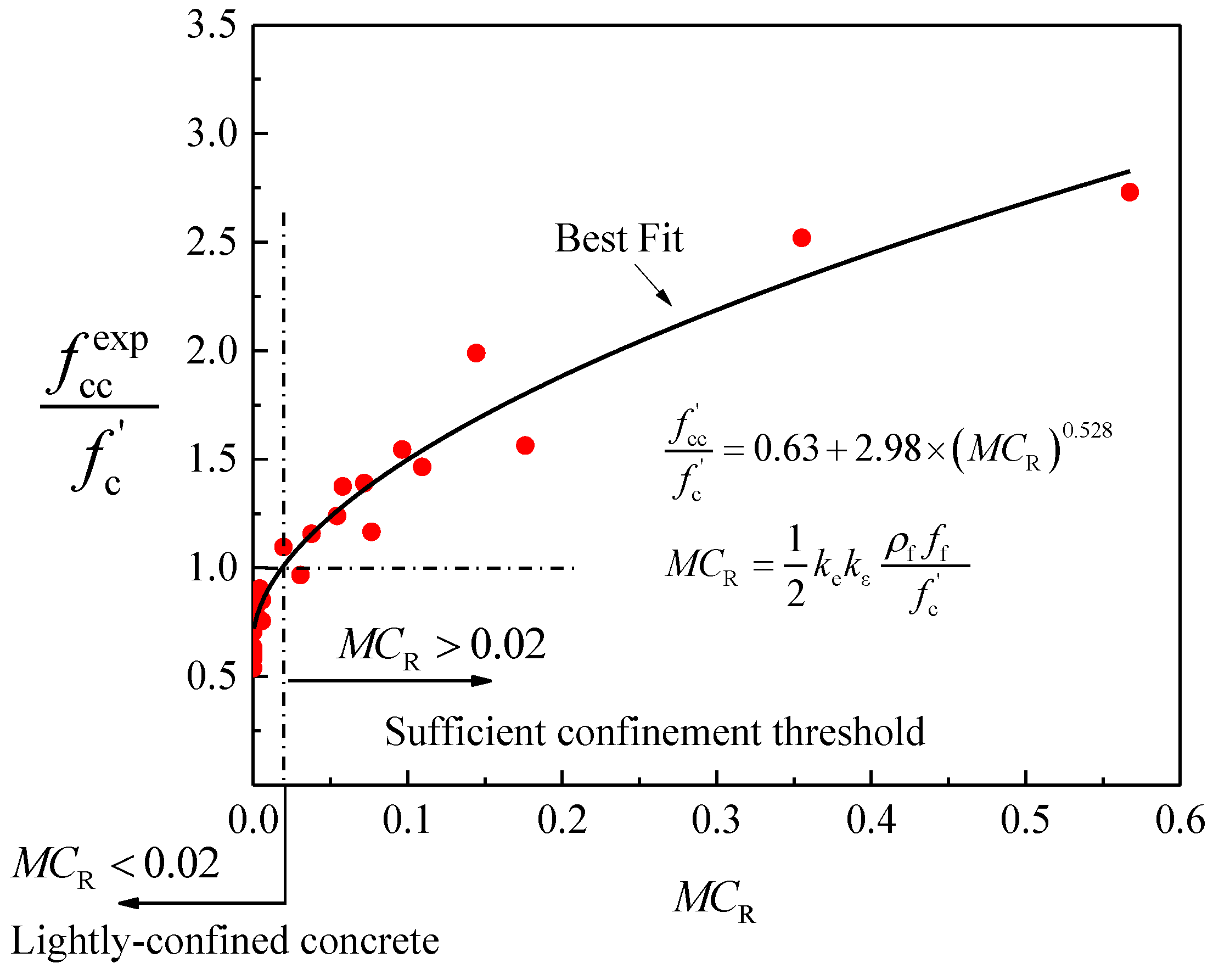
3. Effective Confinement Pressure Ratio
4. Amount of FRP for Sufficiently Confined Concrete
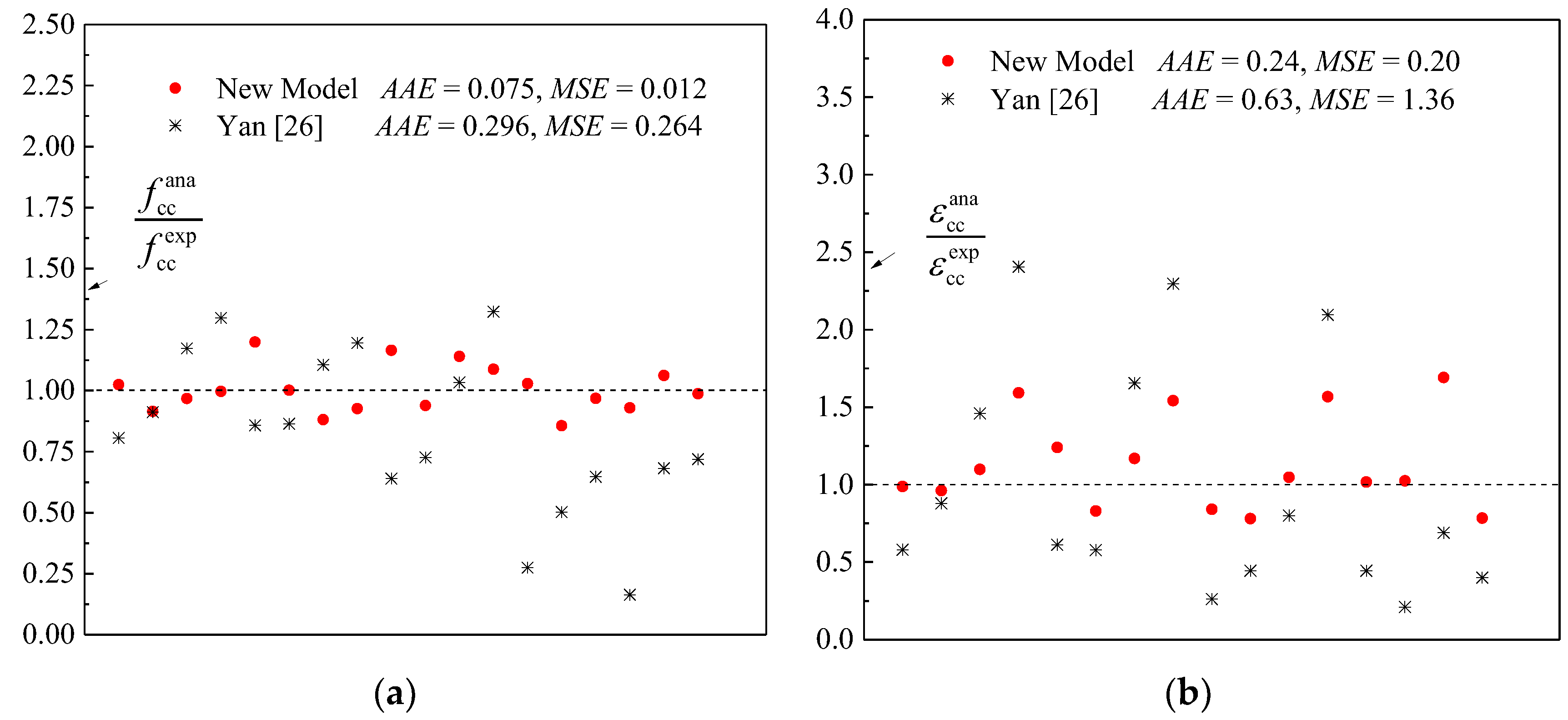
5. Accuracy of the Proposed and Existing Strength and Strain Models
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Notation
| a&b | width and depth of an elliptical cross section |
| a/b | aspect ratio of an elliptical cross-section |
| twrap | thickness of FRP composite layers |
| Ef | tensile elastic modulus of FRP composite |
| ff | tensile strength of FRP composite |
| εfu | FRP ultimate strain at rupture stage |
| fc′ | strength of unconfined concrete |
| ρf | volumetric ratio of FRP |
| εco | axial strain of unconfined concrete |
| εfe | effective hoop strain of FRP |
| kε | efficiency factor for determining the actual FRP hoop strain |
| ke | coefficient of confinement effectiveness |
| CR or MCR | FRP confinement pressure ratio |
| fcc′ | FRP-confined peak strength |
| εcc | axial strain of confined concrete |
| AAE | average absolute error |
| MSE | mean square error |
| N | total number of tested specimens |
| ana | analytical value given by the model |
| exp | experimental value obtained from tests |
References
- Moran, D.A.; Pantelides, C.P. Stress-strain model for fiber-reinforced polymer-confined concrete. J. Compos. Construct. 2002, 6, 233–240. [Google Scholar] [CrossRef]
- Ilki, A.; Kumbasar, N. Behavior of damaged and undamaged concrete strengthened by carbon fiber composite sheets. Struct. Eng. Mech. 2002, 13, 75–90. [Google Scholar] [CrossRef]
- Albanesi, T.; Nuti, C.; vanzi, I. Closed form constitutive relationship for concrete filled FRP tubes under compression. Const. Build. Mater. 2007, 21, 409–427. [Google Scholar] [CrossRef]
- Vintzileou, E.; Panagiotidou, E. An empirical model for predicting the mechanical properties of FRP-confined concrete. Const. Build. Mater. 2008, 22, 841–854. [Google Scholar] [CrossRef]
- Lignola, G.P.; Prota, A.; Manfredi, G.; Cosenza, E. Unified theory for confinement of RC solid and hollow circular columns. Compos. Part B-Eng. 2008, 39, 1151–1160. [Google Scholar] [CrossRef]
- Micelli, F.; Modarelli, R. Experimental and analytical study on properties affecting the behaviour of FRP-confined concrete. Compos. Part B-Eng. 2013, 45, 1420–1431. [Google Scholar] [CrossRef]
- Lim, J.C.; Ozbakkaloglu, T. Unified stress-strain model for FRP and actively confined normal-strength and high-strength concrete. J. Compos. Construct. 2015, 19, 1–14. [Google Scholar] [CrossRef]
- Cascardi, A.; Micelli, F.; Aiello, M.A. Unified model for hollow columns externally confined by FRP. Eng. Struct. 2016, 111, 119–130. [Google Scholar] [CrossRef]
- Cascardi, A.; Micelli, F.; Aiello, M.A. An artificial networks model for the prediction of compressive strength of FRP-confined concrete circular columns. Eng. Struct. 2017, 140, 199–208. [Google Scholar] [CrossRef]
- Sadeghian, P.; Fillmore, B. Strain distribution of basalt FRP-wrapped concrete cylinders. Case Stud. Construct. Mater. 2018, 9, e00171. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Design-oriented stress-strain model for FRP-confined concrete in rectangular columns. J. Reinf. Plast. Compos. 2003, 22, 1149–1186. [Google Scholar] [CrossRef]
- Anselm, E. Stress-Strain Behavior of Rectangular Columns Confined with FRP Sheets. Master’s Thesis, University of Alabama, Huntsville, AL, USA, 2005. [Google Scholar]
- Pham, T.M.; Hadi, M.N.S. Stress prediction model for FRP confined rectangular concrete columns with rounded corners. J. Compos. Construct. 2014, 18. [Google Scholar] [CrossRef]
- Triantafyllou, G.G.; Roisakis, T.C.; Karabinis, A.I. Axially loaded reinforced concrete columns with a square section partially confined by light GFRP straps. J. Compos. Construct. 2014, 19. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Choutopoulou, E.; Fotaki, E.; Skorda, M.; Stathopoulou, M.; Karlos, K. FRP confinement of wall-like reinforced concrete columns. Mater. Struct. 2016, 49, 651–664. [Google Scholar] [CrossRef]
- Isleem, H.F.; Wang, D.Y.; Wang, Z.Y. A new numerical model for polymer-confined rectangular concrete columns. Proc. Inst. Civ. Eng. ICE Struct. Build. 2018. [Google Scholar] [CrossRef]
- Isleem, H.F.; Wang, D.Y.; Wang, Z.Y. Modeling the axial compressive stress-strain behavior of CFRP-confined rectangular RC columns under monotonic and cyclic loading. Compos. Struct. 2018, 185, 229–240. [Google Scholar] [CrossRef]
- Isleem, H.F.; Wang, Z.Y.; Wang, D.Y.; Smith, S.T. Monotonic and cyclic axial compressive behavior of CFRP-confined rectangular RC columns. J. Compos. Construct. 2018, 22, 292–300. [Google Scholar] [CrossRef]
- Isleem, H.F.; Wang, D.Y.; Wang, Z.Y. Axial stress-strain model for square concrete columns internally confined with GFRP hoops. Mag. Concr. Res. 2018, 70, 1064–1079. [Google Scholar] [CrossRef]
- Isleem, H.F.; Wang, Z.Y. A new strength prediction model for rectangular RC columns strengthened with CFRP wraps and anchors. Proc. Inst. Civ. Eng. Struct. Build. 2018. under review. [Google Scholar]
- Isleem, H.F.; Tahir, M.; Wang, Z.Y.; Wang, D.Y. Axial stress-strain model developed for large-sized rectangular RC columns confined with CFRP wraps and anchors. J. Bridge. Eng. 2018. under review. [Google Scholar]
- Isleem, H.F.A. Cyclic Axial Behavior of Rectangular RC Columns Strengthened with CFRP Composites. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2015. [Google Scholar]
- Wu, Y.F.; Zhou, Y.W. Unified strength model based on Hoek-Brown failure criterion for circular and square concrete columns confined by FRP. J. Compos. Construct. 2010, 14, 175–184. [Google Scholar] [CrossRef]
- Al-Salloum, Y.A. Influence of edge sharpness on the strength of square concrete columns confined with FRP composite laminates. Compos. Part B-Eng. 2007, 38, 640–650. [Google Scholar] [CrossRef]
- Tsai, K.C.; Lin, M.L. Seismic jacketing of RC columns for enhanced axial load carrying performance. J. Chin. Inst. Eng. 2002, 25, 389–402. [Google Scholar] [CrossRef]
- Yan, Z.H. Shape Modification of Rectangular Columns Confined with FRP Composites. Ph.D. Thesis, University of Utah, Salt Lake County, UT, USA, 2005. [Google Scholar]
- Pantelides, C.P.; Yan, Z. Confinement model of concrete with externally bonded FRP jackets or posttensioned FRP shells. J. Struct. Eng. 2007, 133, 1288–1296. [Google Scholar] [CrossRef]
- Yan, Z.; Pantelides, C.P. Concrete column shape modification with FRP shells and expansive cement concrete. Const. Build. Mater. 2011, 25, 396–405. [Google Scholar] [CrossRef]
- Xu, L. Shape Modification of Square Reinforced Concrete Columns Confined with Fiber-Reinforced Polymer and Steel Straps. Master’s Thesis, University of Wollongong, Wollongong, Australia, 2012. [Google Scholar]
- Zeng, J.J.; Guo, Y.C.; Gao, W.Y.; Li, J.Z.; Xie, J.H. Behavior of partially and fully FRP-confined circularized square columns under axial compression. Const. Build. Mater. 2017, 152, 319–332. [Google Scholar] [CrossRef]
- Jameel, M.T.; Sheikh, M.N.; Hadi, M.N.S. Behaviour of circularized and FRP wrapped hollow concrete specimens under axial compressive load. Compos. Struct. 2017, 171, 538–548. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Seible, F.; Xiao, Y.; Verma, R. Steel jacket retrofitting of reinforced concrete bridge columns for enhanced shear strength-Part 1: Theoretical considerations and test design. ACI Struct. J. 1994, 91, 394–405. [Google Scholar]
- Priestley, M.J.N.; Seible, F. Design of seismic retrofit measures for concrete and masonry structures. Const. Build. Mater. 1995, 9, 365–377. [Google Scholar] [CrossRef]
- Alsayed, S.H.; Almusallam, T.H.; Ibrahim, S.M.; Al-Hazmi, N.M.; Al-Salloum, Y.A.; Abbas, H. Experimental and numerical investigation for compression response of CFRP strengthened shape modified wall-like RC columns. Const. Build. Mater. 2014, 63, 72–80. [Google Scholar] [CrossRef]
- Teng, J.G.; Lam, L. Compressive behavior of carbon fiber reinforced polymer-confined concrete in elliptical columns. J. Struct. Eng. 2002, 128, 1535–1543. [Google Scholar] [CrossRef]
- Parvin, A.; Schroeder, J.M. Investigation of eccentrically loaded CFRP-confined elliptical concrete columns. J. Compos. Construct. 2008, 12, 93–101. [Google Scholar] [CrossRef]
- Rochette, P.; Labossiére, P. Axial testing of rectangular column models confined with composites. J. Compos. Construct. 2000, 4, 129–136. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, D.Y.; Smith, S.T.; Lu, D.G. CFRP-confined square RC columns. I: Experimental investigation. J. Compos. Construct. 2012, 16, 150–160. [Google Scholar] [CrossRef]
- Wu, G.; Wu, Z.S.; Lu, Z.T. Design-oriented stress-strain model for concrete prisms confined with FRP composites. Const. Build. Mater. 2007, 21, 1107–1121. [Google Scholar] [CrossRef]
- Teng, J.G.; Jiang, T.; Lam, L.; Luo, Y.Z. Refinement of a design-oriented stress-strain model for FRP-confined concrete. J. Compos. Construct. 2009, 13, 269–278. [Google Scholar] [CrossRef]
- Shao, Y.; Zhu, Z.; Mirmiran, A. Cyclic modeling of FRP-confined concrete with improved ductility. Cem. Concr. Compos. 2006, 28, 959–968. [Google Scholar] [CrossRef]
- Karantzikis, M.; Papanicolaou, C.G.; Antonopoulos, C.P.; Triantafillou, T.C. Experimental Investigation of Nonconventional Confinement for Concrete Using FRP. J. Compos. Construct. 2005, 9, 480–487. [Google Scholar] [CrossRef]
- Campione, G.; Fossetti, M. Compressive behaviour of concrete elliptical columns confined by single hoops. Eng. Struct. 2007, 29, 408–417. [Google Scholar] [CrossRef]
- Bournas, D.A.; Triantafillou, T.C. Bar Buckling in RC Columns Confined with Composite Materials. J. Compos. Construct. 2011, 15, 393–403. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Karabinis, A.I. Adequately FRP confined reinforced concrete columns under axial compressive monotonic or cyclic loading. Mater. Struct. 2012, 45, 957–975. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Tourtoutas, I.S. Modeling of passive and active external confinement of RC columns with elastic material. J. Appl. Math. Mech. 2015. [Google Scholar] [CrossRef]
- Bai, Y.L.; Dai, J.G.; Teng, J.G. Buckling of steel reinforcing bars in FRP-confined RC columns: An experimental study. Const. Build. Mater. 2017, 140, 403–415. [Google Scholar] [CrossRef]
- Zeng, J.J.; Lin, G.; Teng, J.G.; Li, L.J. Behavior of large-scale FRP-confined rectangular RC columns under axial compression. Eng. Struct. 2018, 174, 629–645. [Google Scholar] [CrossRef]
- Rousakis, T.C. Inherent seismic resilience of RC columns externally confined with nonbonded composite ropes. Compos. Part B-Eng. 2018, 135, 142–148. [Google Scholar] [CrossRef]
- Wan, B.; Jiang, C.; Wu, Y.F. Effect of defects in externally bonded FRP reinforced concrete. Const. Build. Mater. 2018, 172, 63–76. [Google Scholar] [CrossRef]
- Ilki, A.; Peker, O.; Karamuk, E.; Demir, C.; Kumbasar, N. FRP retrofit of low and medium strength circular and rectangular reinforced concrete columns. J. Mater. Civ. Eng. 2008, 20, 169–188. [Google Scholar] [CrossRef]
- Hany, N.F.; Hantouche, E.G.; Harajli, M.H. Axial stress-strain model of CFRP-confined concrete under monotonic and cyclic loading. J. Compos. Construct. 2015, 16. [Google Scholar] [CrossRef]
- Hany, N.F.; Hantouche, E.G.; Harajli, M.H. Generalized axial stress-strain response of rectangular columns confined using CFRP jackets and anchors. J. Compos. Construct. 2017, 21. [Google Scholar] [CrossRef]
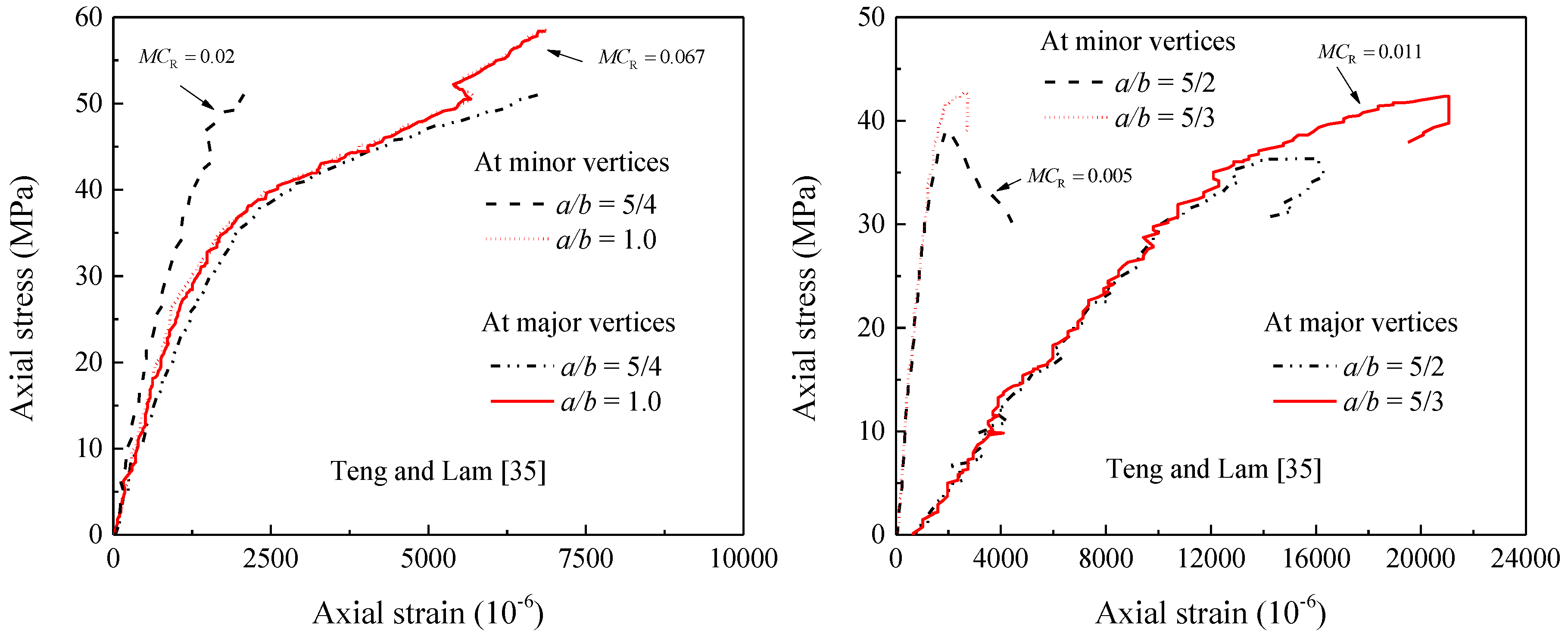
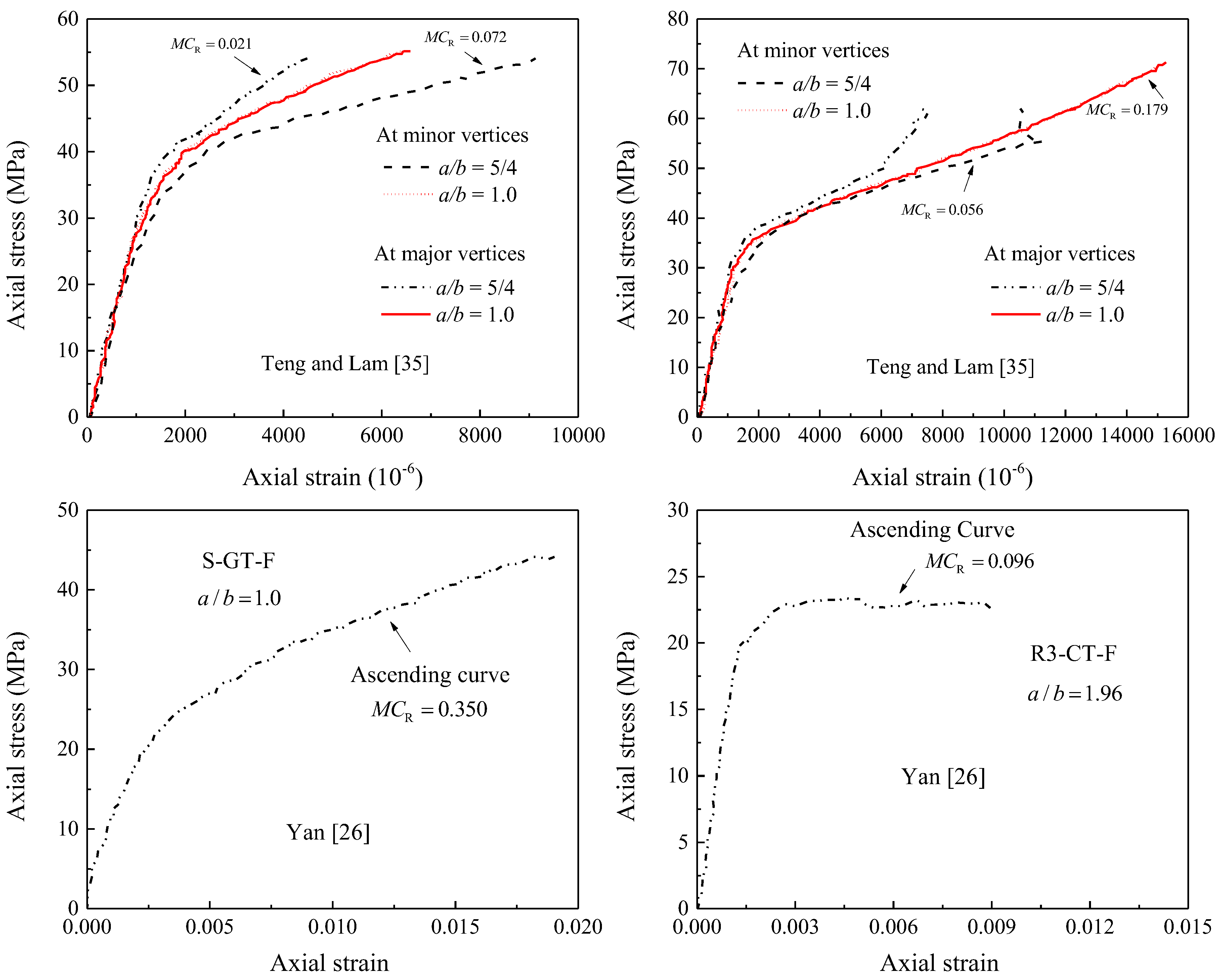
| No. | Specimen | Section Details | Material Properties | ||||||
|---|---|---|---|---|---|---|---|---|---|
| a (mm) | b (mm) | a/b | fc′ (MPa) | twrap (mm) | ff (MPa) | Ef (GPa) | εfu (%) | ||
| Teng and Lam [35] | |||||||||
| Series 1 | |||||||||
| 1 | S1.0L1 | 152.2 | 152.2 | 1.00 | 48.8 | 0.165 | 3983 | 263 | 1.514 |
| 2 | S5/4L1 | 168.2 | 131.6 | 1.28 | 48.8 | 0.165 | 3983 | 263 | 1.514 |
| 3 | S5/3L1 | 194.8 | 115.6 | 1.69 | 48.8 | 0.165 | 3983 | 263 | 1.514 |
| 4 | S5/2L1 | 237.6 | 94.8 | 2.51 | 48.8 | 0.165 | 3983 | 263 | 1.514 |
| Series 2 | |||||||||
| 5 | S1.0L1 | 151.6 | 151.6 | 1.00 | 47.1 | 0.110 | 3824 | 276 | 1.386 |
| 6 | S5/4L1 | 168.4 | 131.6 | 1.28 | 47.1 | 0.165 | 3983 | 263 | 1.514 |
| 7 | S5/3L1 | 194.9 | 114.8 | 1.70 | 47.1 | 0.165 | 3983 | 263 | 1.514 |
| 8 | S5/2L1 | 236.5 | 95.0 | 2.49 | 47.1 | 0.165 | 3983 | 263 | 1.514 |
| Series 3 | |||||||||
| 9 | S1.0L0 | 151.9 | 151.9 | 1.00 | 43.5 | - | - | - | - |
| 10 | S5/4L0 | 168.5 | 131.6 | 1.28 | 43.5 | - | - | - | - |
| 11 | S5/3L0 | 194.8 | 115.9 | 1.68 | 43.5 | - | - | - | - |
| 12 | S5/2L0 | 237.8 | 94.6 | 2.51 | 43.5 | - | - | - | - |
| Series 4 | |||||||||
| 13 | S1.0L0 | 152.0 | 152.0 | 1.00 | 44.6 | - | - | - | - |
| 14 | S5/4L0 | 168.7 | 131.4 | 1.28 | 44.6 | - | - | - | - |
| 15 | S5/3L0 | 194.8 | 115.0 | 1.69 | 44.6 | - | - | - | - |
| 16 | S5/2L0 | 236.8 | 94.6 | 2.50 | 44.6 | - | - | - | - |
| Series 5 | |||||||||
| 17 | S1.0L2 | 152.3 | 152.3 | 1.00 | 45.8 | 0.220 | 3824 | 276 | 1.386 |
| 18 | S5/4L2 | 168.2 | 131.9 | 1.28 | 45.8 | 0.220 | 3824 | 276 | 1.386 |
| 19 | S5/3L2 | 194.8 | 115.0 | 1.69 | 45.8 | 0.220 | 3824 | 276 | 1.386 |
| 20 | S5/2L2 | 237.6 | 94.6 | 2.51 | 45.8 | 0.220 | 3824 | 276 | 1.386 |
| Yan [26] | |||||||||
| Series 1 | |||||||||
| 21 | S-CT-F | 406.4 | 406.4 | 1.00 | 15.1 | 1.930 | 1220.4 | 86.9 | 1.442 |
| 22 | R2-CT-F | 647.7 | 419.1 | 1.55 | 15.2 | 1.930 | 1220.4 | 86.9 | 1.405 |
| 23 | R3-CT-F | 746.1 | 381.0 | 1.96 | 15.2 | 1.930 | 1220.4 | 86.9 | 1.405 |
| Series 2 | |||||||||
| 24 | S-GT-F | 406.4 | 406.4 | 1.00 | 17.6 | 9.754 | 227.5 | 16.9 | 1.365 |
| 25 | R2-GT-F | 692.2 | 355.6 | 1.95 | 15.2 | 9.754 | 227.5 | 16.9 | 1.347 |
| 26 | R3-GT-F | 739.8 | 311.2 | 2.38 | 15.2 | 9.754 | 227.5 | 16.9 | 1.347 |
| Published Model | Specimen Type | Boundary Value |
|---|---|---|
| Pham and Hadi [13] | Circular, rectangular | CR2 ≥ 0.15 |
| Yan [26] | Circular, rectangular, and elliptical | CR1 ≥ 0.2 |
| Shao et al. [41] | Circular | CR3 ≥ 0.3 |
| Source/Specimen | S1.0L1 | S5/4L1 | S5/3L1 | S5/2L1 | S1.0L1 | S5/4L1 |
| fcc′/fc′ | 1.240 | 1.096 | 0.852 | 0.770 | 1.166 | 1.157 |
| Pham and Hadi [13] | 0.129 | 0.159 | 0.159 | 0.157 | 0.134 | 0.165 |
| Evaluation | satisfied | unsuitable | satisfied | satisfied | Satisfied | unsuitable |
| Yan [26] | 0.047 | 0.034 | 0.020 | 0.002 | 0.049 | 0.035 |
| Evaluation | unsuitable | unsuitable | satisfied | satisfied | unsuitable | unsuitable |
| Shao et al. [41] | 0.177 | 0.126 | 0.119 | 0.105 | 0.184 | 0.131 |
| Evaluation | unsuitable | unsuitable | satisfied | satisfied | unsuitable | unsuitable |
| Proposed MCR | 0.054 | 0.020 | 0.006 | 0.003 | 0.077 | 0.038 |
| Evaluation | satisfied | satisfied | satisfied | satisfied | Satisfied | satisfied |
| Source/Specimen | S5/3L1 | S5/2L1 | S1.0L2 | S5/4L2 | S5/3L2 | S5/2L2 |
| fcc′/fc′ | 0.904 | 0.837 | 1.563 | 1.376 | 0.967 | 0.755 |
| Pham and Hadi [13] | 0.165 | 0.163 | 0.171 | 0.211 | 0.211 | 0.209 |
| Evaluation | unsuitable | unsuitable | satisfied | satisfied | unsuitable | unsuitable |
| Yan [26] | 0.020 | 0.002 | 0.064 | 0.047 | 0.027 | 0.002 |
| Evaluation | satisfied | satisfied | unsuitable | unsuitable | satisfied | satisfied |
| Shao et al. [41] | 0.123 | 0.109 | 0.241 | 0.172 | 0.162 | 0.144 |
| Evaluation | satisfied | satisfied | unsuitable | unsuitable | satisfied | satisfied |
| Proposed MCR | 0.004 | 0.003 | 0.176 | 0.058 | 0.031 | 0.006 |
| Evaluation | satisfied | satisfied | satisfied | satisfied | satisfied | satisfied |
| Source/Specimen | S-CT-F | R2-CT-F | R3-CT-F | S-GT-F | R2-GT-F | R3-GT-F |
| fcc′/fc′ | 2.730 | 1.989 | 1.545 | 2.520 | 1.465 | 1.390 |
| Pham and Hadi [13] | 0.520 | 0.491 | 0.482 | 0.421 | 0.484 | 0.499 |
| Evaluation | satisfied | satisfied | satisfied | satisfied | satisfied | satisfied |
| Yan [26] | 0.210 | 0.080 | 0.041 | 0.168 | 0.042 | 0.014 |
| Evaluation | satisfied | unsuitable | unsuitable | unsuitable | unsuitable | unsuitable |
| Shao et al. [41] | 0.766 | 0.401 | 0.371 | 0.621 | 0.375 | 0.365 |
| Evaluation | unsuitable | unsuitable | unsuitable | unsuitable | satisfied | satisfied |
| Proposed MCR | 0.553 | 0.144 | 0.096 | 0.350 | 0.109 | 0.072 |
| Evaluation | satisfied | Satisfied | satisfied | satisfied | satisfied | satisfied |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isleem, H.F.; Wang, Z. Axial Compressive Stress-Strain Model Developed for FRP-Confined Concrete Columns with Elliptical Cross Sections. J. Compos. Sci. 2018, 2, 67. https://doi.org/10.3390/jcs2040067
Isleem HF, Wang Z. Axial Compressive Stress-Strain Model Developed for FRP-Confined Concrete Columns with Elliptical Cross Sections. Journal of Composites Science. 2018; 2(4):67. https://doi.org/10.3390/jcs2040067
Chicago/Turabian StyleIsleem, Haytham F., and Zhenyu Wang. 2018. "Axial Compressive Stress-Strain Model Developed for FRP-Confined Concrete Columns with Elliptical Cross Sections" Journal of Composites Science 2, no. 4: 67. https://doi.org/10.3390/jcs2040067
APA StyleIsleem, H. F., & Wang, Z. (2018). Axial Compressive Stress-Strain Model Developed for FRP-Confined Concrete Columns with Elliptical Cross Sections. Journal of Composites Science, 2(4), 67. https://doi.org/10.3390/jcs2040067





