2.1. Functionally Graded Materials
Functionally graded materials are characterized for their continuous properties variation, in one or more directions, according to the requirements that one needs to satisfy. Theoretically, this variation can be mathematically defined following a determined distribution law; however, when thinking about a real structure, it will be necessary to take into consideration the technological capabilities and limitations of the manufacturing process. This is also a reason for the existence of studies that have focused on the use of the discrete approximations of these material systems by considering a stacking of layers where within each of them, there exists a mean constant material composition.
In the present study, one considers a dual-phase exponential law distribution (Bouchafa et al. [
21], Bernardo et al. [
22]) that resembles a sandwich, where the outer layers are constituted by the individual phases, and the core results from the phases’ exponentially graded mixture. In
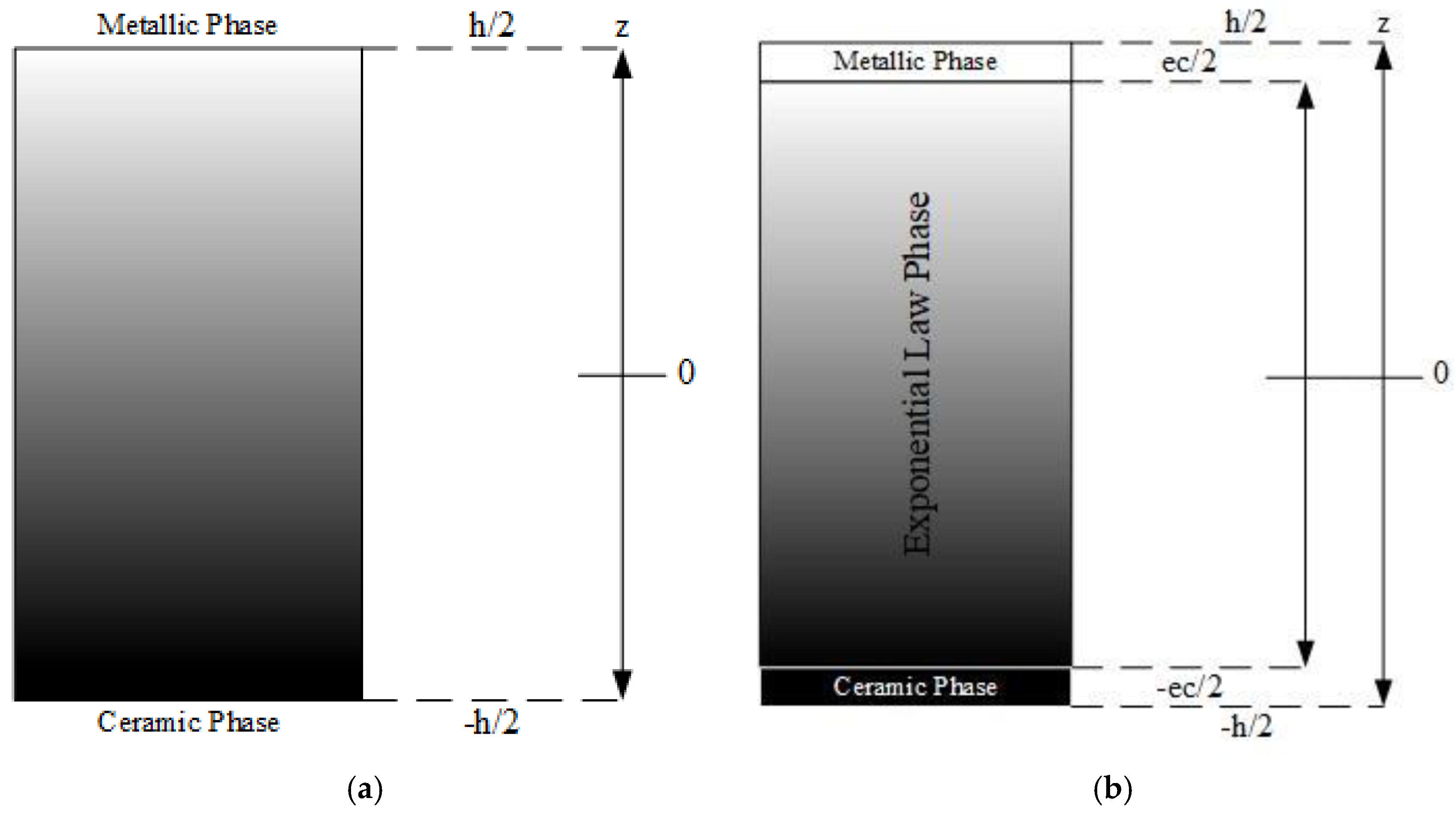
Figure 1, it is possible to observe the more commonly studied power exponent law distribution (
Figure 1a) and the one considered in this study, the exponential law (
Figure 1b), assuming that, as it is the case, one has a dual-phase metallic–ceramic FGM, with a through-thickness mixture variation.
In the power exponent law configuration, the volume fraction distribution of ceramic inclusions through the plate thickness
h is presented in Equation (1) (Loja et al. [
23]). Note that the thickness is associated with the
z coordinate of the Cartesian reference system, and the
xy plane is located at the plate mid-plane, which is being represented in
Figure 1 by the null
z coordinate.
where
Vc denotes the volume fraction of the ceramic phase, and
p denotes the exponent. Based on a selected distribution law, the material properties can be determined using Voigt’s rule of mixtures, among other possible homogenization schemes:
with
standing for any material property associated respectively to the graded composite, the ceramic phase, and the metallic phase, for instance the elasticity modulus
and the Poisson’s ratio
. The subscripts
m and
c denote the metallic and the ceramic phases of the FGM, respectively.
As previously mentioned, this work is focused on the exponential law configuration, whose constitution resembles a sandwich. According to
Figure 1, this FGM has its top and bottom layers made exclusively from its metallic and ceramic phases, i.e., there is no mixture of these two phases on the outer layers. On the contrary, on the middle layer, there is a dual-phase FGM following an exponential distribution; the mathematical representation is expressed as follows:
with
and
. The parameter (
ec) denotes the FGM middle layer thickness and
h denotes the total plate thickness, as can be observed in
Figure 1b. As mentioned,
represents a generic material property of the FGM, namely the elasticity modulus and the Poisson’s ratio.
2.4. Multiple Linear Regression Model
Aiming to obtain a set of non-deterministic models to relate multiple variables with an expected response result, this study considers a statistical classical approach, assuming that, for a generic problem, such variables will follow a linear relation, as:
where
denotes the number of independent input parameters,
is the zero intercept,
is the predictor slope for the
k-th variable,
is the
k-th input parameter variable,
is the real response of the model, and
is the Gaussian error term.
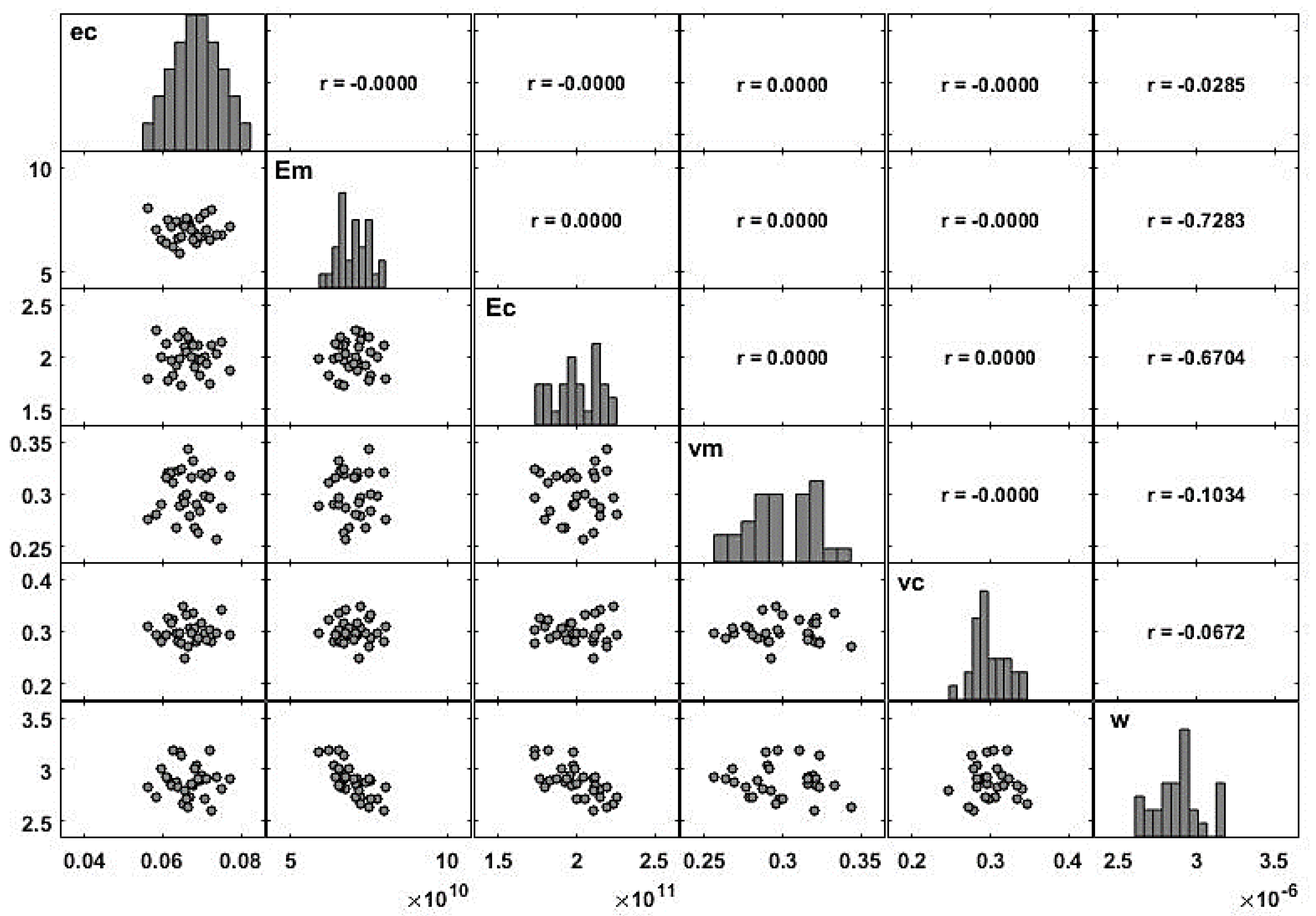
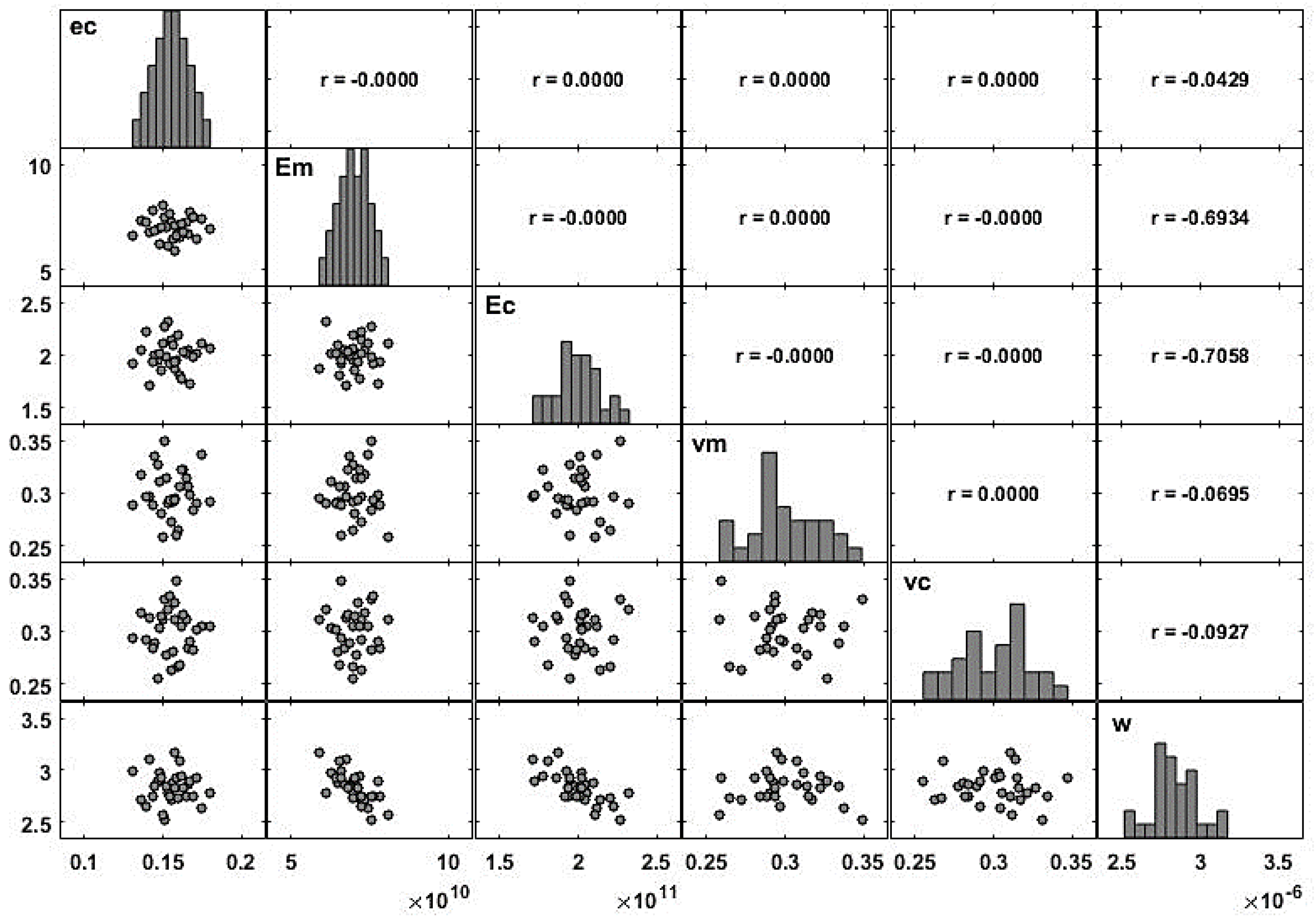
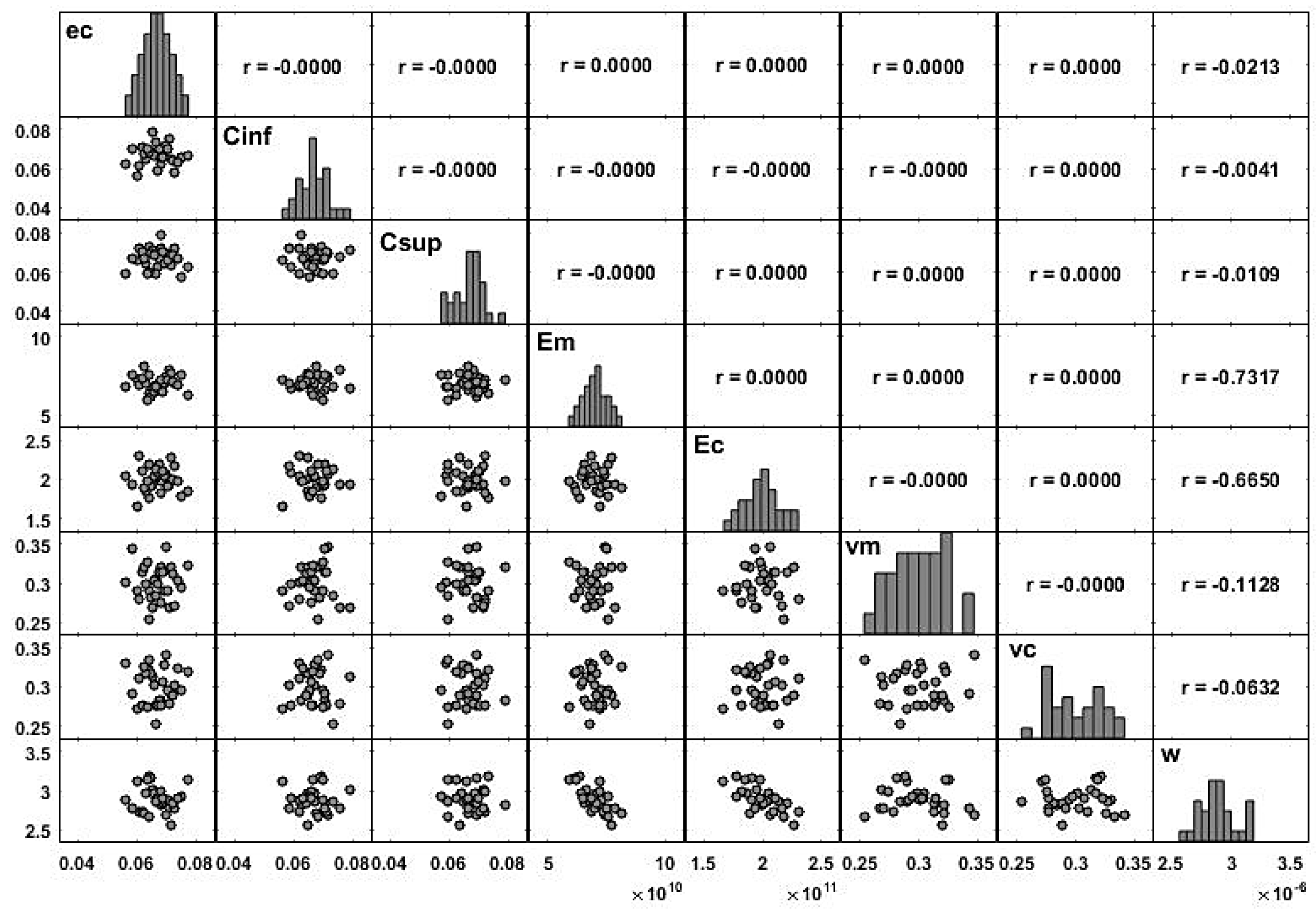
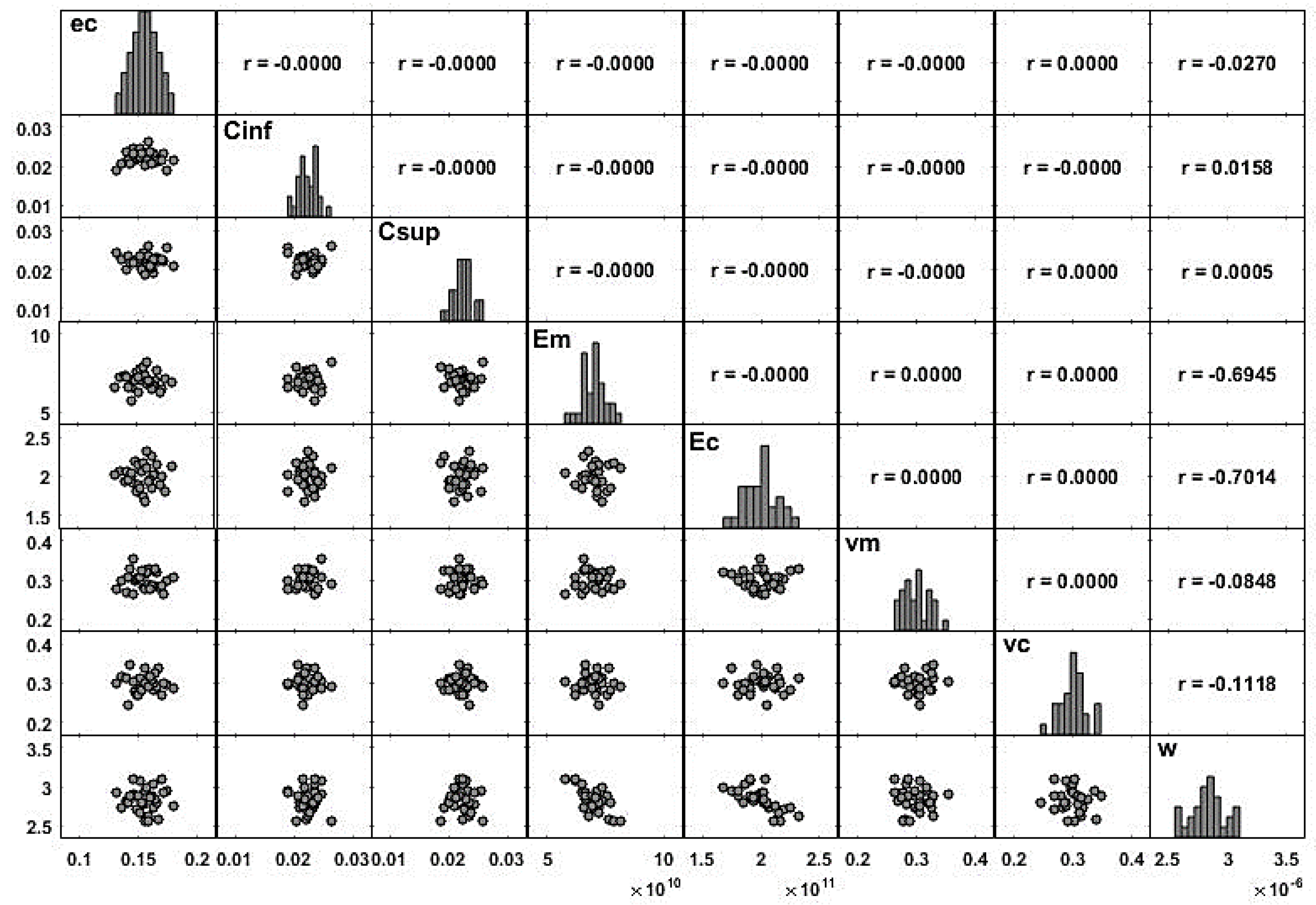
When there is more than one variable defined on a probability space, it is important to understand the relation between the random variables that are involved. A common measure of the linear relation between two random variables is the covariance (denoted in this sub-section by ) which is given as . The covariance measures the linear relation between two variables but depends on the magnitude of the variables. So, it is common to scale the covariance by the standard deviation of each variable (denoted in this sub-section by ), which leads to the correlation, . This measure can be used for comparison purposes, as it is easier to analyze. For any pair of variables , the correlation ranges between , and a null coefficient means that the variables are not linearly correlated. If this coefficient is close to 1 (or ), the two variables are linearly correlated in the positive (or negative) direction. In order to avoid multicollinearity problems, the model requires independence of the input variables, which is ensured by the use of the LHS technique. This independence can be easily verified through the correlation coefficients between the samples of the input variables.
Sometimes, it is necessary to include the interaction effects in the multiple linear regression (MLR) methods, which will be represented, if necessary, by a cross-product term in the model, such as .
The model may also be represented using matrix notation. In such case, for
k independent variables and
n observations, (
xi1,
xi2,
…,
xin),
i = 1, 2, …,
n, and the dependent variable, one has:
This model is a system with
n equations, which can be expressed as:
where:
The residuals describe the error in the fit of the model to the observations. The acceptance of the model requires the residuals to be independent, normally distributed, with null average, and with constant standard deviation, i.e., ∼N(0,σ2). If the assumptions of this model are verified, a response prediction can be estimated via the least squares method from the sampled values.
For a descriptive study, the correlation coefficient between two samples, and can be defined as . Using some data, it is possible to estimate a multiple linear regression model defined according to Equation (9), and the contribution of each regressor is estimated through the regression coefficients .
Also, in order to assess the quality of the model, the coefficient of multiple determination,
, or the adjusted
(Adj-
R2) can be used. These coefficients are global statistics and provide a measure of the percentage of variability of the dependent variable that is explained by the model (for details, see Montgomery [
31]).
For an inferential study, the sampled results can be generalized to the population. With the analysis of variance (ANOVA), one can test the significance of the model based on the
p-value of the
F-test (Montgomery [
31]). The idea is to divide the total variability of the response variable into meaningful components; i.e., the total sum of squares,
, is partitioned into a sum of squares due to regression,
, and a sum of squares due to error,
,
For a given significant level
α (usually 5%), if the null hypothesis is rejected, the model is significant (
p-value ≤
α). In those cases, at least one of the slopes is non-zero. Under these conditions, the
t-test gives the significance of each individual independent variable or model parameter (Montgomery [
31]).
For simplicity, usually the linear regression model (LRM) output displays significant codes for the different p-values: from the most significant p-value ≅ 0 (‘***’), 0.001 (‘**’), 0.01 (‘*’), 0.05 (‘.’), to the less significant 0.1 (‘·’). Frequently, the higher significant level is 10%; above this value, the null hypothesis is not rejected, and the model (F-test) or coefficient (t-test) is not significant. With these partial results, it is possible to build new models with the most significant regressors. Moreover, it is possible to construct confidence intervals for the partial slopes.
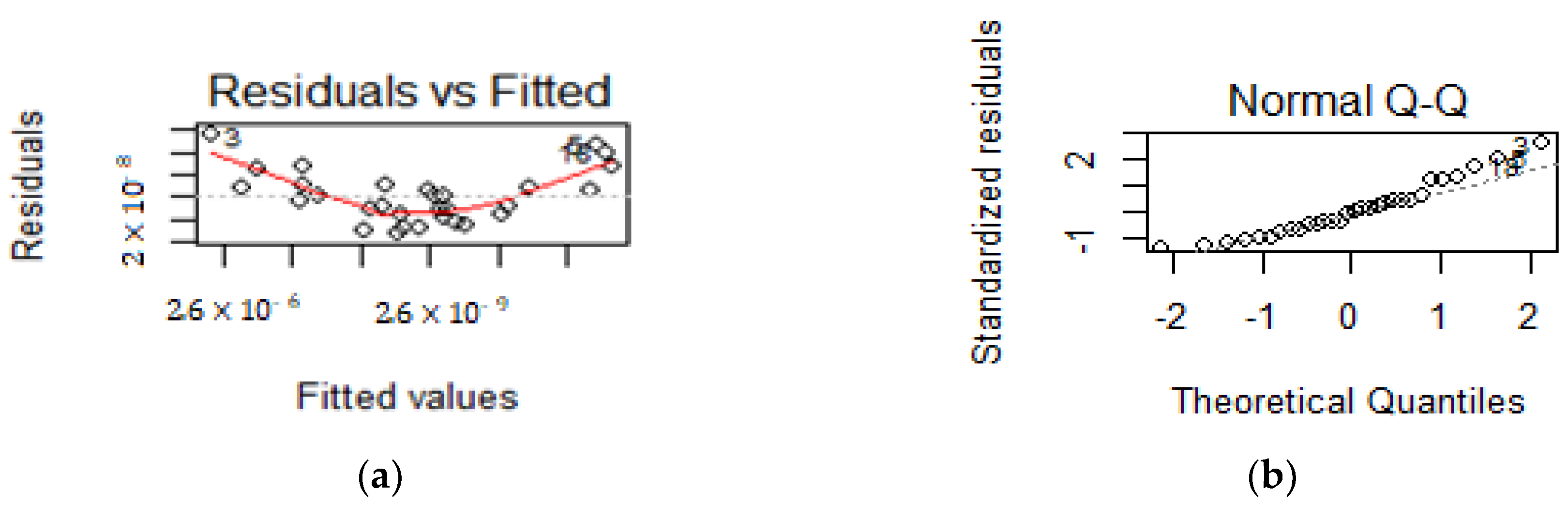
Once the model is chosen, one has to be sure of the validity of the model, namely on the residuals’ assumptions. To validate the null average of the residual, one can use the usual hypothesis testing for the mean (Montgomery [
31]). The normality assumption can be visually checked by a normal quantile–quantile plot (NQQP) or a normal probability plot (NPP), and confirmed with a goodness of fit test, such as the Kolmogorov–Smirnov test (Montgomery [
31]). To check the other two assumptions (independence and equal variance), one can inspect the plot of the residuals against the fitted values. If a pattern appears, it means that there is no independence of the residuals; so, the independence assumption isn’t validated. Also, if the same plot suggests non-constant variance along the fitted values, the variance homoscedasticity is not guaranteed (Montgomery [
31]). In such circumstances, another model should be considered.