Cruciform Specimen Design for Biaxial Tensile Testing of SMC
Abstract
:1. Introduction
1.1. Motivation
1.2. State-of-the-Art
1.3. Present Work
2. Materials and Experiment
2.1. Materials and Manufacturing Process
2.2. Biaxial Tensile Experiments
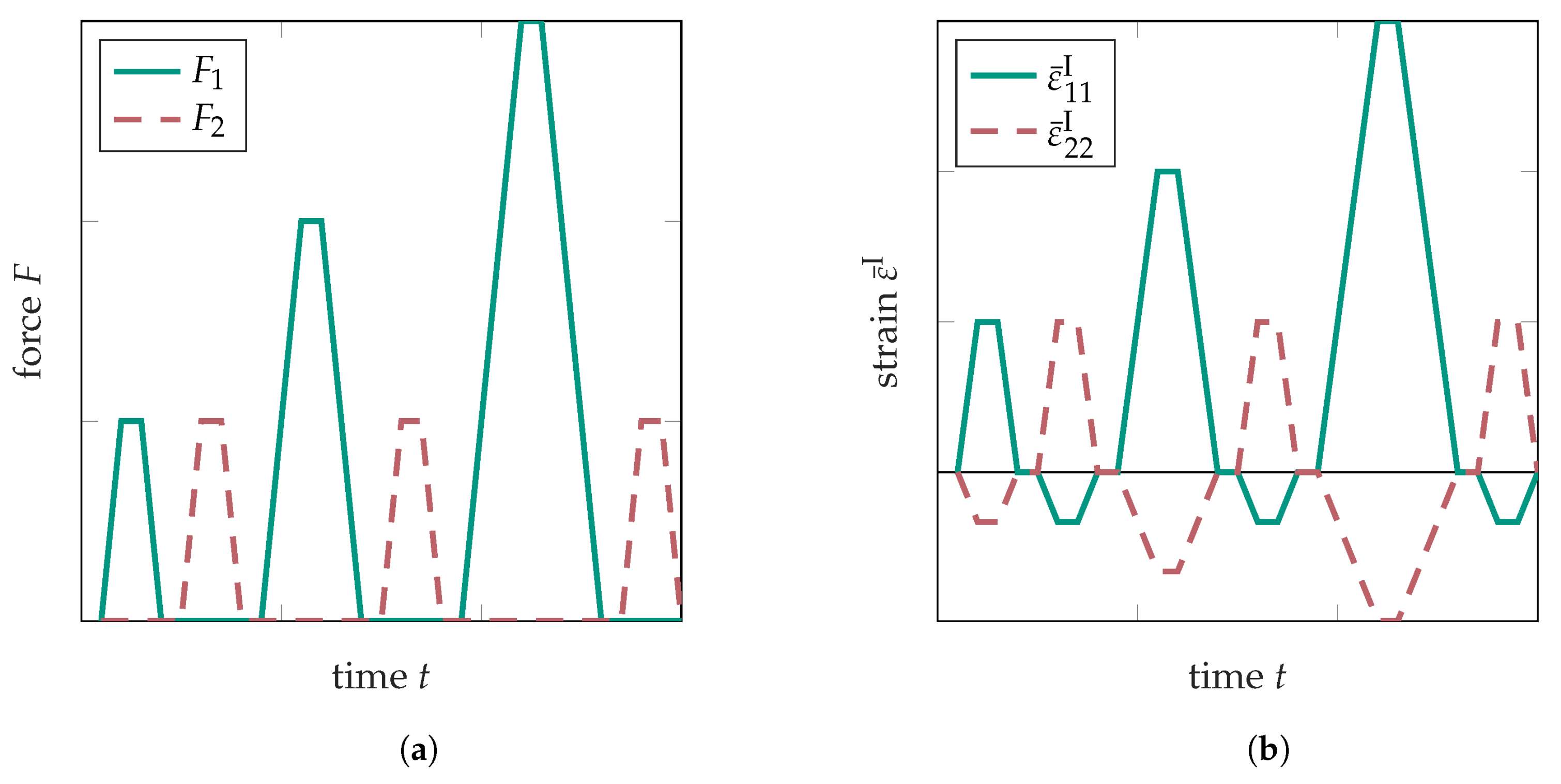
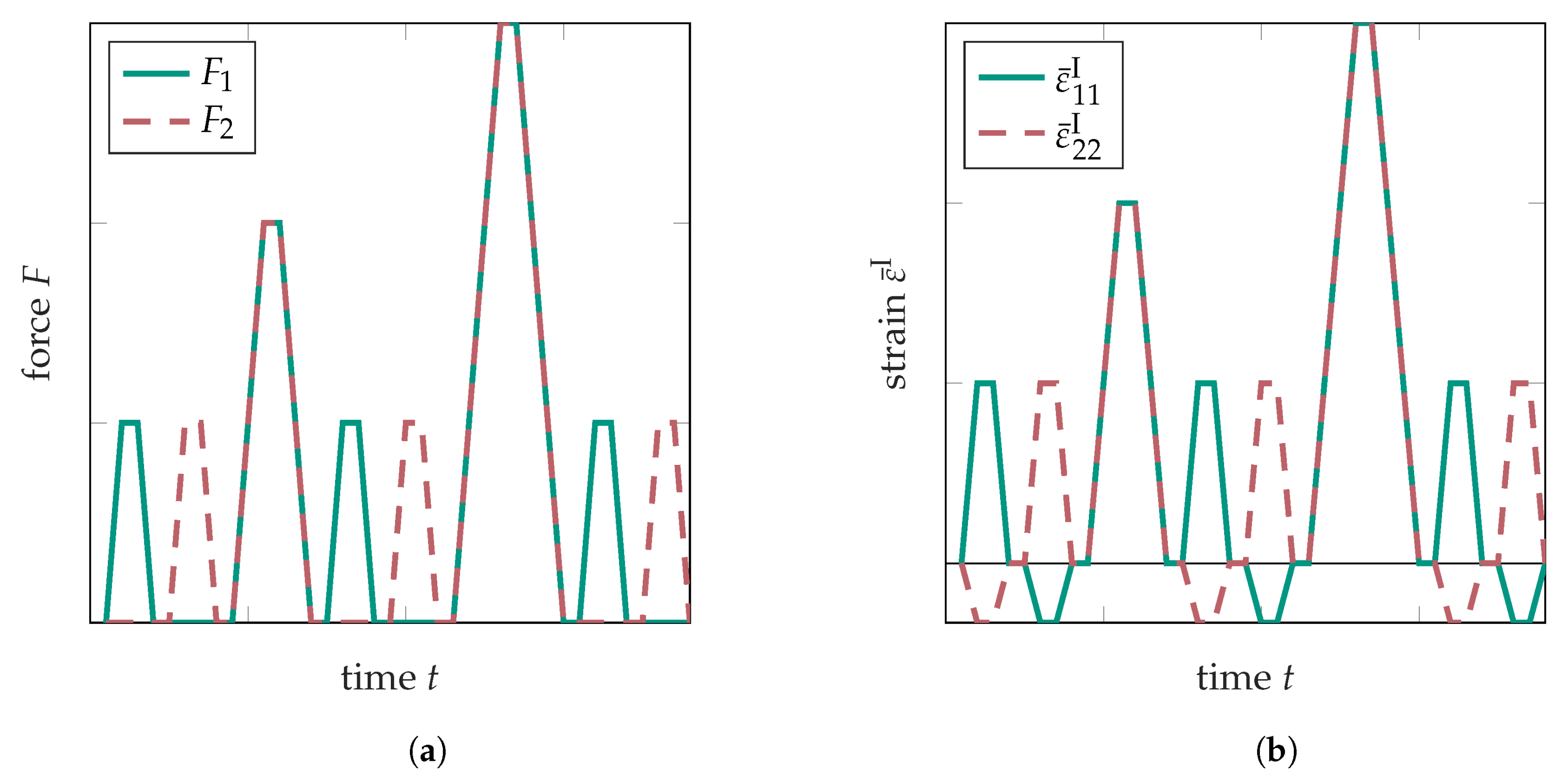
2.2.1. Fundamentals of Biaxial Tensile Testing
2.2.2. Experimental Procedures
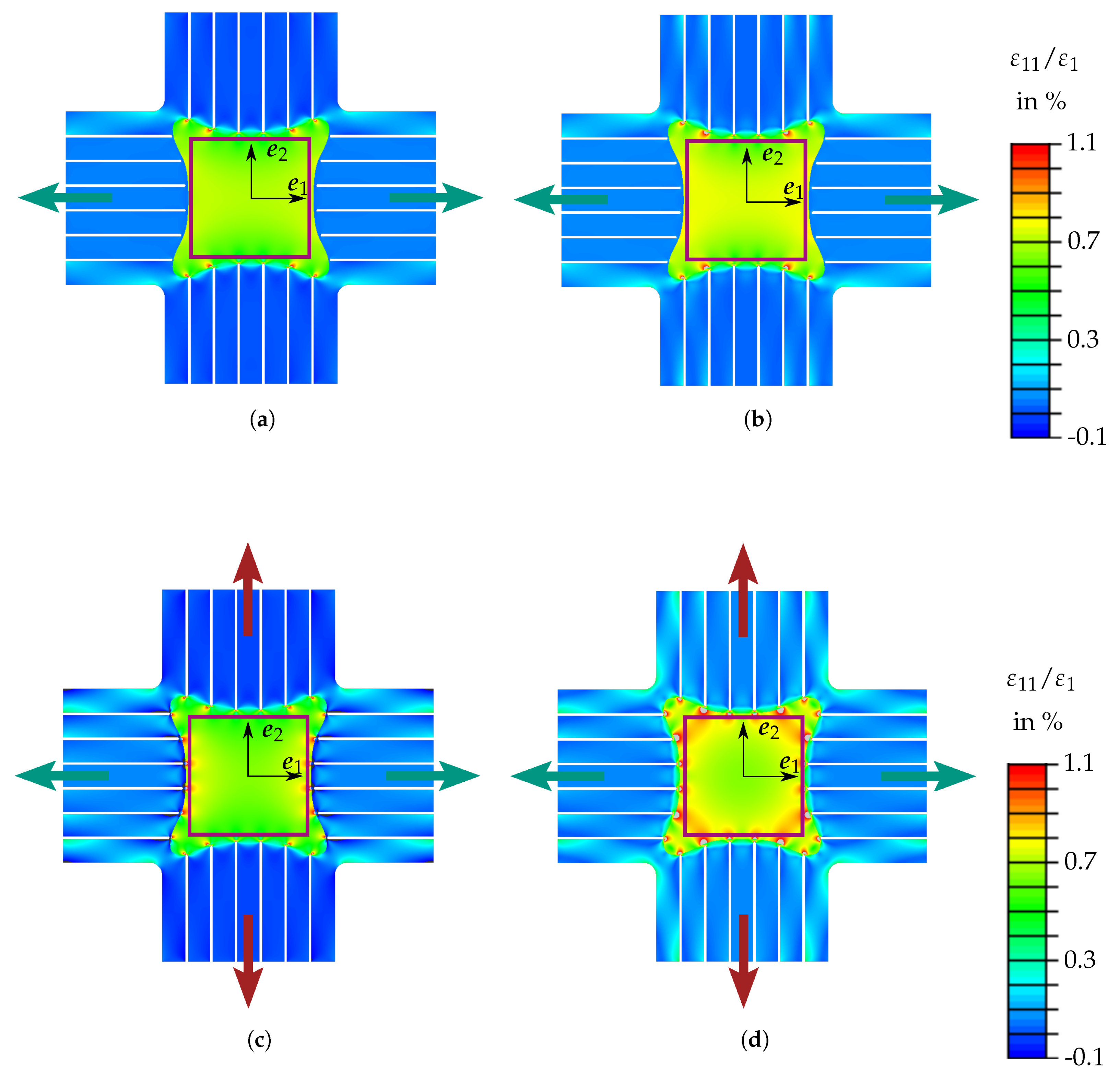
3. Specimen Designs and Experimental Results
3.1. Specimen Requirements
- (1)
- Wide range of achievable stress states. An optimal specimen geometry allows for all biaxial tension stress states, i.e., ratios between normal stresses. By coordinate transformation, all planar stress states (not in magnitude, but in relation to each other) are covered. The measurement of all stress states with the same geometry does not only ensure a good comparability in contrast to multiple specimen geometries, but also allows for a straightforward application of non-monotonic loading paths.
- (2)
- Damage dominantly in the area of interest. Since it is our goal to inspect damage in the area of interest, we would like to avoid premature specimen failure in the arms, and thus analyze the material behavior at highest possible strains in the area of interest.
- (3)
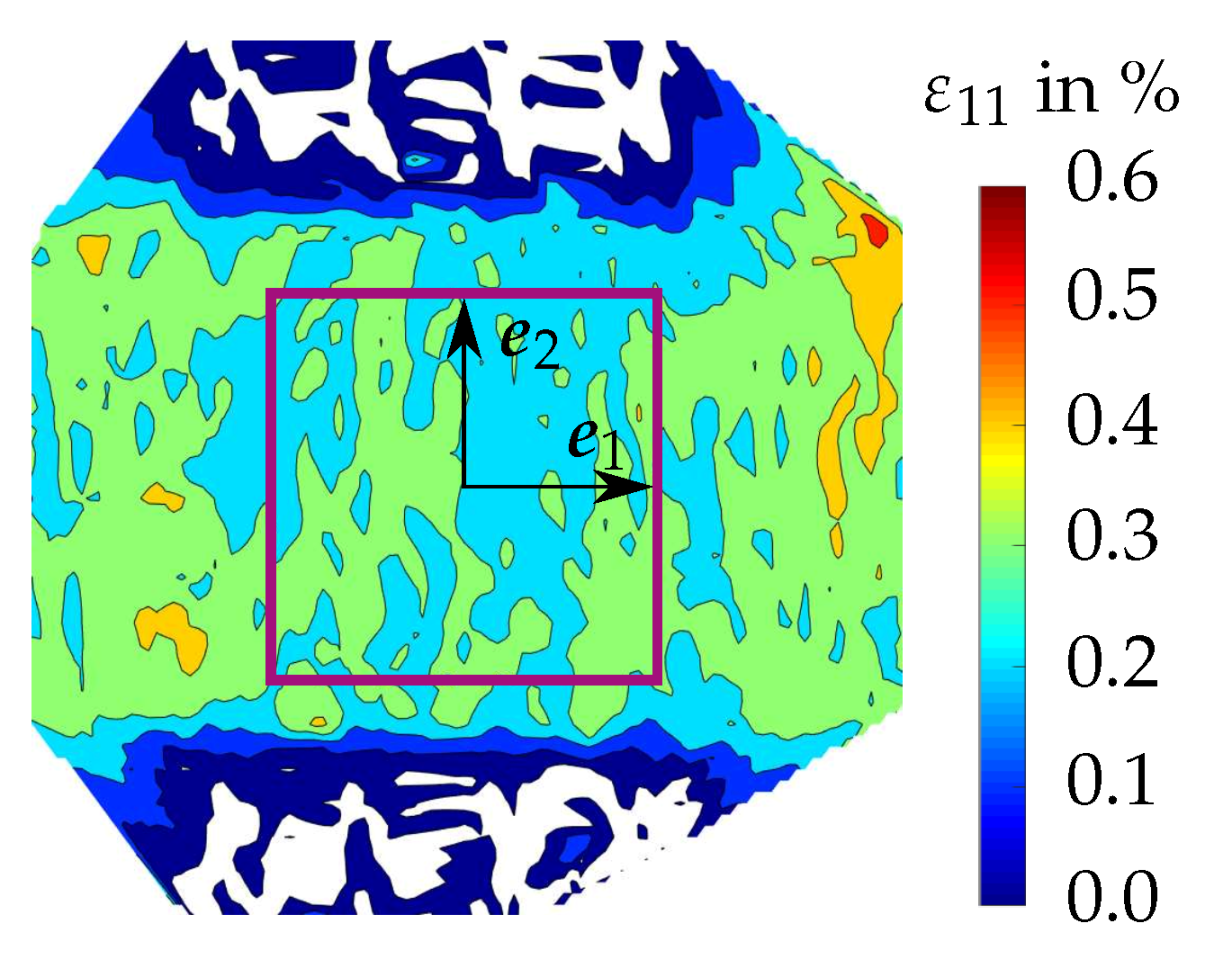
- Homogeneity of stress state in the area of interest. For the analysis of damage, it is desirable to reach a homogeneous stress state in the area of interest. This implies the demand to avoid stress concentrations.
- (4)
- Robust parameter identification. The parameter identification must be a well-posed problem and robust with respect to noise of measured quantities (forces and strain field) [26]. A robust parameter identification is essential for reproducibility. The robustness of the parameter identification is, however, not considered in this paper.
- (5)
- Large area of interest. The microstructural dimensions are in case of SMC, compared to other discontinuous fiber reinforced polymers, relatively large. The typical fiber roving length is , whereas one roving is assembled of thousands of filaments. As the specimen size is limited, it is our goal to achieve a considerably large area of interest.
- (6)
- Low production effort. In contrast to uniaxial tensile specimens, the load ratio is an additional parameter to be considered in the design of experiments. SMC is known to show significant scatter in experimental results. Additionally, the anisotropy and inhomogeneity must be considered in the design of experiments. The resulting high number of required experiments can better be coped with, if the economical effort for the specimen production is low.
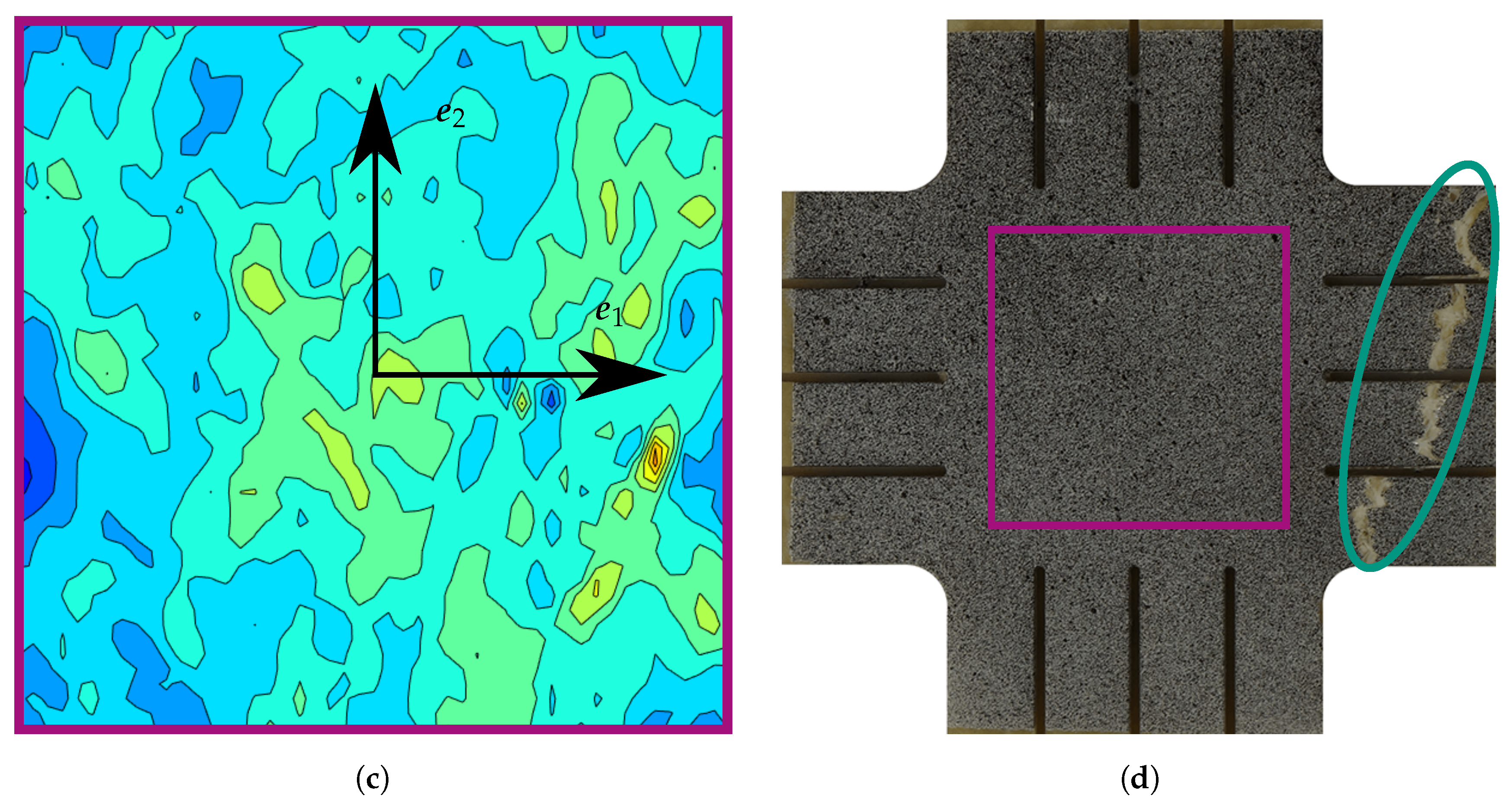
3.2. Unreinforced Specimen Arms
3.2.1. Specimen Design
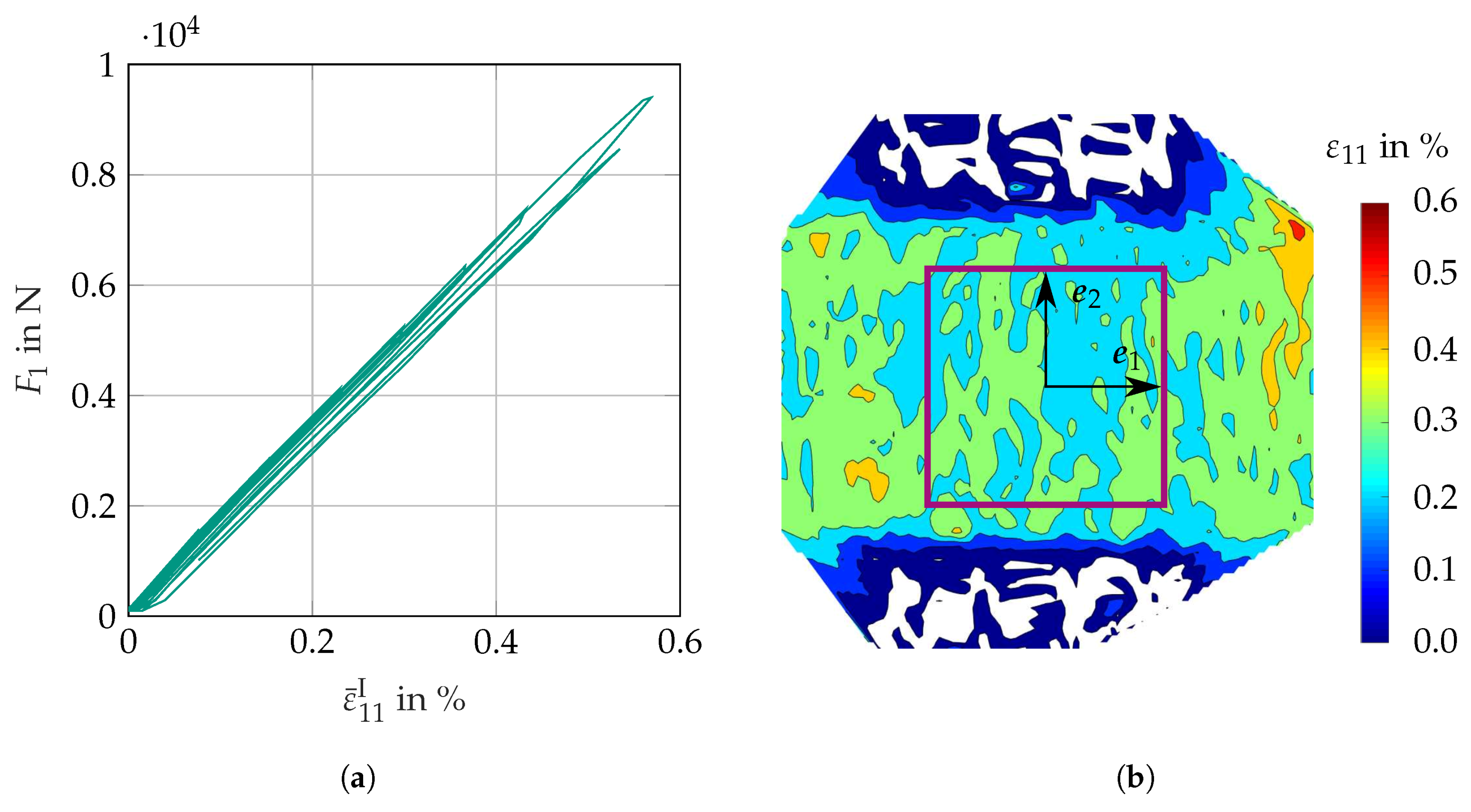
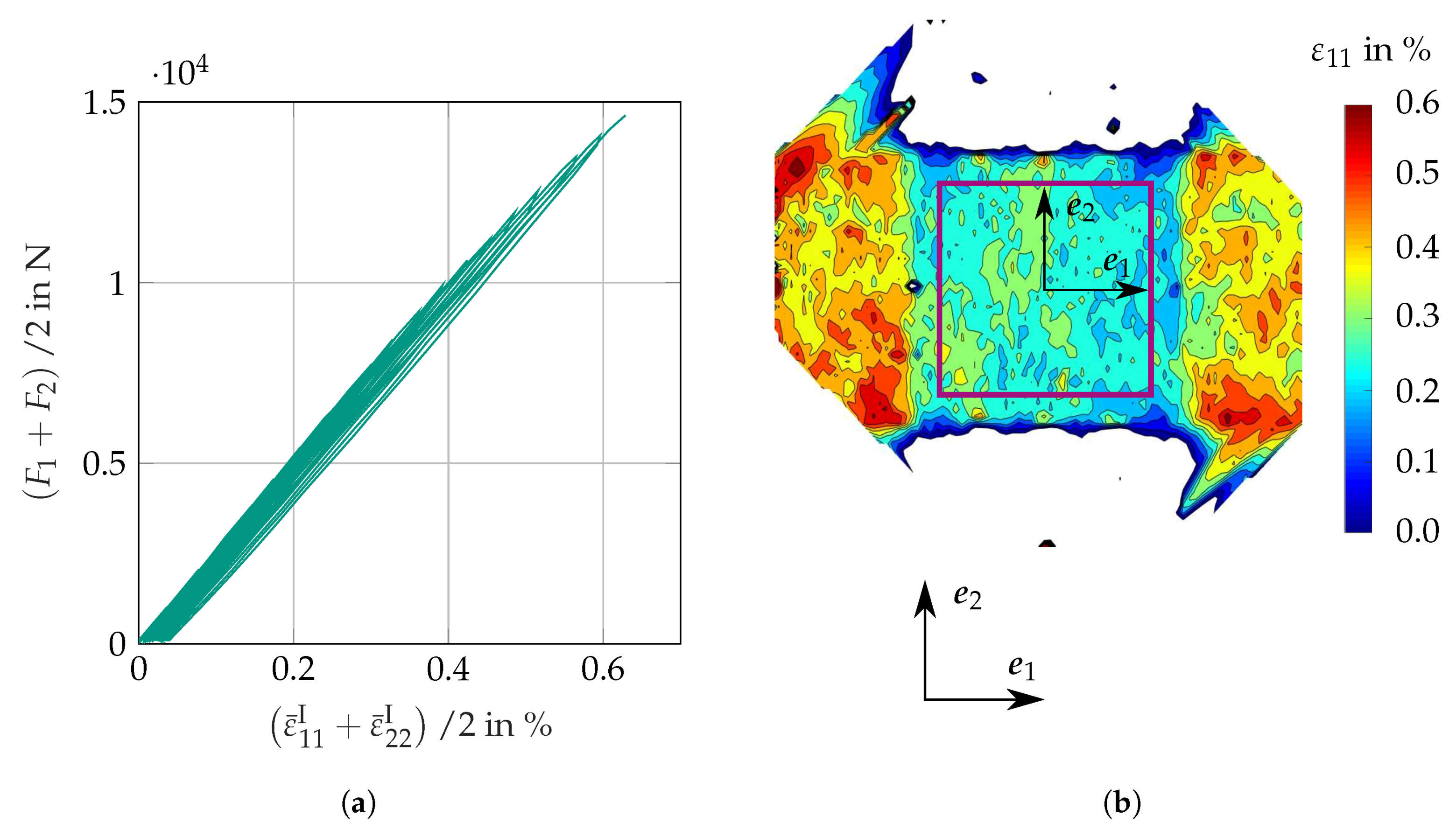
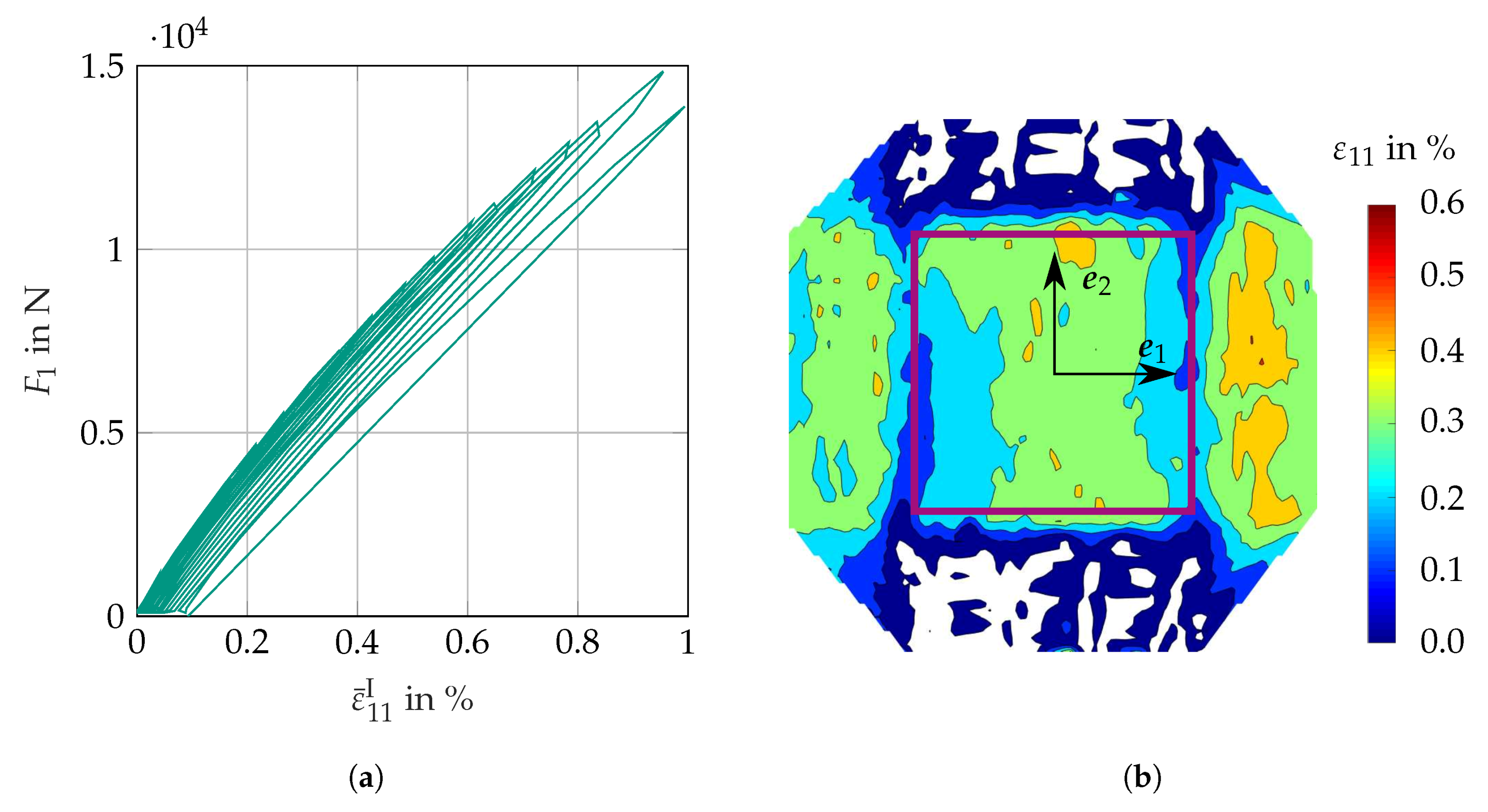
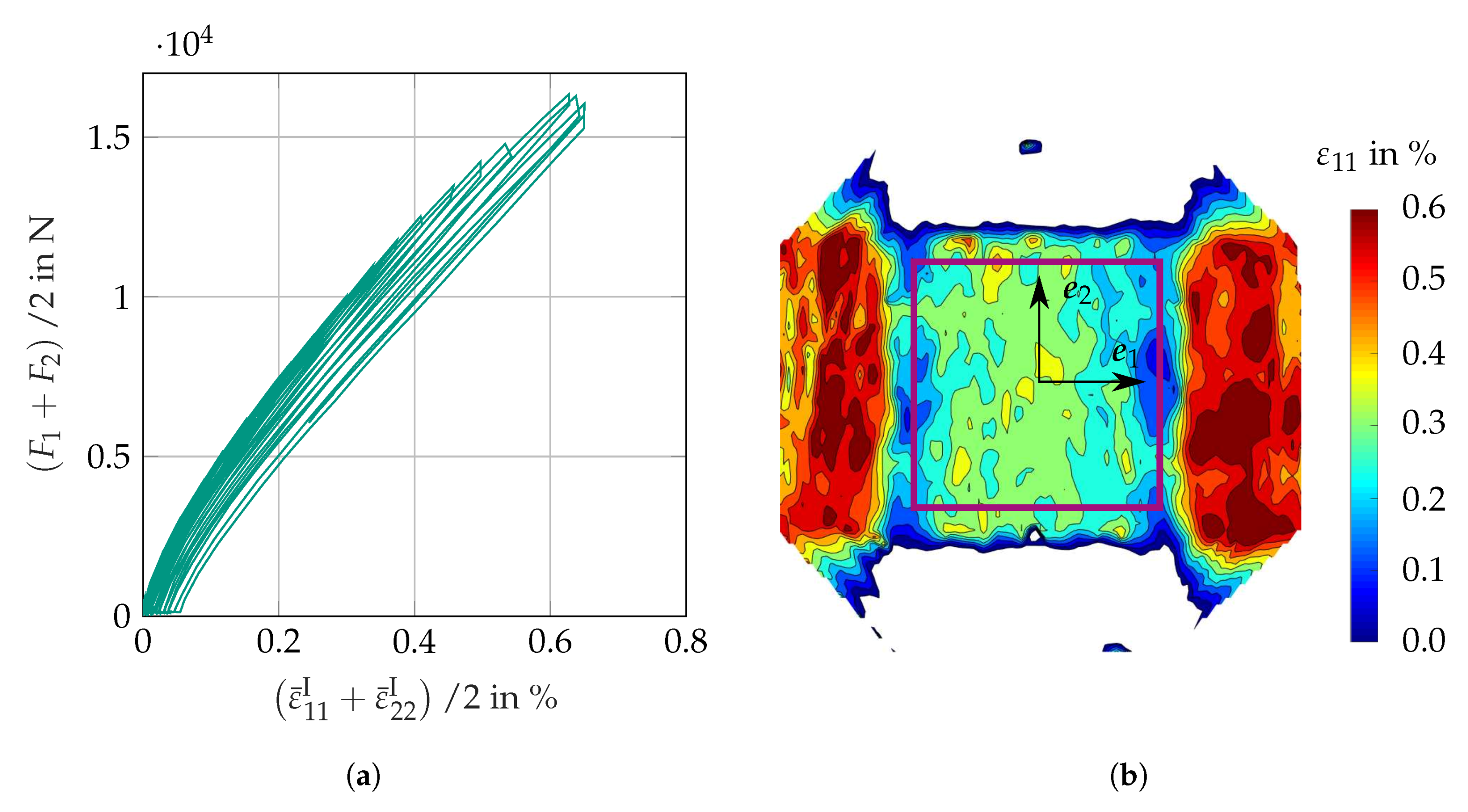
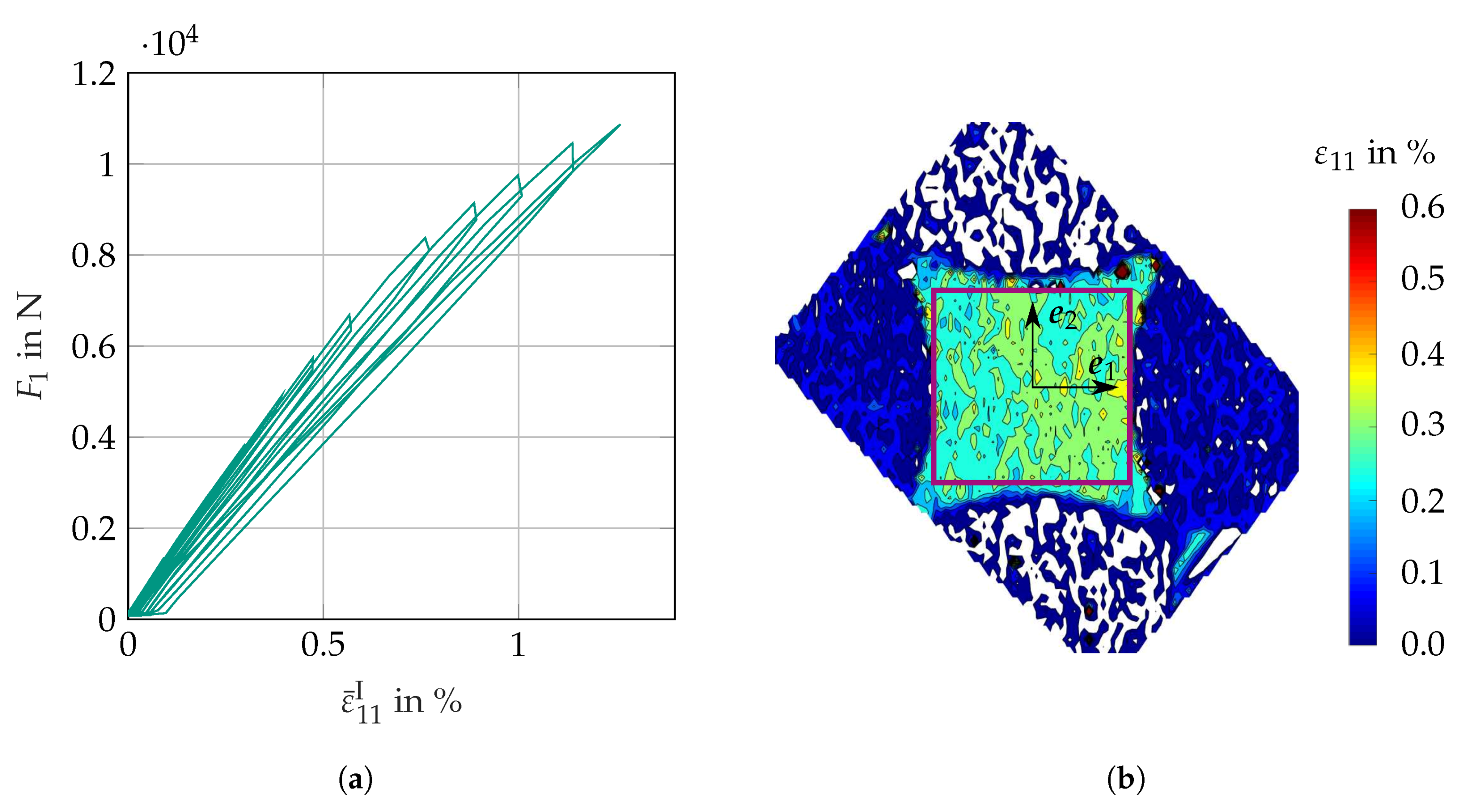
3.2.2. Results
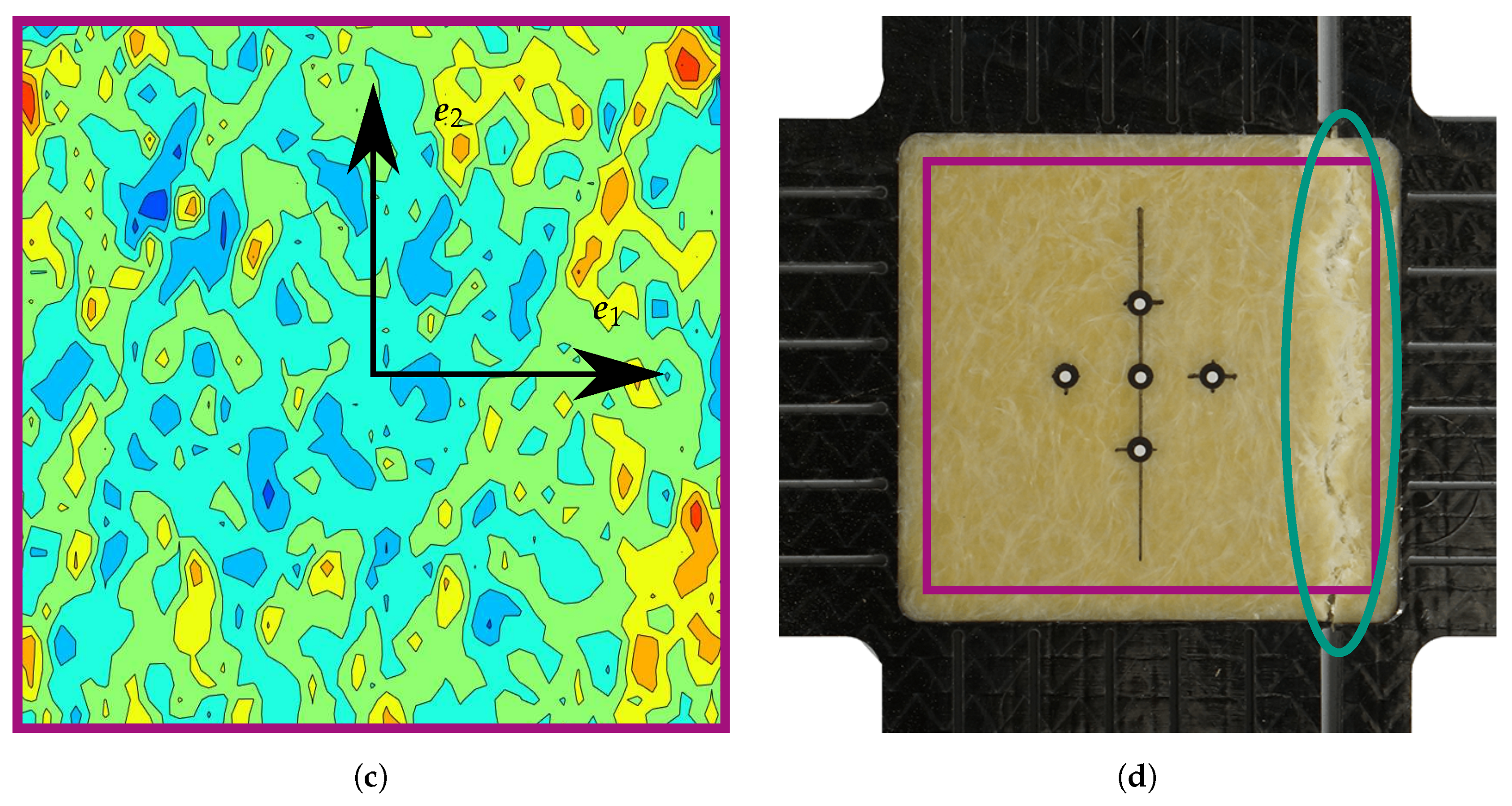
3.3. Bonded Reinforcements on the Arms
3.3.1. Specimen Design
3.3.2. Results
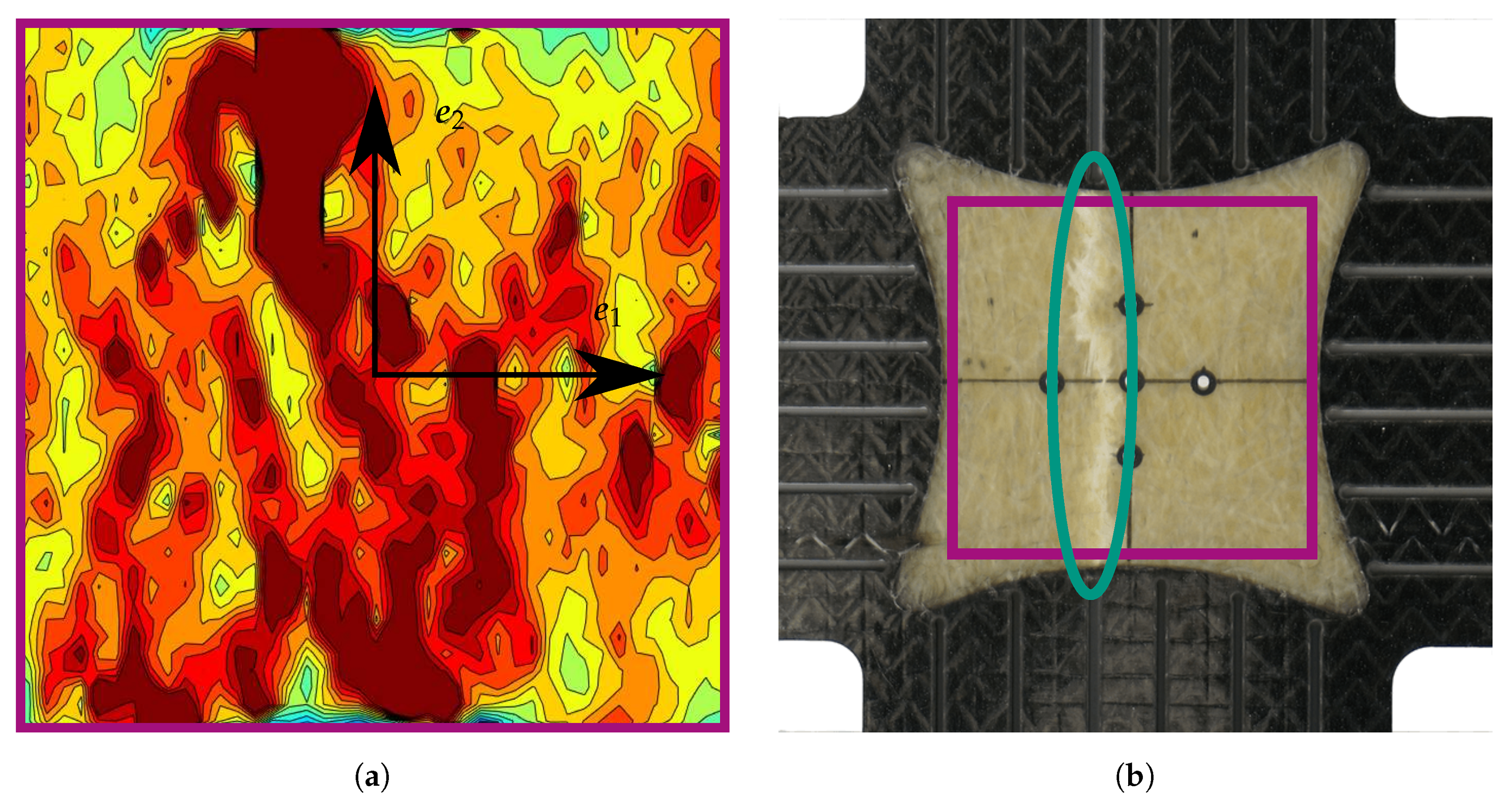
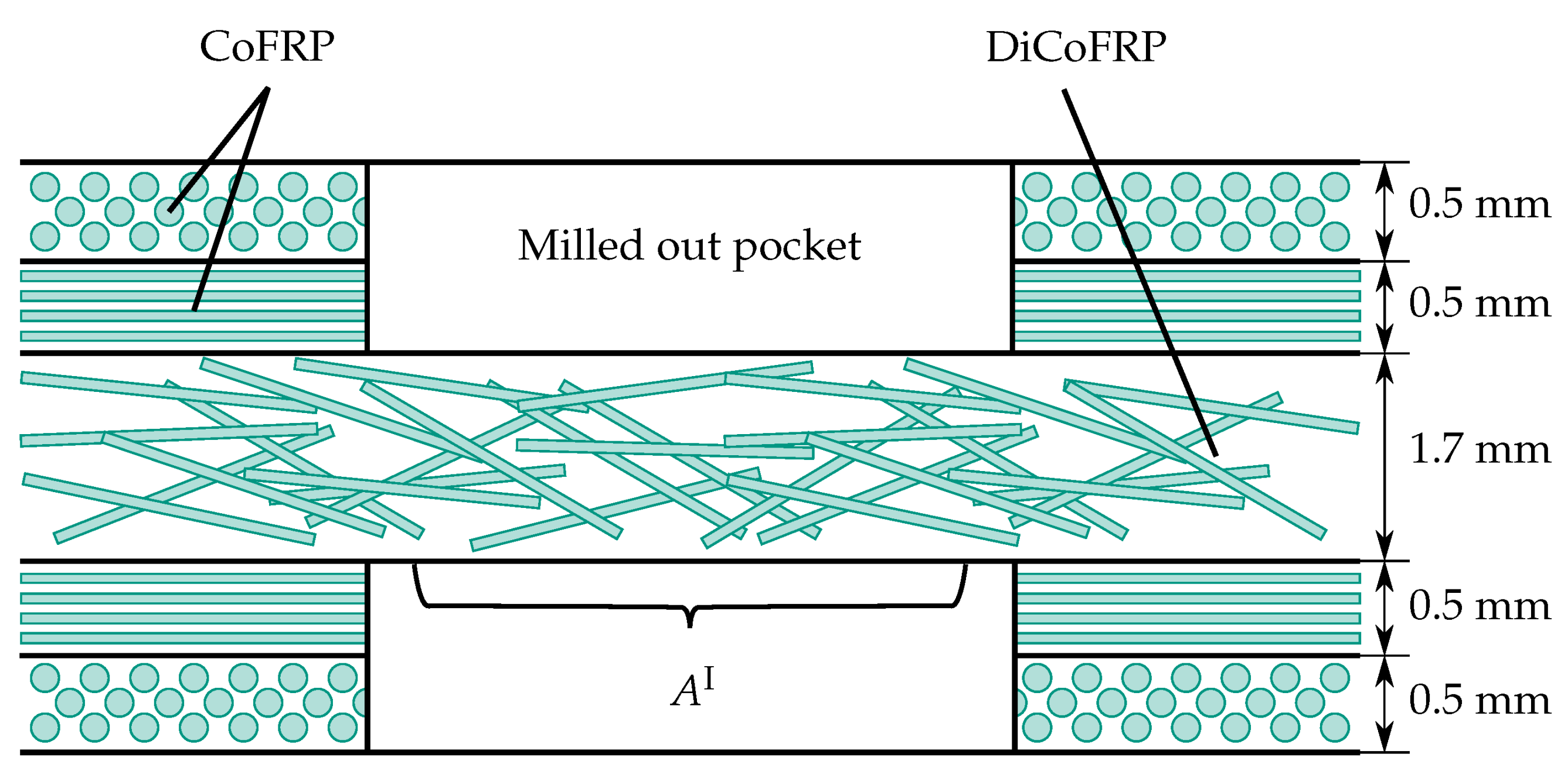
3.4. Continuous Fiber Reinforced Arms
3.4.1. Particularities in Specimen Manufacturing
3.4.2. Specimen Design
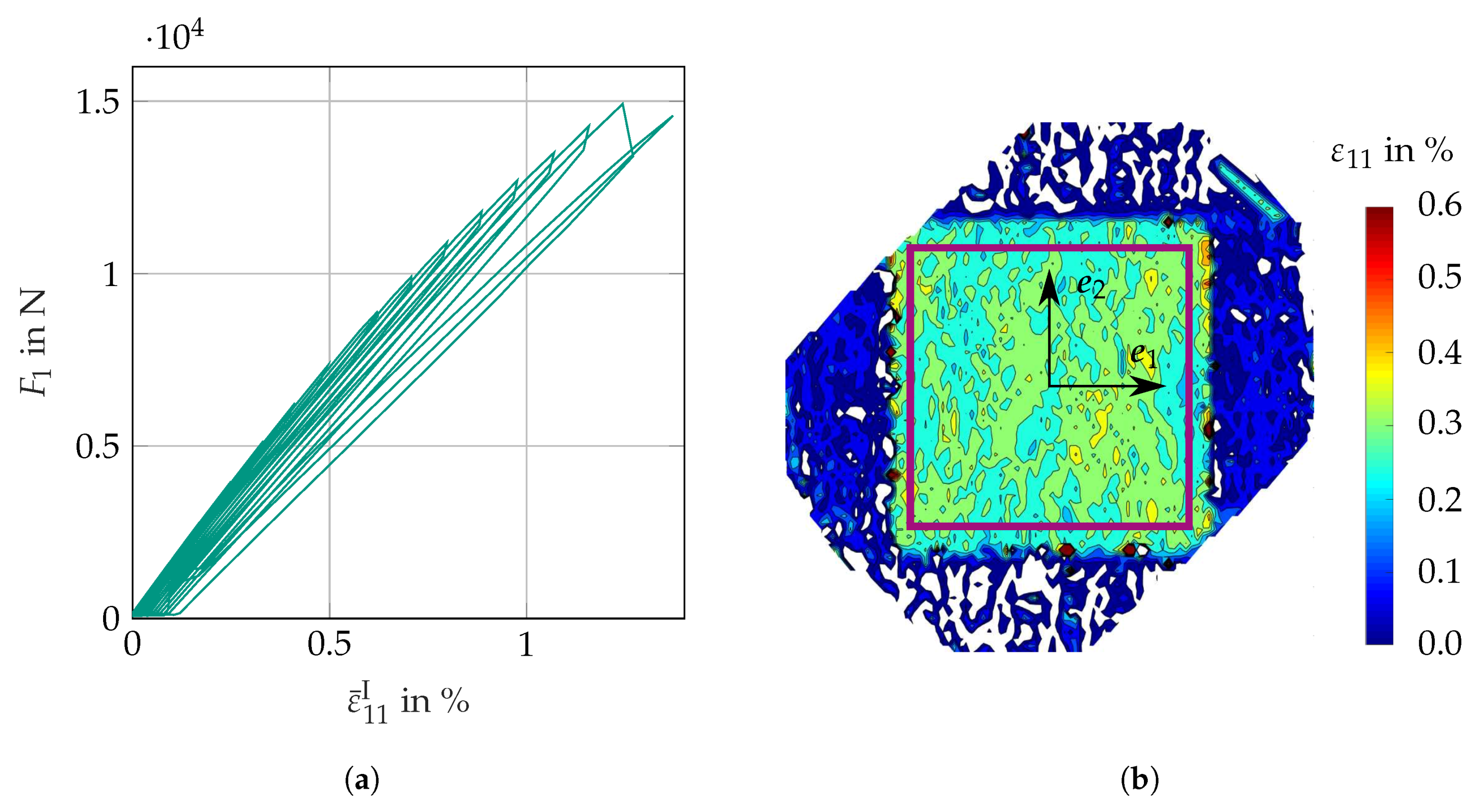
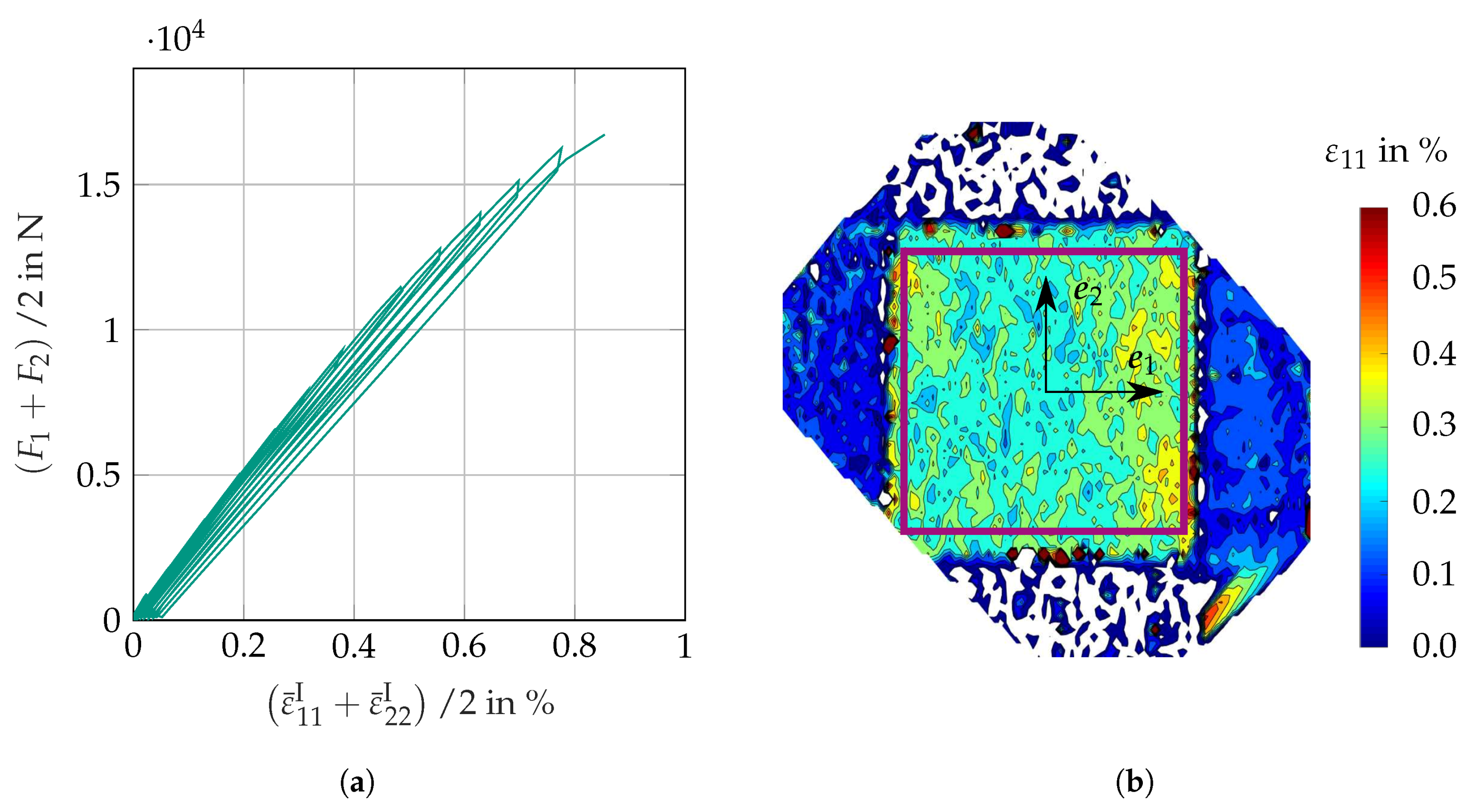
3.4.3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Strain Fields Shortly before Failure and Images of Failed Specimens
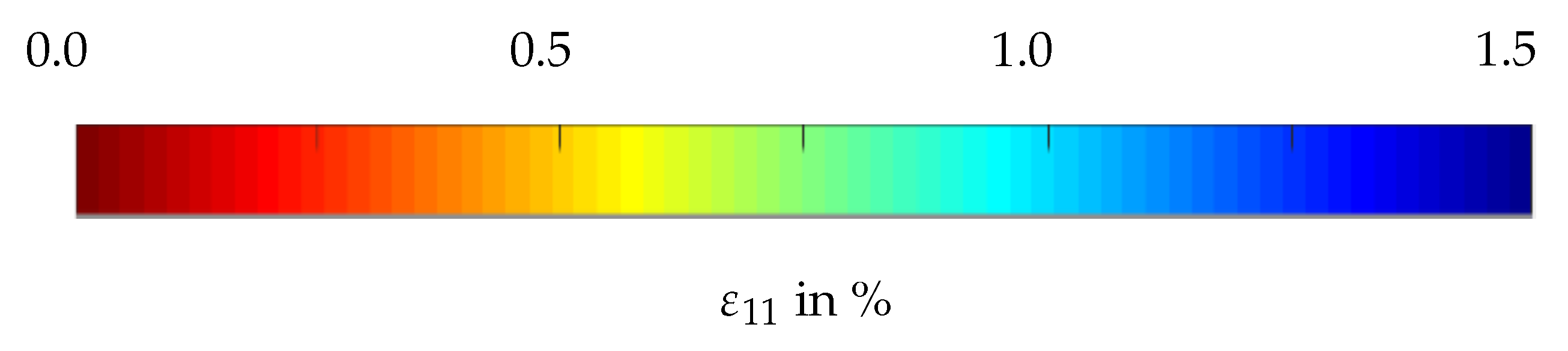
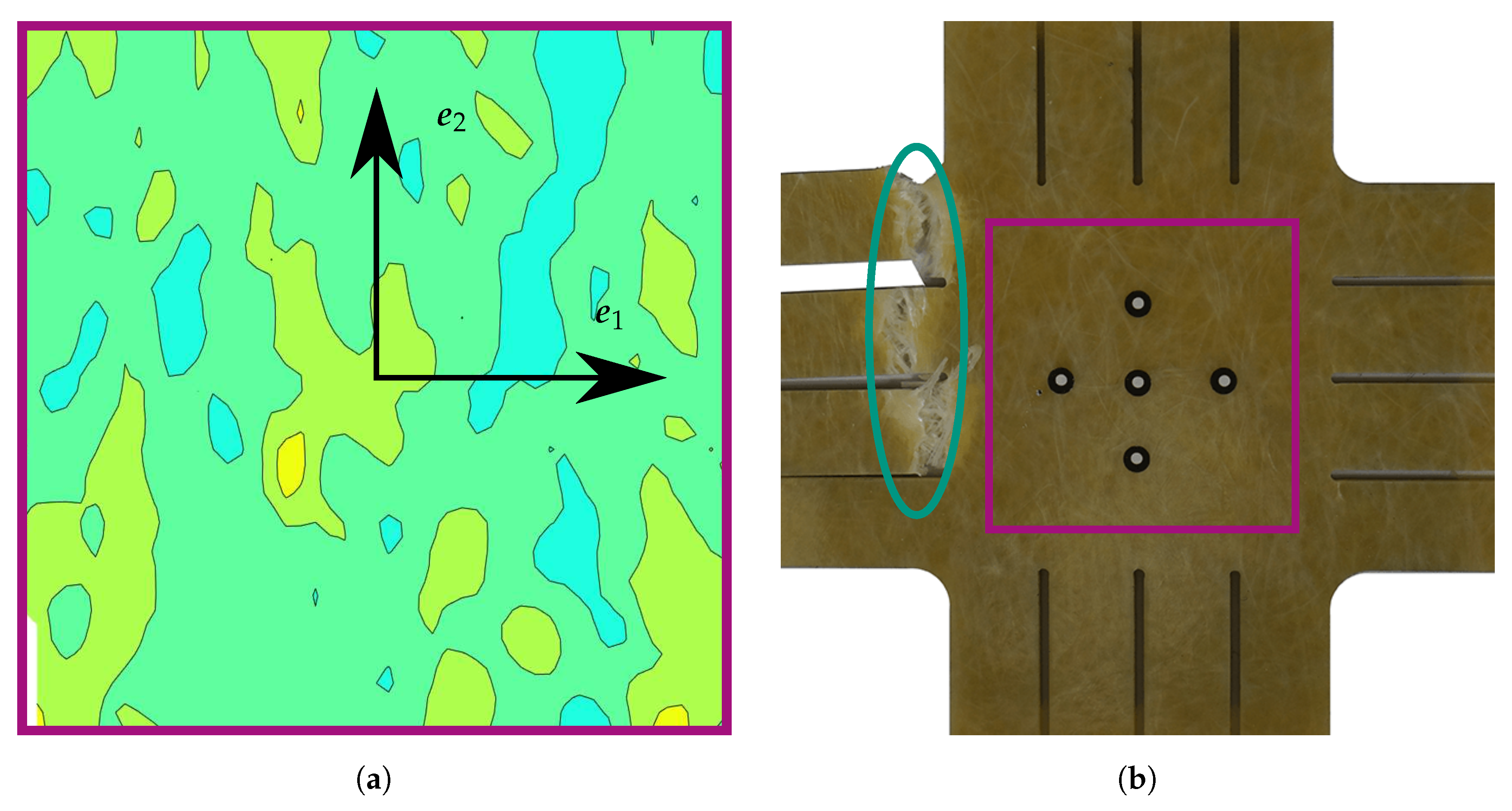
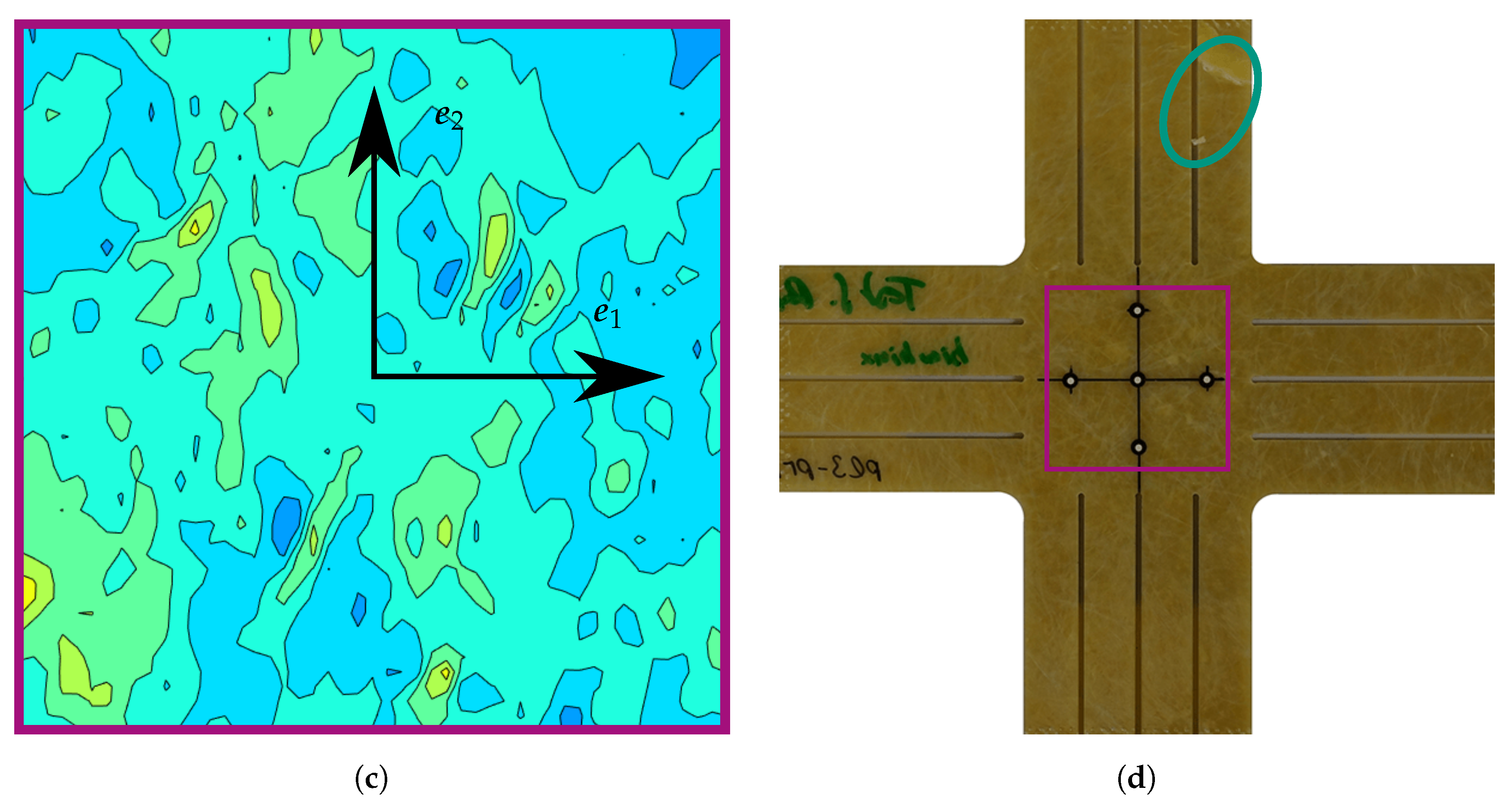
References
- Ohtake, Y.; Rokugawa, S.; Masumoto, H. Geometry determination of cruciform-type specimen and biaxial tensile test of C/C composites. Key Eng. Mater. 1999, 164–165, 151–154. [Google Scholar] [CrossRef]
- Deng, N.; Kuwabara, T.; Korkolis, Y.P. Cruciform specimen design and verification for constitutive identification of anisotropic sheets. Exp. Mech. 2015, 55, 1005–1022. [Google Scholar] [CrossRef]
- Kuwabara, T.; Ikeda, S.; Kuroda, K. Measurement and analysis of differential work hardening in cold-rolled steel sheet under biaxial tension. J. Mater. Process. Technol. 1998, 80–81, 517–523. [Google Scholar] [CrossRef]
- Makinde, A.; Thibodeau, L.; Neale, K.W. Development of an apparatus for biaxial testing using cruciform specimens. Exp. Mech. 1992, 32, 138–144. [Google Scholar] [CrossRef]
- Demmerle, S.; Boehler, J.P. Optimal design of biaxial tensile cruciform specimens. J. Mech. Phys. Solids 1993, 41, 143–181. [Google Scholar] [CrossRef]
- Kelly, D.A. Problems in creep testing under biaxial stress systems. J. Strain Anal. 1976, 11, 1–6. [Google Scholar] [CrossRef]
- Boehler, J.P.; Demmerle, S.; Koss, S. A new direct biaxial testing machine for anisotropic materials. Exp. Mech. 1994, 34, 1–9. [Google Scholar] [CrossRef]
- Hoferlin, E.; Van Bael, A.; Van Houtte, P.; Steyaert, G.; De Maré, C. Design of a biaxial tensile test and its use for the validation of crystallographic yield loci. Model. Simul. Mater. Sci. Eng. 2000, 8, 423–433. [Google Scholar] [CrossRef]
- Hannon, A.; Tiernan, P. A review of planar biaxial tensile test systems for sheet metal. J. Mater. Process. Technol. 2008, 198, 1–13. [Google Scholar] [CrossRef]
- International Organization for Standardization. Metallic Materials—Sheet and Strip—Biaxial Tensile Testing Method Using a Cruciform Test Piece; ISO 16842; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- Green, D.E.; Neale, K.W.; MacEwen, S.R.; Makinde, A.; Perrin, R. Experimental investigation of the biaxial behaviour of an aluminum sheet. Int. J. Plast. 2004, 20, 1677–1706. [Google Scholar] [CrossRef]
- Smits, A.; Van Hemelrijck, D.; Philippidis, T.P.; Cardon, A. Design of a cruciform specimen for biaxial testing of fibre reinforced composite laminates. Compos. Sci. Technol. 2006, 66, 964–975. [Google Scholar] [CrossRef]
- Van Hemelrijck, D.; Ramault, C.; Markis, A.; Clarke, A.R.; Williamson, C.; Gower, M.; Shaw, R.; Mera, R.; Lamkanfi, E.; Van Paepegem, W. Biaxial testing of fibre reinforced composites. In Proceedings of the 16th International Conference on Composite Materials, Xi’an, China, 20–25 August 2007; pp. 1–8. [Google Scholar]
- Makris, A.; Vandenbergh, T.; Ramault, C.; Van Hemelrijck, D.; Lamkanfi, E.; Van Paepegem, W. Shape optimisation of a biaxially loaded cruciform specimen. Polym. Test. 2010, 29, 216–223. [Google Scholar] [CrossRef]
- Lamkanfi, E.; Van Paepegem, W.; Degrieck, J.; Ramault, C.; Makris, A.; Van Hemelrijck, D. Strain distribution in cruciform specimens subjected to biaxial loading conditions. Part 2: Influence of geometrical discontinuities. Polym. Test. 2010, 29, 132–138. [Google Scholar] [CrossRef]
- Gower, M.R.L.; Shaw, R.M. Towards a planar cruciform specimen for biaxial characterisation of polymer matrix composites. Appl. Mech. Mater. 2010, 24–25, 115–120. [Google Scholar] [CrossRef]
- Serna Moreno, M.; Martínez Vicente, J.; López Cela, J. Failure strain and stress fields of a chopped glass-reinforced polyester under biaxial loading. Compos. Struct. 2013, 103, 27–33. [Google Scholar] [CrossRef]
- Hohberg, M.; Kärger, L.; Bücheler, D.; Henning, F. Rheological In-Mold Measurements and Characterizations of Sheet-Molding-Compound (SMC) Formulations with Different Constitution Properties by Using a Compressible Shell Model. Int. Polym. Process. 2017, 32, 659–668. [Google Scholar] [CrossRef]
- Asadi, A.; Miller, M.; Sultana, S.; Moon, R.J.; Kalaitzidou, K. Introducing cellulose nanocrystals in sheet molding compounds (SMC). Compos. Part A Appl. Sci. Manuf. 2016, 88, 206–215. [Google Scholar] [CrossRef]
- Mahnken, R.; Stein, E. A unified approach for parameter identification of inelastic material models in the frame of the finite element method. Comput. Methods Appl. Mech. Eng. 1996, 136, 225–258. [Google Scholar] [CrossRef]
- Mahnken, R.; Stein, E. Parameter identification for viscoplastic models based on analytical derivatives of a least-squares functional and stability investigations. Int. J. Plast. 1996, 12, 451–479. [Google Scholar] [CrossRef]
- Cooreman, S.; Lecompte, D.; Sol, H.; Vantomme, J.; Debruyne, D. Identification of mechanical material behavior through inverse modeling and DIC. Exp. Mech. 2007, 48, 421–433. [Google Scholar] [CrossRef]
- Lecompte, D.; Smits, A.; Sol, H.; Vantomme, J.; Van Hemelrijck, D. Mixed numerical-experimental technique for orthotropic parameter identification using biaxial tensile tests on cruciform specimens. Int. J. Solids Struct. 2007, 44, 1643–1656. [Google Scholar] [CrossRef]
- Schemmann, M.; Brylka, B.; Müller, V.; Kehrer, L.; Böhlke, T. Mean field homogenization of discontinous fiber reinforced polymers and parameter identification of biaxial tensile tests through inverse modeling. In Proceedings of the 20th International Conference on Composite Materials, Copenhagen, Denmark, 19–24 July 2015. [Google Scholar]
- Schemmann, M.; Gajek, S.; Böhlke, T. Biaxial tensile tests and microstructure-based inverse parameter identification of inhomogeneous SMC composites. In Advances in Mechanics of Materials and Structural Analysis: In Honor of Reinhold Kienzler; Altenbach, H., Jablonski, F., Müller, W.H., Naumenko, K., Schneider, P., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 80, pp. 329–342. [Google Scholar]
- Hartmann, S.; Gilbert, R.R. Identifiability of material parameters in solid mechanics. Arch. Appl. Mech. 2017, 1, 1–24. [Google Scholar] [CrossRef]
- Bücheler, D.; Trauth, A.; Damm, A.; Böhlke, T.; Henning, F.; Kärger, L.; Seelig, T.; Weidenmann, K.A. Processing of continuous-discontinuous-fiber-reinforced thermosets. In Proceedings of the SAMPE Europe Conference 2017, Leinfelden-Echterdingen, Germany, 14–16 November 2017; pp. 1–8. [Google Scholar]
- Bücheler, D. Locally Continuous-Fiber Reinforced Sheet Molding Compound. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2017. [Google Scholar]
- Bauer, J.; Priesnitz, K.; Schemmann, M.; Brylka, B.; Böhlke, T. Parametric shape optimization of biaxial tensile specimen. Proc. Appl. Math. Mech. 2016, 16, 159–160. [Google Scholar] [CrossRef]
- Brylka, B.; Schemmann, M.; Wood, J.; Böhlke, T. DMA based characterization of stiffness reduction in long fiber reinforced polypropylene. Polym. Test. 2018, 66, 296–302. [Google Scholar] [CrossRef]





| Component | Trade Name | Weight Fraction |
|---|---|---|
| UPPH resin | Daron ZW 14142 | |
| Adherent and flow aids | BYK 9085 | |
| Impregnation aid | BYK 9076 | |
| Deaeration aid | BYK A-530 | |
| Inhibitor | pBQ | |
| Peroxide | Trigonox 117 | |
| Isocyanate | Lupranat M20R |
| Reinforcement Type | None | Bonded SMC | Cont. Geom. 1 | Cont. Geom. 2 | Uniax. Bone | |
|---|---|---|---|---|---|---|
| 0.57% | 1.00% | 1.37% | 1.26% | 1.57% | ||
| 0.63% | 0.65% | 0.85% | 0.76% | - | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schemmann, M.; Lang, J.; Helfrich, A.; Seelig, T.; Böhlke, T. Cruciform Specimen Design for Biaxial Tensile Testing of SMC. J. Compos. Sci. 2018, 2, 12. https://doi.org/10.3390/jcs2010012
Schemmann M, Lang J, Helfrich A, Seelig T, Böhlke T. Cruciform Specimen Design for Biaxial Tensile Testing of SMC. Journal of Composites Science. 2018; 2(1):12. https://doi.org/10.3390/jcs2010012
Chicago/Turabian StyleSchemmann, Malte, Juliane Lang, Anton Helfrich, Thomas Seelig, and Thomas Böhlke. 2018. "Cruciform Specimen Design for Biaxial Tensile Testing of SMC" Journal of Composites Science 2, no. 1: 12. https://doi.org/10.3390/jcs2010012
APA StyleSchemmann, M., Lang, J., Helfrich, A., Seelig, T., & Böhlke, T. (2018). Cruciform Specimen Design for Biaxial Tensile Testing of SMC. Journal of Composites Science, 2(1), 12. https://doi.org/10.3390/jcs2010012





