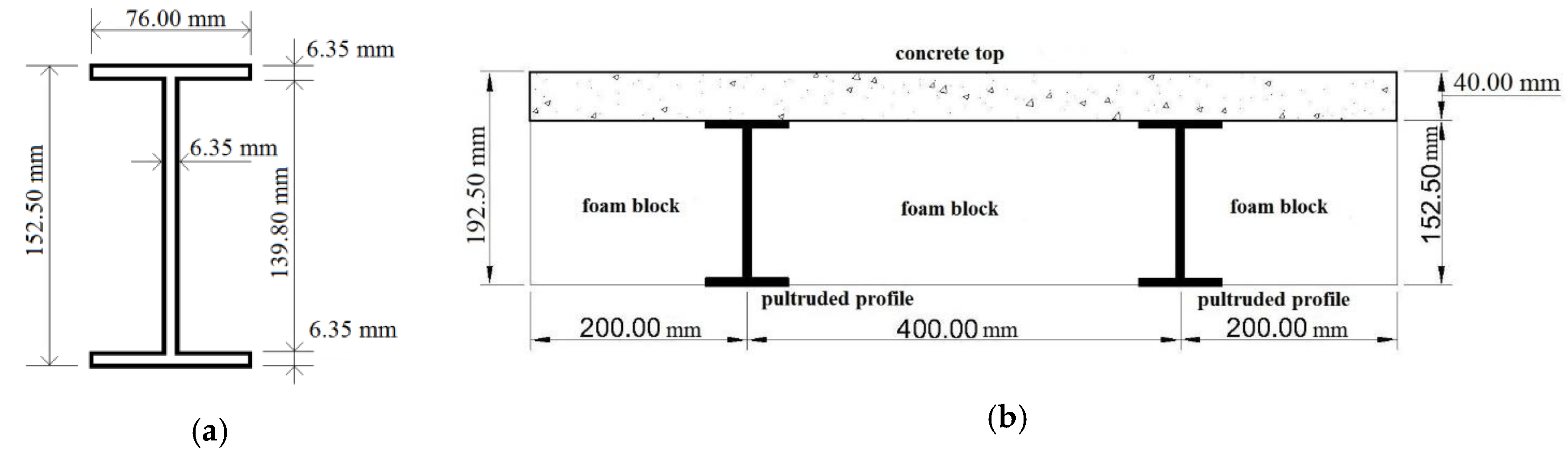
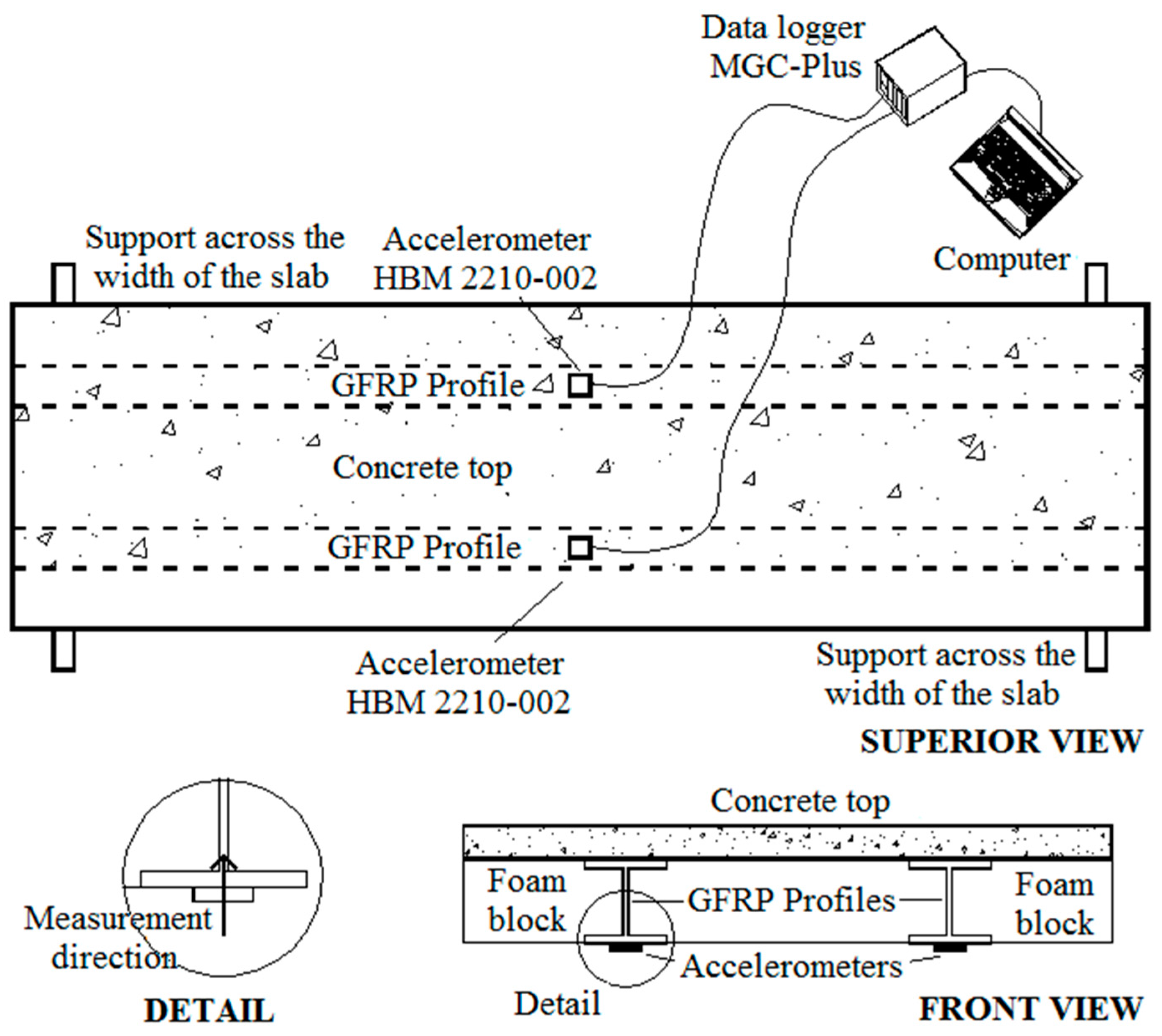
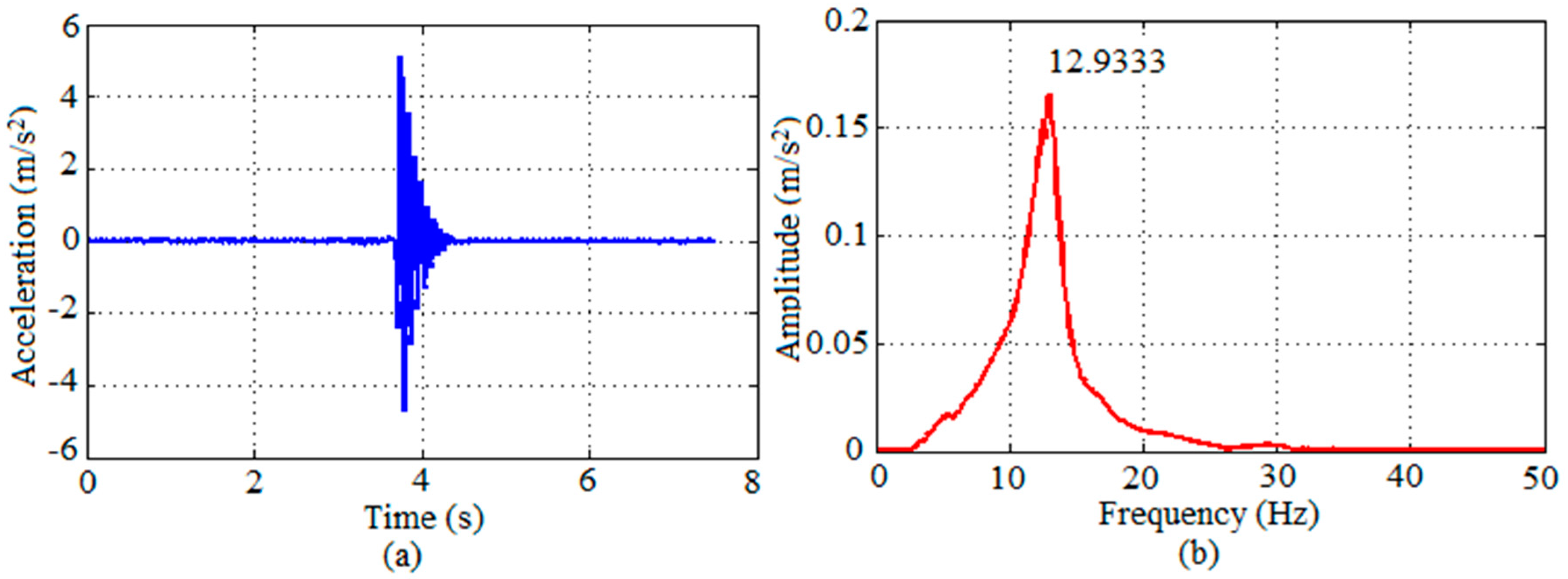
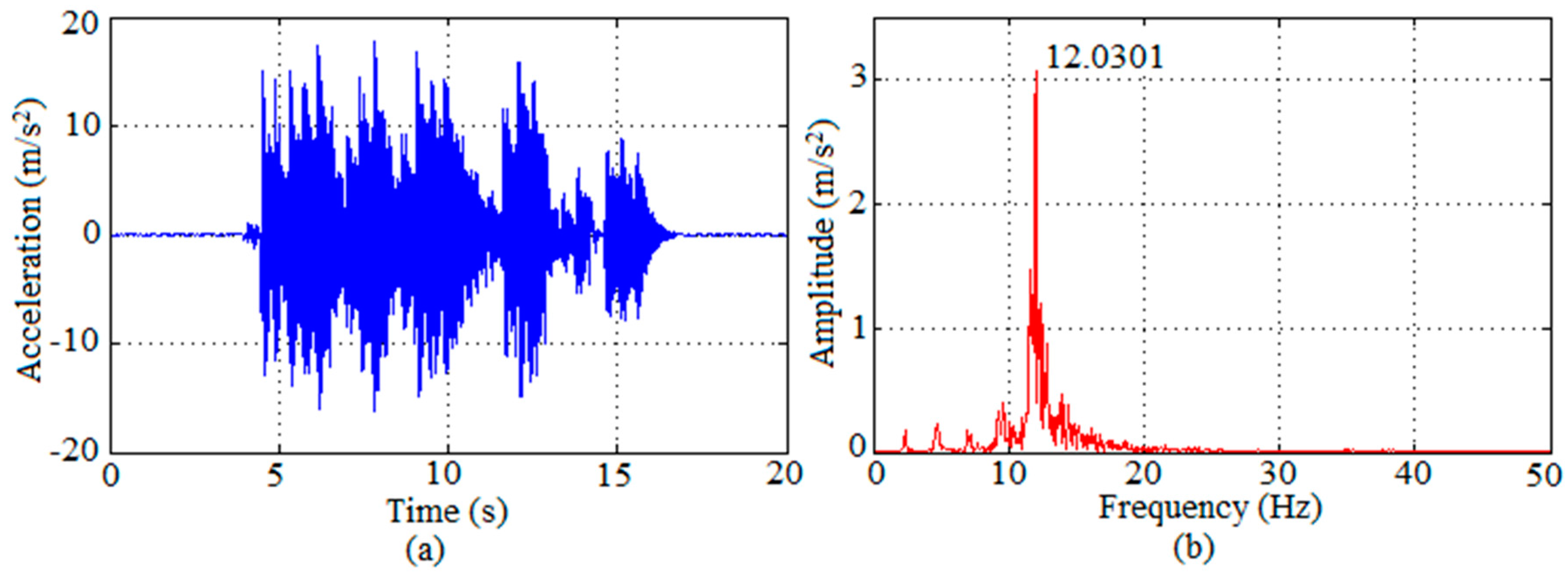
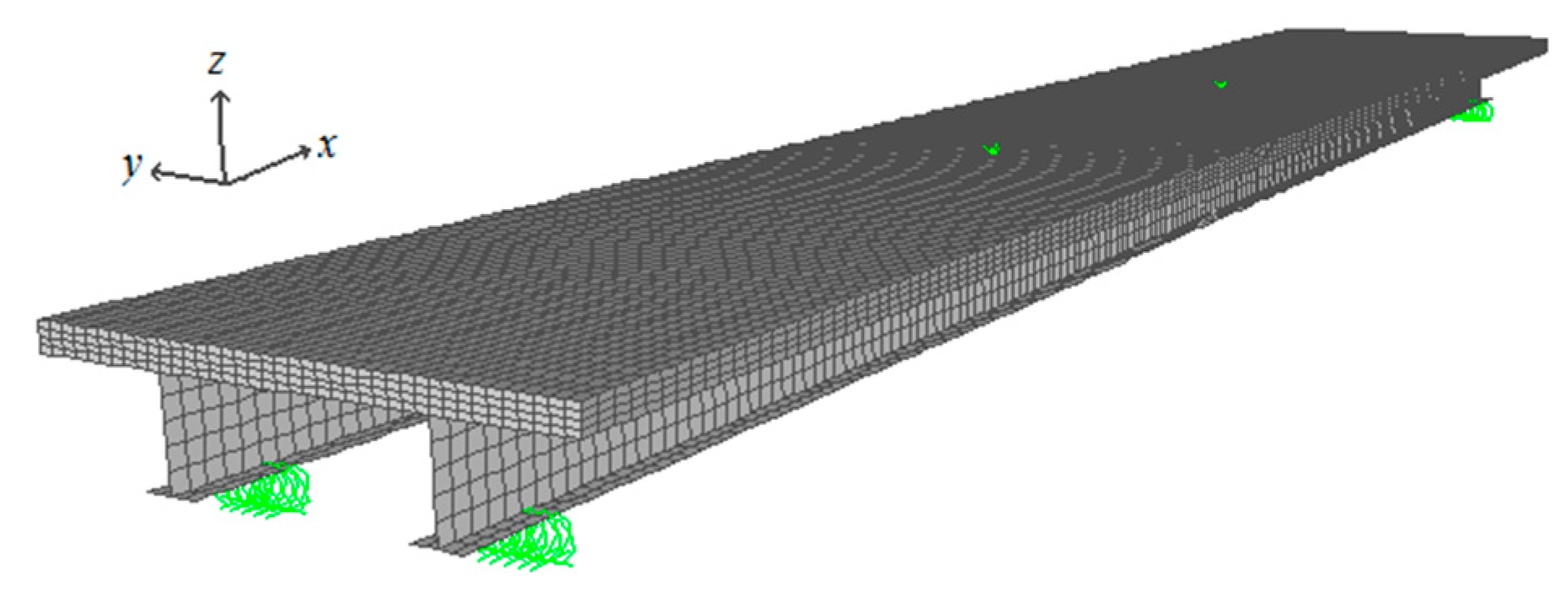
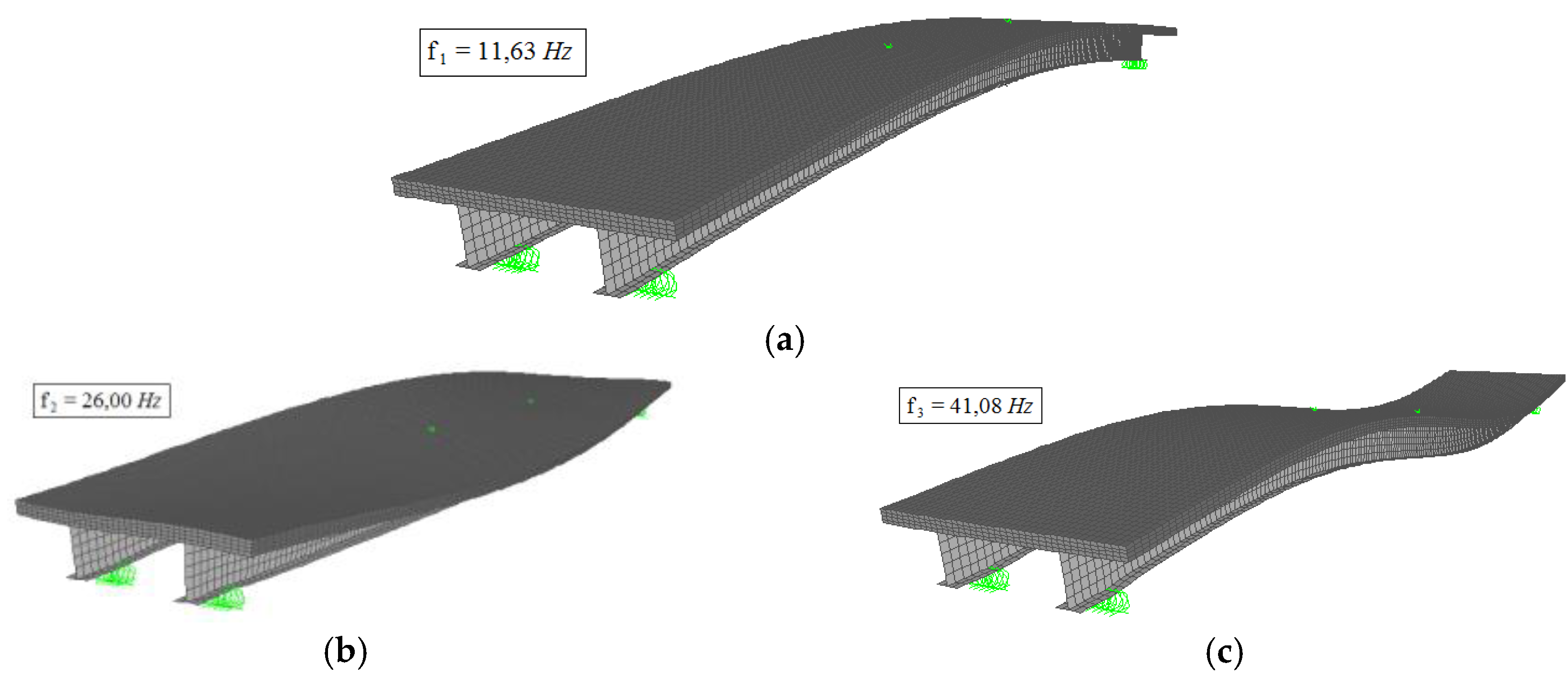
This slab system can be employed either supported by longitudinal beams, with the profiles axis disposed perpendicular to the footbridge longitudinal axis, or supported by transverse beams, with the profiles axis disposed parallel to the footbridge longitudinal axis.
3.1. Material Properties
The selected GFRP profiles are composed of fiber glass rovings (disposed parallel to the profile longitudinal axis) embedded in a polyester matrix, with a fiber volume fraction of 60%, and of laminates made of continuous strand mats (CSM), consisting of randomly-oriented fibers.
It is initially assumed that the profile web and flanges are laminated composites with the same lay-up and equivalent orthotropic mechanical properties. The mechanical elastic properties of each individual laminae can be obtained using the Rule of Mixtures by using the elastic properties of the fibers, resin, and mats as given by the fabricator [
21]. The profile elastic properties can then be estimated from the laminae properties by using the Classical Lamination Theory with results shown in
Table 1.
The elastic properties of the GFRP profiles were also obtained experimentally from three-point bending tests by following a procedure proposed by Bank [
22] based on the Timoshenko Beam Theory. It considers that the profile behaves as an equivalent isotropic material. The equivalent longitudinal (
E) and shear (
G) moduli of the GFRP profiles were found to be 26.21 and 4.29 GPa, respectively. A more detailed description of this procedure and experiments can be found in Santos Neto and La Rovere [
23].
Concrete was designed for a compressive strength of 30 MPa at 28 days. The secant modulus of elasticity (
Ec) was obtained according to ACI 318 recommendation [
24] yielding a value of 26.07 GPa. The usual value of 0.2 was adopted for Poisson´s coefficient, resulting in a shear modulus (
Gc) of 10.86 GPa.
3.2. Design and Static Analysis
Previous studies [
1] have shown that the Serviceability Limit State (SLS) tends to govern the design of composite slabs made of concrete and GFRP materials for footbridge deck applications. The composite slab under study was then initially designed under bending for service loads, without considering long term effects. A representative slab strip of 0.8 m width (see section shown in
Figure 6) was selected for the analysis. A total dead load (
DL) equal to the self-weight (0.846 kN/m) plus an additional load of 1.2 kN/m, due to wearing surface and guardrails, plus a live load (
LL) of 4 kN/m corresponding to the usual pedestrian load of 5 kN/m
2, were considered acting along the span of the simply supported slab strip. One-way action was assumed and the deflections in the slab were calculated using the Timoshenko Beam Theory (TBT), combined with the Transformed Area Approach. The maximum deflection in the slab, at midspan, considering shear deformation, can be found by Equation (10):
where:
v is the maximum displacement;
L is the span;
q is the design service load uniformly distributed along the span;
EI is the flexural stiffness of the transformed section;
GA/fs is the shear stiffness of the transformed section, in which
fs is the shear factor.
The design service load was found considering the quasi-permanent load combination (
q =
DL + 0.4
LL) [
9]. The slab section shown in
Figure 6 was transformed into an equivalent GFRP section, by assuming that concrete and GFRP were perfectly bonded and behaved linear-elastically. It was also assumed that concrete remains uncracked under service loads. By using the equivalent isotropic moduli of the GFRP profiles
E,
G and the estimated values for the concrete moduli
Ec,
Gc, defined in
Section 3.1, the resulting properties of the transformed section were calculated in
Table 2.
By inserting all of these values in Equation (10), and by adopting the allowable limit of
L/250 given in the Brazilian code NBR 6118 [
15] recommendations, a maximum allowable span of 4.65 m was found for the composite slab strip. It then verified the assumption that the concrete top does not crack under service loads.
Next, the composite slab was verified at the Ultimate Limit State (ULS). Three possible failure modes were considered: (1) flexural failure caused by crushing of the extreme compression fiber in the concrete top; (2) shear failure in the GFRP profile at the top flange/web intersection, and (3) bond failure at the GFRP profiles/concrete top interface. For flexural failure, the ultimate bending moment Mu can be calculated from force equilibrium, strain-compatibility conditions and the constitutive behavior of the materials. It was assumed that GFRP materials behave linear-elastically and that concrete was a nonlinear elastic material. The concrete top and the GFRP profiles were assumed to be perfectly bonded and the tensile strength of concrete was neglected. The equivalent rectangular stress block as defined by the ACI 318 [
24] was adopted. Results of ultimate efforts are shown in
Table 3. In this table, the ultimate shear
Vu1 was obtained using an estimated theoretical value for the ultimate shear stress in the GFRP laminae, obtained from Halphin-Tsai equations [
21], and
Vu2 was found from the bond strength at the interface concrete/GFRP, which has been measured experimentally [
1].
For the maximum span of 4.65 m, the design efforts in the simply supported slab strip were found by considering the load combination 1.2
DL + 1.6
LL [
24]. These efforts are shown in
Table 3, with the resulting safety factors (design/ultimate efforts). As it can be observed from
Table 3, the critical failure mode is shear failure in the GFRP profile at the top flange/web intersection (safety factor
Φs1 = 0.51). Although the required safety factors have not yet been established in the Design Codes for the case of concrete/GFRP composite slabs, a safety factor of at most 0.50 should be adopted, since a brittle kind of failure is expected in such structures. Hence, in order to attend both serviceability and ultimate limit states, the span of the composite slab was reduced to 4.0 m (
Φs1 = 0.44).
In order to verify the stiffness and the ultimate efforts estimated in the design of the composite slab under static bending, experimental tests were also carried out. Two slab prototypes of 0.8 m width and 4.0 m of span were tested under 4-point test bending. The loads (P) were applied at a distance (a) of 1.575 m from the supports.
Initially the slab stiffness was investigated by applying on the prototypes two concentrated loads (P) of 4.63 kN, in such a way to obtain the same maximum bending moment produced by a uniformly distributed load (3.646 kN/m) for the service load combination (DL + 0.4 LL). It was observed during the tests that the slab behavior was basically linear elastic under service.
The maximum displacement at midspan can be obtained theoretically using TBT, by means of Equation (11):
where:
v is the maximum displacement;
L is the span;
P are the concentrated loads applied symmetrically on the slab;
a is the distance between the applied loads and the supports;
EI is the flexural stiffness and
GA/fs is the shear stiffness of the transformed section (see
Table 2).
Comparison between theoretical and experimental values of maximum displacement is shown in
Table 4. It can be observed from the table that the theoretical value gives a good estimate for the average value obtained experimentally from the slab prototypes.
Next, the loads were increased on the prototypes (I and II) until failure. Comparison between ultimate efforts estimated theoretically and obtained experimentally is summarized in
Table 5. It can be observed that the prototypes showed different failure modes (I showed bond shear failure, and II showed shear failure in the profile at the web/flange interface). In prototype I, a premature bond shear failure occurred at the interface of the concrete top and only one of the GFRP profiles, which was probably due to bad finishing of the concrete top observed in a small region, giving rise to a non-uniform load application along the slab width. Nevertheless, in spite of the different failure modes, both prototypes fail at a load (
VI = 38.5 kN and
VII = 39.0 kN), close to the estimated one (
Vu = 40.1 kN).
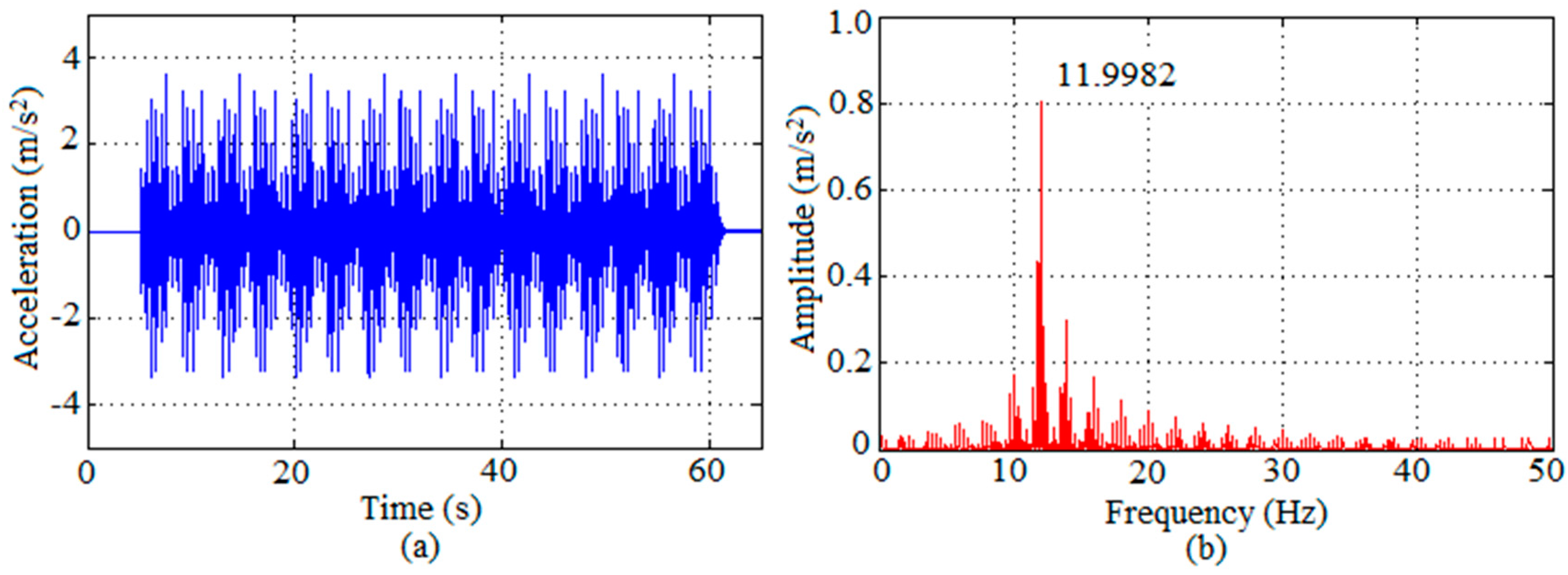
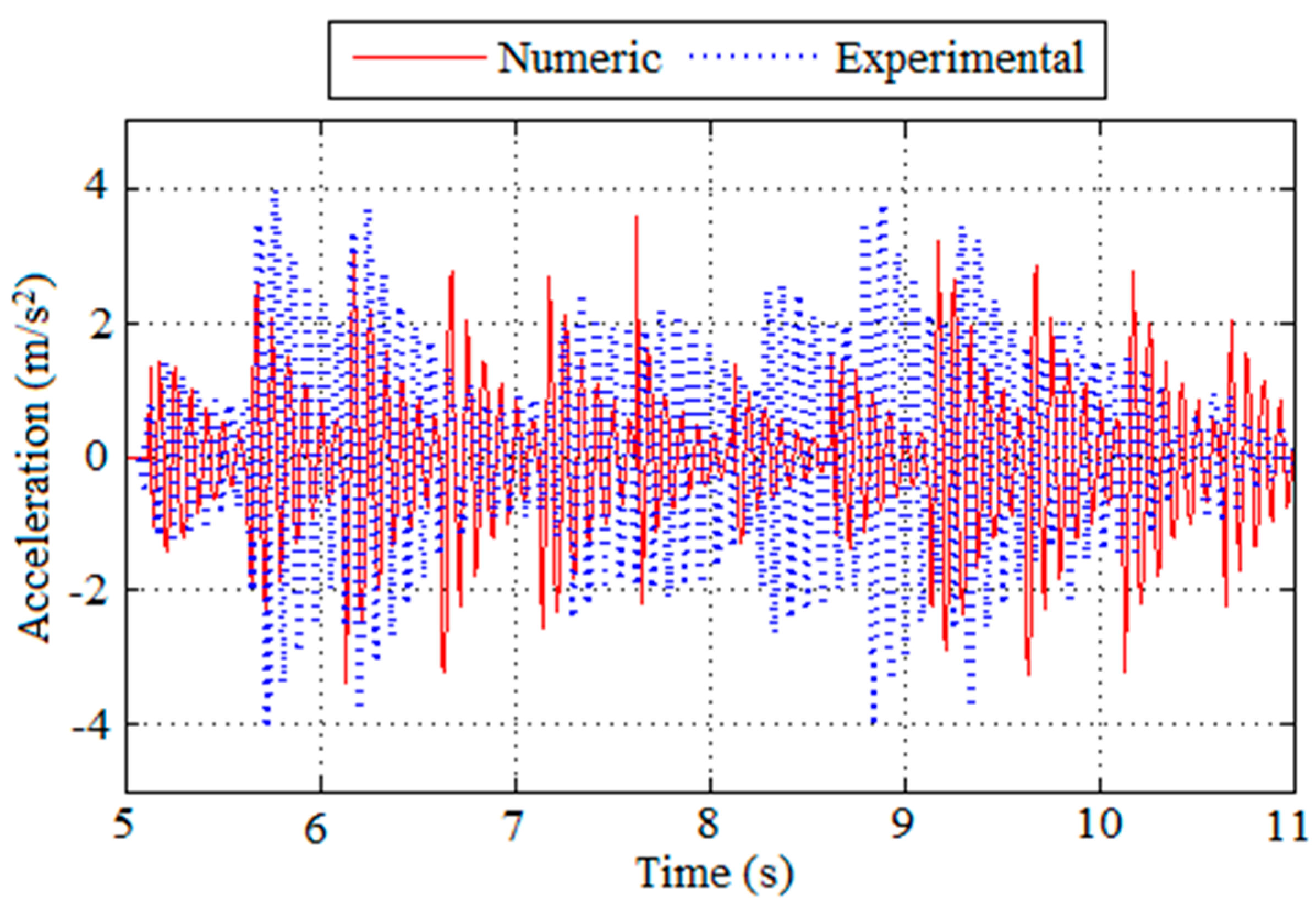
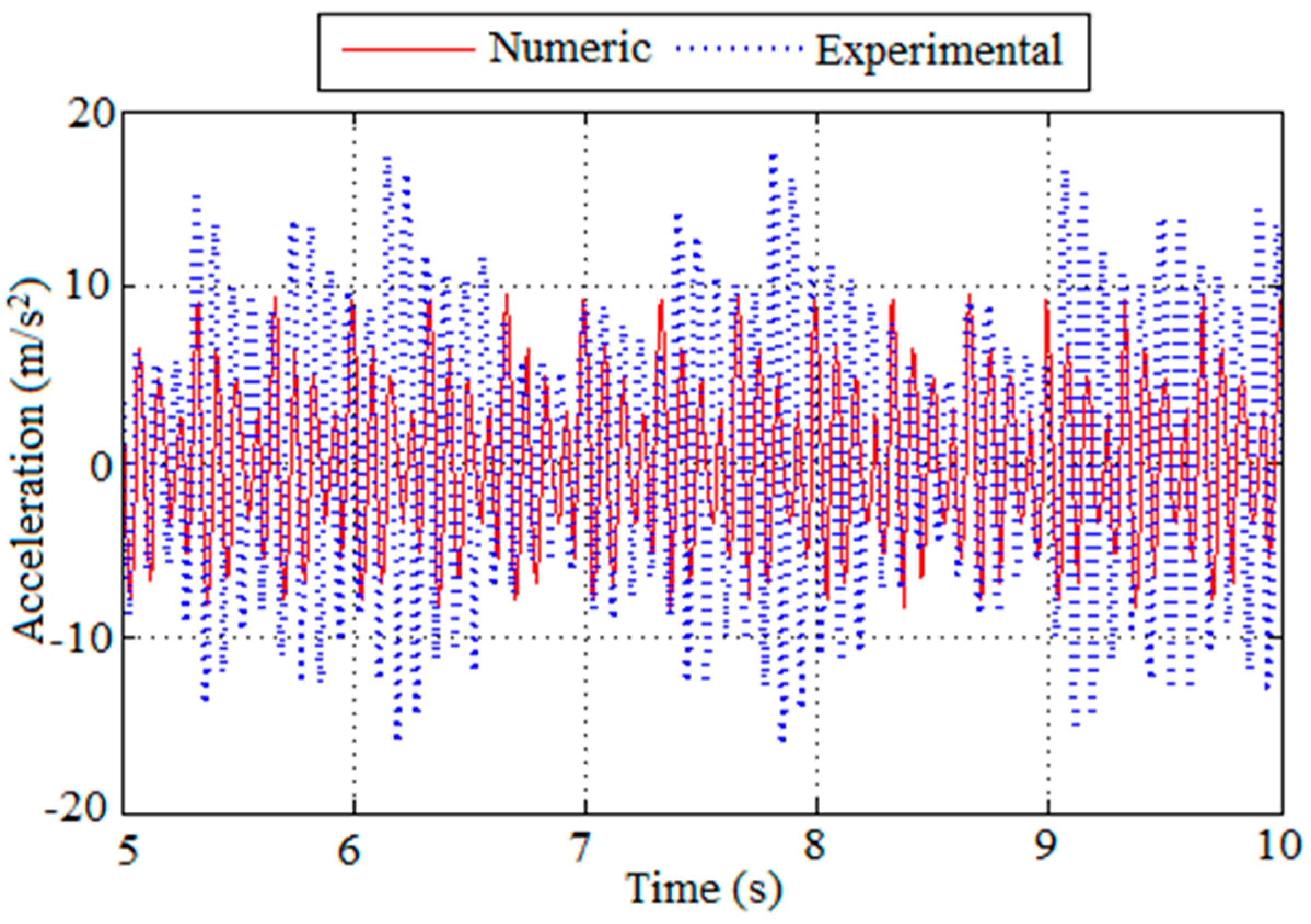
In the following, the dynamic behavior of the composite slab will be investigated.